Next Article in Journal
The Highly Enhanced Efficiency of the Photocatalytic Reduction of CO2 over Bi2WO6 Nanosheets by NaOH Microregulation
Previous Article in Journal
Reliability Evaluation of DC/DC Converter in Direct Current Collection System of Wind Farm Considering the Influence of Control Strategy
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Processes
Volume 11
Issue 10
10.3390/pr11102826
processes-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Permeability Evolution of Intact and Fractured Coal during Progressive Deformation Subjected to True Triaxial Stresses

by
Yubing Liu
1,2,*,
Dong Zhao
1,2,
Yiteng Li
1,2 and
Li Zhang
1,2
1
School of Safety Engineering, China University of Mining and Technology, Xuzhou 221116, China
2
Key Laboratory of Gas and Fire Control for Coal Mines, China University of Mining and Technology, Ministry of Education, Xuzhou 221116, China
*
Author to whom correspondence should be addressed.
Processes 2023, 11(10), 2826; https://doi.org/10.3390/pr11102826
Submission received: 8 September 2023 / Revised: 19 September 2023 / Accepted: 20 September 2023 / Published: 25 September 2023
(This article belongs to the Section Chemical Processes and Systems)
Browse Figures
Versions Notes

Abstract

:
Coal mining is gradually moving towards a deep area of more than 1000 m. At this depth, coal seams are under extremely high stress, leading to the formation of macroscopic fractures. The effects of cleats and macroscopic fractures on permeability evolution and comparative analysis based on established permeability models between intact and fractured coal are still limited. In this study, the permeability of intact and fractured coal specimens was tested by a multi-functional test system. The permeability data were fitted and analyzed based on the established permeability models. Our results show that the permeability curve of fractured coal has an L-shaped trend different from the S-shaped trend of intact coal permeability. The macroscopic fractures increased the permeability of coal samples by 1–3 orders of magnitude. The exponential model had a better fit for the permeability of intact and fractured coal specimens than the cubic model. The mean fitting degrees based on Chen’s and Yu’s models were 0.973 and 0.948, respectively. The slip of the fracture surface resulted in permeability fluctuations during the progressive deformation of fractured coal. The macroscopic fractures increased the slope of permeability in the post-peak stage and reduced coal compressibility and strength.

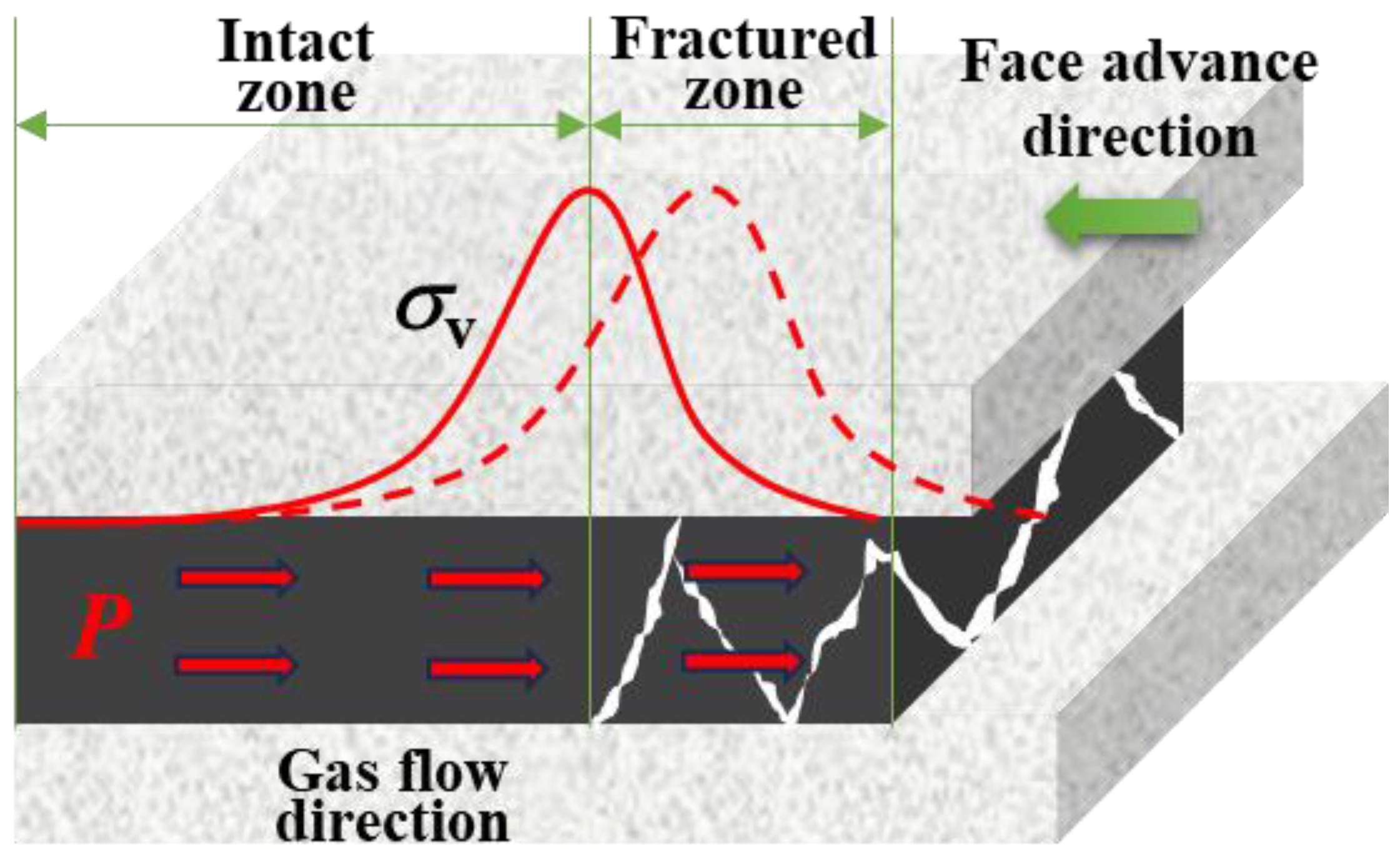
1. Introduction

Coal is an indispensable resource in the energy structure. The shallow reserves above 1000 m of coal resources are gradually depleted with coal exploitation, which could not meet the consumption resources of China. The coal resource, with a depth of more than 1000 m, is still abundant. Entering the coal mining stage of 1000–2000 m is a certain fact in the future [1,2]. There are 47 underground coal mines deeper than 1000 m in China [3]. Coal permeability is a significant variable characterizing gas flow in coal seams. It is of vital importance to the efficiency of gas extraction, CO2 sequestration, and the prevention of gas disasters [4,5,6,7,8]. Deep mines of more than 1000 m are in specially coupled environments with strong disturbances, high gas contents, and ground stress [9,10]. Coal seams are prone to dynamic and gas disasters, which seriously threaten mining safety [11]. The coal structure contains many microscopic fractures called cleats, which are the main channel of gas flow. Coal seams are subjected to overlying rock layers and tectonic features, and macroscopic fractures are easily created in coal seams [12]. A schematic diagram illustrating gas flow surrounding a working face with intact and fractured zones in deep coal mining is shown in Figure 1. The basic theory based on shallow coal mining is not necessarily applicable to deep coal blocks [1]. Therefore, exploring the characteristics of the permeability evolution of fractured coal is of vital significance to CO2 sequestration and disaster prevention [13,14,15].
Compared to other rocks, coal contains many microscopic fractures called cleats, which are naturally anisotropic structures. Many scholars have tested and studied its permeability, mainly focusing on stress conditions, loading rate, initial gas pressures, and bedding plane structure under different load modes [17,18,19,20,21,22]. A direct correlation was found between permeability and aperture. During the loading process, coal permeability showed a trend of first decreasing and then increasing with increasing strain. The coal cleats tended to close due to increasing stress before coal failure, resulting in a rapid decrease in permeability. Due to the limited aperture, coal permeability gradually remained stable. The macroscopic fracture was created after the sample failure, while coal permeability also increased rapidly. As the cleat aperture increased, coal permeability increased during the unloading process. The loading rate, stress conditions, and bedding plane structure all had great influences on coal permeability. Coal permeability had a negative correlation with the loading rate. The change rate of coal permeability had a positive correlation with loading stress. Permeability along the bedding plane direction was higher than in other directions. Permeability evolution at different bedding plane angles also showed significant differences.
Experiments showed that fracture porosity determined coal permeability [23,24,25,26]. As deep coal is in a highly stressed and strongly disturbed environment, it is particularly prone to the formation of damaged fractures. The presence of damaged fractures has a huge impact on coal permeability. Studies [27] showed that the permeability of damaged coal was higher than that of other intact coals and increased by 1–3 orders of magnitude. Many scholars have studied the relationship between coal cleats and permeability evolution [28,29,30]. Their results showed that the size and number of microscopic fractures had a certain influence on coal permeability evolution, resulting in increasing coal permeability. However, research on the permeability evolution of coal throughout macroscopic fractures is still limited. Additionally, the deep coal seams are affected by mining, and some areas will be subjected to true triaxial stress states.
The prediction of coal permeability can provide a data reference for gas extraction methods and CO2 sequestration, so a realistic permeability model is very important. The simplified conceptual coal model is necessary to save calculations. Extensive research about permeability evolution was based on the double porosity model [31,32,33,34,35]. The double porosity model included a matchstick model, sphere model, cube model, etc., according to the specific division. The coal strain was caused by changing mean effective stress, leading to permeability changes [36]. Permeability could be deduced and obtained by coal strain or changing mean effective stress. J. Q. Shi and S. Durucan [37] treated coal as a continuous medium and analyzed the effect of effective stress on permeability, establishing a permeability model called the S&D model. Palmer and Mansoori [38] explored the relationship among permeability, matrix shrinkage, and effective stress and proposed a novel model called the P&M model. Many scholars had also conducted extensive exploration of permeability models based on different influence factors of permeability [39,40,41]. These permeability models are built on the foundation of coal containing only micro-fractures, and their applicability is unclear for fractured coal containing macroscopic fractures.
The permeability evolution of intact and fractured coal under true triaxial stress conditions is studied in this paper. Three different orthogonal directions are designed in the experiment, and the experimental results during progressive deformation are provided. A comparative analysis of permeability evolution for intact and fractured coal is conducted. The effect of cleats and fractures on permeability evolution is systematically analyzed. The modified model based on the logical growth function and the cubic model are used to fit the permeability results of intact and fractured coal. The parameters in the established permeability model are analyzed.

2. Material and Experimental Procedure

2.1. Experimental Materials

The coal specimens were selected from the Baijiao coal mine at an underground depth of about 600 m. Intact coal was made into a cube shape of 0.1 m × 0.1 m × 0.1 m. The end faces of the coal samples were flattened. Coal specimens were dried to remove the moisture in the drying vessel. Fractured coal samples were prepared by compressing intact coal specimens under true triaxial stress before the experiment. During the pre-fracturing process of fractured coal, the specimen was subjected to true triaxial compression until failure. The stress loading path of true triaxial compression is shown in Figure 2. The schematic diagram of coal samples before and after true triaxial compression is shown in Figure 3. Prior to conducting the permeability test, basic mechanical property experiments were performed to obtain the fundamental parameters as shown in Table 1. Elastic moduli of coal samples with directions parallel and normal to the bedding plane were 3.42 GPa and 2.95 GPa, respectively. The uniaxial compressive strengths of coal with directions parallel and normal to the bedding plane were 20.03 MPa and 25.28 MPa, respectively.

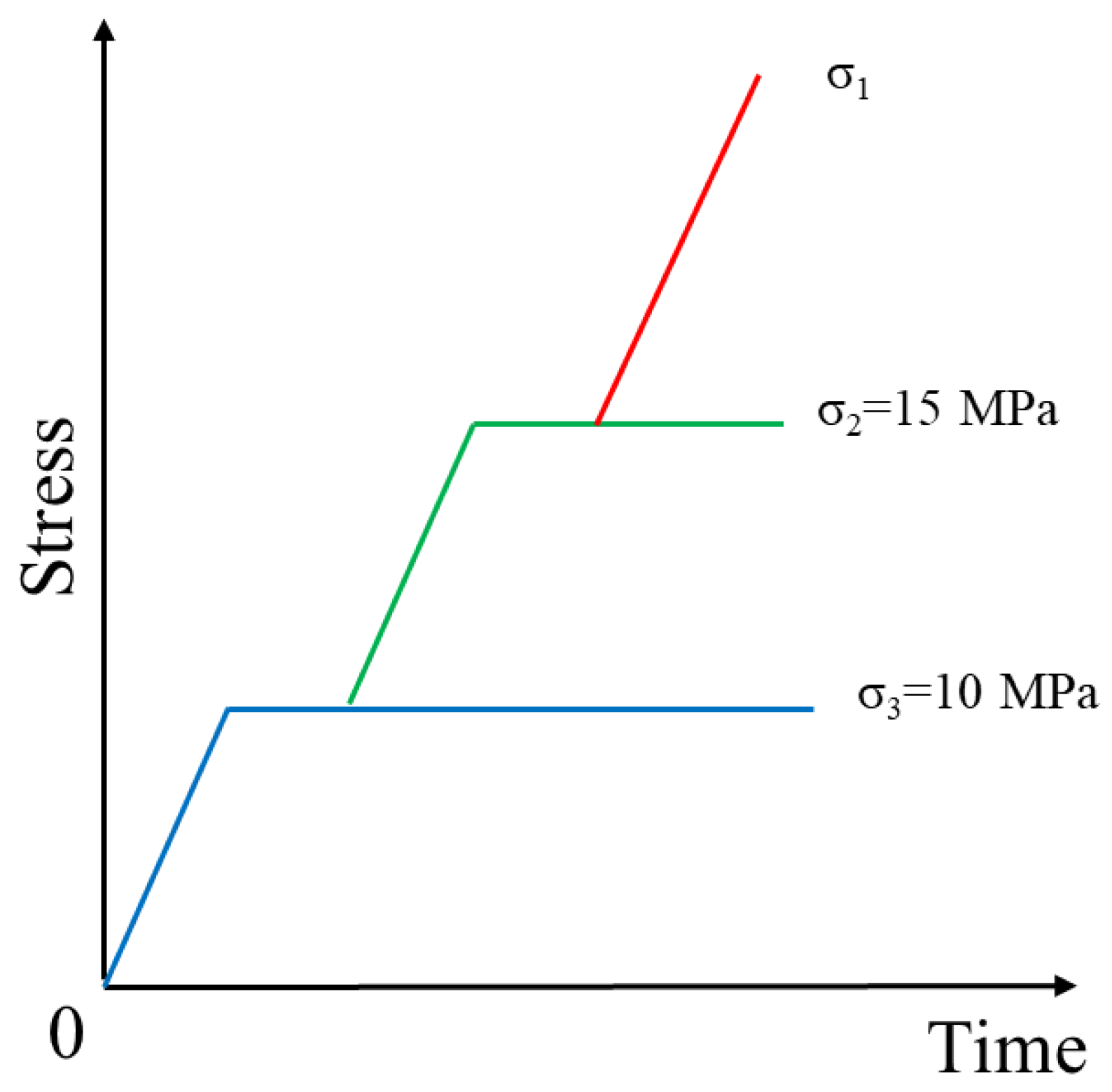
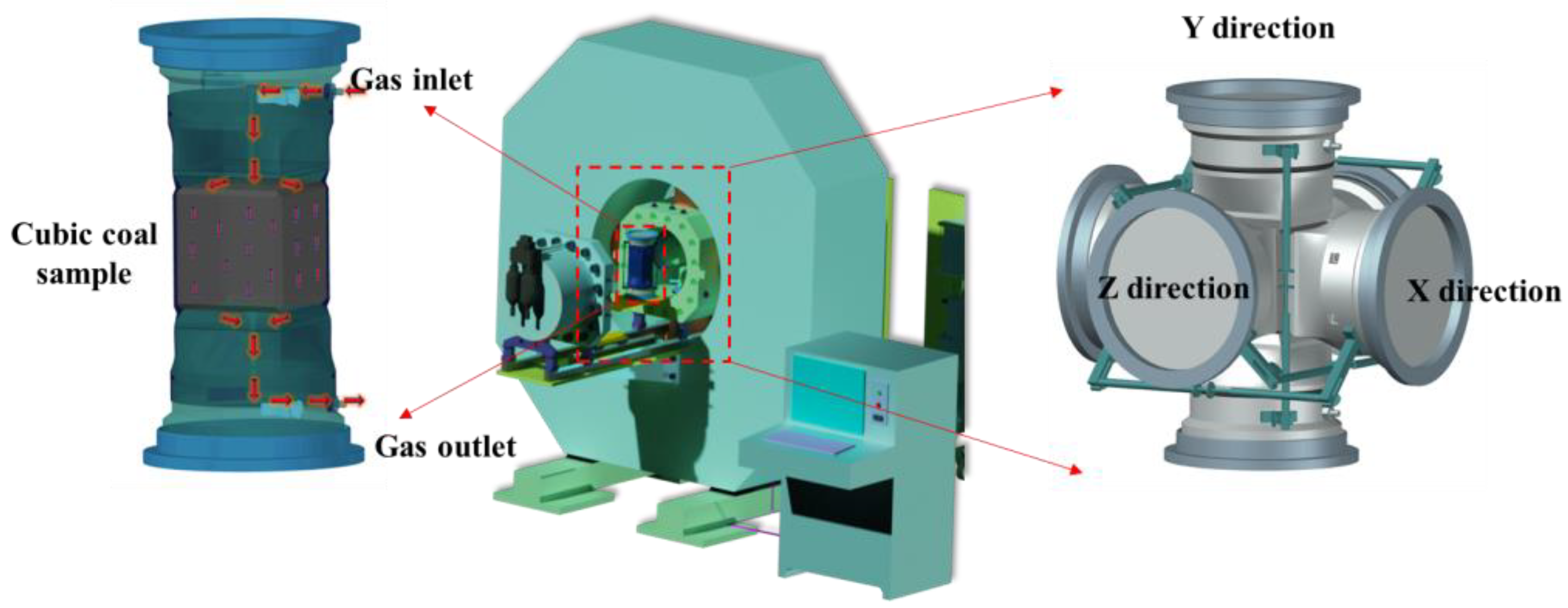
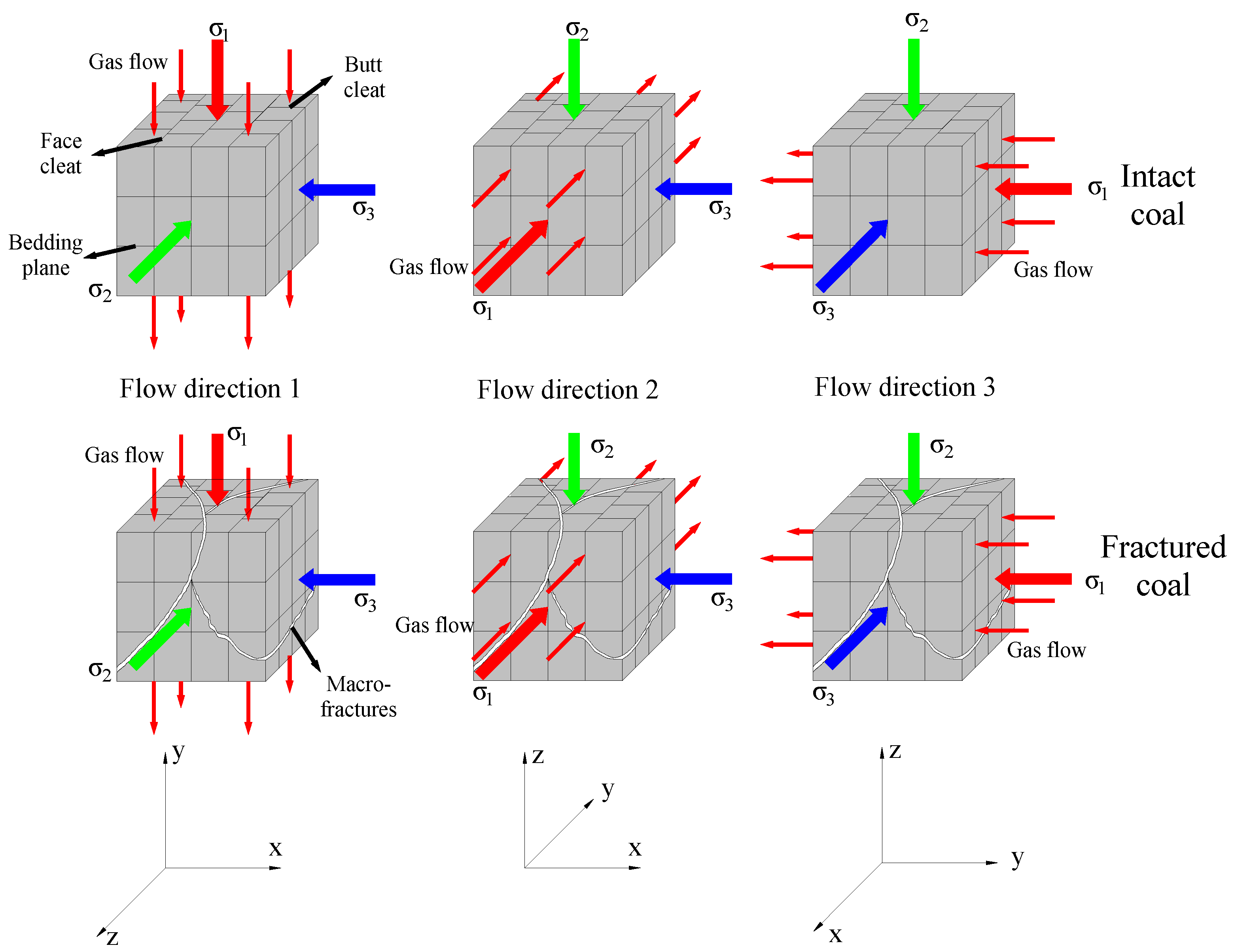
2.2. Experimental Procedure and Setup

A multi-functional true triaxial instrument (TTG) was used to test intact and fractured coal samples. The loading system can provide true triaxial stress conditions during the permeability test. The parameters of gas flow can be measured by the test system. The schematic diagram of the experimental apparatus is shown in Figure 4. The prepared specimen was packed in shrink tubes and placed in the true triaxial chamber. Then the specimen was subjected to true triaxial stress by the multi-functional instrument system. The stress provided by the loading device can reach a magnitude of 600 MPa in the X and Y directions and 400 MPa in the Z direction, and confining stress can reach 40 MPa. The deformation of coal specimens was measured by the linear variable differential transform (LVDT), which ranged from 0 to 40 mm. During the experiment, the gas pressure injected with CO2 was set to 1.0 MPa, and the output gas pressure was kept stable. Monitoring the gas flow was achieved through a mass flow meter that ranged from 0 to 5 L/min. Prior to this experiment, all samples underwent a process of CO2 gas adsorption for 48 h.
During the permeability test, the X-axis, Y-axis, and Z-axis directions were set to the directions of minimum principal stress, maximum principal stress, and intermediate principal stress, respectively. The gas flow direction was consistent with the direction of maximum principal stress. During this experiment, all specimens were tested for permeability using the same stress loading path as shown in Figure 2. It was consistent with the fracturing process prior to this experiment. First, in this experiment, the loading rate of stress was maintained at 0.5 MPa/s in the three directions. The loading stresses in the directions of minimum and intermediate principal stress were halted and kept at the pre-set value when they reached the preset value, respectively. Then the loading rate of maximum principal stress was maintained at 0.002 mm/s. Stress loading was stopped after stress reached its peak and residual value. The stress preset values along the direction of intermediate and minimum principal stress were 15 MPa and 10 MPa, respectively. In this experiment, three different orthogonal directions were designed to carry out permeability test experiments according to the coal structure. The diagram of the three flow directions is shown in Figure 5. The flow direction normal to the bedding plane was set to flow direction 1, and parallel to the face and butt cleat were flow directions 2 and 3, respectively. The flow direction of CO2 was consistent with the Y direction. At the same time, calculating permeability was achieved by a stable Darcy’s law during the loading process.

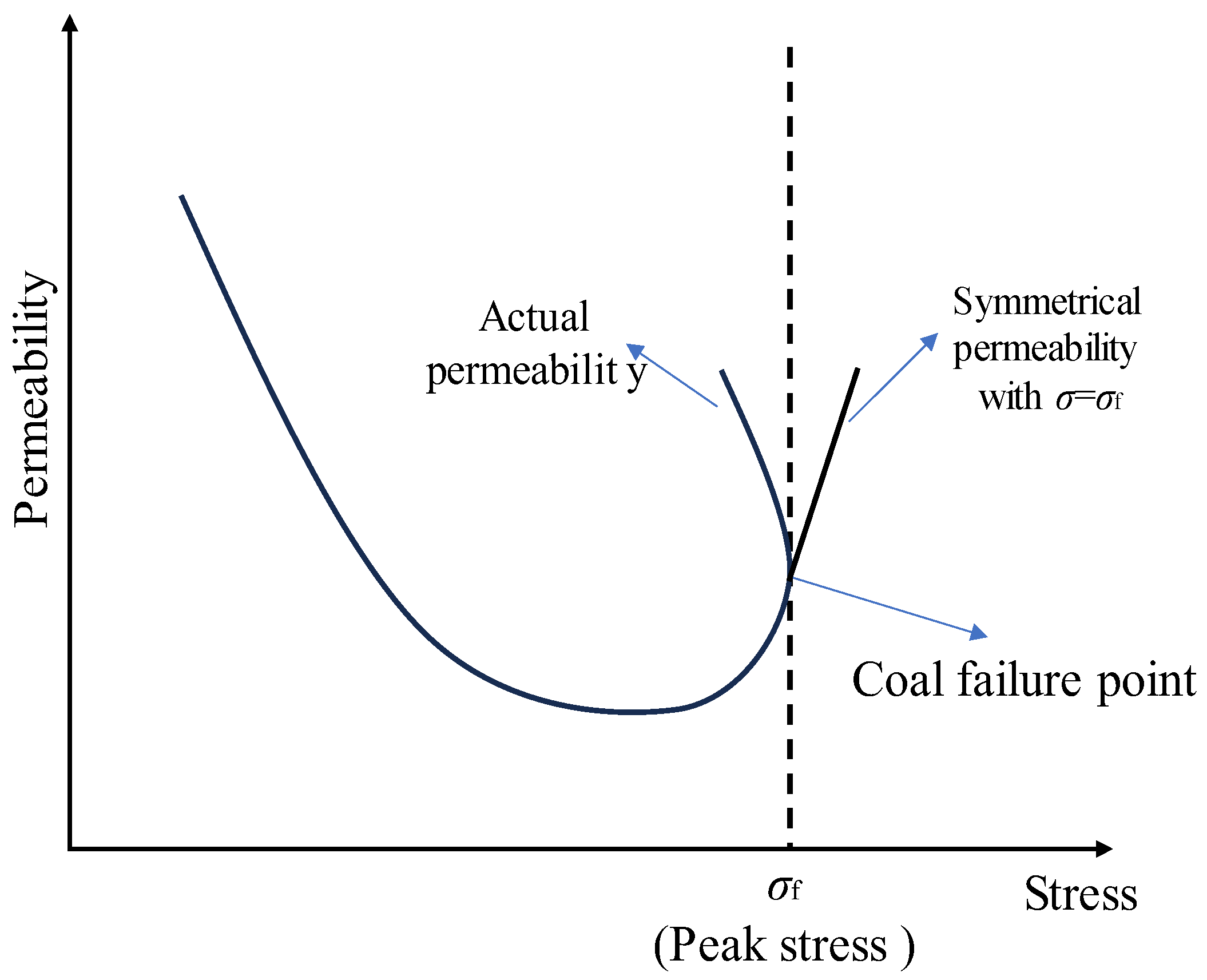
2.3. Permeability Model

Chen [36] introduced a variable L in the curves of the damage and failure stages based on the classic model. Chen’s permeability model considering coal compaction during the elastic stage is [42]:
k = k 0 ⋅ exp ( − 3 C f ( σ m − σ m 0 ) )
where k represents the coal permeability, k0 represents the initial permeability, Cf represents the coal cleat compressibility, σm represents the mean effective stress, and σm0 represents the initial mean effective stress. The equation for σm is:
σ m = ( σ 1 + σ 2 + σ 3 ) / 3
where σ1, σ2, and σ3 represent the principal stress in the X, Y, and Z directions, respectively. Chen’s permeability model during the damage and failure stages is:
k = k 0 ⋅ exp ( − 3 C f ( σ m − σ m 0 ) + γ 1 + exp ( − α ( σ 1 − σ 3 − β ) ) )
where α, β, and γ represent fitting parameters.
However, the stress falls rapidly after specimen failure. The change in permeability with stress is no longer a functional relationship. For a more accurate investigation of the permeability evolution law of intact coal, a segmented permeability model based on Chen’s work during progressive deformation was established. The permeability results with respect to peak stress σf (coal strength) are identified as the segmented point (as shown in Figure 6). The symmetrical permeability after post-peak stress was fitted by Chen’s model. The permeability–stress results of intact coal after post-peak stress are replaced by symmetrical permeability after this article.
Considering the strain caused by fracture and matrix deformation, Yu et al. [43] deduced the permeability model with respect to strain, which is:
k = k 0 ( 1 − α h 9 K φ 0 ( ε 1 s 1 K m l − b 1 K p l + ε 2 s 2 K m l − b 2 K p l + ε 3 s 3 K m l − b 3 K p l ) ) 3
where αh represents the effective stress coefficient (Biot’s coefficient) for bulk strain; K denotes the bulk modulus; φ0 denotes the fracture porosity; ε1, ε2, and ε3 denote the strain of coal in flow directions 1, 2, and 3, respectively; b1, b2, and b3 denote the fracture length in flow directions 1, 2, and 3, respectively; s1, s2, and s3 denote the matrix length in flow directions 1, 2, and 3, respectively; Km denotes the bulk modulus of the coal matrix; Kp denotes the bulk modulus of fractures and pores; l is the length of coal samples; and E denotes the elastic modulus.
Considering the strain caused by damage-induced fracture and matrix deformation, the permeability model is:
k = k 0 ( 1 + α h 9 K φ 0 ( ε 1 s 1 K m l − b 1 K p l + s 1 E l ( s 1 D 1 b 1 ( D 1 − 1 ) + 1 ) + ε 2 s 2 K m l − b 2 K p l + s 2 E l ( s 2 D 2 b 2 ( D 2 − 1 ) + 1 ) + ε 3 s 3 K m l − b 3 K p l + s 3 E l ( s 3 D 3 b 3 ( D 3 − 1 ) + 1 ) ) ) 3
where D1, D2, and D3 denote the damage variables in flow directions 1, 2, and 3, respectively. The damage variable is a function with respect to strain, as follows [44]:
D i = 1 − | ε c i 0 ε i | 2
where εci0 is the maximum compression strain in each flow direction.

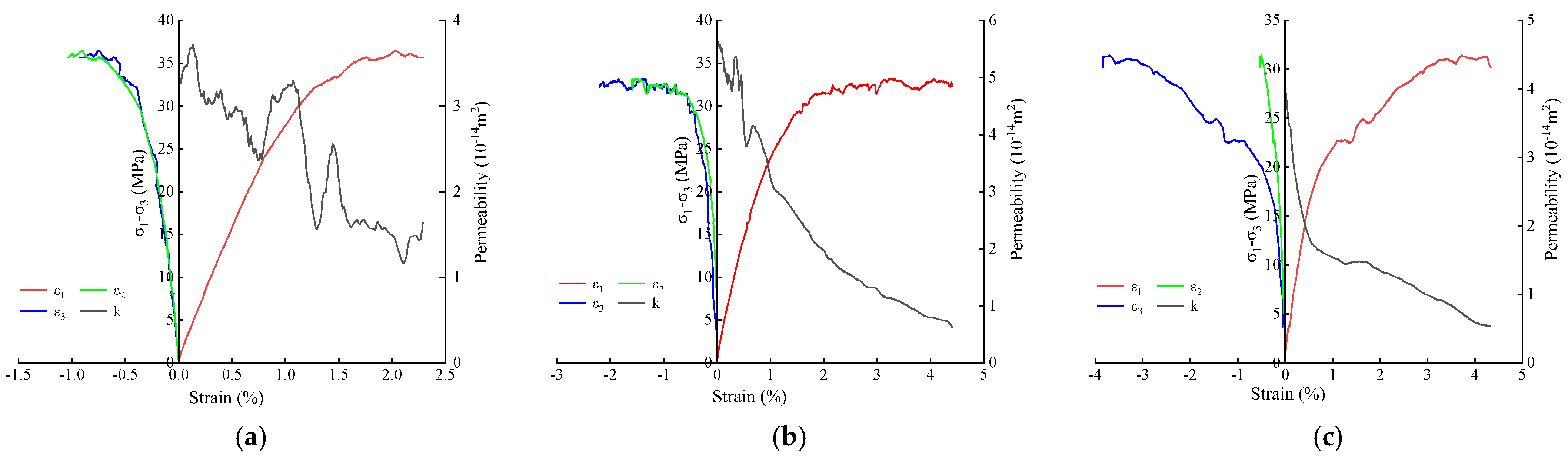
3. Results and Analysis

Figure 7 shows the permeability results of intact coal specimens under varying flow directions. The stress–strain curves of intact coal showed a stress decrease in different flow directions. The platform of the stress–strain curve was not found in the three flow directions. The specimens of intact coal exhibited brittle failure. Intact coal failures were observed at different peak stresses in three flow directions, as shown in Figure 7. The peak stress of intact coal varied from 57.11 MPa to 62.68 MPa. The strain-versus-failure point of intact coal specimens varied from 1.0% to 2.5%. The permeability curves of intact coal samples had the same S-shaped trend with strain. The permeability of intact coal first decreased, then remained stable, then slowly rose, and finally increased rapidly to a certain value after the sample failure. Detailed true triaxial experimental data for intact coal specimens is shown in Table 2.
Figure 8 shows the permeability results of fractured coal specimens under varying flow directions. The stress–strain curves of fractured coal specimens showed a leveling-off of the stress platform in the different flow directions. Macroscopic fractures were found at the fractured coal in flow directions 1 and 3, but not in flow direction 2. It indicates that the modes of fractured coal were the transitional modes from brittle failure to ductile failure. The peak stress of fractured coal varied from 34.82 MPa to 41.51 MPa. The strain-versus-peak-stress point of fractured coal specimens varied from 2.0% to 3.7%. The permeability curves showed the same L-shaped trend for all fractured coal samples. The permeability of fractured coal first decreased and then remained stable with the increase in strain. Detailed true triaxial experimental data for fractured coal specimens is shown in Table 3.

4. Discussion

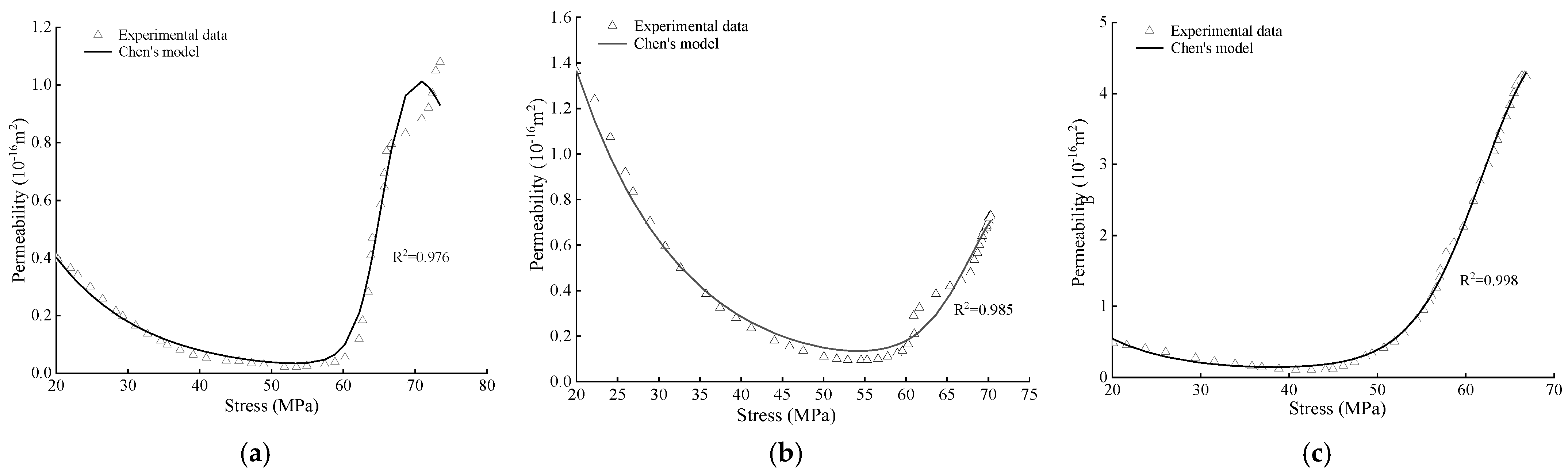
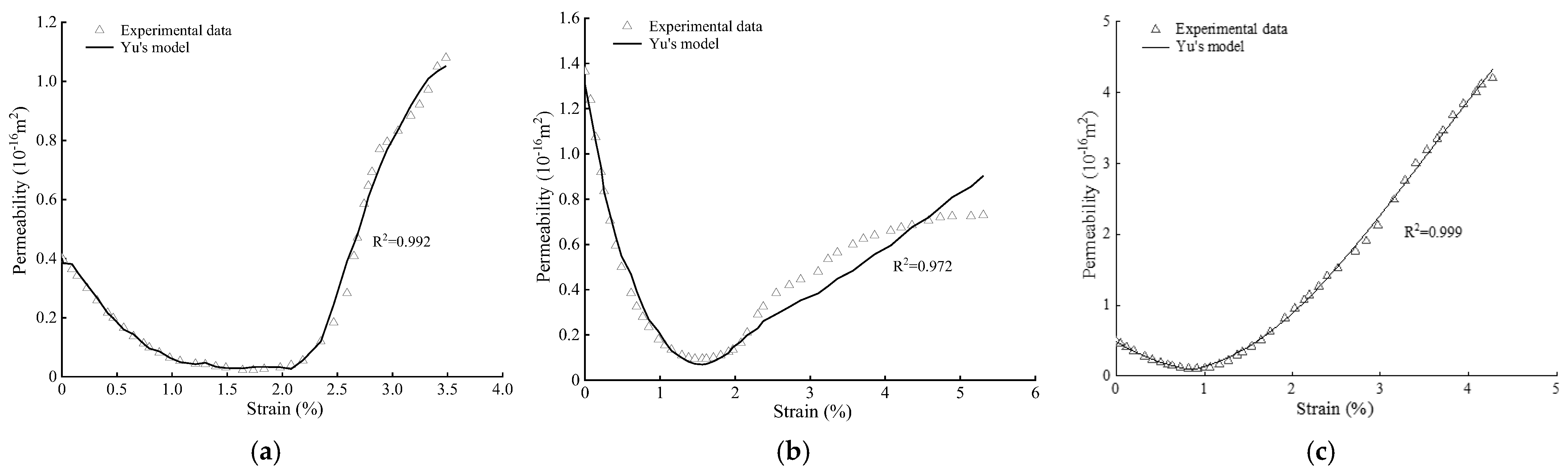
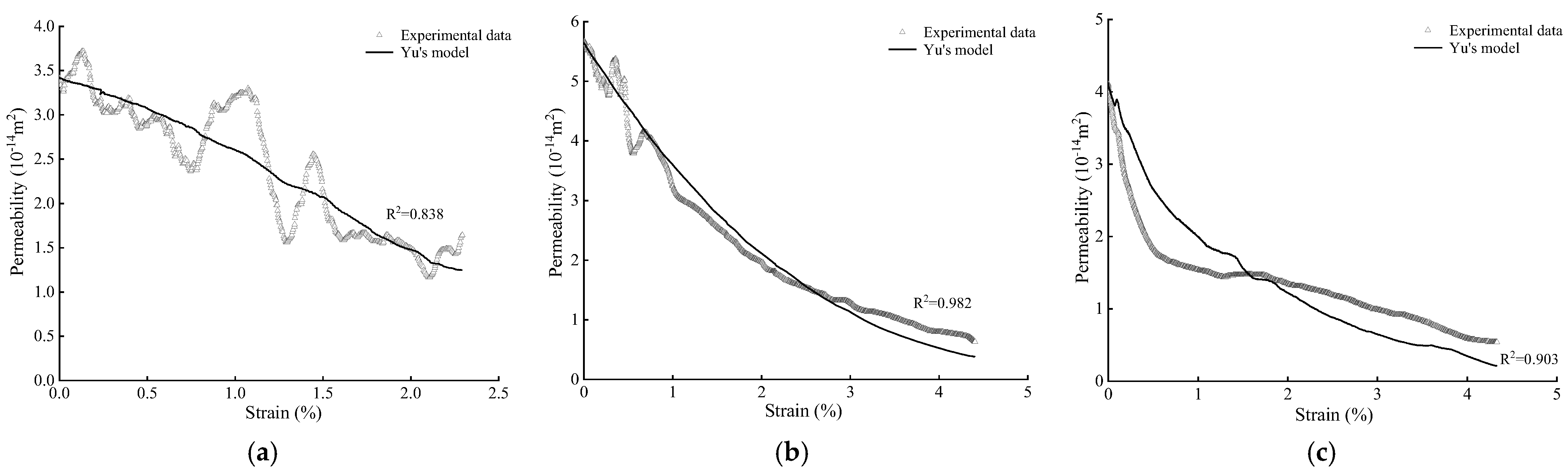
4.1. Validation of the Permeability Model

The steps to determine the parameters of Chen’s model are as follows: Cf was fitted by Equation (1) using the data from the elastic compression stage to obtain the best fitting result; after the Cf was determined, the parameters α, β, and γ were fitted according to Equation (3) to obtain the best fitting value. We obtained parameters E, K, φ0, l, etc. in Yu’s model with experiment or calculation, and the remaining parameters could be obtained by fitting analysis. Parameters in Yu’s model are shown in Table 4.
The permeability data of intact coal was fitted by Chen’s model. Figure 9 shows the permeability data and fitting curves of intact coal based on Chen’s model. It can be observed from Figure 9 that the fitting curve aligned well with the fitting degrees of 0.976, 0.985, and 0.998 in the three flow directions, respectively.
The permeability results of intact coal were then fitted by the model of Yu et al. to obtain the value of the fitting parameters. Figure 10 shows the experimental data and fitting curve of intact coal specimens with the change in strain in the direction of maximum principal stress. It can be found that the permeability model of Yu et al. had high applicability to the permeability results of intact coal. The fitting degrees of the permeability–stress curve were 0.992, 0.972, and 0.999 in the three flow directions, respectively.
The permeability results of fractured coal were fitted by the modified model based on Chen’s work. The experimental data and fitting curve with stress are shown in Figure 11. The permeability of fractured coal generally decreases with increasing stress during progressive deformation. There were some small ranges of increasing permeability. Chen’s model also had a good fit for the test results of fractured coal samples, and the fitting degrees of the permeability–strain curve were 0.924, 0.929, and 0.985 in the three flow directions, respectively.
The permeability results of fractured coal samples were fitted by Yu’s permeability model. The experimental data and fitting curve with respect to strain during progressive deformation are shown in Figure 12. Yu’s model had a good fit for the permeability results of fractured coal samples, and the fitting degrees of curves in flow directions 2 and 3 were 0.982 and 0.903, respectively. Permeability fluctuations were found in the curve of flow direction 1, as shown in Figure 12a. The fitting degree of Yu’s model in flow direction 1 was 0.838, and Chen’s permeability model had a better fit than Yu’s model for permeability fluctuations.

4.2. Permeability Evolution of Intact and Fractured Coal Samples

The permeability curves of intact coal showed the same trend in the three loading directions, as shown in Figure 7. Coal permeability first decreased, then remained stable, then rose slowly, and finally increased rapidly after failure strain during progressive deformation, which was S-shaped. The same situation was found in the permeability test subjected to triaxial compression [45]. The permeability curves had the same trend for fractured coal samples, as shown in Figure 8. As the strain increased, the permeability first decreased and then remained stable, which was an L-shaped curve. The maximum strain of intact coal varied from 3.4% to 5.3% in the three flow directions. The maximum strain of fractured coal varied from 2.29% to 4.41% in the three flow directions. The permeability of intact coal decreased by 94.53%, 93.04%, and 78.51%, then increased by 48.1, 8.5, and 39.9 times, respectively, in the three flow directions during progressive deformation. The permeability of fractured coal decreased by 51.92%, 88.84%, and 68.02%, respectively, in the three flow directions during progressive deformation. The permeability evolution of intact and fractured coal exhibited anisotropy. The greatest reduction in permeability was observed in the direction perpendicular to the bedding plane for intact coal. A similar situation was found in the permeability evolution of shale [46]. The permeability evolution of fractured coal was inconsistent with this situation. We believe that the network was changed during the progressive deformation of intact coal.
The initial permeability of intact and fractured coal in flow direction 2 was higher than others, and the initial permeability in flow direction 3 was higher than in flow direction 2, as shown in Table 2 and Table 3. The minimum permeability of intact coal in flow direction 2 was lower than in other directions. The minimum permeability of intact coal in flow directions 2 and 3 was close, but no similar situation was found in fractured coal. The maximum rebound permeability of intact coal in flow direction 3 was higher than in other directions. The phenomenon of permeability rebound did not appear in fractured coal during progressive deformation. The permeability curve of fractured coal had small fluctuations with the change in strain during progressive deformation, as shown in Figure 8a. It is induced by the surface slip of macroscopic fractures [47]. The phenomenon of permeability fluctuation did not appear in intact coal during progressive deformation.
The fractured coal had a higher permeability of 1–3 orders of magnitude than that of intact coal samples. The reason was that the existence of macroscopic fractures made the coal porosity greater in the fractured coal. It was also found in similar results that the introduction of large fractures increased coal permeability under triaxial stress conditions [48].

4.3. Analysis of Permeability Model Parameters in Different Flow Directions

The parameter fitting results of intact and fractured coal samples based on Chen’s model are shown in Table 5. It can be found that the Cf of fractured coal samples was smaller than that of intact coal samples in different flow directions. The existence of fractures reduced coal compressibility. This may be related to the formation of pulverized coal and separated fragments during the progressive deformation of fractured coal [27]. In Chen’s permeability model, α indicates the slope of permeability with stress after peak strength of coal, and the permeability increases fast for the higher α. β indicates the strength resistant to shear failure. γ indicates that the coal is not compact, and many fractures are easy to produce during the failure process [43]. The α values of fractured coal specimens were greater than those of intact coal in different flow directions, as shown in Table 5. Thus, it can be considered that the existence of the fracture increased the slope of permeability change. The β values of fractured coal samples were less than those of intact coal in different flow directions. It can be considered that the existence of fractures reduced coal strength and its resistance to shear failure. The γ values of fractured coal samples in different flow directions were less than those of intact coal. The fractured coal had fewer fractures created than that of intact coal during progressive deformation. It is consistent with the test results that the fractured coal sample does not have obvious failure during progressive deformation.
The fitting results of permeability parameters based on Yu’s permeability model for intact and fractured coal samples are shown in Table 6.
αh is Biot’s coefficient, which indicates the interrelationship between matrix particles and pore pressure [49]. Biot’s coefficient has an interrelationship with fracture aperture [43]. The Biot’s coefficient values of the fractured coal were higher than those of the intact coal. The mean slope of the permeability curve before failure strain for fractured coal was greater than that of intact coal, indicating that the initial macroscopic fracture increased the change rate of permeability with strain before coal failure.
Additionally, the Walsh model is commonly used to describe the dependence of fracture permeability on effective stress [50,51]. The Walsh model has the ability to determine some parameters describing the gas flow fracture. In future studies, we will explore the modeling of intact and fractured coal permeability using the Walsh model.

5. Conclusions

Coal contains many natural microscopic fractures. The macroscopic fractures have a significant effect on permeability evolution. In an environment of high stress and strong disturbance, a coal block can easily create macro-fractures. The effect of macro-fractures on the permeability evolution and comparative analysis of intact and fractured coal based on an established model is still limited. In this paper, the permeability of intact and fractured coal specimens was measured. The experimental permeability data were fitted based on established models. The differences in the permeability evolution of intact and fractured coal samples were compared. The fitting parameters of intact and fractured coal in Chen’s model and Yu’s model were analyzed. The results are as follows:
(1)
The permeability of intact coal first decreased, then remained stable, then rose slowly, and finally increased rapidly after the failure strain during progressive deformation, which presented an L-shaped trend. Most of the fractured coal showed failure during progressive deformation. The permeability of fractured coal remained gradually stable after the first drop, and the overall trend was L-shaped. The permeability of intact and fractured coal exhibited anisotropy.
(2)
The permeability exponential and cubic models had a good fit for most of the intact and fractured coal samples in different flow directions. The mean fitting degree of permeability based on Chen’s model was 0.973, and the result based on Yu’s model was 0.948. Chen’s model had a higher fitting degree than Yu’s model in the case of permeability fluctuations.
(3)
The existence of macroscopic fractures increased the permeability of coal samples by 1–3 orders of magnitude. During the progressive deformation of fractured coal, the surface slips between the macroscopic fractures, resulting in permeability fluctuations. There were no permeability fluctuations in intact coal during progressive deformation. The presence of macroscopic fractures increased the slope of the curve after post-peak stress and reduced the coal compressibility and coal strength resistant to shear failure.

Author Contributions

Conceptualization, Y.L. (Yubing Liu); methodology, Y.L. (Yubing Liu); validation, D.Z. and Y.L. (Yiteng Li); formal analysis, D.Z. and Y.L. (Yiteng Li); investigation, Y.L. (Yubing Liu); resources, Y.L. (Yubing Liu); data curation, D.Z.; writing—original draft, D.Z. and L.Z.; writing—review and editing, D.Z.; project administration, Y.L. (Yubing Liu); funding acquisition, Y.L. (Yubing Liu). All authors have read and agreed to the published version of the manuscript.

Funding

This research is funded by the National Key R&D Program of China (2022YFC3004705) and the National Natural Science Foundation of China (52104231).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Acknowledgments

The authors are grateful for the financial support of the National Key R&D Program of China (2022YFC3004705) and the National Natural Science Foundation of China (52104231).

Conflicts of Interest

The authors declare that they have no known competing financial interest or personal relationship that could have appeared to influence the work reported in this article.

References

  1. Xie, H. Research framework and anticipated results of deep rock mechanics and mining theory. Gongcheng Kexue Yu Jishu/Adv. Eng. Sci. 2017, 49, 1–16. [Google Scholar]
  2. Ranjith, P.G.; Zhao, J.; Ju, M.H.; De Silva, R.V.S.; Rathnaweera, T.D.; Bandara, A. Opportunities and challenges in deep mining: A brief review. Engineering 2017, 3, 546–551. [Google Scholar] [CrossRef]
  3. Shen, J.; Wan, L.; Zuo, J. Non-linear shear strength model for coal rocks. Rock Mech. Rock Eng. 2019, 52, 4123–4132. [Google Scholar] [CrossRef]
  4. Tan, Y.; Pan, Z.; Liu, J.; Zhou, F.; Connell, L.D.; Sun, W.; Haque, A. Experimental study of impact of anisotropy and heterogeneity on gas flow in coal. Part II: Permeability. Fuel 2018, 230, 397–409. [Google Scholar] [CrossRef]
  5. Zou, Q.; Liu, H.; Jiang, Z.; Wu, X. Gas flow laws in coal subjected to hydraulic slotting and a prediction model for its permeability-enhancing effect. Energ. Source. Part A 2021, 1–15. [Google Scholar] [CrossRef]
  6. Lu, S.Q.; Li, M.J.; Ma, Y.K.; Wang, S.C.; Zhao, W. Permeability changes in mining-damaged coal: A review of mathematical models. J. Nat. Gas Sci. Eng. 2022, 106, 30. [Google Scholar] [CrossRef]
  7. Vishal, V.; Ranjith, P.G.; Singh, T.N. CO2 permeability of Indian bituminous coals: Implications for carbon sequestration. Int. J. Coal Geol. 2013, 105, 36–47. [Google Scholar] [CrossRef]
  8. Viete, D.R.; Ranjith, P.G. The effect of CO2 on the geomechanical and permeability behaviour of brown coal: Implications for coal seam CO2 sequestration. Int. J. Coal Geol. 2006, 66, 204–216. [Google Scholar] [CrossRef]
  9. Xie, H.; Gao, F.; Ju, Y.; Gao, M.; Ru, Z.; Gao, Y.; Liu, J.; Xie, L.Z. Quantitative definition and investigation of deep mining. Meitan Xuebao/J. China Coal Soc. 2015, 40, 1–10. [Google Scholar]
  10. Chen, X.; Li, L.; Wang, L.; Qi, L. The current situation and prevention and control countermeasures for typical dynamic disasters in kilometer-deep mines in China. Saf. Sci. 2019, 115, 229–236. [Google Scholar] [CrossRef]
  11. Fairhurst, C. Some challenges of deep mining. Engineering 2017, 3, 527–537. [Google Scholar] [CrossRef]
  12. Ghorbani, Y.; Nwaila, G.T.; Zhang, S.E.; Bourdeau, J.E.; Canovas, M.; Arzua, J.; Nikadat, N. Moving towards deep underground mineral resources: Drivers, challenges and potential solutions. Resour. Policy 2023, 80, 15. [Google Scholar] [CrossRef]
  13. Wang, F.; Xiao, Z.; Liu, X.; Ren, J.; Xing, T.; Li, Z.; Li, X.; Chen, Y. Strategic design of cellulose nanofibers@zeolitic imidazolate frameworks derived mesoporous carbon-supported nanoscale CoFe2O4/CoFe hybrid composition as trifunctional electrocatalyst for Zn-air battery and self-powered overall water-splitting. J. Power Sources 2022, 521, 230925. [Google Scholar] [CrossRef]
  14. Li, Q.; Han, Y.; Liu, X.; Ansari, U.; Cheng, Y.; Yan, C. Hydrate as a by-product in CO2 leakage during the long-term sub-seabed sequestration and its role in preventing further leakage. Environ. Sci. Pollut. R 2022, 29, 77737–77754. [Google Scholar] [CrossRef]
  15. Li, Q.; Wang, F.; Wang, Y.; Forson, K.; Cao, L.; Zhang, C.; Zhou, C.; Zhao, B.; Chen, J. Experimental investigation on the high-pressure sand suspension and adsorption capacity of guar gum fracturing fluid in low-permeability shale reservoirs: Factor analysis and mechanism disclosure. Environ. Sci. Pollut. R 2022, 29, 53050–53062. [Google Scholar] [CrossRef]
  16. Liu, Y.; Wang, E.; Li, M.; Song, Z.; Zhang, L.; Zhao, D. Mechanical response and gas flow characteristics of pre-drilled coal subjected to true triaxial stresses. Gas Sci. Eng. 2023, 111, 204927. [Google Scholar] [CrossRef]
  17. Yang, X.L.; Cao, J.; Cheng, X.Y.; Liu, Y.H.; Li, X.L.; Sun, Z.G.; Guo, J.J. Mechanical response characteristics and permeability evolution of coal samples under cyclic loading. Energy Sci. Eng. 2019, 7, 1588–1604. [Google Scholar] [CrossRef]
  18. Pan, R.K.; Cheng, Y.P.; Yuan, L.; Yu, M.G.; Dong, J. Effect of bedding structural diversity of coal on permeability evolution and gas disasters control with coal mining. Nat. Hazards 2014, 73, 531–546. [Google Scholar] [CrossRef]
  19. Chen, Z.Y.; Li, G.F.; Wang, Y.; Li, Z.M.; Chi, M.B.; Zhang, H.W.; Tian, Q.L.; Wang, J.H. An experimental investigation of the gas permeability of tectonic coal mineral under triaxial loading conditions. Minerals 2022, 12, 70. [Google Scholar] [CrossRef]
  20. Somerton, W.H.; Söylemezoḡlu, I.M.; Dudley, R.C. Effect of stress on permeability of coal. Int. J. Rock Mech. Min. 1975, 12, 129–145. [Google Scholar] [CrossRef]
  21. Siriwardane, H.; Haljasmaa, I.; McLendon, R.; Irdi, G.; Soong, Y.; Bromhal, G. Influence of carbon dioxide on coal permeability determined by pressure transient methods. Int. J. Coal Geol. 2009, 77, 109–118. [Google Scholar] [CrossRef]
  22. Liu, Y.; Wang, E.; Zhao, D.; Zhang, L.J.S. Energy evolution characteristics of water-saturated and dry anisotropic coal under true triaxial stresses. Sustainabilitiy 2023, 15, 1431. [Google Scholar] [CrossRef]
  23. Kudasik, M. Investigating permeability of coal samples of various porosities under stress conditions. Energies 2019, 12, 762. [Google Scholar] [CrossRef]
  24. Prusty, B.K.; Pal, S.K.; Kumar, J.H. Study of porosity and permeability of coal and coal measure rocks from raniganj coalfield of India. In Proceedings of the 24th International Mining Congress of Turkey, Antalya, Turkey, 14–17 April 2015. [Google Scholar]
  25. Wang, G.; Qin, Y.; Shen, J.; Chen, S.Y.; Han, B.B.; Zhou, X.T. Dynamic-change laws of the porosity and permeability of low-to medium-rank coals under heating and pressurization treatments in the eastern junggar basin, China. J. Earth Sci. 2018, 29, 607–615. [Google Scholar] [CrossRef]
  26. Liu, Y.; Lebedev, M.; Zhang, Y.; Wang, E.; Li, W.; Liang, J.; Feng, R.; Ma, R. Micro-cleat and permeability evolution of anisotropic coal during directional CO2 flooding: An in situ micro-CT study. Nat. Resour. Res. 2022, 31, 2805–2818. [Google Scholar] [CrossRef]
  27. Liu, Y.B.; Wang, E.Y.; Jiang, C.B.; Zhang, D.M.; Li, M.H.; Yu, B.C.; Zhao, D. True triaxial experimental study of anisotropic mechanical behavior and permeability evolution of initially fractured coal. Nat. Resour. Res. 2023, 32, 567–585. [Google Scholar] [CrossRef]
  28. Ju, Y.; Zhang, Q.G.; Zheng, J.T.; Wang, J.G.; Chang, C.; Gao, F. Experimental study on CH4 permeability and its dependence on interior fracture networks of fractured coal under different excavation stress paths. Fuel 2017, 202, 483–493. [Google Scholar] [CrossRef]
  29. Pan, R.K.; Chen, L.; Li, Z.F.; Yu, M.G. The characteristic of micro-fracture evolution and gas permeability effect in the different bedding structure of coal. J. Nanosci. Nanotechnol. 2017, 17, 6670–6676. [Google Scholar] [CrossRef]
  30. Purl, R.; Evanoff, J.; Brugler, M. Measurement of coal cleat porosity and relative permeability characteristics. In Proceedings of the SPE Gas Technology Symposium, Houston, TX, USA, 22 January 1991. [Google Scholar]
  31. Guo, H.J.; Wang, K.; Cheng, Y.P.; Yuan, L.; Xu, C. Model development and analysis of coal permeability based on the equivalent characteristics of dual-porosity structure. J. Geophys. Eng. 2020, 17, 313–327. [Google Scholar] [CrossRef]
  32. Gao, Q.; Liu, J.; Huang, Y.; Li, W.; Shi, R.; Leong, Y.-K.; Elsworth, D. A critical review of coal permeability models. Fuel 2022, 326, 125124. [Google Scholar] [CrossRef]
  33. Wu, Y.; Liu, J.; Elsworth, D.; Chen, Z.; Connell, L.; Pan, Z. Dual poroelastic response of a coal seam to CO2 injection. Int. J. Greenh. Gas Con. 2010, 4, 668–678. [Google Scholar] [CrossRef]
  34. Kumar, H.; Elsworth, D.; Mathews, J.; Marone, C.J.G. Permeability evolution in sorbing media: Analogies between organic-rich shale and coal. Geofluids 2016, 16, 43–55. [Google Scholar] [CrossRef]
  35. Nazarova, L.A.; Nazarov, L.A. Evolution of stresses and permeability of fractured-and-porous rock mass around a production well. J. Min. Sci. 2016, 52, 424–431. [Google Scholar] [CrossRef]
  36. Chen, D.; Pan, Z.J.; Shi, J.Q.; Si, G.Y.; Ye, Z.H.; Zhang, J.L. A novel approach for modelling coal permeability during transition from elastic to post-failure state using a modified logistic growth function. Int. J. Coal Geol. 2016, 163, 132–139. [Google Scholar] [CrossRef]
  37. Shi, J.Q.; Durucan, S. Drawdown induced changes in permeability of coalbeds: A new interpretation of the reservoir response to primary recovery. Transp. Porous Media 2004, 56, 1–16. [Google Scholar] [CrossRef]
  38. Palmer, I.; Mansoori, J. How permeability depends on stress and pore pressure in coalbeds: A new model. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 6–9 October 1996. [Google Scholar]
  39. Wang, G.; Ren, T.; Wang, K.; Zhou, A. Improved apparent permeability models of gas flow in coal with Klinkenberg effect. Fuel 2014, 128, 53–61. [Google Scholar] [CrossRef]
  40. Pan, Z.; Connell, L.D. Modelling permeability for coal reservoirs: A review of analytical models and testing data. Int. J. Coal Geol. 2012, 92, 1–44. [Google Scholar] [CrossRef]
  41. Liu, T.; Lin, B.; Yang, W. Impact of matrix–fracture interactions on coal permeability: Model development and analysis. Fuel 2017, 207, 522–532. [Google Scholar] [CrossRef]
  42. Zhou, H.W.; Zhao, J.W.; Su, T.; Zhang, L.; Zhong, J.C.; Liu, Z.L. Characterization of gas flow in backfill mining-induced coal seam using a fractional derivative-based permeability model. Int. J. Rock Mech. Min. 2021, 138, 104571. [Google Scholar] [CrossRef]
  43. Yu, B.C.; Zhang, D.M.; Li, S.J.; Xu, B.; Liu, C.; Liu, Y.B. Biot’s coefficient and permeability evolution of damaged anisotropic coal subjected to true triaxial stress. Rock Mech. Rock Eng. 2023, 56, 237–260. [Google Scholar] [CrossRef]
  44. Zhu, W.C.; Wei, C.H. Numerical simulation on mining-induced water inrushes related to geologic structures using a damage-based hydromechanical model. Environ. Earth Sci. 2011, 62, 43–54. [Google Scholar] [CrossRef]
  45. Wang, C.; Zhao, Y.; Ning, L.; Bi, J. Permeability evolution of coal subjected to triaxial compression based on in-situ nuclear magnetic resonance. Int. J. Rock Mech. Min. 2022, 159, 105213. [Google Scholar] [CrossRef]
  46. Li, M.; Yin, G.; Xu, J.; Cao, J.; Song, Z. Permeability evolution of shale under anisotropic true triaxial stress conditions. Int. J. Coal Geol. 2016, 165, 142–148. [Google Scholar] [CrossRef]
  47. Phillips, T.; Kampman, N.; Bisdom, K.; Forbes Inskip, N.D.; den Hartog, S.A.M.; Cnudde, V.; Busch, A. Controls on the intrinsic flow properties of mudrock fractures: A review of their importance in subsurface storage. Earth-Sci. Rev. 2020, 211, 103390. [Google Scholar] [CrossRef]
  48. Cai, Y.; Liu, D.; Mathews, J.P.; Pan, Z.; Elsworth, D.; Yao, Y.; Li, J.; Guo, X. Permeability evolution in fractured coal—Combining triaxial confinement with X-ray computed tomography, acoustic emission and ultrasonic techniques. Int. J. Coal Geol. 2014, 122, 91–104. [Google Scholar] [CrossRef]
  49. Zoback, M.D.; Byerlee, J.D. Permeability and Effective Stress1. AAPG Bull. 1975, 59, 154–158. [Google Scholar]
  50. Lee, K.; Advani, S. In Stress and displacement responses of porous-permeable media under thermo-mechanical loading. In Proceedings of the Arma Us Rock Mechanics/Geomechanics Symposium, Reno, NV, USA, 1–3 May 1978. [Google Scholar]
  51. Zhao, Y.; Wang, Z.; Ye, J.; Sun, H.; Gu, J. Lattice Boltzmann simulation of gas flow and permeability prediction in coal fracture networks. J. Nat. Gas Sci. Eng. 2018, 53, 153–162. [Google Scholar] [CrossRef]
Processes 11 02826 g001
Figure 1. The schematic diagram illustrating gas flow surrounding a working face with intact and fractured zones in deep coal mining modified by [16]. σv represents vertical stress states surrounding a working face. P represents the gas pressure in coal seams.
Figure 1. The schematic diagram illustrating gas flow surrounding a working face with intact and fractured zones in deep coal mining modified by [16]. σv represents vertical stress states surrounding a working face. P represents the gas pressure in coal seams.
Processes 11 02826 g001
Processes 11 02826 g002
Figure 2. The loading path of true triaxial compression.
Figure 2. The loading path of true triaxial compression.
Processes 11 02826 g002
Processes 11 02826 g003
Figure 3. The schematic diagram of intact and fractured coal samples.
Figure 3. The schematic diagram of intact and fractured coal samples.
Processes 11 02826 g003
Processes 11 02826 g004
Figure 4. The schematic diagram of the experimental apparatus modified by [27].
Figure 4. The schematic diagram of the experimental apparatus modified by [27].
Processes 11 02826 g004
Processes 11 02826 g005
Figure 5. The diagram of the three flow directions.
Figure 5. The diagram of the three flow directions.
Processes 11 02826 g005
Processes 11 02826 g006
Figure 6. The diagram of permeability evolution with respect to stress.
Figure 6. The diagram of permeability evolution with respect to stress.
Processes 11 02826 g006
Processes 11 02826 g007
Figure 7. The permeability results of intact coal specimens under varying flow directions (σ2 = 15 MPa, σ3 = 10 MPa). (a) Flow direction 1; (b) Flow direction 2; (c) Flow direction 3.
Figure 7. The permeability results of intact coal specimens under varying flow directions (σ2 = 15 MPa, σ3 = 10 MPa). (a) Flow direction 1; (b) Flow direction 2; (c) Flow direction 3.
Processes 11 02826 g007
Processes 11 02826 g008
Figure 8. The permeability results of fractured coal samples under true triaxial stress and varying flow directions (σ2 = 15 MPa, σ3 = 10 MPa). (a) Flow direction 1; (b) Flow direction 2; (c) Flow direction 3.
Figure 8. The permeability results of fractured coal samples under true triaxial stress and varying flow directions (σ2 = 15 MPa, σ3 = 10 MPa). (a) Flow direction 1; (b) Flow direction 2; (c) Flow direction 3.
Processes 11 02826 g008
Processes 11 02826 g009
Figure 9. The permeability–stress data and fitting curve of intact coal based on Chen’s model. (a) Flow direction 1; (b) Flow direction 2; (c) Flow direction 3.
Figure 9. The permeability–stress data and fitting curve of intact coal based on Chen’s model. (a) Flow direction 1; (b) Flow direction 2; (c) Flow direction 3.
Processes 11 02826 g009
Processes 11 02826 g010
Figure 10. The experimental data and fitting curve of intact coal with strain based on Yu’s model. (a) Flow direction 1; (b) Flow direction 2; (c) Flow direction 3.
Figure 10. The experimental data and fitting curve of intact coal with strain based on Yu’s model. (a) Flow direction 1; (b) Flow direction 2; (c) Flow direction 3.
Processes 11 02826 g010
Processes 11 02826 g011
Figure 11. The permeability–stress fitting curve of fractured coal based on Chen’s model. (a) Flow direction 1; (b) Flow direction 2; (c) Flow direction 3.
Figure 11. The permeability–stress fitting curve of fractured coal based on Chen’s model. (a) Flow direction 1; (b) Flow direction 2; (c) Flow direction 3.
Processes 11 02826 g011
Processes 11 02826 g012
Figure 12. The experimental data and fitting curve of fractured coal based on Yu’s model. (a) Flow direction 1; (b) Flow direction 2; (c) Flow direction 3.
Figure 12. The experimental data and fitting curve of fractured coal based on Yu’s model. (a) Flow direction 1; (b) Flow direction 2; (c) Flow direction 3.
Processes 11 02826 g012
Table 1. The fundamental mechanical parameters of coal.
Table 1. The fundamental mechanical parameters of coal.
Direction Elastic Modulus (GPa)Uniaxial Compressive Strength (MPa)
parallel to bedding plane3.4220.03
normal to bedding plane2.9525.28
Table 2. Detailed true triaxial experimental data for intact coal specimens.
Table 2. Detailed true triaxial experimental data for intact coal specimens.
Sample IDElastic Modulus (GPa)Peak Strength (MPa)Strain at the Time of Failure (%)Initial Permeability
(×10−16 m2)		Minimum
Permeability
(×10−16 m2)		The Maximum
Rebound Permeability (×10−16 m2)
Coal-int-11.8962.682.470.4020.0221.080
Coal-int-22.3261.012.161.3650.0950.905
Coal-int-32.4057.112.520.4840.1044.256
Sample ID refers to intact coal samples, i.e., Coal-int-1 represents the intact coal sample in flow direction 1.
Table 3. Detailed true triaxial experimental data for fractured coal specimens.
Table 3. Detailed true triaxial experimental data for fractured coal specimens.
Sample IDInitial Permeability (×10−14 m2)Minimum Permeability (×10−14 m2)Strain at the Time of Peak Stress (%)Peak Stress (MPa)Elastic Modulus (GPa)
Coal-fra-13.4191.6442.2934.822.99
Coal-fra-25.6430.6304.4138.193.26
Coal-fra-34.1091.3145.5541.512.48
Sample ID refers to fractured coal samples, i.e., Coal-fra-1 represents the fractured coal sample in flow direction 1.
Table 4. Parameters used in Yu’s model.
Table 4. Parameters used in Yu’s model.
ParameterValue
φ06.42%
E (GPa)2.1
K (GPa)1.75
Km (GPa)11.841
Kp (GPa)0.597
s1, s2, s3 (m)0.095, 0.097, 0.094
b1, b2, b3 (m)0.005, 0.003, 0.006
l (m)0.1
Table 5. Fitting parameter results of intact and fractured coal in Chen’s model.
Table 5. Fitting parameter results of intact and fractured coal in Chen’s model.
Sample IDCf (MPa−1)α (MPa−1)β (MPa)γR2
Coal-int-10.08170.92752.1604.3290.976
Coal-int-20.07950.20655.2174.5110.985
Coal-int-30.12730.12844.1959.7510.998
Coal-fra-10.01111.04725.9730.7220.992
Coal-fra-20.01941.11328.7041.8580.972
Coal-fra-30.04750.78725.1921.0740.999
R2 refers to the fitting degree of the model.
Table 6. Parameters in Yu’s permeability model for intact and fractured coal samples.
Table 6. Parameters in Yu’s permeability model for intact and fractured coal samples.
Sample IDαhR2Mean Slope before Failure Strain (10−14 m2)
Coal-int-10.6650.9240.361
Coal-int-20.5960.9691.141
Coal-int-30.6290.9850.477
Coal-fra-10.8690.8381.443 × 102
Coal-fra-20.7560.9822.277 × 102
Coal-fra-30.8040.9031.536 × 102
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Liu, Y.; Zhao, D.; Li, Y.; Zhang, L. Permeability Evolution of Intact and Fractured Coal during Progressive Deformation Subjected to True Triaxial Stresses. Processes 2023, 11, 2826. https://doi.org/10.3390/pr11102826

AMA Style

Liu Y, Zhao D, Li Y, Zhang L. Permeability Evolution of Intact and Fractured Coal during Progressive Deformation Subjected to True Triaxial Stresses. Processes. 2023; 11(10):2826. https://doi.org/10.3390/pr11102826

Chicago/Turabian Style

Liu, Yubing, Dong Zhao, Yiteng Li, and Li Zhang. 2023. "Permeability Evolution of Intact and Fractured Coal during Progressive Deformation Subjected to True Triaxial Stresses" Processes 11, no. 10: 2826. https://doi.org/10.3390/pr11102826

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop