A PBM-Based Procedure for the CFD Simulation of Gas–Liquid Mixing with Compact Inline Static Mixers in Pipelines
Abstract
1. Introduction
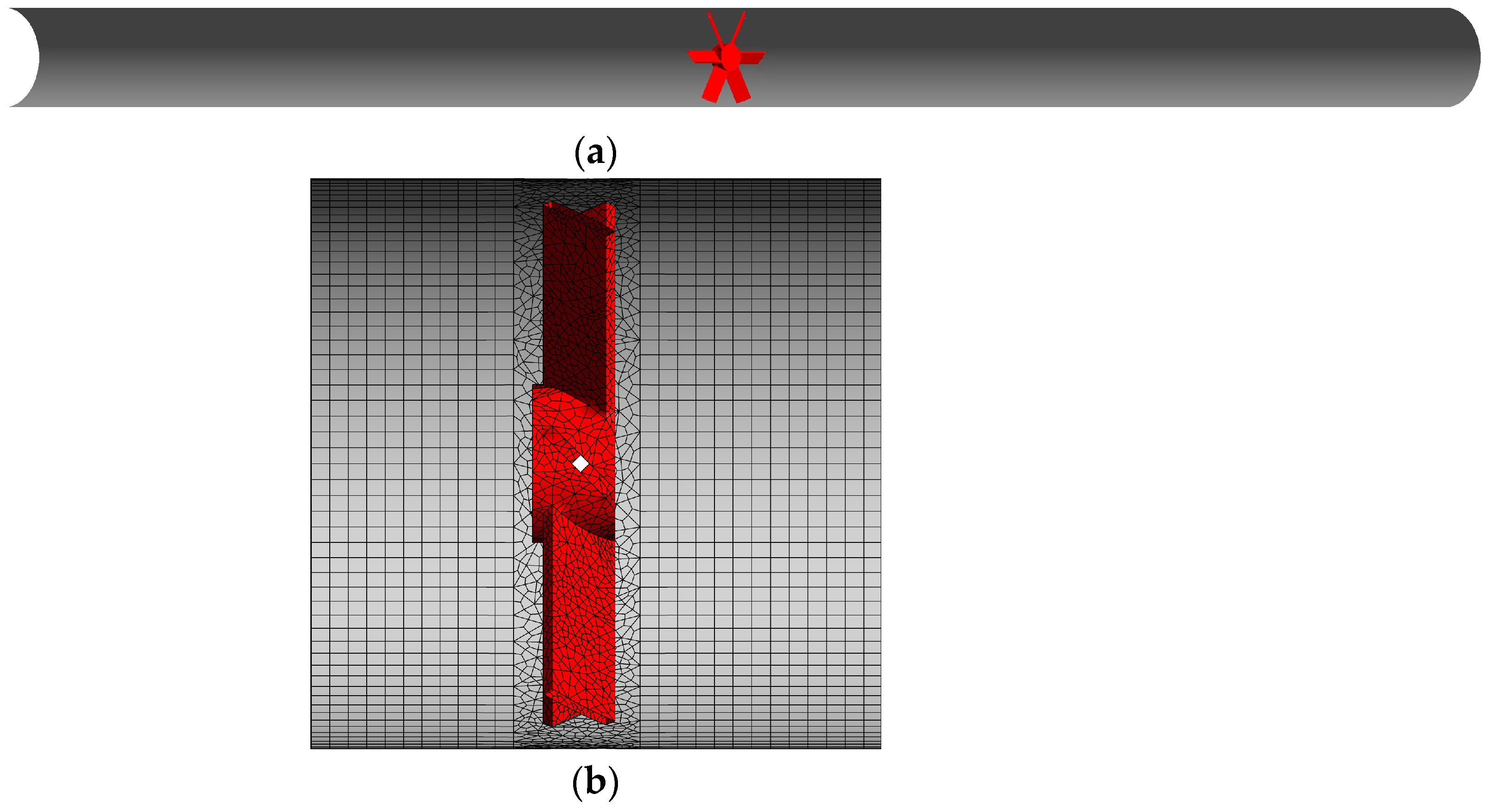
2. Investigated System and Operative Conditions
3. Computational Model
3.1. RANS-TFM Equations
3.2. Interphase Mass Transfer Model
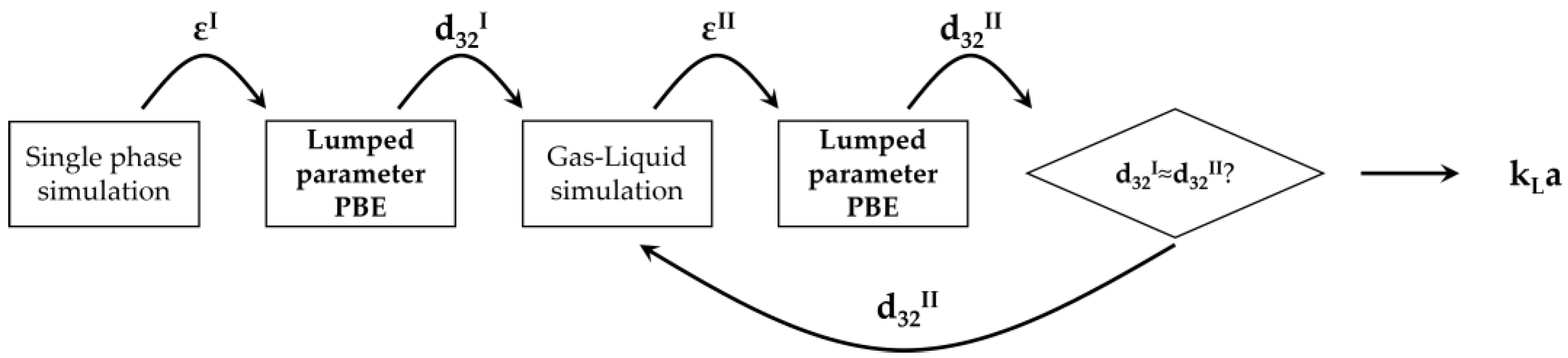
3.3. PBM-Based Procedure for Bubble Size Determination
4. Numerical Solution
5. Results and Discussion
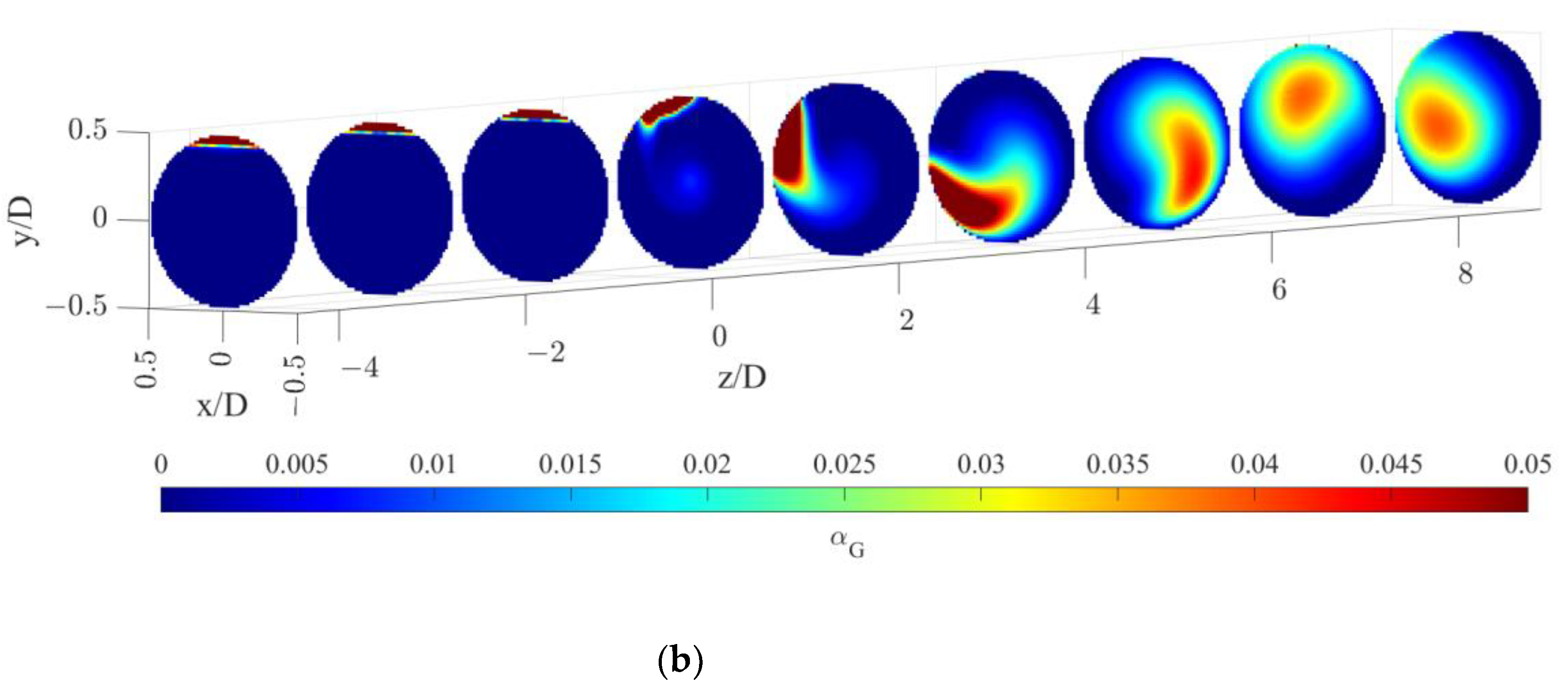
5.1. Bubble Size and Gas Volume Fraction Distribution
5.2. kLa and Mass Transfer Rate
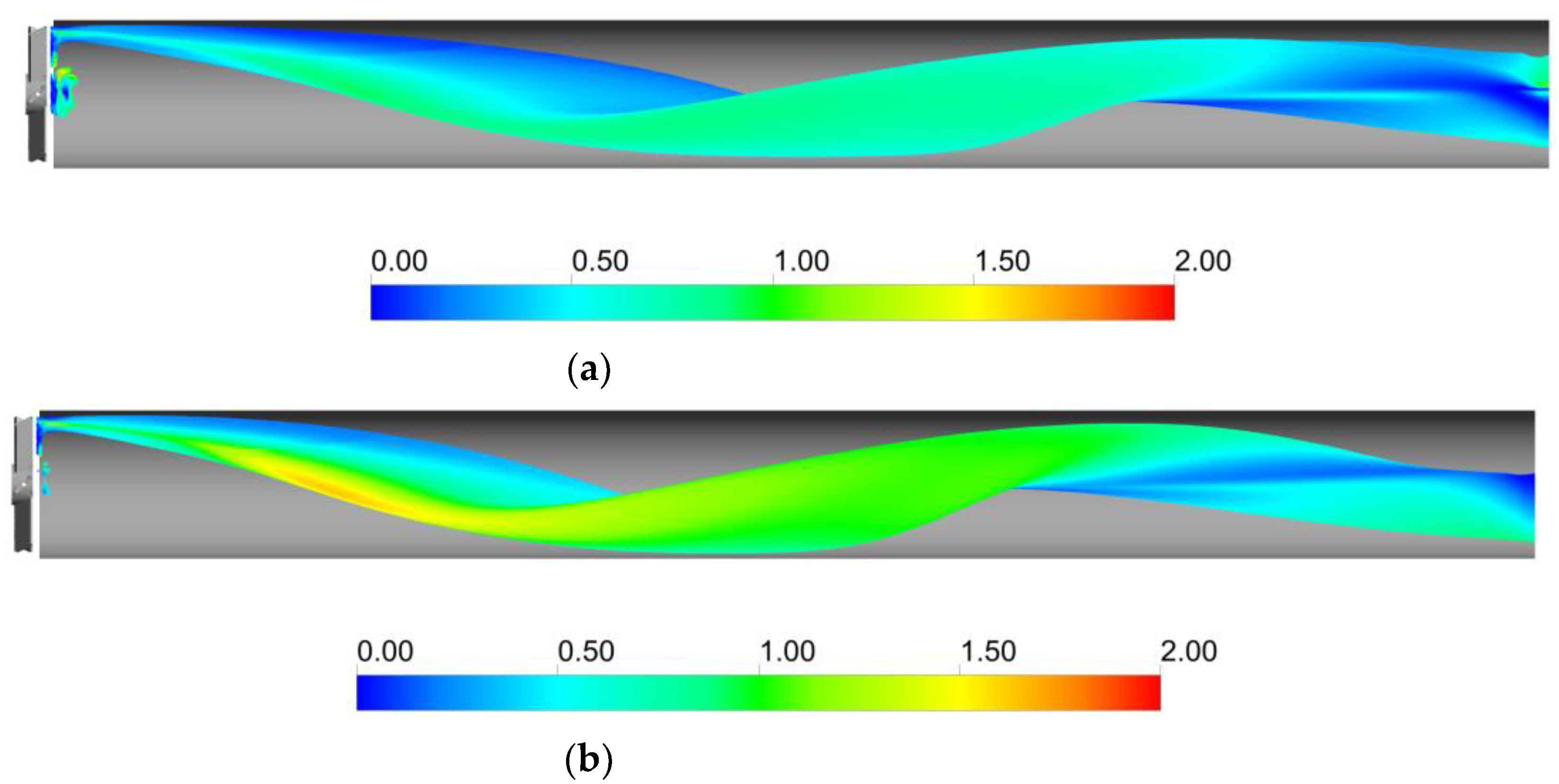
5.3. Local Analysis of the Interphase Mass Transfer Phenomena
6. Conclusions
- Upstream of the static mixer, the gas bubbles accumulate towards the top of the pipe, resulting in a high coefficient of variations of the gas hold-up and low volumetric mass transfer coefficients, thus determining negligible oxygen transfer rates despite a high interphase mass transfer driving force;
- Just downstream of the static mixer, the lighter phase starts to rotate following the liquid phase and gradually reduces the segregation, which lasts to axial coordinates up until 4–5 pipe diameters downstream of the static mixer. Despite the relatively high liquid side mass transfer coefficient, the oxygen transfer rate is limited by the available specific interfacial area;
- At higher axial coordinates, the reduced interphase mass transfer driving force limits the oxygen transfer rate, even though very low coefficients of variations of the gas hold-up are found, indicating sufficient mixedness of the gas–liquid dispersion, together with relatively high values of kLa;
- Modification of the hub geometry is suggested in order to better exploit the low-pressure region downstream of the static mixer to improve the gas distribution in the zone where kL is higher.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thakur, R.; Vial, C.; Nigam, K.; Nauman, E.; Djelveh, G. Static Mixers in the Process Industries—A Review. Chem. Eng. Res. Des. 2003, 81, 787–826. [Google Scholar] [CrossRef]
- Van Gerven, T.; Stankiewicz, A. Structure, Energy, Synergy, Time—The Fundamentals of Process Intensification. Ind. Eng. Chem. Res. 2009, 48, 2465–2474. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, L.; Wang, Y.; Qian, Y.; Wang, H.; Xu, Y.; Yang, X. Gas-liquid flow pattern identification and bubble characteristics analysis in a static mixer based HiPOxTM reactor. Chem. Eng. Sci. 2023, 267, 118269. [Google Scholar] [CrossRef]
- Schrimpf, M.; Esteban, J.; Rösler, T.; Vorholt, A.J.; Leitner, W. Intensified reactors for gas-liquid-liquid multiphase catalysis: From chemistry to Engineering. Chem. Eng. J. 2019, 372, 917–939. [Google Scholar] [CrossRef]
- Scala, M.; Gamet, L.; Malbec, L.-M.; Li, H.-Z. Hydrodynamics of gas-liquid dispersion in transparent Sulzer static mixers SMXTM. Chem. Eng. Sci. 2019, 213, 115398. [Google Scholar] [CrossRef]
- Tepper, M.; Eminoglu, Y.; Mehling, N.; Walorski, J.; Roth, H.; Wessling, M. Rotation-in-a-Spinneret integrates static mixers inside hollow fiber membranes. J. Membr. Sci. 2022, 656, 120599. [Google Scholar] [CrossRef]
- Lehwald, A.; Janiga, G.; Thévenin, D.; Zähringer, K. Simultaneous investigation of macro- and micro-mixing in a static mixer. Chem. Eng. Sci. 2012, 79, 8–18. [Google Scholar] [CrossRef]
- Alberini, F.; Simmons, M.; Ingram, A.; Stitt, E. Assessment of different methods of analysis to characterise the mixing of shear-thinning fluids in a Kenics KM static mixer using PLIF. Chem. Eng. Sci. 2014, 112, 152–169. [Google Scholar] [CrossRef]
- Alberini, F.; Simmons, M.J.H.; Ingram, A.; Stitt, E.H. Use of an areal distribution of mixing intensity to describe blending of non-newtonian fluids in a kenics KM static mixer using PLIF. AIChE J. 2013, 60, 332–342. [Google Scholar] [CrossRef]
- FEng, H.; Olsen, M.G.; Hill, J.C.; Fox, R.O. Investigation of passive scalar mixing in a confined rectangular wake using simultaneous PIV and PLIF. Chem. Eng. Sci. 2010, 65, 3372–3383. [Google Scholar] [CrossRef]
- Rabha, S.; Schubert, M.; Grugel, F.; Banowski, M.; Hampel, U. Visualization and quantitative analysis of dispersive mixing by a helical static mixer in upward co-current gas–liquid flow. Chem. Eng. J. 2015, 262, 527–540. [Google Scholar] [CrossRef]
- Jegatheeswaran, S.; Ein-Mozaffari, F.; Wu, J. Process intensification in a chaotic SMX static mixer to achieve an energy-efficient mixing operation of non-newtonian fluids. Chem. Eng. Process. Process. Intensif. 2018, 124, 1–10. [Google Scholar] [CrossRef]
- Jaworski, Z.; Pianko-Oprych, P.; Marchisio, D.; Nienow, A. CFD Modelling of Turbulent Drop Breakage in a Kenics Static Mixer and Comparison with Experimental Data. Chem. Eng. Res. Des. 2007, 85, 753–759. [Google Scholar] [CrossRef]
- Montante, G.; Carletti, C.; Maluta, F.; Paglianti, A. Solid Dissolution and Liquid Mixing in Turbulent Stirred Tanks. Chem. Eng. Technol. 2019, 42, 1627–1634. [Google Scholar] [CrossRef]
- Paglianti, A.; Carletti, C.; Montante, G. Liquid Mixing Time in Dense Solid-Liquid Stirred Tanks. Chem. Eng. Technol. 2017, 40, 862–869. [Google Scholar] [CrossRef]
- Maluta, F.; Paglianti, A.; Montante, G. RANS-based predictions of dense solid–liquid suspensions in turbulent stirred tanks. Chem. Eng. Res. Des. 2019, 147, 470–482. [Google Scholar] [CrossRef]
- Kumar, V.; Shirke, V.; Nigam, K. Performance of Kenics static mixer over a wide range of Reynolds number. Chem. Eng. J. 2008, 139, 284–295. [Google Scholar] [CrossRef]
- Byrde, O.; Sawley, M. Optimization of a Kenics static mixer for non-creeping flow conditions. Chem. Eng. J. 1999, 72, 163–169. [Google Scholar] [CrossRef]
- Visser, J.E.; Rozendal, P.F.; Hoogstraten, H.W.; Beenackers, A.A. Three-dimensional numerical simulation of flow and heat transfer in the Sulzer SMX static mixer. Chem. Eng. Sci. 1999, 54, 2491–2500. [Google Scholar] [CrossRef]
- Montante, G.; Coroneo, M.; Paglianti, A. Blending of miScible liquids with different densities and viscosities in static mixers. Chem. Eng. Sci. 2016, 141, 250–260. [Google Scholar] [CrossRef]
- Zidouni, F.; Krepper, E.; Rzehak, R.; Rabha, S.; Schubert, M.; Hampel, U. Simulation of Gas–Liquid flow in a helical static mixer. Chem. Eng. Sci. 2015, 137, 476–486. [Google Scholar] [CrossRef]
- Putra, R.A.; Neumann-Kipping, M.; Schäfer, T.; Lucas, D. Comparison of Gas–Liquid Flow Characteristics in Geometrically Different Swirl Generating Devices. Energy 2019, 12, 4653. [Google Scholar] [CrossRef]
- Maluta, F.; Paglianti, A.; Montante, G. Experimental and numerical study of a compact inline swirler for Gas–Liquid separation. Chem. Eng. Sci. 2023, 265, 118219. [Google Scholar] [CrossRef]
- Maluta, F.; Paglianti, A.; Montante, G. Towards a CFD-PBE simulation of aerated stirred tanks at high gas hold ups and different flow regimes. Chem. Eng. Res. Des. 2021, 180, 425–436. [Google Scholar] [CrossRef]
- Buffo, A.; Vanni, M.; Renze, P.; Marchisio, D. Empirical drag closure for polydisperse Gas–Liquid systems in bubbly flow regime: Bubble swarm and micro-scale turbulence. Chem. Eng. Res. Des. 2016, 113, 284–303. [Google Scholar] [CrossRef]
- Yacilom, A.M. Turbulence, 2nd ed.; McGraw-Hill Publishing Co.: New York, NY, USA, 1977. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, A. Über die grundlegenden berechnungen bei der schwerkraftbereitung. Z. Des Ver. Dtsch. Ing. 1933, 77, 318–321. [Google Scholar]
- Burns, A.D.; Frank, T.; Hamill, I.; Shi, J.-M.M. The Favre Averaged Drag Model for Turbulent Dispersion in Eulerian Multi-Phase Flows. In Proceedings of the Fifth International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004; pp. 1–17. [Google Scholar]
- Simonnet, M.; Gentric, C.; Olmos, E.; Midoux, N. Experimental determination of the drag coefficient in a swarm of bubbles. Chem. Eng. Sci. 2007, 62, 858–866. [Google Scholar] [CrossRef]
- Maluta, F.; Paglianti, A.; Montante, G. Prediction of gas cavities size and structure and their effect on the power consumption in a gas-liquid stirred tank by means of a two-fluid RANS model. Chem. Eng. Sci. 2021, 241, 116677. [Google Scholar] [CrossRef]
- Maluta, F.; Paglianti, A.; Montante, G. Two-fluids RANS predictions of gas cavities, power consumption, mixing time and oxygen transfer rate in an aerated fermenter scale-down stirred with multiple impellers. Biochem. Eng. J. 2020, 166, 107867. [Google Scholar] [CrossRef]
- Lamont, J.C.; Scott, D.S. An eddy cell model of mass transfer into the surface of a turbulent liquid. AIChE J. 1970, 16, 513–519. [Google Scholar] [CrossRef]
- Maluta, F.; Paglianti, A.; Montante, G. Modelling of biohydrogen production in stirred fermenters by Computational Fluid Dynamics. Process Saf. Environ. Prot. 2018, 125, 342–357. [Google Scholar] [CrossRef]
- Hänsch, S.; Lucas, D.; Krepper, E.; Höhne, T. A multi-field two-fluid concept for transitions between different scales of interfacial structures. Int. J. Multiph. Flow 2012, 47, 171–182. [Google Scholar] [CrossRef]
- Luo, H.; Svendsen, H.F. Theoretical model for drop and bubble breakup in turbulent dispersions. AIChE J. 1996, 42, 1225–1233. [Google Scholar] [CrossRef]
- Prince, M.J.; Blanch, H.W. Bubble coalescence and break-up in air-sparged bubble columns. AIChE J. 1990, 36, 1485–1499. [Google Scholar] [CrossRef]
- Cheung, S.C.; Yeoh, G.; Tu, J. On the numerical study of isothermal vertical bubbly flow using two population balance approaches. Chem. Eng. Sci. 2007, 62, 4659–4674. [Google Scholar] [CrossRef]
- Ekambara, K.; Sanders, R.; Nandakumar, K.; Masliyah, J. CFD simulation of bubbly two-phase flow in horizontal pipes. Chem. Eng. J. 2008, 144, 277–288. [Google Scholar] [CrossRef]
- Marchisio, D.L.; Fox, R.O. Computational Models for Polydisperse Particulate and Multiphase Systems; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Munter, R. Comparison of Mass Transfer Efficiency and Energy Consumption in Static Mixers. Ozone Sci. Eng. 2010, 32, 399–407. [Google Scholar] [CrossRef]


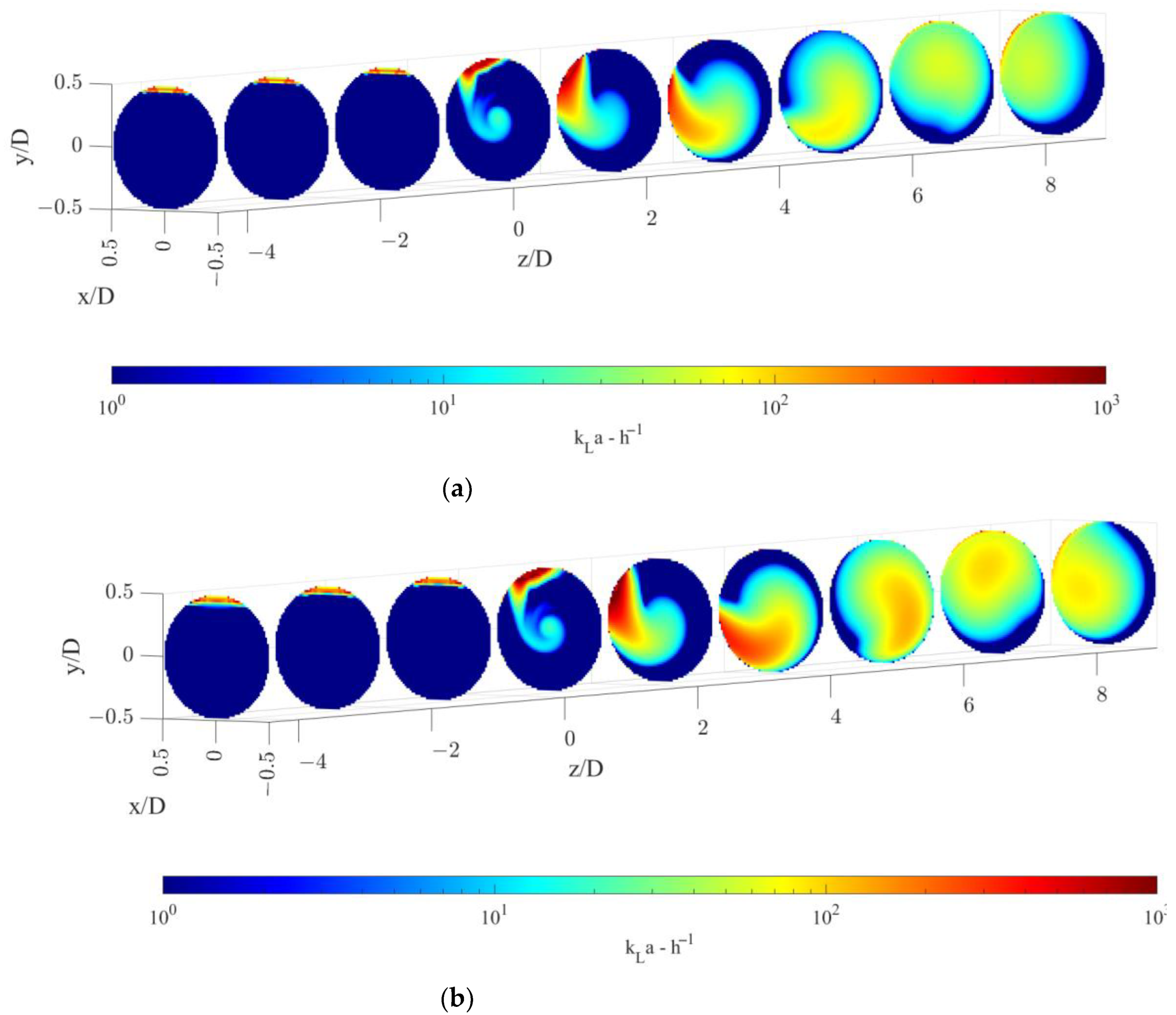
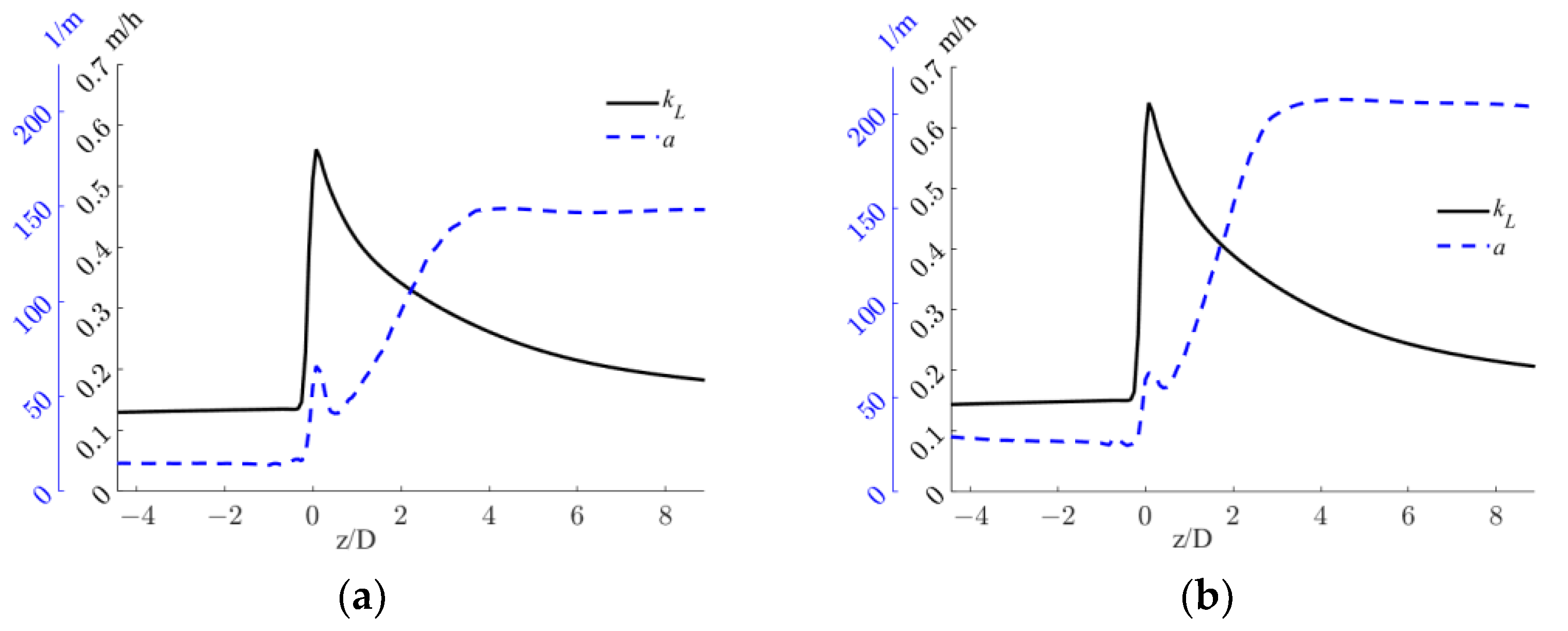
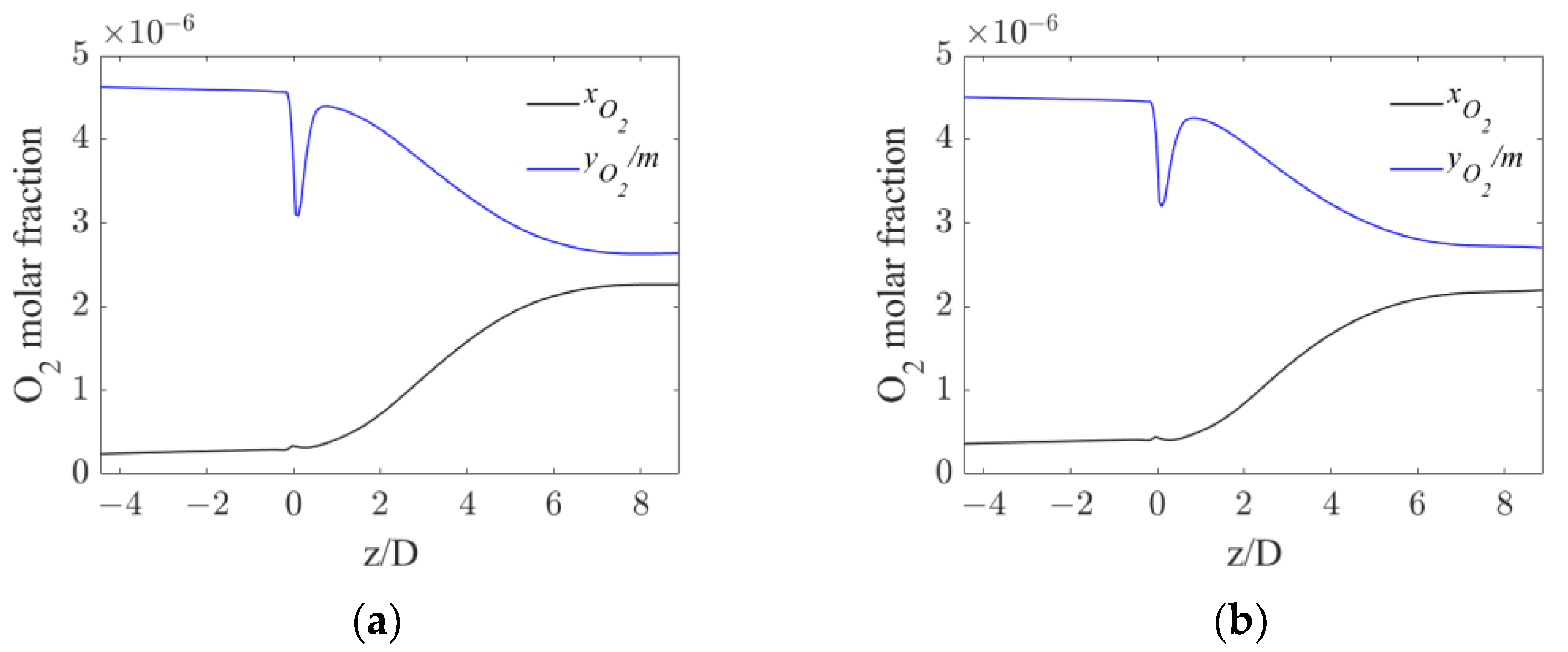


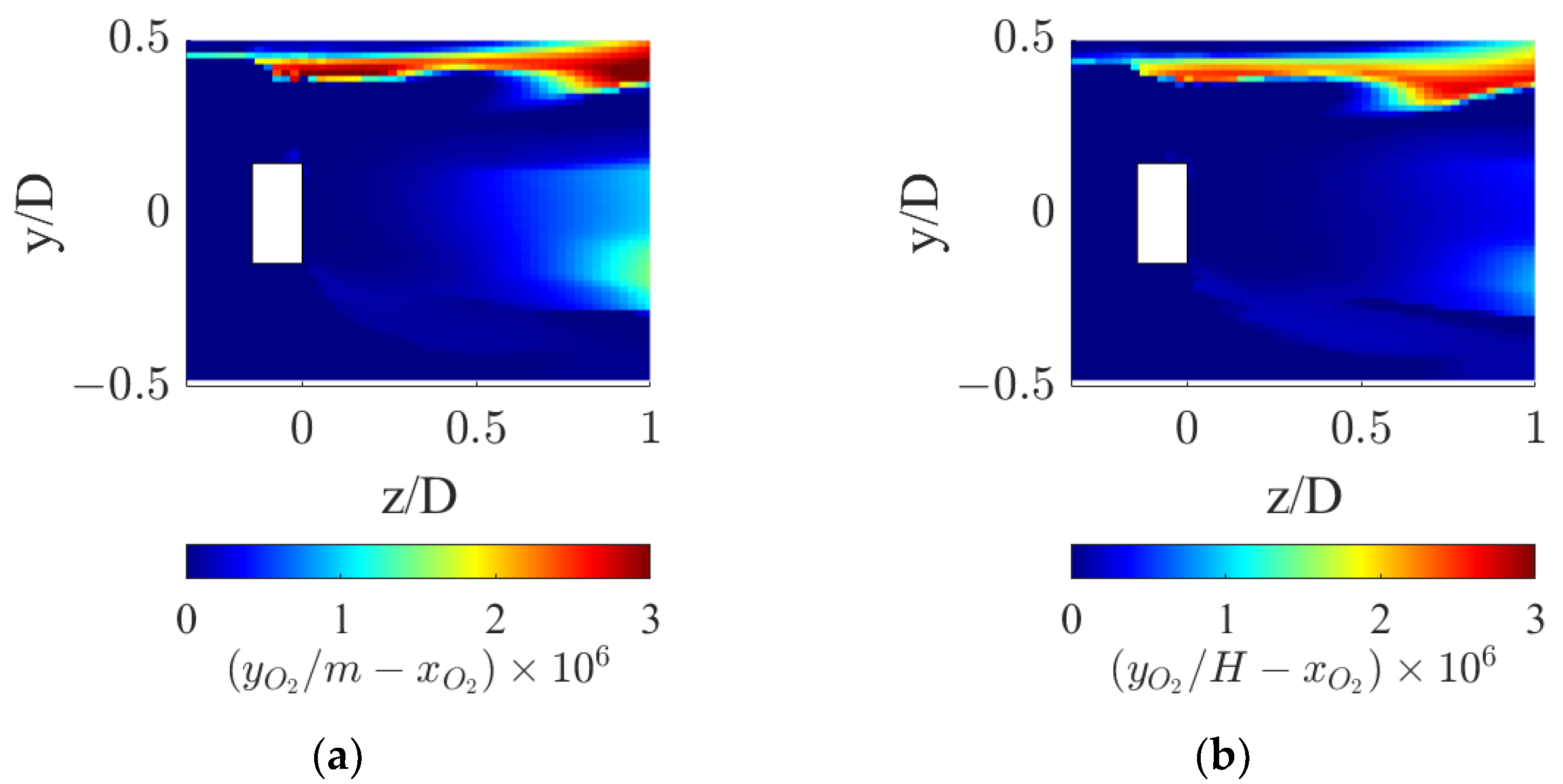
| QL (m3/h) | QG (L/min) | εSM (m2/s3) | d32 (m) | Ut (m/s) |
|---|---|---|---|---|
| 25 | 0 | 3.78 | 7.4 × 10−4 | 0.084 |
| 25 | 3.75 | 3.56 | 7.7 × 10−4 | 0.087 |
| 30 | 0 | 10.07 | 5.2 × 10−4 | 0.058 |
| 30 | 7.5 | 9.81 | 5.4 × 10−4 | 0.060 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maluta, F.; Paglianti, A.; Montante, G. A PBM-Based Procedure for the CFD Simulation of Gas–Liquid Mixing with Compact Inline Static Mixers in Pipelines. Processes 2023, 11, 198. https://doi.org/10.3390/pr11010198
Maluta F, Paglianti A, Montante G. A PBM-Based Procedure for the CFD Simulation of Gas–Liquid Mixing with Compact Inline Static Mixers in Pipelines. Processes. 2023; 11(1):198. https://doi.org/10.3390/pr11010198
Chicago/Turabian StyleMaluta, Francesco, Alessandro Paglianti, and Giuseppina Montante. 2023. "A PBM-Based Procedure for the CFD Simulation of Gas–Liquid Mixing with Compact Inline Static Mixers in Pipelines" Processes 11, no. 1: 198. https://doi.org/10.3390/pr11010198
APA StyleMaluta, F., Paglianti, A., & Montante, G. (2023). A PBM-Based Procedure for the CFD Simulation of Gas–Liquid Mixing with Compact Inline Static Mixers in Pipelines. Processes, 11(1), 198. https://doi.org/10.3390/pr11010198






