Abstract
This paper presents a descriptor representation-based guaranteed cost design methodology for polynomial fuzzy systems. This methodology applies the descriptor representation for presenting the closed-loop system of the polynomial fuzzy model with a parallel distributed compensation (PDC) based fuzzy controller. By the utility of descriptor representation, the guaranteed cost control (GCC) design analysis can utilize polynomial fuzzy slack matrices for obtaining less conservative results. The proposed GCC design is presented as the sum-of-squares (SOS) conditions. The application of polynomial fuzzy slack matrices leads to the double fuzzy summation issue in the control design. Accordingly, the copositive relaxation works out the problem well and is adopted in the control design analysis. The GCC design minimizes the upper limit of a predesignated cost function. According to the performance function, two simulation examples are provided to demonstrate the validity of the proposed GCC design. In these two examples, the proposed design obtains superior results.
1. Introduction
In recent decades, the Takagi–Sugeno (T-S) fuzzy model has been quite celebrated for its ability to represent nonlinear dynamical systems [1], and widely discussed in numerous studies [2,3,4]. The parallel distributed compensation (PDC) technique [5] applying the same membership functions of the T-S fuzzy model for the fuzzy controller is usually utilized for the control design of T-S fuzzy systems. It is well known that the control design is expressed as linear matrix inequality (LMI) conditions for T-S fuzzy systems [6]. Moreover, it is mentioned in [7] that the double fuzzy summation (DFS) issue exists in the control design analysis of T-S fuzzy systems with PDC control.
In [8], the T-S fuzzy system relied on the PDC control is transformed as a descriptor representation. The descriptor representation reduced the DFS issue in the PDC-based control design analysis to a single fuzzy summation issue. This way, the number of control design conditions can be dramatically reduced, especially for the T-S fuzzy systems with many fuzzy rules. Because of the great advantage mentioned above, the descriptor representation-based design for T-S fuzzy systems has been done by some research [9,10,11].
Besides the descriptor representation for T-S fuzzy systems, a polynomial form of the T-S fuzzy model was also proposed as the polynomial fuzzy model (PFM) [12]. Instead of only constants in the T-S fuzzy model, polynomials are contained in the system matrices of the PFM. Control design for polynomial fuzzy systems is usually associated with Lyapunov function candidates, which contain polynomial matrices [13,14,15]. Furthermore, the analysis and design conditions for polynomial fuzzy systems are demonstrated in sum-of-squares (SOS) rather than LMIs. During the decade, the polynomial fuzzy system has been widely studied [16,17,18,19,20,21,22,23,24,25,26,27,28]. A typical type of study for PFM-based control systems aims to acquire relaxed stabilization conditions [23,24,25]. The study [26] investigates the observer-based control for positive PFMs with unknown time delay. In [27], to control velocity and position in marine equipment, nonlinear system dynamics are built in a PFM-based structure. Additionally, the descriptor representation-based design has also been applied to polynomial fuzzy control systems [28].
For T-S and polynomial fuzzy systems, different control issues such as control [18,29,30], robust control [31,32,33], adaptive control [34,35], and optimization control [36,37,38] have been studied. In the optimization control issues, guaranteed cost control (GCC), which minimizes the upper limit of a predesignated cost function, has been applied in diversified fields [39,40,41]. It guarantees the system stability and ensures a performance index value shall never exceed the upper limit. Besides, GCC has also been designed for T-S fuzzy systems [42] and polynomial fuzzy systems [43]. In [44], a descriptor representation-based GCC approach for T-S fuzzy systems is also proposed. Nevertheless, no study contains the GCC design based on the descriptor representation for polynomial fuzzy systems.
This study proposes a descriptor representation-based GCC design methodology for polynomial fuzzy systems. At the beginning of this design methodology, the closed-loop system of PFM applying the PDC-based control is converted into the descriptor representation. By taking advantage of descriptor representation, less conservative results are obtained by introducing fuzzy slack matrices. Because of introducing fuzzy slack matrices, the DFS issue comes about in the control design analysis. Thus, the copositivity relaxation approach is adopted to cope with the DFS issue. The GCC design is represented as an SOS-based optimization problem to minimize the upper limit of a predesignated cost function with a known initial condition. The novelties of this paper are enumerated as follows:
- A descriptor representation-based methodology is proposed for the GCC design of PFM;
- The operation domain is considered in the proposed GCC design for solving the negative highest order term infeasible issue, which frequently happens in the SOS-based GCC design of [43];
- The fuzzy slack matrices are applied to descriptor representation-based GCC design for relaxation.
To the authors’ knowledge, this work is the first study to design GCC for polynomial fuzzy systems based on the descriptor representation. Moreover, the design examples given in this paper demonstrate some superior results compared with the existing design.
Throughout this paper, a matrix () represents is a positive definite (semidefinite) matrix. A function in the form of is defined as a monomial in , where are nonnegative integers [45]. The degree of a monomial is . A linear combination of finite monomials with real coefficients is defined as a polynomial. If the polynomial is an SOS, it means that there exist polynomials such that . Manifestly, a SOS means for all .
2. Descriptor Representation of the Closed-Loop Polynomial Fuzzy System
Consider the PFM [12] as the following equation:
where and are the premise variables; denotes the number of model rules; is the membership function that links the ith model rule and jth premise variable; and are polynomial system matrices in ; is the state vector; is the input vector, and is a column vector whose entries are all monomials in such that iff . The defuzzification output of the PFM (1) can be represented as
where and
with the following properties:
We presume the PFM (1) is built in the following operation domain containing :
where and are the lower and upper bound of the operation domain for the state , respectively. For control design, the PDC-based fuzzy controller sharing the identical membership functions of the PFM (1) is applied:
where is the local feedback gain. In order to turn the fuzzy system into the descriptor representation, the fuzzy controller (1) is altered to
Moreover, the transformation matrix [28] represents the relevance between and as
Applying (7), the descriptor representation for the closed-loop system of the PFM (2) with the PDC-based fuzzy controller (6) can be obtained as
where
From here on, the notation concerning time t is neglected for conciseness. For instance, will be used instead of .
3. Guaranteed Cost Control Design
The objective of this study is to design GCC for the PFM (2) based on the descriptor representation (8). The outputs for the PFM (2) are defined as
where are polynomial output matrices. Moreover, the cost function in the following equation is considered:
where and are positive definite matrices and
The GCC aims to stabilize the closed-loop polynomial fuzzy system and minimize the upper limit of the cost function (10).
For introducing the Lyapunov function candidate, let denote the row indices of whose corresponding row is equal to zero, and define . The Lyapunov function candidate applied in this study is given as
where is a symmetric positive definite polynomial matrix in . In order to apply the descriptor representation (8) for the GCC design, the Lyapunov function candidate (12) is rewritten as
where ,
in which
are fuzzy slack matrices and are polynomial matrices in .
Since the fuzzy slack matrices (15) are introduced for obtaining less conservative results, the problem of DFS appears in the control design analysis. It is well known that copositive relaxation is an efficient method to cope with the DFS issue [19]. The copositive relaxation [45] is described as follows. The copositivity of a given matrix can be verified by checking whether
for and . The copositivity checking can be done by writing and examining if
where , and s is a nonnegative integer.
Based on the descriptor representation (8) and the Lyapunov candidate (12), the proposed GCC design is provided in the subsequent theorem.
Theorem 1.
The closed-loop system of the PFM (2) and the PDC-based fuzzy controller (6) with the outputs (11) is asymptotically stable in the operation domain (4). Furthermore, the upper limit of the cost function (10) is minimized if polynomial matrices and , a symmetric polynomial matrix and polynomials exist to be the solutions for the following optimization problem:
where , and are vectors being independent of ; s is a nonnegative integer; polynomial for , and
in which > 0 for and
Moreover, the local feedback gains of the PDC-based fuzzy controller (5) achieving the GCC can be designed as .
Proof of Theorem 1.
Considering the Lyapunov candidate (12) for which being positive definite is guaranteed if (18) holds. The time derivative of is obtained as the following equation:
Let expresses the kth row of . Since denotes the row indices of whose corresponding row is equivalent to zero, it can be obtained that
for , and
for . Furthermore, due to , the following equation holds [12]:
Moreover, in the operation domain (4), the following inequality is fulfilled:
where being guaranteed by (19). Let
where and for . From the membership function property (3), we have for . Since is a symmetric positive definite matrix and (29) holds in , the following inequality holds for :
The inequality (32) can be rewritten as
Multiply (35) from left and right sides by and respectively, it is obtained that
which is equivalent to
Applying Schur complement and letting , the inequality (37) holds if
which is able to be guaranteed by
Through the copositive relaxation (16) and (17), the condition (38) is fulfilled by (20). As a short summary, if the solutions are found to satisfy (20), then (31) holds for . Since and are positive definite matrices, the condition (31) holding for implies for . Therefore, the closed-loop system of the PFM (2) with the PDC-based fuzzy controller (6) is asymptotically stable. Furthermore, it is noted that (31) is equivalent to
Since the system is asymptotically stable, by integrating the condition (40) from 0 to ∞, it can be obtained that
For minimizing the upper limit of the cost function J, the following relation is considered:
By Schur complement, the inequality
can be rewritten as
which can be guaranteed by (21). In conclusion, if the SOS conditions (18)–(21) are satisfied, then the closed-loop polynomial fuzzy system is asymptotically stable and is fulfilled. Therefore, by minimizing subject to (18)–(21), the GCC can be designed to minimize the upper limit of the cost function J. □
4. Design Examples
In this section, two design examples are given to validate the viability and effectiveness of the proposed GCC design methodology. For a PFM in the first example, the cost function of the proposed descriptor representation-based GCC design methodology is less (better) than the existing GCC approach. The second example clarifies that the proposed Theorem 1 could acquire more relaxed results than the existing SOS-based GCC design method.
4.1. Example 1
The PFM (2) is considered with , and the following system matrices
The membership functions with are given below:
In addition, we consider the following operation domain:
For , and the initial condition , the cost function values J given by the guaranteed cost controllers designed by the proposed and existing methods are shown in Table 1. From Table 1, for the same initial conditions, it could be noticed that the cost function values J of the proposed design are about two-thirds of the values of the existing one [43]. It means that the proposed design is superior to the compared one for this example. Besides, Figure 1 and Figure 2 present the time responses and control inputs of the proposed guaranteed cost controllers with two different initial conditions. It is seen from Figure 1 and Figure 2 that the controlled systems are asymptotically stable.

Table 1.
Comparison of the cost function value J in Example 1.
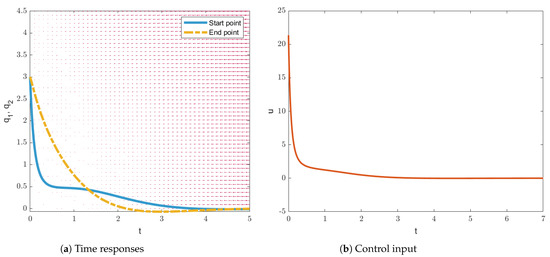
Figure 1.
The time responses and the control input of the proposed guaranteed cost controller for the initial condition in Example 1.
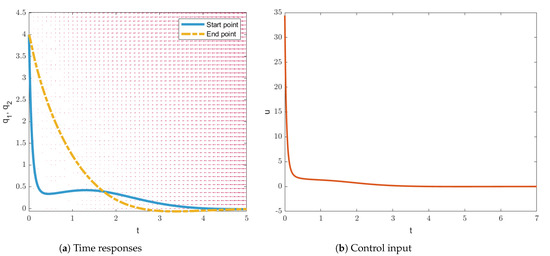
Figure 2.
The time responses and the control input of the offered guaranteed cost controller for the initial condition in Example 1.
4.2. Example 2
The PFM (2) is considered with , and the following system matrices
The membership functions with are given below:
In addition, we consider the following operation domain:
In this case, no solution can be found by applying the existing SOS-based GCC design method (i.e., Theorem 1 of [43]). By contrast, utilizing the proposed Theorem 1 with and , the cost function values J for six different initial conditions are given in Table 2. Therefore, the proposed Theorem 1 has more relaxed results in this example. Moreover, Figure 3 shows the phase plot of trajectories for the six initial conditions mentioned in Table 2. According to Figure 3, the closed-loop system is asymptotically stable. To show the robustness of the proposed design, the two matrices of and are exchanged for further simulation. With the six same initial conditions, Table 3 and Figure 4 show the cost function values J and the phase plot for the simulation results with exchanging and . From Table 3 and Figure 4, it shows that the proposed GCC design is still feasible and the controlled systems are still asymptotically stable.

Table 2.
The cost function values J of the proposed GCC design methodology with six different initial conditions in Example 2.
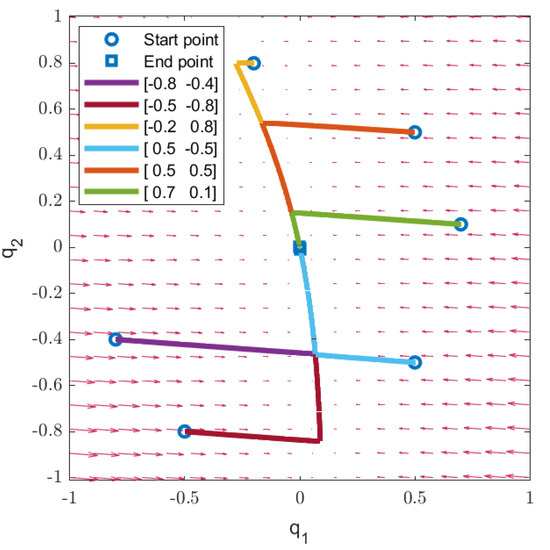
Figure 3.
The phase plot of the control results in Example 2.

Table 3.
The cost function values J of the proposed GCC design methodology by exchanging and in Example 2.
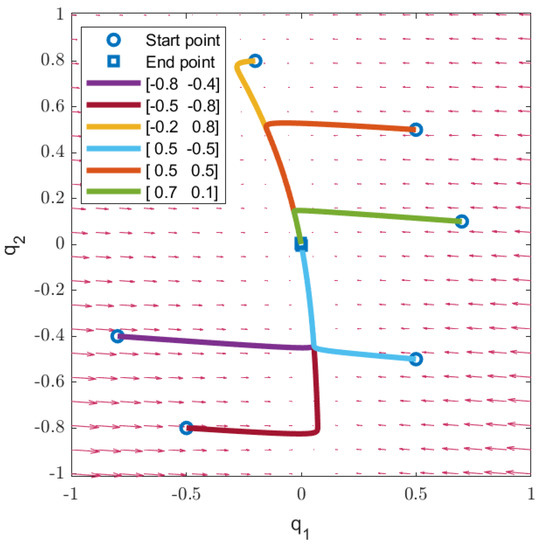
Figure 4.
The phase plot of the control results which exchanging and in Example 2.
5. Conclusions
This paper has presented a descriptor representation-based guaranteed cost design methodology for polynomial fuzzy systems. The design methodology converts the closed-loop polynomial fuzzy system applying the PDC-based fuzzy control into the descriptor representation. The polynomial fuzzy slack matrices are taken into the GCC design analysis to obtain less conservative results by taking advantage of the descriptor representation. The proposed GCC design has relied on the SOS decomposition of multivariate polynomials. The DFS issue comes about in the control design analysis owing to the application of polynomial fuzzy slack matrices. Accordingly, the copositive relaxation is adopted and works out well for the DFS issue in the control design analysis. As a result, the GCC design can minimize the upper limit of a provided cost function for the polynomial fuzzy system. Eventually, two simulation examples have been given to illustrate that the proposed methodology is effectual and has obtained superior results.
Author Contributions
Conceptualization, Y.-J.C., W.-J.W. and K.T.; methodology, Y.-H.S., Y.-J.C. and F.-N.Y.; software, Y.-H.S.; validation, Y.-H.S., Y.-J.C. and F.-N.Y.; formal analysis, Y.-H.S. and Y.-J.C.; investigation, Y.-J.C.; data curation, Y.-H.S.; writing—original draft preparation, Y.-H.S. and Y.-J.C.; supervision, Y.-J.C.; funding acquisition, Y.-J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Technology of Taiwan, under Grant MOST 111-2628-E-155-004.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. B Cybern. 1985, SMC-15, 116–132. [Google Scholar] [CrossRef]
- Wu, H.; Li, H. Finite-Dimensional Constrained Fuzzy Control for a Class of Nonlinear Distributed Process Systems. IEEE Trans. Syst. Man Cybern. B Cybern. 2007, 37, 1422–1430. [Google Scholar] [CrossRef]
- Chen, Y.; Ohtake, H.; Tanaka, K.; Wang, W.; Wang, H.O. Relaxed Stabilization Criterion for T–S Fuzzy Systems by Minimum-Type Piecewise-Lyapunov-Function-Based Switching Fuzzy Controller. IEEE Trans. Fuzzy Syst. 2012, 20, 1166–1173. [Google Scholar] [CrossRef]
- Vu, V.P.; Wang, W.J. Robust observer synthesis for the uncertain large-scale T–S fuzzy system. IET Control Theory Appl. 2019, 13, 134–145. [Google Scholar] [CrossRef]
- Wang, H.O.; Tanaka, K.; Griffin, M.F. An approach to fuzzy control of nonlinear systems: Stability and design issues. IEEE Trans. Fuzzy Syst. 1996, 4, 14–23. [Google Scholar] [CrossRef]
- Feng, G. A Survey on Analysis and Design of Model-Based Fuzzy Control Systems. IEEE Trans. Fuzzy Syst. 2006, 14, 676–697. [Google Scholar] [CrossRef]
- Tanaka, K.; Wang, H.O. Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Tanaka, K.; Ohtake, H.; Wang, H.O. A Descriptor System Approach to Fuzzy Control System Design via Fuzzy Lyapunov Functions. IEEE Trans. Fuzzy Syst. 2007, 15, 333–341. [Google Scholar] [CrossRef]
- Guelton, K.; Bouarar, T.; Manamanni, N. Robust dynamic output feedback fuzzy Lyapunov stabilization of Takagi-Sugeno systems—A descriptor redundancy approach. Fuzzy Sets Syst. 2009, 160, 2796–2811. [Google Scholar] [CrossRef]
- Chadli, M.; Aouaouda, S.; Karimi, H.R.; Shi, P. Robust fault tolerant tracking controller design for a VTOL aircraft. J. Frankl. Inst. 2013, 350, 2627–2645. [Google Scholar] [CrossRef]
- Aouaouda, S.; Chadli, M.; Karimi, H.R. Robust static output-feedback controller design against sensor failure for vehicle dynamics. IET Control Theory Appl. 2014, 8, 728–737. [Google Scholar] [CrossRef]
- Tanaka, K.; Yoshida, H.; Ohtake, H.; Wang, H.O. A Sum-of-Squares Approach to Modeling and Control of Nonlinear Dynamical Systems With Polynomial Fuzzy Systems. IEEE Trans. Fuzzy Syst. 2009, 17, 911–922. [Google Scholar] [CrossRef]
- Sala, A.; AriÑo, C. Polynomial Fuzzy Models for Nonlinear Control: A Taylor Series Approach. IEEE Trans. Fuzzy Syst. 2009, 17, 1284–1295. [Google Scholar] [CrossRef]
- Narimani, M.; Lam, H.K. SOS-Based Stability Analysis of Polynomial Fuzzy-Model-Based Control Systems Via Polynomial Membership Functions. IEEE Trans. Fuzzy Syst. 2010, 18, 862–871. [Google Scholar] [CrossRef]
- Chen, Y.J.; Tanaka, M.; Tanaka, K.; Ohtake, H.; Wang, H.O. Discrete polynomial fuzzy systems control. IET Control Theory Appl. 2014, 8, 288–296. [Google Scholar] [CrossRef]
- Vu, V.P.; Wang, W.J. Polynomial Controller Synthesis for Uncertain Large-Scale Polynomial T–S Fuzzy Systems. IEEE Trans. Cybern. 2021, 51, 1929–1942. [Google Scholar] [CrossRef] [PubMed]
- Vu, V.P.; Wang, W.J. Decentralized Observer-Based Controller Synthesis for a Large-Scale Polynomial T–S Fuzzy System With Nonlinear Interconnection Terms. IEEE Trans. Cybern. 2021, 51, 3312–3324. [Google Scholar] [CrossRef] [PubMed]
- Tsai, S.H.; Wang, J.W.; Song, E.S.; Lam, H.K. Robust H∞ Control for Nonlinear Hyperbolic PDE Systems Based on the Polynomial Fuzzy Model. IEEE Trans. Cybern. 2021, 51, 3789–3801. [Google Scholar] [CrossRef]
- Chen, Y.J.; Tanaka, K.; Tanaka, M.; Tsai, S.H.; Wang, H.O. A Novel Path-Following-Method-Based Polynomial Fuzzy Control Design. IEEE Trans. Cybern. 2021, 51, 2993–3003. [Google Scholar] [CrossRef]
- Xiao, B.; Lam, H.K.; Zhou, H.; Gao, J. Analysis and Design of Interval Type-2 Polynomial-Fuzzy-Model-Based Networked Tracking Control Systems. IEEE Trans. Fuzzy Syst. 2021, 29, 2750–2759. [Google Scholar] [CrossRef]
- Fu, L.; Lam, H.K.; Liu, F.; Xiao, B.; Zhong, Z. Static Output-Feedback Tracking Control for Positive Polynomial Fuzzy Systems. IEEE Trans. Fuzzy Syst. 2022, 30, 1722–1733. [Google Scholar] [CrossRef]
- Yu, G.R.; Chiu, Y.S.; Huang, L.W. Polynomial Fuzzy Control of an Underactuated Robot Using Sum of Squares. In Proceedings of the 12th Asian Control Conference (ASCC), Kitakyushu, Japan, 9–12 June 2019; pp. 895–900. [Google Scholar]
- Lam, H.K.; Lo, J.C. Output Regulation of Polynomial-Fuzzy-Model-Based Control Systems. IEEE Trans. Fuzzy Syst. 2013, 21, 262–274. [Google Scholar] [CrossRef]
- Zhao, Y.; He, Y.; Feng, Z.; Shi, P.; Du, X. Relaxed Sum-of-Squares Based Stabilization Conditions for Polynomial Fuzzy-Model-Based Control Systems. IEEE Trans. Fuzzy Syst. 2019, 27, 1767–1778. [Google Scholar] [CrossRef]
- Meng, A.; Lam, H.K.; Liu, F.; Zhang, C.; Qi, P. Output Feedback and Stability Analysis of Positive Polynomial Fuzzy Systems. IEEE Trans. Syst. Man Cybern. B Cybern. 2021, 51, 7707–7718. [Google Scholar] [CrossRef]
- Han, M.; Lam, H.K.; Li, Y.; Liu, F.; Zhang, C. Observer-based control of positive polynomial fuzzy systems with unknown time delay. Neurocomputing 2019, 349, 77–90. [Google Scholar] [CrossRef]
- Khooban, M.H.; Vafamand, N.; Dragičević, T.; Blaabjerg, F. Polynomial fuzzy model-based approach for underactuated surface vessels. IET Control Theory Appl. 2018, 12, 914–921. [Google Scholar] [CrossRef]
- Yu, F.N.; Chen, Y.J.; Tanaka, M.; Tanaka, K.; Tsai, S.-H. Descriptor Form Design Methodology for Polynomial Fuzzy-Model-Based Control Systems. Int. J. Fuzzy Syst. 2022, 24, 841–854. [Google Scholar] [CrossRef]
- Liu, J.; Wei, L.; Cao, J.; Fei, S. Hybrid-driven H∞ filter design for T–S fuzzy systems with quantization. Nonlinear Anal. Hybrid Syst. 2019, 31, 135–152. [Google Scholar] [CrossRef]
- Tsai, S.H.; Jen, C.Y. H∞ Stabilization for Polynomial Fuzzy Time-Delay System: A Sum-of-Squares Approach. IEEE Trans. Fuzzy Syst. 2018, 26, 3630–3644. [Google Scholar] [CrossRef]
- Teng, L.; Wang, Y.; Cai, W.; Li, H. Robust Fuzzy Model Predictive Control of Discrete-Time Takagi–Sugeno Systems With Nonlinear Local Models. IEEE Trans. Fuzzy Syst. 2018, 26, 2915–2925. [Google Scholar] [CrossRef]
- Yang, W.; Feng, G.; Zhang, T. Robust Model Predictive Control for Discrete-Time Takagi–Sugeno Fuzzy Systems With Structured Uncertainties and Persistent Disturbances. IEEE Trans. Fuzzy Syst. 2014, 22, 1213–1228. [Google Scholar] [CrossRef]
- Tanaka, K.; Tanaka, M.; Chen, Y.J.; Wang, H.O. A New Sum-of-Squares Design Framework for Robust Control of Polynomial Fuzzy Systems With Uncertainties. IEEE Trans. Fuzzy Syst. 2016, 24, 94–110. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Du, H.; Karimi, H.R. Adaptive Sliding Mode Control for Takagi–Sugeno Fuzzy Systems and Its Applications. IEEE Trans. Fuzzy Syst. 2018, 26, 531–542. [Google Scholar] [CrossRef]
- Chen, C.; Xu, J.; Lin, G. Fuzzy adaptive control particle swarm optimization based on T-S fuzzy model of maglev vehicle suspension system. J. Mech. Sci. Technol. 2020, 34, 43–54. [Google Scholar] [CrossRef]
- de Sousa, M.A.T.; Madrid, M.K. Optimization of Takagi-Sugeno fuzzy controllers using a genetic algorithm. In Proceedings of the Ninth IEEE International Conference on Fuzzy Systems, San Antonio, TX, USA, 7–10 May 2000; pp. 30–35. [Google Scholar]
- Wang, F.; Wang, H.; Zhang, Y.; Guo, X. T-S Fuzzy-Based Optimal Control for Minimally Invasive Robotic Surgery with Input Saturation. J. Sens. 2018. [Google Scholar] [CrossRef]
- Kumaresan, N. Optimal Control for Stochastic Singular Integro-Differential Takagi-Sugeno Fuzzy System Using Ant Colony Programming. Filomat 2012, 26, 415–426. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, Y.; Su, H.; Liu, C. Event-Driven Guaranteed Cost Control Design for Nonlinear Systems With Actuator Faults via Reinforcement Learning Algorithm. IEEE Trans. Fuzzy Syst. 2020, 50, 4135–4150. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, H.; Yang, F.; Zhan, X.; Peng, C. Event-Triggered Asynchronous Guaranteed Cost Control for Markov Jump Discrete-Time Neural Networks With Distributed Delay and Channel Fading. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3588–3598. [Google Scholar] [PubMed]
- Zeng, T.; Ren, X.; Zhang, Y.; Li, G.; Na, J. An Integrated Optimal Design for Guaranteed Cost Control of Motor Driving System With Uncertainty. IEEE/ASME Trans. Mechatron. 2019, 24, 2606–2615. [Google Scholar] [CrossRef]
- Wu, Z.G.; Dong, S.; Shi, P.; Su, H.; Huang, T.; Lu, R. Fuzzy-Model-Based Nonfragile Guaranteed Cost Control of Nonlinear Markov Jump Systems. IEEE Trans. Syst. Man Cybern. B Cybern. 2017, 47, 2388–2397. [Google Scholar] [CrossRef]
- Tanaka, K.; Ohtake, H.; Wang, H.O. Guaranteed Cost Control of Polynomial Fuzzy Systems via a Sum of Squares Approach. IEEE Trans. Syst. Man Cybern. B Cybern. 2009, 39, 561–567. [Google Scholar] [CrossRef]
- Sun, C.; Wang, W.; Chen, Y. A descriptor system approach to fuzzy guaranteed cost control system design. In Proceedings of the 2009 IEEE International Conference on Fuzzy Systems, Jeju, Korea, 20–24 August 2009; pp. 1288–1293. [Google Scholar]
- Prajna, S.; Papachristodoulou, A.; Wu, F. Nonlinear control synthesis by sum of squares optimization: A Lyapunov-based approach. In Proceedings of the 5th Asian Control Conference, Melbourne, VIC, Australia, 20–23 July 2004; pp. 157–165. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).