Minimizing Foaming and Bulking in Activated Sludge with Bacteriophage Treatment: A Review of Mathematical Modeling

Abstract

The interest in the ability of phages to control bacterial populations has extended from medical applications into the fields of agriculture, aquaculture, and the food industry. In particular, several authors have proposed using bacteriophages as an alternative method to control foaming and bulking in wastewater treatment. This strategy has shown successful results at the laboratory scale. However, this technology is still in development, and there are several challenges to overcome before bacteriophages can be widely used to control foaming and bulking in pilot or larger-scale treatment plants. Several models of the infection mechanisms in individual bacteria–phage pairs have been reported, i.e., for controlled systems with only one bacterium species in the presence of one phage species. However, activated sludge treatment systems largely differ from this situation, which opens a large horizon for future research. Mathematical models will play a key role in this development process, and this review offers an overview of the proposed models: their applications, potential, and challenges. A particular focus is placed on the model properties, such as parameter identifiability and states’ observability, which are essential for process prediction, monitoring, or dynamic optimization.

1. Introduction

Clean, accessible water for all is an essential part of the world we want to live in, and there is enough freshwater on the planet to achieve this. However, more than 2 billion people are living with the risk of reduced access to freshwater resources, and by 2050, at least one in four people is likely to live in a country affected by chronic or recurring shortages of fresh water [1]. Drought afflicts some of the world’s poorest countries, worsening hunger and malnutrition. Fortunately, there has been significant progress made in the past decade regarding drinking sources and sanitation, whereby over 90% of the world’s population now has access to improved drinking water sources [1].

Nevertheless, more than 80 percent of wastewater resulting from human activities is discharged into rivers or sea without any pollution removal, a fact that generates concern [1]. Therefore, wastewater treatment, which is used to remove contaminants from wastewater or sewage and convert it into an effluent that can be returned to the water cycle with minimum impact on the environment or be directly reused, is receiving ever-increasing interest.

The Activated Sludge (AS) process has been used to treat industrial and municipal wastewaters for nearly a century. Currently, this process is the most widely implemented for wastewater treatment. AS systems can reach organic material removal rates between 85% and 95% at the end of secondary treatment [2]. Despite the significant efficiency of AS treatment, the process is not without problems. The most severe issues are caused by filamentous bacteria, with phenomena known as bulking and foaming. In the bulking process, the sludge in the aeration basin does not sediment and develops a biological foam on the surface. The foam is characterized as persistent, viscous, and brown in color in the foaming process. Due to these problems, the effluent is contaminated, the aeration basin population drops because the sludge cannot be recirculated, and noxious odors are formed when the foam (which contains organic material) is degraded outside of the AS system [3].

While several technical strategies exist for controlling these problems, e.g., the addition of chlorine or hydrogen peroxide to the recycled AS, the alteration of the dissolved oxygen concentration or the waste inflow in the aeration basin to modify the F/M ratio, the addition of principal nutrients (such as nitrogen and phosphorus) or trace metals and growth factors, and, more recently, the addition of inorganic talc or coagulating polymers, they have, however, not been proven effective in all cases. Their associated costs are relatively high, and their use affects the effluent quality, even when they are effective [4,5,6,7,8,9]. At the industrial level, large amounts of chlorine are used. Adding chlorine is effective in 63% of cases. Still, it can potentially create toxic chlorinated organic compounds in low concentrations and, therefore, can be counterproductive to the water treatment process. Manipulation of the sludge recycling flow and increasing the aeration to control filamentous bacteria have associated operational costs and are ineffective considering the influent’s complexity [3,10,11].

Bacteriophages are viruses that infect and lyse bacteria. Interest in the ability of phages to control bacterial populations has extended from medical applications into the fields of agriculture, aquaculture, and the food industry [12,13,14,15,16,17,18,19,20,21,22]. Phage treatments have the potential to control environmental wastewater process problems such as foaming and bulking in activated sludge plants [23,24].

There are several academic studies where bacteriophages were proposed to treat bulking or foaming in activated sludge plants as a biological control, unlike the traditional chemical treatment. In these studies, bacteriophages have been validated to eliminate the foam-producing filamentous bacteria. The lytic phages for these bacteria can reduce the number of bacterial cells causing foaming below the threshold required for a stable foam to occur [25,26].

However, the successful application of phage therapy to wastewater treatment does require further understanding of wastewater microbial community dynamics and interactions in order to become effective solutions to wastewater treatment problems and optimization [27,28,29].

Mathematical modeling of microbial populations has a long history of application in ecology and biology. Although consideration has been given to modeling bacterial populations affected by phage activity, this has not been a major focus of the research field, particularly in wastewater treatment.

A review of mathematical modeling of bacteria–phage interactions is available in [30]. The motivation behind this work is to build upon this review, with a focus on the wastewater treatment on the one side and on important mathematical model properties, such as identifiability, that must be taken into account in order to estimate the model parameters from experimental data while providing a proper validation. Of course, there is paramount importance for further use of the models for dynamic prediction and process monitoring.

This paper is organized as follows; first, a review of the models published to date is presented; based on the literature, a candidate model of bacteria and phage populations was developed. The study of the model is composed of simulations, estimation of equilibrium points, the identifiability, and the observability of the model. Finally, some practical computational applications of the models, highlighting their challenges and perspectives, are presented, emphasizing the importance of their study.

2. Phage Treatment: Description and Reported Applications

Bacteriophages are usually prepared at a laboratory scale in shake flasks. These protocols are adjusted to batch cultures with low cell densities and regulation conditions producing low phage concentration. Bioreactors in batch mode are used when a higher bacteriophage concentration is required. Although batch mode is operationally simpler than the continuous mode, sterile conditions in a higher cell density mean increased cost [13,15,18,31].

The microorganisms that constitute the AS are protozoans, fungi, algae, filamentous organisms, viruses, and bacteria, the latter being the dominant group responsible for the more significant part of the process (90% to 95%) [32].

More than 300 species of bacteria have been isolated from AS systems. Filamentous bacteria are common in ASs, and a moderate presence of these organisms contributes to proper consistency in the flocs. Filamentous bacteria are capable of connecting with each other to form flocs, an important characteristic of ASs that allows for a highly efficient secondary sedimentation process and, therefore, greater transparency and higher quality in the final effluent [24,33].

An increase in filamentous bacteria can prevent the sludge from settling appropriately (sludge bulking) or can generate persistent foams, up to 1 m thick in extreme cases, covering the aeration basins [34]. Due to these processes, some of the sludge can leave the sedimentation system, contaminating the treated water and lowering the efficiency of the process.

Viral communities in the AS systems are incredibly diverse. Compared to bacterial community analysis, research on viral communities in wastewater or wastewater treatment systems is limited. There is an estimated amount of 108–109 phage genotypes in 1 mL of activated sludge, which is a number comparable to or greater than the number of phages found in most aquatic systems [34].

Therefore, using phages to control environmental wastewater processes such as foaming and bulking in activated sludge plants could improve effluent and sludge emissions into the environment [24,25].

Several academic studies have proposed bacteriophage use to treat bulking or foaming in activated sludge plants as a biological control, unlike the traditional chemical treatment. In these studies, the use of bacteriophages has been validated to eliminate the foaming-producing filamentous bacteria, such as Haliscomenobacter hydrossis, Sphaerotilus natans, Tetrasphaera jenkinsii, Gordonia, Beggiatoa, Nocardia, and Nostocoida limícola. The lytic phages for these bacteria can be isolated from activated sludge systems such as the GTE7 phage (Siphoviridae family) that has lytic activity on the Gordonia species and some Nocardia species, which reduce the number of bacterial cells causing foaming below the threshold required for a stable foam to occur. As we can see in

Table 1. Bacteriophages capable of lysing filamentous bacteria model.

Filamentous Bacteria Model	Bacteriophage	Authors
Haliscomenobacter hydrossis, Sphaerotilus natans	SN-phage	Choi et al. [25]
Gordonia terrae, Gordonia malaquae, Gordonia australis, Gordonia amictia and Nocardia nova, Nocaridia asteroides	GTE7	Petrovski et al., Liu et al. [29,35]
Skermania piniformis, Sphaerotilus natans	SPI1	Dyson et al. [36]
Haliscomenobacter	Phage from Myoviridae family	Kotay et al. [23]

, bacteriophages can infect a single or multiple hosts [25,26].

However, the successful application of phage therapy to wastewater treatment does require further understanding of wastewater microbial community dynamics and interactions. Success would also depend on the accurate identification of problem bacteria, effective isolation and unbiased enrichment of phages, and the ability of phages to penetrate flocs and remain infective in situ. Strategies to counter host cell resistance must also be developed. Thus, substantial research is required before phage therapy can be applied successfully to wastewater treatment plants. With a greater understanding of the microbial ecology of wastewater treatment systems, phages may become effective solutions to wastewater treatment problems and optimization [27,28,29]. In addition, a mathematical model can help control the process on a large scale, and the inclusion of a predation mechanism is a new addition to the existing activated sludge models [37]. Much of the study of phage–bacteria interactions has been grounded in pure rather than applied concerns, and models have tended to focus more on ecological and evolutionary issues than on the effectiveness of a particular phage treatment in controlling a bacterial population [28].

3. An Overview of Bacteria–Phage Population Models

To introduce dynamic models of bacteria–phage systems, a good approach is to introduce the concept of compartments, representing the different components of the system, and to go from simple to more detailed models.

As a start, the growth of bacteria, which can be represented by different kinetic laws, has to be described. The kinetic expressions that have been most commonly used in modeling bacterial growth include the Malthusian [38]:

$$\frac{dX}{dt}={\mu }_{max}X,$$

(1)

and Logistic [39]:

$$\frac{dX}{dt}={\mu }_{max}(1-\frac{X}{X_{max}})X,$$

(2)

expressions, where X is the concentration of bacteria, ${\mu }_{max}$ the maximum specific growth rate, and $X_{max}$ is the carrying capacity of the environment. The Malthusian model is appropriate to describe the early exponential growth but has limited applicability. The logistic model has the interesting added feature that it provides an equilibrium state at the carrying capacity, which represents the maximum population that can be sustained by the resources of the environment.

The next logical level is to explain the growth by the consumption of a limiting substrate (S) as represented by the Monod law [40]:

$$\frac{dX}{dt}={\mu }_{max}\left(\frac{S}{K_S+S}\right)X,$$

(3)

where $K_S$ is the half-saturation coefficient.

However, attempts to fit the growth of filamentous organisms in activated sludge with simple models such as those mentioned above have not been successful, due to interactions between microorganisms. Microbial growth in an activated sludge plant occurs in the presence of a diversity of organisms, among which antagonistic and symbiotic relationships exist. To take account of the interaction with a predator, it is necessary to turn to predator–prey models as proposed in the seminal work of [41,42]. This corresponds to a two-compartment model:

$$\begin{array}{cc}\hfill \frac{dX}{dt}& ={\mu }_1\left(P\right)X=(\alpha -\delta P)X,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \frac{dP}{dt}& ={\mu }_2\left(X\right)P=(-\phi +\eta X)P,\hfill \end{array}$$

(5)

where X and P are the prey and predator populations, respectively, and ${\mu }_1\left(P\right)$ and ${\mu }_2\left(X\right)$ are specific growth rates with parameters $\alpha$, $\delta$, $\phi$, and $\eta$ describing the natural growth or decay and the interaction between the two species. This model can be modified in various ways, for instance, by introducing logistic growth, limited predation, the consumption of a limiting substrate following a Monod law, etc.

Campbell [43] proposed such a model under the assumption that a bacterium can only be infected by one phage and the burst size, i.e., the average number of newly synthesized phages released from a single infected bacterium is constant. In a batch (no in- and outflow) reactor, the model of the system could be first written as follows:

$$\begin{array}{cc}\hfill \frac{dX}{dt}& =\mu \left(X\right)X-\delta XP={\mu }_{max}(1-\frac{X}{X_{max}})X-\delta XP,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \frac{dP}{dt}& =-\delta XP+\beta \delta X(t-\tau )P(t-\tau )-{\nu }_{p}P,\hfill \end{array}$$

(7)

where the susceptible bacteria population X grows at a specific rate $\mu \left(X\right)$ in the form of a logistic equation and decays according to the phage infection rate $\delta XP$, where $\delta$ is the adsorption rate which describes the number of phages that bind to the bacterium [44]. The number of free phage particles decays accordingly at the rate $-\delta XP$, in addition to the natural phage inactivation $-{\nu }_{p}P$, and increases in proportion to the production of infected cells with the burst size $\beta$. The production of new phages is not an instantaneous phenomenon, but takes place after a latency phase $\tau$.

Remark 1.

The consideration of a latency phase τ results in a Delay Differential Equation (DDE) system, which is significantly more difficult to solve and to analyze.

To better understand the concept of a latency phase, it is necessary to delve into its principles. The latent period $\tau$ represents the time elapsing from the instant of infection, i.e., when the content of the virus head is injected inside the bacterium, to the instant of the bacterium cell wall lysis, at which a number of copies of assembled phages are released in solution [45]. The processes that occur during the latent period include [46]:

• The translocation of viral genetic material from the periplasm into the cytoplasm;
• The replication of genetic material and production of virus particle components;
• The packaging of viral genomes into viral heads;
• The disruption of the cell surface and release of viral progeny.

In this time span, the eclipse period E is the time it takes for intact virus particles to appear [47], and the moment at which cellular lysis would lead to the potential continuation of a viral infection. The maturation rate R represents the increase in phage progeny per unit of time, occurring in the lapse of time $\tau -E$, and the burst size $\beta$ determines the number of phages released in the event of bacterial lysis or rupture [48,49]. The relationship between these variables is described by the following equation:

$$\beta =(\tau -E)R$$

(8)

Burst size and the phage generation time are controlled by the phage latent period, with a directly proportional relation between burst size and latent period, i.e., greater burst sizes associated with longer latent periods [48].

Levin et al. [50] extended the previous model by considering two distinct bacterial populations, i.e., the susceptible bacteria $X_S$ and the infected bacteria $X_I$, both feeding on a limiting resource S. They also pointed out that Campbell’s model did not take the removal of infected bacteria due to dilution in a continuous process into account. The proposed model takes the following form:

$$\begin{array}{cc}\hfill \frac{d{X}_S\left(t\right)}{dt}& =\mu \left(S\right)X_S\left(t\right)-\delta X_S\left(t\right)P\left(t\right)-D{X}_S\left(t\right),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \frac{d{X}_I\left(t\right)}{dt}& =\delta X_S\left(t\right)P\left(t\right)-e^{D\tau }\delta X_S(t-\tau )P(t-\tau )-D{X}_I\left(t\right),\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \frac{dP\left(t\right)}{dt}& =-\delta X_S\left(t\right)P\left(t\right)+\beta e^{D\tau }\delta X_s(t-\tau )P(t-\tau )-{\nu }_{p}P\left(t\right)-DP\left(t\right),\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \frac{dS\left(t\right)}{dt}& =D(S_{in}-S\left(t\right))-{\nu }_s\mu \left(S\right)X_T\left(t\right)=D(S_{in}-S\left(t\right))-{\nu }_s\mu \left(S\right)(X_S\left(t\right)+X_I\left(t\right)).\hfill \end{array}$$

(12)

where D is the dilution rate and the factor $e^{(-D\tau )}$ represents the dilution effect on a time span $\tau$ (the delayed populations should therefore be divided by this factor), and $S_{in}$ is the substrate concentration in the feed. The growth rate $\mu \left(S\right)$ could follow various laws, e.g., the Monod law.

Remark 2.

An underlying assumption is that the susceptible bacteria grow and the infected bacteria maintain (without growth) at the same rate μ.

Anderson et al. [51] developed a population model of microparasites and invertebrate hosts. This model extends the previous one by the consideration of a death phenomenon affecting the susceptible and infected individuals, a recovery of infected individuals to susceptible ones, and a lysis of infected cells.

$$\begin{array}{cc}\hfill \frac{d{X}_S\left(t\right)}{dt}& =\mu (X_S\left(t\right)+X_I\left(t\right))-\delta X_S\left(t\right)P\left(t\right)-\gamma X_S\left(t\right)+\rho X_I\left(t\right),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill \frac{d{X}_I\left(t\right)}{dt}& =\delta X_S\left(t\right)P\left(t\right)-\eta X_I\left(t\right)-\gamma X_I\left(t\right)-\rho X_I\left(t\right)\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & =\delta X_S\left(t\right)P\left(t\right)-(\eta +\gamma +\rho )X_I\left(t\right),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \frac{dP\left(t\right)}{dt}& =-\delta X_S\left(t\right)P\left(t\right)+\eta X_I\left(t\right),\hfill \end{array}$$

(16)

where $\gamma$ is the death rate of the susceptible and infected bacteria. $\eta$ is the lysis rate giving rise to the release of phages, and $\rho$ is the recovery rate

Remark 3.

This model does not consider a limiting substrate, nor dilution effects. It assumes that both susceptible and infected bacteria grow and die at the same rates, μ and γ, respectively. Interestingly, it relates the lysis and phage production directly to the infected bacteria population, avoiding the explicit consideration of a latency period applied to the susceptible and phage populations. Mathematically speaking, the delay τ is replaced by a time constant $1/\eta$, which has two advantages: (a) the model equations are simple ordinary differential equations and (b) the lysis rate can be different from the infection rate. However, the model assumes that the production of phages also occurs at the same rate η.

Later on, Beretta et al. [45] considered a similar model, with a logistic factor for the growth phenomenon (where $X_{max}$ is the carrying capacity), no recovery rate, but a parameter $\beta$ for the production of phages:

$$\begin{array}{cc}\hfill \frac{d{X}_S\left(t\right)}{dt}& ={\mu }_{max}(1-\frac{X_S\left(t\right)+X_I\left(t\right)}{X_{max}})X_S\left(t\right)-\delta X_S\left(t\right)P\left(t\right),\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \frac{d{X}_I\left(t\right)}{dt}& =\delta X_S\left(t\right)P\left(t\right)-\eta X_I\left(t\right),\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \frac{dP\left(t\right)}{dt}& =-\delta X_S\left(t\right)P\left(t\right)+\beta \eta X_I\left(t\right)-{\nu }_{p}P\left(t\right).\hfill \end{array}$$

(19)

On the other hand, Payne et al. [52] considered a slightly different structure, where both bacteria populations are growing at the same rate $\mu$:

$$\begin{array}{cc}\hfill \frac{d{X}_S\left(t\right)}{dt}& =\mu X_S\left(t\right)-\delta X_S\left(t\right)P\left(t\right),\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill \frac{d{X}_I\left(t\right)}{dt}& =\mu X_I\left(t\right)+\delta X_S\left(t\right)P\left(t\right)-\eta X_I\left(t\right),\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill \frac{dP\left(t\right)}{dt}& =-\delta X_S\left(t\right)P\left(t\right)+\beta \eta X_I\left(t\right)-{\nu }_{p}P\left(t\right).\hfill \end{array}$$

(22)

Remark 4.

The latter models do no longer consider a latency phase, and have the advantage of being described by ordinary differential equations. They differ mostly in the expression of the growth, infection, recovery, lysis, and phage production rates.

Siekmann et al. [53] extended the model of Beretta et al. [45] by adding an evolution equation for viruses $P_I\left(t\right)$ that are confined in their host:

$$\begin{array}{cc}\hfill \frac{d{X}_S\left(t\right)}{dt}& ={\mu }_{max}(1-\frac{X_S\left(t\right)+X_I\left(t\right)}{X_{max}})X_S\left(t\right)-\delta X_S\left(t\right)P\left(t\right),\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill \frac{d{X}_I\left(t\right)}{dt}& =\delta X_S\left(t\right)P\left(t\right)-\eta X_I\left(t\right),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill \frac{d{P}_I\left(t\right)}{dt}& ={\mu }_{max}{P}_I\left(t\right)-c\frac{P_I^2\left(t\right)}{X_I\left(t\right)}-\alpha \eta P_I\left(t\right)+\delta X_S\left(t\right)P\left(t\right),\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill \frac{dP\left(t\right)}{dt}& =\alpha \eta P_I\left(t\right)-\delta X_S\left(t\right)P\left(t\right)-{\nu }_{p}P\left(t\right),\hfill \end{array}$$

(26)

where $0\le \alpha \le 1$.

Remark 5.

This model assumes a logistic growth of the susceptible bacteria (carrying capacity $X_{max}$) and of the host viruses (carrying capacity $X_I$). It is, however, questionable why the same unlimited growth rate ${\mu }_{max}$ applies to both $X_S$ and $P_I$, since $P_I$ is related to $X_I$, which has no growth.

In systems where infection occurs, the possibility exists that the pathogen becomes resistant to the treatment (e.g., bacteria may become resistant to antibiotics, which must then be administered in specific doses within a certain time to prevent the occurrence of this phenomenon). Similarly, the susceptible bacteria could become resistant to the phage treatment due to natural mutation. Cairns et al. [28] included a mutation rate $\epsilon$ from susceptible $X_S\left(t\right)$ to resistant bacteria $X_R\left(t\right)$, leading to:

$$\begin{array}{cc}\hfill \frac{d{X}_S\left(t\right)}{dt}& =\mu X_S\left(t\right)-\delta X_S\left(t\right)P\left(t\right)-\epsilon X_S\left(t\right),\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill \frac{d{X}_I\left(t\right)}{dt}& =\delta X_S\left(t\right)P\left(t\right)-\delta X_S(t-\tau )P(t-\tau ),\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill \frac{d{X}_R\left(t\right)}{dt}& =\mu X_R\left(t\right)+\epsilon X_S\left(t\right),\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill \frac{dP\left(t\right)}{dt}& =-\delta X_S\left(t\right)P\left(t\right)+\beta \delta X_S(t-\tau )P(t-\tau )-{\nu }_{p}P\left(t\right).\hfill \end{array}$$

(30)

Santos et al. [54] slightly modified the previous model by including a limiting substrate as in some of the earlier models Levin et al. [50]:

$$\begin{array}{cc}\hfill \frac{d{X}_S\left(t\right)}{dt}& =\mu \left(S\right)X_S\left(t\right)-\delta X_S\left(t\right)P\left(t\right),\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill \frac{d{X}_I\left(t\right)}{dt}& =\delta X_S\left(t\right)P\left(t\right)-\delta X_S(t-\tau )P(t-\tau ),\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill \frac{d{X}_R\left(t\right)}{dt}& =\mu \left(S\right)X_R\left(t\right),\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill \frac{dP\left(t\right)}{dt}& =-\delta X_S\left(t\right)P\left(t\right)+\beta \delta X_S(t-\tau )P(t-\tau ),\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill \frac{dS\left(t\right)}{dt}& =-{\nu }_s\mu X_T\left(t\right)=-{\nu }_s\mu (X_S\left(t\right)+X_I\left(t\right)+X_R\left(t\right)).\hfill \end{array}$$

(35)

where $\mu \left(S\right)$ is a Monod law.

Having presented an overview of existing models, the objective of the next section is to propose a simple model that contains most of the distinctive features highlighted in previous studies and would be appropriate to describe the bacteria–phages system in the context of wastewater treatment.

4. A Candidate Model of Bacteria and Phage Populations

A simple model, which would be suitable to describe experimental results in the context of wastewater treatment could take the following factors into account:

• The bacteria–phage populations develop in a bioreactor with a limiting substrate and dilution rate (which can be set to zero for batch operation);
• The growth kinetics $\mu \left(S\right)$ of the susceptible bacteria can take various forms, notably the Monod law;
• The infected bacteria do not grow but are sustained using the same substrate at a rate m (a feature that has not been described in the earlier models, which either assume growth or maintenance at the same rate);
• The infection rate is proportional to $X_S\left(t\right)P\left(t\right)$ with a rate $\delta$;
• $\eta$ is the lysis rate (the lysis and release phenomena are represented by rate equations rather than by introducing a delay, which is a mathematical idealization complexifying the model structure);
• $\beta$ is the release rate of new phages;
• ${\nu }_P$ is the natural decay of the free phages;
• Natural decay rates of the susceptible and infected bacteria (which should probably be set to different values in contrast with the earlier models) could be easily introduced but are not taken into consideration, as probably negligible with respect to the other phenomena.

The resulting model equations are given by:

$$\begin{array}{cc}\hfill \frac{d{X}_S\left(t\right)}{dt}& =\mu \left(S\right)X_S\left(t\right)-\delta X_S\left(t\right)P\left(t\right)-D{X}_S\left(t\right),\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill \frac{d{X}_I\left(t\right)}{dt}& =\delta X_S\left(t\right)P\left(t\right)-\eta X_I\left(t\right)-D{X}_I\left(t\right),\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill \frac{dP\left(t\right)}{dt}& =-\delta X_S\left(t\right)P\left(t\right)+\beta \eta X_I\left(t\right)-{\nu }_{p}P\left(t\right)-DP\left(t\right),\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill \frac{dS\left(t\right)}{dt}& =-{\nu }_s\mu \left(S\right)X_S\left(t\right)-m{X}_I\left(t\right)+D(S_{in}-S\left(t\right)).\hfill \end{array}$$

(39)

This model has the advantage of being in the form of a first-order Ordinary Differential Equation (ODE) system, thus amenable to a classical state-space representation:

$$\begin{array}{cc}\hfill \dot{x}& =f(x,u)\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill y& =Cx\hfill \end{array}$$

(41)

with the following definitions corresponding to Equations (36)–(39):

$$x=\left[\begin{array}{c}{X}_S\\ X_I\\ P\\ S\end{array}\right],f\left(x\right)=\left[\begin{array}{c}{f}_{X_S}\left(x\right)\\ f_{X_I}\left(x\right)\\ f_P\left(x\right)\\ f_P\left(x\right)\end{array}\right]$$

(42)

The vector $y\left(t\right)$ represents the set of measurements that can be collected either for parameter identification purposes or for the design of software sensors monitoring the bioreactor. The matrix C describes the selection or linear combination of specific state variables. Note that this matrix can be different in the two above-mentioned tasks. Indeed, parameter estimation can be based on offline and online measurements, whereas software sensors can only use online measurements. In the following, we focus attention on the model analysis, including equilibrium points, stability, identifiability, and observability, which are of paramount importance in the future exploitation of the model.

This analysis will be conducted for the parameter values given in

Table 2. Model parameter values.

	Parameter	Value
Bacteria growth	${\mu }_{max}$  (h${}^{-1}$)	0.4298
	$K_M$  (mg mL${}^{-1}$)	0.39
Bacteriophages proliferation (Infection)	$\delta$  (mL CFU${}^{-1}$ PFU${}^{-1}$ h${}^{-1}$)	$3.02\times {10}^{-9}$
	$\beta$  (PFU CFU${}^{-1}$)	110
	$\eta$ (h${}^{-1}$)	0.5
Other parameters	${\nu }_S$ (mg mL${}^{-1}$)	$1.23\times {10}^{-6}$
	${\nu }_P$ (h${}^{-1}$)	0.01032
	m (mg CFU${}^{-1}$ h${}^{-1}$)	$1\times {10}^{-6}$
Operational parameters	$S_{in}$ (mg mL${}^{-1}$)	4
	D (h${}^{-1}$)	0.1

CFU: Colony-Forming Unit. PFU: Plaque-Forming Unit.

, where the parameters ${\mu }_{max}$, $\delta$, and $\beta$ were estimated experimentally for the pair Gordonia westfálica and its phage (previously isolated and characterized from a sample of foaming in laboratories at PUCV). These values are within the range of values reported in the literature [44,48,55]. The values of the other parameters are taken from literature [28,52,54].

4.1. Equilibrium Points and Stability

The equilibrium points are the solution of the nonlinear system of algebraic equations:

$$f\left(\overline{x}\right)=0,$$

(43)

where $\overline{x}\in \mathbb{R}$ is an equilibrium point.

The analysis reveals that there are three possible equilibrium points, whose location and stability may depend on the value of the dilution rate:

• Point 1 is the trivial equilibrium, where there is no bacteria and no phage (all populations are extinct);
• Point 2 corresponds to a population of bacteria with no phage and no infection, feeding on a substrate (this situation corresponds to a reactor with no phage treatment);
• Point 3 represents the possible coexistence between the different populations, which is a priori the equilibrium point of interest for our analysis.

The equilibrium points are presented in Figure 1 as a function of the dilution rate.

The evolution of equilibrium point 2 shows that the wash-out occurs when $D>\mu \left(S\right)$ (around D = 0.3901 h${}^{-1}$).

Point 3 is interesting to study, as it corresponds to the phage treatment and the coexistence of the several populations. At low dilution rates, the susceptible bacteria population is much smaller than with no treatment. The infected bacteria population is washed out for dilution rates larger than 0.3451 h${}^{-1}$.

The several equilibrium points have to be analyzed with respect to their stability. An equilibrium point which is locally stable will attract trajectories starting from initial conditions located in a close neighborhood (this neighborhood is called the region of attraction of the equilibrium point).

Local stability is studied by evaluating the Jacobian matrix:

$$A=\left[\begin{array}{cccc}\frac{\partial f_{X_S}}{\partial X_S}& \frac{\partial f_{X_S}}{\partial X_I}& \frac{\partial f_{X_S}}{\partial P}& \frac{\partial f_{X_S}}{\partial S}\\ \frac{\partial f_{X_I}}{\partial X_S}& \frac{\partial f_{X_I}}{\partial X_I}& \frac{\partial f_{X_I}}{\partial P}& \frac{\partial f_{X_I}}{\partial S}\\ \frac{\partial f_P}{\partial X_S}& \frac{\partial f_P}{\partial X_I}& \frac{\partial f_P}{\partial P}& \frac{\partial f_P}{\partial S}\\ \frac{\partial f_S}{\partial X_S}& \frac{\partial f_S}{\partial X_I}& \frac{\partial f_S}{\partial P}& \frac{\partial f_S}{\partial S}\end{array}\right]$$

(44)

at the equilibrium point under consideration. The eigenvalues of A are represented as a function of D in Figure 2.

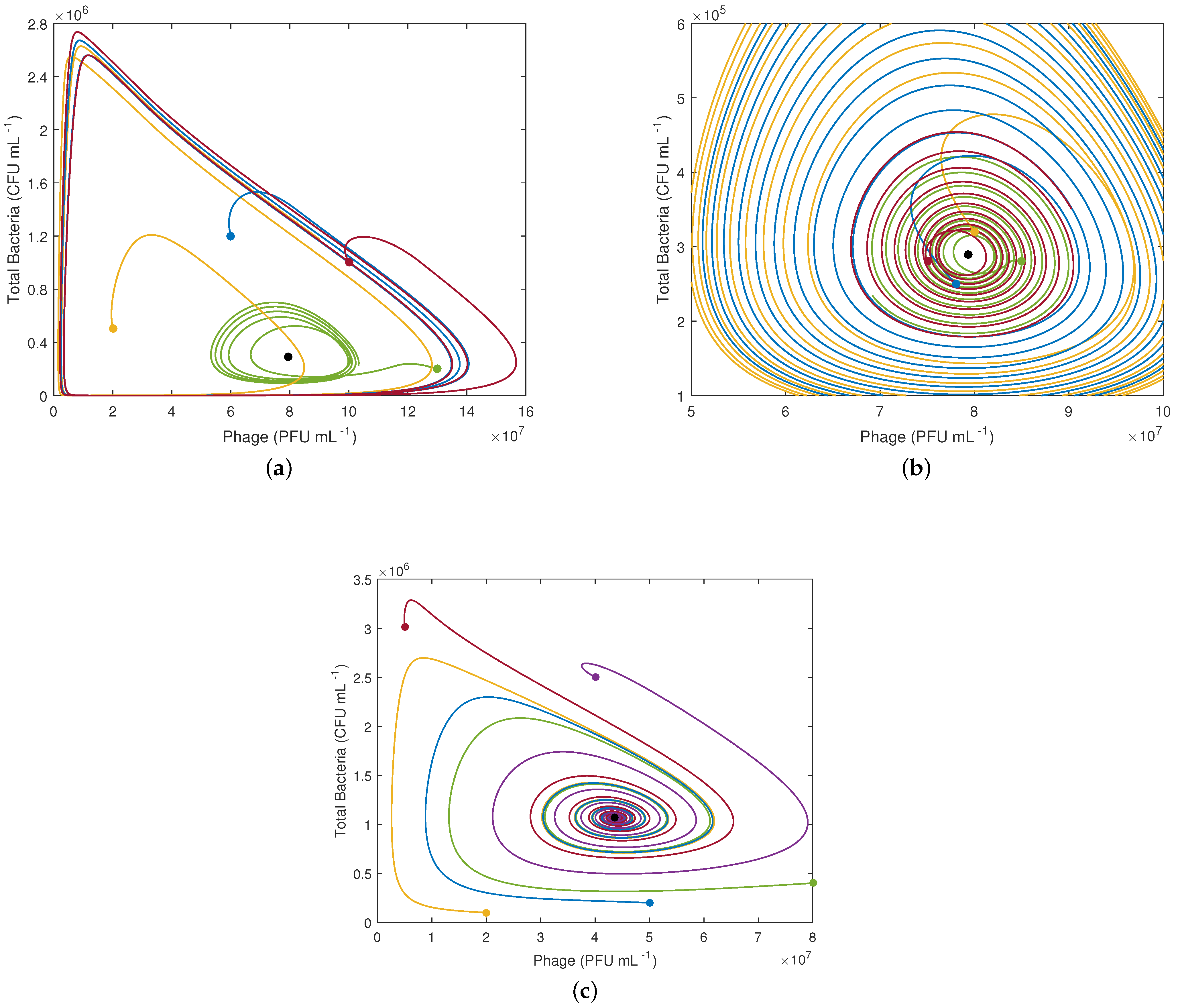
The two first equilibrium points are saddle points, i.e., points characterized by real positive and negative eigenvalues. This reflects the fact that a small perturbation in the populations will generate the onset of bacteria, phages, and infection. The third equilibrium point is characterized by two negative real eigenvalues (stable) and two complex conjugate eigenvalues, which are real negative for D > 0.0951 h${}^{-1}$. For smaller dilution rates (D < 0.0951 h${}^{-1}$), the real part of these latter eigenvalues is positive, yielding an unstable spiral.

Figure 3 presents phase plane plots for D = 0.05 h${}^{-1}$ (Figure 3a and zoom Figure 3b) and D = 0.2 h${}^{-1}$ (Figure 3c) for different initial conditions and the parameters given in Table 2 in order to have a deeper insight into the system trajectories. For D = 0.05 h${}^{-1}$, the trajectories form diverging spirals, which collides into limit cycles, whereas for D = 0.2 h${}^{-1}$, the trajectories form converging spirals towards equilibrium point 3.

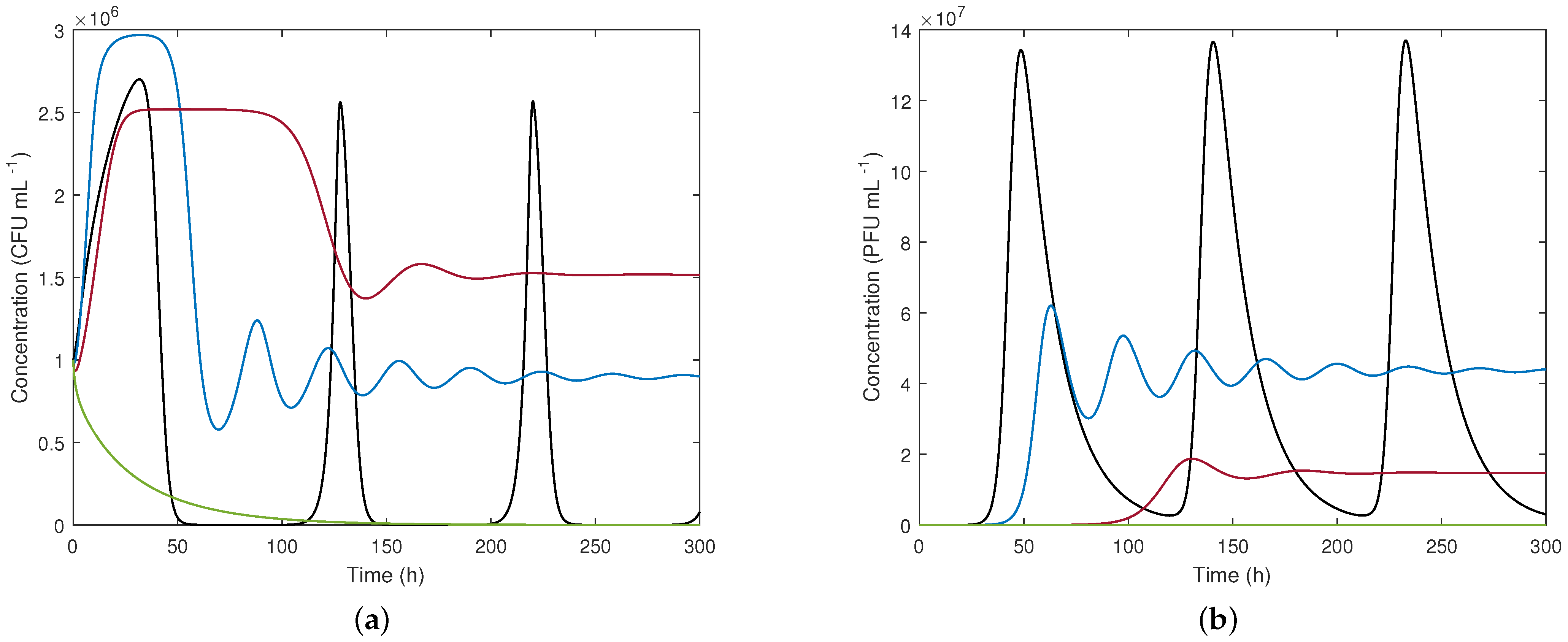
Figure 4 presents time evolution for D = 0.1 h${}^{-1}$, when a phage concentration of $1\times {10}^2$ PFU mL${}^{-1}$ is initially added. As expected, the response converges towards equilibrium point 3 while oscillating. The phage addition is successful from the point of view of controlling the population of unwanted bacteria since even though not all bacteria are eliminated, their excessive growth is mitigated.

Finally, Figure 5 focuses attention on the bacteria populations for four different dilutions rates, e.g., $0.05$, $0.2$, $0.3$, and 0.42 h${}^{-1}$, respectively. In the first case, equilibrium point 3 is unstable and the populations present sustained oscillations. In the second and third cases, the equilibrium point is stable and the populations reach equilibrium values, while in the last case, wash-out conditions are achieved.

4.2. Identifiability

Once a model structure is adopted, the next step in the model derivation is the estimation of the parameter values from experimental data. A natural question arises on whether this is feasible with the data at hand. This question is usually studied in two steps: (a) structural identifiability and (b) practical identifiability. While practical identifiability refers to quantifying the uncertainty in parameter values when estimated from sampled noisy measurements, structural identifiability considers an ideal situation where the data are available in continuous time and with no noise or errors whatsoever [56,57,58,59]. Of course, structural identifiability is a prerequisite, which, if not achieved, should imply questioning about the model structure and parametrization, and possibly a reformulation of the model.

4.2.1. Structural Identifiability Analysis

In this study, structural identifiability is assessed referring to the concept of observability, as suggested by Villaverde [60]. Indeed, structural identifiability can be seen as a particular case of observability if the parameters are considered as constant state variables, and it is possible to simultaneously analyze the observability and structural identifiability of a model using the conceptual tools of differential geometry.

The structural identifiability analysis is carried out for model (36)–(39), regarding the vector of eight parameters

$$p=\left\{\begin{array}{c}{\mu }_{max}{K}_M\delta \beta \eta m{\nu }_S{\nu }_P\end{array}\right\}$$

(45)

and various possible measurement configurations, i.e., matrix C in Equation (41). Operational parameters, $S_{in}$, and D are known as they are under the control of the operator.

This study is achieved using STRIKE-GOLDD [61], a MATLAB toolbox that analyses the local structural identifiability and observability of nonlinear dynamic models with multiple time-varying and possibly unknown inputs. The algorithm adopts a differential geometry approach, recasting the identifiability problem as an observability problem. Essentially, the observability of the model variables (states, parameters, and inputs) is determined by calculating the rank of a generalized observability–identifiability matrix, which is built using Lie derivatives. Unobservable variables exist when the matrix is rank deficient. If these variables are parameters, they are called (structurally) unidentifiable. The procedure determines the subset of identifiable parameters, observable states, and observable (also called reconstructible) inputs, thus performing a “Full Input-State-Parameter Observability” (FISPO) analysis. This approach is directly applicable to many models of small and medium-size; larger systems can be analyzed using additional features of the method [61].

Table 3. Structural identifiability analysis with the STRIKE-GOLDD toolbox.

	Parameters								Identifiable?
	${\mathit{\mu }}_{\mathit{max}}$	${\mathit{K}}_{\mathit{M}}$	${\mathit{\nu }}_{\mathit{S}}$	$\mathit{\delta }$	$\mathit{\beta }$	$\mathit{\eta }$	${\mathit{\nu }}_{\mathit{P}}$	m
4 measurements
$X_S$, $X_I$, P, S	✕	✕	✕	✕	✕	✕	✕	✕	Yes
3 measurements
$X_S$, $X_I$, P	✕	✕	✕	✕	✕	✕	✕	✕	Yes
$X_S$, $X_I$, S	✕	✕	✕	✕	✕	✕	✕	✕	Yes
$X_S$, P, S	✕	✕	✕	✕	✕	✕	✕	✕	Yes
$X_I$, P, S	✕	✕	✕	✕	✕	✕	✕	✕	Yes
$X_T$, P, S	✕	✕	✕	✕	✕	✕	✕	✕	Yes
2 measurements
$X_S$, $X_I$	✕	✕	✕	✕	✕	✕	✕	✕	Yes
$X_S$, P	✕	✕	✕	✕	✕	✕	✕	✕	Yes
$X_S$, S	✕	✕	✕	✕	✕	✕	✕	✕	Yes
$X_I$, P	✕	✕	✕	✕	✕	✕	✕	✕	No
$X_I$, P	✓	✓	✕	✕	✕	✕	✕	✕	Yes
$X_I$, P	✕	✕	✕	✓	✓	✕	✕	✕	Yes
$X_I$, S	✕	✕	✕	✕	✕	✕	✕	✕	Yes
P, S	✕	✕	✕	✕	✕	✕	✕	✕	Yes
$X_T$, P	✕	✕	✕	✕	✕	✕	✕	✕	Yes
$X_T$, S	✕	✕	✕	✕	✕	✕	✕	✕	Yes
1 measurement
$X_S$	✕	✕	✕	✕	✕	✕	✕	✕	No
$X_S$	✓	✓	✕	✓	✓	✕	✕	✕	Yes
$X_I$	✕	✕	✕	✕	✕	✕	✕	✕	No
$X_I$	✓	✓	✕	✓	✓	✕	✕	✕	Yes
P	✕	✕	✕	✕	✕	✕	✕	x	No
P	✓	✓	✕	✓	✓	✕	✕	✕	Yes
S	✕	✕	✕	✕	✕	✕	✕	✕	No
S	✓	✓	✕	✓	✓	✕	✕	✕	Yes
$X_T$	✕	✕	✕	✕	✕	✕	✕	✕	No
$X_T$	✓	✓	✕	✓	✓	✕	✕	✕	Yes

✕ unknown ✓ known.

shows the results of the identifiability study with the STRIKE-GOLDD toolbox. This analysis is first performed assuming that p is unknown while the four states can be measured. Afterwards, other measurement configurations with three, two, or one measurement are also considered.

It is apparent that all the measurement configurations with 4 and 3 measurements (including also the situation where the total biomass $X_T=X_S+X_I$ can be measured) lead to a FISPO system. On the other hand, the choice of measured variables becomes critical when only 2 measurements are available, and the system is not identifiable with only 1 measurement.

Unidentifiable scenarios are therefore re-evaluated, assuming that some of the parameters are a priori known and do not require further identification. In practice, some preliminary experimental results may sometimes be available beforehand, which could be exploited to fix some of the parameters, e.g., ${\mu }_{max}$ and $K_M$ could be estimated experimentally based on a growth curve, $\delta$ through an adsorption curve, and $\beta$ from a one-step test [62]. Then, a few one- and two-measurement configurations lead to a structurally identifiable system, where it would be possible to estimate the remaining unknown parameters.

4.2.2. Practical Identifiability: Parametric Sensitivity Analysis

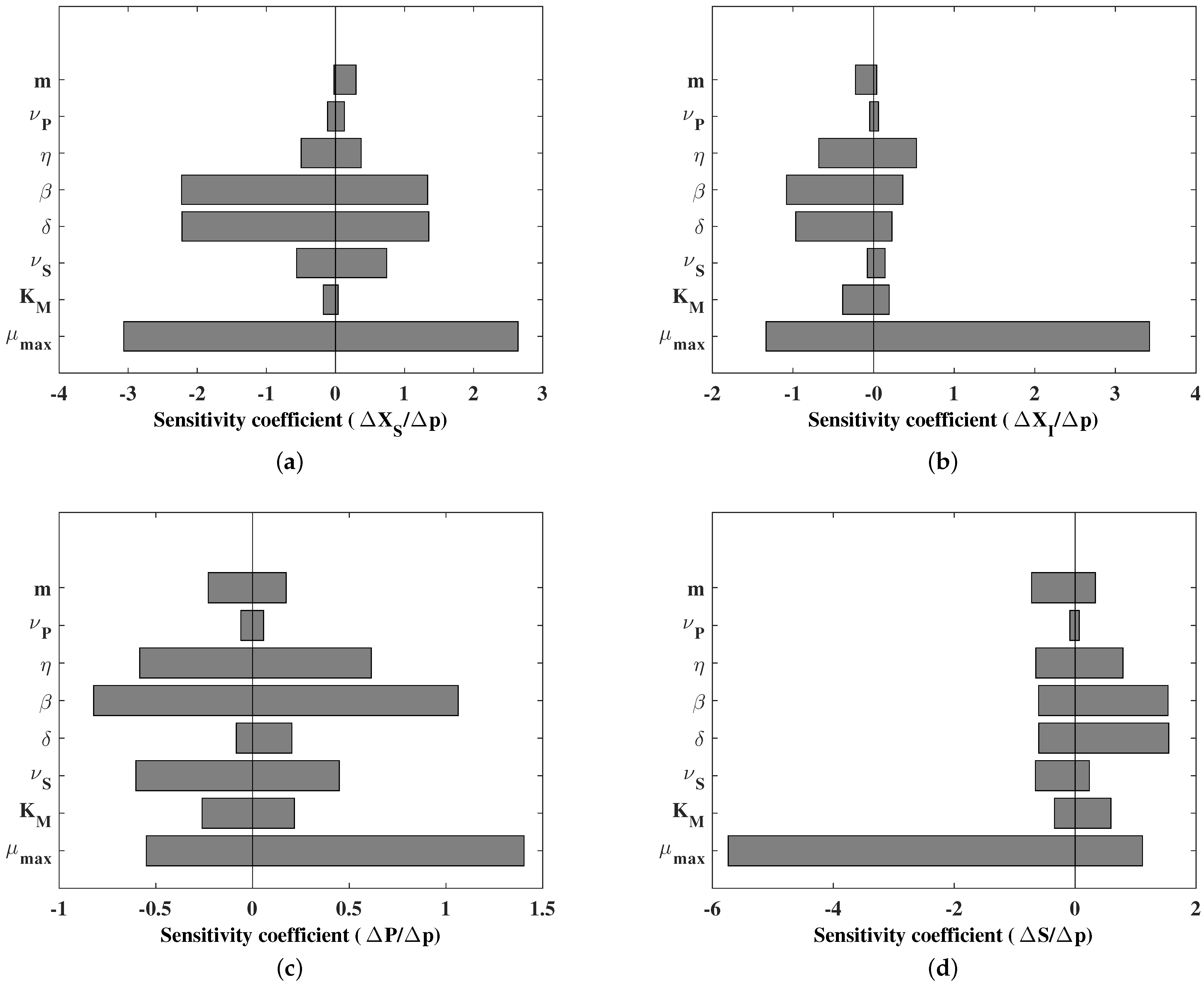
Practical identifiability focuses on the information content of the data and the influence of sampling and noise. Here, the analysis is performed in simulation and is restricted to a local parameter sensitivity analysis around the equilibrium point corresponding to the conditions in Table 2. To this end, changes of $5\%$ are affected in the parameter values. The results are presented in Figure 6.

This analysis confirms that if all the variables are measured, information is a priori available to estimate all the parameters. The less sensitive parameters are ${\nu }_P$ and $K_M$. The natural phage inactivation coefficient ${\nu }_P$ accounts for the stability of the phage over time, a very important physical parameter in the infection but that does not depend on the operational parameters. Classically, the half-saturation coefficient $K_M$ is more delicate to estimate if the feed to the reactor is not varied enough to reach the appropriate range of substrate concentrations (too high concentrations hide this parameters, while too low concentrations make it linearly dependent with ${\mu }_{max}$). These aspects have to be explored based on the a posteriori estimates of the uncertainty on the actual identification results, for instance, on the basis of the Fisher Information Matrix. We will not explore further these aspects which are beyond the scope of this review and refer the interested reader to texts focusing on parameter estimation (for instance, [63]).

4.3. Observability

Observability is the next interesting model property in view of the design of state estimators or observers, or, in a more technical language, software sensors, dedicated to the reconstruction of non-measured variables. This is particularly important in real case applications, where online instrumentation is limited and the deployment of software sensors is a key asset to monitor the plant at minimal costs. Software sensors blend, or fuse, the predictive information of a dynamic model of the process together with the measurement information from available hardware sensors. A wide range of such state estimators, including the extended Kalman filters, are available (see for instance, refs. [64,65] for more details and references).

The concept of observability describes the theoretical possibility of inferring the state vector of a system from observations of the output vector. Observability considers only the dynamic equations of the model, including the definition of inputs and outputs but not the actual characteristics of the experimental measurements, such as the noise level.

Local observability can be easily evaluated by calculating the rank of an observability matrix, which is built as follows.

Consider a linear time-invariant system with n state variables given by:

$$\dot{x}=Ax+Bu,y=Cx$$

(46)

where A, B, and C are the state transition, input, and output matrices, respectively. In the case of a nonlinear system, these matrices can be obtained by computing Jacobian matrices at the point under consideration (for instance, matrix A has been evaluated for our model in Equation (44)).

The observability matrix is defined by:

$$O=\left[\begin{array}{c}C\\ CA\\ C{A}^2\\ ⋮\\ C{A}^n\end{array}\right]$$

(47)

and the system is locally observable if and only if this matrix is full row-rank (the rank calculation can be easily carried out in Matlab using the sequence $rank\left(obsv\right(A,C\left)\right)$).

This local analysis reveals that the model is observable around equilibrium 3 for all possible combinations of the measurements, including $X_S$, $X_I$, the total biomass $X_T=X_S+X_I$, P, and S, starting with a single measurement of one of these variables. In practice, the availability of more measurement signals will allow improving the convergence and robustness of the software sensor. It will also avoid losing observability in the case where the measured signal vanishes, provided the additional measurement signals do not vanish at the same time of course.

The results of this local analysis are confirmed by the use of the Matlab toolbox STRIKE-GOLDD, introduced earlier for the identifiability analysis. The advantage of this tool is that it considers the original nonlinear model and provides a global analysis. In conclusion, with at least one measured state (no matter which one), the system is observable, and all state variables can be estimated with an appropriate software sensor.

5. Modeling Challenges

Parameter estimation is probably the biggest challenge in view of the difficulty of collecting informative experimental data.

Monitoring bacterial growth kinetics could be based on the relations presented in the previous sections, obtaining the parameters associated with logistic and Monod laws (specific growth rate, carrying capacity, etc.). This approach is mostly useful in pure cultures, where it is easy to collect data, but it is much more delicate, or even impossible, in full-scale operation with consortia of micro-organisms.

On the other hand, the infection parameters can be determined with additional tests. For instance, the latent period and burst size can be determined by one-step growth assays, and the adsorption constant can be determined according to a standard protocol [62]. However, it is also observed that these parameters could be time-varying and that additional modeling effort is required [20,48,54,66,67].

De Leeuw et al. [68] used microtiter plates (which served as multiple micro-scale ecosystems) and studied the predator–prey relationship between bacteria and phage isolated from wastewater treatment bioreactors. The shifts in the bacterial population were monitored through the optical readings from the plate reader, and a mathematical model incorporating phage–bacteria interactions was developed and calibrated using Matlab. However, only the total bacterial population was observed, whereas monitoring the phage population and substrate concentrations would be valuable, and represents an actual challenge in monitoring and controlling wastewater treatment.

Nabergoj et al. [69] investigated how dilution rate, defining bacterial growth rate in continuous culture, affects adsorption constant, latent period, and burst size and, consequently, also bacteriophage population growth rate. They used a well-studied phage T4 and E. coli K-12 as a host in a chemostat. The authors demonstrated that bacterial growth rate had an important influence on three phage growth parameters, e.g., adsorption constant, latent period, and burst size, determining the bacteriophage population growth rate. In addition, bacteriophage population growth rate as a function of dilution rate was found to be accurately described by a simple Monod equation. From these results, the question emerges if these changes in infection parameters are general or depend on the choice of a phage–host system, which adds to the difficulties of parameter estimation.

Another challenge for the application of bacteriophage treatment at the industrial level is the large number of phages that should be produced, so that cost-effective and scalable methods for phage production are required to meet the demand. In this connection, computational models could also assist the optimization of such production processes, and are an open research avenue. In this connection, Krysiak-Baltyn et al. [70] proposed a model for a two-stage, self-cycling process, which was successfully operated without showing the evidence of resistant bacteria. The model developed for a setup with multiple reactors provided simple cost estimates as a function of operational parameters such as substrate concentration, feed volume, and cycling times. They concluded that the approach is flexible and could be used to optimize phage production at a laboratory or industrial scale by minimizing costs or maximizing productivity.

6. Practical Applications of Computational Models in Activated Sludge Processes

Single reactor models have been essential to increasing our understanding of some aspects of the system dynamics, but these models may not be adequate to simulate the spread and propagation of phages in the complex and varied configurations of real-world systems, including the sewage pipes and wastewater treatment plants. In that sense, few authors have studied phage treatment.

One of the first foaming studies was accomplished by Blackall et al. [71], who analyzed the onset of foam formation and subsequent persistence of foaming in terms of a mathematical model for Nocardia amarae (filamentous bacteria) described by two balance equations. Using experimental data, the authors determined that the foam acted as a significant source for continued bacteria growth in the mixed liquor, which would make it difficult for the microorganisms to washout. In addition, activated sludge systems are sensitive to changes in key variables that could lead to the onset or disappearance of foam. They concluded that such a model is helpful, but that there are difficulties in obtaining meaningful values for some parameters, especially if more than one filamentous organisms are dominant [72].

Hao et al. [73] presented a model to simulate a sequencing batch reactor (SBR) system enriching polyphosphate-accumulating organisms (PAOs). For this purpose, they proposed extending the Activated Sludge Model No. 2d (ASM2d) to incorporate predation and viral infection processes. In order to include predation and viral infection, the decay process in ASM2d was split into three individual processes, e.g., predation-induced decay, viral infection-induced decay, and decay induced by other factors (e.g., toxic substances, natural cell death, etc.). Correspondingly, the stoichiometric matrix and kinetic rate expressions related to predation and viral infection were added to the extended ASM2d.

For foaming treatment, Liu et al. [29] isolated Gordonia species from activated sludge of a commercial wastewater treatment plant, and four isolated phages were applied to sludge, reducing Gordonia host levels in a wastewater sludge model by approximately 10-fold as compared to non-phage-treated reactors. In addition to controlling Gordonia levels in activated sludge, phage-treated sludge at the end of the experiment showed better settling properties and lower foaming potential in the supernatant after settlement compared to the control. They concluded that phages applied for bio-control could survive during sludge aeration, providing significant potential for phage application in controlling Gordonia-associated foaming and bulking during wastewater treatment [29].

Recently, Krysiak-Baltyn et al. [74] proposed a model incorporating phage dynamics in wastewater treatment for two reactor configurations, SBR and PFR (Plug Flow Reactor), to investigate the potential use of phages as a tool to reduce foaming or bulking. The model couples wastewater treatment dynamics within the commercial software GPS-X (Hydromantis Inc., Hamilton, Canada) with phage dynamics through a newly developed add-on called PhageDyn. Simulations predict that immediately after phage dosing, there is a lag period during which no apparent changes are observed, followed by a sudden and quick increase in the phage concentration and reduction in foaming biomass. ‘Normalization’ without foaming is achieved within 1–2 weeks after dosing. The system may subsequently relapse to foaming, requiring additional phage dosing, or be “cured” such that the added phages keep the problematic foaming biomass indefinitely at bay. The behavior described by Krysiak-Baltyn et al. [74] has been the closest to reality, although the DDE system had to be reformulated into a set of ODEs since its computation was impossible. They concluded that the kinetic parameters describing the behavior of the phages and reactor configuration are vital determinants of the outcome.

7. Conclusions and Perspectives

In recent times, biological wastewater treatment has found a larger and more prominent place in global concerns. Generally speaking, the problems arising from their operation are more complex than those of more classical industrial processes, and the need for efficient control strategies is obvious. Despite the ever increasing advanced automation of wastewater treatment processes, there are are still open issues that require more analysis and the deployment of model-based control strategies.

To this end, dynamic models must be available, including parameter estimation and model validation. These models are of course less mature in novel approaches such as the treatment of filamentous bacteria with bacteriophages. The difficulty to develop models is also related to the lack of affordable and reliable instrumentation to measure online the essential process variables.

Bacteriophage treatment for foaming control might be the basis for a more efficient, economic, and sustainable control than the current practice based on chemical treatments. This biological treatment has shown its effectiveness in some experimental studies. However, the understanding of the underlying phenomena remain only partial. Mathematical models still require further analysis and experimental validation.

In this article, in addition to a review of the literature about modeling, analysis and applications of phages-bacteria population systems, we have highlighted the importance of carefully formulating models and analyzing their properties, including stability, identifiability, and observability. Particularly, the development of software sensors, based on these models, would allow significant advances in monitoring important biological variables, such as the time evolution of the concentration of filamentous bacteria, and would alleviate the lack of online hardware sensors to achieve such tasks.