Numerical Investigation and Optimization of the Flow Characteristics of Bend Pipe with Different Bending Angles
Abstract
:1. Introduction
2. Physical and Numerical Methods
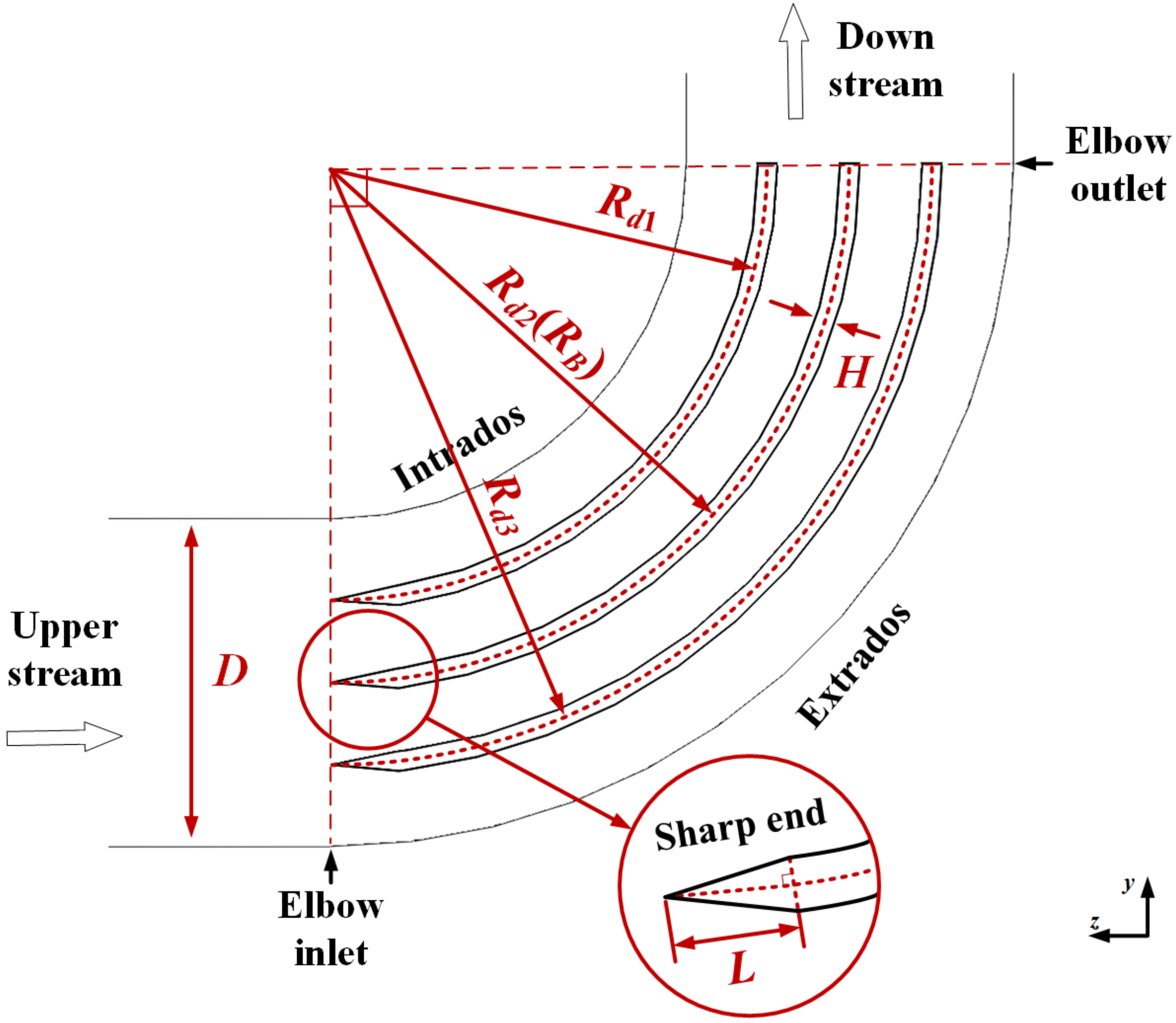
2.1. Physical Models
2.2. Numerical Methods
3. Results and Discussion
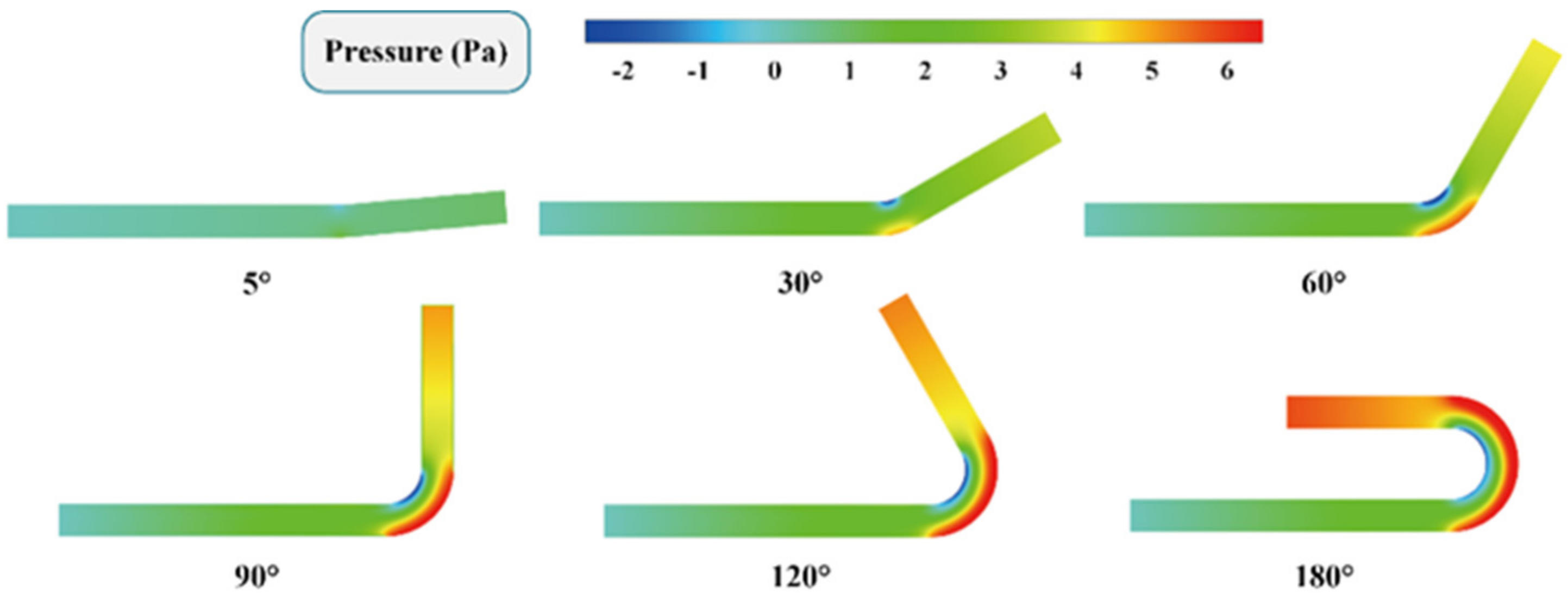
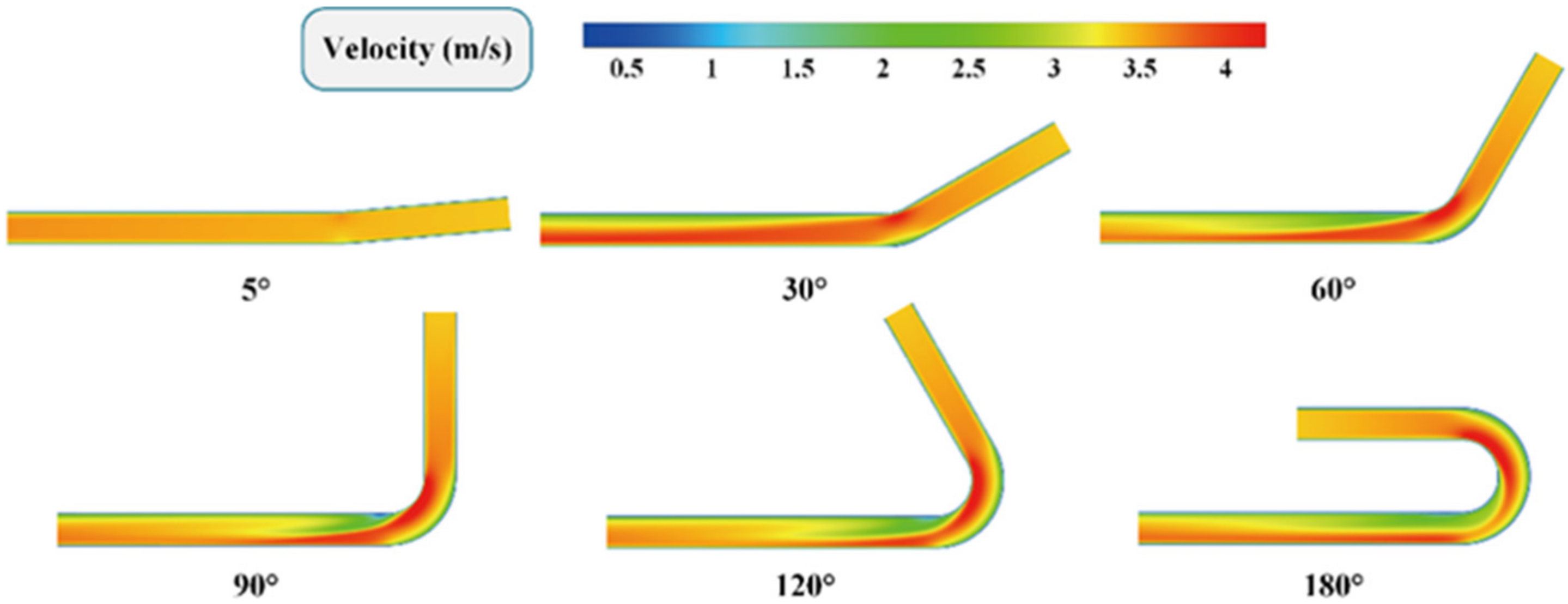
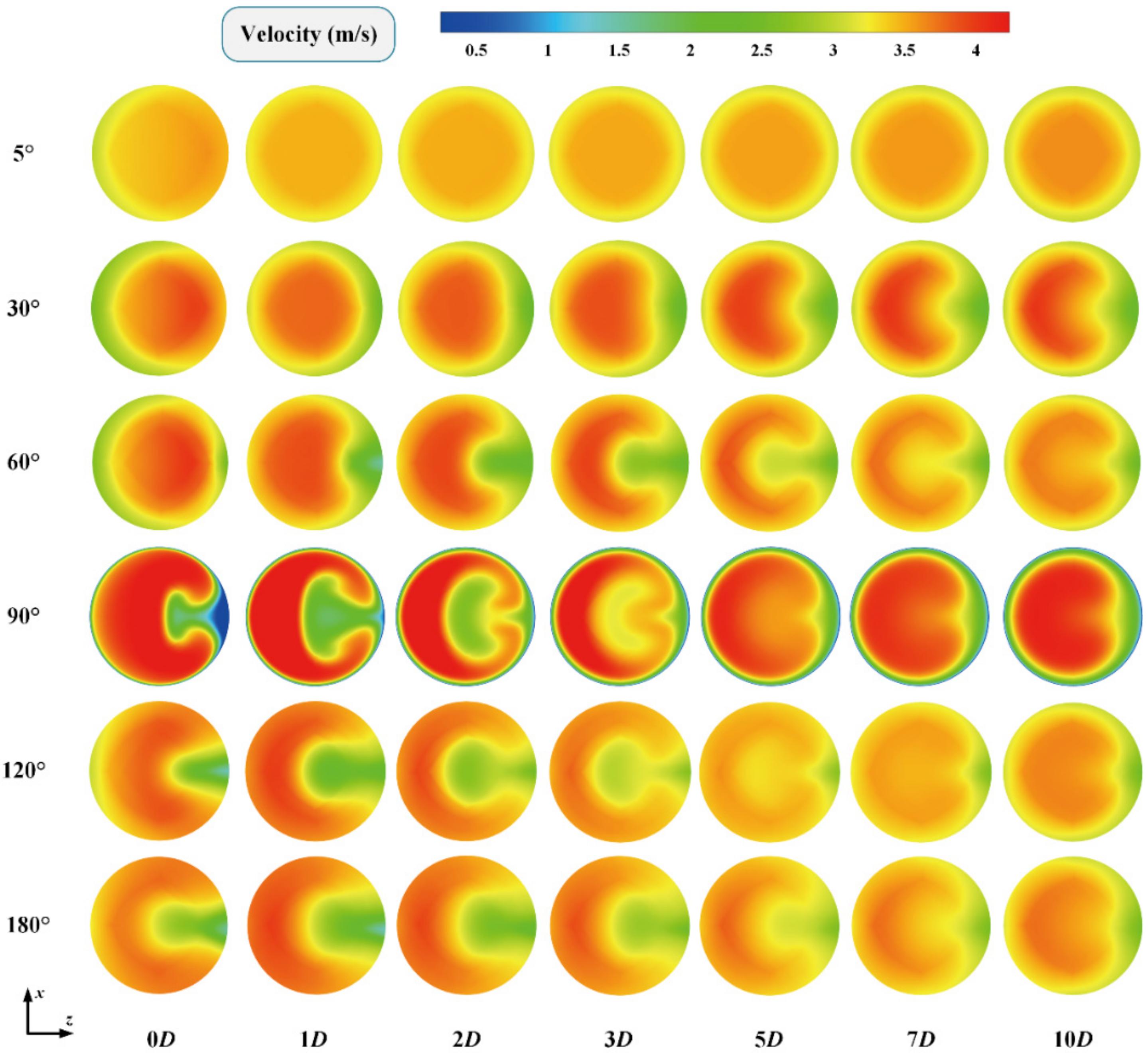
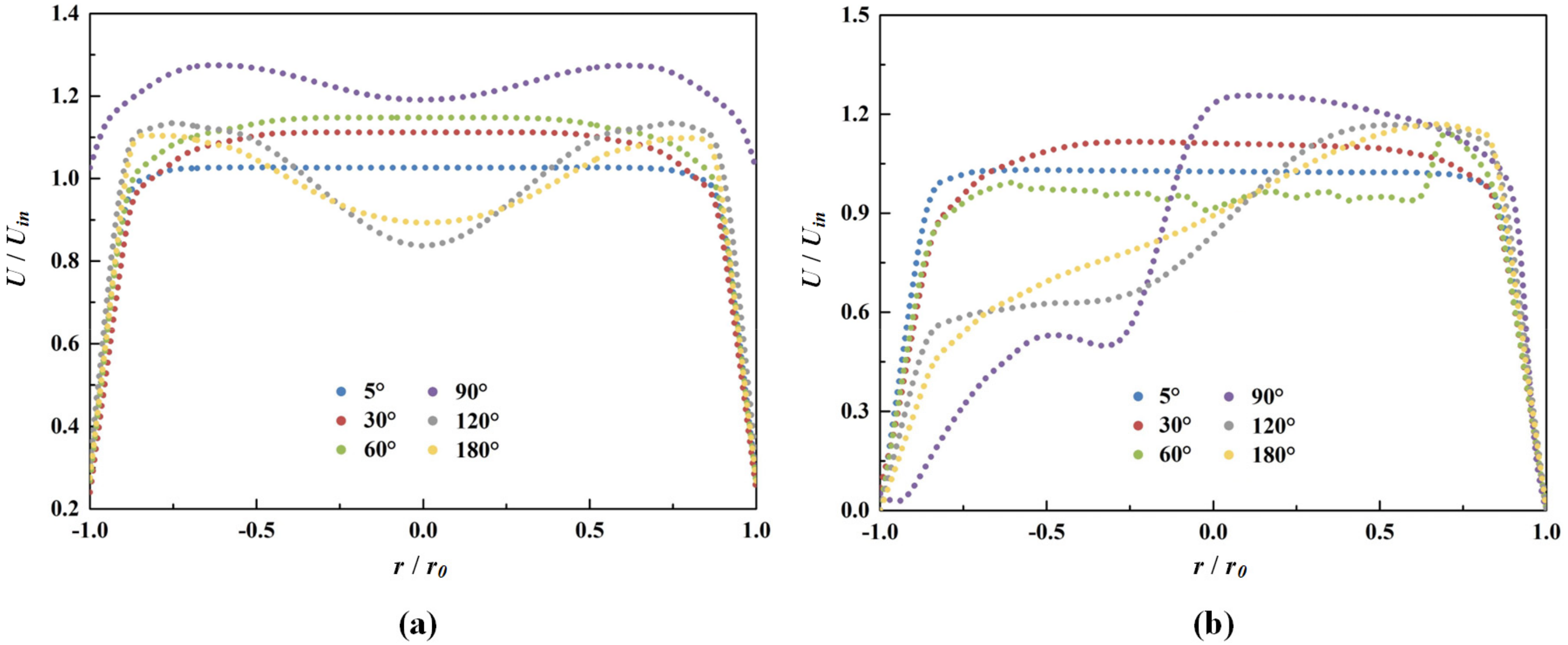
3.1. Global Flow Analysis
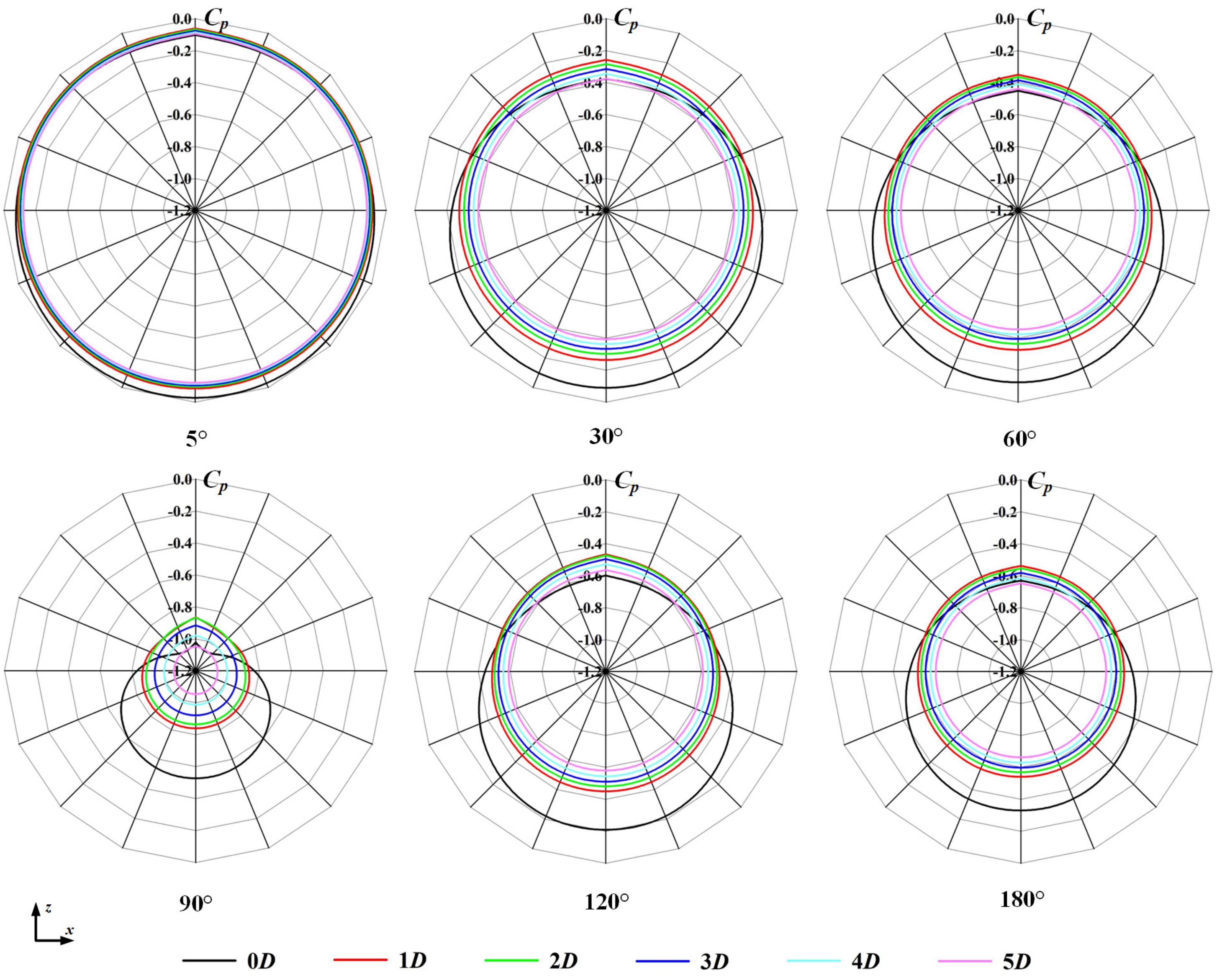
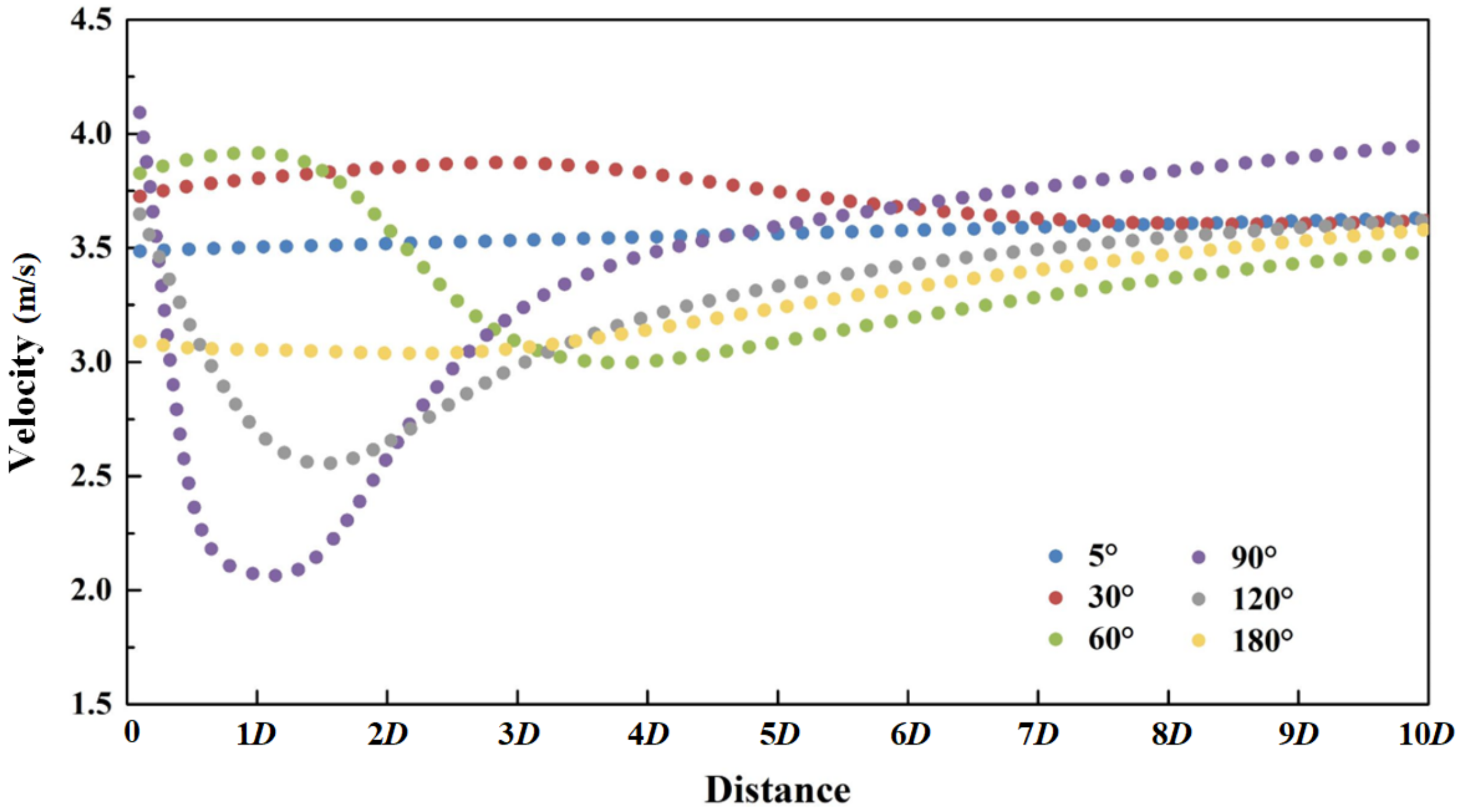
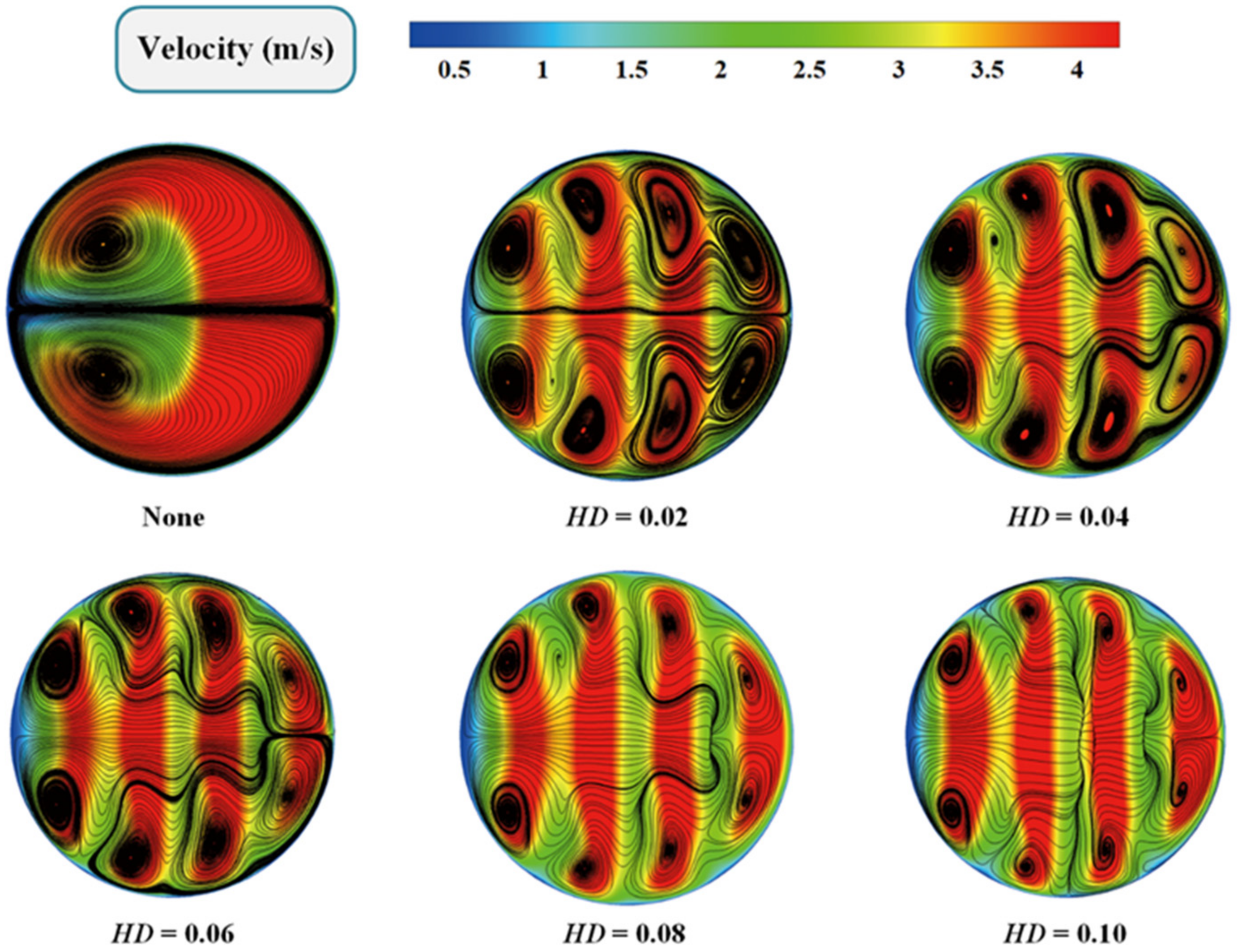
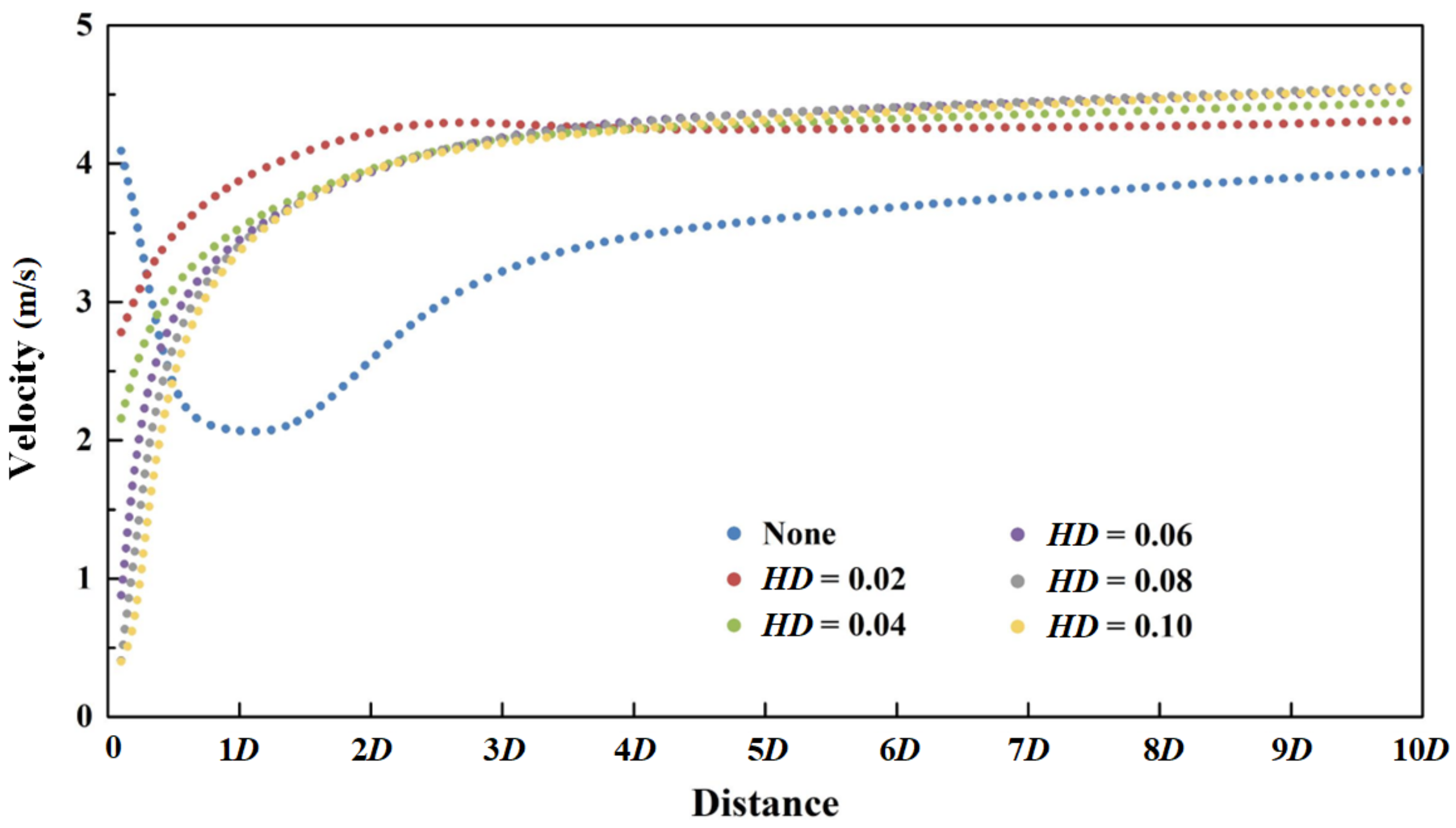
3.2. Wake Development
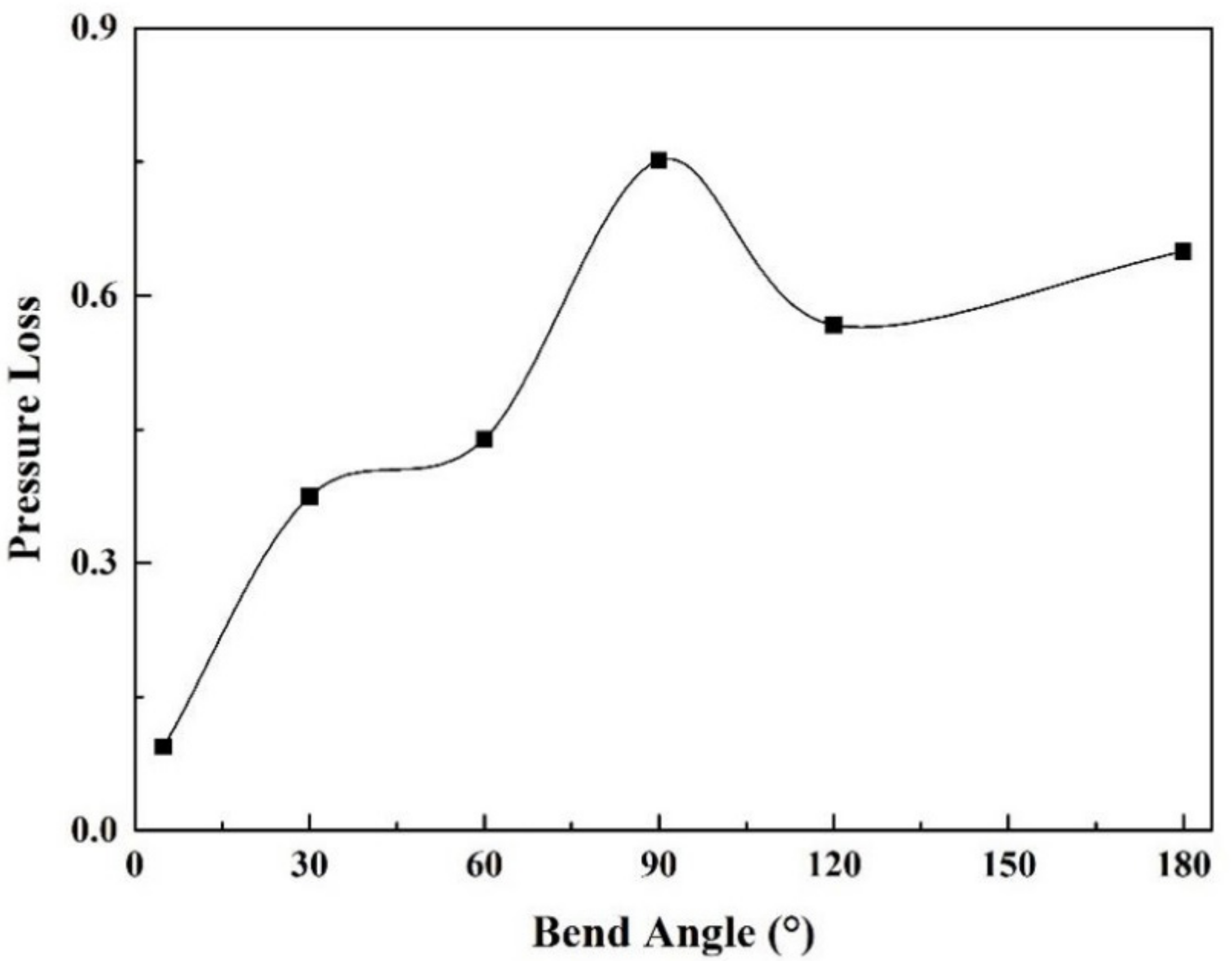
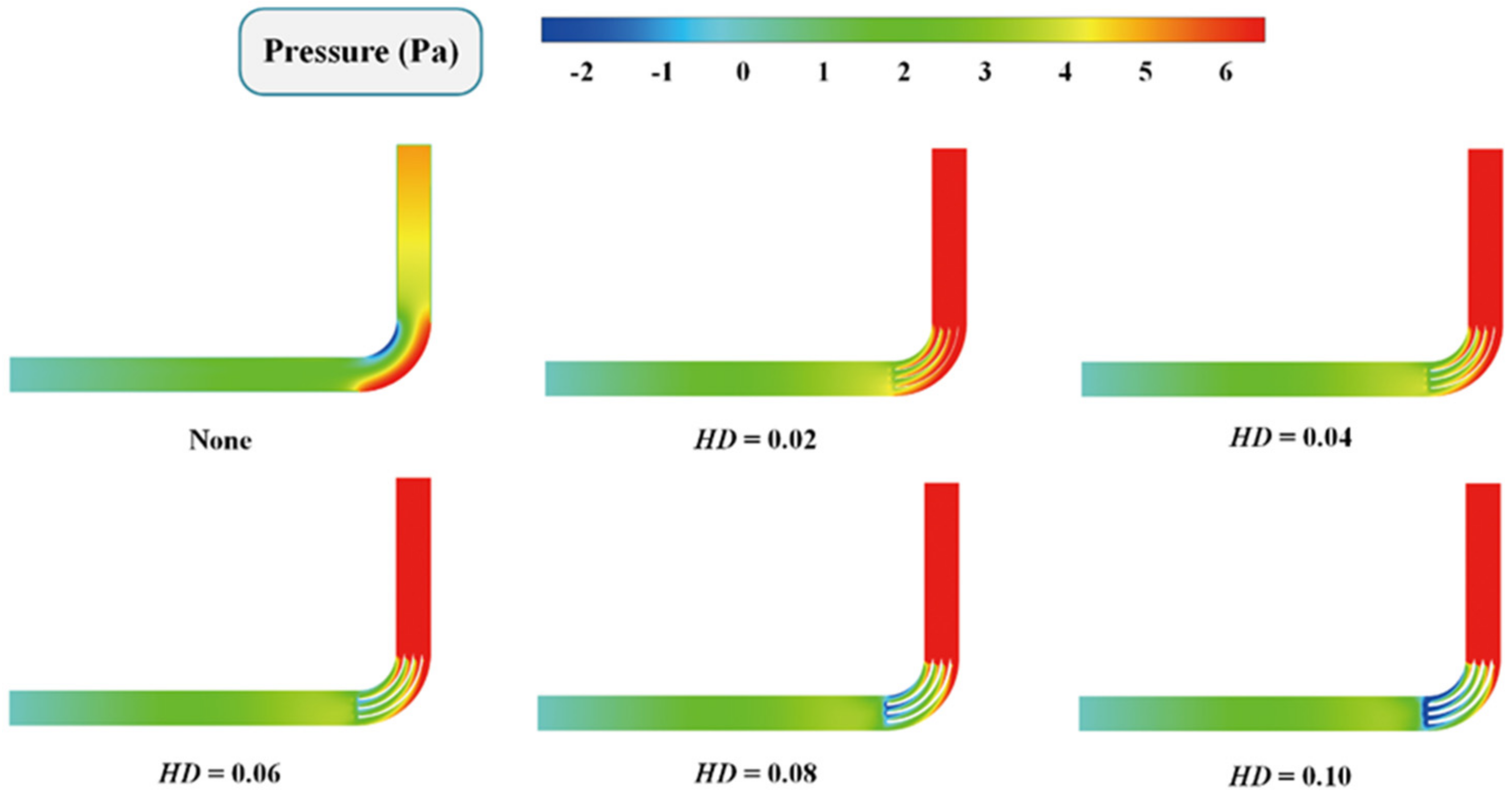
3.3. Pressure Loss
4. Structure Optimization
4.1. Different Thick-Diameter Ratio
4.2. Different Length-Diameter Ratio
5. Conclusions and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, Y.; Liu, S.; Dou, H.-S.; Wu, S.; Chen, T. Numerical prediction and similarity study of pressure fluctuation in a prototype Kaplan turbine and the model turbine. Comput. Fluids 2012, 56, 128–142. [Google Scholar] [CrossRef]
- Kamyar, A.; Aminossadati, S.M.; Leonardi, C.R.; Sasmito, A.P.; Poncet, S. Flow characterisation of monopropylene glycol ice slurry through a horizontal U-bend: A numerical approach. Eur. J. Mech. B/Fluids 2020, 82, 93–105. [Google Scholar] [CrossRef]
- Fellouah, H.; Castelain, C.; Ould-El-Moctar, A.; Peerhossaini, H. The Dean instability in power-law and Bingham fluids in a curved rectangular duct. J. Non-Newton. Fluid Mech. 2010, 165, 163–173. [Google Scholar] [CrossRef]
- Skillen, A.; Zimon, M.J.; Sawko, R.; Tunstall, R.; Moulinec, C.; Emerson, D.R. Thermal transients in a U-bend. Int. J. Heat Mass Transf. 2020, 148, 119039. [Google Scholar] [CrossRef]
- Kumar, P.; Singh, J. Computational study on effect of Mahua natural surfactant on the flow properties of heavy crude oil in a 90° bend. Mater. Today Proc. 2021, 43, 682–688. [Google Scholar] [CrossRef]
- Akar, S.; Esfahani, J.A.; Shaegh, S.A.M. A numerical investigation on the Magnetophoretic-guided stem cells delivery in a bend blood vessel. J. Magn. Magn. Mater. 2019, 498, 166110. [Google Scholar] [CrossRef]
- Dean, W.R. Fluid motion in a curved channel. Proc. R. Soc. A Math. Phys. Eng. Sci. 1928, 121, 402–420. [Google Scholar]
- Hashemi, A.; Fischer, P.F.; Loth, F. Direct numerical simulation of transitional flow in a finite length curved pipe. J. Turbul. 2018, 19, 664–682. [Google Scholar] [CrossRef]
- Canton, J.; Schlatter, P.; Örlü, R. Modal instability of the flow in a toroidal pipe. J. Fluid Mech. 2016, 792, 894–909. [Google Scholar] [CrossRef]
- Ji, Y.; Wilson, C.; Chen, H.-H.; Ma, H. Particle shape effect on heat transfer performance in an oscillating heat pipe. Nanoscale Res. Lett. 2011, 6, 296. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kalpakli, A.; Örlü, R. Turbulent pipe flow downstream a 90° pipe bend with and without superimposed swirl. Int. J. Heat Fluid Flow 2013, 41, 103–111. [Google Scholar] [CrossRef]
- Kalpakli, A.; Örlü, R.; Alfredsson, P. Vortical patterns in turbulent flow downstream a 90° curved pipe at high Womersley numbers. Int. J. Heat Fluid Flow 2013, 44, 692–699. [Google Scholar] [CrossRef]
- Lupi, V.; Canton, J.; Schlatter, P. Global stability analysis of a 90°-bend pipe flow. Int. J. Heat Fluid Flow 2020, 86, 108742. [Google Scholar] [CrossRef]
- Wang, Z.; Örlü, R.; Schlatter, P.; Chung, Y.M. Direct numerical simulation of a turbulent 90° bend pipe flow. Int. J. Heat Fluid Flow 2018, 73, 199–208. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Tu, S.; Dong, D.; Guo, L.; Joseph, D.D.; Matsumoto, Y.; Sommerfeld, Y.; Wang, Y. Numerical simulation of flow characteristic in three-dimensional bend pipes. In Proceedings of the 6th International Symposium on Multiphase Flow, Heat Mass Transfer and Energy Conversion, Xi’an, China, 11–15 July 2009; pp. 424–428. [Google Scholar]
- Dutta, P.; Saha, S.K.; Nandi, N.; Pal, N. Numerical study on flow separation in 90° pipe bend under high Reynolds number by k-ε modelling. Eng. Sci. Technol. Int. J. 2016, 19, 904–910. [Google Scholar] [CrossRef] [Green Version]
- Ran, L.Y.; Zhao, J.; Qin, H.B.; Hu, S.G.; Tian, X.L. The Analysis of Field Characteristics and Measurement for Centrifugal Fan and 90° Bend Pipe. Appl. Mech. Mater. 2014, 628, 266–269. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Sun, H.; Chen, M.; Lu, X.; Wang, Y.; Liu, X. Pressure of Newtonian fluid flow through curved pipes and elbows. J. Therm. Sci. 2013, 22, 372–376. [Google Scholar] [CrossRef]
- Chowdhury, R.R.; Biswas, S.; Alam, M.; Islam, A.K.M.S. Turbulent flow analysis on bend and downstream of the bend for different curvature ratio. In Proceedings of the 11th International Conference on Mechanical Engineering, Dhaka, Bangladesh, 18–20 December 2015; p. 040020. [Google Scholar]
- Kim, Y.-J.; Oh, C.-S. Limit loads for pipe bends under combined pressure and in-plane bending based on finite element limit analysis. Int. J. Press. Vessel. Pip. 2006, 83, 148–153. [Google Scholar] [CrossRef]
- Li, J.; Zhou, C.-Y.; Xue, J.-L.; He, X.-H. Limit loads for pipe bends under combined pressure and out-of-plane bending moment based on finite element analysis. Int. J. Mech. Sci. 2014, 88, 100–109. [Google Scholar] [CrossRef]
- Qian, X.; Yang, Y.; Lee, S.W. Design and evaluation of the lab-ccale shell and tube heat exchanger (STHE) for poultry litter to energy production. Processes 2020, 8, 500. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, F.; Yang, Z.; Li, G.; Zuo, J. Simulation of the Transient Characteristics of Water Pipeline Leakage with Different Bending Angles. Water 2019, 11, 1871. [Google Scholar] [CrossRef] [Green Version]
- Li, S.-J.; Zhou, C.-Y.; Li, J.; Pan, X.-M.; He, X.-H. Effect of bend angle on plastic limit loads of pipe bends under different load conditions. Int. J. Mech. Sci. 2017, 131–132, 572–585. [Google Scholar] [CrossRef]
- Silambarasan, R.; Veerappan, A.R.; Shanmugam, S. Effect of structural deformations and bend angle on the collapse load of pipe bends subjected to in-plane closing bending moment. World J. Eng. 2021, 19, 594–603. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Lee, K.-H.; Oh, C.-S.; Yoo, B.; Park, C.-Y. Effect of bend angle on plastic loads of pipe bends under internal pressure and in-plane bending. Int. J. Mech. Sci. 2007, 49, 1413–1424. [Google Scholar] [CrossRef]
- Li, S.; Zhou, C.; Li, J.; Miao, X. Effect of Bend Angle on Plastic Limit Loads of Pipe Bends Under In-Plane Bending Moment. In Proceedings of the ASME Pressure Vessels and Piping Conference, Vancouver, BC, Canada, 17–21 July 2016. [Google Scholar]
- Bezyan, B.; Porkhial, S.; Mehrizi, A.A. 3-D simulation of heat transfer rate in geothermal pile-foundation heat exchangers with spiral pipe configuration. Appl. Therm. Eng. 2015, 87, 655–668. [Google Scholar] [CrossRef]
- Arun, G.; Babu, S.K.; Natarajan, S.; Kulasekharan, N. Study of flow behaviour in sharp and mitred pipe bends. Mater. Today Proc. 2019, 27, 2101–2108. [Google Scholar] [CrossRef]
- Valsala, R.R.; Son, S.W.; Suryan, A.; Kim, H.D. Study on reduction in pressure losses in pipe bends using guide vanes. J. Vis. 2019, 22, 795–807. [Google Scholar] [CrossRef]
- Enayet, M.; Gibson, M.; Taylor, A.; Yianneskis, M. Laser-Doppler measurements of laminar and turbulent flow in a pipe bend. Int. J. Heat Fluid Flow 1982, 3, 213–219. [Google Scholar] [CrossRef] [Green Version]
- Sudo, K.; Sumida, M.; Hibara, H. Experimental investigation on turbulent flow in a circular-sectioned 90-degree bend. Exp. Fluids 1998, 25, 42–49. [Google Scholar] [CrossRef]
- Sudo, K.; Sumida, M.; Hibara, H. Experimental investigation on turbulent flow through a circular-sectioned 180° bend. Exp. Fluids 2000, 28, 51–57. [Google Scholar] [CrossRef]
- Carlsson, C.; Alenius, E.; Fuchs, L. Swirl switching in turbulent flow through 90° pipe bends. Phys. Fluids 2015, 27, 085112. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, D.; Tao, J.; Zhu, Z.; Guo, X. Transient Regulating Characteristics of V-Port Ball Valve in Opening and Closing Process. J. Fluids Eng. 2022, 144, 101201. [Google Scholar] [CrossRef]
- Wang, X.; He, M. Numerical simulation of wing-body junction turbulence flow. Appl. Math. Mech. 1993, 14, 581–587. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Akin, A.; Kahveci, H.S. Effect of turbulence modeling for the prediction of flow and heat transfer in rotorcraft avionics bay. Aerosp. Sci. Technol. 2019, 95, 105453. [Google Scholar] [CrossRef]
- Tian, Z.F.; Tu, J.Y.; Yeoh, G. CFD Studies of Indoor Airflow and Contaminant Particle Transportation. Part. Sci. Technol. 2007, 25, 555–570. [Google Scholar] [CrossRef]
- Qian, Z.D.; Hu, X.Q.; Huai, W.X.; Amador, A. Numerical simulation and analysis of water flow over stepped spillways. Sci. China Ser. E Technol. Sci. 2009, 52, 1958–1965. [Google Scholar] [CrossRef]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Liu, L.; Li, S.; Guo, P.; Wang, X. Natural wind impact analysis of transiting test method to measure wind pressure coefficients. Wind. Struct. 2020, 30, 199–210. [Google Scholar] [CrossRef]
- Xu, B.; Feng, J.; Shen, X.; Zhang, D.; Zhang, W. Numerical investigation of cavitation suppression in an inducer for water and liquid nitrogen with emphasis on thermodynamic effect. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 212. [Google Scholar] [CrossRef]
- Zou, Q.; Li, Z.; Wu, H.; Kuang, R.; Hui, Y. Wind pressure distribution on trough concentrator and fluctuating wind pressure characteristics. Sol. Energy 2015, 120, 464–478. [Google Scholar] [CrossRef]
- Cui, B.; Lin, Z.; Zhu, Z.; Wang, H.; Ma, G. Influence of opening and closing process of ball valve on external performance and internal flow characteristics. Exp. Therm. Fluid Sci. 2017, 80, 193–202. [Google Scholar] [CrossRef]
- Tao, J.; Lin, Z.; Ma, C.; Ye, J.; Zhu, Z.; Li, Y.; Mao, W. An Experimental and Numerical Study of Regulating Performance and Flow Loss in a V-Port Ball Valve. ASME J. Fluids Eng. 2020, 142, 021207. [Google Scholar] [CrossRef]

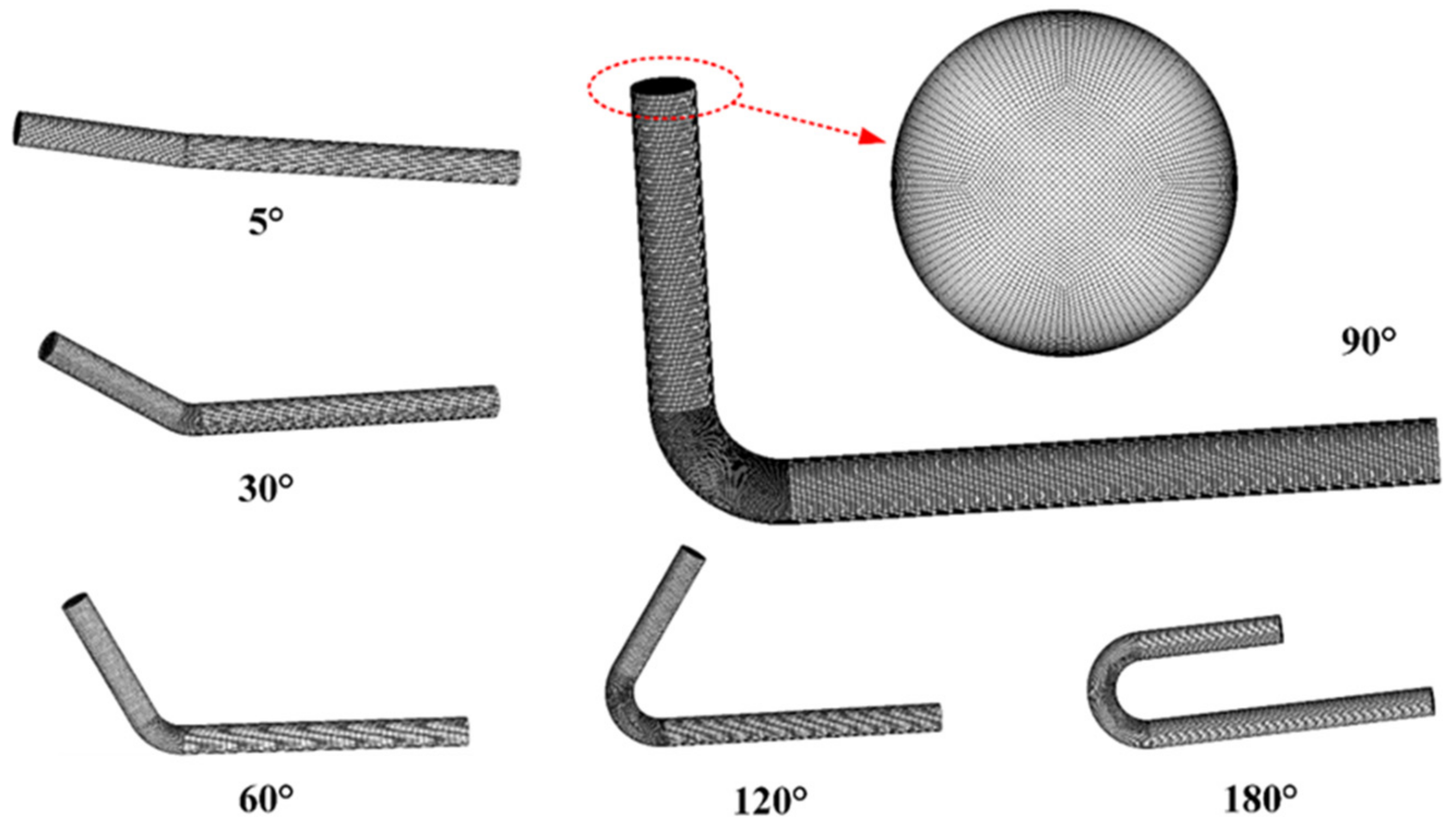



| No. | Mesh Number (×104) | Pressure Coefficient | Relative Error (%) |
|---|---|---|---|
| 1 | 45 | 1.3972 | 0.59 |
| 2 | 90 | 1.4055 | 1.03 |
| 3 | 140 | 1.4201 | 0.53 |
| 4 | 170 | 1.4277 | 0.16 |
| 5 | 200 | 1.4300 | 0.26 |
| 6 | 260 | 1.4336 | —— |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, D.; Wang, W.; Zhu, Z. Numerical Investigation and Optimization of the Flow Characteristics of Bend Pipe with Different Bending Angles. Processes 2022, 10, 1510. https://doi.org/10.3390/pr10081510
Zhang J, Wang D, Wang W, Zhu Z. Numerical Investigation and Optimization of the Flow Characteristics of Bend Pipe with Different Bending Angles. Processes. 2022; 10(8):1510. https://doi.org/10.3390/pr10081510
Chicago/Turabian StyleZhang, Jianyi, Dongrui Wang, Weiwei Wang, and Zuchao Zhu. 2022. "Numerical Investigation and Optimization of the Flow Characteristics of Bend Pipe with Different Bending Angles" Processes 10, no. 8: 1510. https://doi.org/10.3390/pr10081510
APA StyleZhang, J., Wang, D., Wang, W., & Zhu, Z. (2022). Numerical Investigation and Optimization of the Flow Characteristics of Bend Pipe with Different Bending Angles. Processes, 10(8), 1510. https://doi.org/10.3390/pr10081510





