Abstract
A continuous nonsingular fast terminal sliding mode (CNFTSM) control strategy with an automated double power reaching law is proposed to improve the performance of speed dynamic response and accuracy tracking for the permanent magnet synchronous motor (PMSM) servo system. In pursuit of robustness against system uncertainties, a finite-time convergent extended state observer (ESO) is designed to estimate external disturbances, parameter variation, and unmodeled dynamics as a feedforward compensation to the output feedback control system. The developed controller, based on Lyapunov stability theory analysis, can guarantee finite time stability from any initial state in the presence of internal and external disturbances. The modified sliding mode reaching law can achieve enough convergence rate compared with the exponential reaching law, and the inherent chattering of sliding mode is reduced when system states approach the equilibrium point. Theoretical analysis and simulation results demonstrate that the proposed composite controller can achieve higher performance than the conventional sliding mode method.
1. Introduction
As a typical alternating current electric machine drive system, the permanent magnet synchronous motor (PMSM) attracts huge attention because of its advantages, such as high efficiency, high power density, high torque to inertia ratio, low noise, and simple maintenance, which is widely considered as a higher precision machine drive with the most potential application [1,2]. Not surprisingly, ensuring the fast-tracking and anti-interference performance of linear and nonlinear dynamic control systems has always been a fundamental problem of modern control theory [3]. To achieve the desired high precision servo performance, the design of the PMSM controller is still crucial and challenging due to the large quantities of disturbances and uncertainties which are derived from the multiple sources of disturbances [4]: induced torque, mechanical and electrical parameters, load torque, to name but a few [5,6]. When the ambient temperature of the motor changes, the parameters of the motor vary accordingly, it is generally assumed that the variation is within a specific range. In the practical PMSM system, the external load signal is complex and usually contains high-frequency components, which are difficult to measure directly and eliminate. In addition, although the magnetic field orientation mechanism is generally employed, it is still nonlinear and strongly coupled during the electromagnetic conversion in the PMSM system [7].
The sliding mode control (SMC) technique as a particular approach to a robust nonlinear control system has the excellent advantage of fast transient response, insensitivity to uncertainties, and simplicity of practical application [8,9,10,11,12,13]. In recent decades, much fruitful research based on sliding mode control for PMSM has been vigorously investigated. In the reference [14], to improve the convergence rate, the nonlinear sliding surface proposed in the reference [8] is used for the speed closed-loop control of PMSM. Because of the existence of a terminal attractor, the states converge to the origin in finite time; compared with the linear sliding surface, the convergence performance is improved, and chattering is reduced to some extent. Further, A global fast terminal sliding mode (FTSM) has been introduced for the PMSM drive system in [15]. In [16], by introducing a virtual control, a continuously improved sliding mode controller is developed based on the terminal sliding mode surface and has globally asymptotic stability for the PMSM drive system with matched and mismatched disturbances. Compared with the terminal sliding mode (TSM), the PMSM control system achieves faster convergence in both the sliding mode stage and the arrival stage, resulting in fast response and high control accuracy. Nevertheless, it should be pointed out that the robustness and rapidity of the sliding mode controller, mainly referring to the insensitivity to system uncertainties, are guaranteed by increasing the switch gain. Consequently, the control gain will cause greater chattering with the significant disturbance. In this respect, it is essential to avoid the tradeoff by adjusting the sliding mode reaching law, with which the reaching rate is increased accordingly before getting to the setpoint of the motor speed. At the same time, the acceptable chattering level of the controller can be maintained when it is close to the sliding mode surface.
Another attractive topic is to combine SMC with other disturbance estimation techniques to reject the disturbance and improve the robustness. The main advantage is that the online estimation of the system uncertainty can be compensated to the feedback controller to achieve the so-called dynamic compensation linearization [17,18] and reach the control effect of the nominal system. This idea of disturbance feedforward compensation control has been applied in PMSM drive motion systems [5,19,20,21]. The combination of disturbance observer and sliding mode control not only improves the ability to reject disturbances of the system but also is authentically resultful in weakening the requirement of control gain for chattering. These methods have been widely used and tested in PMSM drive control systems, and the test results show that good performance can be obtained.
In recent years, the ESO-based SMC method has provided an intuitive solution for robustness and chattering attenuation [4,7,22]. However, it is worth noting that only asymptotic convergence can be achieved due to the structural limitation of linear extended state observer (LESO), not the fast finite-time convergence property. Further, as a disturbance observer in the PMSM system, the estimation error is obviously not small enough for the application, which affects the high control performance.
In this paper, a continuous nonlinear sliding mode surface is introduced to the FTSM controller for the speed closed-loop PMSM drive system. Involving the absolute value and signum operator [23], it is naturally singularity-free; as a result of that, there is not any negative fractional power term. For the adaptability of reaching law, the coefficient of which takes the tracking error as an adjustable parameter; thus, an improved double power reaching law (DPRL) is designed to obtain a faster speed when it is far from the origin and less chattering when close to the equilibrium point. Besides, a finite time ESO based on the PMSM state equation is proposed for rejecting disturbance actively, which can estimate the total disturbance [24] caused by parameter perturbation, unmodeled dynamics, and external load torque. Combined with the output-feedback sliding mode control, a comprehensive controller is constituted via the feedforward method and disturbance observer (DO) technique to achieve high-performance motion control. The paper’s main contribution is summarized as follows: (1) for the practical PMSM servo system under a disturbance observer-based SMC strategy, the control problems on reducing the adverse effects caused by excessive gains are considered and addressed. Unlike the solutions seeking a method different from the composite strategy, the proposed method in this paper aims to improve sliding mode reaching law and develop the extended state observer for enhancing fast convergence and rejecting disturbance ability. (2) a continuous nonsingular fast terminal sliding mode with an improved double power reaching law is proposed to ensure rapid convergence near and far from the equilibrium point, naturally avoiding the singularity problem. As a matter of fact, the variation range of the PMSM speed will be relatively large; this will inevitably result in the need for a larger control gain to obtain a better tracking dynamic. Therefore, based on this proposed sliding mode controller, enough tracking speed can be obtained precisely due to the adaptable reaching law, compared with other results of PMSM servo control methods. 3) instead of the traditional design, a reconstructed nonlinear extended state observer (NESO) with finite-time convergence is proposed to improve the disturbance observing ability. The estimation error can be reduced exponentially in contrast to the traditional LESO under the same observer gains. In this way, the adverse effects of the composite control scheme, such as chattering, are acceptable largely depending on the observer’s accuracy.
The rest context of this paper is arranged as follows. The dynamic model of the PMSM is described in Section 2. Based on the adaptive fast power approach law, a continuous nonsingular fast terminal sliding mode (CNFTSM) controller is designed in Section 3. In Section 4, a finite time nonlinear extended state observer for disturbances estimation is studied. The paper is concluded in Section 5.
2. Dynamic Model of PMSM
According to the motor vector control (VC) theory, through coordinate transformation, the current vector is decomposed into the current components generating flux and torque. These two components are perpendicular and independent of each other; in this way, they can be adjusted separately for the double closed-loop control similar to the direct current (DC) motor. Making d-axis consistent with the excitation axis of the permanent magnet, the electrical and mechanical dynamic equations of PMSM can be described in the rotor rotating coordinates (d-q axis) as follows:
where is the rotor velocity; , , , , , denote stator currents, stator voltages, and inductances of the d-axis and q-axis, respectively; denotes the load torque, which is usually unknown disturbance; is the stator resistance; is the number of pole pairs, is the rotor flux linkage; is the moment of inertia and is the viscous frictional coefficient. is defined as the torque constant.
In this paper, the surface-mounted PMSM, i.e., , is studied. The corresponding electromagnetic torque is obtained as
From (2), the torque is linearly related to the q-axis current so that the speed of PMSM can be controlled by adjusting the q-axis current. In the field-oriented control (FOC), the maximum torque control can be achieved by keeping the d-axis current at zero. Consequently, the decoupling dynamic equation can be expressed as
where is the control signal. It is obvious that the load torque here is the unmatched disturbance [25].
Although the definite motion model is established, a practical PMSM servo system still has to face multiple sources of uncertainties/disturbances arising from the current sensor, encoder, inverter module, flux harmonics, and the external torque. This paper attempts to design a composite high-performance speed controller for a PMSM system based on the sliding mode theory and disturbance observer so that the output of the system can track its given speed with rapid response and small fluctuation as possible under matched and unmatched uncertainties.
3. Design of the NFTSM Controller for PMSM
The objective of the proposed control strategy is that the PMSM speed tracking system can not only run reliably and achieve satisfactory dynamic response and accuracy tracking performance but also be strongly robust to model uncertainties and external disturbances with the attenuated chattering caused by switching. As shown in Figure 1, the schematic diagram of the proposed PMSM control system is a typical cascade control structure [26]. Under the FOC strategy, the PMSM drive system consists of two current loops that adopt standard proportional-integral (PI) controllers for the stability of the d-axis and q-axis current [7]. Subsequently, we will pay attention to exploring a controller for the speed loop to obtain higher performance. The proposed control method based on the sliding mode feedback control and a nonlinear ESO is illustrated as follows.
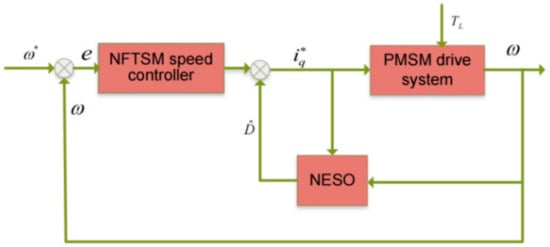
Figure 1.
Schematic diagram of PMSM control system.
3.1. Speed Control Model
For the electromagnetic parameters of the motor varying with the external working conditions (i.e., temperature), the PMSM mathematical model is perturbed. Considering these variations, we can define
where are perturbations of electrical and mechanical parameters.
Let , , , then the first equation in the speed loop of (3) can be rewritten as
In addition, considering the electromagnetic characteristics of the motor, such as magnetic circuit saturation, hysteresis, and eddy current loss, as well as the nonsinusoidal spatial distribution of the magnetic field, which is also the unique uncertainty of the motor system, the lumped uncertainties of PMSM, can be expressed as follows:
where denotes other uncertainties caused by unmodeled dynamics. It should be pointed out that in the practical system, the value can not be absolutely zero, and there is always a dynamic change. However, it is very small for the stabilization of closed-loop systems with linear controllers. In summary, is an entirely unknown uncertainty in a comprehensive sense.
Substituting (6) into (5) gives
Define the tracking error between reference speed and output speed as
where is the reference speed.
The error differential equation of (8) becomes
where represents the lumped disturbances, including the system uncertainties and the external disturbance .
In the speed control system, let the state variable , the output feedback state equation is described as follows:
From (10), the load torque in (3) has been lumped into , which meets the matched condition so that the traditional sliding mode control method can be designed for the PMSM system. However, due to the constraints of including the uncertainties originating from the system hardware itself and model parameters with the exception of , a large control gain is needed. This will, in turn, produce adverse effects on the system, such as amplifying measurement noise. Ideally, an observer is designed to estimate the disturbance and then compensate it to the output feedback controller to obtain the nominal performance of the system [18].
3.2. Nonsingular Fast Terminal Sliding Surface
To enhance the rapidity of system response, the terminal sliding mode (TSM) controller [27] and the fast terminal sliding mode (FTSM) controller [28] are developed to achieve finite-time convergence using adopting nonlinear sliding surfaces. The difference is that the FTSM has ensured a faster convergence rate when states are both far from and close to the equilibrium point.
For system (10), the robust nonsingular fast terminal sliding mode surface [29] is designed as follows:
where the symbol sign denotes the signum function,
and
are the positive constants, and .
By using the sliding surface described in Equation (11), the system can quickly converge from any initial state to zero in finite time, yet without singularity [26]. In fact, the first item of (11) guarantees fast convergence when the system state is far away from the equilibrium point. In contrast, when it is close to equilibrium, the second item plays a leading role in ensuring the system converges in finite time.
After reaching the sliding surface, i.e., , the dynamic trajectory of the system state is determined by
It is not hard to observe that the state variables from any initial condition in finite time with dynamics described by (11), and the settling time is discussed and given in [29]. In SMC application, the control law should be designed after selecting the above sliding surface so that the system can achieve finite-time convergence even in the presence of disturbances. For this goal, the following assumption is required.
Assumption 1.
The derivative of lumped disturbances in (10) is bounded, satisfying for , where denotes the upper bound of the lumped disturbances.
3.3. Double Power Fast Reaching Law
For the speed tracking control system of PMSM, the sliding mode variables often have a significant initial value when the motor starts or the speed of its changes. In view of this control characteristic, this paper proposes a fast double power reaching law with a variable coefficient to improve the convergence rate in the reaching phase. At the same time, the control effect will adjust based on the distance between the state and the equilibrium point to reduce the chattering while maintaining faster convergence.
To make the tracking error dynamic system fast converge to the sliding surface (11) from the initial state, the double power sliding mode reaching law is designed as
where .
The outstanding advantage of the double power reaching law is that it can achieve fast convergence when the initial value of sliding mode is large due to the interaction of the two terms in the Equation (13). Furthermore, the dynamics of (13) without any disturbances can converge in a fixed time, and the settling time is bounded by [30].
From (14), it can be seen that the four constant parameters determine the convergence rate regardless of the initial conditions . This means that the settling time can be arbitrarily tuned; however, too large gains will increase the chattering in practical application. From this point of view, it is impossible to achieve absolute perfection, which is restricted by the nature of the sliding mode control method. On the other hand, when in the presence of uncertainties and external disturbances, the system state s can not be guaranteed to converge to zero but to a neighborhood of the origin in finite time. In this way, for the PMSM speed tracking system, the parameters can be designed appropriately according to the control accuracy index for the dynamic and steady-state performance requirements.
To overcome the influence of disturbances, the consequent system chattering also occurs due to the action of the switching signal. It is better to control the system to maintain a small enough neighborhood of zero, which is entirely acceptable relative to the enormous initial state value. On the other hand, the convergence rate is still expected to be relatively large when the state value is outside the origin until the system dynamic approaches the equilibrium point. Given this, we propose a variable coefficient fast double power reaching law based on tracking error state for the quicker convergence in the approaching phase, yet reducing chattering near the equilibrium point.
The new reaching law is designed as follows:
where and are the modified factor. Letting , it can be observed that the added coefficient term is monotonically increasing with respect to the error e. This means that if the system state is far away from the origin, the gain is large, and the reaching speed is fast, even when ; while close to the origin, it is precisely because the value of is positive in the state space beside the equilibrium point that the stable convergence of the system can be guaranteed.
Remark 1.
Parameterandin (14) determine the intrinsic velocity of the designed approach law; if too large, it will produce oscillation. This tradeoff problem can be solved by the adjusting parameter, which is mainly used to vastly accelerate the convergence speed when the error is large.
3.4. CNFTSM Control Law
To achieve fast convergence of the state variables , in the Equation (10) to zero in the presence of the disturbances, we have to drive the variable s in the equation (11) to zero in finite time and then make the system states stay on the sliding surface utilizing the control in the Equation (10).
By setting , which is a necessary condition for the states maintaining on the sliding surface, then we have
Substituting the Equation (10) into (16), the overall control signal is derived as
To facilitate the analysis, the following lemma is introduced.
Lemma 1.
Ref. [31] Suppose thatis a continuously differentiable function and it is positive definite, there exists an open neighborhoodof the originsuch that,and. Then the equilibriumis finite-time stable. Moreover, when,is globally finite-time stable.
The main result of the proposed control law is summarized as follows.
Theorem 1.
Consider the uncertain system 10 satisfying the condition of Assumption 1. Given the sliding mode surface (11), the reaching law (13), and the control law (17), the system trajectory will reach the following neighborhood
of in finite time. That is
The system states that it will reach the following neighborhood and of in a finite time. That is
Proof.
A candidate Lyapunov function is introduced, taking the form
By differentiating (20) and substituting (10) into it, we obtain
Substituting (17) into (21) yields
Let . Then, in terms of Assumption 1, it is obtained
Therefore, for the case , i.e., , as long as the condition is satisfied, we can get
Where . From Lemma 1, it can be recognized that the system is finite-time stable, but with the convergence region
Then for , substituting (16) into system (10) yields
For both and , we can obtain and . Thus it shows that is not an attractor if . Therefore, the sliding mode will be reached within a finite time in the area .
When system states enter the convergence region, there exists , satisfying
Simply transforming yields
Considering (11), it is deduced that when , the system can be guaranteed to converge in finite time, but the trajectory is limited in the region of , not zero point. Thus, the convergence region is obtained
Using the same procedure, the convergence region can be obtained
Therefore, the sliding mode (11) can be reached into , stats and of the system (10) will reach into and , respectively. Thus, the proof is completed. □
Remark 2.
From (17), it can be seen that there exists no high-speed switching term, which is nonsingular and continuous in the control law, thus avoiding the chattering enlarging caused by frequent switching.
Remark 3.
Without any disturbance, it can be obtained from Theorem 1 that the system states will converge to zero in a finite time; that is, no static error tracking can be realized. When disturbances exist, the system states will converge to a neighborhood of in finite time. In this case, the disturbances can be estimated by designing an observer and compensating into the control law. Therefore, even if disturbances exist, the stable convergence of the system can be guaranteed, and the convergence region can be reduced to meet the requirements of control accuracy.
4. Disturbance Observer
It can be seen from (25), (29), and (30) that the error convergence performance of the speed tracking system largely depends on the amount of the uncertain part of the system and the control parameters. Obviously, the method of increasing the control gain is practical and easy to achieve. However, the well-known reason is that this will consume more control energy and increase the chattering of the system, although the chattering has been reduced by using the reaching law (13), compared with the constant rate reaching law (CRRL).
For another way of thinking, the total disturbance can be estimated and then compensated as a feedforward control segment to attenuate or even eliminate the influence of the disturbances, that is, diminishing in (25), to realize active disturbance rejection control. To achieve this goal, a new disturbance observer is introduced.
Considering (7) and (9), the dynamic equation of PMSM can be expressed as
According to the theoretical method of ESO, is defined as a new extended state, then the state equation of PMSM can be obtained as
where is the derivative of . For (28), a second-order extended state observer can be designed as follows
where and denote the estimates of and , respectively; , ; the observer parameters and are designed such that the characteristic polynomial is Hurwitz and , .
Substituting (34) from (33), the error dynamic equation can be obtained
Remark 4.
Referring to [32], the selected parameters can ensure that the reduced system of (34) with, i.e., is stable in finite time.
The convergence of (34) is guaranteed by the following theorem.
Theorem 2.
Suppose that the extended state observer (33) for (32) in which the disturbance is satisfying the condition of Assumption 1. Then the system (34) is stable, and the disturbance D of (33) can be estimated byin finite time with the observer error convergent to the small neighborhood near the origin, satisfying that
Proof.
Consider a Lyapunov function candidate for (34)
It can be seen that is Lipschitz continuous, then the derivative of (36) along the dynamic of (34) is
According to Assumption 1, we can obtain
From (38), if , then . This means that the dynamics of (34) will enter the neighborhood defined by (35) in finite time. Thus, the proof is completed. □
Remark 5.
The main objective of this designed disturbance observer is to track the internal system dynamic uncertainties and external disturbances in time and quickly, not considering the convergence of stateof (33). Certainly, its effectiveness has been verified by the subsequent simulation. Compared with the traditional linear observer, it has the characteristics of finite-time stability.
5. Simulation Results
Simulation analysis is carried out to verify the performance of the proposed nonlinear extended state disturbance observer and the effectiveness of the continuous NFTSM control strategy for speed tracking response of PMSM. The simulations are implemented in MATLAB/Simulink, and the PMSM parameters are listed in Table 1. For performance comparison with our proposed control strategy, the other four methods are nonsingular terminal sliding mode with fast power reaching law (NTSM-FPRL) [23], nonsingular terminal sliding mode with double power reaching law (NFTSM-DPRL), the proposed NFTSM control with state-based double reaching law without disturbance observer (NFTSM-SBDPRL) and the algorithm NFTSM-SBDPRL with the linear extended state observer (NFTSM-SBDPRL-LESO) are also employed for the speed loop of the PMSM system. The LESO method and parameter design refer to the paper [7]. The same PI controller is employed for the d-axis and q-axis current loop with the same parameters: proportional gain and integral gain .

Table 1.
Parameters of PMSM system in simulations when the ambient temperature is 25 °C.
The parameters of the proposed NFTSM-DPRL-NESO method are designed as , , , , , , , , , , , , , .
For fairly and effectively showing the superiority of the designed control strategy, the parameters of the other four control methods are consistent. The simulations are carried out with the variation of load torque and motor parameters for practicality. In practice, the change is mainly caused by the external temperature. See Table 2 for the specific parameter variation. The following simulation scenarios are set: sudden load disturbance for , time-varying load disturbance for , and motor working temperature varying from 20 degrees to 100 degrees for . Response curves of speed control under the four methods are shown in Figure 2. The corresponding q-axis voltage signals are shown in Figure 3, and the three-phase currents signals of the PMSM in Figure 4.

Table 2.
Parameters of PMSM system in simulations when the ambient temperature is 150 °C.
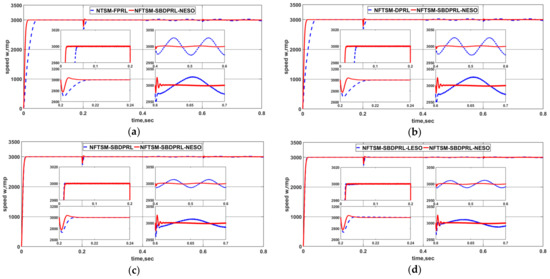
Figure 2.
Response curves of the PMSM under NFTSM-SBDPRL-NESO and the other four control methods for comparison: (a) NTSM-FPRL and NFTSM-SBDPRL-NESO, (b) NFTSM-DPRL and NFTSM-SBDPRL-NESO, (c) NFTSM-SBDPRL and NFTSM-SBDPRL-NESO, (d) NFTSM-SBDPRL-LESO and NFTSM-SBDPRL-NESO.
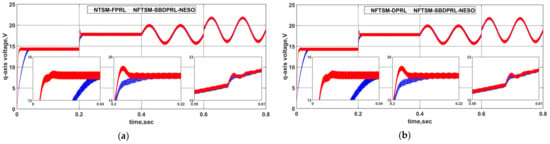
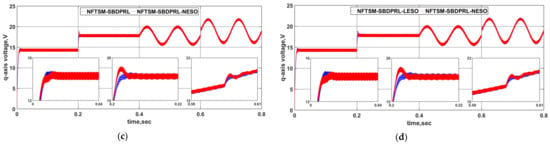
Figure 3.
Control signals (q-axis voltage) of the PMSM under the five control methods for comparison: (a) NTSM-FPRL and NFTSM-SBDPRL-NESO, (b) NFTSM-DPRL and NFTSM-SBDPRL-NESO, (c) NFTSM-SBDPRL and NFTSM-SBDPRL-NESO, (d) NFTSM-SBDPRL-LESO and NFTSM-SBDPRL-NESO.
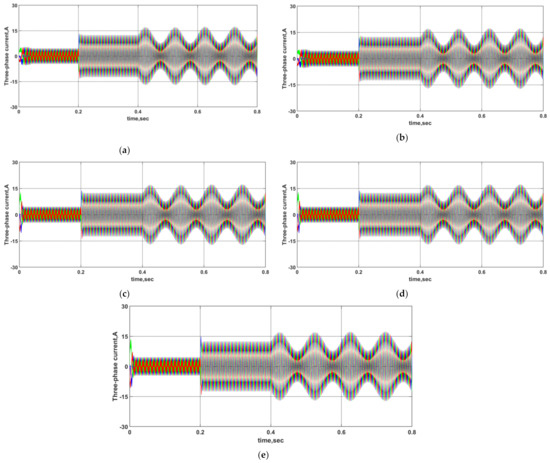
Figure 4.
Three-phase currents of the PMSM under the five control methods for comparison: (a) NTSM-FPRL, (b) NFTSM-DPRL, (c) NFTSM-SBDPRL, (d) NFTSM-SBDPRL-LESO, (e) NFTSM-SBDPRL-NESO.
From Figure 2, it can be observed from 0 to 0.2 that the convergence rate of the proposed NFTSM-SBDPRL algorithm is obviously better than the traditional NTSM-FPRL and NFTSM-DPRL. It is mainly due to the effect of changing coefficient , as stated in Remark 1. When a sudden load torque of 0.5 Nm is imposed on the PMSM at 0.2 , the motor speed appears drooped and is regulated to the target speed after a short transient. For the ability of our improved NESO to estimate the constant torque disturbance in advance and a more accurate estimate than LESO, the proposed NFTSM-SBDPRL-NESO controller has better disturbance rejection performance from the transient response.
To verify the robustness of the control algorithm to time-varying disturbance, a sinusoidal torque is applied to the motor at . From the operation results, the advantages of the algorithm presented in this paper are illustrated: after a short transient, it is almost entirely unaffected by the sinusoidal time-varying disturbance compared with the other four controllers, which can be observed apparently in Figure 5. Finally, the practical scenario simulation of the motor parameters changed due to the temperature varying from 25 °C to 150 °C at shows that the proposed NFTSM-SBDPRL-NESO controller can regulate the motor speed to the desired setpoint flowing a short transient with the fourth-smallest fluctuation.
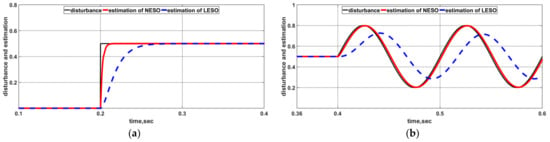
Figure 5.
Performance comparison of two observers under the disturbance of (a) and (b) .
It is noted here that the classical terminal sliding mode and double power reaching law do not show a convincing effect for the high-speed motor servo system, as shown in Figure 2. However, the tracking performance and disturbance resistance ability are greatly improved by using our improved reaching law and disturbance observer for compensation under the same parameters condition. Furthermore, the control scheme integrated with a remarkable disturbance observer shows nominal performance recovery property in the presence of disturbances. Given all of that, all of the above is consistent with the theoretical results, which illustrates the effect of the proposed control method.
6. Conclusions
An improved continuous nonsingular fast terminal sliding mode control algorithm is proposed for the speed tracking of permanent magnet synchronous motor. Moreover, to solve the problem of performance degradation caused by external torque disturbances and motor parameters perturbation, a modified nonlinear extended state observer is designed to estimate these disturbances to feedforward compensation into the sliding mode controller, thus improving the robustness and rapidity of PMSM servo control system. The simulation results and theoretical analysis show that there are several significant properties. Firstly, a reaching law based on speed error adjusting is proposed to make fast-tracking whether the system state is far from or close to the equilibrium point. Secondly, the proposed method involved continuous sliding mode surface and reaching law can alleviate the chattering essentially. Finally, using the designed disturbance observer, the restraining disturbance ability of the system is vastly improved comparatively confronting, whether external or internal disturbances. Further, for the practical application of PMSM, it is crucial to use the composite control strategy that overcomes defects from the feedback control and observer gains effectively.
The major strength of this study is the application significance for actual output tracking systems in the presence of disturbances. Further study is warranted for more experimental results to verify the superiority of the proposed controller. In addition, we have begun investigating a robust finite-time disturbance observer to obtain an unbiased estimation. In this way, by using the feedforward compensation, the finite-time stability of the system can be easily realized through smooth output feedback control for higher performance, which is divorced from the disadvantages of high gain on the system.
Author Contributions
Conceptualization, Y.G. and Y.Y.; methodology, Y.Y.; validation, Y.Y., Y.G. and W.W.; data curation, W.W.; writing—original draft preparation, Y.Y. and W.W.; writing—review and editing, Y.Y., Y.G. and W.W.; supervision, Y.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 62033008), Shandong Provincial Natural Science Foundation (Grant No. ZR2021QF037), the Fundamental Research Funds for the Central Universities (Grant No. 22CX06035A) and the Shandong Key R&D Program-International Science and Technology Cooperation Project (Grant No. 2019GHZ001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Krishnan, R. Electric Motor Drives: Modeling, Analysis, and Control; Prentice-Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Errouissi, R.; Ouhrouche, M.; Chen, W.-H.; Trzynadlowski, A.M. Robust nonlinear predictive controller for permanent magnet synchronous motors with optimized cost function. IEEE Trans. Ind. Electron. 2012, 59, 2849–2858. [Google Scholar] [CrossRef]
- Jiang, T.; Huang, C.; Guo, L. Control of uncertain nonlinear systems based on observers and estimators. Automatica 2015, 59, 11–23. [Google Scholar] [CrossRef]
- Yan, Y.; Yang, J.; Sun, Z.; Zhang, C.; Li, S.; Yu, H. Robust Speed Regulation for PMSM Servo System With Multiple Sources of Disturbances via an Augmented Disturbance Observer. IEEE/ASME Trans. Mechatron. 2018, 23, 769–780. [Google Scholar] [CrossRef]
- Yang, J.; Chen, W.H.; Li, S.; Guo, L.; Yan, Y. Disturbance/Uncertainty Estimation and Attenuation Techniques in PMSM Drives–A Survey. IEEE Trans. Ind. Electron. 2016, 64, 3273–3285. [Google Scholar] [CrossRef] [Green Version]
- Ding, S.; Chen, W.H.; Mei, K.; Murray-Smith, D.J. Disturbance Observer Design for Nonlinear Systems Represented by Input-Output Models. IEEE Trans. Ind. Electron. 2020, 67, 1222–1232. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Liu, H.; Ding, S. A speed control for a PMSM using finite-time feedback control and disturbance compensation. Trans. Inst. Meas. Control. 2010, 32, 170–187. [Google Scholar]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Jin, M.; Lee, J.; Chang, P.H. Practical nonsingular terminal sliding-mode control of robot manipulators for high-accuracy tracking control. IEEE Trans. Ind. Electron. 2009, 56, 3593–3601. [Google Scholar]
- de Loza, A.F.; Cieslak, J.; Henry, D.; Dvila, J.; Zolghadri, A. Sensor fault diagnosis using a non-homogeneous high-order sliding mode observer with application to a transport aircraft. IET Control. Theory Appl. 2015, 9, 598–607. [Google Scholar] [CrossRef]
- Shahinzadeh, H.; Darougaran, L.; Sani, E.J. Design of Power System Stabilizer Based on Sliding Mode Control Theory for Multi-Machine Power System. J. Intell. Proced. Electr. Technol. 2010, 1, 13–22. [Google Scholar]
- Sabanovic, A. Variable structure systems with sliding modes in motion control-A survey. IEEE Trans. Ind. Inform. 2011, 7, 212–223. [Google Scholar] [CrossRef]
- Feng, Y.; Zheng, J.; Yu, X.; Truong, N.V. Hybrid terminal slidingmode observer design method for a permanent-magnet synchronous motor control system. IEEE Trans. Ind. Electron. 2009, 56, 3424–3431. [Google Scholar] [CrossRef]
- Li, S.; Zhou, M.; Yu, X. Design and Implementation of Terminal Sliding Mode Control Method for PMSM Speed Regulation System. IEEE Trans. Ind. Inform. 2013, 9, 1879–1891. [Google Scholar] [CrossRef]
- Teng, Q.; Jin, Y.; Li, S.; Zhu, J.; Guo, Y. GFTSM-based Model Predictive Torque Control for PMSM Drive System With Single Phase Current Sensor. Acta Autom. Sin. 2017, 43, 1644–1655. [Google Scholar]
- Liu, X.; Yu, H. Continuous adaptive integral-type sliding mode control based on disturbance observer for PMSM drives. Nonlinear Dyn. 2021, 104, 1429–1441. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Huang, Y.; Xue, W.C. Active disturbance rejection control: Methodology and theoretical analysis. ISA Trans. 2014, 53, 963–976. [Google Scholar] [CrossRef]
- Xu, W.; Junejo, A.K.; Liu, Y.; Islam, M.R. Improved continuous fast terminal sliding mode control with extended state observer for speed regulation of pmsm drive system. IEEE Trans. Veh. Technol. 2019, 68, 10465–10476. [Google Scholar] [CrossRef]
- Li, T.; Liu, X. Non-Cascade Fast Nonsingular Terminal Sliding Mode Control of Permanent Magnet Synchronous Motor Based on Disturbance Observers. J. Electr. Eng. Technol. 2022, 17, 1061–1075. [Google Scholar] [CrossRef]
- Chang, S.H.; Chen, P.Y.; Ting, Y.H.; Hung, S.W. Robust current control-based sliding mode control with simple uncertainties estimation in permanent magnet synchronous motor drive systems. IET Electr. Power Appl. 2010, 4, 441–450. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, L. Output-Feedback Sliding Mode Control for Permanent Magnet Synchronous Motor Servo System Subject to Unmatched Disturbances. Math. Probl. Eng. 2021, 2021, 6642840. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Guo, B.Z.; Zhao, Z.L. On the convergence of an extended state observer for nonlinear systems with uncertainty. Syst. Control. Lett. 2011, 60, 420–430. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Su, J.; Yu, X. Continuous nonsingular terminal sliding mode control for systems with mismatched disturbances. Automatica 2013, 49, 2287–2291. [Google Scholar] [CrossRef] [Green Version]
- Xia, P.; Deng, Y.; Wang, Z.; Li, H. Speed Adaptive Sliding Mode Control with an Extended State Observer for Permanent Magnet Synchronous Motor. Math. Probl. Eng. 2018, 2018, 6405923. [Google Scholar] [CrossRef] [Green Version]
- Man, Z.; Yu, X.H. Terminal sliding mode control of MIMO linear systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 1065–1070. [Google Scholar]
- Yu, X.; Zhihong, M. Fast terminal sliding-mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2009, 49, 261–264. [Google Scholar]
- Yang, L.; Yang, J. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems. Int. J. Robust Nonlinear Control. 2011, 21, 1865–1879. [Google Scholar] [CrossRef]
- Li, H.; Cai, Y. On SFTSM control with fixed-time convergence. IET Control. Theory Appl. 2017, 11, 766–773. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-Time Stability of Continuous Autonomous Systems. SIAM J. Control. Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Geometric homogeneity with applications to finite-time stability. Math. Control. Signals Syst. 2005, 17, 101–127. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).