Sigmoid-like Event-Triggered Security Cruise Control under Stochastic False Data Injection Attacks
Abstract
:1. Introduction
- A novel Sigmoid-like ETS is proposed to cope with the co-design of the control and communication of CCSs. Compared with the traditional static ETSs [23], adaptive ETSs [21,22] and dynamic ETSs [6,11], the proposed Sigmoid-like ETS will guarantee the upper bound of event-triggered thresholds while making full use of the state perception;
- The security control of CCSs under stochastic FDI attacks is well characterized with the proposed Sigmoid-like ETS. Rather than detecting the FDI attacks in a complicated way [18,19,24], the studied event-triggered security control of CCSs is of performance even on the condition that the FDI attack detection fails.
2. Preliminaries
2.1. Sigmoid-like ETS
- The is a monotonic decreasing function along with ;
- It is obvious that is held.
2.2. Stochastic FDI Attacks
2.3. Control Objectives
3. Main Results
| Algorithm 1: Find the controller gain , event-triggered parameter and weighting matrix |
| 1: Set the positive scalars , and the initial event-triggered parameter . Give the increasing step and an optimization target ; |
| 2: While ; |
| 3: ; |
| 4: Solve LMIs (18), if there is a feasible solution X, , and satisfying LMIs (18), go to the next step. Otherwise, return 1; |
| 5: Return and calculate , . |
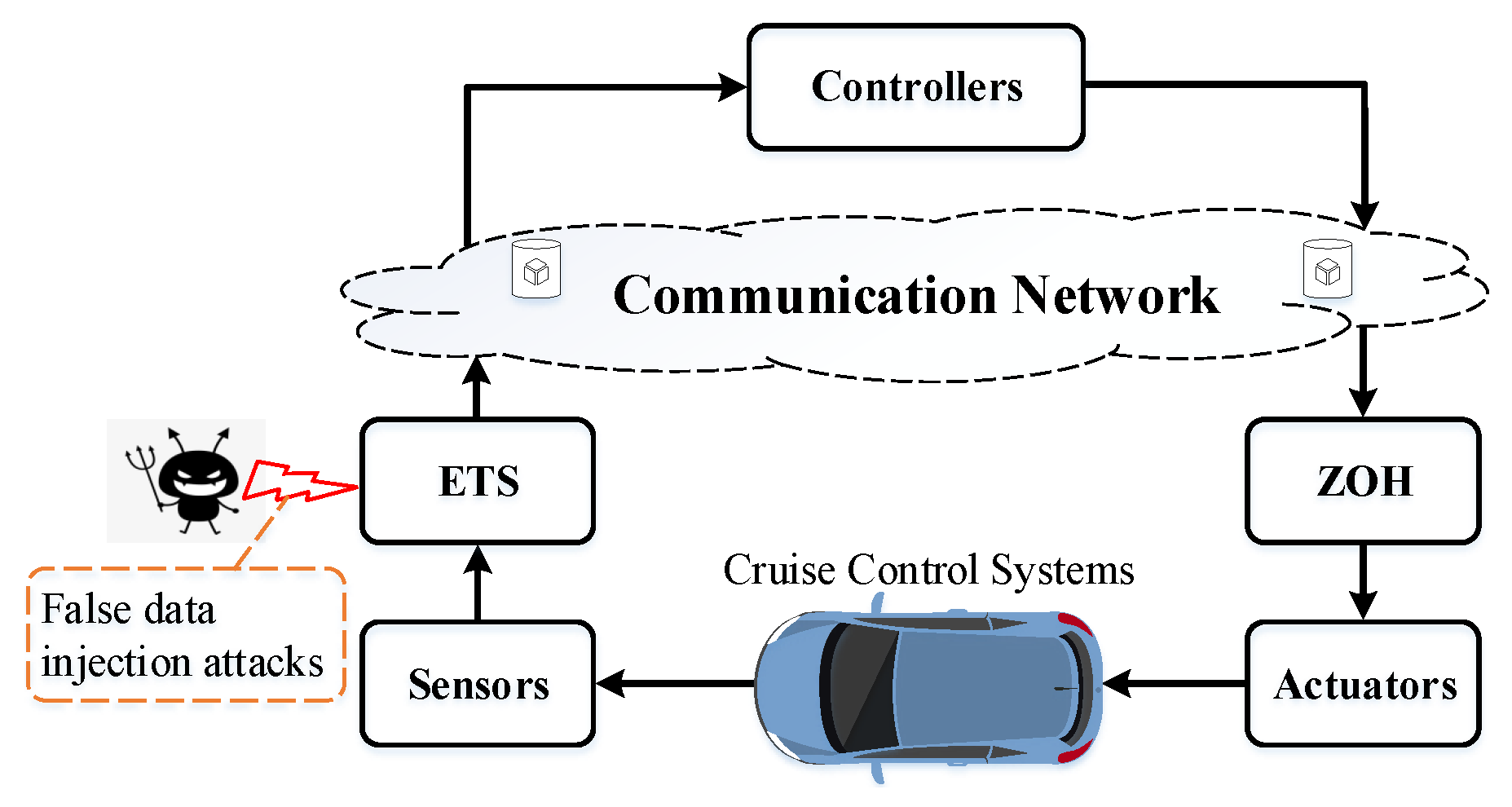
4. Simulation Examples
4.1. Parameters Setting
- System parameters:Set the vehicle to cruise with different velocities: 5 m/s, 10 m/s, 15 m/s. In the system (3), the disturbance is , s, and the other parameters are s, s, s, , , the initial state ;
- FDI attack parameters:The probability of FDI attack is with ⩽ and = ; ; , where the weighting matrix = diag{ };
- Event-triggered parameters:The event-triggered related parameter , , (a is in Sigmoid-like function).
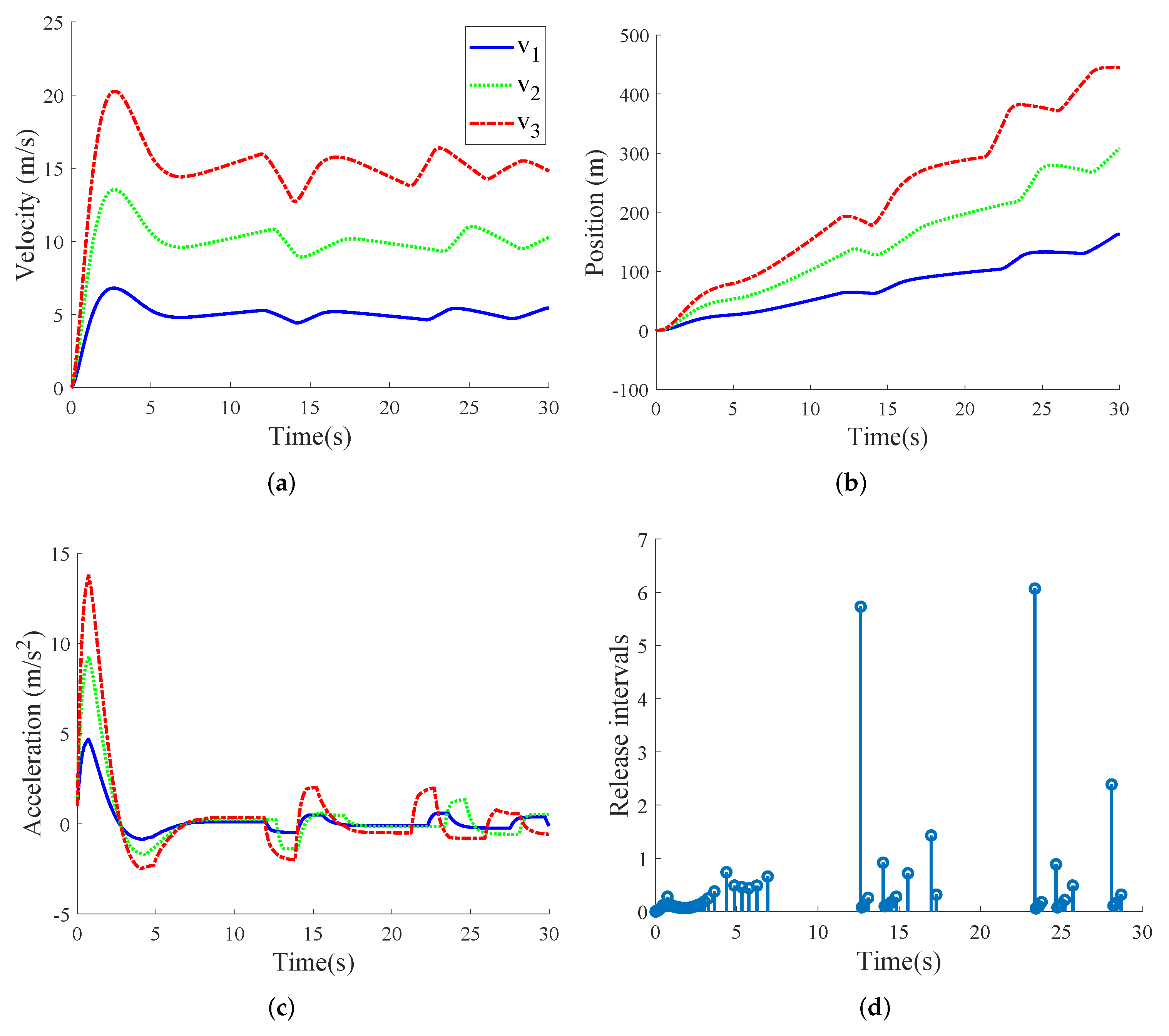
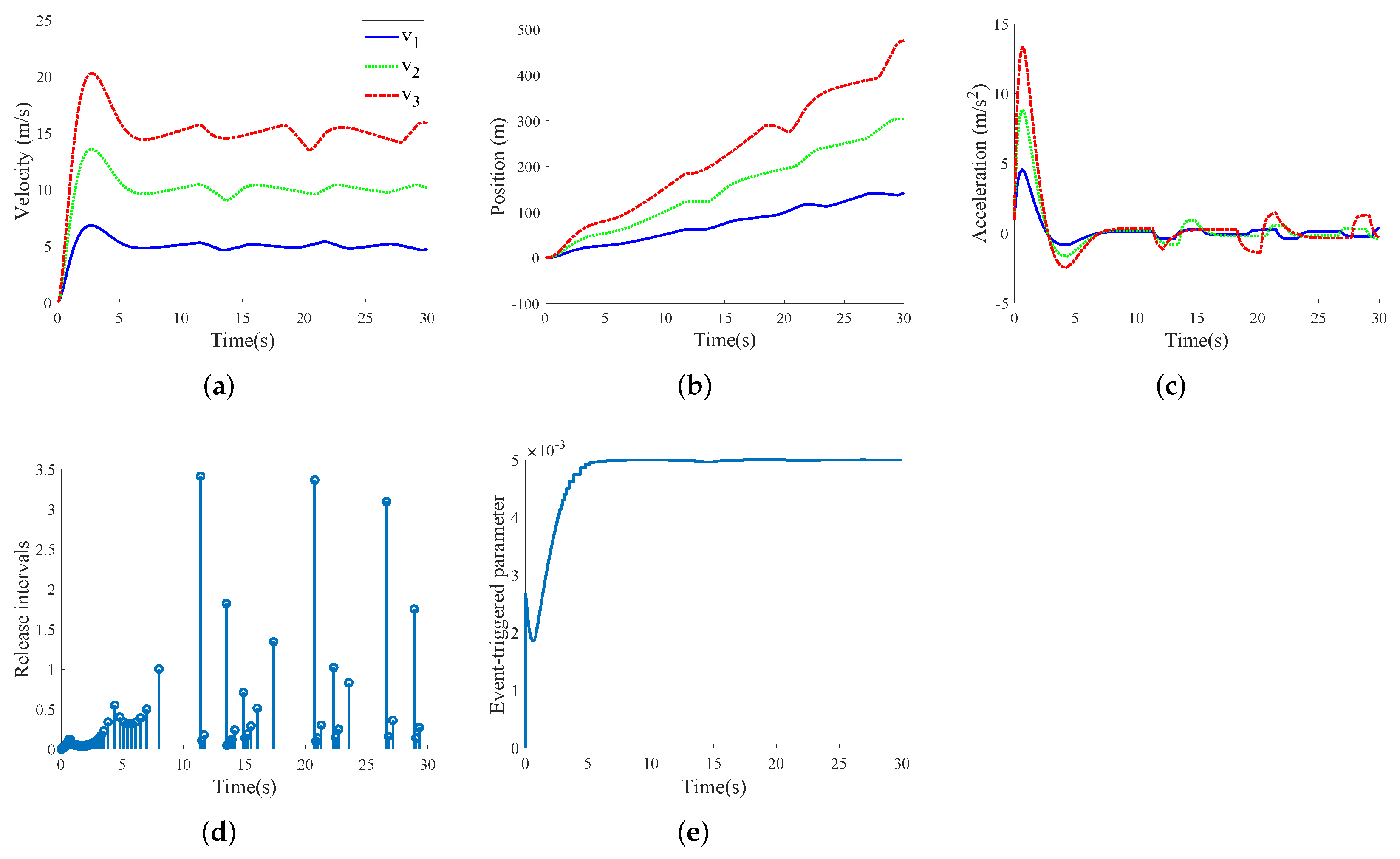
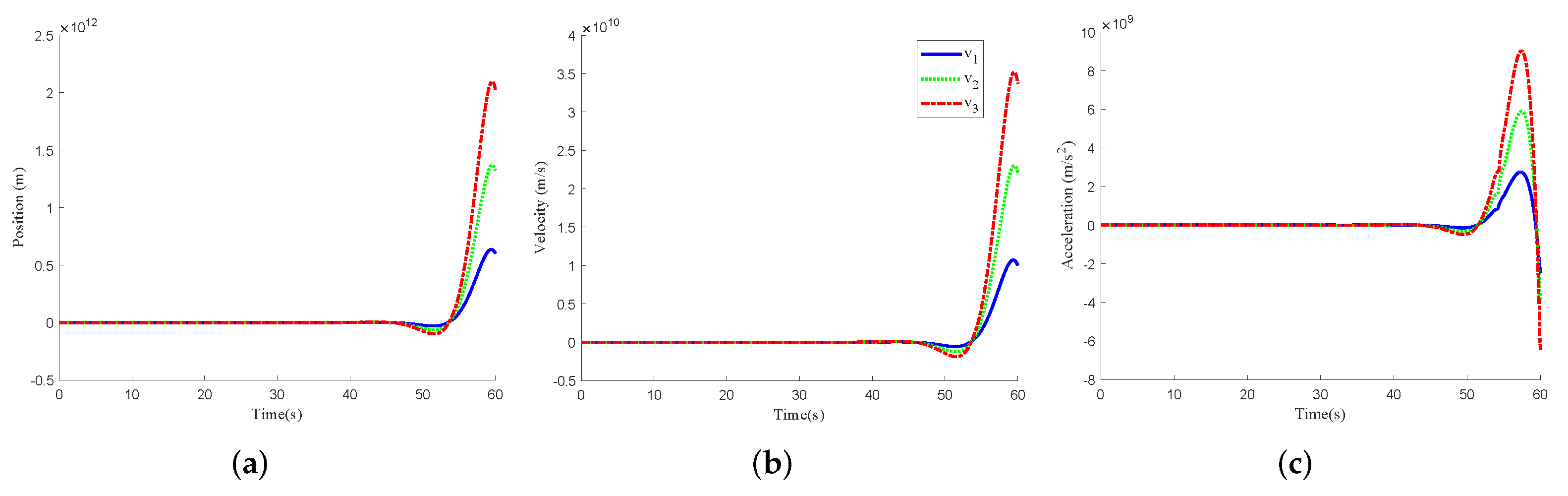
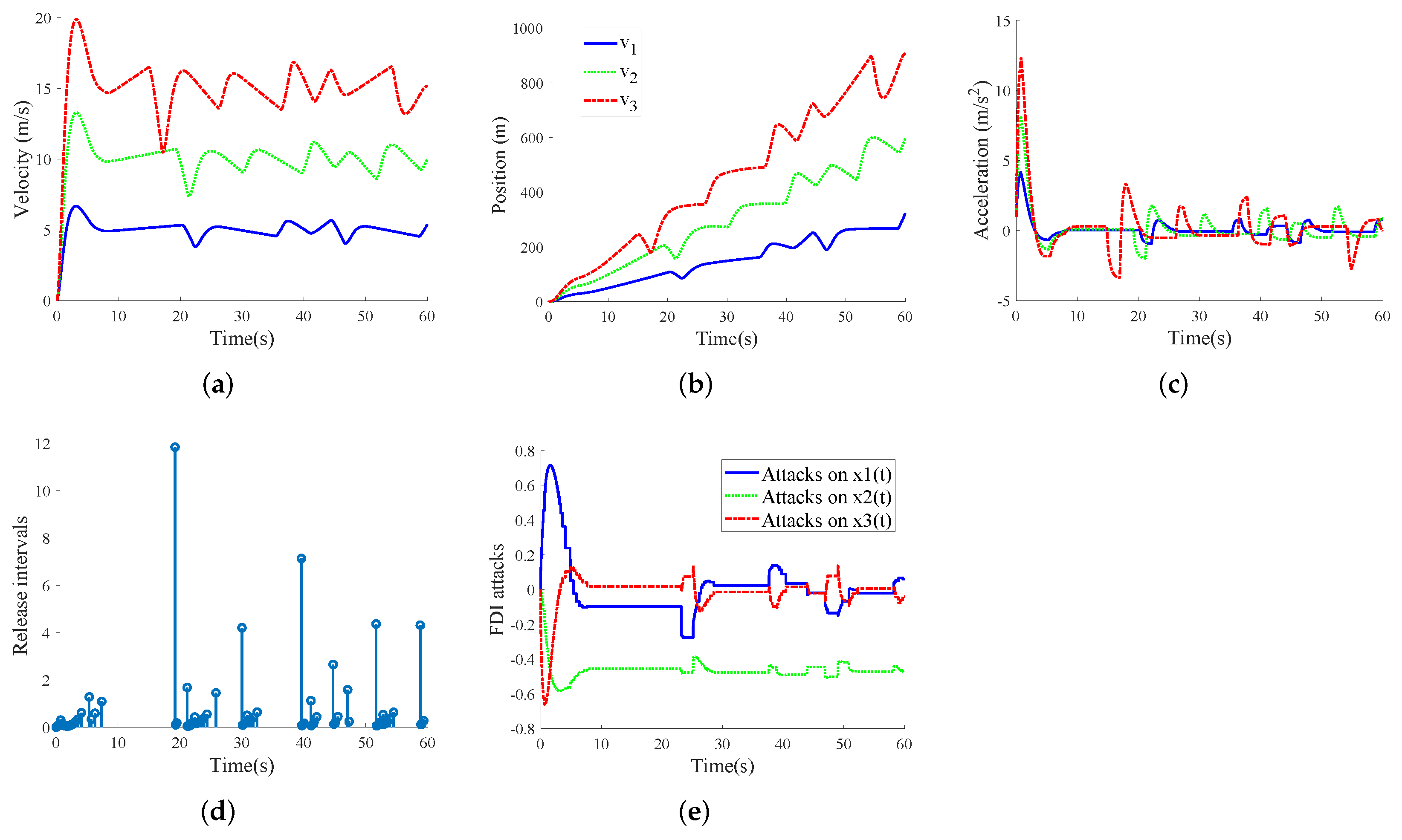
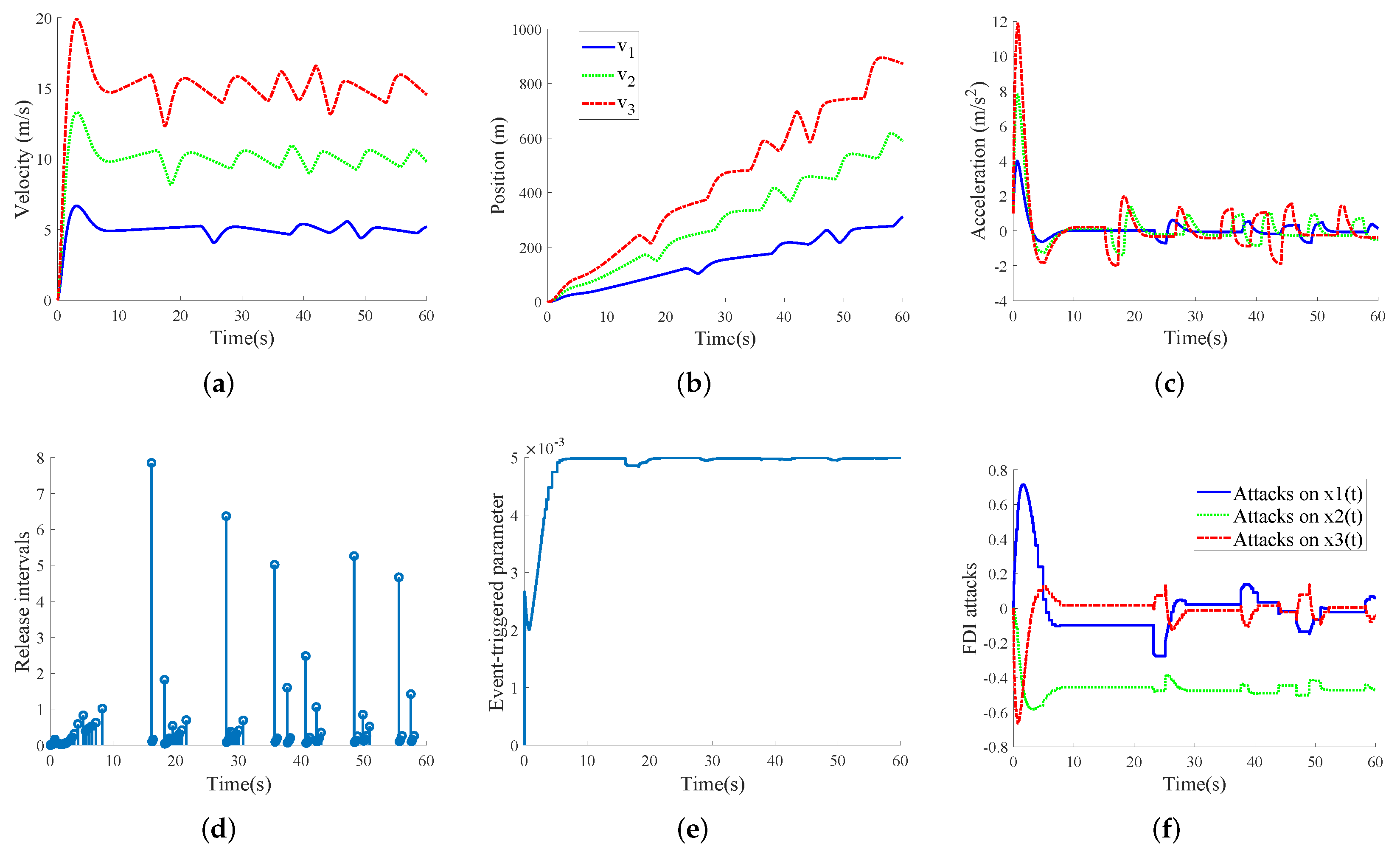
4.2. Discussions of Simulation Results
- Case I: FDI-free case
- Case II: FDI attack case
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Plessen, M.; Bernardini, D.; Esen, H.; Bemporad, A. Spatial-based predictive control and geometric corridor planning for adaptive cruise control coupled with obstacle avoidance. IEEE Trans. Control Syst. Technol. 2018, 26, 38–50. [Google Scholar] [CrossRef]
- Dey, K.; Yan, L.; Wang, X.; Wang, Y.; Shen, H.; Chowdhury, M.; Yu, L.; Qiu, C.; Soundararaj, V. A review of communication, driver characteristics, and controls aspects of cooperative adaptive cruise control. IEEE Trans. Intell. Transp. Syst. 2016, 17, 491–509. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, D.; Zhong, Z. Adaptive optimal control of heterogeneous CACC system with uncertain dynamics. IEEE Trans. Control Syst. Technol. 2019, 27, 1772–1779. [Google Scholar] [CrossRef]
- Dolk, V.; Heemels, M. Event-triggered control systems under packet losses. Automatica 2017, 80, 143–155. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Geng, G.; Yu, J. Delay-optimized multicast tree packing in software-defined networks. IEEE Trans. Serv. Comput. 2021, 1–14. [Google Scholar] [CrossRef]
- Ge, X.; Ahmad, I.; Han, Q.-L.; Wang, J.; Zhang, X.-M. Dynamic event-triggered scheduling and control for vehicle active suspension over controller area network. Mech. Syst. Sig. Process. 2021, 152, 107481. [Google Scholar] [CrossRef]
- Peng, C.; Tian, Y.; Yue, D. Output feedback control of discrete-time systems in networked environments. IEEE Trans. Syst. Man Cybern. A Syst. Humans 2011, 41, 185–190. [Google Scholar] [CrossRef] [Green Version]
- Heemels, W.; Donkers, M. Model-based periodic event-triggered control for linear systems. Automatica 2013, 49, 698–711. [Google Scholar] [CrossRef]
- Xu, W.; Ho, D.; Zhong, J.; Chen, B. Event/self-triggered control for leader-following consensus over unreliable network with DoS attacks. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3137–3149. [Google Scholar] [CrossRef]
- Peng, C.; Yang, M.; Zhang, J. Network-based H∞ control for T-S fuzzy systems with an adaptive event-triggered communication scheme. Fuzzy Sets Syst. 2017, 329, 61–76. [Google Scholar] [CrossRef]
- Dolk, V.; Borgers, D.; Heemels, W.P.M.H. Output-based and decentralized dynamic event-triggered control with guaranteed Lp- gain performance and Zeno-freeness. IEEE Trans. Autom. Control 2017, 62, 34–49. [Google Scholar] [CrossRef]
- Wang, K.; Tian, E.; Liu, J.; Wei, L.; Yue, D. Resilient control of networked control systems under deception attacks: A memory-event-triggered communication scheme. Int. J. Robust Nonlinear Control 2020, 30, 1534–1548. [Google Scholar] [CrossRef]
- Guo, G.; Ding, L.; Han, Q.-L. A distributed event-triggered transmission strategy for sampled-data consensus of multi-agent systems. Automatica 2014, 50, 1489–1496. [Google Scholar] [CrossRef]
- Gu, Z.; Park, J.; Yue, D.; Wu, Z.; Xie, X. Event-triggered security output feedback control for networked interconnected systems subject to cyber-attacks. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 6197–6206. [Google Scholar] [CrossRef]
- Sun, H.-T.; Peng, C.; Ding, F. Self-discipline predictive control of autonomous vehicles against denial of service attacks. Asian J. Control 2022, 1–14. [Google Scholar] [CrossRef]
- Takemori, K.; Mizoguchi, S.; Kawabata, H.; Kubota, A. In-vehicle network security using secure element. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2016, E99.A, 208–216. [Google Scholar] [CrossRef]
- Sun, H.-T.; Peng, C.; Tan, C. Self-discipline predictive control against large-scale packet dropouts using input delay approach. Int. J. Syst. Sci. 2022, 53, 934–947. [Google Scholar] [CrossRef]
- Zivkovic, N.; Saric, A. Detection of false data injection attacks using unscented Kalman filter. J. Mod. Power Syst. Clean Energy 2018, 6, 847–859. [Google Scholar] [CrossRef] [Green Version]
- Deng, R.; Zhuang, P.; Liang, H. CCPA: Coordinated cyber-physical attacks and countermeasures in smart grid. IEEE Trans. Smart Grid 2017, 8, 2420–2430. [Google Scholar] [CrossRef]
- Tian, E.; Peng, C. Memory-based event-triggering H∞ load frequency control for power systems under deception attacks. IEEE Trans. Cybern. 2020, 50, 4610–4618. [Google Scholar] [CrossRef]
- Sun, H.; Peng, C.; Yue, D.; Wang, Y.; Zhang, T. Resilient load frequency control of cyber-physical power systems under QoS-dependent event-triggered communication. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2113–2122. [Google Scholar] [CrossRef]
- Liu, J.; Gu, Y.; Zha, L.; Liu, Y.; Cao, J. Event-triggered H∞ load frequency control for multiarea power systems under hybrid cyber attacks. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1665–1678. [Google Scholar] [CrossRef]
- Peng, C.; Yang, T. Event-triggered communication and H∞ control co-design for networked control systems. Automatica 2013, 49, 1326–1332. [Google Scholar] [CrossRef]
- Musleh, A.; Chen, G.; Dong, Z. A survey on the detection algorithms for false data injection attacks in smart grids. IEEE Trans. Smart Grid 2019, 11, 2218–2234. [Google Scholar] [CrossRef]
- Liu, J.; Xia, J.; Tian, E.; Fei, S. Hybrid-driven-based H∞ filter design for neural networks subject to deception attacks. Appl. Math. Comput. 2018, 320, 157–174. [Google Scholar] [CrossRef]
- Han, Q.-L. Absolute stability of time-delay systems with sector-bounded nonlinearity. Automatica 2005, 41, 2171–2176. [Google Scholar] [CrossRef]

| N | T | |||
|---|---|---|---|---|
| 0.2 | 75 | 114 | 0.3824 | 0.2599 |
| 0.3 | 72 | 111 | 0.3321 | 0.2508 |
| 0.4 | 63 | 118 | 0.4563 | 0.2536 |
| 0.5 | 61 | 158 | 0.4633 | 0.1271 |
| 0.6 | 69 | 418 | 0.4046 | 0.0710 |
| 0.7 | 71 | 2357 | 0.4189 | 0.0126 |
| 0.8 | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Sun, H.; Peng, C.; Tan, C. Sigmoid-like Event-Triggered Security Cruise Control under Stochastic False Data Injection Attacks. Processes 2022, 10, 1326. https://doi.org/10.3390/pr10071326
Zhang P, Sun H, Peng C, Tan C. Sigmoid-like Event-Triggered Security Cruise Control under Stochastic False Data Injection Attacks. Processes. 2022; 10(7):1326. https://doi.org/10.3390/pr10071326
Chicago/Turabian StyleZhang, Pengfei, Hongtao Sun, Chen Peng, and Cheng Tan. 2022. "Sigmoid-like Event-Triggered Security Cruise Control under Stochastic False Data Injection Attacks" Processes 10, no. 7: 1326. https://doi.org/10.3390/pr10071326
APA StyleZhang, P., Sun, H., Peng, C., & Tan, C. (2022). Sigmoid-like Event-Triggered Security Cruise Control under Stochastic False Data Injection Attacks. Processes, 10(7), 1326. https://doi.org/10.3390/pr10071326






