Combined Grey Wolf Optimizer Algorithm and Corrected Gaussian Diffusion Model in Source Term Estimation
Abstract
:1. Introduction
2. Models and Methods
2.1. STE Model Based on Optimization Algorithm
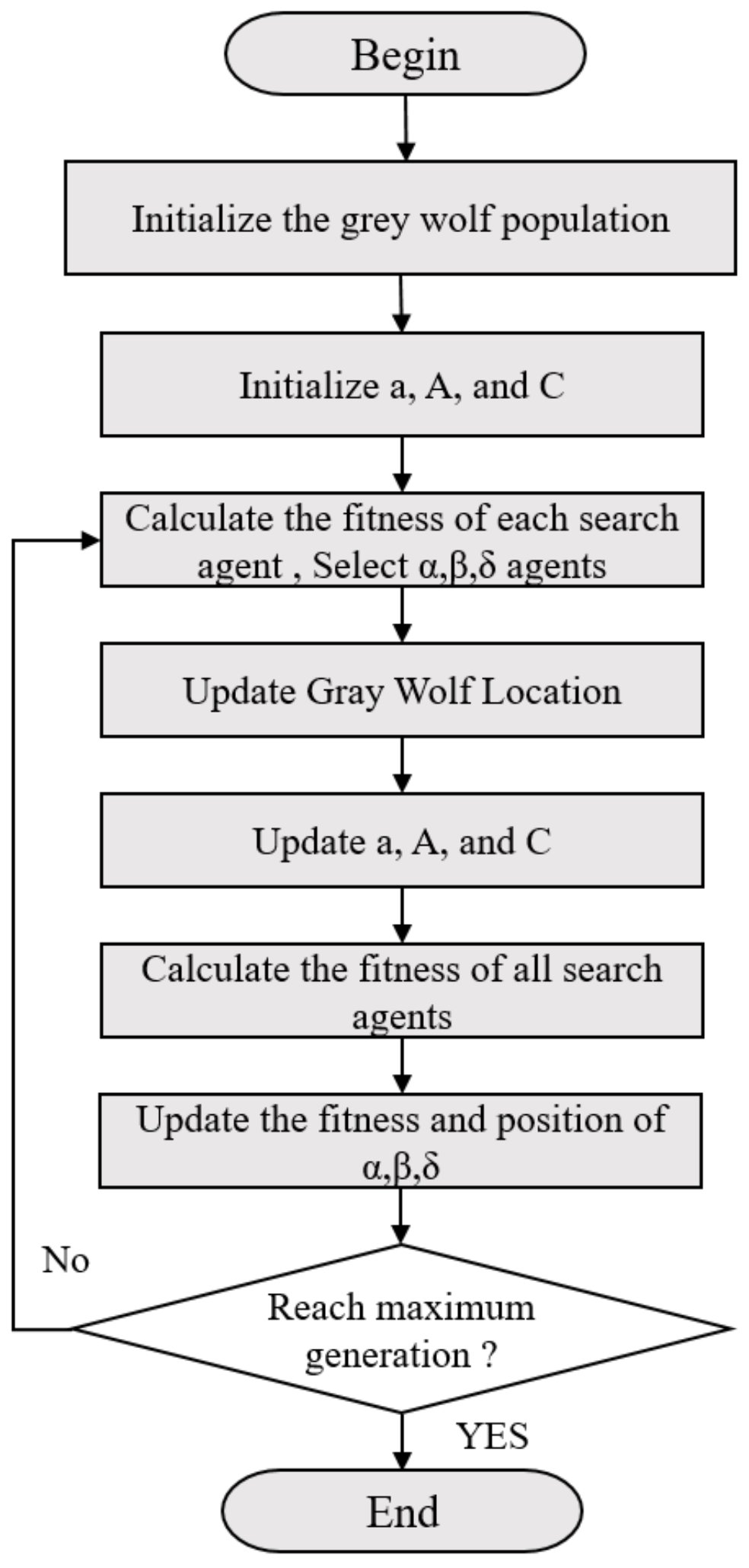
2.2. Grey Wolf Optimizer (GWO)
| Algorithm 1: Pseudo code of the GWO algorithm |
| Initialize the grey wolf population Xi (i = 1, 2, …, n) Initialize a, A, C For Xi (i = 1, 2, …, n) do Calculate fitness End for Save the first three best wolves as Xα, Xβ and Xδ While (t < Max number of iterations) For each search agent Update the position of the current search agent by Equations (9)–(11) End for Update a, A, and C For Xi (i = 1, 2, …, n) do Calculate fitness End for Update a Xα, Xβ and Xδ t = t + 1 End while Return Xα |
2.3. Case Study
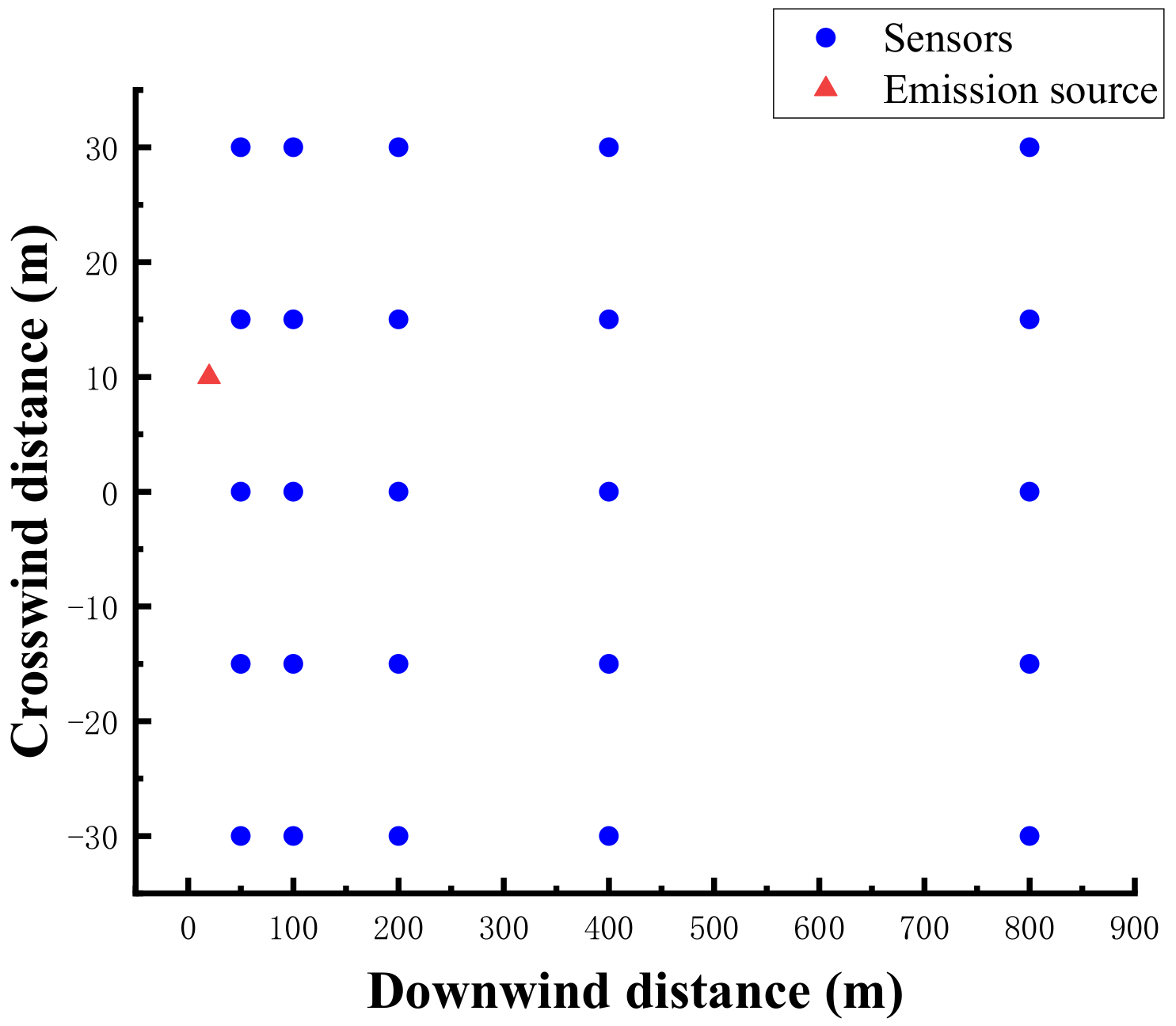
2.3.1. Simulation Cases
2.3.2. Experimental Cases
2.3.3. Skill Scores
3. Results and Discussion
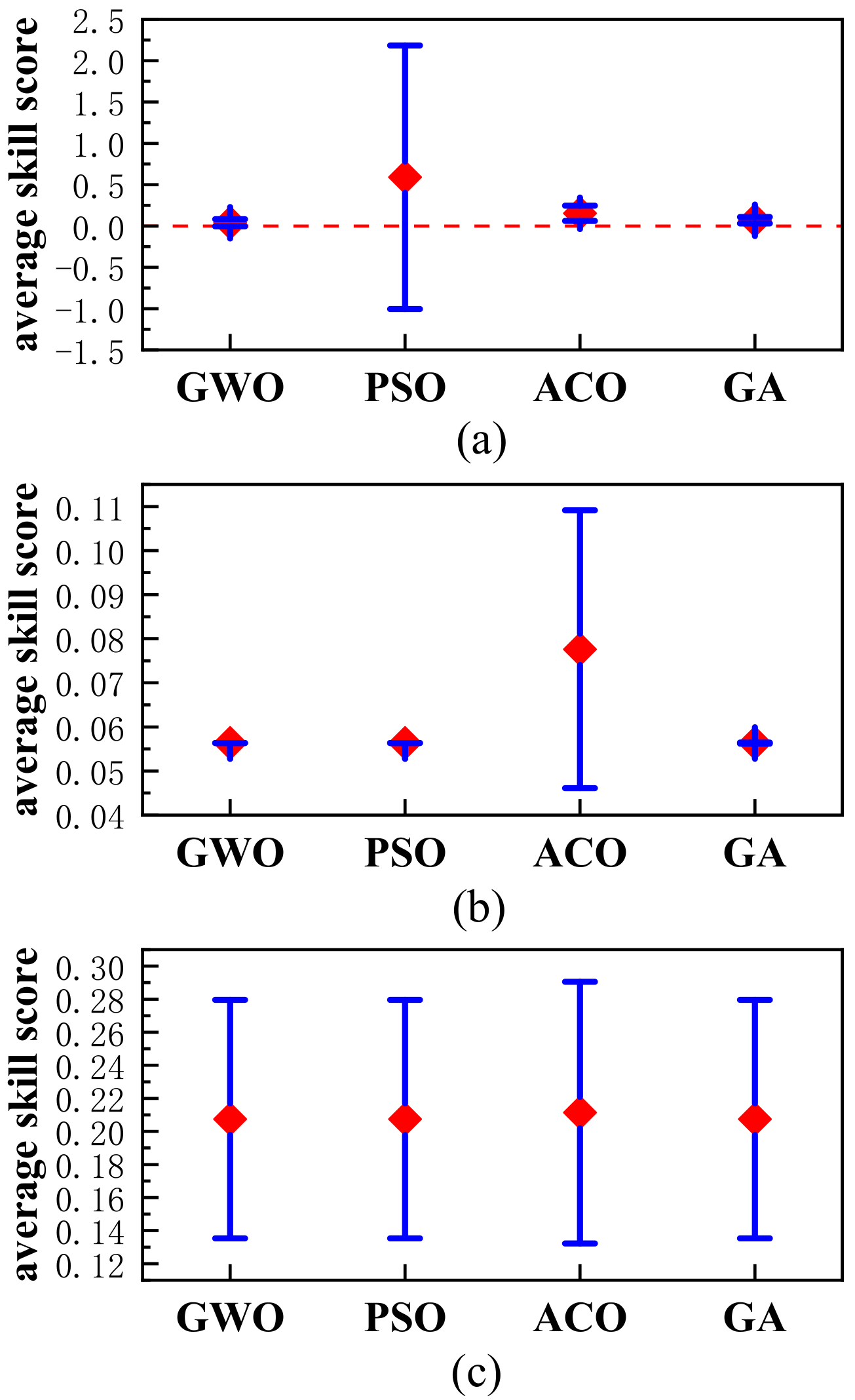
3.1. Estimation Results
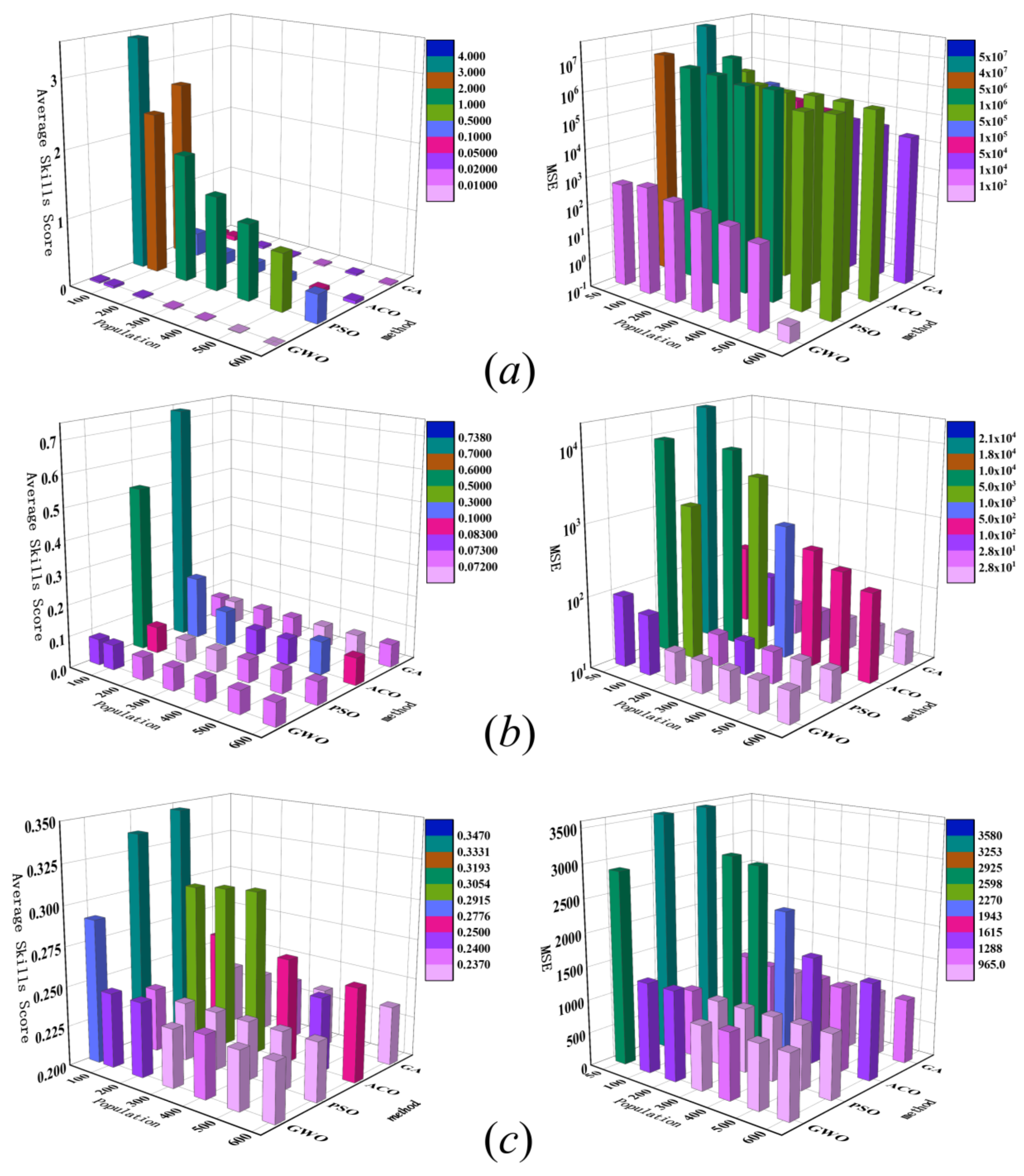
3.2. Effect of Population Size
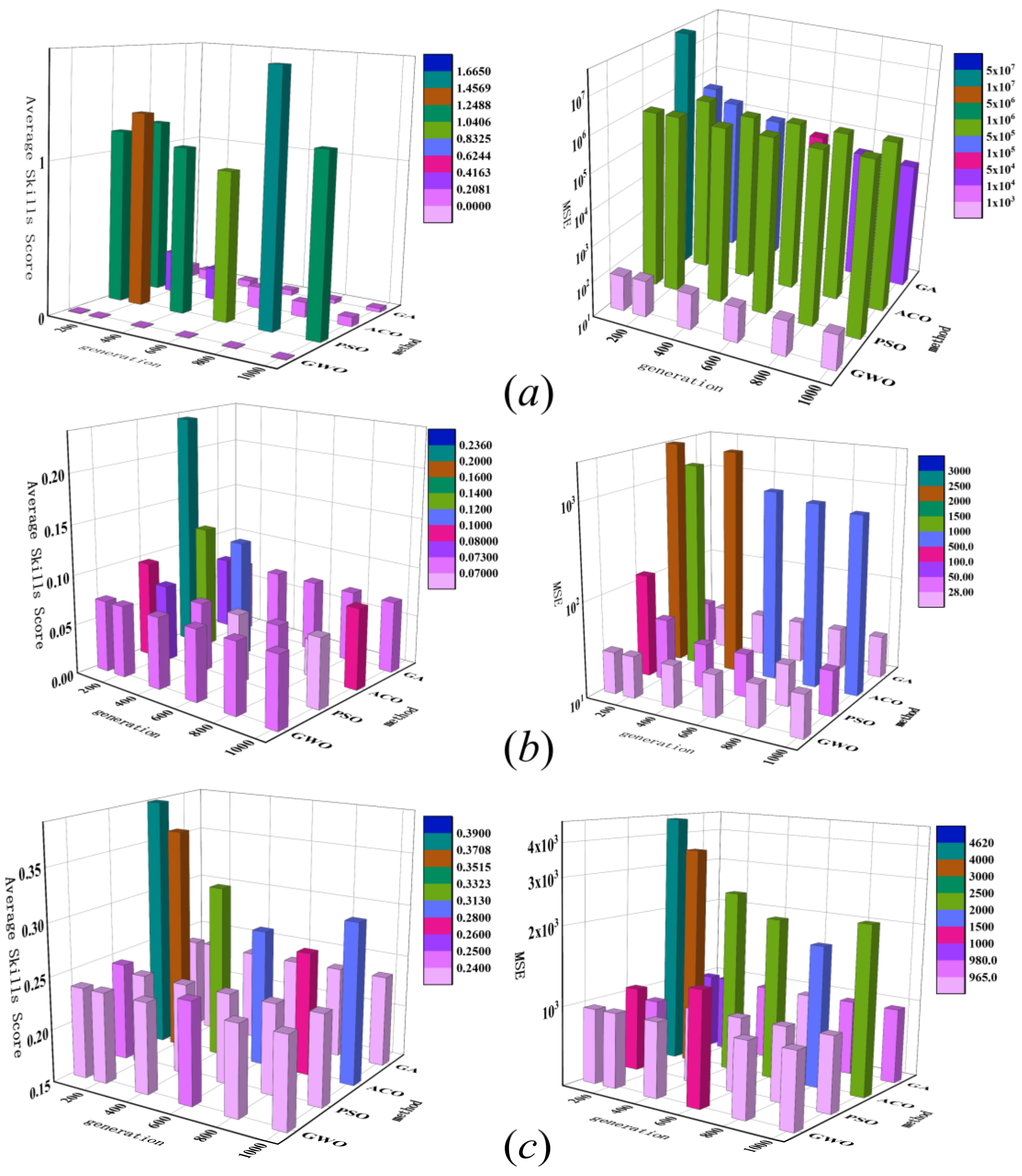
3.3. Effect of the Number of Iterations
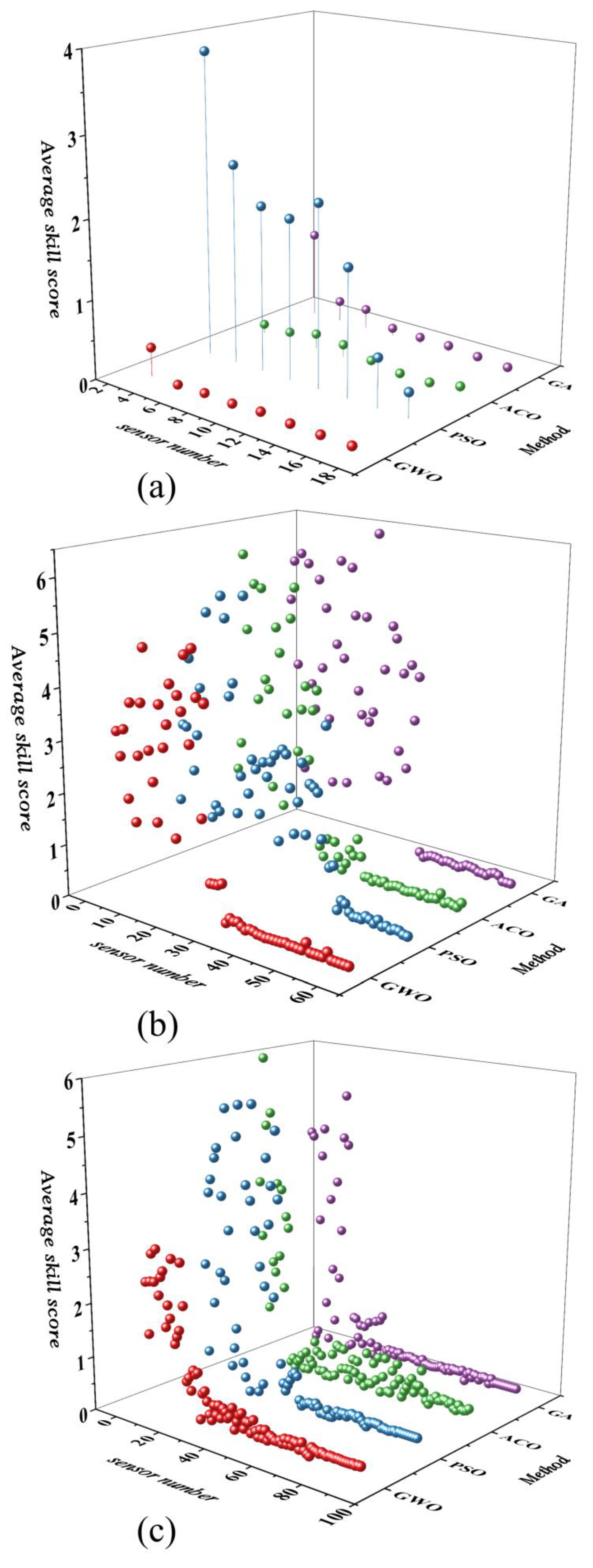
3.4. Effect of Sensor Number
4. Gaussian Diffusion Model with Terrain Parameter Correction
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GWO | Gray Wolf optimizer |
| STE | source term estimation |
| PSO | particle swarm optimization |
| GA | genetic algorithm |
| ACO | ant colony optimization |
| SA | simulated annealing |
| BMC | Bayesian inference and stochastic Monte Carlo methods |
| MCMC | Markov chain Monte Carlo sampling method |
| BFGS | Broyden-Fletcher-Goldfarb-Shanno algorithm |
| CFD | Computational Fluid Dynamics |
| SCIPUFF | The Second-Order Closure Integrated Puff model |
| FA | Firefly algorithm |
| PFA | Passive firefly algorithm |
| AFA | Active firefly algorithm |
Nomenclatures
| Concentration measured by the sensor at the position i; | |
| Concentration predicted by the forward dispersion model; | |
| N | Number of the measurement; |
| Object function; | |
| C(x, y, z) | Gas concentration at position (x, y, z), g/m3; |
| u | Wind speed, m/s; Q is the emission source strength, g/s; |
| H | Height of the plume, m; |
| Distance deviation coefficients in crosswind and vertical direction; | |
| and | Coefficient vectors; |
| Position vector of the prey; | |
| Position vector of a grey wolf; | |
| and | Random vectors in [0, 1]; |
| a | Convergence factor; |
| t | Current iteration number; |
| tmax | The maximum number of iterations; |
| Skill score, where i represents the corresponding source term (x, y, Q); | |
| Location score; | |
| Average skill score; | |
| The estimated value; | |
| The real value; | |
| Diffusion correction coefficients in the horizontal direction; | |
| Diffusion correction coefficients in the vertical direction; | |
| a0–g0 | Empirical correction factors, which have different values at different atmospheric stability. |
References
- Singh, S.K.; Rani, R. Assimilation of concentration measurements for retrieving multiple point releases in atmosphere: A least-squares approach to inverse modelling. Atmos. Environ. 2015, 119, 402–414. [Google Scholar] [CrossRef]
- Hutchinson, M.; Oh, H.; Chen, W.H. A review of source term estimation methods for atmospheric dispersion events using static or mobile sensors. Inf. Fusion 2017, 36, 130–148. [Google Scholar] [CrossRef] [Green Version]
- Sohn, M.D.; Reynolds, P.; Singh, N.; Gadgil, A.J. Rapidly locating and characterizing pollutant releases in buildings. Air Waste Manag. Assoc. 2002, 52, 1422–1432. [Google Scholar] [CrossRef] [PubMed]
- Sohn, M.D.; Sextro, R.G.; Gadgil, A.J.; Daisey, J.M. Responding to sudden pollutant releases in office buildings: 1. Framework and analysis tools. Indoor Air 2003, 13, 267–276. [Google Scholar] [CrossRef] [PubMed]
- Sohn, M.D.; Small, M.J.; Pantazidou, M. Reducing uncertainty in site characterization using Bayes Monte Carlo methods. Environ. Eng.-ASCE 2000, 126, 893–902. [Google Scholar] [CrossRef]
- Qian, S.S.; Stow, C.A.; Borsuk, M.E. On Monte Carlo methods for Bayesian inference. Ecol. Model. 2003, 159, 269–277. [Google Scholar] [CrossRef]
- Senocak, I.; Henuartner, N.W.; Short, M.B.; Daniel, W.B. Stochastic event reconstruction of atmospheric contaminant dispersion using Bayesian inference. Atmos. Environ. 2008, 42, 7718–7727. [Google Scholar] [CrossRef] [Green Version]
- Chow, F.K.; Kosovic, B.; Chan, S. Source inversion for contaminant plume dispersion in urban environments using building-resolving simulations. Appl. Meteorol. Climatol. 2008, 47, 1553–1572. [Google Scholar] [CrossRef] [Green Version]
- Yee, E.; Flesch, T.K. Inference of emission rates from multiple sources using Bayesian probability theory. Environ. Monit. 2010, 12, 622–634. [Google Scholar] [CrossRef]
- Xue, F.; Kikumoto, H.; Li, X.F.; Ooka, R. Bayesian source term estimation of atmospheric releases in urban areas using LES approach. Hazard. Mater. 2018, 349, 68–78. [Google Scholar] [CrossRef]
- Liu, Z.Z.; Li, X.F. The impact of sensor layout on Source Term Estimation in urban neighborhood. Build. Environ. 2022, 213, 108859. [Google Scholar] [CrossRef]
- Jia, H.Y.; Kikumoto, H. Sensor configuration optimization based on the entropy of adjoint concentration distribution for stochastic source term estimation in urban environment. Sust. Cities Soc. 2022, 79, 103726. [Google Scholar] [CrossRef]
- Ling, Y.S.; Huang, T.; Yue, Q.; Shan, Q.; Hei, D.; Zhang, X.; Shi, C.; Jia, W. Improving the estimation accuracy of multi-nuclide source term estimation method for severe nuclear accidents using temporal convolutional network optimized by Bayesian optimization and hyperband. J. Environ. Radioact. 2022, 424, 106787. [Google Scholar] [CrossRef] [PubMed]
- Eslinger, P.W.; Schrom, B.T. Utility of atmospheric transport runs done backwards in time for source term estimation. J. Environ. Radioact. 2019, 203, 98–106. [Google Scholar] [CrossRef]
- Singh, S.K.; Rani, R. A least-squares inversion technique for identification of a point release: Application to Fusion Field Trials 2007. Atmos. Environ. 2014, 92, 104–117. [Google Scholar] [CrossRef]
- Singh, S.K.; Sharan, M.; Issartel, J.P. Inverse modelling methods for identifying unknown releases in emergency scenarios: An overview. Int. J. Environ. Pollut. 2015, 57, 68–91. [Google Scholar] [CrossRef]
- Bieringer, P.E.; Rodriguez, L.M.; Vandenberghe, F.; Hurst, J.G.; Bieberbach, G., Jr.; Sykes, I.; Hannan, J.R.; Zaragoza, J.; Fry, R.N., Jr. Automated source term and wind parameter estimation for atmospheric transport and dispersion applications. Atmos. Environ. 2015, 122, 206–219. [Google Scholar] [CrossRef]
- Annunzio, A.J.; Young, G.S.; Haupt, S.E. A Multi-Entity Field Approximation to determine the source location of multiple atmospheric contaminant releases. Atmos. Environ. 2012, 62, 593–604. [Google Scholar] [CrossRef]
- Thomson, L.C.; Hirst, B.; Gibson, G.; Gillespie, S.; Jonathan, P.; Skeldon, K.D.; Padgett, M.J. An improved algorithm for locating a gas source using inverse methods. Atmos. Environ. 2007, 41, 1128–1134. [Google Scholar] [CrossRef]
- Pan, Y.; Jiang, J.C.; Wang, R.; Jiang, J.J. Predicting the net heat of combustion of organic compounds from molecular structures based on ant colony optimization. J. Loss Prev. Process Ind. 2011, 24, 85–89. [Google Scholar] [CrossRef]
- Qin, X.Q. A prediction model of mine gas emission base on a new ant colony algorithm. Appl. Mech. Mater. 2013, 318, 379–384. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, H.; Huang, L.D.; Zhang, X.L. Source term estimation of hazardous material releases using hybrid genetic algorithm with composite cost functions. Eng. Appl. Artif. Intell. 2018, 75, 102–113. [Google Scholar] [CrossRef]
- Wang, Y.D.; Chen, B.; Zhu, Z.Q.; Wang, R.X.; Chen, F.R.; Yong, Z.; Zhang, L. A hybrid strategy on combining different optimization algorithms for hazardous gas source term estimation in field cases. Process Saf. Environ. Protect. 2020, 138, 27–38. [Google Scholar] [CrossRef]
- Ma, D.L.; Tan, W.; Zhang, Z.X.; Hu, J. Gas emission source term estimation with 1-step nonlinear partial swarm Optimization-Tikhonov regularization hybrid method. Chin. J. Chem. Eng. 2018, 26, 356–363. [Google Scholar] [CrossRef]
- Ma, D.L.; Gao, J.M.; Zhang, Z.X.; Wang, Q.S. An Improved Firefly Algorithm for Gas Emission Source Parameter Estimation in Atmosphere. IEEE Access 2019, 7, 111923–111930. [Google Scholar] [CrossRef]
- Ma, D.L.; Deng, J.Q.; Zhang, Z.X. Comparison and improvements of optimization methods for gas emission source identification. Atmos. Environ. 2013, 81, 188–198. [Google Scholar] [CrossRef]
- Wu, J.S.; Liu, Z.; Yuan, S.Q.; Cai, J.T.; Hu, X.F. Source term estimation of natural gas leakage in utility tunnel by combining CFD and Bayesian inference method. J. Loss Prev. Process Ind. 2020, 68, 104328. [Google Scholar] [CrossRef]
- Haupt, S.E.; Young, G.S.; Allen, C.T. Validation of a receptor-dispersion model coupled with a genetic algorithm using synthetic data. J. Appl. Meteorol. Climatol. 2007, 45, 476–490. [Google Scholar] [CrossRef]
- Briggs, G.A. Diffusion Estimation for Small Emissions; ATDL Contribution File No. 79; Atmospheric Turbulence and Diffusion Laboratory: Oak Ridge, TN, USA, 1973. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Barad, M.L. Project Prairie Grass, a Field Program in Diffusion; Geophysical Research Paper, No. 59; Report AFCRC-TR-58-235(I); Air Force Cambridge Research Center: Cambridge, MA, USA, 1958; pp. 1–305. [Google Scholar]
- Zhang, W.; Zhang, X. Dispersion modeling of important toxic substance spills. J. Saf. Health Environ. 1996, 3, 1–19. [Google Scholar]


| Method | Estimation Results | Relative Error | MSE | Consuming Time/s | ||||
|---|---|---|---|---|---|---|---|---|
| x/m | y/m | Q/g s−1 | x | y | Q | |||
| Real value | 30 | 15 | 8801.20 | - | - | - | - | - |
| GWO | 29.7999 | 14.9950 | 8799.17 | 0.67% | 0.03% | 0.02% | 399.46 | 3.11 |
| PSO | 63.2489 | 15.0886 | 8584.18 | 110.1% | 0.59% | 2.47% | 745,010 | 4.12 |
| ACO | 27.7710 | 15.0098 | 8703.31 | 7.43% | 0.06% | 1.11% | 536,574 | 24.42 |
| GA | 30.8747 | 15.0613 | 8734.84 | 2.92% | 0.41% | 0.75% | 37,644.6 | 3.01 |
| Method | Estimation Results | Relative Error | MSE | Consuming Time/s | ||||
|---|---|---|---|---|---|---|---|---|
| x/m | y/m | Q/g s−1 | x | y | Q | |||
| Real value | 94.6 | 66.8 | 56.5 | - | - | - | - | - |
| GWO | 92.5484 | 68.3096 | 61.0980 | 2.17% | 2.26% | 8.14% | 27.6294 | 1.51 |
| PSO | 92.6823 | 68.3085 | 60.9959 | 1.20% | 2.26% | 7.87% | 28.5197 | 1.81 |
| ACO | 90.7901 | 68.4246 | 63.0258 | 4.25% | 2.43% | 11.55% | 265.8731 | 4.79 |
| GA | 92.5312 | 68.3148 | 61.1095 | 2.19% | 2.27% | 8.16% | 27.8334 | 1.46 |
| Method | Estimation Results | Relative Error | MSE | Consuming Time/s | ||||
|---|---|---|---|---|---|---|---|---|
| x/m | y/m | Q/g s−1 | x | y | Q | |||
| Real value | 109 | 76.6 | 94.7 | - | - | - | - | - |
| GWO | 105.2910 | 81.9778 | 126.711 | 3.41% | 7.00% | 33.80% | 1348.4280 | 1.79 |
| PSO | 105.8041 | 81.9892 | 125.106 | 2.93% | 7.02% | 32.11% | 963.7614 | 2.26 |
| ACO | 103.57635 | 81.8642 | 131.772 | 4.98% | 6.86% | 39.15% | 2077.8503 | 6.50 |
| GA | 105.8167 | 81.9941 | 125.053 | 2.92% | 7.03% | 32.05% | 981.0636 | 1.73 |
| Surface Types | z0 (m) |
|---|---|
| Grassland or open country | ≤0.1 |
| Crop areas | 0.1~0.3 |
| Village or scattered trees | 0.3~1 |
| urban | 1~4 |
| Develop urban | ≥4 |
| Stability Class | A | B | C | D | E | F | |
|---|---|---|---|---|---|---|---|
| 0.042 | 0.115 | 0.15 | 0.38 | 0.3 | 0.57 | ||
| 1.10 | 1.5 | 1.49 | 2.53 | 2.4 | 2.913 | ||
| 0.0364 | 0.045 | 0.0182 | 0.13 | 0.11 | 0.0944 | ||
| 0.4364 | 0.853 | 0.87 | 0.55 | 0.86 | 0.753 | ||
| 0.05 | 0.0128 | 0.01046 | 0.042 | 0.01682 | 0.0228 | ||
| 0.273 | 0.156 | 0.089 | 0.35 | 0.27 | 0.29 | ||
| 0.024 | 0.0136 | 0.0071 | 0.03 | 0.022 | 0.023 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Jiang, Y.; Zhang, X.; Pan, Y.; Qi, Y. Combined Grey Wolf Optimizer Algorithm and Corrected Gaussian Diffusion Model in Source Term Estimation. Processes 2022, 10, 1238. https://doi.org/10.3390/pr10071238
Liu Y, Jiang Y, Zhang X, Pan Y, Qi Y. Combined Grey Wolf Optimizer Algorithm and Corrected Gaussian Diffusion Model in Source Term Estimation. Processes. 2022; 10(7):1238. https://doi.org/10.3390/pr10071238
Chicago/Turabian StyleLiu, Yizhe, Yu Jiang, Xin Zhang, Yong Pan, and Yingquan Qi. 2022. "Combined Grey Wolf Optimizer Algorithm and Corrected Gaussian Diffusion Model in Source Term Estimation" Processes 10, no. 7: 1238. https://doi.org/10.3390/pr10071238
APA StyleLiu, Y., Jiang, Y., Zhang, X., Pan, Y., & Qi, Y. (2022). Combined Grey Wolf Optimizer Algorithm and Corrected Gaussian Diffusion Model in Source Term Estimation. Processes, 10(7), 1238. https://doi.org/10.3390/pr10071238







