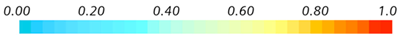Abstract
Solutions that aim to reduce water production in heavy oil wells have led to the design of devices known as rate-controlled production (RCP) autonomous inflow-control device (AICD) valves, which are placed in well completions and autonomously open with the oil inflow and close with water by choking the flow. These devices, which are based on Bernoulli’s principle, use a levitating disk that chokes the flow of the phase with the lowest flow resistance. This study proposes a numerical model based on computational fluid dynamics (CFD) technology to understand these devices’ operations and propose better designs without experimentation. The numerical model was based on dynamic fluid–body interaction (DFBI) and volume of fluid (VOF) models. The model was found to respond as expected depending on the physical properties of the fluids involved in heavy oil production. Finally, some limitations were found in the numerical study that can be improved in future studies.
1. Introduction
The oil and gas (O&G) industry contributes over half of the total energy supply in the world according to International Energy Agency (IEA) data [1]. Figure 1 shows that by 2018, 4.5 million ktoe of oil were used for energy supply. Furthermore, the importance of oil in other industries such as transportation, manufacturing, and services shows that this resource is necessary for the world economy. However, some concerns about its production efficiency are of significant research interest.
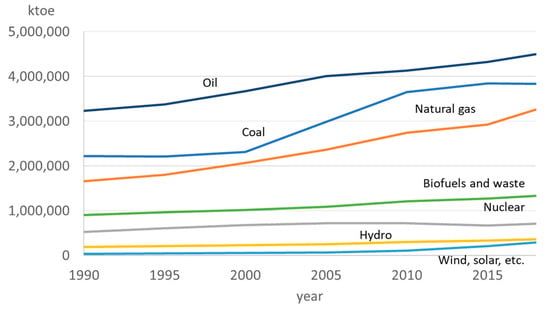
Figure 1.
Total energy supply in ktoe in the world from 1990 to 2018. Extracted from IEA [1].
The O&G industry is constantly improving its operations to reduce costs and the social and environmental impacts of its processes. Nowadays, this industry is interested in mitigating high-water production problems in heavy oil reservoirs, a notorious problem worldwide that causes a significant increase in operational costs, energy consumption, and consequently the carbon footprint. Figure 2 shows that 32% of the remaining reservoirs in Colombia are heavy oil, while more than 50% were considered unconventional by the same group by 2013 [2]. There are various solutions to mitigate this problem. For example, enhanced oil recovery technologies play a vital role in increasing production efficiency. Unfortunately, these are expensive mitigation solutions and are usually long term. For this reason, it is essential to design new active technologies that allow for a reduction in water production in the short term.
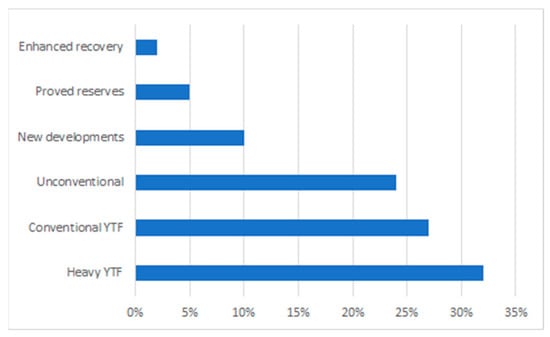
Figure 2.
Distribution of methods used for oil production in Colombia. Extracted from Agencia Nacional Hidrocarburos [2].
Different technologies have been invented to improve oil production, and inflow control valves (ICVs) are among the most innovative ones. These devices are placed in the well completion and are designed to increase oil production in heavy oil reservoirs by reducing the excessive water production by choking the water inflow at the breakthrough event using mechanical and electrical mechanisms [3]. On the contrary, other more straightforward and innovative valves known as autonomous inflow-control devices (AICDs) manage to do the same job autonomously. These devices’ working principle is the interaction between the different reservoir fluids and the internal parts while avoiding mechanical and electrical mechanisms [4]. For example, rated-controlled production (RCP) valves remain open when oil passes through and are closed autonomously when water starts to get through, reducing the inflow. This automatization mechanism is attributed to the differential pressure change that generates the different phases’ physical properties. Predicting these internal parts’ movement can lead to the optimization of pre-existing designs in the industry. This is when cutting-edge technologies such as computational fluid dynamics (CFD) can play a fundamental role by allowing digital twins to fully understand and improve existing designs without building numerous prototypes for on-site laboratory tests. They are usually expensive and dangerous because they are prone to exposure to high-pressure fluids.
AICD valves are small devices that act passively and are placed along production wells to control the inflow, making the entry of fluids other than oil more tortuous. Their method of operation varies depending on the field’s specifications or the private investigations that the companies have carried out. Most of these devices work by reducing the fluids’ velocity at the well’s entrance, thus avoiding the generation of conification phenomena [3]. Halliburton has the most significant examples of patented AICDs in the industry, which have proven to be an effective solution for excessive water and gas production [5]. One significant example of the AICD technology’s success has been in heavy oil reservoirs in the North Sea. These devices were a disruptive solution to high water and gas cuts in the Troll Heavy oil reservoirs. Moreover, these devices’ study and improvement have led to new designs that maximize oil production and make it less expensive and more reliable. One significant example is RCP valves.
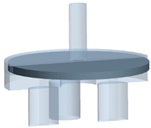
Figure 3 presents an example of an RCP valve. This design has four parts: the nozzle, where the fluids enter from the reservoir; the body, which encases the fluid and moving parts and requires a unique mount in the well casing; the moving part, known as the plate, which is responsible for the controlled process of choking the flow; and the seat, where the plate rests. Once the oil enters, the friction loss increases due to the high viscosity, forcing the plate to remain in the seat and allowing the fluid to flow through the lower orifices toward the tubing or inner liner. This position is known as open. The closed position occurs when the water enters; due to its higher density and lower viscosity, it causes the pressure near the plate to decrease due to the high velocity of the fluid, following Bernoulli’s principle. As the lower part of the plate’s pressure decreases, it rises until it covers the nozzle, choking the flow autonomously. Due to the pressure variation in the system, the plate does not maintain the open or closed position but maintains a permanent oscillation and vibration.
Figure 3.
Typical RCP design. The flow patterns and the plate movement for the open and closed positions are also shown. Additionally, the principle behind the plate movement is based on Bernoulli’s principle.
Figure 4 shows a typical well completion using ICDs. It comprises swell packers, the AICD housing, the location of the RCP, and other standard devices such as the sand screen and the inner liner. The RCPs are placed at different points along the well; thus, when one closes, the velocity dynamics in the shock front change, allowing other surrounding valves to work typically.
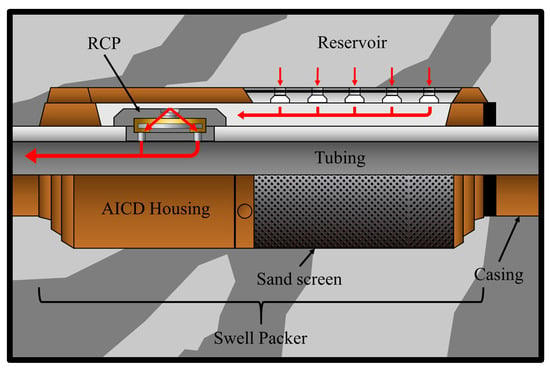
Figure 4.
Installation of an RCP in the casing of a horizontal well.
On the other hand, CFD is a technology derived from fluid mechanics science that is capable of reproducing and predicting different fluids’ behavior based on the numerical solution of the momentum, energy, and mass conservation equations. Based on this principle, other closure models could be added to simulate multiphase flow, porous media flow, energy transfer by radiation, etc.
In this study, a CFD analysis was conducted to predict the plate’s free motion in the RCP for the first time. The dynamic fluid–body interaction (DFBI) model was used to predict numerically how a solid was affected by a surrounding fluid motion. Examples of this model are a ship affected by sea waves or a floating tank filled with fluids showing how the motion changes due to the differential pressure in the interior and the atmosphere. On the other hand, the geometry’s discretization must capture the plate’s motion. Therefore, the mesh morphing model was considered due to its capabilities in complex geometries with small gaps, such as the one under study, over other discretization methodologies such as the overset mesh model.
1.1. Inflow Controller Classification
This subsection describes the different inflow control technologies; i.e., the ICVs and AICDs mentioned previously. Both are distinct and belong to different inflow control technologies: ICVs and ICDs. The first one requires an electrical or hydraulic impulse to act and generate the corresponding fluid choking. In contrast, the second one works without any external mechanism, taking advantage of physical principles to reduce excessive water/gas production. ICDs can be divided into the first generation of passive inflow control devices (PICDs) and the second generation of AICDs. The first category includes those devices that increase friction to allow the fluid with a higher viscosity and lower density to enter higher volumes. The second category is further divided into fluidic diodes, which use a balance between inertial and viscous forces to make the undesired phases generate a vortex and impede its production while keeping oil on the most straightforward path, increasing its production. These rate controlled production (RCP) valves, which were under study in this research, act under Bernoulli’s principle, causing the mechanism to act with the densest fluid’s entry and stopping its production. Figure 5 summarizes the different inflow technologies [6].
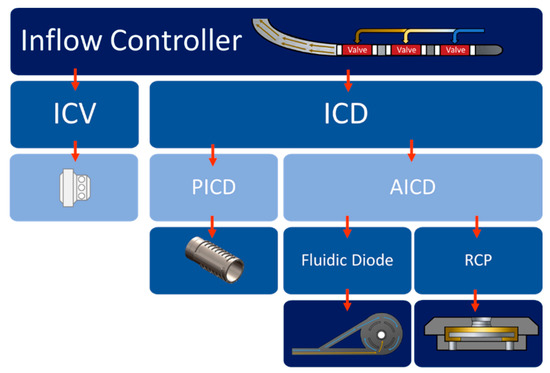
Figure 5.
Schematic representation of the types of inflow controllers to reduce water and gas production.
Among the disadvantages of ICVs is the requirement for a control system and extended cables that reach the ground surface to maintain its operation. The disadvantage of PICDs is that they maintain a constant inflow resistance, implying that more water is produced than oil until the breakthrough occurs. Fluidic-diode-type devices, on the other hand, only delay the production of the less viscous fluid but do not stop its production altogether. The RCPs’ disadvantage is the plate’s integrity because high velocities cause the plate to hit against the chamber’s walls, resulting in damaged or a loss in functionality [6].
1.2. Previous Works
This subsection summarizes a literature review on the numerical study of ICDs. Table 1 summarizes the significant contributions of each study. The following results were found: this technology is brand new, which implies that it is still under constant research. Therefore, adjusting to the needs of different oil wells maintains a continuous improvement and optimization, from the principles involved in the device to its geometry and materials. Another aspect to consider is that it is indispensable for researchers to construct computational models to reduce experimental costs because new designs are developed computationally and tested without extensive and demanding laboratory work. Many researchers have opted for the technology provided by CFD. However, specifically for RCPs, no work was found to replicate the plate’s motion inside the valve, and works were limited to only analyzing flow dynamics while assuming a single-phase flow and with the plate remaining static. The lack of research on the subject led to designing a computational model that replicated the movement mentioned above, which will be an excellent tool for future research in the field of RCPs that will allow new researchers to change, for example, the design of the immersed fluids and obtain results without the need to create prototypes in laboratories.

Table 1.
Compilation of previous works on inflow control devices where the principal aim was to optimize designs using computational models.
1.3. CFD Governing Equations
This study first undertook a validation process for the numerical model using experimental data found in the literature. The experimental data was acquired with only one phase in the valve. Afterward, an analysis of the device’s dynamic behavior was sought for a multiphase flow system while considering water and oil. This section presents the mathematical models that described the system under study.
1.3.1. Continuity Equation
The continuity equation integrates the mass conservation equation in which the mass entering the system, mass exiting the system, and the production are quantified. The first term analyzes the change in mass in time, the second one quantifies the net change in mass while subtracting outlet less inlet, and the last is the mass source term, which is related to the density; the term is a user-defined source term (Equation (1)) [9].
The valve is activated due to the plate’s interaction with the water; afterward, when the oil returns to the domain, the active body descends to maintain the production rate. In order to reproduce this case study, the Eulerian multiphase VOF model was implemented. This model has excellent behavior in describing immiscible systems and uses the high-resolution interface-capturing (HRIC) scheme to track the interface in conjunction with the interfacial tension [10]. Since the system analyzed involved two different fluids determined by the VOF model, the equation changed in the definition of the terms compared with Equation (1) along with the momentum equation, since they must be specified in volume fraction. The volume fraction of the i-phase in a given cell is defined as the volume of the i-phase in the cell over the cell’s total volume (Equation (2)). Furthermore, the sum of all fractions over the cell must be equal to 1 (Equation (3)).
At the interface, fluid properties are evaluated as a mixture. Therefore, density and viscosity are defined as the sum of the property in the i-phase multiplied by the volume fraction in that cell (Equations (4) and (5)).
Equation (6) is the total mass conservation law for all phases in a volume. The equation is the same as for the single-phase case, except for the density term of the i-phase and the , which is a user-defined source term of the i-phase (Equation (7)).
1.3.2. Momentum Equation
The general equations that describe the dynamics of fluids are the mass, momentum, and energy conservation laws. The Navier–Stokes (NS) equations solve the law of conservation of linear momentum when the fluids are assumed to be incompressible and Newtonian, which were valid considerations for the model proposed in this study. Equation (8) shows the final expression developed for a single-phase flow where is the unity tensor, is the stress tensor, is the vector of body forces, and is the user-specified source term [9].
Equation (9) shows the final expression developed for the multiphase flow while considering a VOF Eulerian model, which shows similarities with the single-phase case except for the definition of the densities and the final term that quantifies momentum in the mixture, with as the diffusion velocity.
1.3.3. Turbulence Equation
The modeling of turbulent systems requires new models that primarily describe the behavior of the eddies immersed in the flow. The Reynolds average Navier–Stokes (RANS) equations achieve this by making assumptions and solving the NS equations. The primary assumption is that the system variables’ behavior can be divided into fluctuating and averaging. Additional models have been developed to describe how the properties of the vortices change in the system by calculating their viscosity and diffusivity. Two equation models have been developed by using approximations to perform these calculations and close the RANS equations correctly. One of these models is the k-ε model, which describes the turbulent kinetic energy (k) and the dissipated turbulent energy (ε) [11]. The realizable k-ε transport equations are as follows:
The first term of the equations describes the variable’s change over time; the second term describes the transfer by convection; the third term describes the diffusive transport; and the remaining terms correspond to the production and destruction rate of turbulent kinetic energy and the dissipated turbulent energy. The term refers to eddy viscosity, and are the Prandtl numbers of the variables, is a function depending on the source terms, and and are constants [11].
Continuing with the two-equation models, one of the most widely used is the Menter SST k-ω model, which analyzes the turbulence frequency (ω) and not the dissipated turbulent energy (ε). The transport equations for this model are as follows:
As with the realizable k-ε equations, the first term describes the change in time of the variable, the second term is its convection, the third term describes the turbulent diffusion, and the remaining terms describe the rates of production and dissipation. The terms , , , , , and are experimental constants [11].
Another model is based on the RANS solution, which has a higher complexity; this model is called the Reynolds stress turbulence. The complexity lies in the fact that it has a turbulence equation for each of the Reynolds stresses, which increases the computational time; however, it correctly describes flow patterns such as vorticities, among others. In contrast to the two-equation models that calculate the eddy viscosity, this method calculates the stresses directly to close the RANS equations. The general transport equation is as follows:
Each of the terms describes one of the various Reynolds stresses (). The first term refers to the rate of change, the second to convection, the third to production, the fourth to diffusion, the fifth to dissipation, the sixth to transport due to pressure and strain interactions, and the last is the rotation term [11].
1.3.4. DFBI Equation
A body’s motion using the DFBI scheme is due to the sum of all the forces and momentums acting. Equation (15) shows that the total force is the sum of forces such as , which is the fluid pressure force acting on the body; , which is the fluid shear force, , which is the gravity force; and the last term, which is the sum of external forces. On the other hand, Equation (16) shows the different moment sources such as , which is the fluid pressure moment; , which is the fluid shear moment; and the last term, which is the sum of external moments. In both equations, the first term is the time-ramping function, as it is possible to specify the release time and the ramp time of the body [12].
Contact coupling is a mathematical method used to determine the physical boundaries of a system. The plate had two main limits on the motion axis (the seat and the stop); these contacts were necessary to define two parameters: the elastic and damping coefficients (Equations (17) and (18)). These parameters were used to calculate the counter-movement force sufficient for the body to stop in contact. Both coefficients depended on the body’s mass (), the contact area (), the relative speed of the body (), the minimum contact distance (), and the effective range ); in the case of the damping coefficient, it depended on a constant factor () that described the amount of damping, which was usually less than 1. Equation (19) indicates the time required for the body to stop due to the contact; this value was essential while selecting the simulation’s time step because it must be small enough to consider the stopping process [13].
2. Materials and Methods
A workstation with an Intel Xeon CPU E5-2690 v3 @ 2.60 GHz and 128 GB of RAM was used to conduct the numerical study. Additionally, the CFD code STAR-CCM+ v14.06 was used. The procedure to create the model began with developing the domain. The design studied by Askvik and Johannessen was considered mainly because of experimental data available to validate the numerical model [4]. Then, the system’s spatial discretization was constructed using an unstructured mesh with nonorthogonal elements. Additionally, a turbulence model analysis was conducted to determine the model’s sensitivity to the variations in the hydrodynamic profile and the plate’s movement over this variable.
2.1. Valve Geometry and Experimental Data
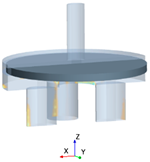
The following study analyzed the interaction between the fluids immersed in an oil production operation and the mechanical components of a standard RCP valve used in the industry. Thus, the design proposed by the Norwegian oil company Equinor (formerly Statoil) and improved by Askvik and Johannessen was used [4]. The valve was 9 cm in diameter and 3.2 cm in thickness and had three parts assembled with only one moving component, as shown in Figure 6. The geometry was designed using CAD software (Autodesk Inventor 2020).
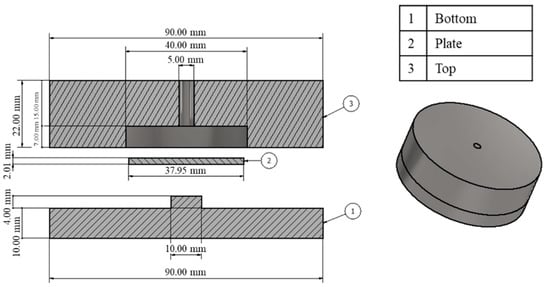
Figure 6.
RCP valve proposed by Askvik and Johannessen [4].
The active part of the valve was the plate, which was made of aluminum, measured 3.795 cm in diameter and 0.201 cm in thickness, and weighed 6 g; additionally, it had a space of 0.3 cm to move between the bottom and the top sits. This model was attractive because it did not present great difficulty in its construction and assembly, making it a better option for the industry.
Experimental data found in the literature was used to corroborate the model to contrast the simulations’ production curves. Askvik and Johannessen’s work analyzed the existing analytical models to calculate the pressure drop in RCP valves using experimental findings, similar to the present study [4]. They performed experiments with water and oil separately and analyzed whether the valve acted correctly depending on the fluid. For simulation purposes, only the experimental data for water and its respective analytical prediction were considered (Figure 7).
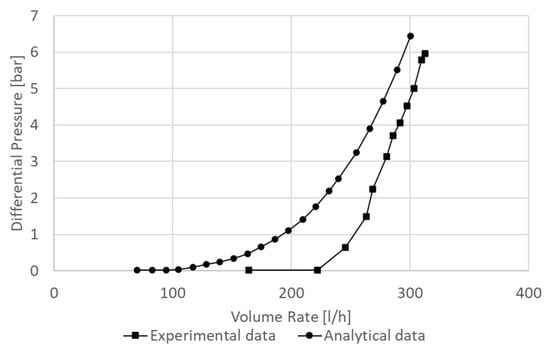
Figure 7.
Experimental and analytical water data in the RCP valve designed by Statoil and improved by Askvik and Johannessen [4].
The analytical model shown in the Figure 7 corresponded to an estimate of this style’s pressure loss across valves. The function depended on the geometry of the valve and the density and viscosity of the fluid in the domain. It was determined that the pressure loss across the valve followed a fourth-order relationship concerning the flow rate entering the valve; it also showed that the pressure loss across the valve followed a cubic proportional relationship with the density and was inversely quadratic proportional with the viscosity. This showed why these systems promote the production of oil over that of water.
2.2. Creation and Validation of the Numerical Model
The numerical model was validated using the experimental water data; the validation was performed in one phase with the realizable k-ε turbulence model while controlling the pressure drop and obtaining the volume rate. Finally, a study was conducted to analyze a real case using a multiphase model. The system was initialized fully with oil; water entered the valve at the zero time. Then, a period of time passed until the plate closed the inlet, after which oil was again introduced to analyze whether the plate returned to its open position.
The realizable k-ε model was selected because the meshing analysis did not include a detailed description of the boundary layer for the flow near the wall due to the complexity of the system under study. Therefore, using another turbulence model such as the k-ω would be highly inefficient because more complex models require a high mesh resolution near the walls to describe the flow in those areas [14].
2.2.1. Models
The initial model approximation was carried out to compare the experimental curve and the analytical data shown in Figure 7. These curves were developed using water. Therefore, a multiphase model was not employed yet. The turbulent flow was assumed and analyzed using the realizable k-ε RANS model. Additionally, gravity was considered an external body force. To achieve the interaction between the fluid and the plate, the DFBI and mesh morphing models were considered. A summary of the models implemented is shown in Figure 8. To analyze the computational model with a real scenario likely to occur in a typical reservoir, a multiphase model with excellent oil/water interaction performance was implemented. An Eulerian model was used; precisely, the volume of fluid (VOF) model. In addition, all models remained exact (Figure 8).
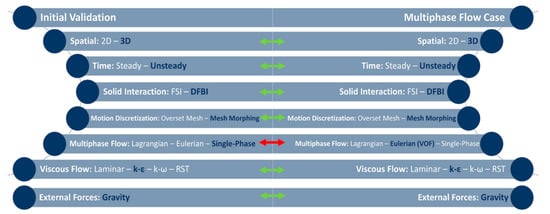
Figure 8.
Comparison of the models used for the two analyses conducted.
2.2.2. Domain, Initial, and Boundary Conditions for Validation
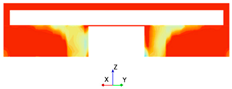
The boundary conditions were defined by the differential pressure between the inlet and outlet of the valve. The inlet’s pressure depended on the experimental point to be simulated. In contrast, the four outlets were set at 0 bar, achieving the experimental pressure drop. A schematic showing the computational domain and boundary conditions is shown in Figure 9.
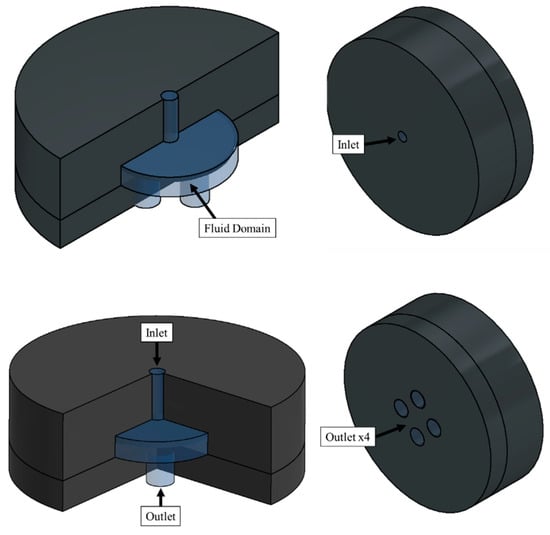
Figure 9.
Computational domain generated from the internal fluid and boundary conditions for the validation.
The DFBI model was used to simulate the plate’s movement due to the interaction with the fluids. Furthermore, the movement had to be constrained between the top and bottom seats in the stop and seat. Therefore, contact conditions had to be defined as shown in Figure 9. The contact coupling condition required the iterative and manual tuning of parameters to generate an opposing force, such as the effective distance, and the elastic and damping coefficients, depending on the body’s velocity and mass and the boundary’s contact area. Although these parameters could be manually calculated based on the model’s analytical equations for single-phase flow (Equations (17) and (18)), they became the first approximation because they required a further iterative manual tunning for multiphase flows. The plate was initially in the center of the chamber. Moreover, the valve was left wholly filled with water; this same fluid was injected into the inlet in the initial conditions. The properties of the water are shown in Table 2.

Table 2.
Properties of the fluids employed at 15 °C.
The boundary conditions of the multiphase case are shown in Figure 10. A differential pressure of 1.3 bar was defined between the inlet and the four outlets of the valve as in the experimental study.
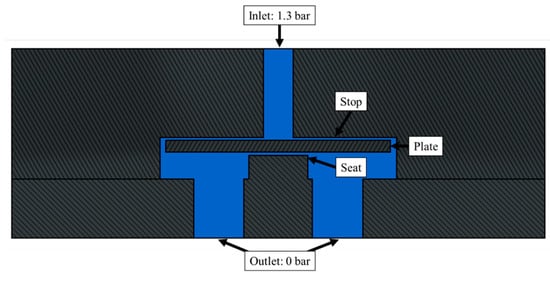
Figure 10.
Computational domain generated from the internal fluid and boundary condition for the real-case analysis.
The VOF model’s initial condition was the domain fully loaded with oil; at time 0 s, the water flowed at the inlet. The properties of the fluids are shown in Table 2. The oil analyzed had an API of 33.61, corresponding to light oil.
2.3. Discretization of the Domain
The mesh morphing and DFBI models were coupled to simulate the plate’s motion. The mesh morphing model deformed the mesh cells to be less computationally expensive and more comfortable to generate compared to other methods such as the overset mesh model. However, the plate did not overlap entirely with the mesh morphing model at the upper and lower sits. This could lead to excessive shrinking of the cells between the plate and the sits, which could cause negative volume cells in the domain and consequently numerical instabilities and convergence issues. Therefore, an advanced mesh design was used to create the nodes in a vertical positioning. In addition, it was essential to use the model in conjunction with the contact coupling condition mentioned above. Each vertical section had to define the source and target surface to build the mesh. The target surface was the top of the mesh extrusion. A hand-built mesh also had to be defined on the source surface. The number of layers through the section was also defined; this was the extrusion’s vertical division. Figure 11 shows the complete mesh. Finally, the mesh consisted of 43,728 cells after conducting a mesh independence test.
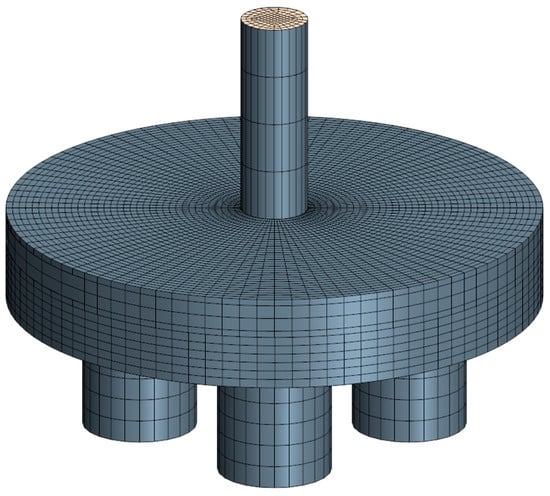
Figure 11.
Result of the directed mesh via domain discretization.
2.3.1. Mesh Independence through GCI Analysis
A mesh-independence test using the grid convergence index (GCI) was conducted to determine the most appropriate element count for modeling the RCP valve. This analysis was crucial to developing a computational model to find the influence of spatial discretization on the solution. There are many different mesh-independence test methodologies, but the most widely recommended is the grid convergence index analysis (GCI), whereby a numerical calculation is used to quantify how much variation the mesh generates in the results obtained. The ASME guideline for the GCI analysis was considered in this study [15].
Two different mesh independence analyses were conducted based on the computational model’s nature: one in a steady-state, single-phase flow without the plate’s movement; and the second in an unsteady state while considering the movement of the plate in a single-phase flow resembling the validation model. These two cases were conducted to determine the impacts of DFBI and mesh morphing on the GCI results. Three different meshes were studied for the two cases containing 84,864, 43,728, and 27,816 cells. The analysis was carried out with two variables: pressure drop and mass flow. Each of the meshes was generated to maintain a single layer at the top and bottom of the plate in order to correctly solve the DFBI model coupled with the mesh morphing tool; the refinement was concentrated in areas such as the inlet and outlet of the valve, as well as in the increase in cells radially and not axially in the area of the chamber.
2.4. Turbulence Analysis
An additional analysis of the effect of the turbulence models was conducted to validate the experimental data model. The experimental curve was replicated by changing the turbulence equations and the absence while assuming laminar flow. The laminar case was analyzed because the researchers who obtained the experimental data shown in Figure 7 considered this flow regime for the analytical modeling of the valve [4]. Four curves were made: one for the laminar case, another for the realizable k-ε, another for the Menter SST k-ω, and finally for the Reynolds stress transport (RST) model, thus analyzing the two existing approximations in the RANS models, the approximation through the calculation of the eddy viscosity, and the RST model [16]. Note that the flow was turbulent when using the experimental values and the diameter of the inlet at the valve, showing a Reynold’s number greater than 11,555.
3. Results
3.1. Validation and Real-Case Analysis
3.1.1. Validation
The validation attempted to replicate the operational conditions of the experiment conducted by Askvik and Johannessen. In addition, the second set of simulations was developed without the DFBI model to contrast both conditions. Figure 12 presents the simulation results with and without DFBI, the experimental values, and the analytical water prediction.
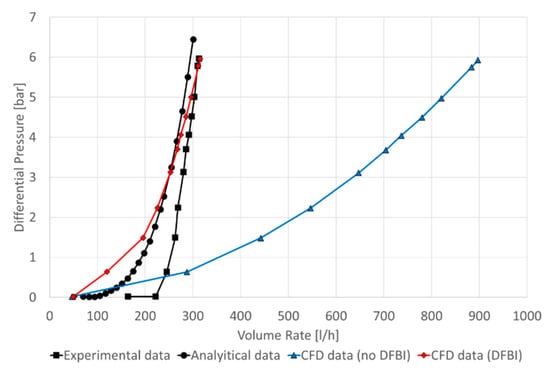
Figure 12.
Results of the validation with the simulated, experimental, and analytical data.
The experimental and analytical data showed that the pressure difference axis began to behave asymptotically at a certain point in the curve. This behavior was due to the choking effect of the valve in stopping the water inlet. The data simulated using DFBI showed this behavior correctly, demonstrating that a choking effect was achieved in the system. On the other hand, the data without DFBI were similar to a flow in a pipe because it does not rise asymptotically. This showed that the DFBI managed to replicate the natural behavior of the valve. Further analysis showed that the simulation’s behavior was closer to the analytical conditions for low-pressure differences while it resembled the experimental conditions for high-pressure differences. These differences could be attributed to the fact that the simulation conditions did not consider the upstream effects of the experiments.
Figure 13 presents the percentual differences between the data obtained using the DFBI model and the experimental data found in the literature.
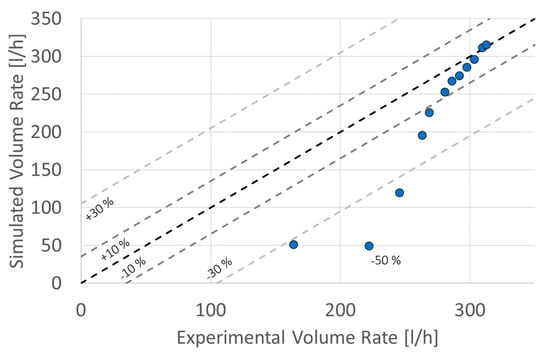
Figure 13.
Percentual differences between the simulated data with DFBI and experimental results.
The values grouped in the ±10% error area corresponded to pressure differences between 3.13 and 5.96 bar, which meant that the model worked correctly for high-pressure values. For pressure changes between 1.49 and 2.23 bar, the data were in the −30% error area. The furthest value corresponded to an error of −50%, corresponding to the data with a pressure difference of 0.018 bar. The model was found to have an excellent performance when the effect of the choke was high. Coincidentally, these conditions were generally found in the field [4].
3.1.2. Multiphase Flow
Validation of the meshing strategy
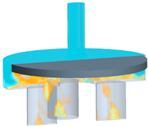
An essential element of the model was the discretization of the moving body. The implementation of mesh morphing achieved this; this tool had to adapt the cells to the body’s motion and adapt to the stopping process near the walls as best as possible. The mesh had to maintain a single cell above and below the plate to avoid overlapping nodes and generating nonpositive cell errors. To achieve this objective, polyhedral and tetrahedral meshes were discarded because their cell arrangements were disorderly. Therefore, a hand-built mesh was considered to control the number of vertical cells above and below the body, which obtained a better coupling of the contact between the plate and the walls. Figure 14 shows the dynamic behavior of the mesh obtained in two different stages of the process. At the initial position, the cells above and below the plate had the same thickness; then, the system was filled with water and the oil re-entered (final phase). The plate then moved down to the seat, deforming the thickness of the cells and showing the correct adaptability of the discretization to the DFBI model.
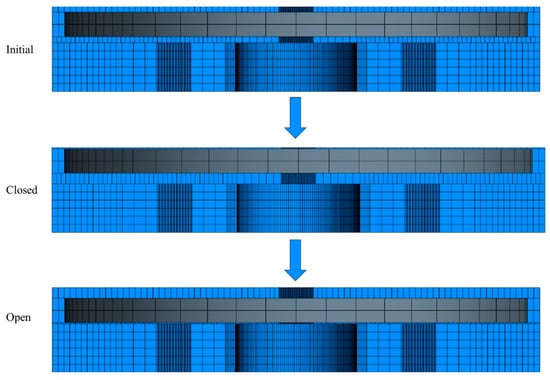
Figure 14.
The mesh’s behavior in three different plate positions: at the initial stage, with the water inlet (closed position), and finally with the oil inlet (open position).
The Figure 14 shows that the mesh cells could not disappear or have an area equal to zero because that would generate an error in the discretization. On the other hand, the cells that closed horizontally to the side of the plate did not suffer any deformation; this was defined to maintain the plate’s geometry without variations. Thus, the deformation was implemented only in the vertical direction.
RCP internal motion
Mainly the DFBI model was expected to act differently with water and oil. Specifically, the plate had to rise in the presence of water while the plate sunk with oil. Furthermore, according to Askvik and Johannessen, the plate oscillated when the valve closed, which was expected to be emulated in the numerical model [4]. However, it is essential to emphasize that no experimental results were available regarding this vibration’s behavior when both fluids were present because the experimental setup did not consider the multiphase flow. Therefore, this study was the first to analyze these flow dynamics inside the valve.
Table 3 shows the results of the DFBI model for three different stages of the process:

Table 3.
Plate motion at different stages of the process.
- The first stage (0.00 s): the domain was filled with oil, water began to flow in, and the plate was static in the middle of the chamber.
- The second stage (0.04 s): there was a quasistatic behavior in the plate’s motion in the closed position due to the water. In this step, the oil entered the valve again.
- The third stage (0.15 s): the water left the domain at the end of the process.
As expected, the model reacted accordingly, demonstrating that when water was in contact with the plate, it rose until it stopped, causing the valve to close; contrary to the oil inlet, when the plate descended to allow the fluid to flow. The multiphase flow behavior was also correct because there was an adequate displacement of both phases in the process’s different moments.
The model had to predict the plate’s vibration or oscillation in a closed position; therefore, analyzing the displacement through time had to reveal this behavior. Figure 15 shows the translation and velocity of the plate throughout time.
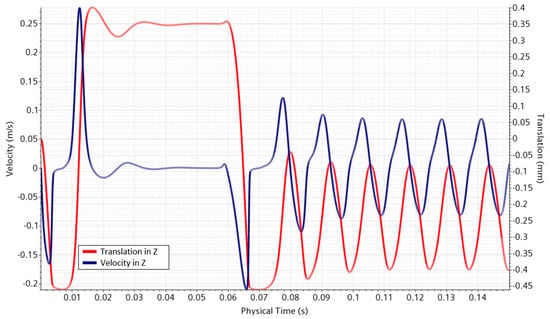
Figure 15.
The plate’s velocity and translation profile in the valve with a differential pressure of 1.3 bar. The water began to enter at 0 s, then the oil entered at 0.04 s.
The translation and velocity were calculated using the plate’s center mass. Therefore, negative translation values implied a descending behavior of the plate on the vertical axis. The vibration was quickly damped between 0.015 s and 0.04 s. The valve’s behavior in the open position showed a constant oscillation between 0.4 mm and 0.1 mm in the opposite direction of the flow. Oscillation was visible, as were changes in the presence of different fluids in the domain.
Production rates
Under the boundary conditions considered, a production of more than 0.000184 m3/s (100 Bbl/day) was expected; however, this value was strongly affected when water entered. Figure 16 shows the production rate profiles for both oil and water.
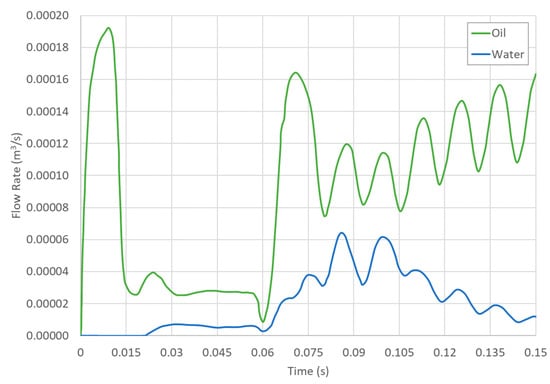
Figure 16.
Production rate profile of the oil and the water vs. process time.
The oil’s profile increased immediately above the expected 0.000184 m3/s or 100 barrels per day, decreased due to water entry, and had a small oscillation similar to the plate’s translation. As this stabilized quickly, production increased in an oscillatory manner with the oil entry. This was well matched to the plate’s behavior at this stage. On the other hand, water production was almost zero until 0.0216 s, when it remained stable but below 9.2 × 10−6 m3/s (5 barrels per day). With the oil entry, the production oscillated until it reached 7 × 10 × 10−6 m3/s (38 barrels per day); it decreased with the same behavior.
3.2. Mesh Independency
Two different sets of simulations were analyzed. In the first case, steady-state simulations were performed. The simulations were performed in an unsteady state in the second case while considering the DFBI and mesh morphing models. For both cases, there three different meshes were considered (Ni). In each case, the pressure drop and mass flow were analyzed. The analyses of the cases were carried out to determine how the meshing independence results with the mesh morphing and DFBI model and with a different temporal discretization could change. The results of the GCI analysis are shown in Table 4.

Table 4.
Results of mesh independence with the GCI parameters were calculated for the two different cases with the three defined meshes. , , and are the element counts from the most refined mesh ( ) to the coarser mesh ( ).
The results showed a grid convergence index of less than 4.6%, which indicated that convergence was achieved independent of the discretization used. The unsteady-state case results were better than those of the steady-state case because the convergence values were lower by at least one order of magnitude. For the pressure difference, a value of 0.5% was obtained in the unsteady case, while for the steady case, it was 1.3%; for the flow rate, the difference was more significant because it had a GCI value in the unsteady state equal to 0.034%, while for the steady case, it was 4.6%. The relative errors between the most refined meshes (1 and 2) showed that the most significant variation was 9.4% for the flow rate in the stationary solution; this value improved when analyzing the unsteady-state case, dropping to 4.2%. Regarding the extrapolated error, which attempted to quantify the difference in the solution if the discretization was further refined, we observed that for the unsteady-state case, the values were lower by between one and two orders of magnitude compared to the steady-state results. In conclusion, the unsteady-state discretization presented better results for all of the GCI parameters. Table 5 shows the mesh element count, the approximate base size in the domain, and the computational time to run the simulations in the unsteady-state case.

Table 5.
The computational time for the unsteady-state simulation with DFBI running for 0.11 s of physical time.
The difference in computational times was about 1 h between meshes. Since minimizing the computational time was essential when running multiple simulations and considering the GCI results, mesh 2 was the best option. This decision was supported by the GCI results of 0.5% for the differential pressure and 0.034% for the flow rate, as well as the possibility of saving one hour of computational time.
3.3. Turbulence Analysis
A total of four datasets were simulated. The first one, which handled the flow regime, was laminar; the other three, under the realizable k-ε, Menter SST k-ω, and RST models, were based on the RANS formulation and analyzing the turbulent flow. The results of these simulations and the experimental and analytical data are given in Figure 17.
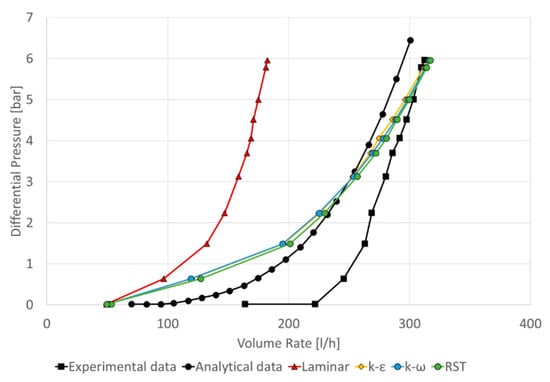
Figure 17.
The model results for one laminar and three turbulence models based on RANS formulation (k-ε, k-ω, and RST) contrasted with the experimental and analytical data.
The simulated curves showed a choking effect via an asymptotic behavior in the differential pressure. However, the results that corresponded to the laminar flow were distant from both the experimental curve and the analytical data. On the other hand, the three simulated results with a turbulent flow regime presented the same behavior and the differences between the data were negligible. The turbulence models followed the same behavior as the data used for the validation, as seen in Figure 12: the pressure difference for low volume rates was distant from the experimental data but close to analytical data. As the volume rate was increased, the data approached the experimental curve. The percentage differences between the experimental and simulated data are shown in Figure 18.
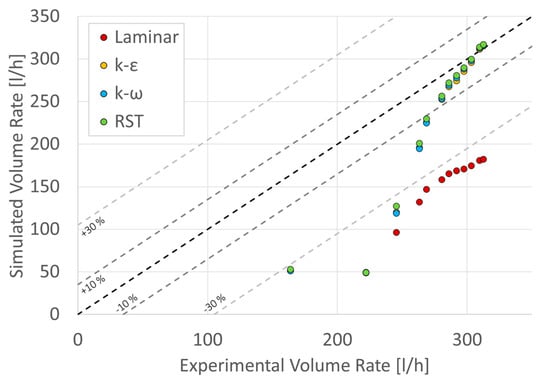
Figure 18.
Percentual differences between simulated results for one laminar and three turbulence models based on RANS formulation (k-ε, k-ω, and RST) contrasted with the experimental data.
The behavior for high volume rates was close to the experimental values (around ±10%). As the variable decreased, the RST model presented a lower percentage error; however, the difference between the two-equation models was less than 1%. All values of the laminar curve had an error between −30% and −50%, which indicated that the model did not correctly predict the experimental results, contrary to Askvik and Johannessen’s statement. Since the computational cost of solving a simulation with RST is higher than solving it with either k-ε or k-ω, it is recommended to use the two-equation models because the difference in results is small. The simulation results showed that for low-pressure differentials, the flow rates were lower compared to the experimental values; calculating the Reynolds number using the lowest volumetric flow determined that the flow was in transition; this should be considered because there are turbulence models for low Reynolds numbers that are capable of describing regimes in transition adequately.
4. Conclusions
- The single-phase model using DFBI and mesh morphing showed excellent results in describing the valve behavior when choking occurred. This meant that the model prediction had a deviation between 30% and 50% for low-pressure differences compared to the experimental data. One reason for the deviation could be that the experimental data contemplated the flow dynamics upstream of the measurement point, which was not considered in the simulations. On the other hand, for high differential pressures, the error between experimental and simulated data was less than 10% when choking occurred. These pressure conditions were the most common in reservoirs reaching differential pressures up to 20 bar; however, Askvik and Johannessen could only reach up to 6 bar experimentally.
- In contrast, the model for low differential pressures fit the analytical data better, resulting in errors below 10%; this may have shown that conditions that were not considered in the analytical model and in the CFD model that was considered in the experimental process became evident for low pressures. Conditions such as material roughness, radial movements, and fluid emulsions, among others, could affect the solution. Therefore, the CFD model should consider that low differential pressure means low flow velocities close to regimes in transition; this implies that the turbulence models chosen should contemplate a correction for low Re. This condition is highly linked to having a y+ below 1, something that was not considered when designing the mesh.
- The prediction performed without the model plate’s motion resulted in values distant from the experimental data. This was expected because without body motion, the model did not analyze the natural behavior of an RCP.
- It was determined that mesh morphing and DFBI actively responded depending on the fluid flowing into the device when analyzing a real-life case. When water flowed in, the plate rose to plug the nozzle; the plate lowered and allowed the flow to pass through when oil flowed in.
- An essential consideration of the DFBI model was the need to add contact constraints on the inner walls of the valve to contain the plate properly. However, due to the geometric scale and the high velocities of the plate, setting the contact conditions was of high complexity. Therefore, one of the assumptions that had to be made for the model was to dampen the motion of the plate. This is evident in Figure 15, which shows that the plate’s translation oscillated when the water entered but was damped and remained constant until the oil enters. This did not occur in real life; the expected behavior was the plate closing when the inlet began to vibrate due to the pressure variations.
- Although there were difficulties in emulating the oscillation of the plate, the results obtained showed an excellent prediction of the valve’s performance, as shown in the validation of the model. Therefore, the present computational analysis and the model generated are recommended for predicting results such as the curves of the pressure difference versus the flow rate and analyzing the device’s behavior for different geometrical considerations to optimize the process.
- Mesh independence showed that the unsteady-state case had a lower GCI than the steady-state case. There was not much in the literature on applying this analysis method to models with mesh morphing.
- Assuming a laminar flow showed results far from reality (more than a 30% error). Few differences between models were found when a turbulent flow regime was considered. The RST model was the most complete among the RANS models because it described the domain’s flow dynamics, making it an excellent choice. However, the computational cost of this model was higher by 22% compared to the computational time for solving the two-equation models. Since the difference between the turbulent regime solutions was small, we recommend using the realizable k-ε or SST k-ω model.
- For future work, we recommend finding a method for implementing the contacts inside the valve so that the oscillations of the plate are replicated. Using the present model, it is possible to analyze conditions that Askvik and Johannessen could not detail in their experimental process due to operational problems such as reaching pressure conditions of 20 bar or analyzing different oil viscosities for the valve they designed. Something that can also be analyzed is the effect of the oil and gas flow inside the valve. Due to the density difference between the phases, it is expected that something similar will happen with the water at the gas inlet (the plate moving to a closed position).
- Sources of errors that could affect the validation of the model include a lack of information on the upstream and downstream data of the valve during the experimental process; these variations can affect the flow dynamics and cause the computational model to be far from reality. Another aspect of the experimental data was that it did not detail whether the valve was vertical or horizontal, which would change how gravity affected it; in this study, it was assumed that the valve was vertical. A final source of error was that only the motion of the plate in the vertical direction was considered and not in other possible directions, which may have affected the results in predicting the outflow. Finally, the mesh treatment for the no-slip condition was not considered, so parameters such as y+ were not analyzed; this could have caused the values obtained to be different from reality.
Author Contributions
Conceptualization, L.A.R.C., J.A.P., N.R.R., M.A.; Methodology, L.A.R.C. and J.A.P.; Software, L.A.R.C.; Validation, L.A.R.C. and J.A.P.; Formal Analysis, L.A.R.C.; Investigation, L.A.R.C. and J.A.P.; Resources, N.R.R.; Writing—Original Draft Preparation, L.A.R.C.; Writing—Review and Editing, L.A.R.C., J.A.P. and N.R.R.; Supervision, N.R.R. and M.A.; Funding Acquisition, N.R.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Surface area (m2) | User-defined source term (-) | ||
| AICD | Autonomous inflow control device | Time (s) | |
| DFBI | Dynamic fluid–body interaction | Velocity of the fluid (m/s) | |
| Relative error (-) | Diffusion velocity (m2/s) | ||
| Extrapolated relative error (-) | Volume of i-phase in a cell (m3) | ||
| Gravity (m/s2) | Total volume of a cell (m3) | ||
| GCI | Grid convergence index | VOF | Volume of fluid |
| ICD | Inflow control device | Volume fraction of i-phase in a cell (-) | |
| ICV | Inflow control valve | Greek | |
| Mesh element count (-) | Solution at defined discretization (-) | ||
| Order of accuracy (-) | Extrapolated solution (-) | ||
| Pressure (Pa) | Viscosity (Pa·s) | ||
| PICD | Passive inflow control device | Viscosity of i-phase (Pa·s) | |
| Refinement ratio (-) | Density (kg/m3) | ||
| RCP | Rate controlled production | Density of i-phase (kg/m3) | |
| User-defined source term of i-phase (-) |
References
- IEA. Key World Energy Statistics 2020. IEA Publications. 2020. Available online: https://www.iea.org/reports/key-world-energy-statistics-2020 (accessed on 1 March 2021).
- Agencia Nacional Hidrocarburos. Colombia Open for Business. 2013. Available online: https://hydrocarbonscolombia.com/article/colombia-open-for-business/ (accessed on 1 March 2021).
- Bellaraby, J. Well Completion Design; Elsevier: Amsterdam, The Netherlands, 2009; Volume 56. [Google Scholar]
- Askvik, S.M.; Johannessen, I.L. Dynamic Autonomous Inflow Control Device; Norwegian University of Science and Technology: Trondheim, Norway, 2017. [Google Scholar]
- Halliburton. Inflow Control Devices. 2019. Available online: https://www.halliburton.com/en-US/ps/completions/sand-control/screens/inflow-control/default.html# (accessed on 23 May 2022).
- Zeng, Q.; Wang, Z.; Wang, X.; Li, Y.; Zou, W.; Xiao, J.; Chen, T.; Yang, G.; Zhang, Q. A novel autonomous inflow control device design: Improvements to hybrid ICD. In Proceedings of the International Petroleum Technology Conference 2014, IPTC 2014—Innovation and Collaboration: Keys to Affordable Energy, Kuala Lumpur, Malaysia, 10–12 December 2014; Volume 1, pp. 702–710. [Google Scholar]
- Fripp, M.; Zhao, L.; Least, B. The theory of a fluidic diode autonomous inflow control device. In Proceedings of the SPE Middle East Intelligent Energy Conference and Exhibition 2013, Manama, Bahrain, 28–30 October 2013; pp. 28–30. [Google Scholar]
- Corona, G.; Yin, W.; Felten, F. Enhanced nozzle inflow control device development for wall shear stress minimization in high-production application. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2016; Volume 1, pp. 713–719. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. Chapter two: Conservation laws of fluid motion and boundary conditions. In An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson: Upper Saddle River, NJ, USA, 2007; pp. 9–39. [Google Scholar]
- Hirt, C.; Nichols, B. Volume of Fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. Chapter three: Turbulence and its modeling. In An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson: Upper Saddle River, NJ, USA, 2007; pp. 40–114. [Google Scholar]
- SIEMENS. 6-DOF Rigid Body Motion. Forces and Moments; SIEMENS: Munich, Germany, 2020; pp. 1–3. [Google Scholar]
- SIEMENS. 6-DOF Rigid Body Motion. Body Connections; SIEMENS: Munich, Germany, 2020; pp. 4–6. [Google Scholar]
- Argyropoulos, C.D.; Markatos, N.C. Recent advances on the numerical modelling of turbulent flows. Appl. Math. Model. 2015, 39, 693–732. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar]
- SIEMENS. Reynolds-Averaged Navier-Stokes (RANS) Turbulence Models; SIEMENS: Munich, Germany, 2021; pp. 1–3. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).