Remaining Useful Life Prediction of Gear Pump Based on Deep Sparse Autoencoders and Multilayer Bidirectional Long–Short–Term Memory Network
Abstract
1. Introduction
2. Theoretical Background
2.1. DSAE
2.1.1. SAE
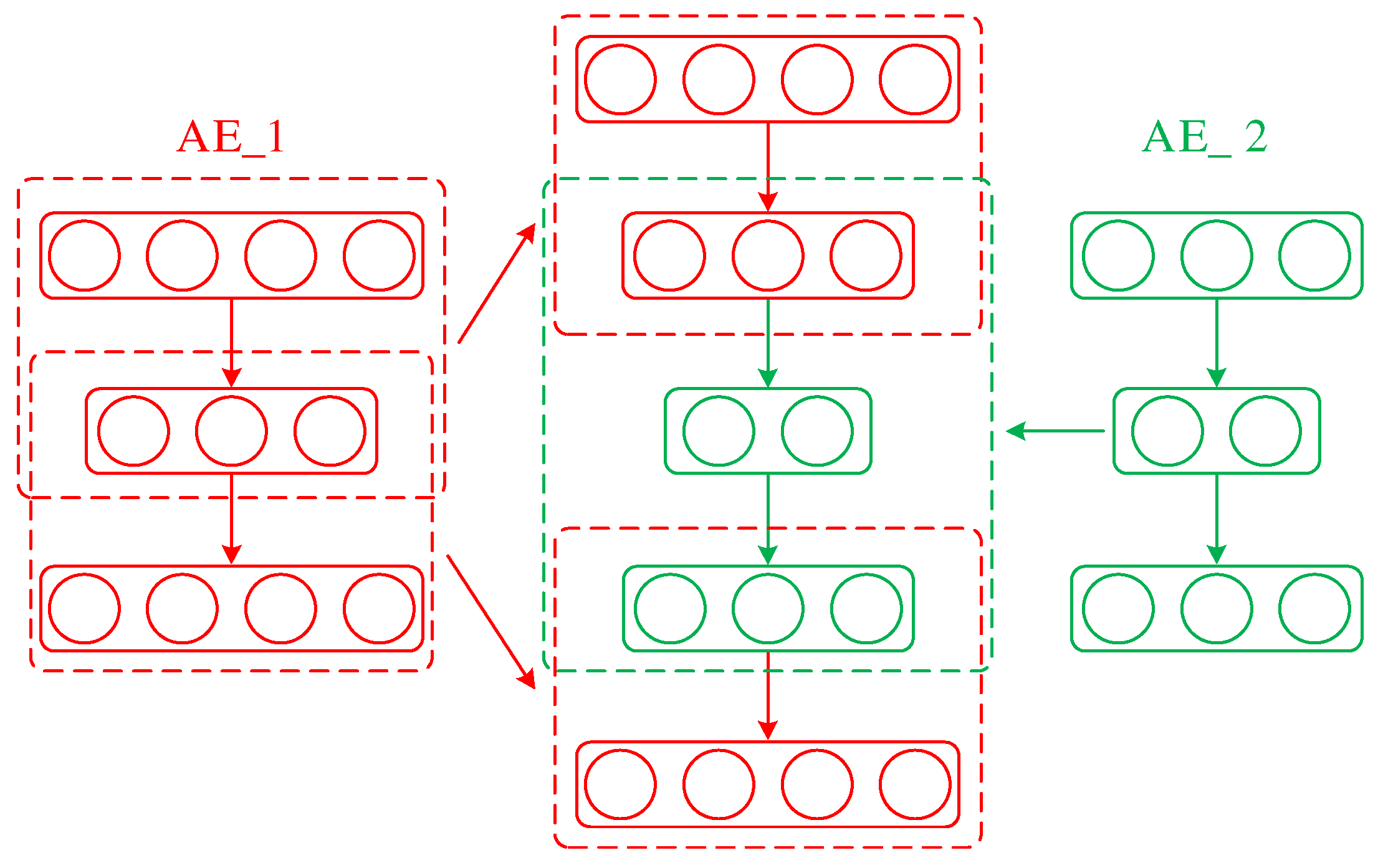
2.1.2. DSAE
2.2. SVDD
2.3. Multilayer Bi–LSTM Network
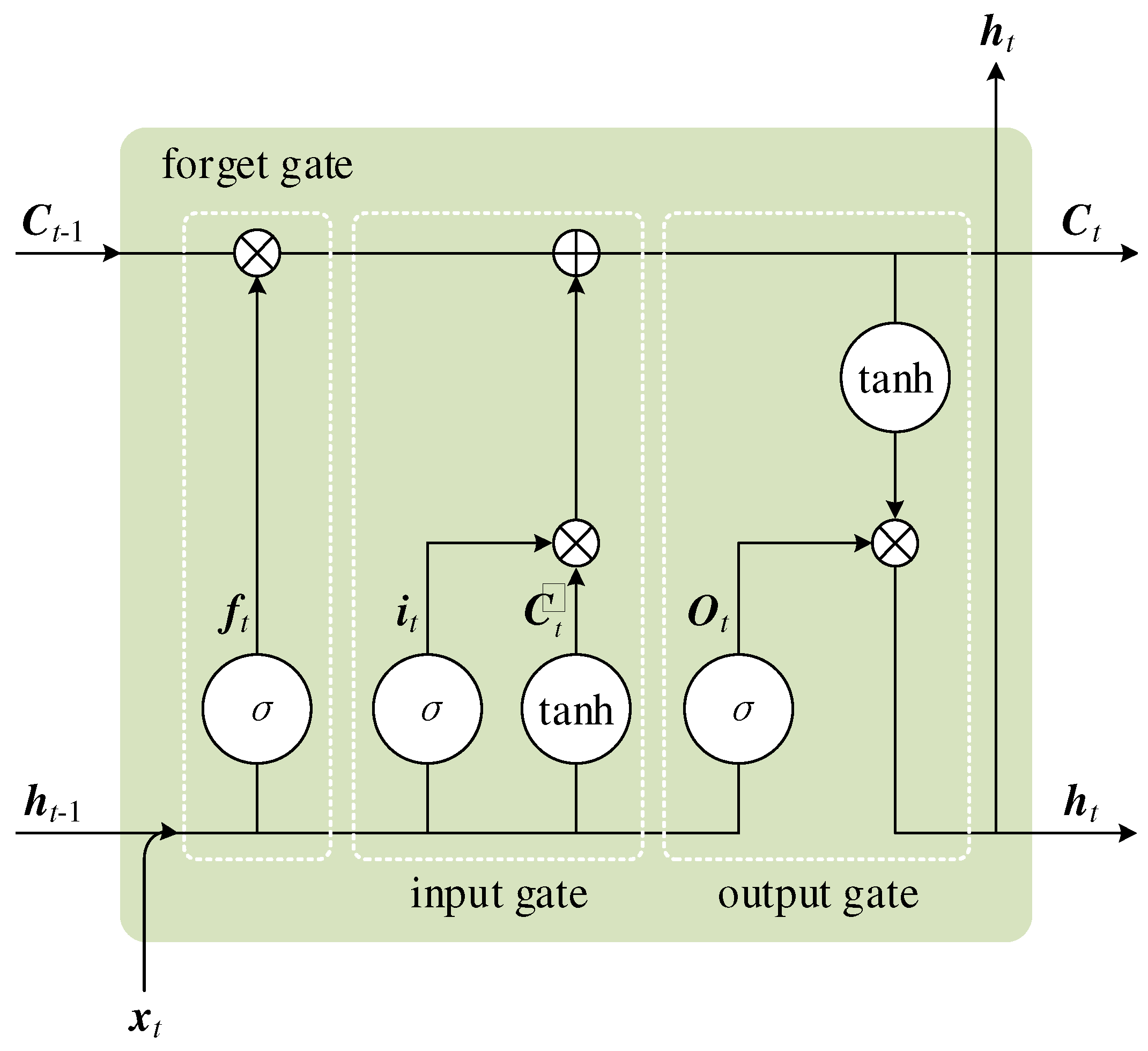
2.3.1. LSTM
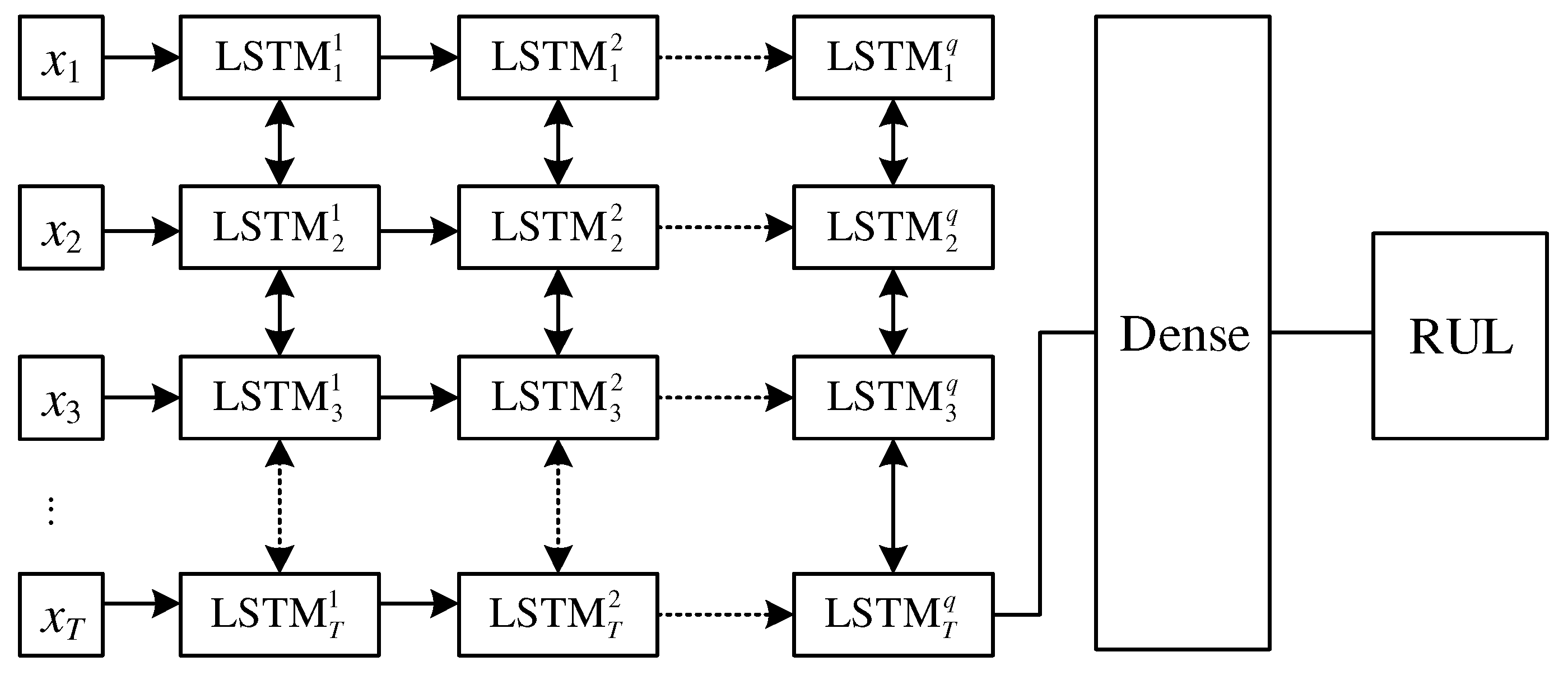
2.3.2. Multilayer Bi–LSTM Network
3. Experiment and Calculation
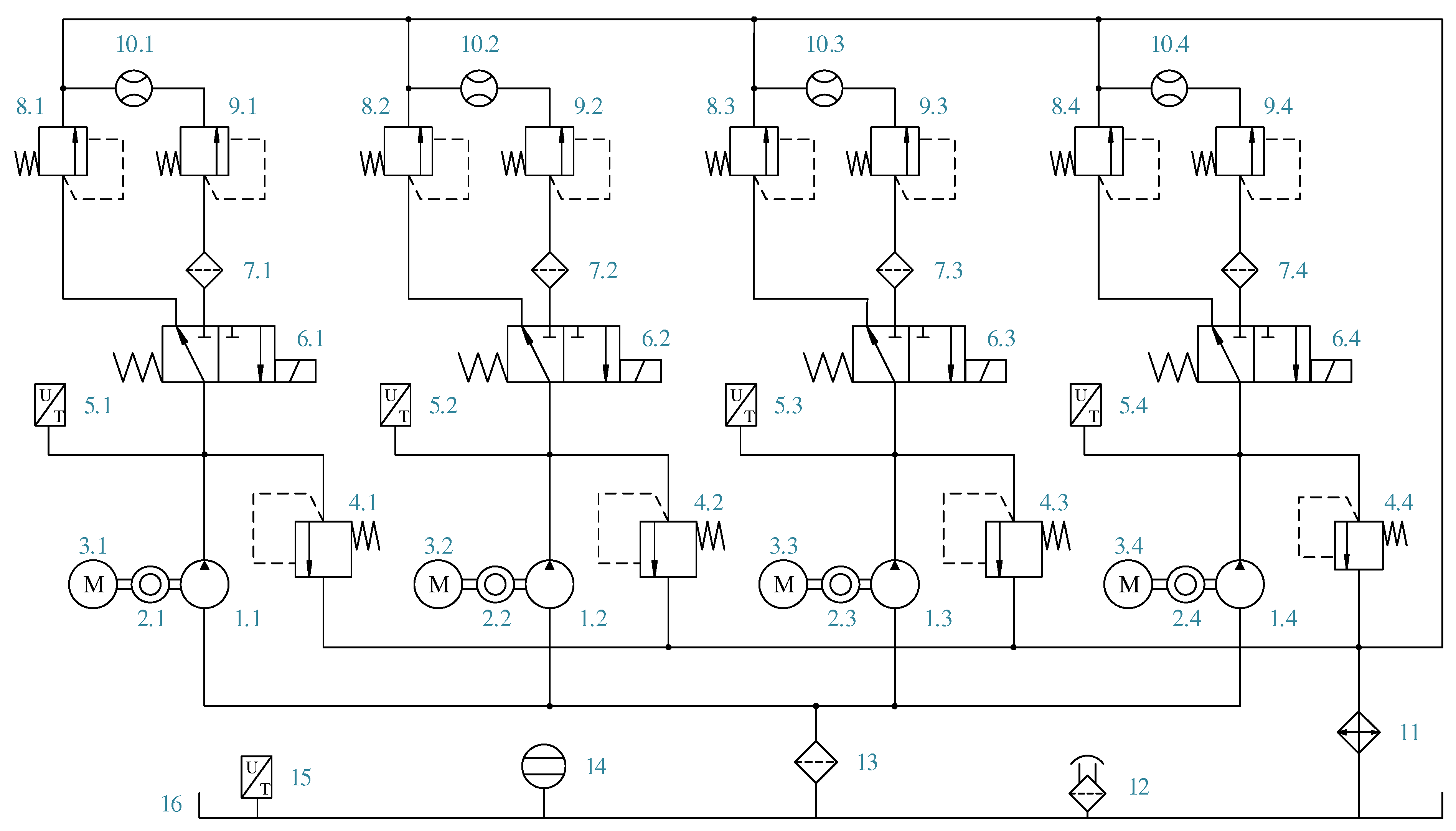
3.1. Full–Life Test of Gear Pump
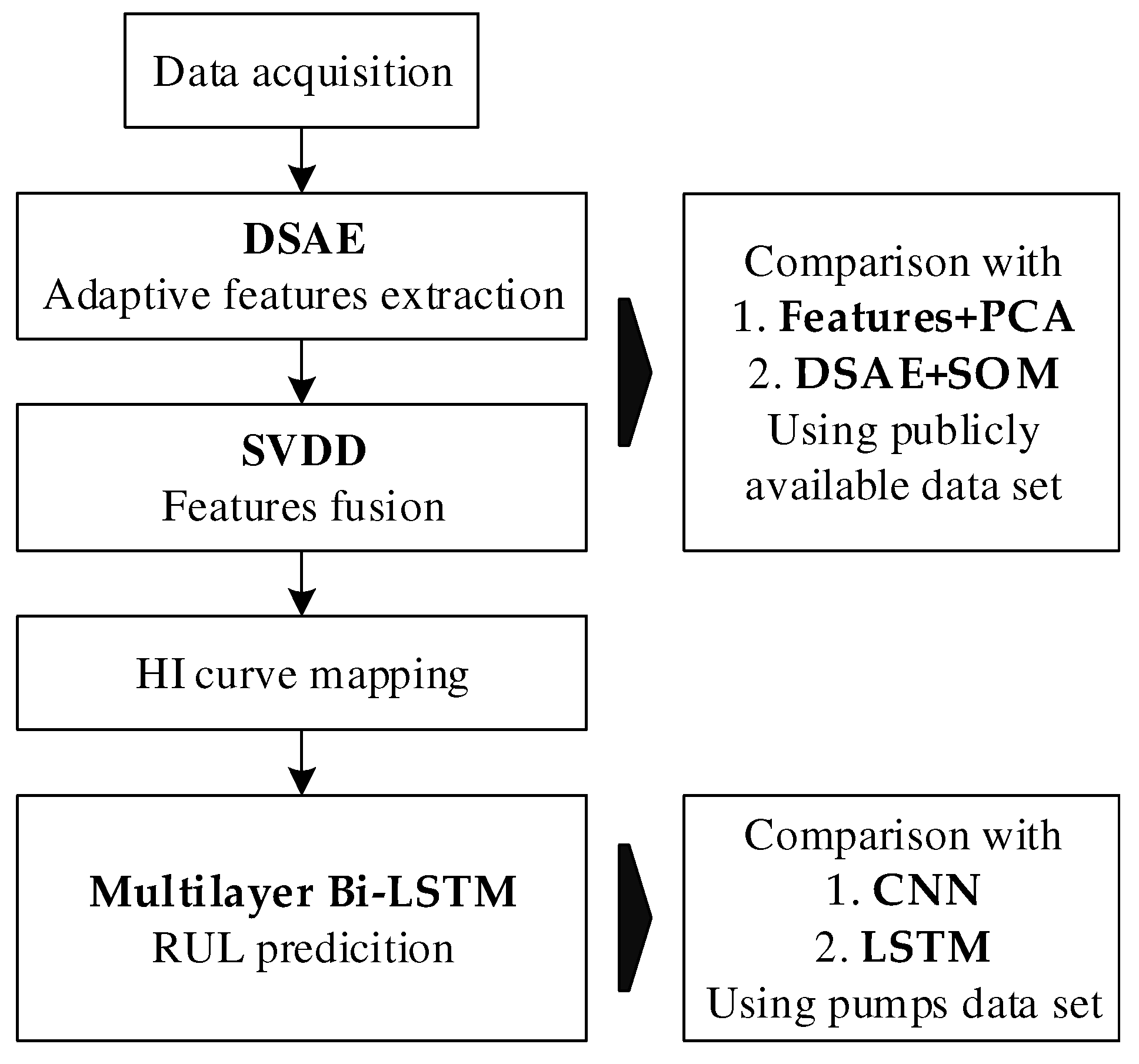
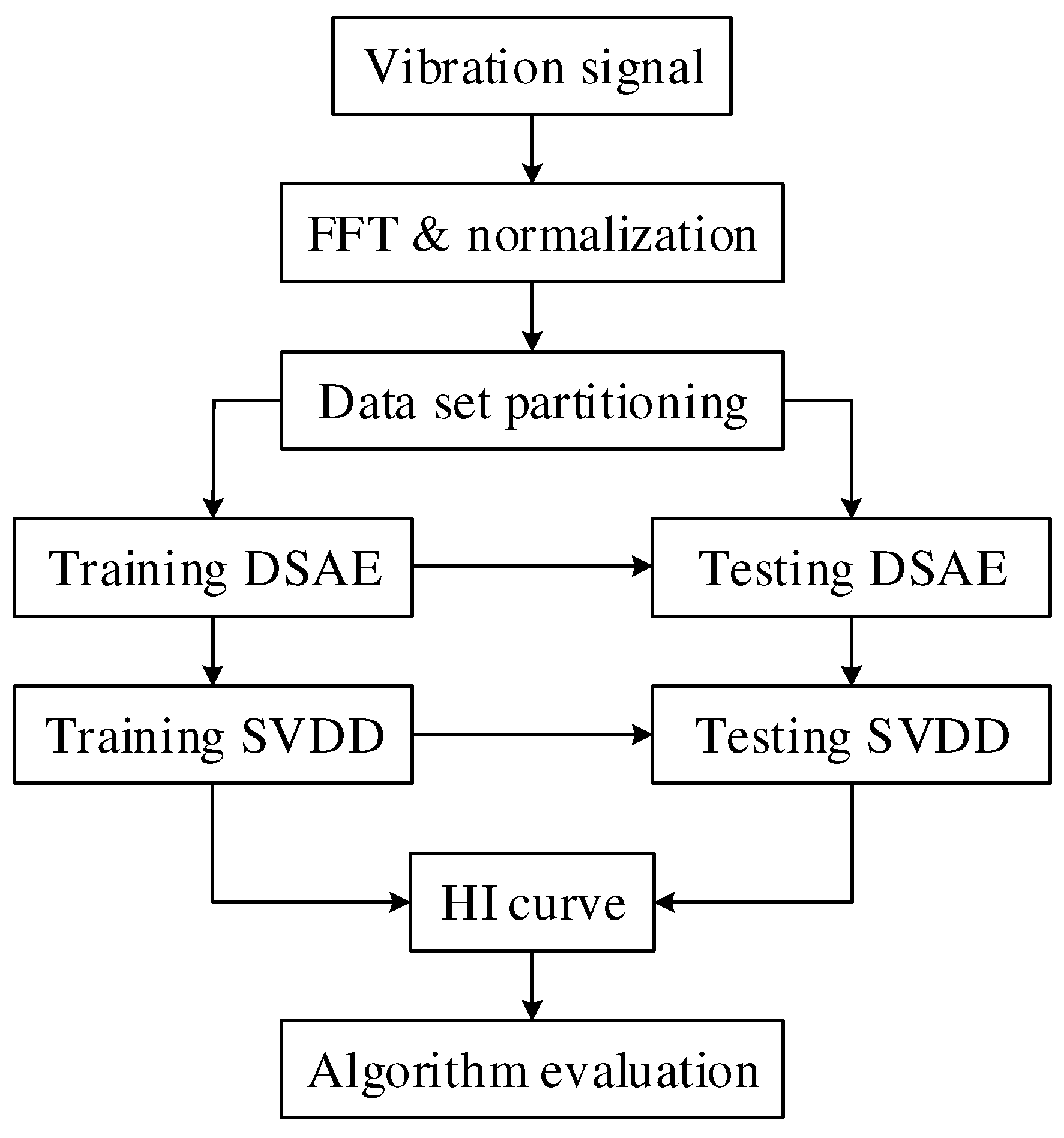
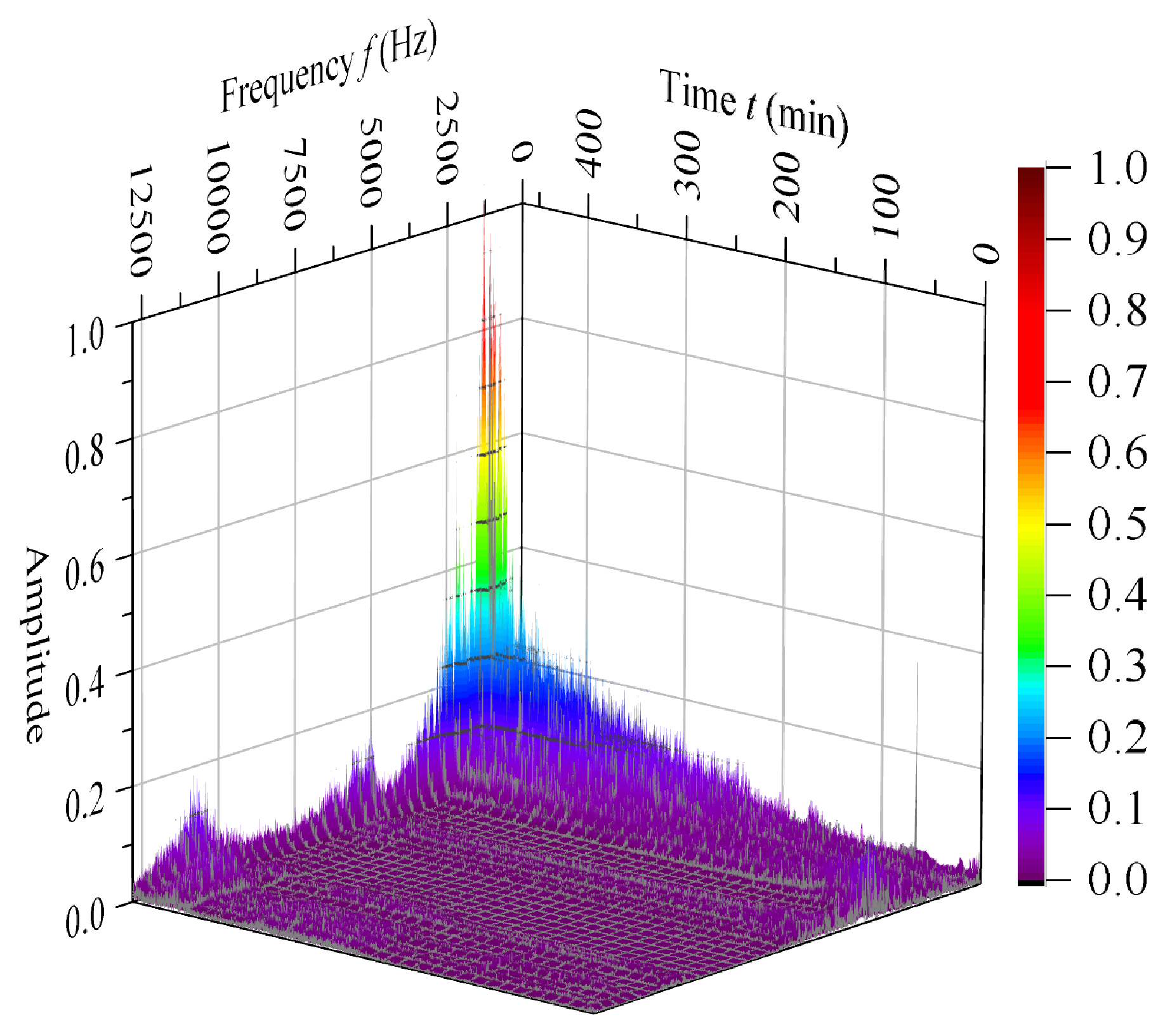
3.2. Plotting the Health Indicator Curve by DSAE + SVDD
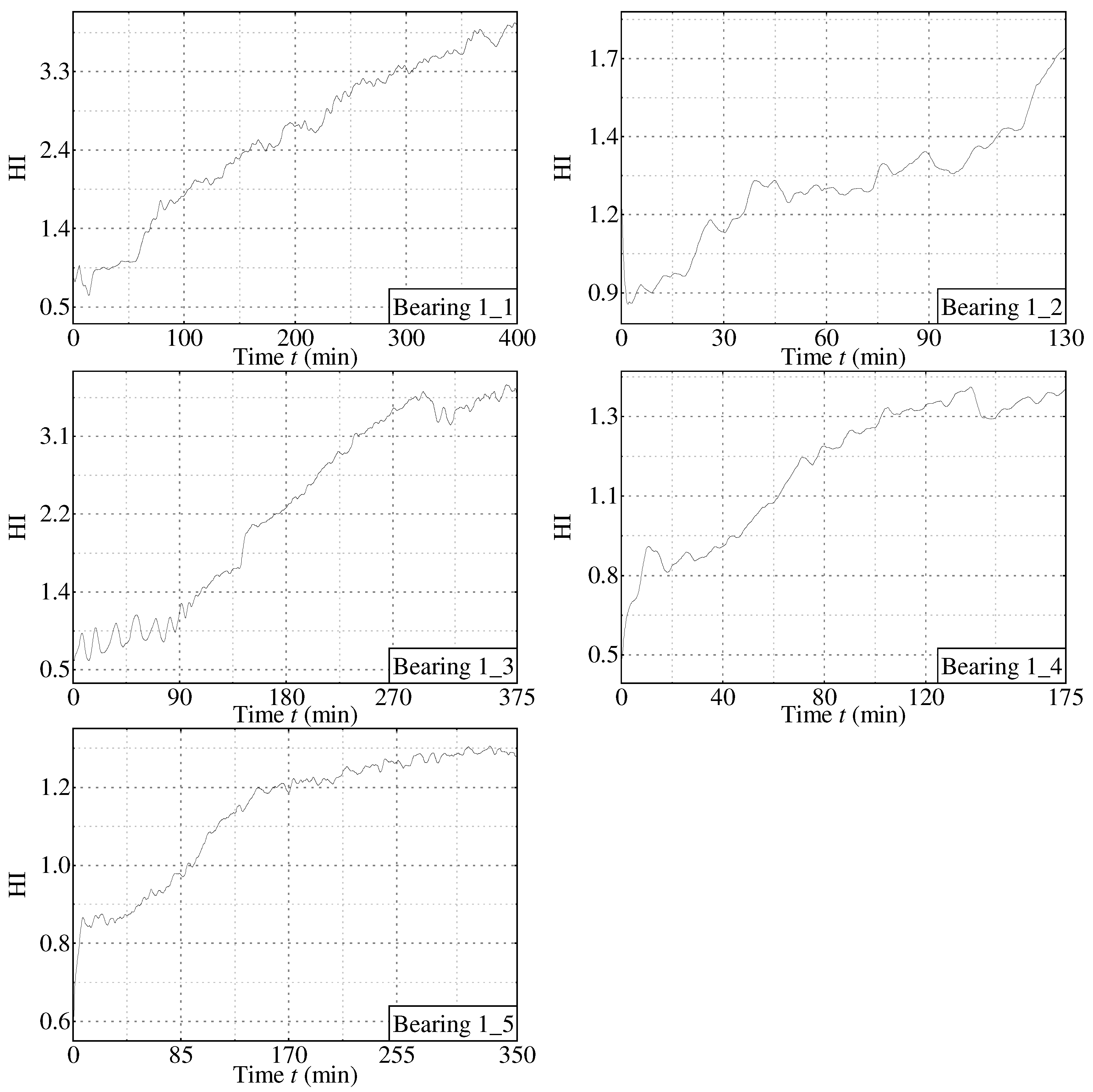
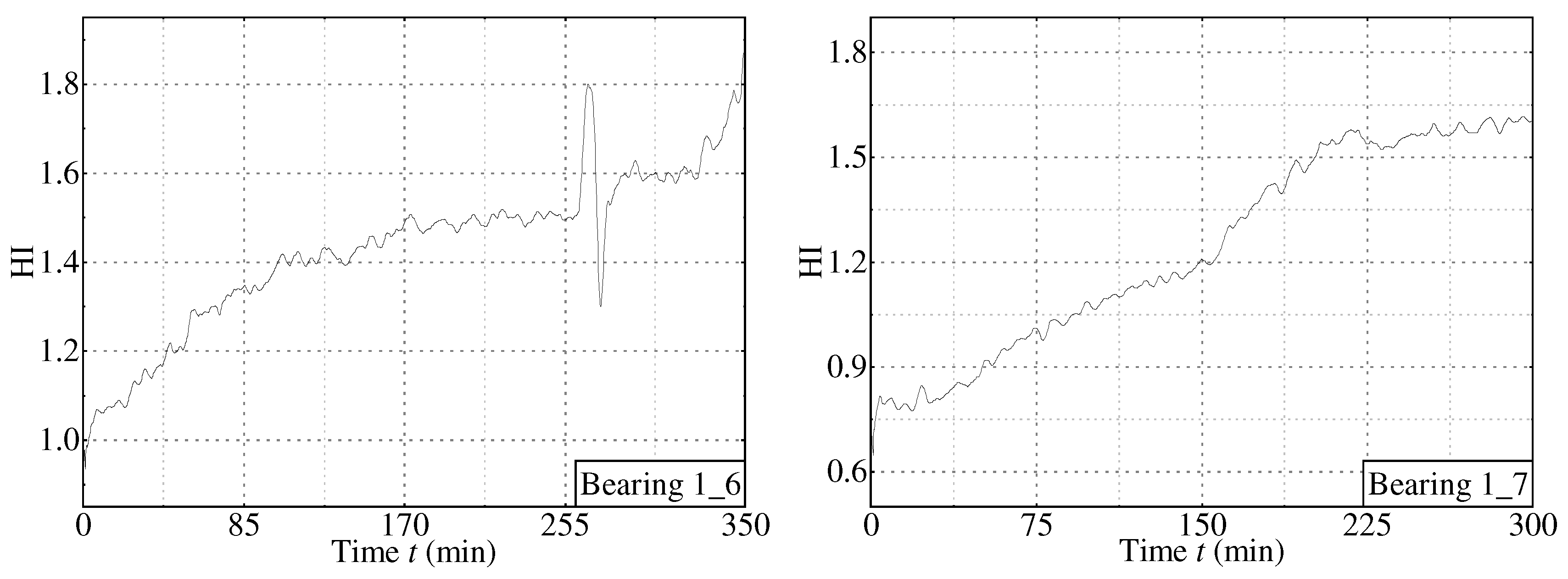
3.2.1. Verifying the Proposed Method by the Public Dataset
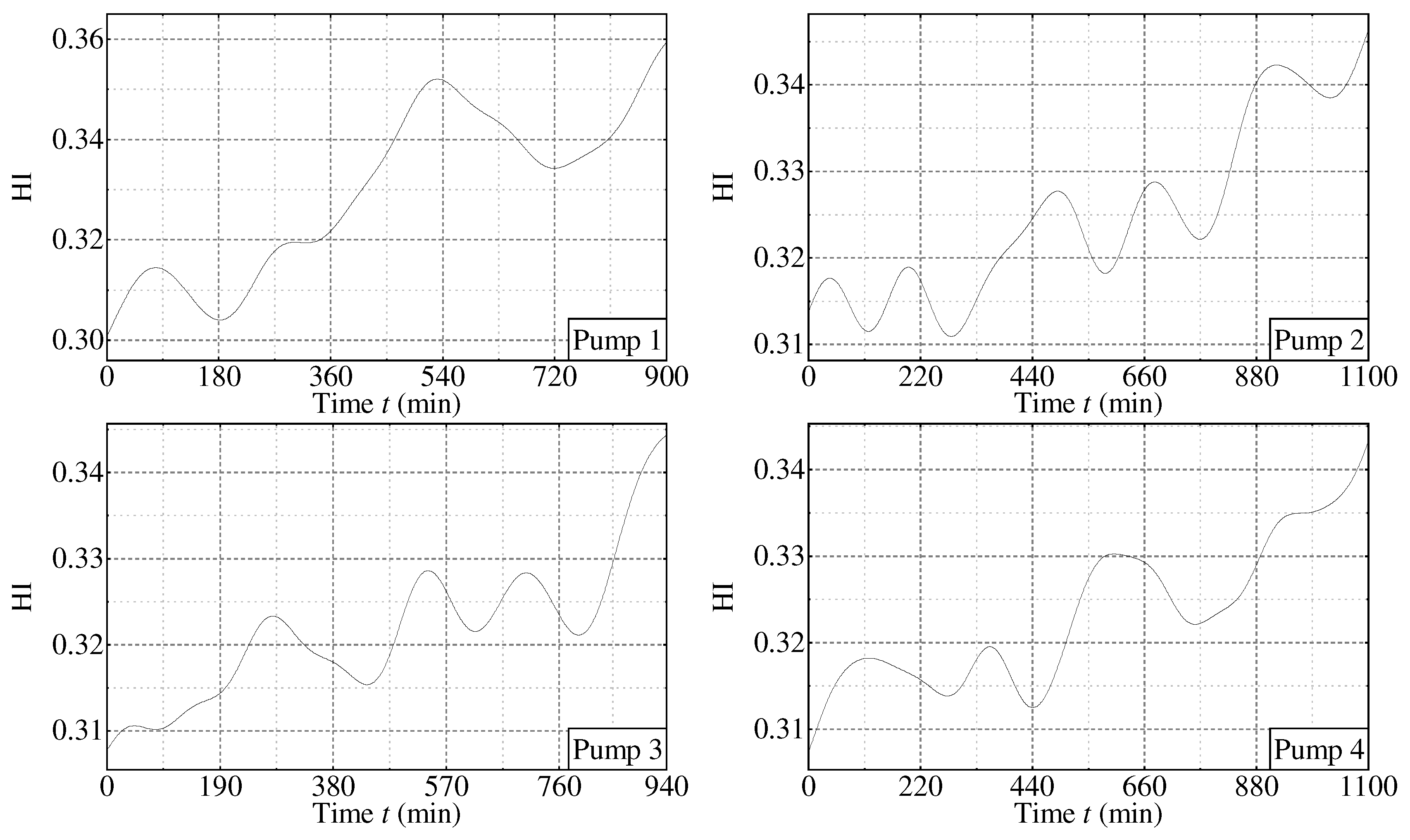
3.2.2. Processing Gear Pump Data Using the Proposed Method
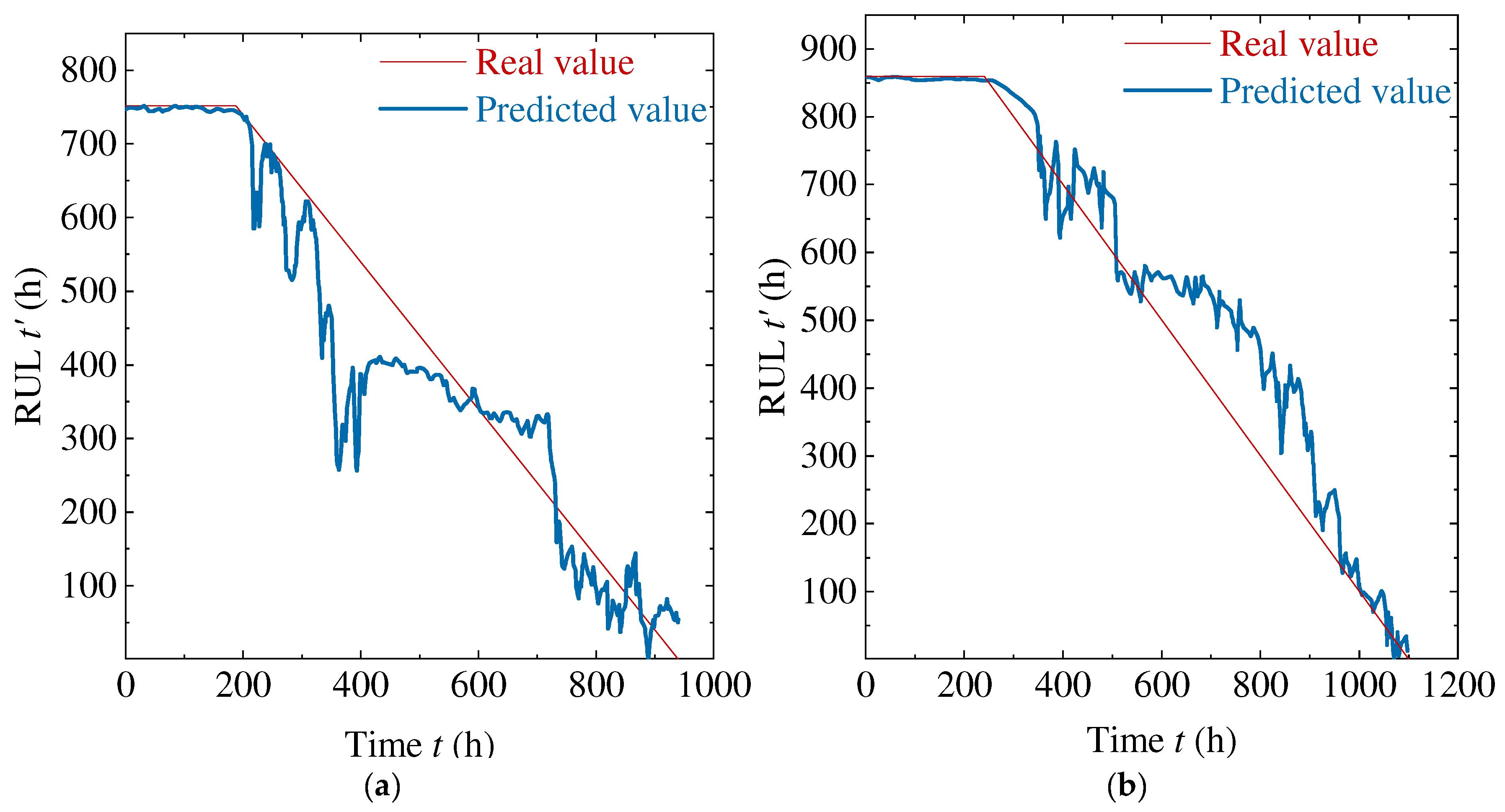
3.3. Predicting RUL Using Multilayer Bi–LSTM
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Xi, B.; Wang, C.; Xi, W.; Liu, Y.; Wang, H.; Yang, Y. Experimental investigation on the water hammer characteristic of stalling fluid in eccentric casing–tubing annulus. Energy 2022, 253, 124113. [Google Scholar] [CrossRef]
- Chao, Q.; Gao, H.; Tao, J.; Wang, Y.; Zhou, J.; Liu, C. Adaptive decision–level fusion strategy for the fault diagnosis of axial piston pumps using multiple channels of vibration signals. Sci. China Technol. Sci. 2022, 65, 470–480. [Google Scholar] [CrossRef]
- Chao, Q.; Zhang, J.; Xu, B.; Wang, Q.; Lu, F.; Li, K. Integrated slipper retainer mechanism to eliminate slipper wear in high–speed axial piston pumps. Front. Mech. Eng. 2022, 17, 1. [Google Scholar] [CrossRef]
- Tang, S.N.; Zhu, Y.; Yuan, S.Q. An Improved Convolutional Neural Network with an Adaptable Learning Rate towards Multi–signal Fault Diagnosis of Hydraulic Piston Pump. Adv. Eng. Inform. 2021, 50, 101406. [Google Scholar] [CrossRef]
- Yuan, X.M.; Wang, W.Q.; Zhu, X. Theory Model of Dynamic Bulk Modulus for Aerated Hydraulic Fluid. Chin. J. Mech. Eng. 2022, 35, 121. [Google Scholar] [CrossRef]
- Tang, S.N.; Zhu, Y.; Yuan, S.Q. A Novel Adaptive Convolutional Neural Network for Fault Diagnosis of Hydraulic Piston Pump with Acoustic Images. Adv. Eng. Inform. 2022, 52, 101554. [Google Scholar] [CrossRef]
- Tang, S.N.; Zhu, Y.; Yuan, S.Q. An adaptive deep learning model towards fault diagnosis of hydraulic piston pump using pressure signal. Eng. Fail. Anal. 2022, 138, 106300. [Google Scholar] [CrossRef]
- Li, N.; Lei, Y.; Lin, J.; Ding, S.X. An Improved Exponential Model for Predicting Remaining Useful Life of Rolling Element Bearings. IEEE Trans. Ind. Electron. 2015, 62, 7762–7773. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Hu, C.H.; Fan, H.D. Real–Time Remaining Useful Life Prediction for a Nonlinear Degrading System in Service: Application to Bearing Data. IEEE/ASME Trans. Mechatron. 2018, 23, 211–222. [Google Scholar] [CrossRef]
- Nian, F. Viewpoints about the prognostic and health management. Chin. J. Sci. Instrum. 2018, 39, 1–14. [Google Scholar]
- Liu, H.; Liu, Z.; Jia, W.; Zhang, D.; Tan, J. Current research and challenges of deep learning for equipment remaining useful life prediction. Comput. Integr. Manuf. Syst. 2021, 27, 34–52. [Google Scholar]
- Pei, H.; Hu, C.; Si, X.; Zhang, J.; Pang, Z.; Zhang, P. Review of Machine Learning Based Remaining Useful Life Prediction Methods for Equipment. J. Mech. Eng. 2019, 55, 1–13. [Google Scholar] [CrossRef]
- Peng, C.; Qian, F.; Du, X. New nonlinear degradation modeling and residual life prediction. Comput. Integr. Manuf. Syst. 2019, 25, 1647–1654. [Google Scholar]
- Guo, J.; Li, Z.; Li, M. A Review on Prognostics Methods for Engineering Systems. IEEE Trans. Reliab. 2020, 69, 1110–1129. [Google Scholar] [CrossRef]
- Guo, X.J.; Chen, L.; Shen, C.Q. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Measurement 2016, 93, 490–502. [Google Scholar] [CrossRef]
- Wang, Z.J.; Yang, N.N.; Li, N.P.; Du, W.H.; Wang, J.Y. A new fault diagnosis method based on adaptive spectrum mode extraction. Struct. Health Monit. Int. J. 2021, 20, 3354–3370. [Google Scholar] [CrossRef]
- Jiang, W.; Li, Z.; Li, J.; Zhu, Y.; Zhang, P. Study on a Fault Identification Method of the Hydraulic Pump Based on a Combi–nation of Voiceprint Characteristics and Extreme Learning Machine. Processes 2019, 7, 894. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. Intelligent fault diagnosis of hydraulic piston pump based on deep learning and Bayesian optimization. ISA Trans. 2022, 129, 555–563. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Li, W.H. Multisensor Feature Fusion for Bearing Fault Diagnosis Using Sparse Autoencoder and Deep Belief Network. IEEE Trans. Instrum. Meas. 2017, 66, 1693–1702. [Google Scholar] [CrossRef]
- Zhao, M.H.; Kang, M.S.; Tang, B.P.; Pecht, M. Multiple Wavelet Coefficients Fusion in Deep Residual Networks for Fault Diagnosis. IEEE Trans. Ind. Electron. 2019, 66, 4696–4706. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Xu, L.; Liu, L.Z.; Silva, C.W. Fault Diagnosis for Rotating Machinery Using Multiple Sensors and Convolutional Neural Networks. IEEE ASME Trans. Mechatron. 2018, 23, 101–110. [Google Scholar] [CrossRef]
- Ben Ali, J.; Chebel–Morello, B.; Saidi, L.; Malinowski, S.; Fnaiech, F. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network. Mech. Syst. Signal Process. 2015, 56–57, 150–172. [Google Scholar] [CrossRef]
- Guo, R.; Li, Y.; Zhao, L.; Zhao, J.; Gao, D. Remaining Useful Life Prediction Based on the Bayesian Regularized Radial Basis Function Neural Network for an External Gear Pump. IEEE Access 2020, 8, 107498–107509. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, W.; Zhang, S.; Xue, D.; Zhang, S. Research on Prediction Method of Hydraulic Pump Remaining Useful Life Based on KPCA and JITL. Appl. Sci. 2021, 11, 9389. [Google Scholar] [CrossRef]
- Xu, G.W.; Liu, M.; Jiang, Z.F.; Shen, W.M.; Huang, C.X. Online Fault Diagnosis Method Based on Transfer Convolutional Neural Networks. IEEE Trans. Instrum. Meas. 2020, 69, 509–520. [Google Scholar] [CrossRef]
- Welling, M.; Hinton, G.E. A new learning algorithm for Mean Field Boltzmann Machines. Lect. Notes Comput. Sci. 2002, 2415, 351–357. [Google Scholar]
- Lecun, Y. Modèles Connexionnistes de L’apprentissage. Ph.D. Thesis, Pierre and Marie Curie University, Paris, France, 1985. [Google Scholar]
- Le, Q. Building high–level features using large scale unsupervised learning. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Liu, H.; Taniguchi, T.; Takano, T.; Tanaka, Y.; Takenaka, K.; Bando, T. Visualization of driving behavior using deep sparse autoencoder. In Proceedings of the IEEE Intelligent Vehicles Symposium, Dearborn, MI, USA, 8–11 June 2014. [Google Scholar]
- Al–Zaidy, R.A.; Caragea, C.; Giles, C.L. Bi–LSTM–CRF sequence labeling for key phrase extraction from scholarly documents. In Proceedings of the Web Conference 2019—Proceedings of the World Wide Web Conference, New York, NY, USA, 13 May 2019. [Google Scholar]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Wang, C.; Jiang, W.; Yue, Y.; Zhang, S. Research on Prediction Method of Gear Pump Remaining Useful Life Based on DCAE and Bi–LSTM. Symmetry 2022, 14, 1111. [Google Scholar] [CrossRef]
- Wang, S.H.; Li, H.C.; Zhang, J.W. Research on Life Estimation of Aero–Engine Fuel Gear Pump. Mach. Des. Manuf. 2012, 8, 138–140. [Google Scholar]
- Jiang, W.L.; Li, Z.B.; Lei, Y.F.; Zhang, S.; Tong, X.W. Deep learning based rolling bearing fault diagnosis and performance degradation degree recognition method. J. Yanshan Univ. 2020, 44, 526–635. [Google Scholar]
- Hu, C.H.; Pei, H.; Si, X.S.; Du, D.B.; Pang, Z.N.; Wang, X. A prognostic model based on DBN and diffusion process for degrading bearing. IEEE Trans. Ind. Electron. 2020, 67, 8767–8777. [Google Scholar] [CrossRef]
- Sun, W.; Shao, S.; Yan, R. Induction motor fault diagnosis based on deep neural network of sparse auto–encoder. J. Mech. Eng. 2016, 52, 65–71. [Google Scholar] [CrossRef]
- Shin, H.C.; Orton, M.R.; Collins, D.J.; Doran, S.J.; Leach, M.O. Stacked autoencoders for unsupervised feature learning and multiple organ detection in a pilot study using 4D patient data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1930–1943. [Google Scholar] [CrossRef]
- Bengio, Y.; Lamblin, P.; Popovici, D.; Larochelle, H. Greedy Layer–Wise Training of Deep Networks; MIT Press: Cambridge, MA, USA, 2007; pp. 153–160. [Google Scholar]
- Werbos, P.J. Backpropagation through Time: What It Does and How to Do It. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Kohonen, T. The self–organizing map. Neurocomputing 1998, 21, 1–6. [Google Scholar] [CrossRef]
- Porotsky, S.; Bluvband, Z. Remaining useful life estimation for systems with non–trendability behavior. In Proceedings of the Prognostics and Health Management, Denver, CO, USA, 18–21 June 2012. [Google Scholar]
- Tax, D.M.J.; Duin, R.P.W. Support Vector Data Description. Mach. Learn. 2014, 54, 45–66. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in neural networks: An overview. Neural Netw. 2015, 61, 379–394. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.R.; Hinton, G.E. Speech recognition with deep recurrent neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short–Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Li, Z.B.; Jiang, W.L.; Wu, X.; Zhang, S.Q.; Chen, D.N. Study on Health Indicator Construction and Health Status Evaluation of Hydraulic Pumps Based on LSTM–VAE. Processes 2022, 10, 1869. [Google Scholar] [CrossRef]
- She, D.; Jia, M.; Pecht, M.G. Sparse auto–encoder with regularization method for health indicator construction and remaining useful life prediction of rolling bearing. Meas. Sci. Technol. 2020, 31, 105005. [Google Scholar] [CrossRef]
- Babu, G.S.; Zhao, P.; Li, X.L. Deep convolutional neural network based regression approach for estimation of remaining useful life. Lect. Notes Comput. Sci. 2016, 9642, 214–228. [Google Scholar]
- Tang, S.N.; Zhu, Y.; Yuan, S.Q. Intelligent Fault Identification of Hydraulic Pump Using Deep Adaptive Normalized CNN and Synchrosqueezed Wavelet Transform. Reliab. Eng. Syst. Saf. 2022, 224, 108560. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, G.P.; Tang, S.N.; Wang, R.; Su, H.; Wang, C. Acoustic Signal–based Fault Detection of Hydraulic Piston Pump using a Particle Swarm Optimization Enhancement CNN. Appl. Acoust. 2022, 192, 108718. [Google Scholar] [CrossRef]








| Name | Model Number | Remarks |
|---|---|---|
| Gear pump | CBWF–304 | Rated pressure: 20 MPa, maximum pressure: 25 MPa, rated rotating speed: 2500 r/min, displacement: 4 mL/r. |
| Meter of rotating speed and torque | CYT–302 | Measurable torque range: 0–50 N·m, Measurable rotating speed range: 0–3000 r/min, accuracy: 0.5 FS. |
| Electromotor | Y90L–4B35 | Rated rotating speed: 1470 r/min, power: 3 kW. |
| Relief valve | DBDS6P1X/200 | Maximum pressure: 31.5 MPa, maximum flow: 80 L/min. |
| Pressure sensor | PU5400 | Maximum measurable value: 40 MPa. |
| Solenoid directional valve | 3WE6A50/G24 | Maximum flow: 60 L/min. |
| High–pressure filter | ZU–H40X30 | Maximum flow: 40 L/min, filter fineness: 30 μm. |
| Flow meter | MG015 | Maximum flow: 40 L/min. |
| Cooler | DEL–4 | Heat release: 0.3 kW/°C, flow range: 15–80 L/min. |
| Oil filter | TF–63X100F–Y | Nominal flow: 63 L/min, filter fineness: 100 μm, latus rectum: 25 mm. |
| Liquid level gauge | YWT–250 | Pressure range: 0.1–0.15 MPa. |
| DAQ card | NI PXIe–6363 | Analog acquisition channel: 32, resolution: 16–bit, maximum sampling rate: 2 MS/s |
| Temperature sensor | CWDZ11 | Measurable temperature range: −50–100 °C, accuracy: 0.5 FS |
| Acceleration sensor | YD–36D | Sensitivity: 0.002 V/m·s−2, frequency response: 10 Hz–5 kHz (−3 dB), maximum acceleration: 2500 m/s2, resolution: 0.01 m/s2. |
| Category | Condition_1 | Condition_2 | Condition_3 |
|---|---|---|---|
| Training dataset | Bearing1_1 | Bearing2_1 | Bearing3_1 |
| Bearing1_2 | Bearing2_2 | Bearing3_2 | |
| Testing dataset | Bearing1_3 | Bearing2_3 | Bearing3_3 |
| Bearing1_4 | Bearing2_4 | ||
| Bearing1_5 | Bearing2_5 | ||
| Bearing1_6 | Bearing2_6 | ||
| Bearing1_7 | Bearing2_7 |
| Category | Dataset | Number of Used Samples | Number of All Samples |
|---|---|---|---|
| Training dataset | Bearing1_1 | 2660 | 2803 |
| Bearing1_2 | 826 | 871 | |
| Bearing1_3 | 2329 | 2375 | |
| Bearing1_4 | 1055 | 1428 | |
| Bearing1_5 | 2217 | 2463 | |
| Testing dataset | Bearing1_6 | 2080 | 2448 |
| Bearing1_7 | 2033 | 2259 |
| Dataset | Features + PCA | DSAE + SOM | DSAE + SVDD | |||
|---|---|---|---|---|---|---|
| Vmon | Vtre | Vmon | Vtre | Vmon | Vtre | |
| Bearing1_1 | 0.13 | 0.86 | 0.17 | 0.66 | 0.21 | 0.96 |
| Bearing1_2 | 0.07 | 0.19 | 0.03 | 0.31 | 0.27 | 0.94 |
| Bearing1_3 | 0.13 | 0.73 | 0.14 | 0.64 | 0.34 | 0.97 |
| Bearing1_4 | 0.09 | 0.91 | 0.16 | 0.95 | 0.41 | 0.94 |
| Bearing1_5 | 0.16 | 0.91 | 0.17 | 0.92 | 0.19 | 0.92 |
| Bearing1_6 | 0.04 | 0.19 | 0.11 | 0.82 | 0.20 | 0.93 |
| Bearing1_7 | 0.06 | 0.56 | 0.08 | 0.29 | 0.21 | 0.96 |
| Algorithm | Evaluation Index | Pump 3 | Pump 4 |
|---|---|---|---|
| CNN | MAE | 119.65 | 55.35 |
| RMSE | 138.70 | 69.30 | |
| NMSE | 6.10 | 1.43 | |
| LSTM | MAE | 110.00 | 63.82 |
| RMSE | 138.45 | 79.38 | |
| NMSE | 6.08 | 3.12 | |
| Multilayer Bi–LSTM | MAE | 38.78 | 52.82 |
| RMSE | 43.17 | 73.37 | |
| NMSE | 0.76 | 1.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Jiang, W.; Shi, X.; Zhang, S. Remaining Useful Life Prediction of Gear Pump Based on Deep Sparse Autoencoders and Multilayer Bidirectional Long–Short–Term Memory Network. Processes 2022, 10, 2500. https://doi.org/10.3390/pr10122500
Zhang P, Jiang W, Shi X, Zhang S. Remaining Useful Life Prediction of Gear Pump Based on Deep Sparse Autoencoders and Multilayer Bidirectional Long–Short–Term Memory Network. Processes. 2022; 10(12):2500. https://doi.org/10.3390/pr10122500
Chicago/Turabian StyleZhang, Peiyao, Wanlu Jiang, Xiaodong Shi, and Shuqing Zhang. 2022. "Remaining Useful Life Prediction of Gear Pump Based on Deep Sparse Autoencoders and Multilayer Bidirectional Long–Short–Term Memory Network" Processes 10, no. 12: 2500. https://doi.org/10.3390/pr10122500
APA StyleZhang, P., Jiang, W., Shi, X., & Zhang, S. (2022). Remaining Useful Life Prediction of Gear Pump Based on Deep Sparse Autoencoders and Multilayer Bidirectional Long–Short–Term Memory Network. Processes, 10(12), 2500. https://doi.org/10.3390/pr10122500





