Nonstationary Process Monitoring Based on Alternating Conditional Expectation and Cointegration Analysis
Abstract
1. Introduction
2. Theory and Method
2.1. Difference and Unit Root Test
2.2. Cointegration Theory
2.3. Cointegration Test
2.3.1. Engle and Granger Test
2.3.2. Johansen Test
2.4. Alternating Conditional Expectation
2.5. Monitoring Statistics
3. The Proposed Monitoring Strategy
3.1. Offline Modeling
3.2. Online Monitoring
4. Case and Result
4.1. Two-Dimensional Simulation Case
4.1.1. Data Construction
4.1.2. ACE and EG Test
4.2. Multidimensional Simulation Case
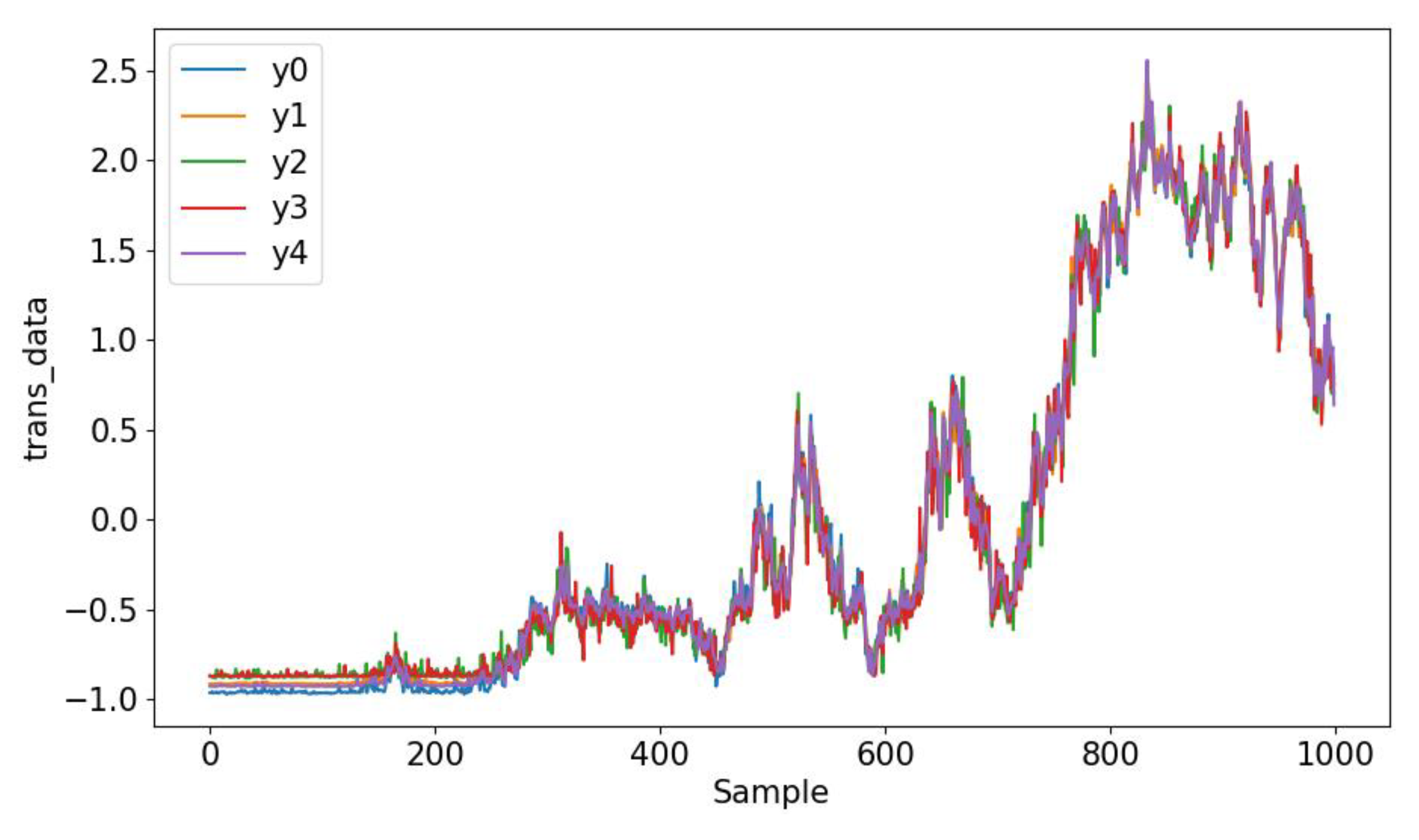
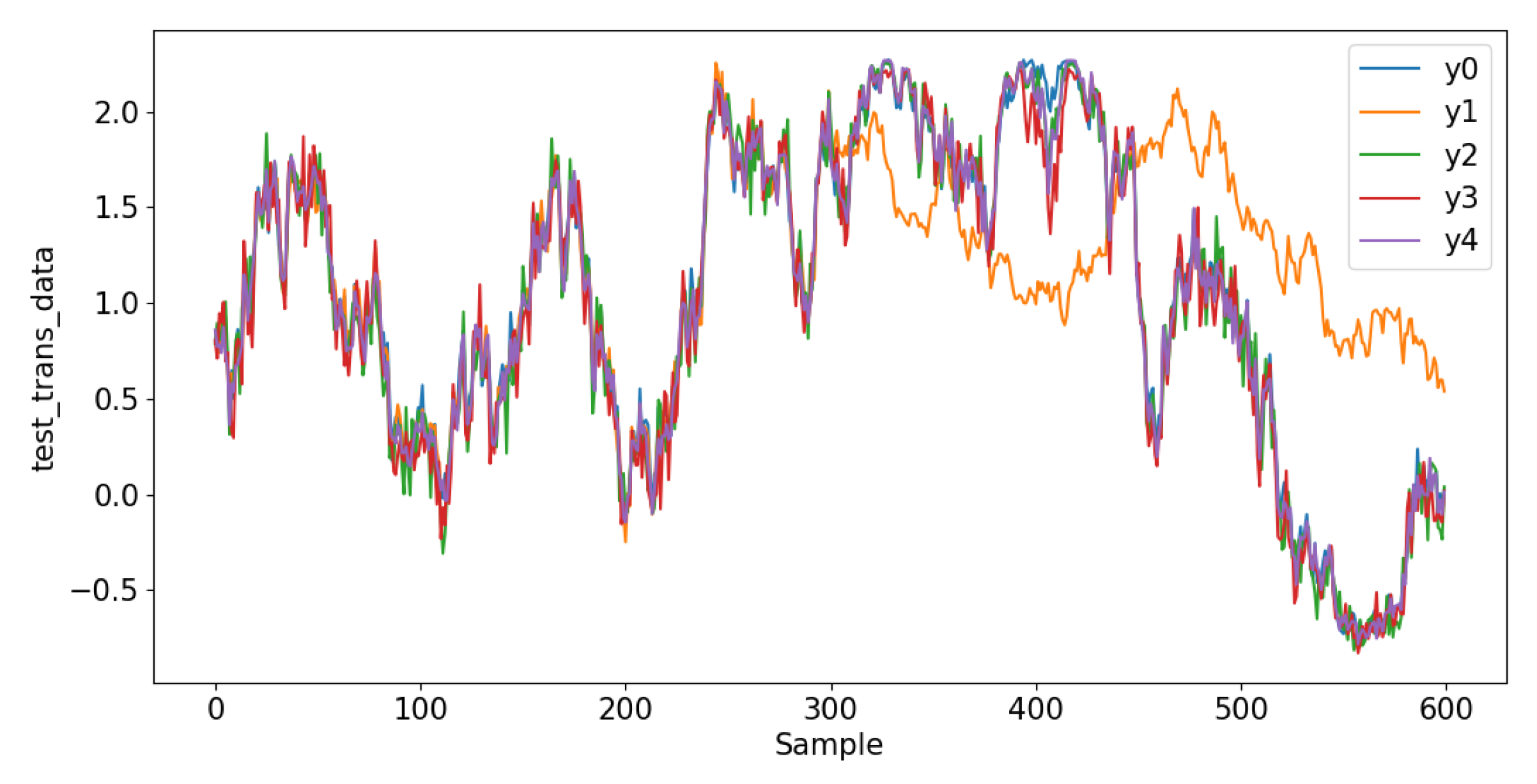
4.2.1. Data Construction
4.2.2. ACE and Johansen Test
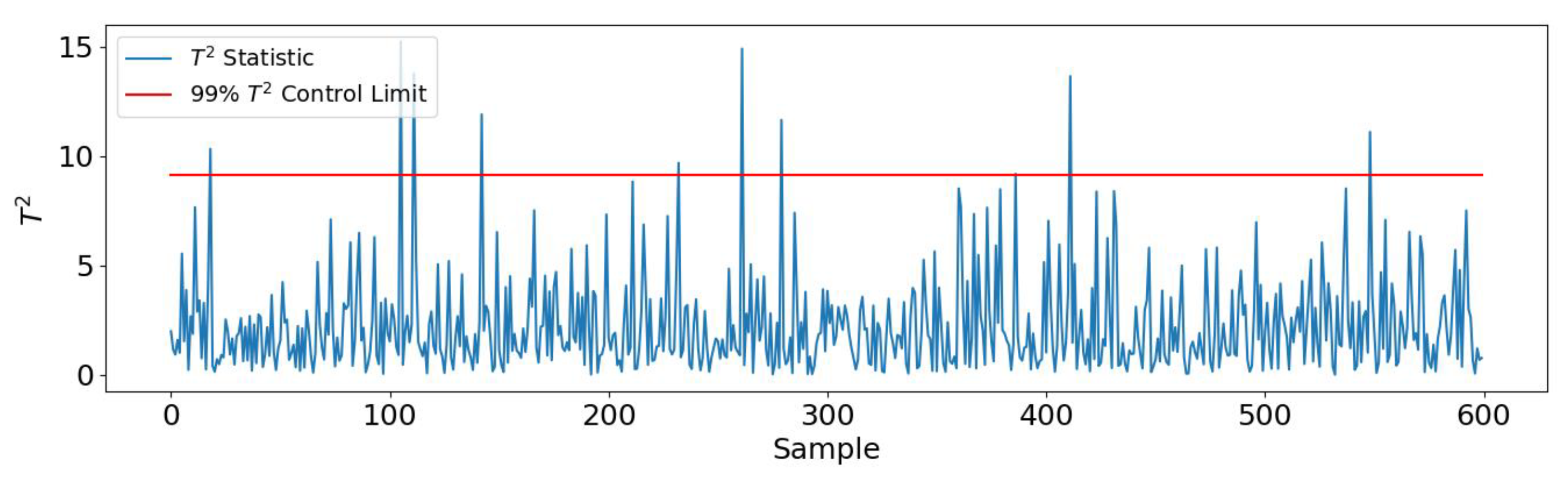
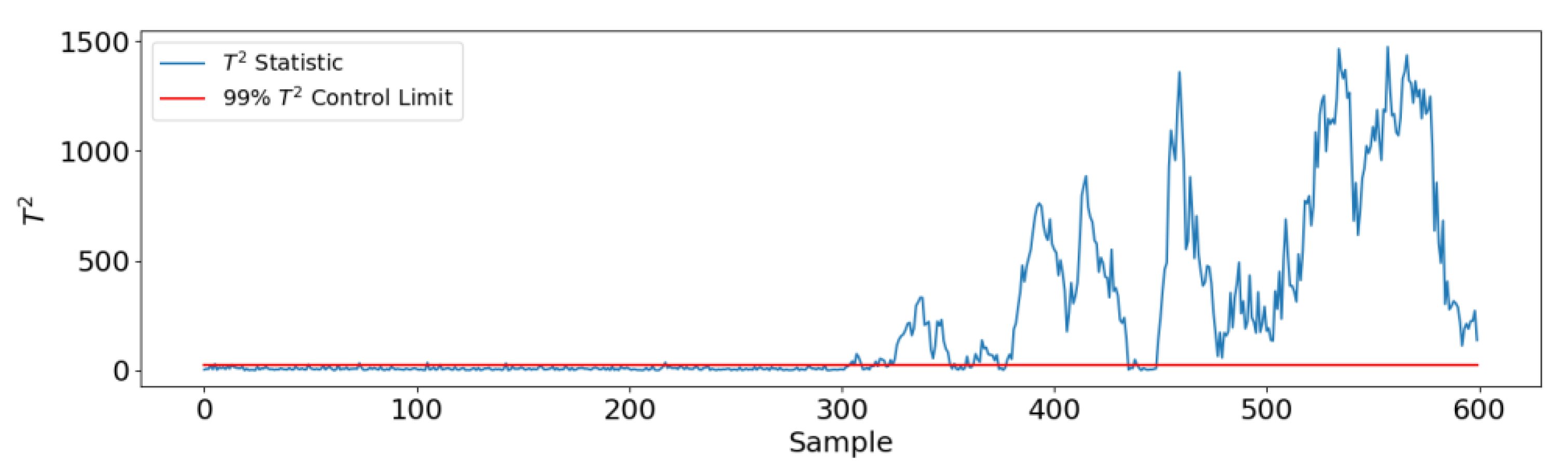
4.2.3. Monitoring Results
4.3. Industrial Case
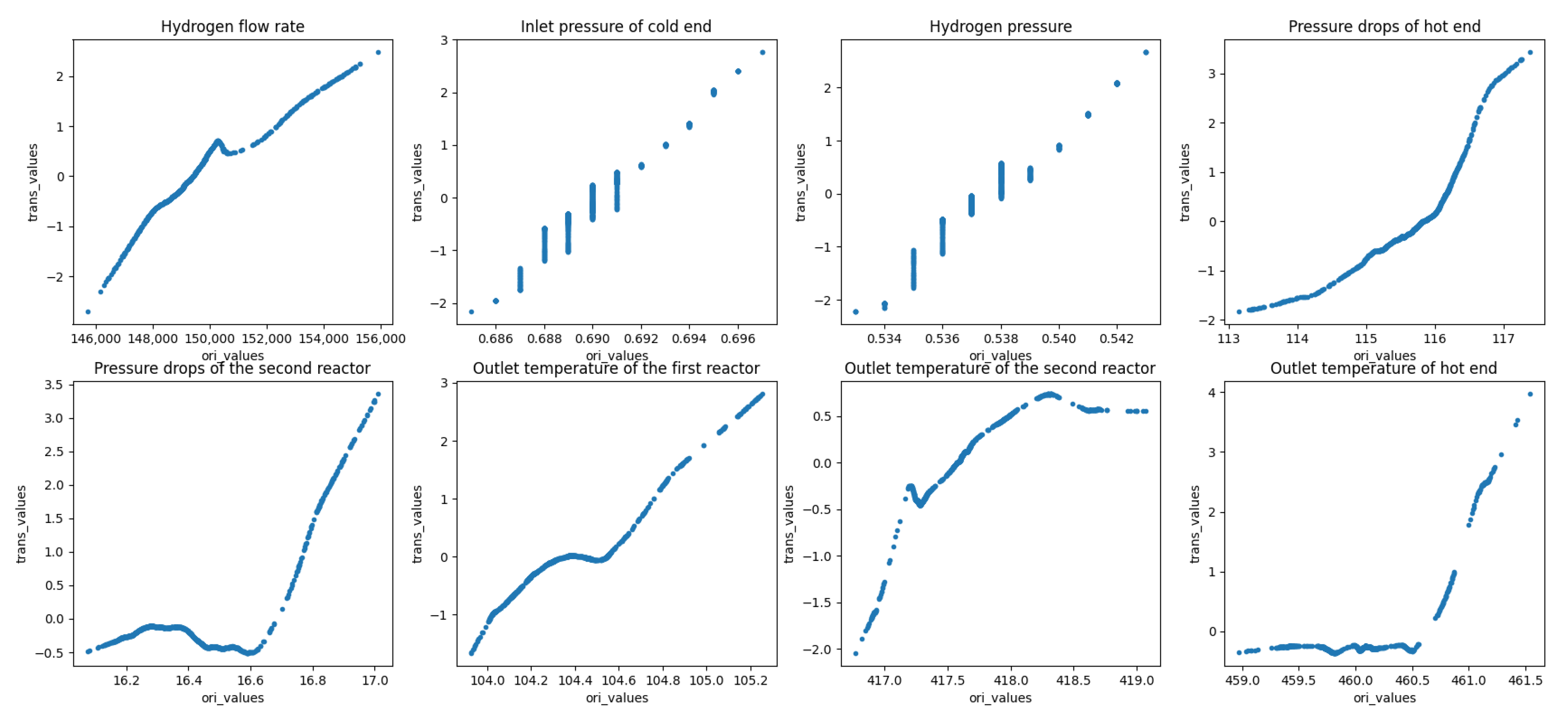
4.3.1. Introduction
4.3.2. Modeling
4.3.3. Monitoring Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ge, Z.; Song, Z.; Gao, F. Review of Recent Research on Data-Based Process Monitoring. Ind. Eng. Chem. Res. 2013, 52, 3543–3562. [Google Scholar] [CrossRef]
- Ji, C.; Sun, W. A Review on Data-Driven Process Monitoring Methods: Characterization and Mining of Industrial Data. Processes 2022, 10, 335. [Google Scholar] [CrossRef]
- Julieta, C.; Daniel, S.; Barbara, G. Monitoring Wine Fermentation Deviations Using An ATR-MIR Spectrometer and MSPC Charts. Chemom. Intell. Lab. Syst. 2020, 201, 104011. [Google Scholar]
- Tong, C.; Shi, X. Mutual Information Based PCA Algorithm with Application in Process Monitoring. CIESC J. 2015, 10, 6. [Google Scholar]
- Li, Z.; Liang, L.; Han, C. Multi-Rate Process Fault Detection Based on Partial Least Squares. Comput. Simul. 2016, 10, 5. [Google Scholar]
- Pollanen, K.; Hakkinen, A.; Reinikainen, S. Dynamic PCA-Based MSPC Charts for Nucleation Prediction in Batch Cooling Crystallization Processes. Chemom. Intell. Lab. Syst. 2016, 84, 126–133. [Google Scholar] [CrossRef]
- Ji, C.; Ma, F.; Wang, J.; Sun, W. Early Identification of Abnormal Deviations in Nonstationary Processes by Removing Non- Stationarity. Comput. Aided Chem. Eng. 2022, 49, 1393–1398. [Google Scholar]
- Ku, W.; Storer, R.H.; Georgakis, C. Disturbance Detection and Isolation by Dynamic Principal Component Analysis. Chemom. Intell. Lab. Syst. 1995, 30, 179–196. [Google Scholar] [CrossRef]
- Rato, T.J.; Reis, M.S. Advantage of Using Decorrelated Residuals in Dynamic Principal Component Analysis for Monitoring Large-Scale Systems. Ind. Eng. Chem. Res. 2013, 52, 13685–13698. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, G.M. Time Series Analysis, Forecasting, and Control; John Willey & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Engle, R.F.; Granger, C. Cointegration and Error-Correction: Representation, Estimation and Testing. Econometrica 1987, 55, 251–276. [Google Scholar] [CrossRef]
- Granger, C. Some Properties of Time Series Data and Their Use in Econometric Model Specification. J. Econom. 1981, 16, 121–130. [Google Scholar] [CrossRef]
- Chen, Q.; Pan, Y. Application of Cointegration Testing Method to Condition Monitoring and Fault Diagnosis of Nonstationary FCCU System. Acta Pet. Sin. 2007, 23, 69–76. [Google Scholar]
- Xu, Z. Nonstationary Process Monitoring and Fault Diagnosis Using Cointegration with Structural Change Testing Method. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, December 2007. [Google Scholar]
- Yu, W.; Zhao, C.; Huang, B. Recursive Cointegration Analytics for Adaptive Monitoring of Nonstationary Industrial Processes with both Static and Dynamic Variations. J. Process Control 2020, 92, 319–332. [Google Scholar] [CrossRef]
- Wen, J.; Li, Y. Nonstationary Process Monitoring Based on Cointegration Theory and Multiple Order Moments. Processes 2022, 10, 169. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H. Estimating Optimal Transformations for Multiple Regression and Correlation. Publ. Am. Stat. Assoc. 1985, 80, 580–598. [Google Scholar] [CrossRef]
- Xue, G. Optimal Transformations for Multiple Regression: Application to Permeability Estimation from Well Logs. Spe Form. Eval. 1997, 12, 85–94. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, S. A Reconsideration to the Nonlinear Transformation of the Integrated Time Series. J. Syst. Eng. 1998, 13, 8. [Google Scholar]
- Lu, F. Complex Dynamic Engineering System Codition Monitoring Research Using Cointegration Theory. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, November 2010. [Google Scholar]
- Johansen, S. Statistical Analysis of Cointegration Vectors. J. Econ. Dyn. Control 1988, 12, 231–254. [Google Scholar] [CrossRef]
- Johansen, S. Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models. Econometrica 1991, 59, 1551–1580. [Google Scholar] [CrossRef]
- Li, G.; Qin, S.J.; Yuan, T. Nonstationarity and Cointegration Tests for Fault Detection of Dynamic Processes. IFAC Proc. Vol. 2014, 47, 10616–10621. [Google Scholar] [CrossRef]
- Zhu, H.; Li, S.; Zeng, H. Test for Bayesian Nonlinear Cointegration in Nonparametric ACE Transformed Model. J. Manag. Sci. China 2011, 14, 52–64. [Google Scholar]
- Özmen, A.; Weber, G.W.; Batmaz, İ. RCMARS: Robustification of CMARS with Different Scenarios under Polyhedral Uncertainty Set. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4780–4787. [Google Scholar] [CrossRef]
- Özmen, A.; Weber, G.W.; Batmaz, İ. The New Robust CMARS (RCMARS) Method. Vectors 2010, 1, 362–368. [Google Scholar]










| A | 3.803 × 10−7 | −2.346 × 10−6 | 7.105 × 10−6 | −5.025 × 10−7 | −2.341 × 10−8 |
| B | 9.533 × 10−5 | 1.788 × 10−4 | 1.308 × 10−3 | −7.445 × 10−4 | −2.182 × 10−5 |
| C | 4.193 × 10−3 | −1.713 × 10−3 | 5.973 × 10−2 | 3.087 × 10−2 | 5.489 × 10−4 |
| D | −4.106 × 10−2 | 2.945 × 10−3 | 8.172 × 10−1 | −1.893 × 10−1 | 6.948 × 10−2 |
| E | −9.707 × 10−1 | −8.798 × 10−1 | 2.565 | −5.595 × 10−1 | 6.563 × 10−2 |
| Johansen H0 Hypothesis | Trace Statistics | Critical Value (5%) |
|---|---|---|
| 549.353 | 3.8415 | |
| 286.844 | 15.4943 | |
| 65.3606 | 29.7961 | |
| 1.85367 | 47.8545 | |
| 0 | 69.8189 |
| Johansen H0 Hypothesis | Trace Statistics | Critical Value (5%) |
|---|---|---|
| 566.01 | 3.8415 | |
| 276.362 | 15.4943 | |
| 11.0395 | 29.7961 | |
| 2.89588 | 47.8545 | |
| 0 | 69.8189 |
| Variable | Test Statistic | Critical Value (1%) | Variable | Test Statistic | Critical Value (1%) |
|---|---|---|---|---|---|
| Inlet flow of cold end | −30.5959 | −3.43764 | Inlet temperature of hot end | −4.4610 | −3.43765 |
| Hydrogen flow rate | −2.8303 | −3.43766 | Inlet temperature of cold end | −5.0377 | −3.43765 |
| Inlet pressure of cold end | −3.3003 | −3.43766 | Outlet temperature of cold end | −4.0436 | −3.43766 |
| Hydrogen pressure | −2.8968 | −3.43766 | Outlet temperature of the first furnace | −15.7487 | −3.43766 |
| Outlet pressure of hot end | −11.3220 | −3.43766 | Outlet temperature of the second furnace | −19.9573 | −3.43765 |
| Pressure drops of hot end | −3.1284 | −3.43766 | Outlet temperature of the first reactor | −3.3998 | −3.43766 |
| Pressure drops of cold end | −3.4391 | −3.43766 | Outlet temperature of the second reactor | −3.1017 | −3.43766 |
| Pressure drops of the first reactor | −3.6682 | −3.43766 | Outlet temperature of the third furnace | −19.2434 | −3.43766 |
| Pressure drops of the second reactor | −2.8726 | −3.43766 | Outlet temperature of the third reactor | −4.2464 | −3.43766 |
| Pressure drops of the third reactor | −3.5858 | −3.43766 | Outlet temperature of the fourth furnace | −18.8509 | −3.43766 |
| Pressure drops of the fourth reactor | −3.8137 | −3.43766 | Temperature drops of the third furnace | −9.2383 | −3.43766 |
| Inlet pressure of the fourth reactor | −3.8399 | −3.43766 | Temperature drops of the fourth furnace | −7.7637 | −3.43766 |
| Pressure drops of cold end filter | −12.1079 | −3.43766 | Temperature drops of the second furnace | −4.3286 | −3.43766 |
| Outlet temperature of hot end | −2.8410 | −3.43766 |
| Johansen H0 Hypothesis | Trace Statistics | Critical Value (5%) |
|---|---|---|
| 419.515 | 3.8415 | |
| 215.018 | 15.4943 | |
| 121.076 | 29.7961 | |
| 50.9084 | 47.8545 | |
| 26.0231 | 69.8189 | |
| 9.88992 | 95.7542 | |
| 2.44853 | 125.618 | |
| 0 | 159.529 |
| Johansen H0 Hypothesis | Trace Statistics | Critical Value (5%) |
|---|---|---|
| 419.486 | 3.8415 | |
| 250.82 | 15.4943 | |
| 161.232 | 29.7961 | |
| 96.6288 | 47.8545 | |
| 54.8984 | 69.8189 | |
| 20.8353 | 95.7542 | |
| 6.35215 | 125.618 | |
| −0 | 159.529 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, J.; Ji, C.; Wen, J.; Wang, J.; Sun, W. Nonstationary Process Monitoring Based on Alternating Conditional Expectation and Cointegration Analysis. Processes 2022, 10, 2003. https://doi.org/10.3390/pr10102003
Rao J, Ji C, Wen J, Wang J, Sun W. Nonstationary Process Monitoring Based on Alternating Conditional Expectation and Cointegration Analysis. Processes. 2022; 10(10):2003. https://doi.org/10.3390/pr10102003
Chicago/Turabian StyleRao, Jingzhi, Cheng Ji, Jiatao Wen, Jingde Wang, and Wei Sun. 2022. "Nonstationary Process Monitoring Based on Alternating Conditional Expectation and Cointegration Analysis" Processes 10, no. 10: 2003. https://doi.org/10.3390/pr10102003
APA StyleRao, J., Ji, C., Wen, J., Wang, J., & Sun, W. (2022). Nonstationary Process Monitoring Based on Alternating Conditional Expectation and Cointegration Analysis. Processes, 10(10), 2003. https://doi.org/10.3390/pr10102003







