New Insights from Locally Resolved Hydrodynamics in Stirred Cell Culture Reactors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Cultivation Procedures
2.1.1. Pre-Culture
2.1.2. Main Culture
2.2. Analytical Methods
2.3. CFD Simulations
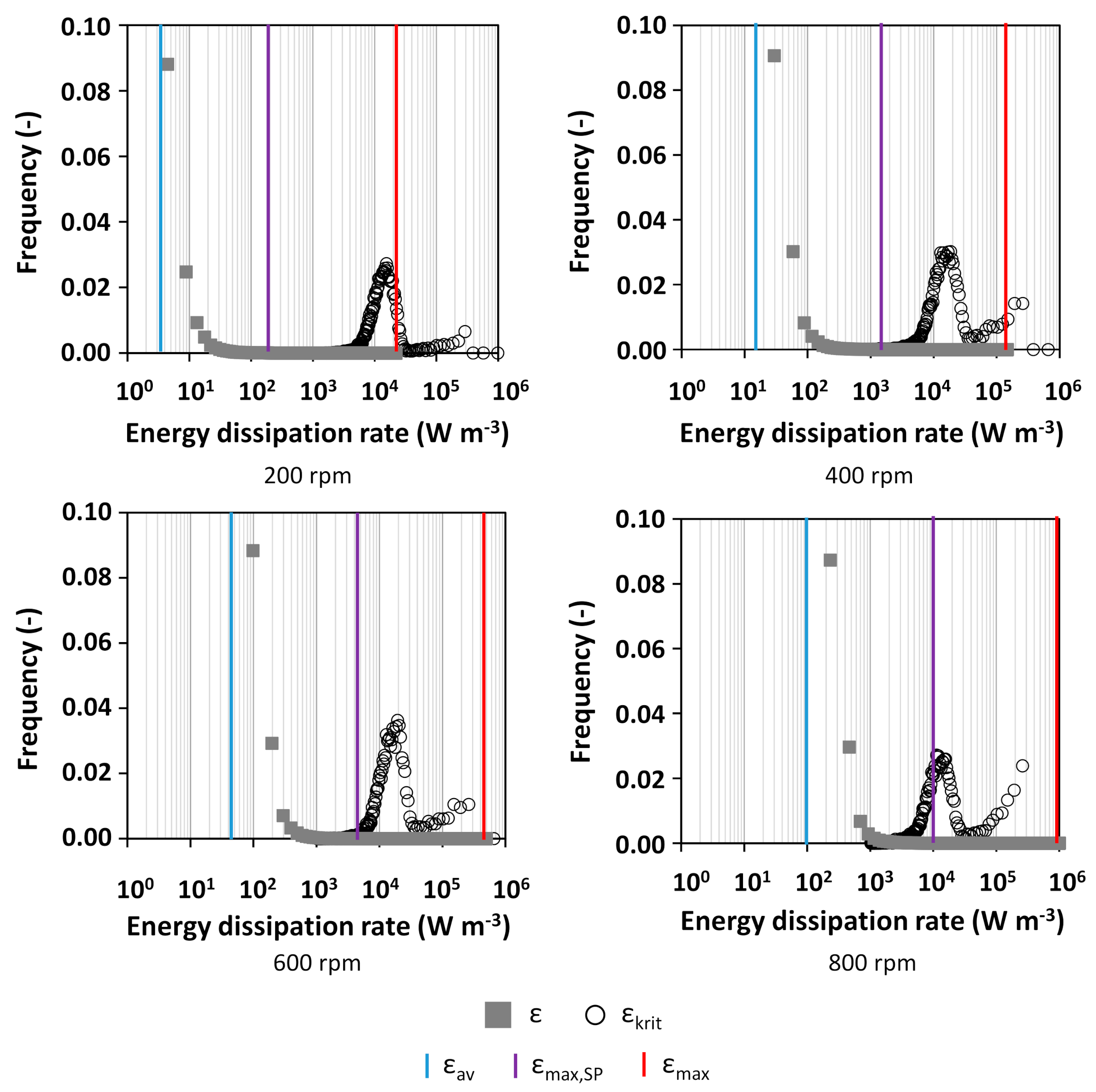
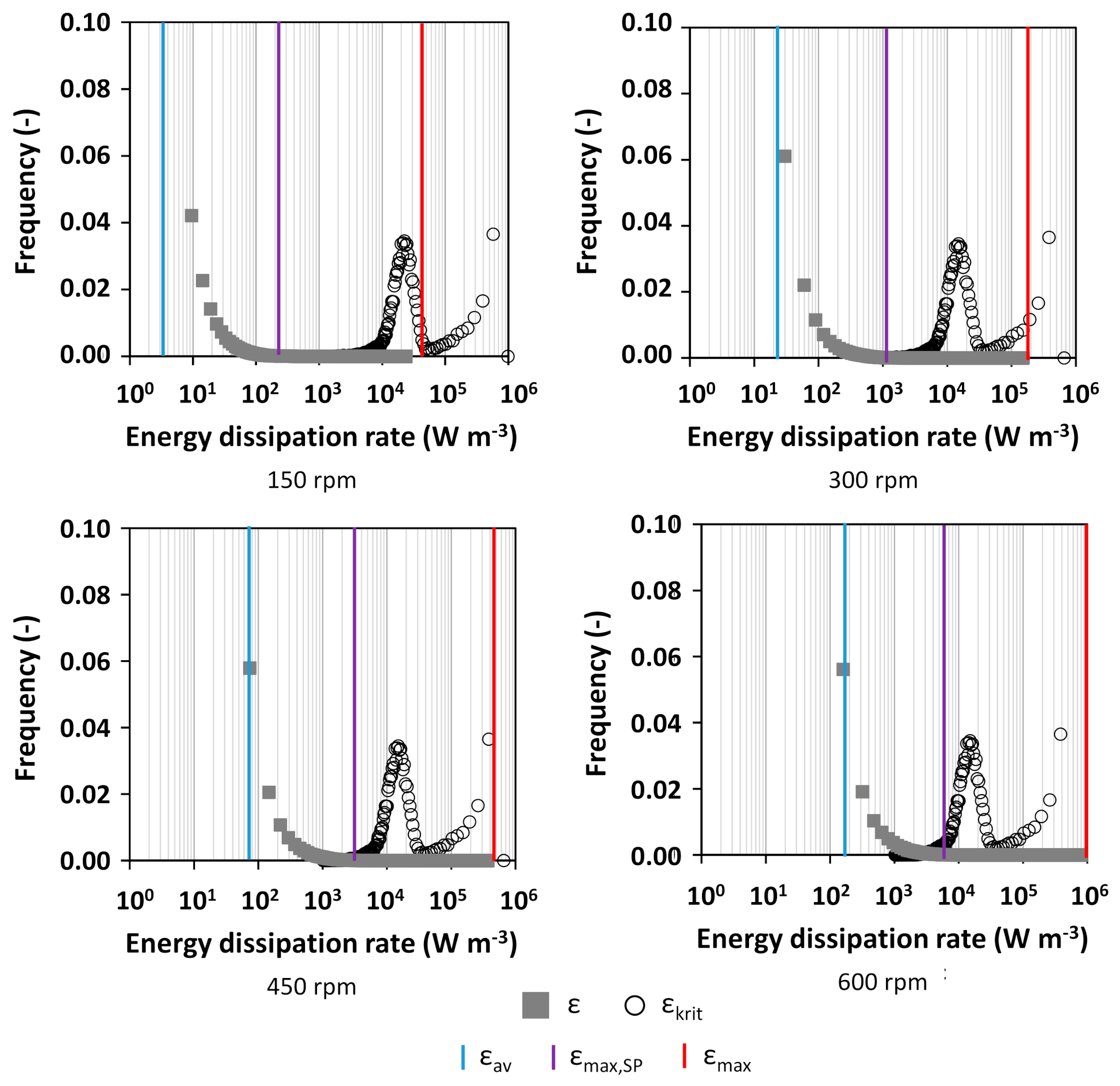
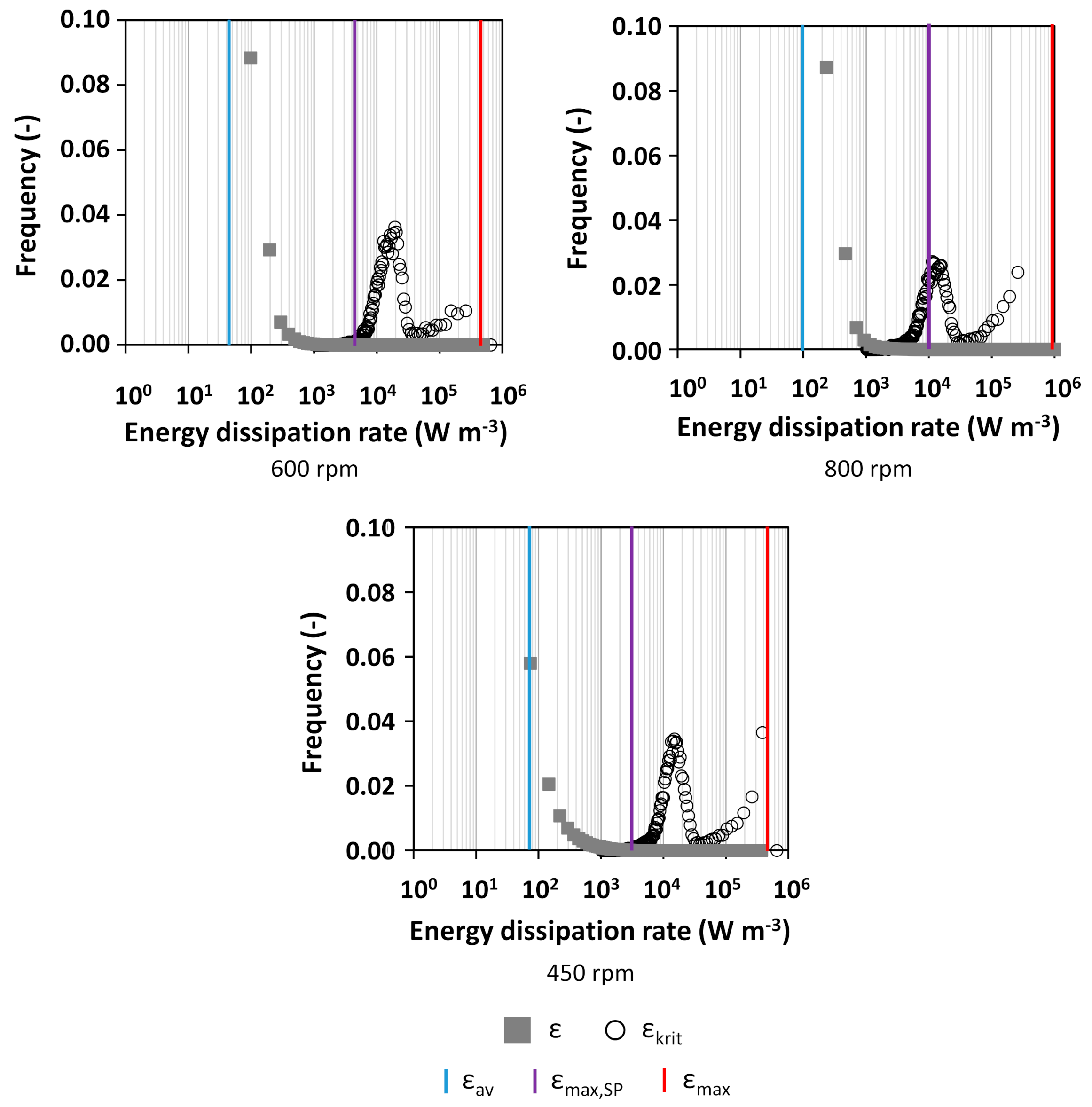
2.4. Calculation of the Critical Energy Dissipation Rate
3. Results
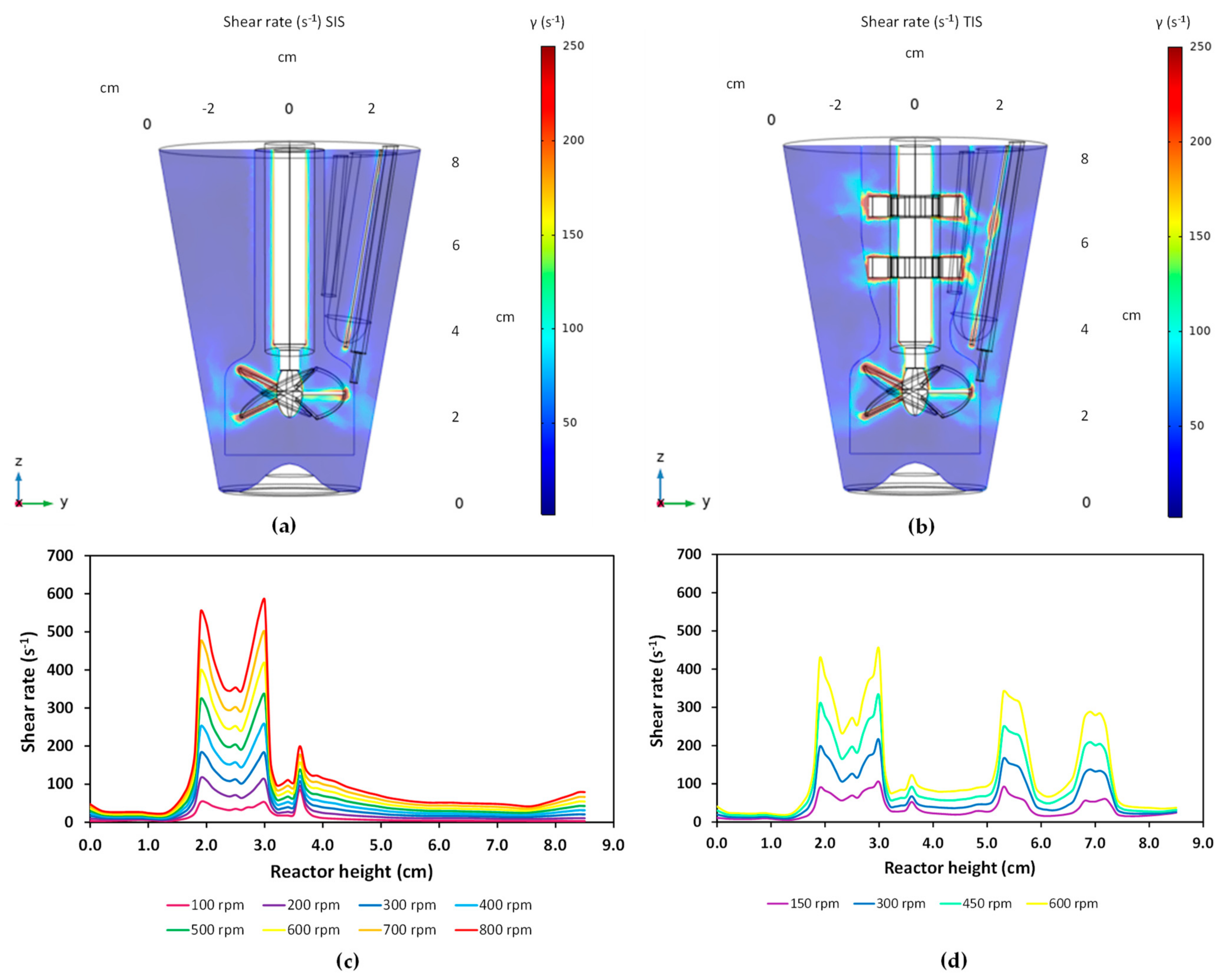
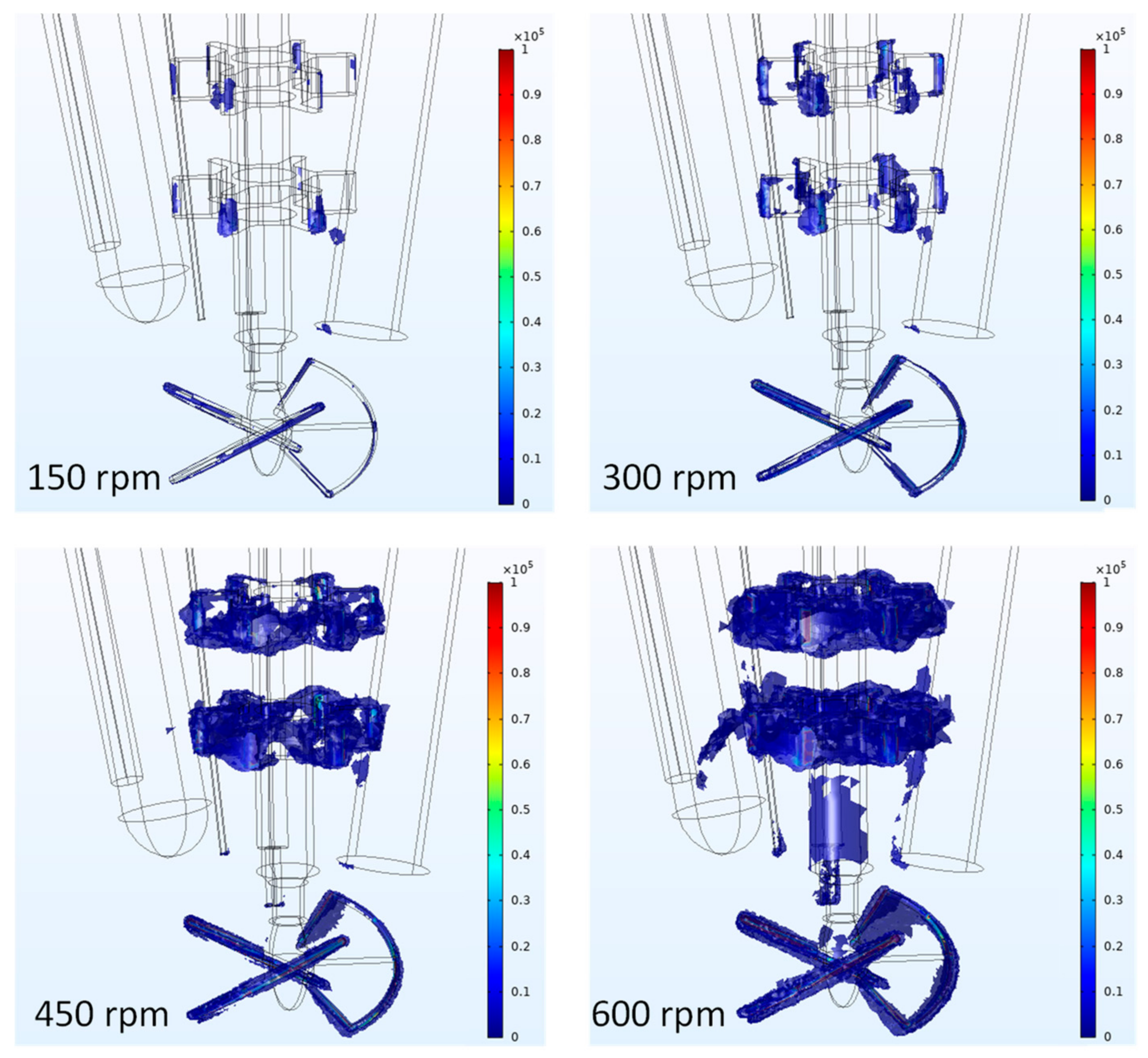
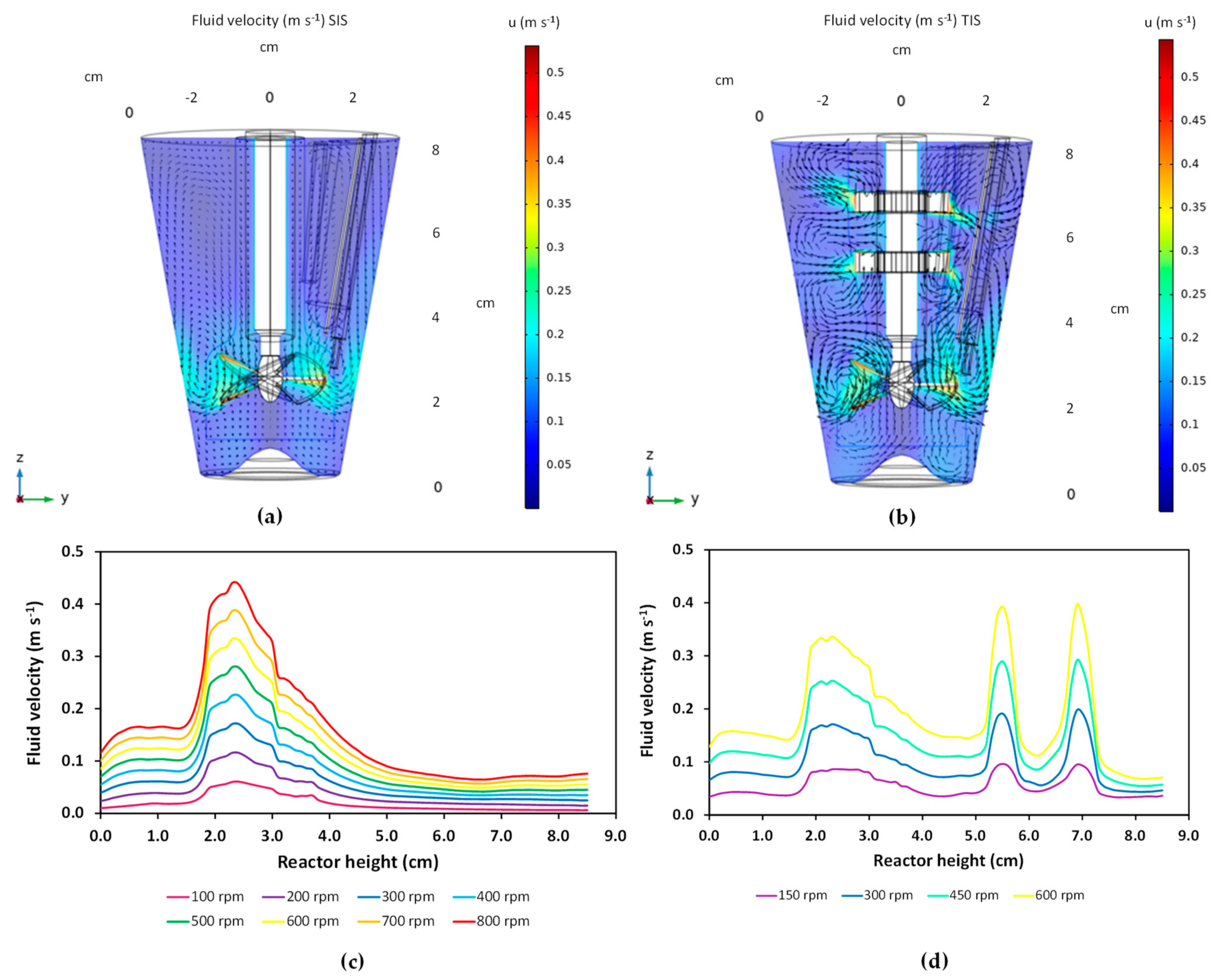
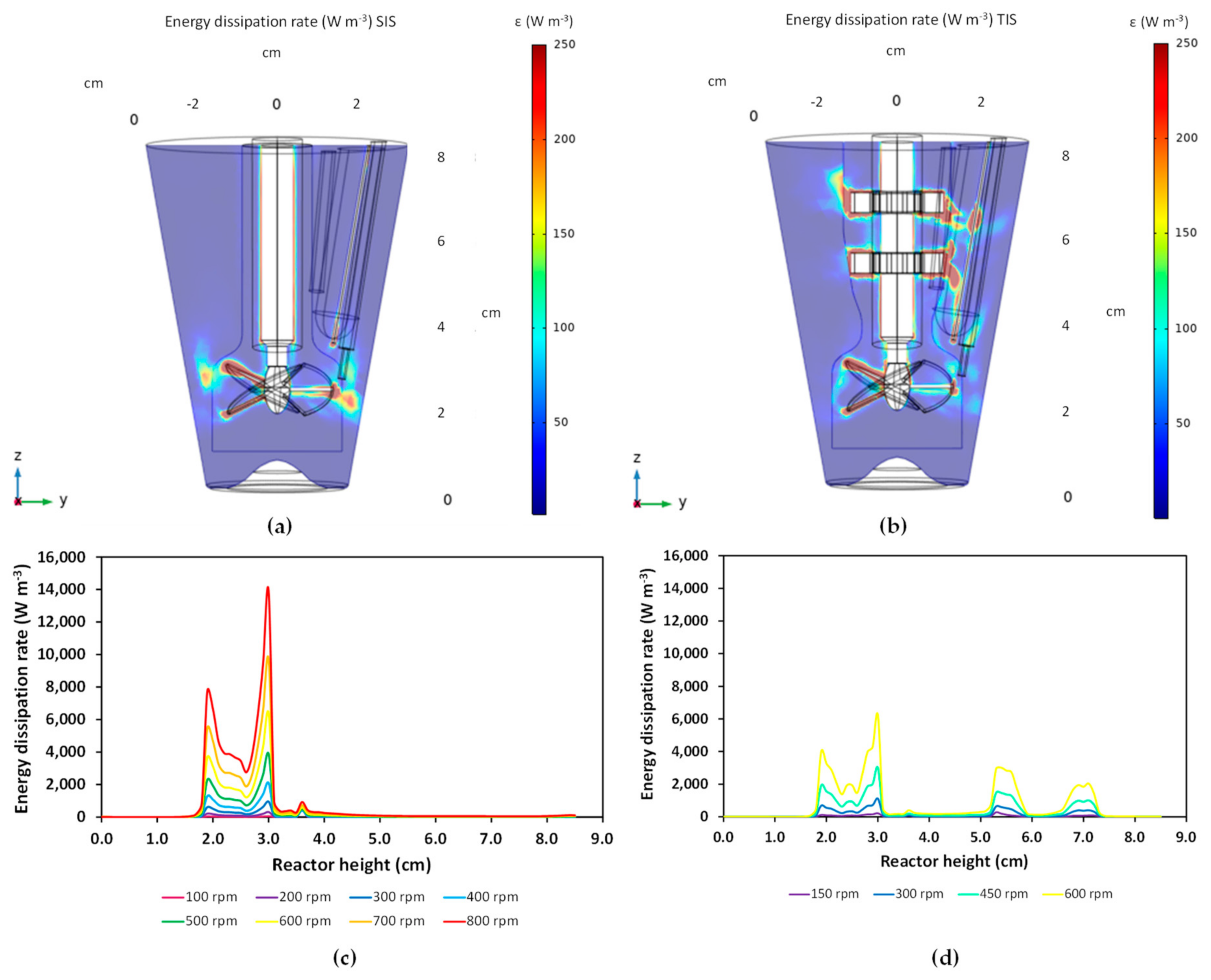
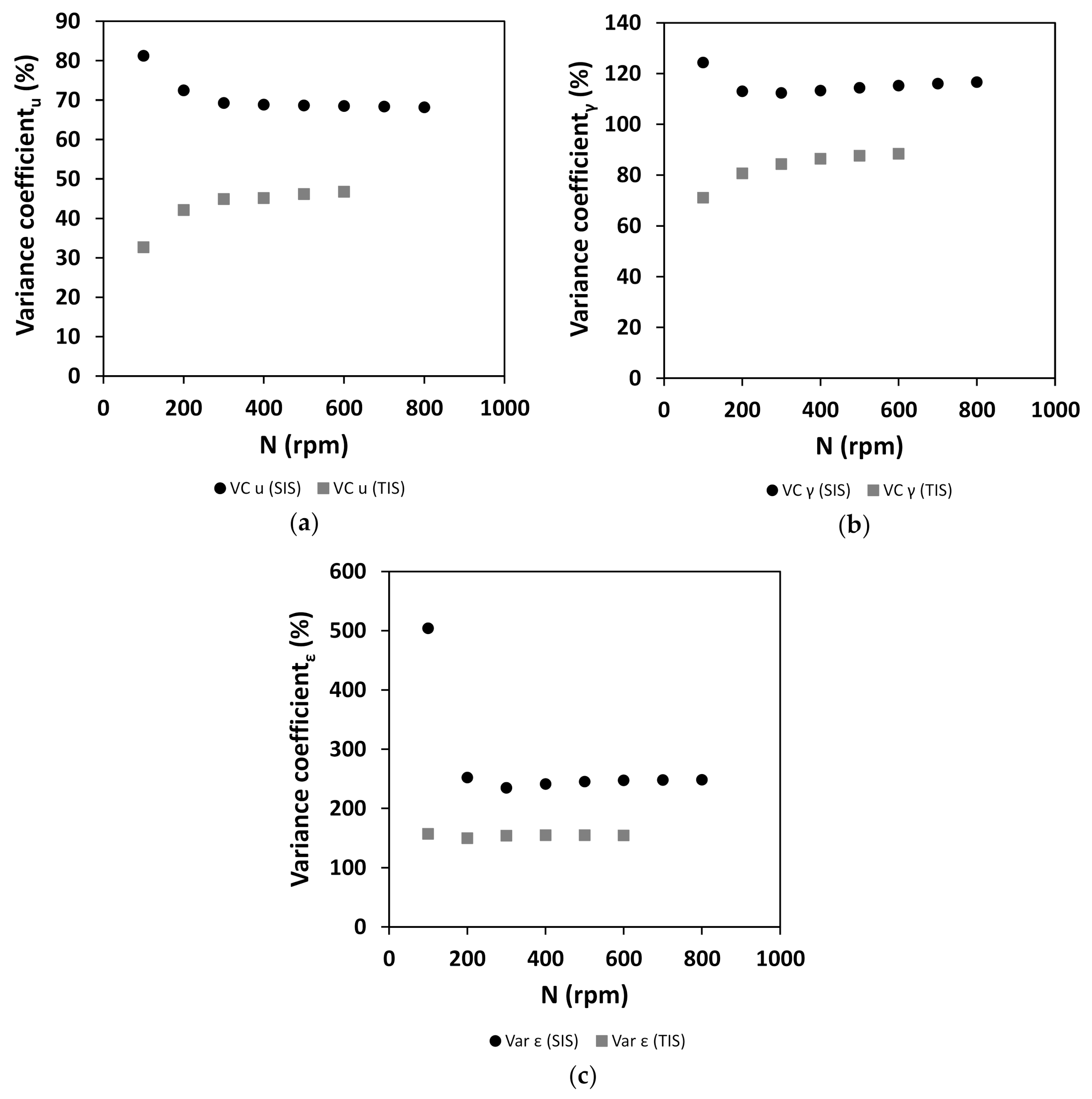
3.1. Characterization of Hydrodynamics of Single- and Multiple-Impeller Setups with CFD Methods
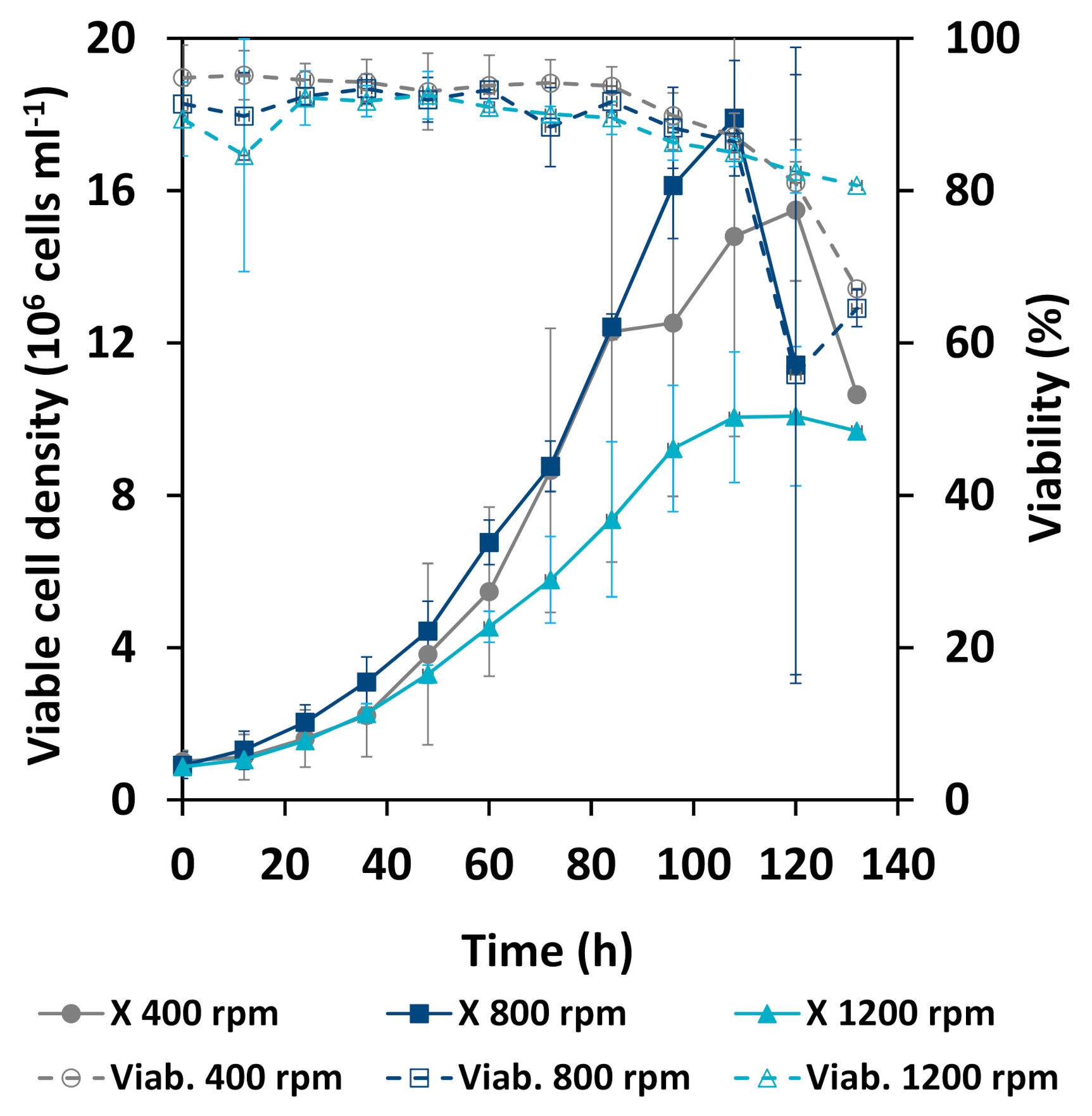
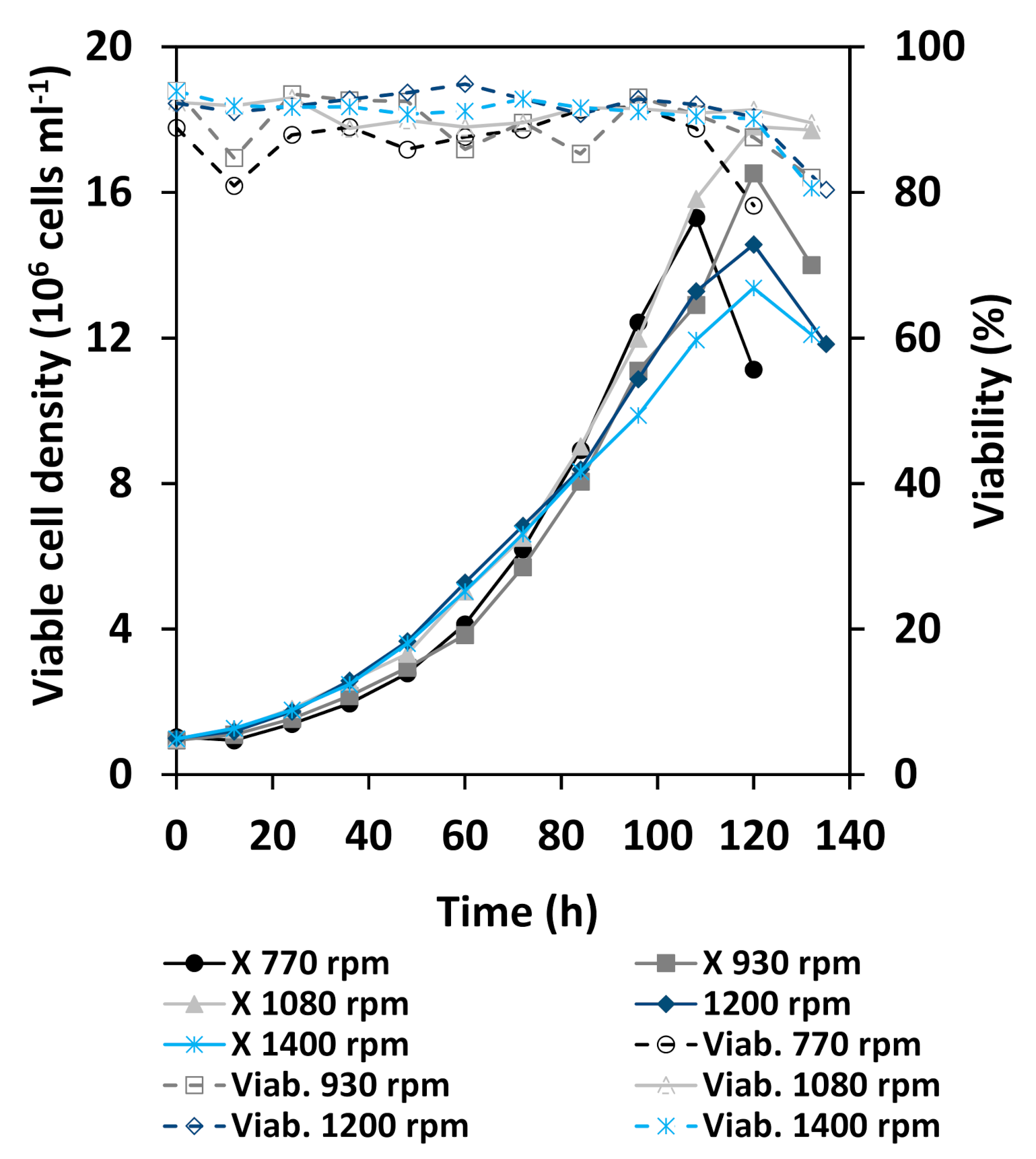
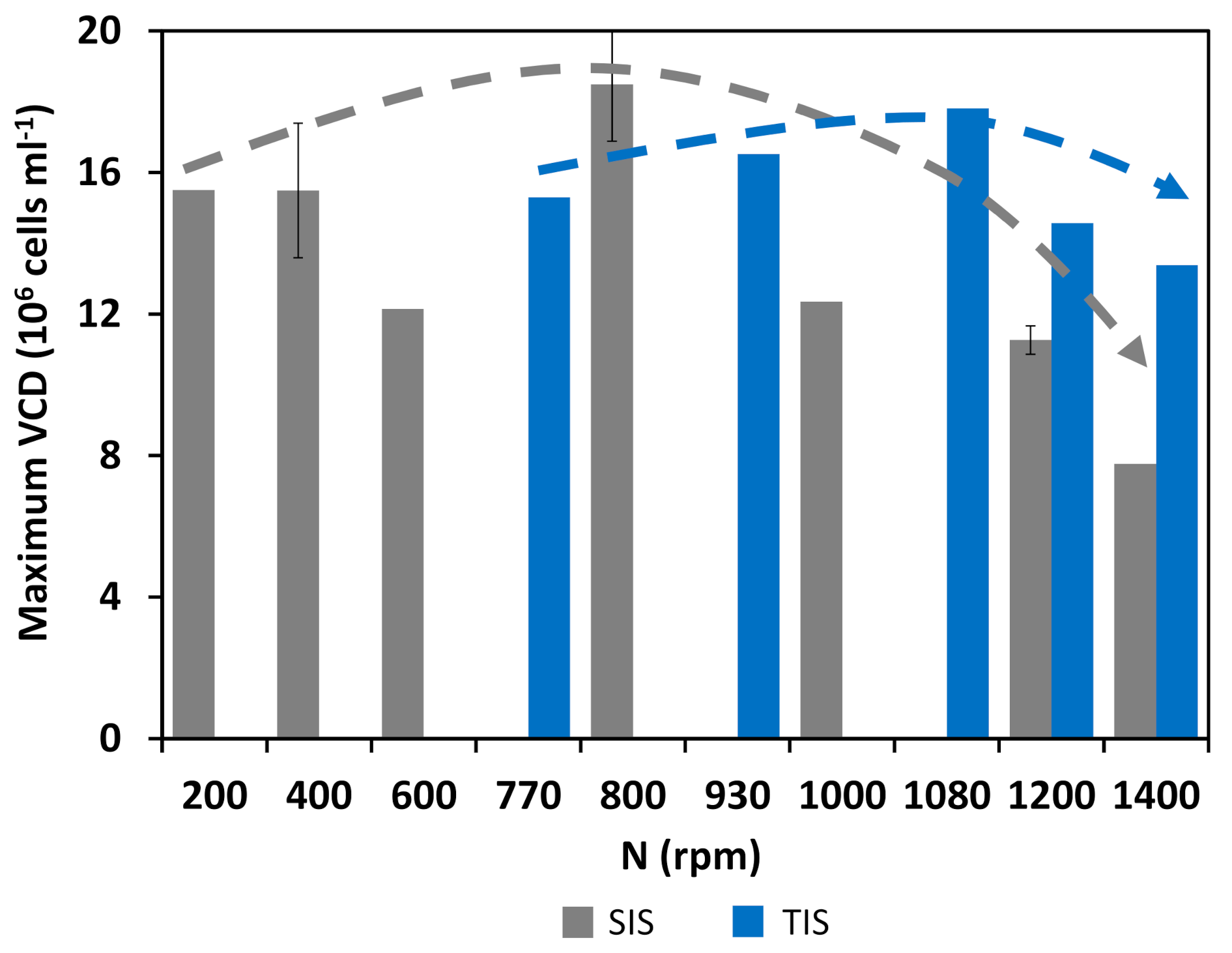
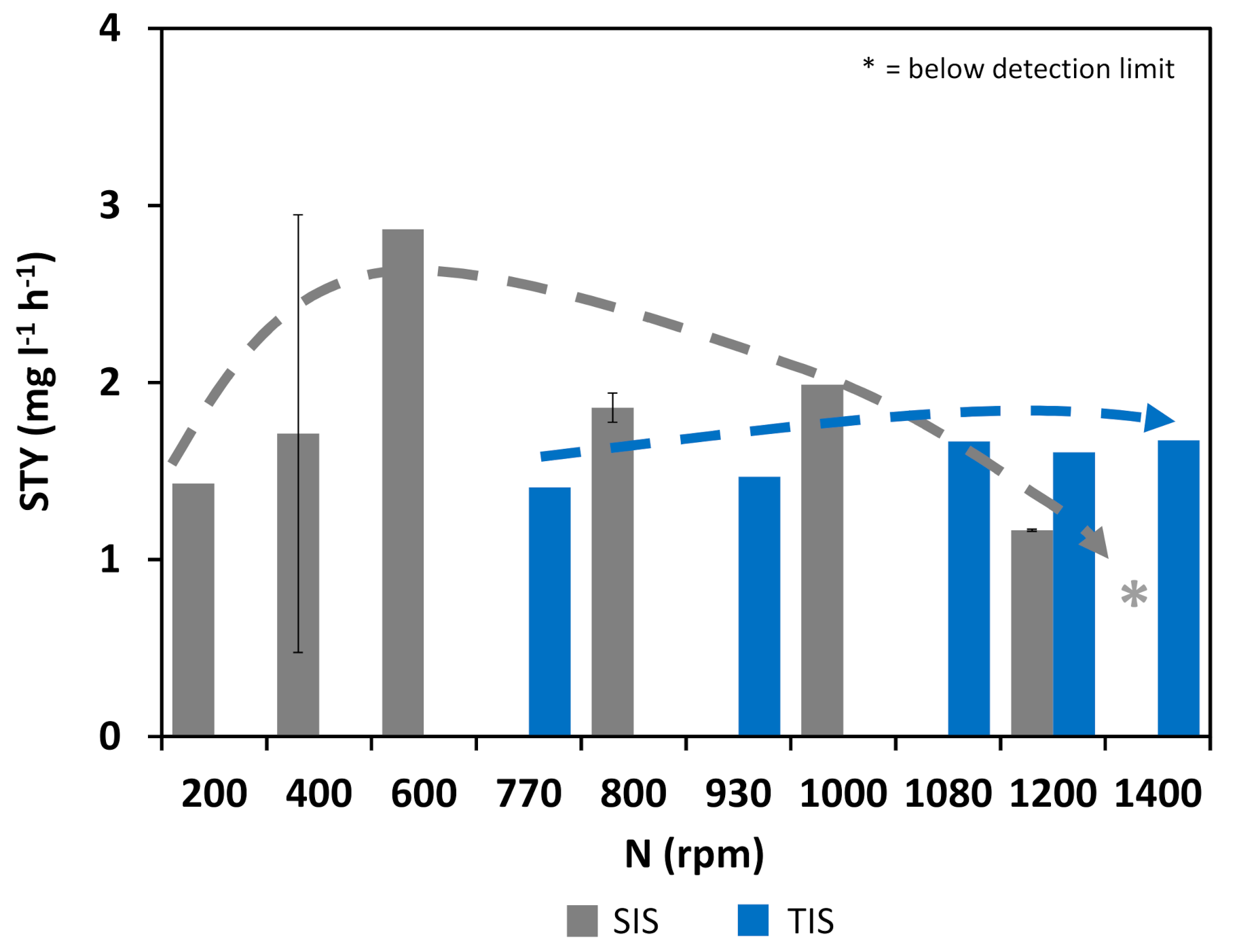
3.2. Cultivation Results
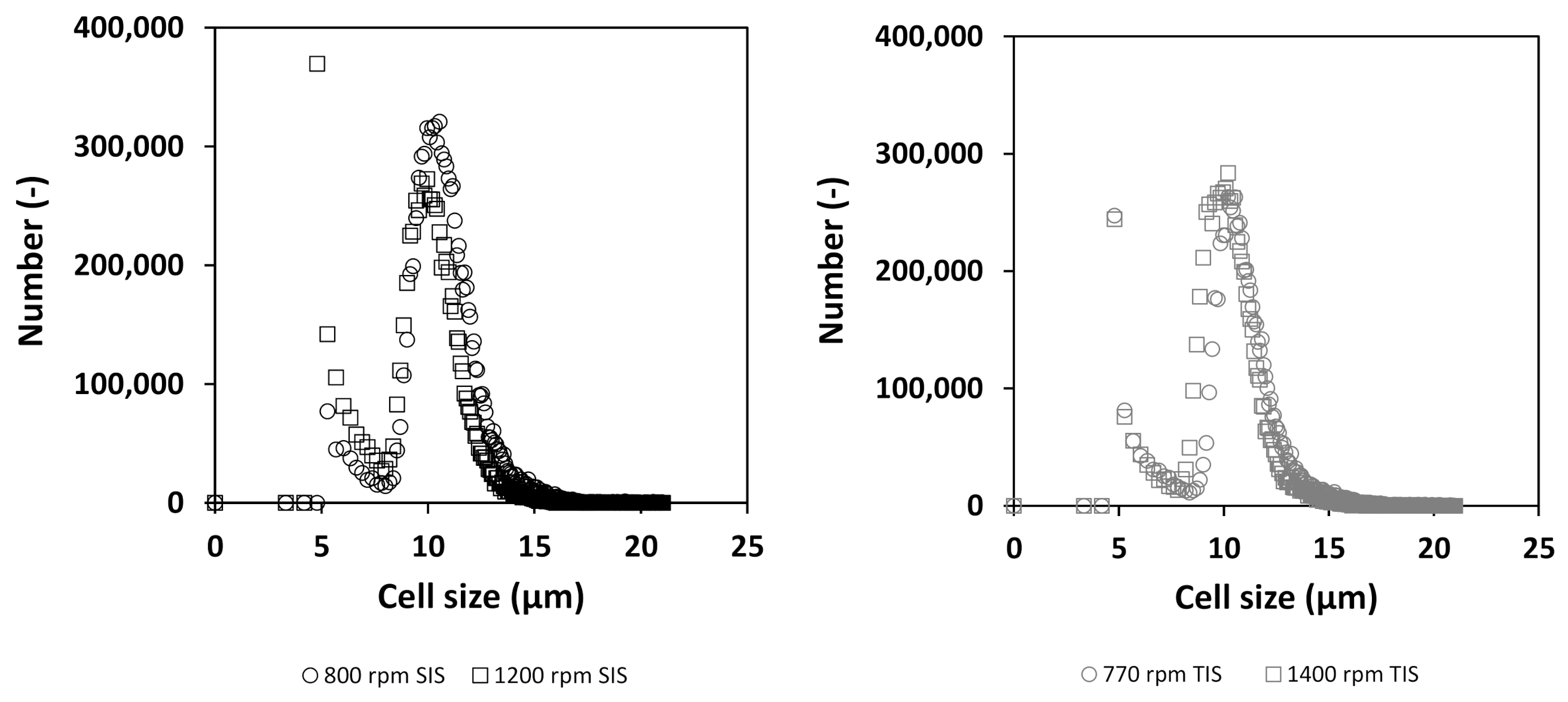
3.3. Comparison of Cellular Behavior and Hydrodynamic Parameters
4. Discussion
4.1. Hydrodynamic Differences for Single and Multi-Stage Impellers
4.2. Stability of Cell Culture Processes Related to Locally Resolved Hydrodynamics
4.3. Evaluation of Concepts for Estimation of Shear Related Parameters
4.4. Learning for Reactor Scale-Up and Scale-Down
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A
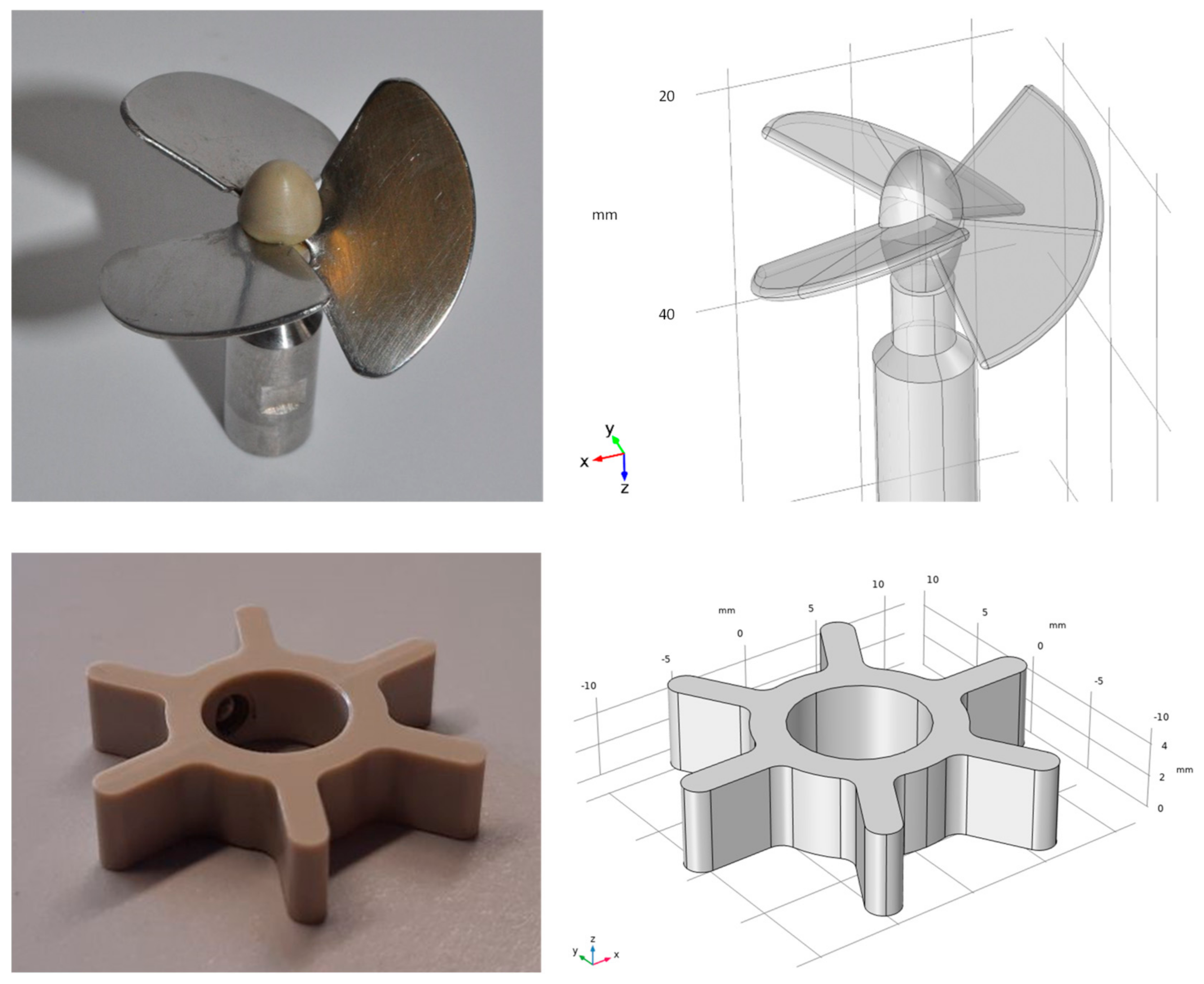

| N (rpm) | uav (m s−1) | γav (s−1) | εav (W m−3) | εmax (W m−3) | εmax,SP (W m−3) |
|---|---|---|---|---|---|
| 200 | 0.032 | 10.06 | 2.39 | 22,169 | 214 |
| 400 | 0.068 | 21.23 | 15.35 | 146,510 | 1575 |
| 600 | 0.103 | 32.22 | 47.35 | 491,767 | 4959 |
| 800 | 0.138 | 43.15 | 107.12 | 1,159,628 | 11,001 |
| 1000 | 0.171 | 53.56 | 203.56 | 2,265,066 | 20,239 |
| 1200 | 0.205 | 64.27 | 345.05 | 3,932,425 | 33,194 |
| 1400 | 0.240 | 74.99 | 540.50 | 6,286,050 | 50,385 |
| N (rpm) | uav (m s−1) | γav (s−1) | εav (W m−3) | εmax (W m−3) | εmax,SP (W m−3) |
|---|---|---|---|---|---|
| 150 | 0.039 | 13.24 | 3.63 | 45,738 | 221 |
| 300 | 0.081 | 28.62 | 23.86 | 194,000 | 1118 |
| 450 | 0.125 | 43.93 | 72.90 | 479,000 | 3014 |
| 600 | 0.159 | 55.53 | 176.93 | 1,010,000 | 6247 |
| 770 | 0.208 | 72.98 | 454.35 | 2,007,732 | 12,103 |
| 930 | 0.252 | 88.15 | 964.25 | 3,401,191 | 20,258 |
| 1080 | 0.292 | 102.36 | 1744.79 | 5,172,104 | 30,686 |
| 1200 | 0.325 | 113.74 | 2633.29 | 6,952,684 | 41,252 |
| 1400 | 0.379 | 132.69 | 4742.49 | 10,725,752 | 63,867 |
References
- Hu, W.; Berdugo, C.; Chalmers, J.J. The Potential of Hydrodynamic Damage to Animal Cells of Industrial Relevance: Current Understanding. Cytotechnology 2011, 63, 445–460. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Godoy-Silva, R.; Chalmers, J.J.; Casnocha, S.A.; Bass, L.A.; Ma, N. Physiological responses of CHO cells to repetitive hydrodynamic stress. Biotechnol. Bioeng. 2009, 103, 1103–1117. [Google Scholar] [CrossRef] [PubMed]
- Chalmers, J.J.; Ma, N. Hydrodynamic Damage to Animal Cells. In Animal Cell Culture; Al-Rubeai, M., Ed.; Springer International Publishing: Basel, Switzerland, 2015; pp. 169–183. [Google Scholar]
- Nienow, A.W.; Scott, W.H.; Hewitt, C.J.; Thomas, C.R.; Lewis, G.; Amanullah, A.; Kiss, R.; Meier, S.J. Scale-down studies for assessing the impact of different stress parameters on growth and product quality during animal cell culture. Chem. Eng. Res. Des. 2013, 91, 2265–2274. [Google Scholar] [CrossRef] [Green Version]
- Jossen, V.; Eibl, D.; Eibl, R. Numerical Methods for the Design and Description of In Vitro Expansion Processes of Human Mesenchymal Stem Cells. Adv. Biochem. Eng. Biotechnol. 2020, 177, 185–228. [Google Scholar] [CrossRef]
- Arndt, L.; Wiegmann, V.; Kuchemüller, K.B.; Baganz, F.; Pörtner, R.; Möller, J. Model-based workflow for scale-up of process strategies developed in miniaturized bioreactor systems. Biotechnol. Prog. 2021, 37, e3122. [Google Scholar] [CrossRef]
- Doran, P.M. Bioprocess Engineering Principles, 2nd ed.; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Storhas, W. Bioverfahrensentwicklung; John Wiley & Sons: Hoboken, NJ, USA, 2003; ISBN 3-527-28866-X. [Google Scholar]
- Xu, S.; Hoshan, L.; Jiang, R.; Gupta, B.; Brodean, E.; O’Neill, K.; Seamans, T.C.; Bowers, J.; Chen, H. A practical approach in bioreactor scale-up and process transfer using a combination of constant P/V and vvm as the criterion. Biotechnol. Prog. 2017, 33, 1146–1159. [Google Scholar] [CrossRef]
- Scully, J.; Considine, L.B.; Smith, M.T.; McAlea, E.; Jones, N.; O’Connell, E.; Madsen, E.; Power, M.; Mellors, P.; Crowley, J.; et al. Beyond heuristics: CFD-based novel multiparameter scale-up for geometrically disparate bioreactors demonstrated at industrial 2kL–10kL scales. Biotechnol. Bioeng. 2020, 117, 1710–1723. [Google Scholar] [CrossRef]
- Rosseburg, A.; Fitschen, J.; Wutz, J.; Wucherpfennig, T.; Schlüter, M. Hydrodynamic inhomogeneities in large scale stirred tanks—Influence on mixing time. Chem. Eng. Sci. 2018, 188, 208–220. [Google Scholar] [CrossRef]
- Kolmogorov, A. Dissipation of Energy in the Locally Isotropic Turbulence. Dokl. Akad. Nauk SSSR 1941, 32, 538–541. [Google Scholar]
- Kolmogorov, A. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds Numbers. Dokl. Akad. Nauk SSSR 1941, 30, 301–305. [Google Scholar]
- Cherry, R.S.; Papoutsakis, E.T. Hydrodynamic Effects on Cells in Agitated Tissue Culture Reactors. Bioprocess Eng. 1986, 1, 29–41. [Google Scholar] [CrossRef]
- Cherry, R.S.; Papoutsakis, E.T. Physical mechanisms of cell damage in microcarrier cell culture bioreactors. Biotechnol. Bioeng. 1988, 32, 1001–1014. [Google Scholar] [CrossRef]
- Cherry, R.S.; Papoutsakis, E.T. Growth and death rates of bovine embryonic kidney cells in turbulent microcarrier bioreactors. Bioprocess Eng. 1989, 4, 81–89. [Google Scholar] [CrossRef]
- Hua, J.; Erickson, L.E.; Yiin, T.Y.; Glasgow, L.A. A review of the effects of shear and interfacial phenomena on cell viability. Crit. Rev. Biotechnol. 1993, 13, 305–328. [Google Scholar] [CrossRef]
- Cherry, R.S. Animal cells in turbulent fluids: Details of the physical stimulus and the biological response. Biotechnol. Adv. 1993, 11, 279–299. [Google Scholar] [CrossRef]
- Croughan, M.S.; Hamel, J.F.; Wang, D.I. Hydrodynamic Effects on Animal Cells Grown in Microcarrier Cultures. Biotechnol. Bioeng. 1987, 29, 130–141. [Google Scholar] [CrossRef]
- Wang, G.; Haringa, C.; Tang, W.; Noorman, H.; Chu, J.; Zhuang, Y.; Zhang, S. Coupled metabolic-hydrodynamic modeling enabling rational scale-up of industrial bioprocesses. Biotechnol. Bioeng. 2020, 117, 844–867. [Google Scholar] [CrossRef]
- Ueki, M.; Tansho, N.; Sato, M.; Kanamori, H.; Ito, Y.; Kato, Y. Improved cultivation of CHO cells in bioreactor with reciprocal mixing. Authorea 2020. [Google Scholar] [CrossRef]
- Kuschel, M.; Fitschen, J.; Hoffmann, M.; von Kameke, A.; Schlüter, M.; Wucherpfennig, T. Validation of Novel Lattice Boltzmann Large Eddy Simulations (LB LES) for Equipment Characterization in Biopharma. Processes 2021, 9, 950. [Google Scholar] [CrossRef]
- Jossen, V.; Schirmer, C.; Mostafa Sindi, D.; Eibl, R.; Kraume, M.; Pörtner, R.; Eibl, D. Theoretical and practical issues that are relevant when scaling up hMSC microcarrier production porocesses. Stem Cells Int. 2016, 2016, 4760414. [Google Scholar] [CrossRef] [Green Version]
- Isu, G.; Morbiducci, U.; Nisco, G.d.; Kropp, C.; Marsano, A.; Deriu, M.A.; Zweigerdt, R.; Audenino, A.; Massai, D. Modeling methodology for defining a priori the hydrodynamics of a dynamic suspension bioreactor. Application to human induced pluripotent stem cell culture. J. Biomech. 2019, 94, 99–106. [Google Scholar] [CrossRef]
- Kaiser, S.; Jossen, V.; Schirmaier, C.; Eibl, D.; Brill, S.; van den Bos, C.; Eibl, R. Fluid Flow and Cell Proliferation of Mesenchymal Adipose-Derived Stem Cells in Small-Scale, Stirred, Single-Use Bioreactors. Chem. Ing. Tech. 2013, 85, 95–102. [Google Scholar] [CrossRef]
- Möller, J.; Kuchemüller, K.B.; Steinmetz, T.; Koopmann, K.S.; Pörtner, R. Model-assisted Design of Experiments as a concept for knowledge-based bioprocess development. Bioprocess Eng. 2019, 42, 867–882. [Google Scholar] [CrossRef]
- Ghasemian, M.; Layton, C.; Nampe, D.; Zur Nieden, N.I.; Tsutsui, H.; Princevac, M. Hydrodynamic characterization within a spinner flask and a rotary wall vessel for stem cell culture. Biochem. Eng. J. 2020, 157, 107533. [Google Scholar] [CrossRef]
- Platas Barradas, O.; Jandt, U.; Minh Phan, L.D.; Villanueva, M.E.; Schaletzky, M.; Rath, A.; Freund, S.; Reichl, U.; Skerhutt, E.; Scholz, S.; et al. Evaluation of Criteria for Bioreactor Comparison and Operation Standardization for Mammalian Cell Culture. Eng. Life Sci. 2012, 12, 518–528. [Google Scholar] [CrossRef]
- Fitschen, J.; Hofmann, S.; Wutz, J.; Hoffmann, M.; Wucherpfennig, T.; Schlüter, M. Novel evaluation method to determine the local mixing time distribution in stirred tank reactors. Chem. Eng. Sci. X 2021, 10, 100098. [Google Scholar] [CrossRef]
- Möller, J.; Hernández Rodríguez, T.; Müller, J.; Arndt, L.; Kuchemüller, K.B.; Frahm, B.; Eibl, R.; Eibl, D.; Pörtner, R. Model uncertainty-based evaluation of process strategies during scale-up of biopharmaceutical processes. Comput. Chem. Eng. 2020, 134, 106693. [Google Scholar] [CrossRef]
- Bates, R.L.; Fondy, P.L.; Corpstein, R.R. Examination of Some Geometric Parameters of Impeller Power. Ind. Eng. Chem. Proc. Des. Dev. 1963, 2, 310–314. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freiberger, F.; Budde, J.; Ateş, E.; Schlüter, M.; Pörtner, R.; Möller, J. New Insights from Locally Resolved Hydrodynamics in Stirred Cell Culture Reactors. Processes 2022, 10, 107. https://doi.org/10.3390/pr10010107
Freiberger F, Budde J, Ateş E, Schlüter M, Pörtner R, Möller J. New Insights from Locally Resolved Hydrodynamics in Stirred Cell Culture Reactors. Processes. 2022; 10(1):107. https://doi.org/10.3390/pr10010107
Chicago/Turabian StyleFreiberger, Fabian, Jens Budde, Eda Ateş, Michael Schlüter, Ralf Pörtner, and Johannes Möller. 2022. "New Insights from Locally Resolved Hydrodynamics in Stirred Cell Culture Reactors" Processes 10, no. 1: 107. https://doi.org/10.3390/pr10010107
APA StyleFreiberger, F., Budde, J., Ateş, E., Schlüter, M., Pörtner, R., & Möller, J. (2022). New Insights from Locally Resolved Hydrodynamics in Stirred Cell Culture Reactors. Processes, 10(1), 107. https://doi.org/10.3390/pr10010107









