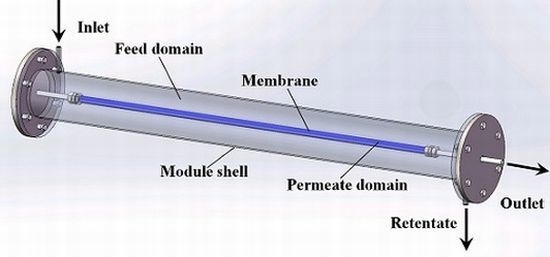
Scale-Up Design Analysis and Modelling of Cobalt Oxide Silica Membrane Module for Hydrogen Processing

Abstract

This work shows the application of a validated mathematical model for gas permeation at high temperatures focusing on demonstrated scale-up design for H₂ processing. The model considered the driving force variation with spatial coordinates and the mass transfer across the molecular sieve cobalt oxide silica membrane to predict the separation performance. The model was used to study the process of H₂ separation at 500 °C in single and multi-tube membrane modules. Parameters of interest included the H₂ purity in the permeate stream, H₂ recovery and H₂ yield as a function of the membrane length, number of tubes in a membrane module, space velocity and H₂ feed molar fraction. For a single tubular membrane, increasing the length of a membrane tube led to higher H₂ yield and H₂ recovery, owing to the increase of the membrane area. However, the H₂ purity decreased as H₂ fraction was depleted, thus reducing the driving force for H₂ permeation. By keeping the membrane length constant in a multi-tube arrangement, the H₂ yield and H₂ recovery increase was attributed to the higher membrane area, but the H₂ purity was again compromised. Increasing the space velocity avoided the reduction of H₂ purity and still delivered higher H₂ yield and H₂ recovery than in a single membrane arrangement. Essentially, if the membrane surface is too large, the driving force becomes lower at the expense of H₂ purity. In this case, the membrane module is over designed. Hence, maintaining a driving force is of utmost importance to deliver the functionality of process separation.

1. Introduction

Global climate change is closely associated with energy production, particularly CO₂ emissions from power generation and transportation using fossil fuels. One of the options to address this problem is the utilization of hydrogen, a clean energy carrier. In combustion or chemical processes to generate energy, hydrogen has the unique property of reacting with oxygen and producing water. Low temperature fuel cells are a clear example, where hydrogen disassociates into protons and electrons and, subsequently, recombines with oxygen from air to generate water. The major advantages of using hydrogen in fuel cell systems, such as polymer electrolyte fuel cells, include high efficiencies of up to 64% [1], high energy densities (relative to batteries) and the ability to operate on clean fuels, while emitting no pollutants [2].

The most viable process to produce hydrogen is via natural gas reforming or coal gasification [3]. The problem here is that fossil fuels are still being used and emitting greenhouse gases, such as CO₂. However, as hydrogen can be generated by a single plant, this facilitates CO₂ capture storage for a single point source, a major advantage to tackle greenhouse gases in non-diffuse sources. In these processes, there is a need to separate hydrogen from CO₂. Conventional industrial processes for gas separation include amine absorption strippers and pressure swing adsorption. These processes are energy intensive, because the gases produced at high temperatures (>800 °C) needed to be cooled down to meet the temperature requirements for these technologies in order to operate effectively at lower temperatures (<50 °C) [4,5]. Another process for consideration is the deployment of membranes. Organic (polymeric) membranes have been extensively used for gas separation, such as polydimethylsilane [6], though operations are generally limited to low temperatures owning to the poor thermo-stability and chemical stability of the polymeric matrix [7,8]. A more promising option is inorganic membranes, which can fulfil these requirements at high temperatures and have attracted great interest in hydrogen separation [9,10,11].

Metal- and silica-based inorganic membranes have been extensively investigated for hydrogen separation. Metal membranes are generally derived from palladium (Pd) and Pd alloy, where hydrogen is solubilised in the metal matrix, and its transport via the membrane follows the Sievert’s law, where the driving force is proportional to the square root of the partial pressure of hydrogen in the feed and the permeate streams. On the other hand, silica-derived membranes follow a molecular sieving transport, where the pore size allows for a very fast diffusion of hydrogen and, generally, hindering the diffusion of CO₂. In this case, the driving force is proportional to the partial pressure difference of hydrogen in the feed and the permeate streams. The molecular sieving transport is temperature-dependent, and generally, the flux of hydrogen increases with temperature, whilst the flux of CO₂ reduces. This is generally the case for silica membranes prepared with the silica precursors, tetraethoxy silane [12,13,14], ethoxysilane ES40 [15], or combined with surfactants [16] and metal oxides, such as nickel oxides [17] and cobalt oxides [18]. This is very attractive in industrial applications, as high temperature separation allows for high selectivities, which is defined as the ratio of hydrogen flux over CO₂ flux. Furthermore, the driving forces for gas permeation in silica-derived membranes are more significant, as any small increase in the partial pressure in the feed stream will increase the driving force instead of the square root law for the metal membranes.

The best silica membranes are those prepared with metal oxides, particularly cobalt oxide. These membranes have been shown to be hydrostable [10] and deliver high H₂/CO₂ selectivities at high temperatures of 500 °C. However, inorganic membrane research has been mainly limited to laboratory scales, with the only exception to date being a multi-tube membrane module operating for 2000 h recently reported by Yacou and co-workers [19]. Small scale tests are generally carried out under special conditions, where the driving forces are mainly constant. This allows researchers to study the transport phenomena of gases under steady state conditions. However, when gas separation modules are scaled up for industrial sizes, there is a greater spatial variation of the driving force in the module [20,21,22,23]. This is caused by the preferential permeation of H₂, reducing its partial pressure in the feed domain and affecting the driving force. In principle, the flux of a gas is proportional to the driving force, which is essentially the partial pressure difference of the gas species of interest. Hence, as gases permeate though a membrane, the driving force reduces along the length of a membrane tube. This tends to affect the membrane performance in terms of H₂ production.

Traditional membrane mass transfer models treat the feed-interface boundary and permeate-interface boundary as constant. However, it is questionable that this constant condition cannot be considered for large-scale modules, due to driving force variation. Hence, a gas transport model must be developed and validated to predict gas separation performance in the process industry using appropriate scales. In this study, a mass transfer model is investigated by incorporating both driving force changes in the gas flow and the mass transfer across a membrane. The simulation is validated against a multi-tube membrane module and, thus, predicting the hydrogen gas separation. The model is therefore applied to membrane modules by taking into consideration important process engineering parameters, such as H₂ recovery, yield and purity in terms of membrane tube length and the number of membrane tubes per module.

2. The Mathematical Modelling Details

A membrane module is depicted in Figure 1 consisting of two parts named as feed domain and permeate domain. The membrane is assembled inside the module via Swagelok connections to steel tubes. The feed gas is introduced from the inlet to the feed domain, thus contacting the outer shell of the membrane tube. The permeable gas diffuses across the membrane to the permeate domain (or inner shell of the membrane tube), and the permeate stream is collected at the permeate outlet. The impermeable gas continues to flow in the feed domain along the longitudinal axis of the membrane tube and, finally, exits the module at another outlet, named as the retentate. The gases in both domains flow in the same direction in a co-current configuration.

Figure 1. The structure of the membrane separation module.

Figure 1. The structure of the membrane separation module.

2.1. Mass Transfer in Gas Phase

There are two important gas diffusion mechanisms, namely: gas-through-gas diffusion and gas diffusion through the membrane. Gas-through-gas diffusion is severe at high temperature, and gases are constantly mixed to maintain the chemical equilibrium. The gas phase diffusivity is about four orders of magnitude of diffusivity across the silica membrane [24]. Given this situation, the concentration polarization phenomenon is very weak [23,24]. Therefore, in this case, we assume that the concentration polarization is negligible.

The basic mass balance in the gas phase can be described by the continuity equation:

(1)

where c is the molar concentration, J the bulk flux, t time, l the space coordinate in the module and S is the source term, which represents the total mass transfer across the membrane. It must be noted that the source term is zero, except at the permeable region [22]. In the membrane feed side, the source term is negative, whereas it is positive in the permeate side.

The component mass balance of H₂ is governed by the following solution conservation equation:

(2)

where x₁ is the molar fraction of H₂, D the diffusivity of H₂ in the other gas, which can be estimated from the Fuller equation [25], and S₁ is the source term for H₂ permeation, which will be further discussed in the following.

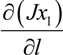It is important to observe that Equation (2) contains both the advection term, , and the diffusion term, 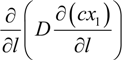. In liquid or low temperature gas separation in small-scale modules, advection is far more intense than diffusion, so diffusion is always omitted in the component mass balance equation [26,27,28,29,30,31]. This is not the case for industrial gas processes, as the diffusion term cannot be overlooked. In addition, the intrinsic properties of molecular sieve silica membranes show temperature-dependent transport, where high selectivities can be expected at high temperatures [32,33,34]. Consequently, the diffusion coefficient increases [25,35] and diffusion becomes prevalent over advection, in this case.

Pressure is an important parameter in determining the driving force for permeation. The correlation between permeate pressure and flow rate is governed by the Hagen-Poiseuille equation [36]

(3)

where p is pressure, η viscosity, F the bulk flow rate, R the gas constant, T the temperature and r is the tube radius.

The source terms in Equations (1) and (2) represent the mass transfer between the feed side and the permeate side and are derived from the following formulas [37,38]:

(4)

(5)

where d and d _H2 are the total permeate flow rate and the hydrogen permeate flow rate, respectively, J_H2 is the hydrogen permeate flux, dA is the permeable area and dV is the computational cell volume. The source terms are zero if the computational cell is not in the permeable region (such as the Swagelok for sealing the membrane and the steel tube). The source terms apply to the permeable region only.

2.2. Mass Transfer across Membrane

The major resistance of mass transfer occurs across the membrane; thus, this is a very important issue for consideration in modelling gas flux in membrane systems in the process industry. The membrane-mass-transfer mechanisms are always associated with the intrinsic properties of the membrane material. The widely used Fick’s law is proven to be less accurate than the Maxwell-Stefan model [39,40], so the latter is used to express the mass transfer across the silica membrane for a multiple component system

(6)

where J_i is the permeate molar flux of component i, Đ_ji in Equation (6) is the inter-exchange coefficient between component i and component j. A common method to estimate Đ_ij is the Vignes correlation [41,42]. x is the molar fraction, and Đ_i is the Maxwell-Stefan diffusivity of single gas i, which can be obtained from a single gas permeation test.

Equation (6) is usually cast into matrix form [43]:

(7)

For an H₂/Ar binary gas system, the elements of [B] are given according to Equation (6) (subscript 1 is for H₂ and 2 is for Ar):

(8)

where Đ₁ is the Maxwell-Stefan single gas diffusivity of H₂ and Đ₂ is that of Ar. Đ₁₂ is the Maxwell-Stefan interchange coefficient inside the membrane.

The permeate flux can be derived from Equation (7) as:

(9)

If the matrix [∆] is defined as [44]:

[∆] = [B]⁻¹

(10)

then the flux of the two species can be obtained from an explicit expression:

(11)

As both [∆] and [∇p] are functions of H₂, fraction x₁, it is necessary to solve the fraction x₁ profile across the membrane thickness in advance by flux conservation.

(12)

where r is the radial coordinate inside the membrane. The technique of obtaining x₁ distribution across the membrane is reported in detail elsewhere [23].

3. Experiment and Model Validation

The experimental data for this work were obtained from Yacou et al. [19] for a metal oxide silica multi-tube membrane operating at high temperatures up to 500 °C. The data for the selected operating conditions are listed in Table 1. The simulations were carried out under the same operating conditions as the experiments, and results are also shown in Table 1. The simulation results fit seemingly well with the experimental work and show very low relative errors for both permeate flow and permeate fraction. Hence, the initial simulation confirmed that the model was accurate enough to carry out the process simulations in this work.

Table 1. The operating conditions for mixture gas separation test.

Temperature	Feed flow rate (mL min−1)	H2 Feed fraction	Permeate flow rate in experiment (mL min−1)	Permeate flow rate in model (mL min−1)	H2 Permeate fraction in experiment	H2 Permeate fraction in model	Relative error for permeate flow	Relative error for permeate fraction
500 °C	253.9	99%	249.2	251.7	100%	99%	0.01	0.01
	49.6	82%	44.2	44.7	90%	88%	0.01	0.02
	35.1	76%	30.7	31.3	85%	82%	0.02	0.03
	13.4	18%	8.9	7.9	24%	26%	0.11	0.05
400 °C	142.7	98%	137.7	140.8	100%	98%	0.02	0.02
	44.6	84%	39.8	40.8	91%	89%	0.03	0.03
	32.4	71%	27.7	25.8	79%	81%	0.07	0.03
	16.8	41%	12.2	10.8	51%	53%	0.11	0.05

Table 1. The operating conditions for mixture gas separation test.

Temperature	Feed flow rate (mL min−1)	H2 Feed fraction	Permeate flow rate in experiment (mL min−1)	Permeate flow rate in model (mL min−1)	H2 Permeate fraction in experiment	H2 Permeate fraction in model	Relative error for permeate flow	Relative error for permeate fraction
500 °C	253.9	99%	249.2	251.7	100%	99%	0.01	0.01
	49.6	82%	44.2	44.7	90%	88%	0.01	0.02
	35.1	76%	30.7	31.3	85%	82%	0.02	0.03
	13.4	18%	8.9	7.9	24%	26%	0.11	0.05
400 °C	142.7	98%	137.7	140.8	100%	98%	0.02	0.02
	44.6	84%	39.8	40.8	91%	89%	0.03	0.03
	32.4	71%	27.7	25.8	79%	81%	0.07	0.03
	16.8	41%	12.2	10.8	51%	53%	0.11	0.05

3.1. Numerical Technique

The finite-difference method was used to solve the gas phase governing equations. The iteration stopped right after the calculation process reached a steady state, when the H₂ mass balance converged to differences smaller than 1e⁻⁵. This value is sufficiently small to attain accurate simulations in this work. The boundary conditions were set as follows: (i) retentate pressure is 6 atm; (ii) permeate outlet pressure is 1 atm; (iii) constant feed flow rate and (iv) constant gas composition at the feed inlet, in each case.

Different grid sizes were run by this model. A grid independence study in Figure 2 was performed to determine the suitable grid size for this model. It showed the H₂ fraction profile along axial positions with different grid sizes. When the grid size, ∆l, is smaller than ­­0.02 m, further reducing the grid size did not lead to any significant changes of the H₂ fraction. Therefore, Δl = 0.02 m was deemed adequate to provide accurate values for describing the physical problems in this work.

Figure 2. Grid independence simulation.

Figure 2. Grid independence simulation.

3.2. Process Parameters of Interest

The process parameters of interest to be investigated in this work are: H₂ purity, H₂ yield and H₂ recovery, as follows:

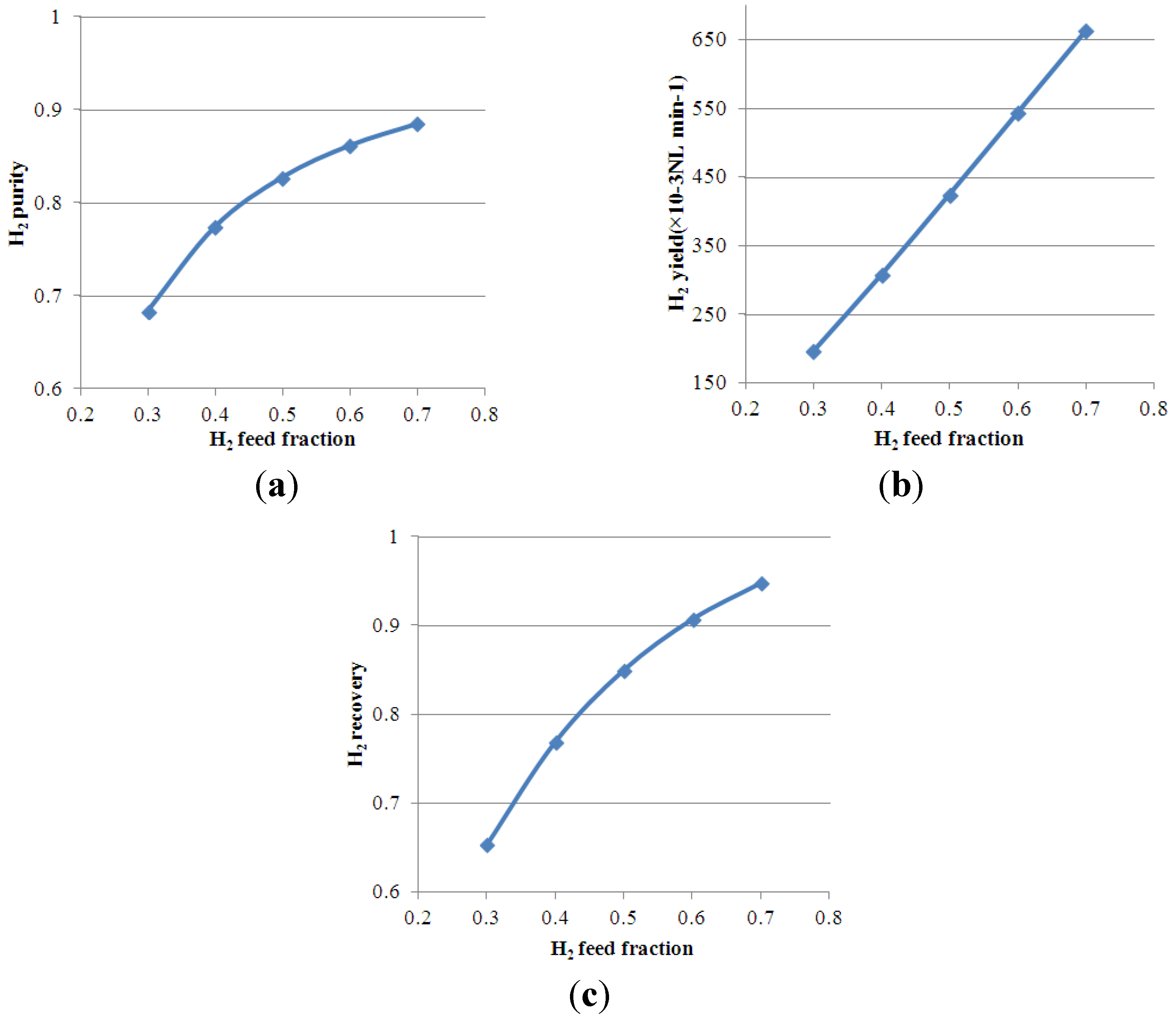
• H₂ purity is defined as the H₂ permeate molar fraction at the permeate outlet.
• H₂ yield is the permeate flow rate at the permeate outlet multiplied by H₂ purity.
• H₂ recovery is the H₂ yield divided by the H₂ feed flow rate.

The parameters of interest were simulated by solving the derivative equations by the finite difference method. The domain (e.g., feed or permeate side) was divided into numerous grids from first (entry) to n^th (exit) along the axis. Upon conversion of the simulated results at steady state conditions, the permeate flow rate and permeate fraction were determined from the n^th grid.

The properties of the membrane and the constant operating conditions were also sought from the work of Yacou et al. [19] and are listed in Table 2 and based on H₂ and Ar separation. The use of Ar instead of CO₂ was to avoid the reverse of the water gas shift reaction, which would result in the production of CO and water. Hence, Ar was used as a subrogated molecule to maintain a binary gas mixture of H₂/Ar instead of a multiple transient gas mixture. In addition, Ar (d_k = 3.42Å) and CO₂ (d_k = 3.3Å) have similar kinetic diameters (d_k) and show similar trends and fluxes and negative apparent energy of activation in high quality silica membranes. These trends are contrary to the smaller kinetic diameter of H₂ (d_k = 2.89Å), showing a positive apparent energy of activation. The simulation in this work investigates these process parameters, which are affected primarily by changing the surface area of the membranes inside a module. This can be done by altering the design specification, either by increasing the length of the membrane tubes or by adding extra tubes of the same length to a membrane module in a parallel configuration.

Table 2. Membrane properties and operating conditions [19].

Operating conditions	Value
Temperature	500 (°C)
H2 permeance	5.80 × 10−8 (mol s−1 m−2 Pa−1)
Ar permeance	5.67 × 10−10 (mol s−1 m−2 Pa−1)
Radius of module	0.05 (m)
Membrane radius	0.007 (m)
Retentate pressure	6 (atm)
Permeate pressure	1 (atm)

Table 2. Membrane properties and operating conditions [19].

Operating conditions	Value
Temperature	500 (°C)
H2 permeance	5.80 × 10−8 (mol s−1 m−2 Pa−1)
Ar permeance	5.67 × 10−10 (mol s−1 m−2 Pa−1)
Radius of module	0.05 (m)
Membrane radius	0.007 (m)
Retentate pressure	6 (atm)
Permeate pressure	1 (atm)

4. Results and Discussion

4.1. Effect of Membrane Length on Process Performance

Figure 3 displays the separation performance for a single membrane tube by varying the length from 1 m and 5 m to 10 m with a constant feed flow condition (feed flow rate = 1 NL min⁻¹, feed H₂ fraction = 0.5). The simulation shows that by increasing the membrane length, it benefited H₂ yield and H₂ recovery, though it was detrimental to H₂ purity. In order to explain the decline of the H₂ purity, it is important to understand the H₂ fraction distribution in the feed side of the membrane in Figure 4. Longer membranes have a higher surface area, which favours a higher hydrogen flux (or yield) and, consequently, a higher hydrogen recovery. By the same token, the H₂ feed fraction reduced from 0.5 to 0.35 for the 1 m length tube. By increasing the membrane length to 5 and 10 m, the hydrogen molar fraction reduced even further to 0.15 and 0.10, respectively. Hence, this caused a significant reduction in the driving force for the hydrogen permeation. Consequently, this allows for the flux of the less permeable gas to increase. As a result, the H₂ purity decreases as a function of the membrane length.

Figure 3. H₂ processing performance as a function of membrane length: (a) H₂ purity; (b) H₂ yield; (c) H₂ recovery.

Figure 3. H₂ processing performance as a function of membrane length: (a) H₂ purity; (b) H₂ yield; (c) H₂ recovery.

Figure 4. H₂ molar fraction distribution along the module for different membrane lengths.

Figure 4. H₂ molar fraction distribution along the module for different membrane lengths.

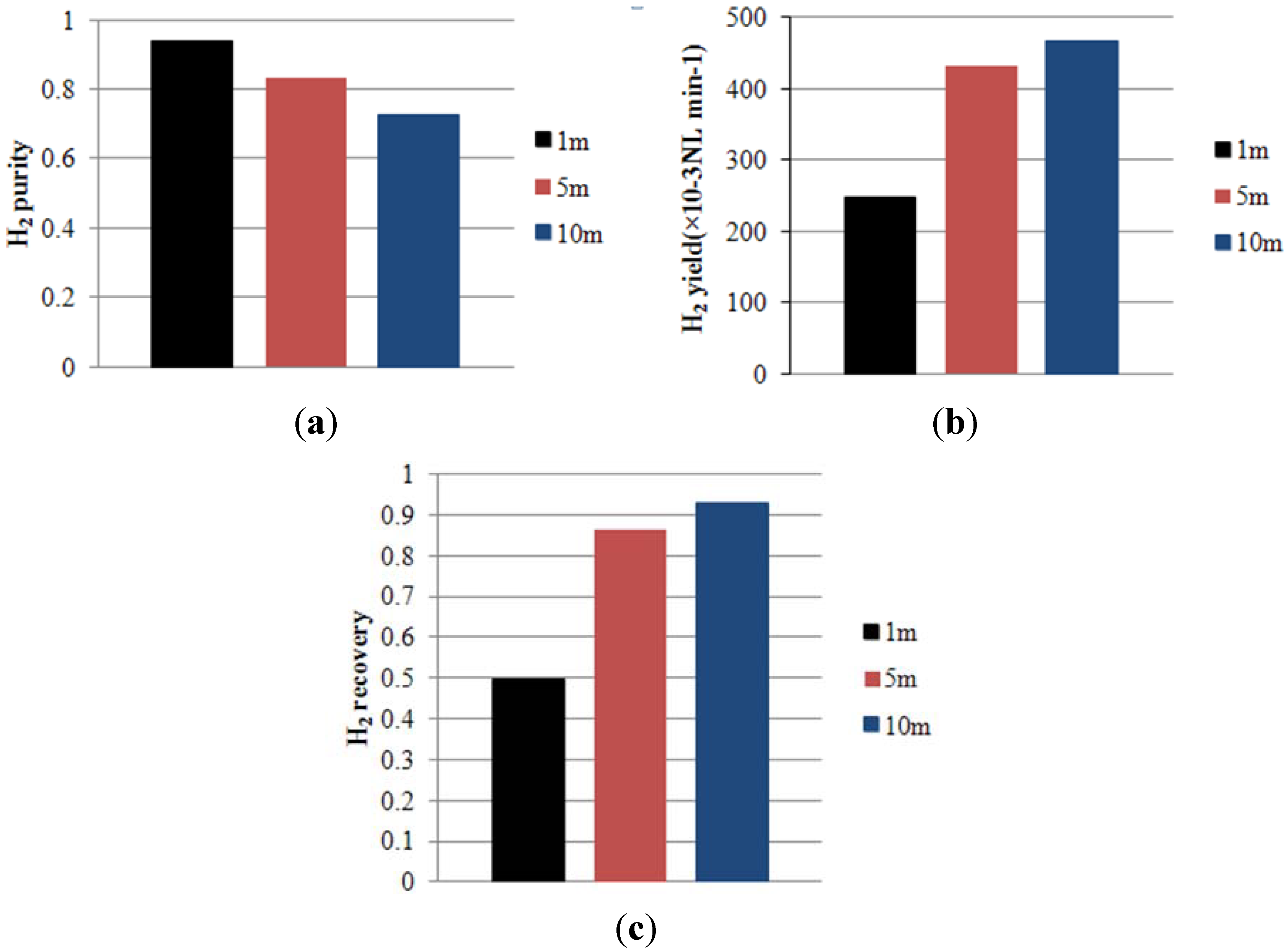
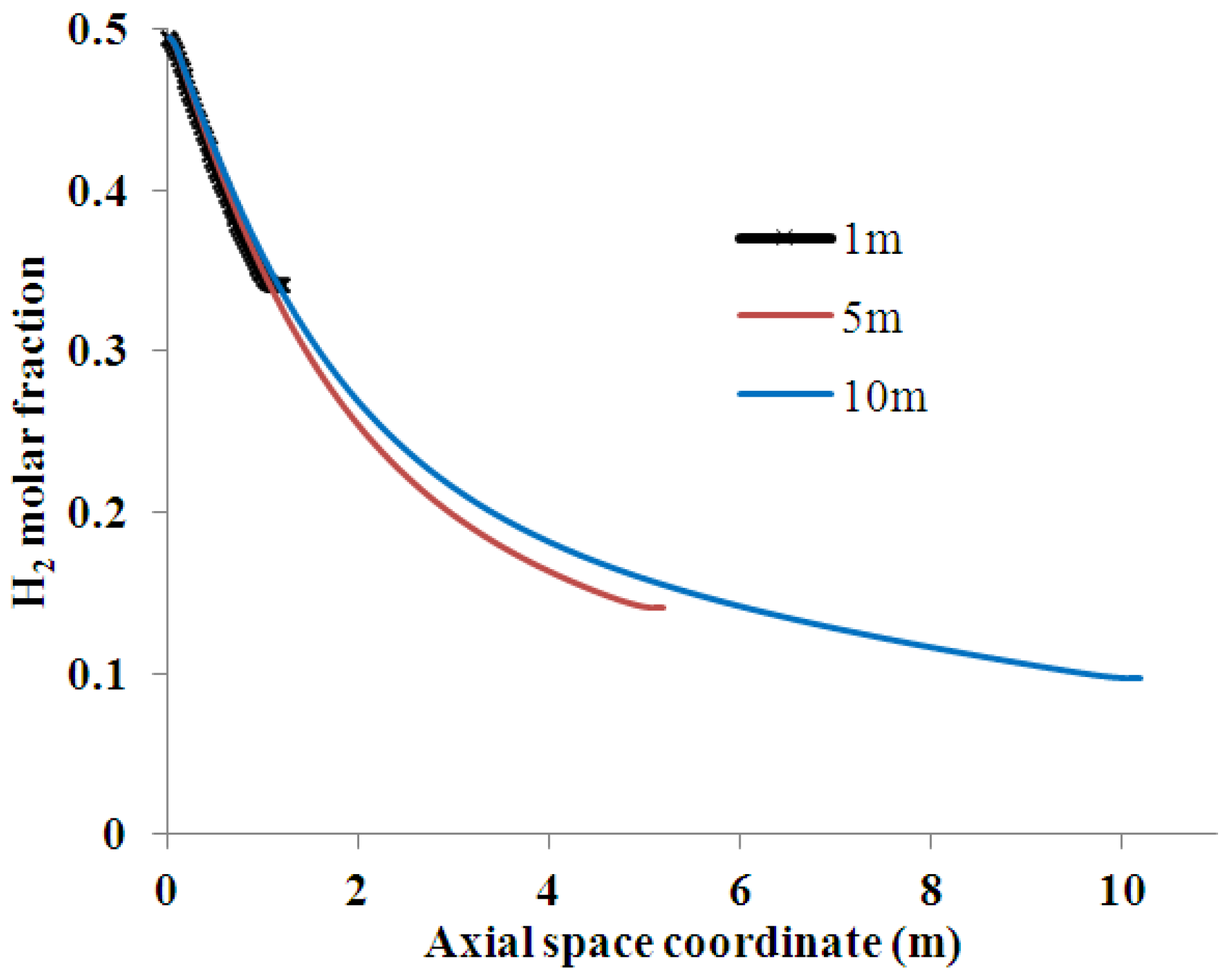
4.2. Effect of Multi-Tube Membranes on Process Performance

In industrial process design, multiple membrane tubes can be fixed in a module. If the membranes are connected in series, then the membranes would be equivalent to a single long membrane with the same total membrane length. Therefore, this section focuses on the separation performance of a multi-tube membrane in parallel, as displayed in Figure 5. As membranes can be set up equidistantly in a parallel arrangement, this allows for increasing the membrane surface area over the membrane module volume. This is an important process engineering parameter, as a high packaging ratio is desirable for industrial applications leading to small footprint units and, more importantly, reduction in capital cost.

Figure 5. The structure of quintuple membranes in parallel.

Figure 5. The structure of quintuple membranes in parallel.

Figure 6 compares the separation performance in parallel arrangement. For the same membrane length, adding extra membranes to a module led to lower H₂ purity, higher H₂ yield and H₂ recovery. The reduction of H₂ purity as a function of the number of membrane tubes in parallel is associated with a reduction of the H₂ molar feed fraction in the feed side, as shown in Figure 7. Again, adding extra tubes in parallel increase the surface area of the membranes and affects the process parameters in a similar manner as increasing the length of a membrane tube discussed above.

Figure 6. H₂ processing performance as a function of the number of membranes in a module: (a) H₂ purity; (b) H₂ yield; (c) H₂ recovery.

Figure 6. H₂ processing performance as a function of the number of membranes in a module: (a) H₂ purity; (b) H₂ yield; (c) H₂ recovery.

Figure 7. H₂ molar fraction distribution along the 1 m membrane of different membrane numbers.

Figure 7. H₂ molar fraction distribution along the 1 m membrane of different membrane numbers.

However, in terms of process design, these results strongly suggest that full recovery of H₂ is conflicting with H₂ purity. Hence, excessive membrane area (five tubes of five metres in length) causes the membrane to deliver H₂ purity almost similar to the H₂ molar ratio in the feed stream. In this case, the membrane module has been over-designed, and its function to separate gases is no longer attainable. Hence, there is a need to maintain a driving force for H₂ permeation through the membrane. If H₂ is depleted because the surface area is too large, then this creates the conditions for other gas/gases to start permeating through the membrane and, likewise, reducing H₂ purity in the permeate stream.

To meet H₂ purity specification, membrane modules cannot have 100% full recovery. While the latter would be ideal for the process industry to reduce product losses, the advantage of using inorganic membranes is associated with separation of gases at high temperatures. To counter balance the losses of H₂, membrane systems attract major gains by dispensing the requirement of conventional energy-intensive cooling down gas stream processes to separate H₂. Further comparison of Figure 6a,c can be drawn for a single tube of 5 m in length and to five multi-tube module of 1 m in length each, thus equivalent to 5 m. In principle, both designs have the same surface area, though the single tube is delivering slightly better performance for H₂ purity (~0.5%), H₂ yield (~2%) and H₂ recovery (~2%). Although these values are modest, in terms of long-term production for large processing plants, this may translate into millions of dollars in savings in production costs.

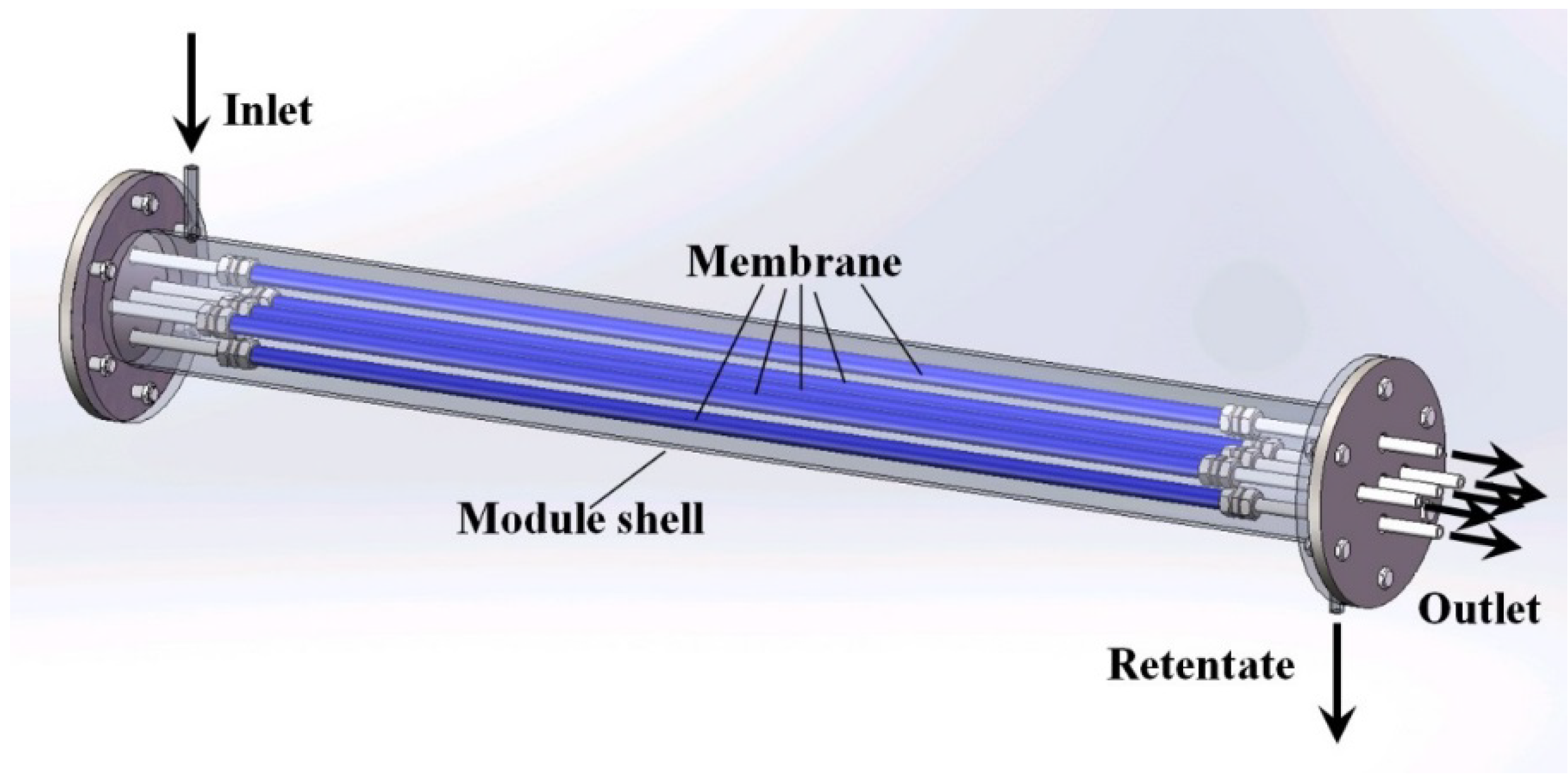
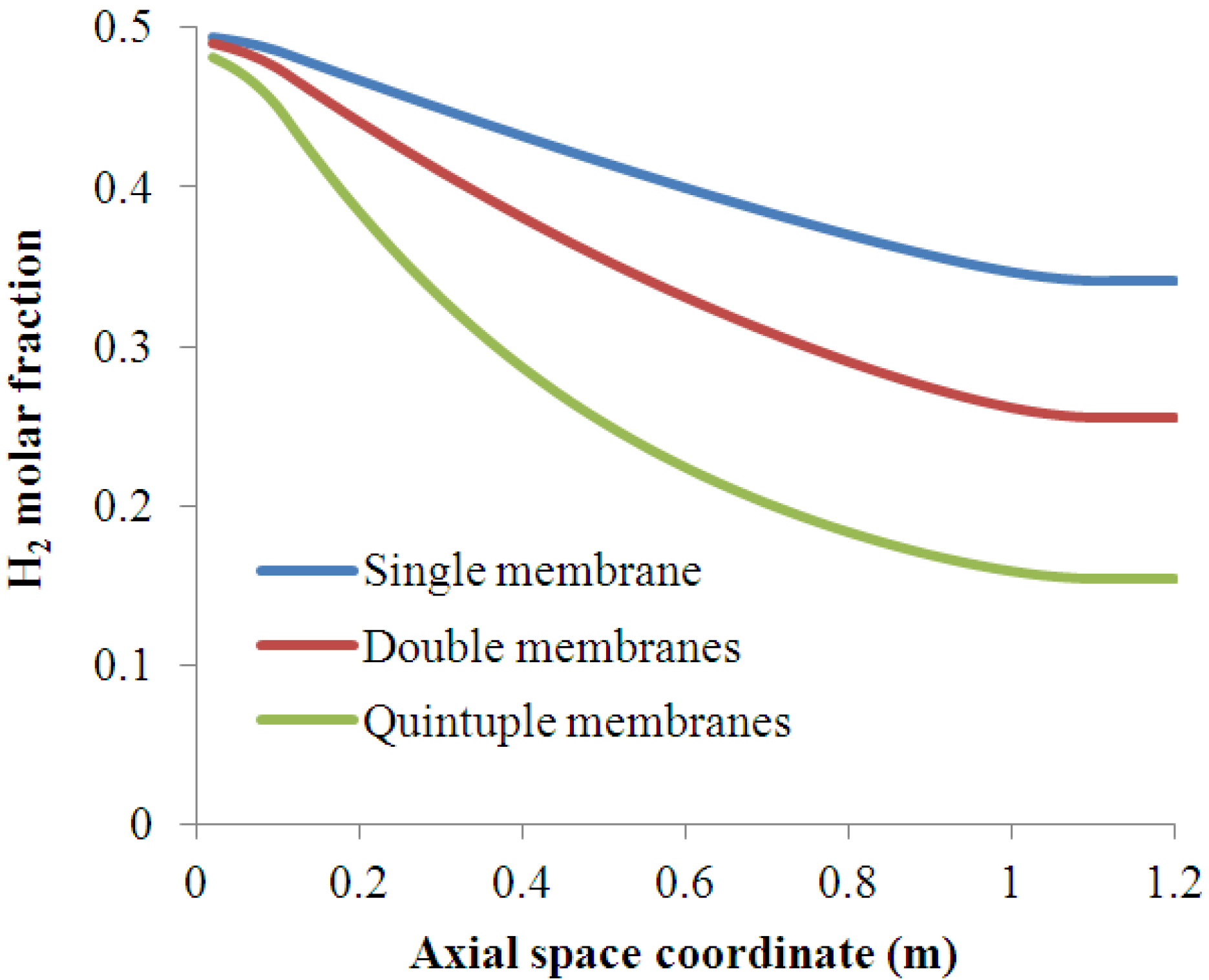
4.3. Effect of Space Velocity on Process Performance

The space velocity of gases inside a vessel or reactor is an important parameter in process design, particularly related to the sizing of a membrane module. In this case, space velocity correlates with the feed flow rate. This means that the faster the feed flow rate, the higher the space velocity or a lower retention time is, and vice versa. In the above examples, the feed flow rate was kept constant and quite low or a lower space velocity. The low feed flow rate was detrimental for H₂ purity, as the surface area of the membrane module increased to a point of being over-designed. One strategy to increase H₂ purity is to increase the feed flow rate or space velocity. Hence, the simulation was carried out for each type of membrane module by increasing the feed flow rate from 1 NL min⁻¹ to 5 NL min⁻¹. In Figure 8, it is observed that the H₂ purity increased slightly with an increasing feed flow rate. Notably, the H₂ yield rose significantly. However, the H₂ recovery deceased as the retention time in the module was reduced.

Figure 8. H₂ processing performance as a function of feed flow rate and number of membranes in a module: (a) H₂ purity; (b) H₂ yield; (c) H₂ recovery.

Figure 8. H₂ processing performance as a function of feed flow rate and number of membranes in a module: (a) H₂ purity; (b) H₂ yield; (c) H₂ recovery.

These results clearly show that using one membrane with a 1 NL min⁻¹ feed flow rate delivered higher H₂ purity, ~94%, as compared with the five membrane module, which reached up to ~83%. However, again, H₂ recovery was compromised, as this high H₂ purity was associated with low H₂ recovery of ~50%. When the feed gas fraction is constant, it is not possible to have both high H₂ purity and H₂ recovery at the same time. However, it must be said that an H₂ purity of ~84% with a recovery rate of ~85% is within industrial targets; in particular, this separation process is aimed at being achieved at 500 °C.

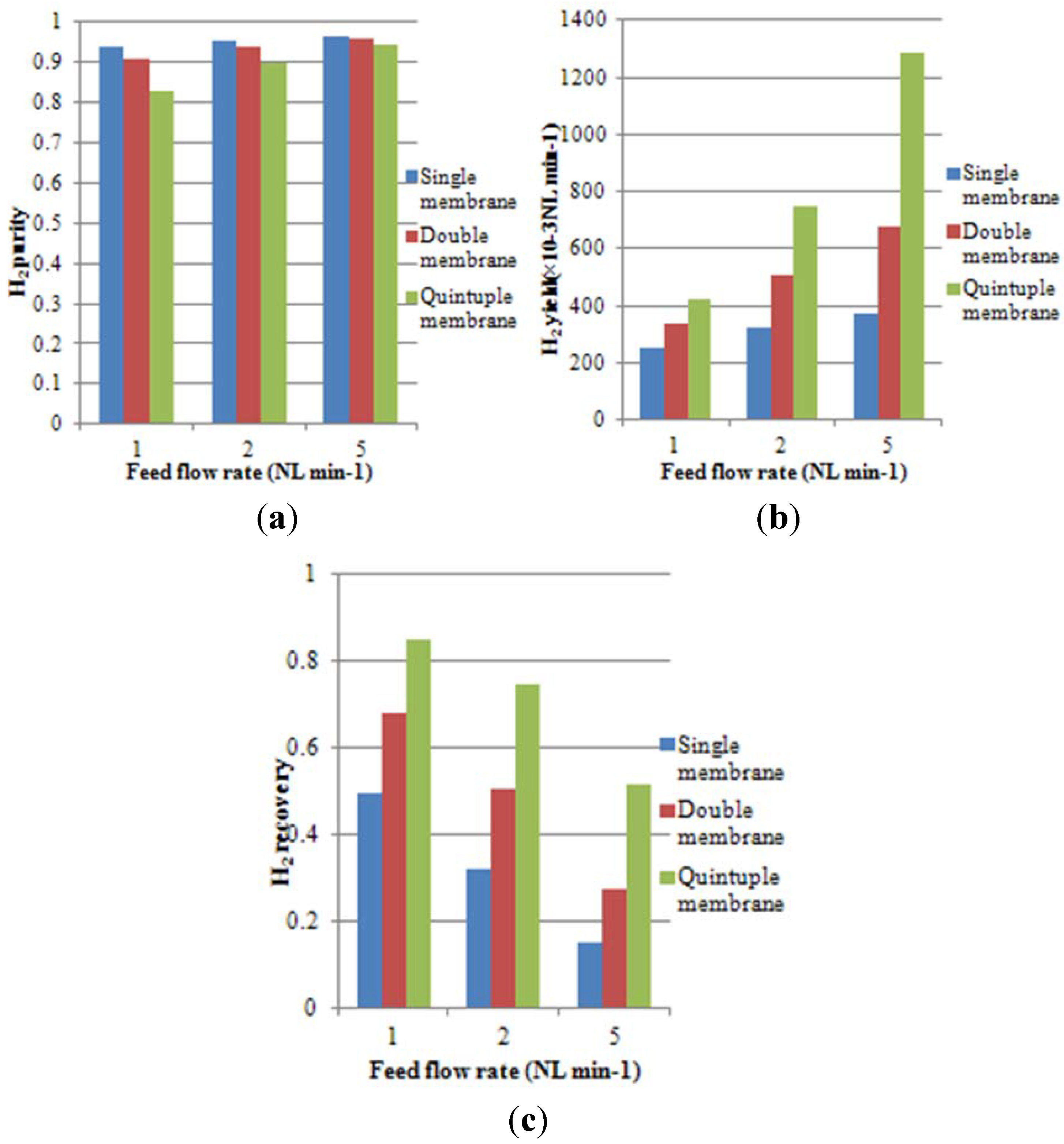
4.4. Effect of H₂ Feed Molar Fraction on Process Performance

The H₂ feed molar fraction also influences the overall separation performance of membrane modules. The variation of the H₂ feed fraction provides different amounts of the H₂ fraction along the length of the membrane module and, in turn, affects the overall driving force accordingly. In Figure 9, the H₂ feed fraction is increased gradually from 0.3 to 0.7, whilst other operating conditions are kept constant, namely feed flow rate (1 NL min⁻¹), membrane length (1 m), number of membrane tubes (5) and temperature (500 °C). It is observed that increasing the H₂ feed fraction resulted in an increase of H₂ purity, H₂ yield and H₂ recovery. H₂ yield shows a linear correlation to H₂ feed fraction, due to the fact that H₂ partial pressure in the feed domain is proportional to the H₂ feed fraction. However, both H₂ purity and H₂ recovery are convex functions to H₂ feed fraction, and essentially, these process parameters will level off and converge to a single value of one.

Figure 9. H₂ processing performance as a function of the H₂ feed molar fraction: (a) H₂ purity; (b) H₂ yield; (c) H₂ recovery.

Figure 9. H₂ processing performance as a function of the H₂ feed molar fraction: (a) H₂ purity; (b) H₂ yield; (c) H₂ recovery.

In terms of process, these results suggest that the H₂ feed molar fraction is effective in controlling the driving force. If H₂ purity cannot be achieved in a single pass, as the H₂ feed fraction is too low, then the permeate stream can be fed in a second pass by another membrane module as a cascade system. For instance, in a first pass, 30% of the H₂ feed fraction will be processed to 68% H₂ purity in the permeate stream, which can be used as a feed stream in a second pass delivering an H₂ purity of 88%. Similarly, H₂ purities and H₂ yields will also be affected accordingly. All of these parameters must be traded off to achieve the optimal membrane performance of an H₂ product specification for industrial process separation.

5. Conclusions

This study presents a model to simulate the membrane separation performance in a scale-up single and multi-tube membrane module arrangement. Cobalt oxide silica membranes were used to validate the model for H₂ separation at 500 °C. For constant feed flow conditions, longer membrane tubes increased H₂ yield and H₂ recovery, but did not deliver a higher H₂ purity. Multiple membranes in parallel enhanced the H₂ yield and H₂ recovery compared to the single membrane, but the H₂ purity decreased. Increasing the feed flow rate (and space velocity) avoided the reduction of H₂ purity in the parallel arrangement, but at the expense of H₂ recovery. Meanwhile, the H₂ yield and H₂ recovery are observed to be higher in a multi-tube configuration. Increasing the H₂ feed fraction resulted in an increase in all the performance parameters. When the tubes are too long or there is sufficient large surface area to deplete the H₂ concentration in the feed domain, then the driving force for H₂ permeation across the membrane is greatly reduced. As a result, the permeation of the other gases increased slightly, resulting in the reduction of H₂ purity. To improve the H₂ purity, it is possible to increase the space velocity (feed flow rate), which, in turn, reduces H₂ recovery. Hence, all these parameters are interlinked, of which the process conditions and product specification will dictate the optimal process conditions to be deployed in the industry.