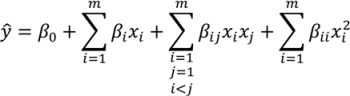Modeling of Particulate Processes for the Continuous Manufacture of Solid-Based Pharmaceutical Dosage Forms
Abstract
1. Introduction
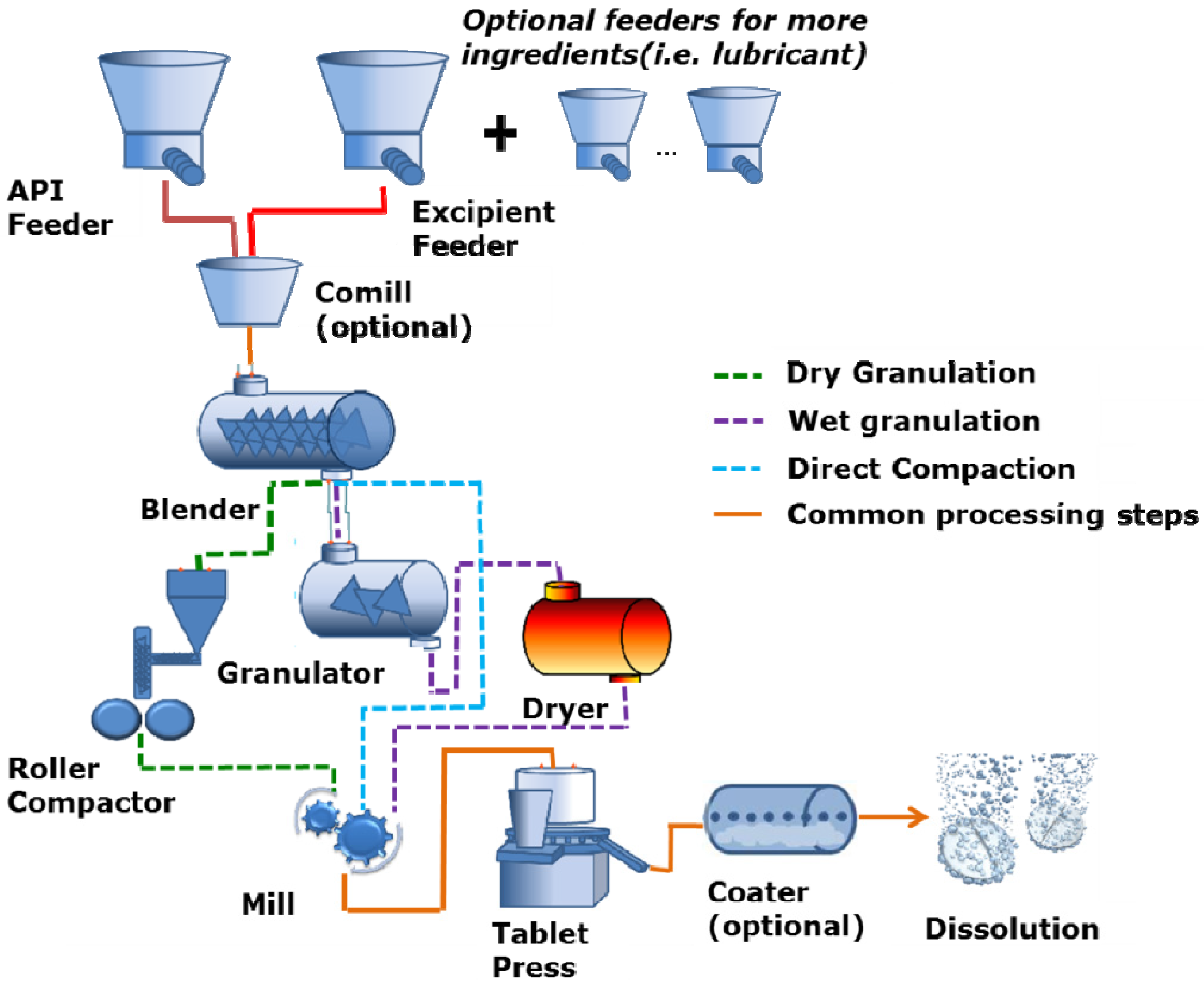
2. Continuous Tablet Manufacturing
2.1. Process Overview
| Unit name | Symbol | Design parameters | Operating parameters |
|---|---|---|---|
| Hopper |  | Shape (conical, wedge) Width Outlet diameter Wall angle Material of construction | Powder flow rate |
| LIW Feeder |  | Tooling (screw, screen) Hopper size Operating mode | Screw speed Flow rate set point |
| Continuous Mixer |  | Vessel length and diameter Agitator size and configuration | Agitator rpm Mixer fill level |
| Twin Screw Extruder |  | Number of screws Screw geometry Barrel length Binding solution properties and addition location | Screw speed Granulation temperature Liquid to solid ratio Powder Flow Rate Binder content |
| Roller Compactor |  | Roll configuration Roll diameter Roll surface Powder feed | Powder feed rate Roll speed Compaction pressure Roll gap |
| Mill |  | Mill type Mill configuration Geometry Screen/selector size Equipment size Air nozzle arrangement | Solids feed rate Rotor speed Grinding pressure |
| Tablet Press |  | Die and punch size and geometry Die feeding method Number of compression stations Die filling method Lubrication method | Powder feed rate Compression force Tableting speed |
2.2. Processing Equipment
2.2.1. Hoppers
2.2.2. Loss-in-Weight Feeders
2.2.3. Continuous Mixers
2.2.4. Wet Granulation
2.2.5. Roller Compactors
2.2.6. Milling
2.2.7. Tablet Press (with Integrated Hopper and Feed Frame)
3. Computational Tools and Mathematical Modeling Approaches
3.1. DEM Simulation
3.2. Population Balance Models
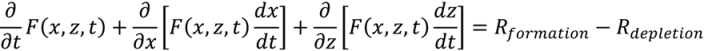
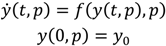
| Method | Description | Pharmaceutically relevant applications | Level of detail | Computational expense |
|---|---|---|---|---|
| DEM | particle level simulation of powder behavior | powder flow, powder mixing, and compaction | Particle level information | high |
| PBM | describes the evolution of populations of entities (particles, granules, droplets) over time | mixing, crystallization, granulation, milling | Description of population of particles | moderate to high—depending on problem dimensionality |
| ROM | approximation of high fidelity models using a variety of estimation and interpolation techniques | various unit operations, simulation-based optimization | Unit operation level description | low |
3.3. Reduced Order Models
3.3.1. Kriging
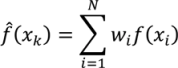
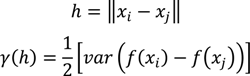
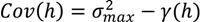
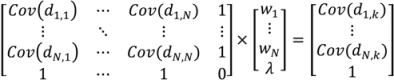
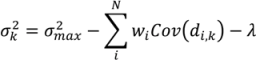
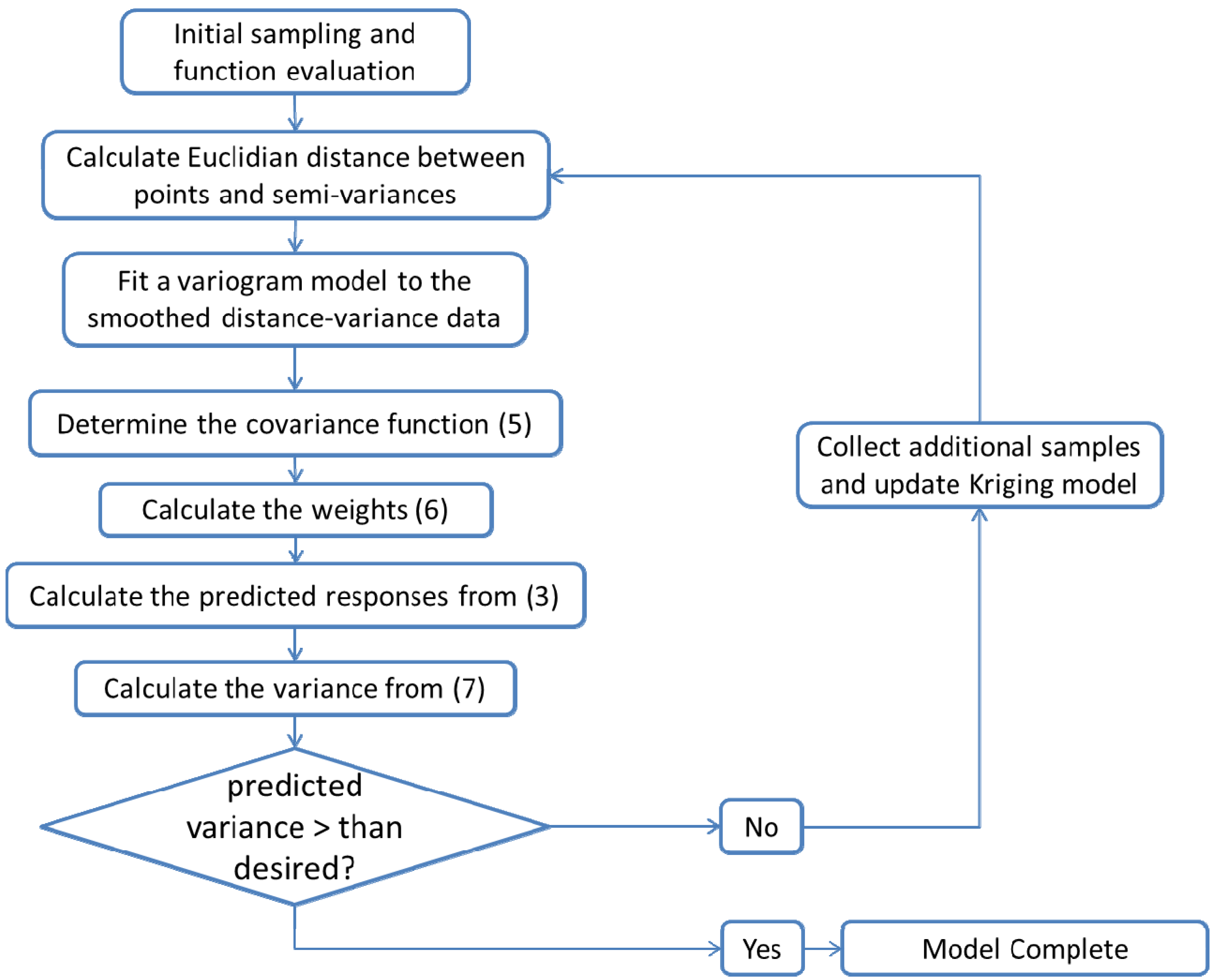
- Select an initial sample set x consisting of NT sample points and evaluate the process or model at these points to obtain the corresponding function evaluations f(x).
- Using the data obtained in step 1, calculate the Euclidian distances h and the corresponding semi-variances γ(h) using Equation (4) for all NT(NT − 1)/2 sampling pairs.
- Smooth the γ(h) vs. h data and fit it to an appropriate variogram model according to a least squares error minimization criterion and/or a secondary criterion for computational efficiency.
- Based on the variogram model, determine the covariance function as in Equation (5).
- For a test point xk calculate the weights from Equation (6). Calculate the predicted response f̂(xk) from Equation (3) and the associated variance from Equation (7).
- Optional—If the predicted variance is larger than desired, collect additional sample points in the region of the test point xk and add those to the set NT to develop an updated Kriging model.
3.3.2. Response Surface Methodology (RSM)
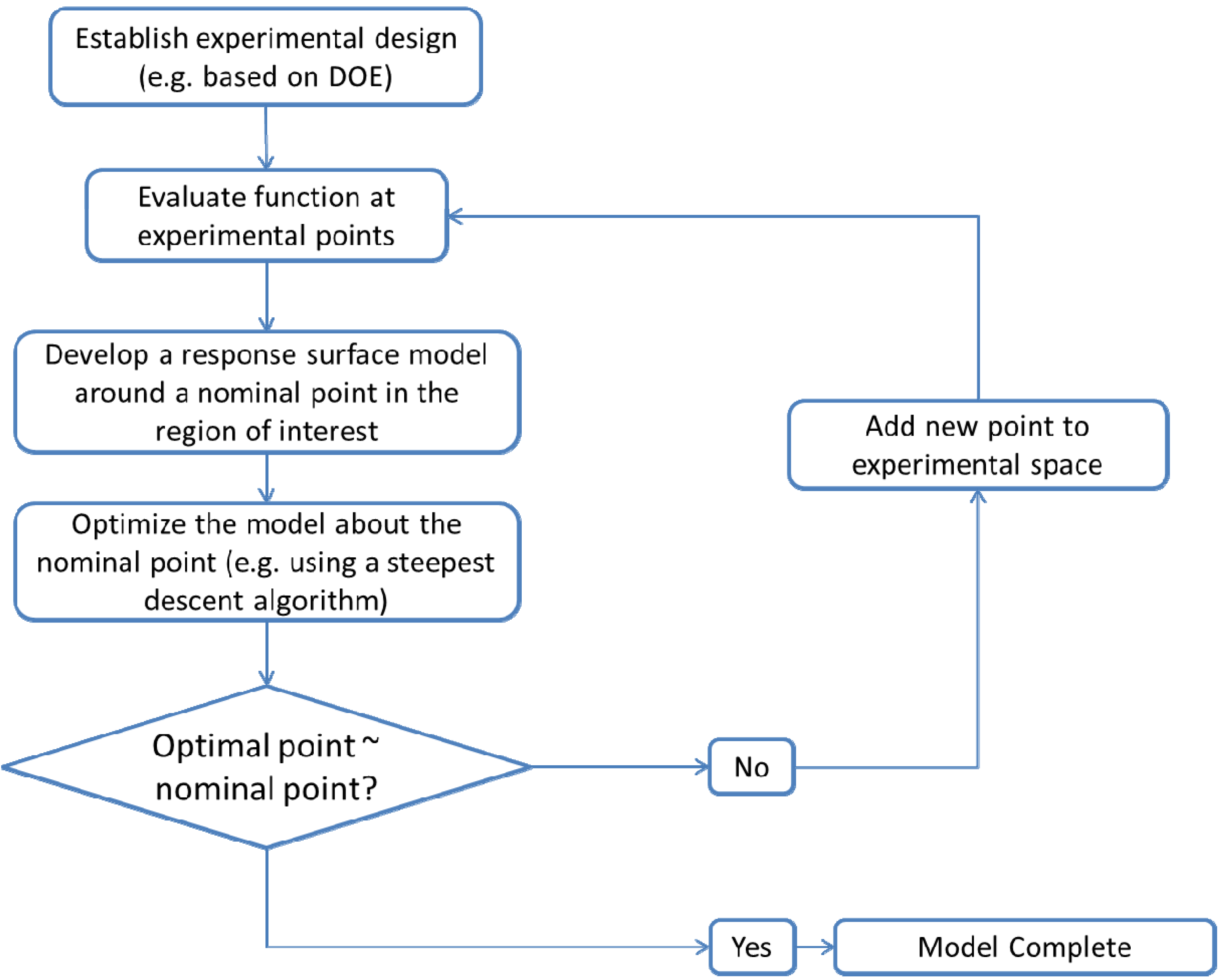
- Establishment of an experimental designA design, D, consisting of n samples can be generated using a design of experiments (DOE) or other appropriate statistical approach.
.
The proper selection of D is critical to ensure that the generated response surface will be an accurate predictor for the response of interest. The number of sampling points should be greater than the number of coefficients to be fitted for the response surface model. For noisy data, the number of sampling points needed may be greater. Further discussion of appropriate designs is provided in the literature [131,132,133]. - Development of a response surface model in the region of interestThe initial response surface model is developed around the nominal sampling point. The form of the model is defined by the modeler. Typically second-order polynomial functions as in Equation (8) are selected for the response functions. Justification for the selection of second order polynomials is provided in the literature [132,133]. The sampled data can then be regressed to the specified model using least squares or other appropriate fitting techniques.ŷ is the estimated response. β0, βi, βij and βii are the model coefficients. xi and xj are the input variables.
- Local model optimizationModel optimization is performed in order to determine the region where expected process improvement can be maximized. The optimization can be completed using a steepest descent search over the sampling region. In this case the local optimum is found iteratively. An initial model is built based on the first sampling point. The optimum of this model then becomes the nominal point for the next iteration and a new response surface is built and optimized, with the addition of new sample points. As the algorithm converges, the nominal and optimal points become one and the same [131]. Other optimization techniques such as ridge analysis can also be applied [132]. If different process designs are to be considered, binary variables can be introduced to indicate the design configuration. This results in a mixed integer nonlinear program (MINLP) optimization problem formulation [12].
3.3.3. High Dimensional Model Representation (HDMR)
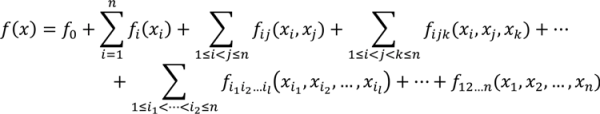
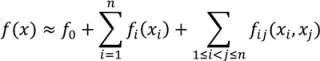
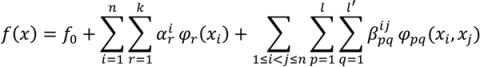
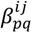 are coefficients for the basis functions φr(xi) and φpq(xi,xj) and k, l and l' are integers [143]. The use of variance reduction methods has also been shown to reduce the sampling required for accurate Monte-Carlo integration of coefficients for RS-HDMR expansions [148,149]. An overview of the algorithm for developing high dimensional model representations is provided in Figure 4.
are coefficients for the basis functions φr(xi) and φpq(xi,xj) and k, l and l' are integers [143]. The use of variance reduction methods has also been shown to reduce the sampling required for accurate Monte-Carlo integration of coefficients for RS-HDMR expansions [148,149]. An overview of the algorithm for developing high dimensional model representations is provided in Figure 4.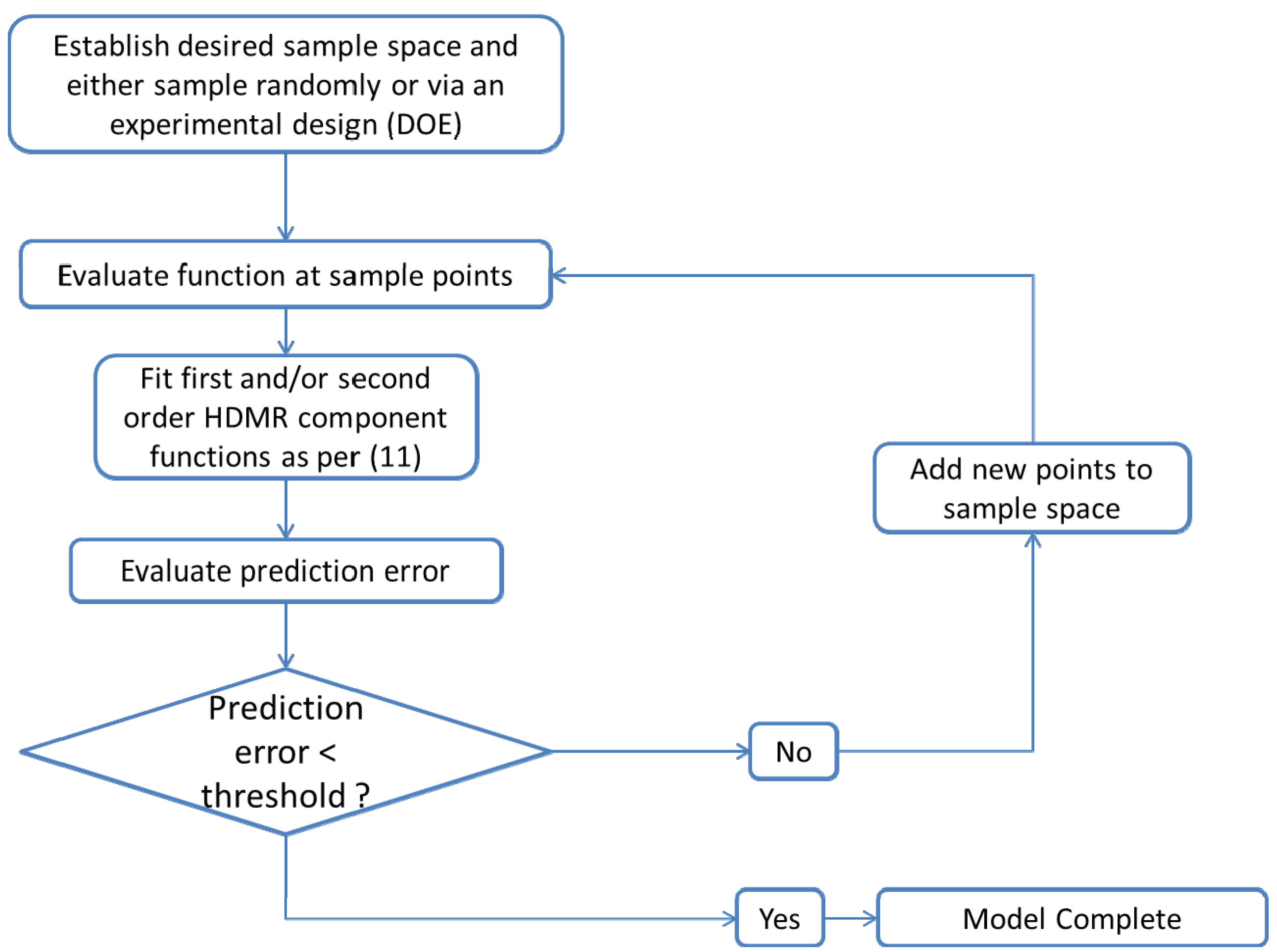
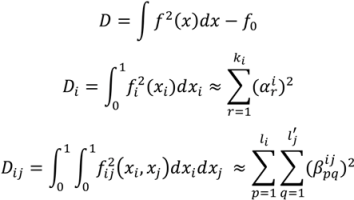
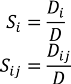

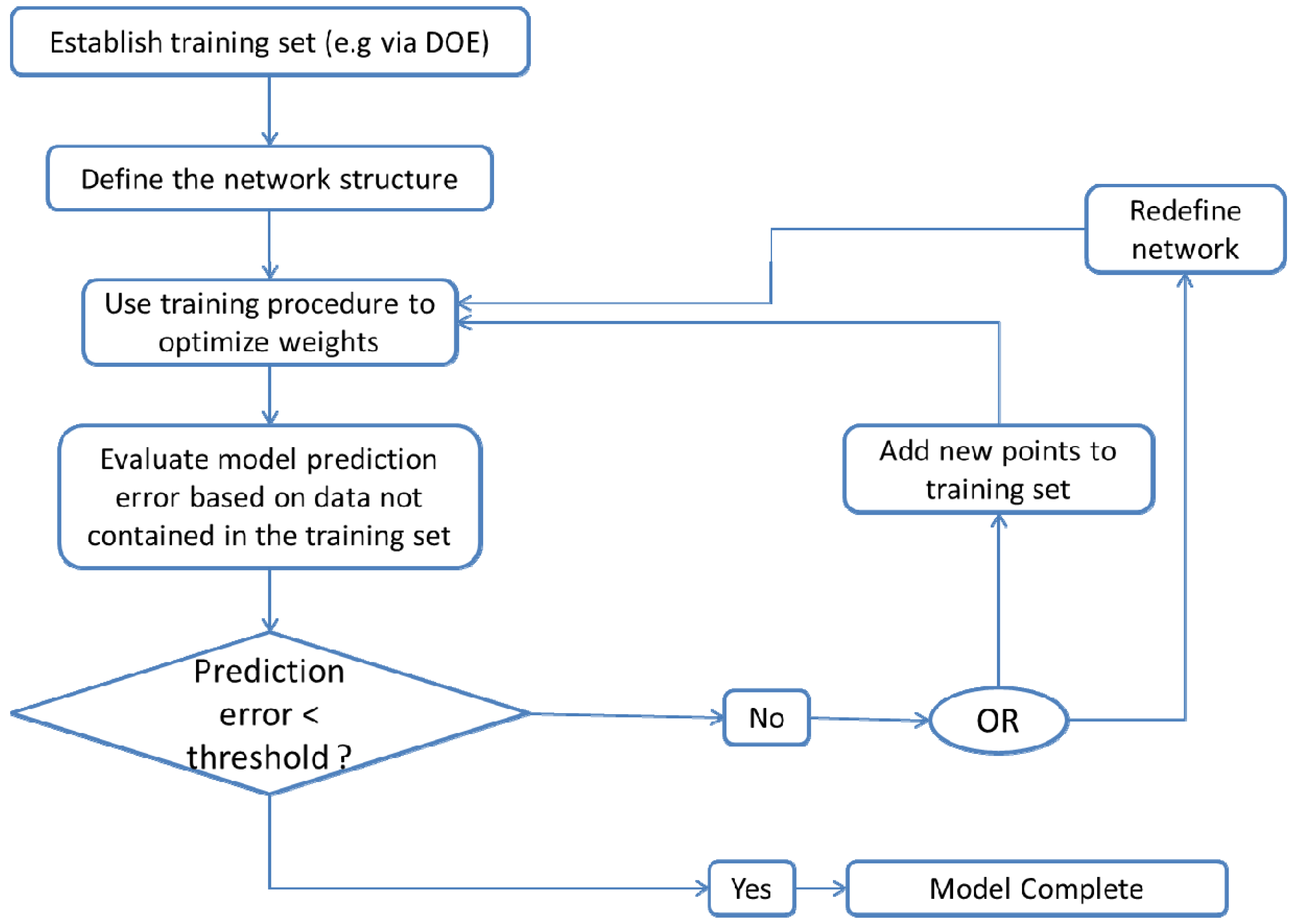
3.3.4. Artificial Neural Networks
- Obtain a training data set e.g., via DOE;
- Define the network: the number of hidden layers, the number of neurons to include in each layer and the type of transfer functions to be implemented;
- Use a training procedure to optimize the weights in such a way that prediction error is minimized. The number of neurons in each layer can also be determined based on the training set, via cross validation;
- Test the developed network against data that was not contained in the original training set to verify that the network has not been over fitted.
3.3.5. Comparison of HDMR, RSM, Kriging and Neural Networks
| Method | Fitted parameters | Number of fitted parameters* | Common basis functions |
|---|---|---|---|
| Kriging | variogram coefficients, regression coefficients | 21 | correlation models: exponential, gaussian, linear, spherical, cubic, spline regression models: polynomial |
| RSM | polynomial coefficients | 15 | Polynomial |
| HDMR | component function coefficients | 20 | Analytical basis functions: orthonormal polynomials, spline functions |
| ANN | neuron weights | 40 | Transfer functions: linear, threshold, sigmoid |
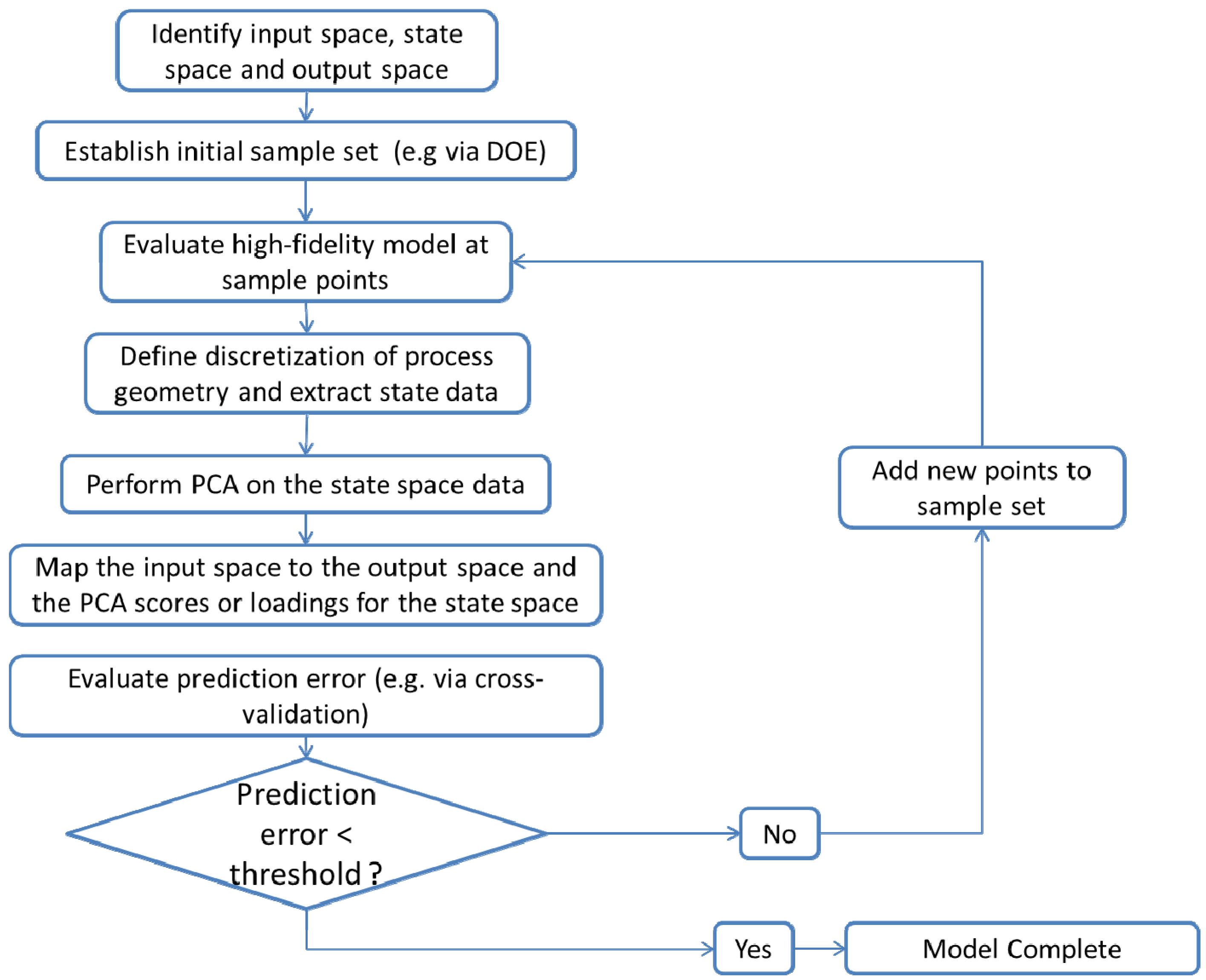
3.3.6. PCA Based ROM
- Identification of the input space (U), the state space (X) and the output space (Y)The input space consists of operating parameters that can be controlled. The output space contains measured responses at the end or outlet of the process. The state space contains variables monitored within the processing unit at various discrete points. The dimensionality of the state space depends on the spatial discretization of the unit. In the case of a continuous mixing operation the inputs might include blade rpms and configurations as well as fill level and total feed rate while API concentration and relative standard deviation (RSD) at the mixer outlet would make up the output space. The state space could include average particle velocities and energies at discrete positions within the geometry of the mixer.
- Determination of the domain of the input space and implementation of an experimental design to define the input sampling space. Performing the computer simulations at the defined sampling points.The levels of input variables to be investigated can be defined based on the operating regime for the process of interest. A design of experiments (DOE) can be used to sample the input space appropriately, resulting in a total of N distinct sampling points within the input space. Simulating the process at each of the sampling points provides the corresponding state space and output space data.
- Definition of the discretization of the process geometry in order to extract the state space dataBoukouvala et al. [110] have indicated that the choice of discretization is critical to successful ROM development. Therefore care should be taken in selecting the mesh for the geometry.
- Performing PCA on the state space dataPCA can be performed as discussed above. Note that PCA is conducted separately for each state. Thus if particle velocity data in the axial and radial directions is extracted from a simulation PCA must be conducted on each velocity component separately.
- Mapping the input space to the output space and to the scores or loadings for the state spaceThe functional form of the input-output mapping U → Y and the input-scores or input-loadings mapping U → P is determined by the modeler. Lang et al. [124,128] have described the use of Neural Networks for this mapping, while Boukouvala et al. [110] have described the use of Kriging. Regardless of the type of mapping used, it is important verify the model accuracy e.g., via cross validation.
3.4. Integrated Flowsheet Modeling Tools
3.4.1. gPROMS™
3.4.2. Aspentech’s AspenOne® utilizing AspenPlus® (V7 and V8) and AspenCustomModeler®
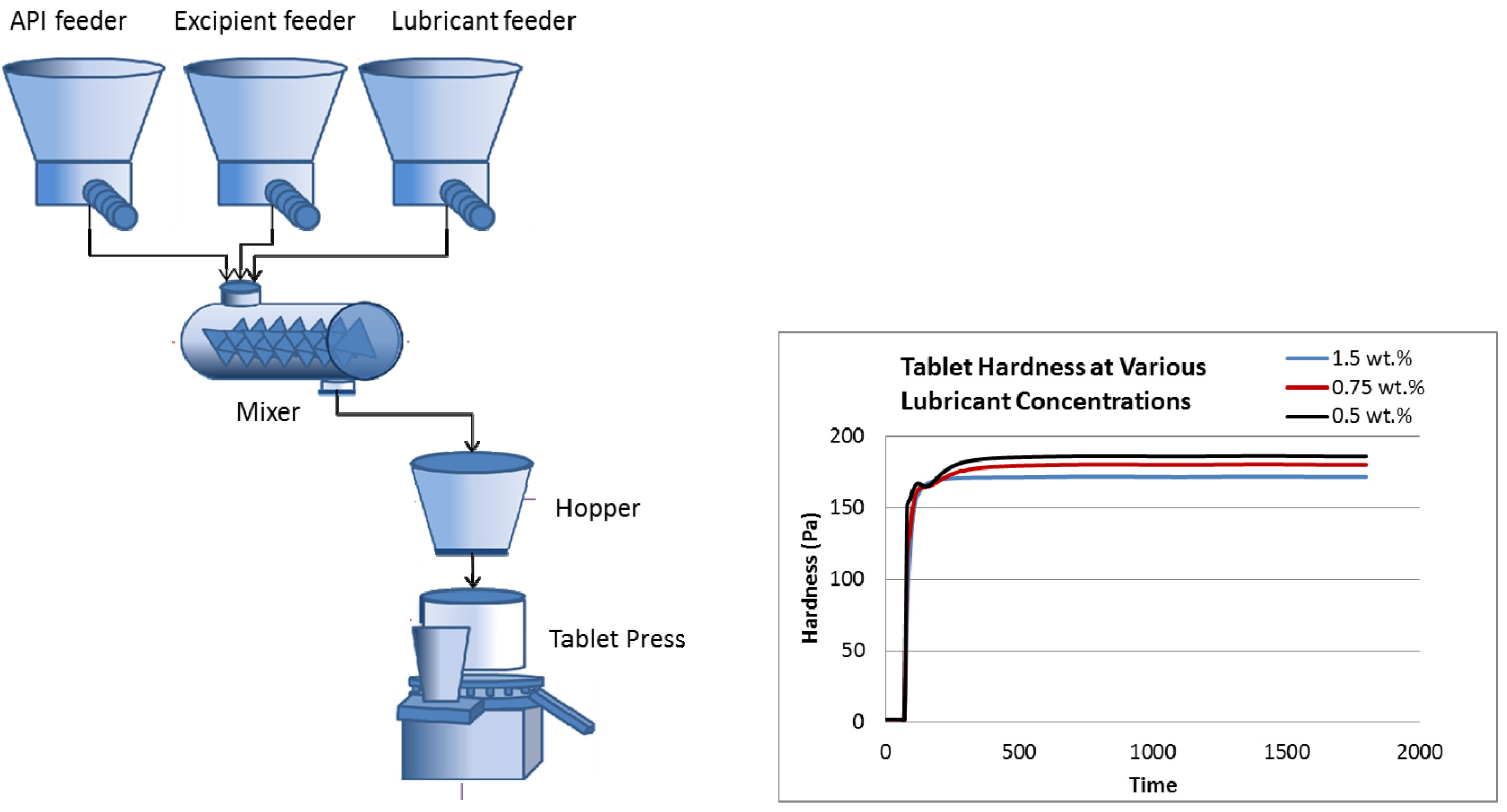
4. Unit Operation Models
4.1. Hopper
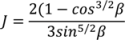
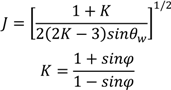
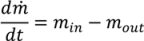
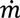 (t) = H (t)Aρbulk (t)
(t) = H (t)Aρbulk (t)
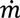 , as a function of the height of the powder within the hopper (H), the cross sectional area of the hopper, A, which may vary as a function of the height and the bulk density of the powder. Equation (19) assumes that bulk density is constant throughout the hopper, which is a reasonable assumption for small hoppers with relatively low holdup.
, as a function of the height of the powder within the hopper (H), the cross sectional area of the hopper, A, which may vary as a function of the height and the bulk density of the powder. Equation (19) assumes that bulk density is constant throughout the hopper, which is a reasonable assumption for small hoppers with relatively low holdup.
4.2. Loss-in-Weight Feeders
 , a time constant (τ f) and a time delay factor
, a time constant (τ f) and a time delay factor 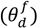 . For the purposes of this model, material bulk density and mean particle size is assumed to be constant throughout the feeder.
. For the purposes of this model, material bulk density and mean particle size is assumed to be constant throughout the feeder.
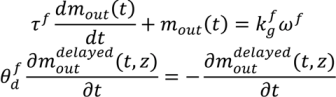
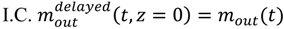
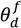 is the experimentally determined time delay and
is the experimentally determined time delay and  is the output feed rate. Equation (23) indicates that for invariant properties, like material bulk density, the feeding process has no effect. This should be experimentally verified prior to using this model for a particular process.
is the output feed rate. Equation (23) indicates that for invariant properties, like material bulk density, the feeding process has no effect. This should be experimentally verified prior to using this model for a particular process. 4.3. Continuous Mixer


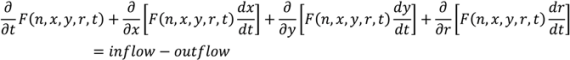
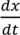 and
and 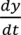 . For implementation, the process geometry is usually discretized in space so that the differentials with respect to y and x can be replaced with finite differences. The same can be done for the particle size. It is typically broken up into size categories or bins defined by upper and lower limits on particle size. In order to calculate the right hand size of Equation (27) the material balance for the mixer is needed. This is provided in Equation (28). Equation (29) provides a means of determining composition-dependent properties at the mixer outlet.
. For implementation, the process geometry is usually discretized in space so that the differentials with respect to y and x can be replaced with finite differences. The same can be done for the particle size. It is typically broken up into size categories or bins defined by upper and lower limits on particle size. In order to calculate the right hand size of Equation (27) the material balance for the mixer is needed. This is provided in Equation (28). Equation (29) provides a means of determining composition-dependent properties at the mixer outlet.
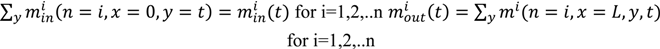
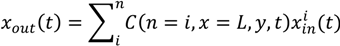
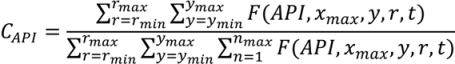
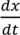 and
and 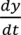 that appear in the PBM can be developed based on DEM data. Boukouvala et al. [110] have demonstrated the use of a technique called DE-ROM to develop predictive models based on data obtained from DEM and have shown that it can be used to develop a predictive model for particle velocities throughout the mixer as a function of input parameters like blade rpm. The developed reduced order model can then be implemented to provide velocity information for the population balance model.
that appear in the PBM can be developed based on DEM data. Boukouvala et al. [110] have demonstrated the use of a technique called DE-ROM to develop predictive models based on data obtained from DEM and have shown that it can be used to develop a predictive model for particle velocities throughout the mixer as a function of input parameters like blade rpm. The developed reduced order model can then be implemented to provide velocity information for the population balance model.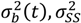 and
and 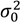 describe the composition variance within the periodic section as a function of time, at steady state, and initially (before mixing begins).
describe the composition variance within the periodic section as a function of time, at steady state, and initially (before mixing begins).
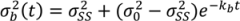
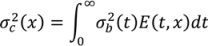
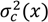 is the variance at position x and can be calculated as in Equation (33) where kc is the variance decay rate for a continuous mixing process
is the variance at position x and can be calculated as in Equation (33) where kc is the variance decay rate for a continuous mixing process
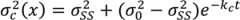
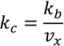

4.4. Wet Granulation
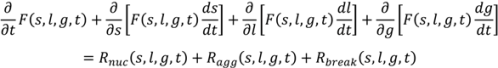

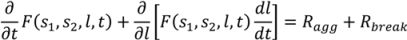
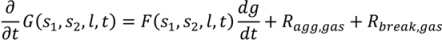
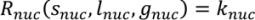
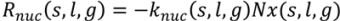
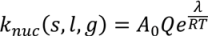
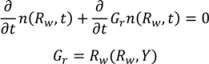
4.5. Roller Compaction
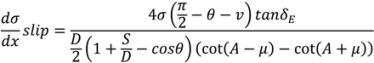
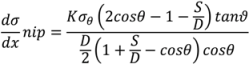
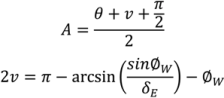
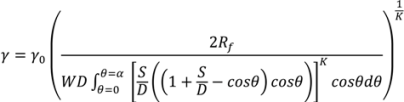
4.6. Milling
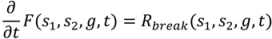
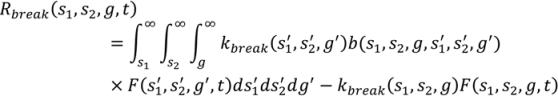
4.7. Tablet Press
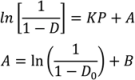
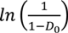 relates to the initial die filling process and B corresponds to densification from slippage and rearrangement of particles [75,211,212]. The Kawakita equation (Equation (50)) assumes that the relationship between applied pressure and powder volume is constant because particles are at equilibrium throughout the compression process.
relates to the initial die filling process and B corresponds to densification from slippage and rearrangement of particles [75,211,212]. The Kawakita equation (Equation (50)) assumes that the relationship between applied pressure and powder volume is constant because particles are at equilibrium throughout the compression process.
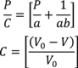
5. Model Validation and Verification
| Validation Method | Metrics | Advantages | Disadvantages | References |
|---|---|---|---|---|
| Data visualization | Qualitative | Straightforward to implement and interpret |
| [62,113,120,189,192,193] |
| Sensitivity analysis | Qualitative | Identifes important sources of process variability |
| [14,225] |
| Direct comparison | Quantitative (R2, SSE) |
| Does not provide an estimate of the prediction error | [191,242] |
| Cross-Validation | Quantitative (MSEP, RMSEP) | Provides a nearly unbiased estimate of prediction error | Can be an unstable error estimator, particularly for small datasets | [42,78,85,110,234,235,243] |
| Bootstrapping | Quantitative (MSEP, RMSEP, etc.) |
| Can become computationally expensive as the number of bootstraps increases | [244,245] |
| Hypothesis Testing | Qualitative result (reject or accept model) based on a Quantitative decision making criteria ( t-test, z-test, or F-test statistic or Bayes factor) |
|
| [41,241] |
6. Conclusions
Acknowledgments
Conflict of Interest
References
- Suresh, P.; Basu, P.K. Improving pharmaceutical product development and manufacturing: Impact on cost of drug development and cost of goods sold of pharmaceuticals. J. Pharm. Innov. 2008, 3, 175–187. [Google Scholar] [CrossRef]
- Shah, N. Pharmaceutical supply chains: Key issues and strategies for optimisation. Comput. Chem. Eng. 2004, 28, 929–941. [Google Scholar] [CrossRef]
- ICH Harmonised Tripartite Guideline: Pharmaceutical Development Q8(r2), Current Step 4 Version. In The International Conference on Harmonisation, Geneva, Switzerland, 2009.
- McKenzie, P.; Kiang, S.; Tom, J.; Rubin, A.E.; Futran, M. Can pharmaceutical process development become high tech? AIChE J. 2006, 52, 3990–3994. [Google Scholar] [CrossRef]
- Food and Drug Administration, Guidance for Industry, Q8 Pharmaceutical Development; Food and Drug Administration: Silver Spring, MD, USA, 2006.
- Reinhardt, U.E. Perspectives on the pharmaceutical industry. Health Aff. (Millwood) 2001, 20, 136–149. [Google Scholar] [CrossRef]
- Basu, P.; Joglekar, G.; Rai, S.; Suresh, P.; Vernon, J. Analysis of manufacturing costs in pharmaceutical companies. J. Pharm. Innov. 2008, 3, 30–40. [Google Scholar] [CrossRef]
- Plumb, K. Continuous processing in the pharmaceutical industry—Changing the mind set. Chem. Eng. Res. Des. 2005, 83, 730–738. [Google Scholar] [CrossRef]
- Buchholz, S. Future manufacturing approaches in the chemical and pharmaceutical industry. Chem. Eng. Process. 2010, 49, 993–995. [Google Scholar] [CrossRef]
- Aksu, B.; de Beer, T.; Folestad, S.; Ketolainen, J.; Linden, H.; Lopes, J.A.; de Matas, M.; Oostra, W.; Rantanen, J.; Weimer, M. Strategic funding priorities in the pharmaceutical sciences allied to quality by design (QBD) and process analytical technology (PAT). Eur. J. Pharm. Sci. 2012, 47, 402–405. [Google Scholar] [CrossRef]
- Schaber, S.D.; Gerogiorgis, D.I.; Ramachandran, R.; Evans, J.M.B.; Barton, P.I.; Trout, B.L. Economic analysis of integrated continuous and batch pharmaceutical manufacturing: A case study. Ind. Eng. Chem. Res. 2011, 50, 10083–10092. [Google Scholar]
- Boukouvala, F.; Muzzio, F.J.; Ierapetritou, M.G. Design space of pharmaceutical processes using data-driven-based methods. J. Pharm. Innov. 2010, 5, 119–137. [Google Scholar] [CrossRef]
- Gernaey, K.V.; Gani, R. A model-based systems approach to pharmaceutical product-process design and analysis. Chem. Eng. Sci. 2010, 65, 5757–5769. [Google Scholar] [CrossRef]
- Boukouvala, F.; Niotis, V.; Ramachandran, R.; Muzzio, F.J.; Ierapetritou, M.G. An integrated approach for dynamic flowsheet modeling and sensitivity analysis of a continuous tablet manufacturing process. Comput. Chem. Eng. 2012, 42, 30–47. [Google Scholar] [CrossRef]
- Gernaey, K.V.; Cervera-Padrell, A.E.; Woodley, J.M. A perspective on PSE in pharmaceutical process development and innovation. Comput. Chem. Eng. 2012, 42, 15–29. [Google Scholar] [CrossRef]
- Akkisetty, P.K.; Lee, U.; Reklaitis, G.V.; Venkatasubramanian, V. Population balance model-based hybrid neural network for a pharmaceutical milling process. J. Pharm. Innov. 2010, 5, 161–168. [Google Scholar] [CrossRef]
- Ramachandran, R.; Arjunan, J.; Chaudhury, A.; Ierapetritou, M.G. Model-based control-loop performance of a continuous direct compaction process. J. Pharm. Innov. 2011, 6, 249–263. [Google Scholar] [CrossRef]
- Singh, R.; Ierapetritou, M.; Ramachandran, R. System-wide hybrid MPC-PID control of a continous pharmaceutical tablet manufacturing process via direct compaction. Eur. J. Pharm. Biopharm. 2013. [Google Scholar] [CrossRef]
- Singh, R.; Ierapetritou, M.; Ramachandran, R. An engineering study on the enhanced control and operation of continuous manufacturing of pharmaceutical tablets via roller compaction. Int. J. Pharm. 2012, 438, 307–326. [Google Scholar] [CrossRef]
- Gao, Y.J.; Muzzio, F.J.; Ierapetritou, M.G. Optimizing continuous powder mixing processes using periodic section modeling. Chem. Eng. Sci. 2012, 80, 70–80. [Google Scholar] [CrossRef]
- Troup, G.M.; Georgakis, C. Process systems engineering tools in the pharmaceutical industry. Comput. Chem. Eng. 2013, 51, 157–171. [Google Scholar] [CrossRef]
- Järvinen, M.A.; Paaso, J.; Paavola, M.; Leivisk, K.; Juuti, M.; Muzzio, F.; Järvinen, K. Continuous direct tablet compression: Effects of impeller rotation rate, total feed rate and drug content on the tablet properties and drug release. Drug Dev. Ind. Pharm. 2012. [Google Scholar] [CrossRef]
- Anand, A.; Curtis, J.S.; Wassgren, C.R.; Hancock, B.C.; Ketterhagen, W.R. Predicting discharge dynamics from a rectangular hopper using the discrete element method (DEM). Chem. Eng. Sci. 2008, 63, 5821–5830. [Google Scholar] [CrossRef]
- Weir, G.J. A mathematical model for dilating, non-cohesive granular flows in steep-walled hoppers. Chem. Eng. Sci. 2004, 59, 149–161. [Google Scholar] [CrossRef]
- Gremaud, P.A.; Matthews, J.V.; Schaeffer, D.G. On the computation of steady hopper flows III: Model comparisons. J. Comput. Phys. 2006, 219, 443–454. [Google Scholar] [CrossRef]
- Faqih, A.M.N.; Alexander, A.W.; Muzzio, F.J.; Tomassone, M.S. A method for predicting hopper flow characteristics of pharmaceutical powders. Chem. Eng. Sci. 2007, 62, 1536–1542. [Google Scholar] [CrossRef]
- Ketterhagen, W.R.; Curtis, J.S.; Wassgren, C.R.; Kong, A.; Narayan, P.J.; Hancock, B.C. Granular segregation in discharging cylindrical hoppers: A discrete element and experimental study. Chem. Eng. Sci. 2007, 62, 6423–6439. [Google Scholar] [CrossRef]
- Ketterhagen, W.R.; Hancock, B.C. Optimizing the design of eccentric feed hoppers for tablet presses using DEM. Comput. Chem. Eng. 2010, 34, 1072–1081. [Google Scholar] [CrossRef]
- Balevičius, R.; Kačianauskas, R.; Mróz, Z.; Sielamowicz, I. Discrete-particle investigation of friction effect in filling and unsteady/steady discharge in three-dimensional wedge-shaped hopper. Powder Technol. 2008, 187, 159–174. [Google Scholar] [CrossRef]
- Engisch, W.E.; Muzzio, F.J. Method for characterization of loss-in-weight feeder equipment. Powder Technol. 2012, 228, 395–403. [Google Scholar] [CrossRef]
- Gao, Y.J.; Muzzio, F.; Ierapetritou, M. Characterization of feeder effects on continuous solid mixing using fourier series analysis. AIChE J. 2011, 57, 1144–1153. [Google Scholar] [CrossRef]
- Yang, S.; Evans, J.R.G. Metering and dispensing of powder; the quest for new solid freeforming techniques. Powder Technol. 2007, 178, 56–72. [Google Scholar] [CrossRef]
- Berthiaux, H.; Marikh, K.; Gatumel, C. Continuous mixing of powder mixtures with pharmaceutical process constraints. Chem. Eng. Process. 2008, 47, 2315–2322. [Google Scholar] [CrossRef]
- Pernenkil, L.; Cooney, C.L. A review on the continuous blending of powders. Chem. Eng. Sci. 2006, 61, 720–742. [Google Scholar] [CrossRef]
- Portillo, P.M.; Ierapetritou, M.G.; Muzzio, F.J. Characterization of continuous convective powder mixing processes. Powder Technol. 2008, 182, 368–378. [Google Scholar] [CrossRef]
- Marikh, K.; Berthiaux, H.; Gatumel, C.; Mizonov, V.; Barantseva, E. Influence of stirrer type on mixture homogeneity in continuous powder mixing: A model case and a pharmaceutical case. Chem. Eng. Res. Des. 2008, 86, 1027–1037. [Google Scholar] [CrossRef]
- Portillo, P.M.; Ierapetritou, M.G.; Muzzio, F.J. Effects of rotation rate, mixing angle, and cohesion in two continuous mixers—A statistical approach. Powder Technol. 2009, 194, 217–227. [Google Scholar] [CrossRef]
- Vanarase, A.U.; Muzzio, F.J. Effect of operating conditions and design parameters in a continuous powder mixer. Powder Technol. 2011, 208, 26–36. [Google Scholar] [CrossRef]
- Portillo, P.M.; Vanarase, A.U.; Ingram, A.; Seville, J.K. Investigation of the effect of impeller rotation rate, powder flowrate, and cohesion on powder flow behavior in a continuous blender using pept. Chem. Eng. Sci. 2010, 65, 5685–5668. [Google Scholar]
- Koller, D.M.; Posch, A.; Horl, G.; Voura, C.; Radl, S.; Urbanetz, N.; Fraser, S.D.; Tritthart, W.; Reiter, F.; Schlingmann, M.; et al. Continuous quantitative monitoring of powder mixing dynamics by near-infrared spectroscopy. Powder Technol. 2011, 205, 87–96. [Google Scholar] [CrossRef]
- Gao, Y.J.; Vanarase, A.; Muzzio, F.; Ierapetritou, M. Characterizing continuous powder mixing using residence time distribution. Chem. Eng. Sci. 2011, 66, 417–425. [Google Scholar] [CrossRef]
- Jarvinen, K.; Hoehe, W.; Jarvinen, M.; Poutiainen, S.; Juuti, M.; Borchert, S. In-line monitoring of the drug content of powder mixtures and tablets by near-infrared spectroscopy during the continuous direct compression tableting process. Eur. J. Pharm. Sci. 2013, 48, 680–688. [Google Scholar] [CrossRef]
- Vanarase, A.U.; Alcala, M.; Rozo, J.I.J.; Muzzio, F.J.; Romanach, R.J. Real-time monitoring of drug concentration in a continuous powder mixing process using NIR spectroscopy. Chem. Eng. Sci. 2010, 65, 5728–5733. [Google Scholar] [CrossRef]
- Martínez, L.; Peinado, A.; Liesum, L.; Betz, G. Use of near-infrared spectroscopy to quantify drug content on a continuous blending process: Influence of mass flow and rotation speed variations. Eur. J. Pharm. Biopharm. 2013, 84, 606–615. [Google Scholar] [CrossRef]
- Marikh, K.; Berthiaux, H.; Mizonov, V.; Barantsev, E. Experimental study of the stirring conditions taking place in a pilot plant continuous mixer of particulate solids. Powder Technol. 2005, 157, 138–143. [Google Scholar] [CrossRef]
- Faure, A.; York, P.; Rowe, R.C. Process control and scale-up of pharmaceutical wet granulation processes: A review. Eur. J. Pharm. Biopharm. 2001, 52, 269–277. [Google Scholar] [CrossRef]
- Lee, K.T.; Ingram, A.; Rowson, N.A. Comparison of granule properties produced using twin screw extruder and high shear mixer: A step towards understanding the mechanism of twin screw wet granulation. Powder Technol. 2013, 238, 91–98. [Google Scholar] [CrossRef]
- Iveson, S.M.; Litster, J.D.; Hapgood, K.; Ennis, B.J. Nucleation, growth and breakage phenomena in agitated wet granulation processes: A review. Powder Technol. 2001, 117, 3–39. [Google Scholar] [CrossRef]
- Betz, G.; Junker-Burgin, P.; Leuenberger, H. Batch and continuous processing in the production of pharmaceutical granules. Pharm. Dev. Technol. 2003, 8, 289–297. [Google Scholar] [CrossRef]
- Vervaet, C.; Remon, J.P. Continuous granulation in the pharmaceutical industry. Chem. Eng. Sci. 2005, 60, 3949–3957. [Google Scholar] [CrossRef]
- Tu, W.D.; Ingram, A.; Seville, J. Regime map development for continuous twin screw granulation. Chem. Eng. Sci. 2013, 87, 315–326. [Google Scholar] [CrossRef]
- Dhenge, R.M.; Cartwright, J.J.; Hounslow, M.J.; Salman, A.D. Twin screw wet granulation: Effects of properties of granulation liquid. Powder Technol. 2012, 229, 126–136. [Google Scholar] [CrossRef]
- Cartwright, J.J.; Robertson, J.; D’Haene, D.; Burke, M.D.; Hennenkamp, J.R. Twin screw wet granulation: Loss in weight feeding of a poorly flowing active pharmaceutical ingredient. Powder Technol. 2013, 238, 116–121. [Google Scholar] [CrossRef]
- Vercruysse, J.; Cordoba Diaz, D.; Peeters, E.; Fonteyne, M.; Delaet, U.; van Assche, I.; de Beer, T.; Remon, J.P.; Vervaet, C. Continuous twin screw granulation: Influence of process variables on granule and tablet quality. Eur. J. Pharm. Biopharm. 2012, 82, 205–211. [Google Scholar] [CrossRef]
- Paltzer, S. Drying of wet agglomerates in a continuous fluid bed: Influence of residence time, air temperature and air-flowrate on the drying kinetics and the amount of oversize particles. Chem. Eng. Sci. 2007, 62, 463. [Google Scholar] [CrossRef]
- Kleinebudde, P. Roll compaction/dry granulation: Pharmaceutical applications. Eur. J. Pharm. Biopharm. 2004, 58, 317–326. [Google Scholar] [CrossRef]
- Yu, S.; Gururajan, B.; Reynolds, G.; Roberts, R.; Adams, M.J.; Wu, C.Y. A comparative study of roll compaction of free-flowing and cohesive pharmaceutical powders. Int. J. Pharm. 2012, 428, 39–47. [Google Scholar] [CrossRef]
- Lecompte, T.; Doremus, P.; Thomas, G.; Perier-Camby, L.; Le Thiesse, J.-C.; Masteau, J.-C.; Debove, L. Dry granulation of organic powders—Dependence of pressure 2d-distribution on different process parameters. Chem. Eng. Sci. 2005, 60, 3933–3940. [Google Scholar] [CrossRef]
- Boswell, S.; Smith, G. Improving solid dosage forms with dry granulation. Pharm. Technol. Eur. 2011, 23, 31. [Google Scholar]
- Sharma, A.; Sharma, A.; Chauhan, C.S. Roller compaction: Imperative process for tablet manufacturing: A review. Int. J. Pharm. Res. Dev. 2012, 4, 40–47. [Google Scholar]
- Reynolds, G.; Ingale, R.; Roberts, R.; Kothari, S.; Gururajan, B. Practical application of roller compaction process modeling. Comput. Chem. Eng. 2010, 34, 1049–1057. [Google Scholar] [CrossRef]
- Bindhumadhavan, G.; Seville, J.P.K.; Adams, N.; Greenwood, R.W.; Fitzpatrick, S. Roll compaction of a pharmaceutical excipient: Experimental validation of rolling theory for granular solids. Chem. Eng. Sci. 2005, 60, 3891–3897. [Google Scholar] [CrossRef]
- Dec, R.T.; Zavaliangos, A.; Cunningham, J.C. Comparison of various modeling methods for analysis of powder compaction in roller press. Powder Technol. 2003, 130, 265–271. [Google Scholar] [CrossRef]
- Miguélez-Morán, A.M.; Wu, C.-Y.; Seville, J.P.K. The effect of lubrication on density distributions of roller compacted ribbons. Int. J. Pharm. 2008, 362, 52–59. [Google Scholar] [CrossRef]
- Nakach, M.; Authelin, J.R.; Chamayou, A.; Dodds, J. Comparison of various milling technologies for grinding pharmaceutical powders. Int. J. Miner. Process. 2004, 74, S173–S181. [Google Scholar] [CrossRef]
- Reynolds, G.K. Modelling of pharmaceutical granule size reduction in a conical screen mill. Chem. Eng. J. 2010, 164, 383–392. [Google Scholar] [CrossRef]
- Verheezen, J.J.; van der Voort Maarschalk, K.; Faassen, F.; Vromans, H. Milling of agglomerates in an impact mill. Int. J. Pharm. 2004, 278, 165–172. [Google Scholar] [CrossRef]
- Vendola, T.A.; Hancock, B.C. The effect of mill type on two dry-granulated placebo formulations. Pharm. Technol. 2008, 32, 72–86. [Google Scholar]
- Samanta, A.K.; Ng, K.Y.; Heng, P.W. Cone milling of compacted flakes: Process parameter selection by adopting the minimal fines approach. Int. J. Pharm. 2012, 422, 17–23. [Google Scholar] [CrossRef]
- Motzi, J.J.; Anderson, N.R. The quantitative evaluation of a granulation milling process ii. Effect of output screen size, mill speed and impeller shape. Drug Dev. Ind. Pharm. 1984, 10, 713–728. [Google Scholar] [CrossRef]
- Inghelbracht, S.; Remon, J.P. Reducing dust and improving granule and tablet quality in the roller compaction process. Int. J. Pharm. 1998, 171, 195–206. [Google Scholar] [CrossRef]
- Mehrotra, A.; Chaudhuri, B.; Faqih, A.; Tomassone, M.S.; Muzzio, F.J. A modeling approach for understanding effects of powder flow properties on tablet weight variability. Powder Technol. 2009, 188, 295–300. [Google Scholar] [CrossRef]
- Kuentz, M.; Lunenberger, H. A new model for the hardness of a compacted particle systems, applied to tablets of pharmaceutical polymers. Powder Technol. 2000, 111, 145–153. [Google Scholar] [CrossRef]
- Gentis, N.D.; Betz, G. Compressibility of binary powder formulations: Investigation and evaluation with compaction equations. J. Pharm. Sci. 2012, 101, 777–793. [Google Scholar] [CrossRef]
- Patel, S.; Kaushal, A.M.; Bansal, A.K. Effect of particle size and compression force on compaction behavior and derived mathematical parameters of compressibility. Pharm. Res. 2007, 24, 111–124. [Google Scholar] [CrossRef]
- Wu, C.Y.; Ruddy, O.M.; Bentham, A.C.; Hancock, B.C.; Best, S.M.; Elliott, J.A. Modelling the mechanical behaviour of pharmaceutical powders during compaction. Powder Technol. 2005, 152, 107–117. [Google Scholar] [CrossRef]
- Podczeck, F. Methods for the practical determination of the mechanical strength of tablets—From empiricism to science. Int. J. Pharm. 2012, 436, 214–232. [Google Scholar] [CrossRef]
- Corredor, C.C.; Bu, D.; Both, D. Comparison of near infrared and microwave resonance sensors for at-line moisture determination in powders and tablets. Anal. Chim. Acta 2011, 696, 84–93. [Google Scholar] [CrossRef]
- Zavaliangos, A.; Galen, S.; Cunningham, J.; Winstead, D. Temperature evolution during compaction of pharmaceutical powders. J. Pharm. Sci. 2008, 97, 3291–3304. [Google Scholar] [CrossRef]
- Onuki, Y.; Kawai, S.; Arai, H.; Maeda, J.; Takagaki, K.; Takayama, K. Contribution of the physicochemical properties of active pharmaceutical ingredients to tablet properties identified by ensemble artificial neural networks and Kohonen’s self-organizing maps. J. Pharm. Sci. 2012, 101, 2372–2381. [Google Scholar] [CrossRef]
- Govedarica, B.; Ilic, I.; Sibanc, R.; Dreu, R.; Srcic, S. The use of single particle mechanical properties for predicting the compressibility of pharmaceutical materials. Powder Technol. 2012, 225, 43–51. [Google Scholar] [CrossRef]
- Wang, J.; Wen, H.; Desai, D. Lubrication in tablet formulations. Eur. J. Pharm. Biopharm. 2010, 75, 1–15. [Google Scholar] [CrossRef]
- Jackson, S.; Sinka, I.C.; Cocks, A.C. The effect of suction during die fill on a rotary tablet press. Eur. J. Pharm. Biopharm. 2007, 65, 253–256. [Google Scholar] [CrossRef]
- Hancock, B.C.; Ketterhagen, W.R. Discrete element method (DEM) simulations of stratified sampling during solid dosage form manufacturing. Int. J. Pharm. 2011, 418, 265–272. [Google Scholar] [CrossRef]
- Otsuka, M.; Yamane, I. Prediction of tablet properties based on near infrared spectra of raw mixed powders by chemometrics: Scale-up factor of blending and tableting processes. J. Pharm. Sci. 2009, 98, 4296–4305. [Google Scholar] [CrossRef]
- Yu, A.B. Discrete element method—An effective way for particle scale research of particulate matter. Eng. Comput. 2004, 21, 205–214. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: Theoretical developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: A review of major applications and findings. Chem. Eng. Sci. 2008, 63, 5728–5770. [Google Scholar] [CrossRef]
- Persson, A.S.; Frenning, G. An experimental evaluation of the accuracy to simulate granule bed compression using the discrete element method. Powder Technol. 2012, 219, 249–256. [Google Scholar] [CrossRef]
- Siiria, S.M.; Antikainen, O.; Heinamaki, J.; Yliruusi, J. 3d simulation of internal tablet strength during tableting. AAPS PharmSciTech 2011, 12, 593–603. [Google Scholar] [CrossRef]
- Jerier, J.F.; Hathong, B.; Richefeu, V.; Chareyre, B.; Imbault, D.; Donze, F.V.; Doremus, P. Study of cold powder compaction by using the discrete element method. Powder Technol. 2011, 208, 537–541. [Google Scholar] [CrossRef]
- Yi, L.Y.; Dong, K.J.; Zou, R.P.; Yu, A.B. Coordination number of the packing of ternary mixtures of spheres: DEM simulations versus measurements. Ind. Eng. Chem. Res. 2011, 50, 8773–8785. [Google Scholar] [CrossRef]
- McCarthy, J.J.; Jasti, V.; Marinack, M.; Higgs, C.F. Quantitative validation of the discrete element method using an annular shear cell. Powder Technol. 2010, 203, 70–77. [Google Scholar] [CrossRef]
- Wu, C.Y.; Cocks, A.C.F. Numerical and experimental investigations of the flow of powder into a confined space. Mech. Mater. 2006, 38, 304–324. [Google Scholar] [CrossRef]
- Ketterhagen, W.R.; Ende, M.T.A.; Hancock, B.C. Process modeling in the pharmaceutical industry using the discrete element method. J. Pharm. Sci. 2009, 98, 442–470. [Google Scholar] [CrossRef]
- Wu, C.Y. DEM simulations of die filling during pharmaceutical tabletting. Particuology 2008, 6, 412–418. [Google Scholar] [CrossRef]
- Wu, C.-Y.; Guo, Y. Numerical modelling of suction filling using DEM/CFD. Chem. Eng. Sci. 2012, 73, 231–238. [Google Scholar] [CrossRef]
- Guo, Y.; Kafui, K.D.; Wu, C.Y.; Thornton, C.; Seville, J.P.K. A coupled DEM/CFD analysis of the effect of air on powder flow during die filling. AIChE J. 2008, 55, 49–62. [Google Scholar]
- Guo, Y.; Wu, C.-Y.; Kafui, K.D.; Thornton, C. Numerical analysis of density-induced segregation during die filling. Powder Technol. 2009, 197, 111–119. [Google Scholar]
- Guo, Y.; Wu, C.Y.; Kafui, K.D.; Thornton, C. 3D DEM/CFD analysis of size-induced segregation during die filling. Powder Technol. 2011, 206, 177–188. [Google Scholar] [CrossRef]
- Gethin, D.T.; Yang, X.S.; Lewis, R.W. A two dimensional combined discrete and finite element scheme for simulating the flow and compaction of systems comprising irregular particles. Comput. Methods Appl. Mech. Eng. 2006, 195, 5552–5565. [Google Scholar] [CrossRef]
- Frenning, G. Compression mechanics of granule beds: A combined finite/discrete element study. Chem. Eng. Sci. 2010, 65, 2464–2471. [Google Scholar] [CrossRef]
- Nwose, E.N.; Pei, C.L.; Wu, C.Y. Modelling die filling with charged particles using DEM/CFD. Particuology 2012, 10, 229–235. [Google Scholar] [CrossRef]
- Bertrand, F.; Leclaire, L.A.; Levecque, G. DEM-based models for the mixing of granular materials. Chem. Eng. Sci. 2005, 60, 2517–2531. [Google Scholar] [CrossRef]
- Marigo, M.; Davies, M.; Leadbeater, T.; Cairns, D.L.; Ingram, A.; Stitt, E.H. Application of positron emission particle tracking (PEPT) to validation a discrete element method (DEM) model of granular flow and mixing in the turbula mixer. Int. J. Pharm. 2013, 66, 1811–1824. [Google Scholar]
- Remy, B.; Khinast, J.G.; Glasser, B.J. Polydisperse granular flows in a bladed mixer: Experiments and simulations of cohesionless spheres. Chem. Eng. Sci. 2011, 66, 1811–1824. [Google Scholar] [CrossRef]
- Remy, B.; Canty, T.M.; Khinast, J.G.; Glasser, B.J. Experiments and simulations of cohesionless particles with varying roughness in a bladed mixer. Chem. Eng. Sci. 2010, 65, 4557–4571. [Google Scholar] [CrossRef]
- Sarkar, A.; Wassgren, C.R. Comparison of flow microdynamics for a continuous granular mixer with predictions from periodic slice DEM simulations. Powder Technol. 2012, 221, 325–336. [Google Scholar] [CrossRef]
- Gao, Y.J.; Muzzio, F.J.; Ierapetritou, M.G. A review of the residence time distribution (RTD) applications in solid unit operations. Powder Technol. 2012, 228, 416–423. [Google Scholar] [CrossRef]
- Boukouvala, F.; Gao, Y.J.; Muzzio, F.; Ierapetritou, M.G. Reduced-order discrete element method modeling. Chem. Eng. Sci. 2013, 95, 12–26. [Google Scholar] [CrossRef]
- Griffin, D.W.; Mellichamp, D.A.; Doherty, M.F. Reducing the mean size of api crystals by continuous manufacturing with product classification and recycle. Chem. Eng. Sci. 2010, 65, 5770–5780. [Google Scholar] [CrossRef]
- Mortier, S.T.F.C.; Gernaey, K.V.; de Beer, T.; Nopens, I. Development of a population balance model of a pharmaceutical drying process and testing of solution methods. Comput. Chem. Eng. 2013, 50, 39–53. [Google Scholar] [CrossRef]
- Barasso, D.; Ramachandran, R. A comparison of model order reduction techniques for a four-dimensional population balance model describing multi-component wet granulation process. Chem. Eng. Sci. 2012, 80, 380–392. [Google Scholar] [CrossRef]
- Langham, Z.A.; Booth, J.; Hughes, L.P.; Reynolds, G.K.; Wren, S.A.C. Mechanistic insights into the dissolution of spray-dried amorphous solid dispersions. J. Pharm. Sci. 2012, 101, 2798–2810. [Google Scholar] [CrossRef]
- Sen, M.; Ramachandran, R. A multi-dimensional population balance model approach to continuous powder mixing processes. Adv. Powder Technol. 2013, 24, 51–59. [Google Scholar]
- Ramkrishna, D. Population Balances: Theory and Applications to Particulate Systems Engineering; Academic Press: London, UK, 2000. [Google Scholar]
- Majumbder, A.; Kariwala, V.; Ansumali, S.; Rajendran, A. Lattice boltzmann method for population balance equations with simultaneous growth, nucleation, aggregation and breakage. Chem. Eng. Sci. 2012, 65, 4884–4893. [Google Scholar]
- Ramachandran, R.; Barton, P.I. Effective parameter estimation within a multi-dimensional population balance model framework. Chem. Eng. Sci. 2010, 65, 4884–4893. [Google Scholar] [CrossRef]
- Sen, M.; Singh, R.; Vanarase, A.; John, J.; Ramachandran, R. Multi-dimensional population balance modeling and experimental validation of continuous powder mixing processes. Chem. Eng. Sci. 2012, 80, 349–360. [Google Scholar] [CrossRef]
- Ramachandran, R.; Immanuel, C.D.; Stepanek, F.; Litster, J.D.; Doyle, F.J. A mechanistic model for breakage in population balances of granulation: Theoretical kernel development and experimental validation. Chem. Eng. Res. Des. 2009, 87, 598–614. [Google Scholar] [CrossRef]
- Immanuel, C.D.; Doyle, F.J. Computationally efficient solution of population balance models incorporating nucleation, growth and coagulation: Application to emulsion polymerization. Chem. Eng. Sci. 2003, 58, 3681–3698. [Google Scholar] [CrossRef]
- Immanuel, C.D.; Doyle, F.J. Solution technique for a multi-dimensional population balance model describing granulation processes. Powder Technol. 2005, 156, 213–225. [Google Scholar] [CrossRef]
- Boukouvala, F.; Dubey, A.; Vanarase, A.; Ramachandran, R.; Muzzio, F.J.; Ierapetritou, M. Computational approaches for studying the granular dynamics of continuous blending processes, 2—Population balance and data-based methods. Macromol. Mater. Eng. 2012, 297, 9–19. [Google Scholar] [CrossRef]
- Lang, Y.D.; Zitney, S.E.; Biegler, L.T. Optimization of IGCC processes with reduced order CFD models. Comput. Chem. Eng. 2011, 35, 1705–1717. [Google Scholar] [CrossRef]
- Zitney, S.E. Process/equipment co-simulation for design and analysis of advanced energy systems. Comput. Chem. Eng. 2010, 34, 1532–1542. [Google Scholar] [CrossRef]
- Brenner, T.A.; Fontenot, R.L.; Cizmas, P.G.A.; O’Brien, T.J.; Breault, R.W. A reduced-order model for heat transfer in multiphase flow and practical aspects of the proper orthogonal decomposition. Comput. Chem. Eng. 2012, 43, 68–80. [Google Scholar] [CrossRef]
- Liberge, E.; Hamdouni, A. Reduced order modelling method via proper orthogonal decomposition (POD) for flow around an oscillating cylinder. J. Fluids Struct. 2010, 26, 292–311. [Google Scholar] [CrossRef]
- Lang, Y.D.; Malacina, A.; Biegler, L.T.; Munteanu, S.; Madsen, J.I.; Zitney, S.E. Reduced order model based on principal component analysis for process simulation and optimization. Energy Fuels 2009, 23, 1695–1706. [Google Scholar] [CrossRef]
- Boukouvala, F.; Muzzio, F.J.; Ierapetritou, M.G. Predictive modeling of pharmaceutical processes with missing and noisy data. AIChE J. 2010, 56, 2860–2872. [Google Scholar] [CrossRef]
- Box, G.E.P. On the experimental attainment of optimum conditions. J. R. Stat. Soc. Ser. B 1951, 13, 1–35. [Google Scholar]
- Jia, Z.; Davis, E.; Muzzio, F.J.; Ierapetritou, M.G. Predictive modeling for pharmaceutical processes using kriging and response surface. J. Pharm. Innov. 2009, 4, 174–186. [Google Scholar] [CrossRef]
- Khuri, A.I.; Mukhopadhyay, S. Response surface methodology. WIREs Comput. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C. Response Surface Methodology Process and Product Optimization Using Designed Experiments; John Wiley & Sons, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Ranjbarian, S.; Farhadi, F. Evaluation of the effects of process parameters on granule mean size in a conical high shear granulator using response surface methodology. Powder Technol. 2013, 237, 186–190. [Google Scholar] [CrossRef]
- Metheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Calder, C.A.; Cressie, N. Kriging and Variogram Models. In International Encyclopedia of Human Geography; Kitchin, R., Thrift, N., Eds.; Elsevier Science: Oxford, UK, 2009; Volume 1, pp. 49–55. [Google Scholar]
- Krige, D.G. A Statistical Approach to Some Mine Valuations and Allied Problems at the Witwatersrand. Master Thesis, University of Witwatersrand, Johannesburg, North Africa, 1951. [Google Scholar]
- Boukouvala, F.; Muzzio, F.J.; Ierapetritou, M.G. Dynamic data-driven modeling of pharmaceutical processes. Ind. Eng. Chem. Res. 2011, 50, 6743–6754. [Google Scholar] [CrossRef]
- Boukouvala, F.; Ierapetritou, M.G. Feasibility analysis of black-box processes using adaptive sampling kriging based method. Comput. Chem. Eng. 2012, 36, 358–368. [Google Scholar] [CrossRef]
- Kleijnen, J.P.C. Kriging metamodeling in simulation: A review. Eur. J. Oper. Res. 2009, 192, 707–716. [Google Scholar] [CrossRef]
- Huang, J.; Kaul, G.; Cai, C.; Chatlapalli, R.; Hernandez-Abad, P.; Gosh, K.; Nagi, A. Quality by design case study: An integrated multivariate approach to drug product and process development. Int. J. Pharm. 2009, 382, 23–32. [Google Scholar] [CrossRef]
- Braumann, A.; Kraft, M.; Mort, P.R. Parameter estimation in a multidimensional granulation model. Powder Technol. 2010, 197, 196–210. [Google Scholar] [CrossRef]
- Li, G.Y.; Wang, S.W.; Rabitz, H. Practical approaches to construct RS-HDMR component functions. J. Phys. Chem. A 2002, 106, 8721–8733. [Google Scholar] [CrossRef]
- Li, G.Y.; Rabitz, H.; Hu, J.S.; Chen, Z.; Ju, Y.G. Regularized random-sampling high dimensional model representation (RS-HDMR). J. Math. Chem. 2008, 43, 1207–1232. [Google Scholar] [CrossRef]
- Li, G.; Rosenthal, C.; Rabitz, H. High dimensional model representations. J. Phys. Chem. A 2001, 105, 7765–7777. [Google Scholar] [CrossRef]
- Ziehn, T.; Tomlin, A.S. Global sensitivity analysis of a 3d street canyon model—Part I: The development of high dimensional model representations. Atmos. Environ. 2008, 42, 1857–1873. [Google Scholar] [CrossRef]
- Li, G.; Wang, S.-W.; Rabitz, H. High dimensional model representations (HDMR): Concepts and applications. Available online: http:// www.ima.umn.edu/talks/workshops/3-15-19.2000/li/hdmr.pdf (accessed on 10 April 2013).
- Li, G.; Rabitz, H.; Wang, S.-W.; Georgopoulos, P.G. Correlation method for variance reduction of Monte Carlo integration in RS-HDMR. J. Comput. Chem. 2003, 24, 277–283. [Google Scholar] [CrossRef]
- Li, G.; Rabitz, H. Ratio control variate method for efficiently determining high-dimensional model representations. J. Comput. Chem. 2006, 27, 1112–1118. [Google Scholar] [CrossRef]
- Banerjee, I.; Pal, S.; Maiti, S. Computationally efficient black-box modeling for feasibility analysis. Comput. Chem. Eng. 2010, 34, 1515–1521. [Google Scholar] [CrossRef]
- Banarjee, I.; Ierapetritou, M.G. Model independent parametric decision making. Ann. Oper. Res. 2004, 132, 135. [Google Scholar] [CrossRef]
- Li, G.Y.; Wang, S.W.; Rabitz, H.; Wang, S.Y.; Jaffe, P. Global uncertainty assessments by high dimensional model representations (HDMR). Chem. Eng. Sci. 2002, 57, 4445–4460. [Google Scholar] [CrossRef]
- Ziehn, T.; Tomlin, A.S. A global sensitivity study of sulfur chemistry in a premixed methane flame model using HDMR. Int. J. Chem. Kinet. 2008, 40, 742–753. [Google Scholar] [CrossRef]
- Ziehn, T.; Tomlin, A.S. GUI–HDMR—A software tool for global sensitivity analysis of complex models. Environ. Model. Softw. 2009, 24, 775–785. [Google Scholar] [CrossRef]
- Basheer, L.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Agatonovic-Kustrin, S.; Beresford, R. Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research. J. Pharm. Biomed. Anal. 2000, 22, 717–727. [Google Scholar] [CrossRef]
- De la Fuente, R.L.N.; Garcia-Munoz, S.; Biegler, L.T. An efficient nonlinear programming strategy for PCA models with incomplete data sets. J. Chemom. 2010, 24, 301–311. [Google Scholar]
- Walczak, B.; Massart, D.L. Dealing with missing data: Part I. Chemom. Intell. Lab. Syst. 2001, 58, 15–27. [Google Scholar] [CrossRef]
- Walczak, B.; Massart, D.L. Dealing with missing data: Part II. Chemom. Intell. Lab. Syst. 2001, 58, 28–42. [Google Scholar]
- Noonan, R.; Wold, H. NIPALS path modelling with latent variables. Scand. J. Educ. Res. 1977, 21, 33–61. [Google Scholar] [CrossRef]
- Boukouvala, F.; Chaudhury, A.; Sen, M.; Zhou, R.J.; Mioduszewski, L.; Ierapetritou, M.G.; Ramachandran, R. Computer-aided flowsheet simulation of a pharmaceutical tablet manufacturing process incorporating wet granulation. J. Pharm. Innov. 2013, 8, 11–27. [Google Scholar] [CrossRef]
- Sen, M.; Chaudhury, A.; Singh, R.; John, J.; Ramachandran, R. Multi-scale flowsheet simulation of an integrated continuous purification-downstream pharmaceutical manufacturing process. Int. J. Pharm. 2013, 445, 29–38. [Google Scholar] [CrossRef]
- Papavasileiou, V.; Koulouris, A.; Siletti, C.; Petrides, D. Optimize manufacturing of pharmaceutical products with process simulation and production scheduling tools. Chem. Eng. Res. Des. 2007, 85, 1086–1097. [Google Scholar] [CrossRef]
- gPROMS ModelBuilder Guide Release v3.6.; Process Systems Enterprise, Ltd.: London, UK, October; 2012.
- Model Developer Guide Release v3.6.; Process Systems Enterprise, Ltd.: London, UK, October; 2012.
- Model Validation Guide Release v3.6.; Process Systems Enterprise, Ltd.: London, UK, October; 2012.
- gPROMS Advanced User Guide Release 2.3.; Process System Enterprise, Ltd.: London, UK, February; 2004.
- Minceva, M.; Rodrigues, A.E. Two-level optimization of an existing SMB for p-xylene separation. Comput. Chem. Eng. 2005, 29, 2215–2228. [Google Scholar] [CrossRef]
- Asteasuain, M.; Brandolin, A. Modeling and optimization of a high-pressure ethylene polymerization reactor using gPROMS. Comput. Chem. Eng. 2008, 32, 396–408. [Google Scholar] [CrossRef]
- Nowee, S.M.; Abbas, A.; Romagnoli, J.A. Optimization in seeded cooling crystallization: A parameter estimation and dynamic optimization study. Chem. Eng. Process. 2007, 46, 1096–1106. [Google Scholar] [CrossRef]
- Nowee, S.M.; Abbas, A.; Romagnoli, J.A. Antisolvent crystallization: Model identification, experimental validation and dynamic simulation. Chem. Eng. Sci. 2008, 63, 5457–5467. [Google Scholar] [CrossRef]
- Bermingham, S.K.; Verheijen, P.J.T.; Kramer, H.J.M. Optimal design of solution crystallization processes with rigorous models. Chem. Eng. Res. Des. 2003, 81, 894–903. [Google Scholar]
- Beck, R. Aspen Plus v8.0 Solids Modeling: A Brief Introduction; Aspen Technology, Inc.: Burlington, MA, USA, 2012. [Google Scholar]
- Levine, J. Jump Start: Solids Process Modeling in Aspen Plus® v8; Aspen Technology, Inc.: Burlington, MA, USA, 2012. [Google Scholar]
- Chemical engineering: Software. Available online: https://uwaterloo.ca/chemical-engineering/resources-services/computing-facilities/software#AspenCustomModeler (accessed on 5 January 2013).
- Aspen Plus, Getting Started Modeling Processes with Solids; Version v7.1; Aspen Technology, Inc.: Burlington, MA, USA, 2009.
- Wei, H.-Y. Computer-aided design and scale-up of crystallization processes: Integrating approaches and case studies. Chem. Eng. Res. Des. 2010, 88, 1377–1380. [Google Scholar] [CrossRef]
- Lau, S.-Y.; Gonawan, F.N.; Bhatia, S.; Kamaruddin, A.H.; Uzir, M.H. Conceptual design and simulation of a plant for the production of high purity (S)-ibuprofen acid using innovative enzymatic membrane technology. Chem. Eng. J. 2011, 166, 726–737. [Google Scholar] [CrossRef]
- Brown, R.L. Minimum energy theorem for flow of dry granular materials through apertures. Nature 1961, 191, 458–461. [Google Scholar] [CrossRef]
- Savage, S.B. The mass flow of granular materials derived from coupled velocity-stress fields. Br. J. Appl. Phys. 1965, 16, 1885–1888. [Google Scholar] [CrossRef]
- Savage, S.B.; Sayed, M.S. Gravity flow of coarse cohesionless granular materials in conical hoppers. J. Appl. Math. Phys. 1981, 2, 125–143. [Google Scholar]
- Brennen, C.; Pearce, J.C. Granular material flow in two dimensional hoppers. J. Appl. Mech. 1978, 45, 43–50. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Brennen, C.; Sabersky, R.H. Gravity flow of granular materials in conical hoppers. J. Appl. Mech. 1979, 46, 529–535. [Google Scholar] [CrossRef]
- Sun, J.; Sundaresan, S. A constitutive model with microstructure evolution for flow of rate-independent granular materials. J. Fluid Mech. 2011, 682, 590–616. [Google Scholar] [CrossRef]
- Weir, G.J. Sound speed and attenuation in dense, non-cohesive air-granulator systems. Chem. Eng. Sci. 2001, 56, 3699–3717. [Google Scholar] [CrossRef]
- Sun, J.; Sundaresan, S. Radial hopper flow prediction using a constitutive model with microstructure evolution. Powder Technol. 2013, 242, 81–85. [Google Scholar] [CrossRef]
- Danckwerts, P.V. Continuous flow systems: Distribution of residence times. Chem. Eng. Sci. 1953, 2, 1–13. [Google Scholar] [CrossRef]
- Gao, Y.; Ierapetritou, M.; Muzzio, F. Periodic section modeling of convective continuous powder mixing processes. AIChE J. 2012, 58, 69–78. [Google Scholar] [CrossRef]
- Bouffard, J.; Bertrand, F.; Chaouki, J. A multiscale model for the simulation of granulation in rotor-based equipment. Chem. Eng. Sci. 2012, 81, 106–117. [Google Scholar] [CrossRef]
- Cameron, I.T.; Wang, F.Y.; Immanuel, C.D.; Stepanek, F. Process systems modelling and applications in granulation: A review. Chem. Eng. Sci. 2005, 80, 3723–3750. [Google Scholar]
- Hounslow, M.J.; Pearson, J.M.K.; Instone, T. Tracer studies of high-shear granulation: II. Population balance modeling. AIChE J. 2001, 47, 1984–1999. [Google Scholar] [CrossRef]
- Biggs, C.A.; Sanders, C.; Scott, A.C.; Willemse, A.W.; Hoffman, A.C.; Instone, T.; Salman, A.D.; Hounslow, M.J. Coupling granule properties and granulation rates in high-shear granulation. Powder Technol. 2003, 130, 162–168. [Google Scholar] [CrossRef]
- Liu, L.X.; Litster, J.D. Population balance modelling of granulation with a physically based coalescence kernel. Chem. Eng. Sci. 2002, 57, 2183–2191. [Google Scholar] [CrossRef]
- Gannt, J.A.; Cameron, I.T.; Litster, J.D.; Gatzke, E.P. Determination of coalescence kernels for high-shear granulation using DEM simulations. Powder Technol. 2006, 170, 53–63. [Google Scholar] [CrossRef]
- Poon, J.M.-H.; Immanuel, C.D.; Doyle, F.J.I.; Litster, J.D. A three-dimensional population balance model of granulation with a mechanistic representation of the nucleation and aggregation phenomena. Chem. Eng. Sci. 2008, 63, 1315–1329. [Google Scholar] [CrossRef]
- Liu, L.X.; Litster, J.D.; Iveson, S.M.; Ennis, B.J. Coalescence of deformable granules in wet granulation processes. AIChE J. 2000, 46, 529–539. [Google Scholar] [CrossRef]
- Marshall, C.L.J.; Rajniak, P.; Matsoukas, T. Multi-component population balance modeling of granulation with continuous addition of binder. Powder Technol. 2013, 235, 211–220. [Google Scholar] [CrossRef]
- Matsoukas, T.; Kim, T.; Lee, K. Bicomponent aggregation with composition-dependent rates and the approach to well-mixed state. Chem. Eng. Sci. 2009, 64, 787–799. [Google Scholar] [CrossRef]
- Sahni, E.K.; Chaudhuri, B. Contact drying: A review of experimental and mechanistic modeling approaches. Int. J. Pharm. 2012, 434, 334–348. [Google Scholar] [CrossRef]
- Mortier, S.T.F.C.; de Beer, T.; Gernaey, K.V.; Remon, J.P.; Vervaet, C.; Nopens, I. Mechanistic modelling of fluidized bed drying processes of wet porous granules: A review. Eur. J. Pharm. Biopharm. 2011, 79, 205–225. [Google Scholar] [CrossRef]
- Mortier, S.T.F.C.; van Daele, T.; Gernaey, K.V.; de Beer, T.; Nopens, I. Reduction of a single granule drying model: An essential step in preparation of a population balance model with a continuous growth term. AIChE J. 2013, 59, 1127–1138. [Google Scholar] [CrossRef]
- Johanson, J.R. A rolling theory for granular solids. J. Appl. Mech. 1965, 32, 842–848. [Google Scholar] [CrossRef]
- Hsu, S.H.; Reklaitis, G.V.; Venkatasubramanian, V. Modeling and control of roller compaction for pharmaceutical manufacturing. Part I: Process dynamics and control framework. J. Pharm. Innov. 2010, 5, 14–23. [Google Scholar] [CrossRef]
- Marshall, E.A. A theory for the compaction of incompressible granular materials by rolling. IMA J. Appl. Math. 1973, 12, 21–36. [Google Scholar] [CrossRef]
- Muliadi, A.R.; Litster, J.D.; Wassgren, J.R. Modeling the powder roll compaction process: Comparison of 2-D finite element method and the rolling theory for granular solids (Johanson’s model). Powder Technol. 2012, 221, 90–100. [Google Scholar] [CrossRef]
- Bilgili, L.; Capece, M. Quantitative analysis of multi-particle interactions during particle breakage: A discrete non-linear population balance framework. Powder Technol. 2011, 213, 162–173. [Google Scholar] [CrossRef]
- Verkoeijen, D.; Pouw, G.A.; Meesters, M.H.; Scarlett, B. Population balances for particulate processes—A volume approach. Chem. Eng. Sci. 2002, 57, 2287–2303. [Google Scholar] [CrossRef]
- Bilgili, E.; Scarlett, B. Population balance modeling of non-linear effects in milling processes. Powder Technol. 2005, 153, 59–71. [Google Scholar] [CrossRef]
- Tsoy, E.N. A modelling approach for derivation of the breakage functions. Chem. Eng. Sci. 2012, 80, 361–364. [Google Scholar] [CrossRef]
- Bilgili, E.; Yepes, J.; Scarlett, B. Formulation of a non-linear framework for population balance modeling of batch grinding: Beyond first-order kinetics. Chem. Eng. Sci. 2006, 61, 33–44. [Google Scholar] [CrossRef]
- Heckel, R.W. An analysis of powder compaction phenomena. Trans. Metall. Soc. AIME 1961, 221, 1001–1008. [Google Scholar]
- Heckel, R.W. Density pressure relationships in powder compaction. Trans. Metall. Soc. AIME 1961, 221, 671–675. [Google Scholar]
- Kawakita, K.; Ludde, K.H. Some considerations on powder compression equations. Powder Technol. 1971, 4, 61–68. [Google Scholar] [CrossRef]
- Kawakita, K.; Hattori, I.; Kishigami, M. Characteristic constants in kawakita’s powder compression equation. J. Powder Bulk Solids Technol. 1977, 1, 3–8. [Google Scholar]
- Kuentz, M.; Leuenberger, H. Pressure susceptibility of polymer tablets as a critical property: A modified Heckel equation. J. Pharm. Sci. 1999, 88, 174–179. [Google Scholar] [CrossRef]
- Singh, R.; Gernaey, K.V.; Gani, R. Icas-pat: A software for design, analysis and validation of PAT systems. Comput. Chem. Eng. 2010, 34, 1108–1136. [Google Scholar] [CrossRef]
- Frenning, G.; Nordström, J.; Alderborn, G. Effective Kawakita parameters for binary mixtures. Powder Technol. 2009, 189, 270–275. [Google Scholar] [CrossRef]
- Mazel, V.; Busignies, V.; Duca, S.; Leclerc, B.; Tchoreloff, P. Original predictive approach to the compressibility of pharmaceutical powder mixtures based on the Kawakita equation. Int. J. Pharm. 2011, 410, 92–98. [Google Scholar] [CrossRef]
- Robinson, S.; Brooks, R.J. Independent verification and validation of an industrial simulation model. Simulation 2010, 86, 405–416. [Google Scholar] [CrossRef]
- Davies, P.K. Generalizing Concepts and Methods of Verification, Validation and Accreditation (VV&A) for Military Simulation; RAND: Santa Monica, CA, USA, 1992. [Google Scholar]
- Sargent, R.G. Verification and Validation of Simulation Models. In Proceedings of the 2010 Winter Simulation Conference, Baltimore, MD, USA, 5–8 December 2010. [Green Version]
- Kremer, D.M.; Hancock, B.C. Process simulation in the pharmaceutical industry: A review of some basic physical models. J. Pharm. Sci. 2006, 95, 517–529. [Google Scholar] [CrossRef]
- Balci, O. Golden rules of verification, validation, testing, and certification of modeling and simulation applications. SCS M&S Mag. 2010. No. 4. [Google Scholar]
- Saltelli, A.; Chan, K.; Scott, E.M. Sensivivity Analysis; John Wiley & Sons Ltd.: Chichester, UK, 2000. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Campolongo, F. Sensitivity analysis as an ingredient of modeling. Stat. Sci. 2000, 15, 377–395. [Google Scholar] [CrossRef]
- Sin, G.; Gernaey, K.V.; Eliasson Lantz, A. Good modelling practice (gmop) for pat applications: Propagation of input uncertainty and sensitivity analysis. Biotechnol. Prog. 2009, 25, 1043–1053. [Google Scholar] [CrossRef]
- Ling, Y.; Mahadevan, S. Quantitative model validation techniques: New insights. Reliab. Eng. Syst. Saf. 2013, 111, 217–231. [Google Scholar] [CrossRef]
- Rodgers, J.L.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 41, 59–66. [Google Scholar]
- Min, F.Y.; Yang, M.; Wang, Z.C. Knowledge-based method for the validation of complex simulation models. Simul. Model. Pract. Theory 2010, 18, 500–515. [Google Scholar] [CrossRef]
- Tedeschi, L.O. Assessment of the adequacy of mathematical models. Agric. Syst. 2006, 9, 225–247. [Google Scholar] [CrossRef]
- Browne, M.W. Cross-validation methods. J. Math. Psychol. 2000, 44, 108–132. [Google Scholar] [CrossRef]
- Efron, B.; Gong, G. A leisurely look at the bootstrap, the jackknife and cross-validation. Am. Stat. 1983, 37, 36–48. [Google Scholar]
- Efron, B. Estimating the error rate of a prediction rule: Improvement on cross-validation. J. Am. Stat. Assoc. 1983, 78, 316–331. [Google Scholar] [CrossRef]
- Tomba, E.; de Martin, M.; Facco, P.; Robertson, J.; Zomer, S.; Bezzo, F.; Barolo, M. General procedure to aid the development of continuous pharmaceutical processes using multivariate statistical modeling—An industrial case study. Int. J. Pharm. 2013, 444, 25–39. [Google Scholar] [CrossRef]
- Hassani, S.; Martens, H.; Qannari, E.M.; Hanafi, M.; Kohler, A. Model validation and error estimation in multi-block partial least squares regression. Chemom. Intell. Lab. Syst. 2012, 117, 42–53. [Google Scholar] [CrossRef]
- Steyerberg, E.W.; Harrell, F.E.J.; Borsboom, G.J.J.M.; Eijkemans, M.J.C.R.; Vergouwe, Y.; Habbema, J.D.F. Internal validation of predictive models: Efficiency of some procedures for logistic regression analysis. J. Clin. Epidemiol. 2001, 54, 775–781. [Google Scholar]
- Gong, G. Cross-validation, the jackknife, and the bootstrap: Excess error estimation in forward logistic regression. J. Am. Stat. Assoc. 1986, 81, 108–113. [Google Scholar] [CrossRef]
- Ji, G.; Zhang, K.; Zhu, Y. A method of MPC model error detection. J. Process Control 2012, 22, 635–642. [Google Scholar] [CrossRef]
- Zhu, Y.; Patwardan, R.; Wagner, S.B.; Zhao, J. Toward a low cost and high performance MPC: The role of system identification. Comput. Chem. Eng. 2013, 51, 124–135. [Google Scholar] [CrossRef]
- Robinson, A.P.; Froese, R.E. Model validation using equivalence tests. Ecol. Model. 2004, 176, 349–358. [Google Scholar] [CrossRef]
- Rebba, R.; Mahadevan, S. Validation of models with multivariate output. Reliab. Eng. Syst. Saf. 2006, 91, 861–871. [Google Scholar] [CrossRef]
- Capece, M.; Bilgile, E.; Dave, R. Identification of the breakage rate and distribution parameters in a non-linear population balance model for batch milling. Powder Technol. 2011, 208, 195–204. [Google Scholar] [CrossRef]
- Vanarase, A.U.; Jarvinen, M.; Passo, J.; Muzzio, F.J. Development of a methodology to estimate error in the on-line measurements of blend uniformity in a continuous powder mixing process. Powder Technol. 2013, 241, 263–271. [Google Scholar] [CrossRef]
- Babamoradi, H.; van den berg, F.; Rinnan, A. Bootstrap based confidence limits in principal component analysis—A case study. Chemom. Intell. Lab. Syst. 2013, 120, 97–105. [Google Scholar] [CrossRef]
- Afanador, N.L.; Tran, T.N.; Buydens, L.M.C. Use of the bootstrap and permutation methods for a more robust variable importance in the projection metric for partial least squares regression. Anal. Chim. Acta 2013, 768, 49–56. [Google Scholar] [CrossRef]
- Ng, K.M. Design and development of solids processes—A process systems engineering perspective. Powder Technol. 2002, 126, 205–210. [Google Scholar] [CrossRef]
- Kimber, J.A.; Kazarian, S.G.; Štěpánek, F. Microstructure-based mathematical modelling and spectroscopic imaging of tablet dissolution. Comput. Chem. Eng. 2011, 35, 1326–1339. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rogers, A.J.; Hashemi, A.; Ierapetritou, M.G. Modeling of Particulate Processes for the Continuous Manufacture of Solid-Based Pharmaceutical Dosage Forms. Processes 2013, 1, 67-127. https://doi.org/10.3390/pr1020067
Rogers AJ, Hashemi A, Ierapetritou MG. Modeling of Particulate Processes for the Continuous Manufacture of Solid-Based Pharmaceutical Dosage Forms. Processes. 2013; 1(2):67-127. https://doi.org/10.3390/pr1020067
Chicago/Turabian StyleRogers, Amanda J., Amir Hashemi, and Marianthi G. Ierapetritou. 2013. "Modeling of Particulate Processes for the Continuous Manufacture of Solid-Based Pharmaceutical Dosage Forms" Processes 1, no. 2: 67-127. https://doi.org/10.3390/pr1020067
APA StyleRogers, A. J., Hashemi, A., & Ierapetritou, M. G. (2013). Modeling of Particulate Processes for the Continuous Manufacture of Solid-Based Pharmaceutical Dosage Forms. Processes, 1(2), 67-127. https://doi.org/10.3390/pr1020067