Hyperparameter Tuning for Machine Learning Algorithms Used for Arabic Sentiment Analysis
Abstract
:1. Introduction
- The paper reviews common hyperparameter tuning techniques, their benefits, and their drawbacks.
- A comprehensive comparative analysis among five hyperparameter tuning algorithms is given, as most of the previous and current literature typically focuses only on Grid Search and Random Search.
- Hyperparameter tuning for six machine learning models is performed to analyze sentiments over an Arabic text.
- The Arabic language is a challenging language; this paper is considered the first hyperparameter tuning study performed on an Arabic text.
2. Related Work
2.1. Hyperparameter Tunning
2.2. Sentiment Analysis
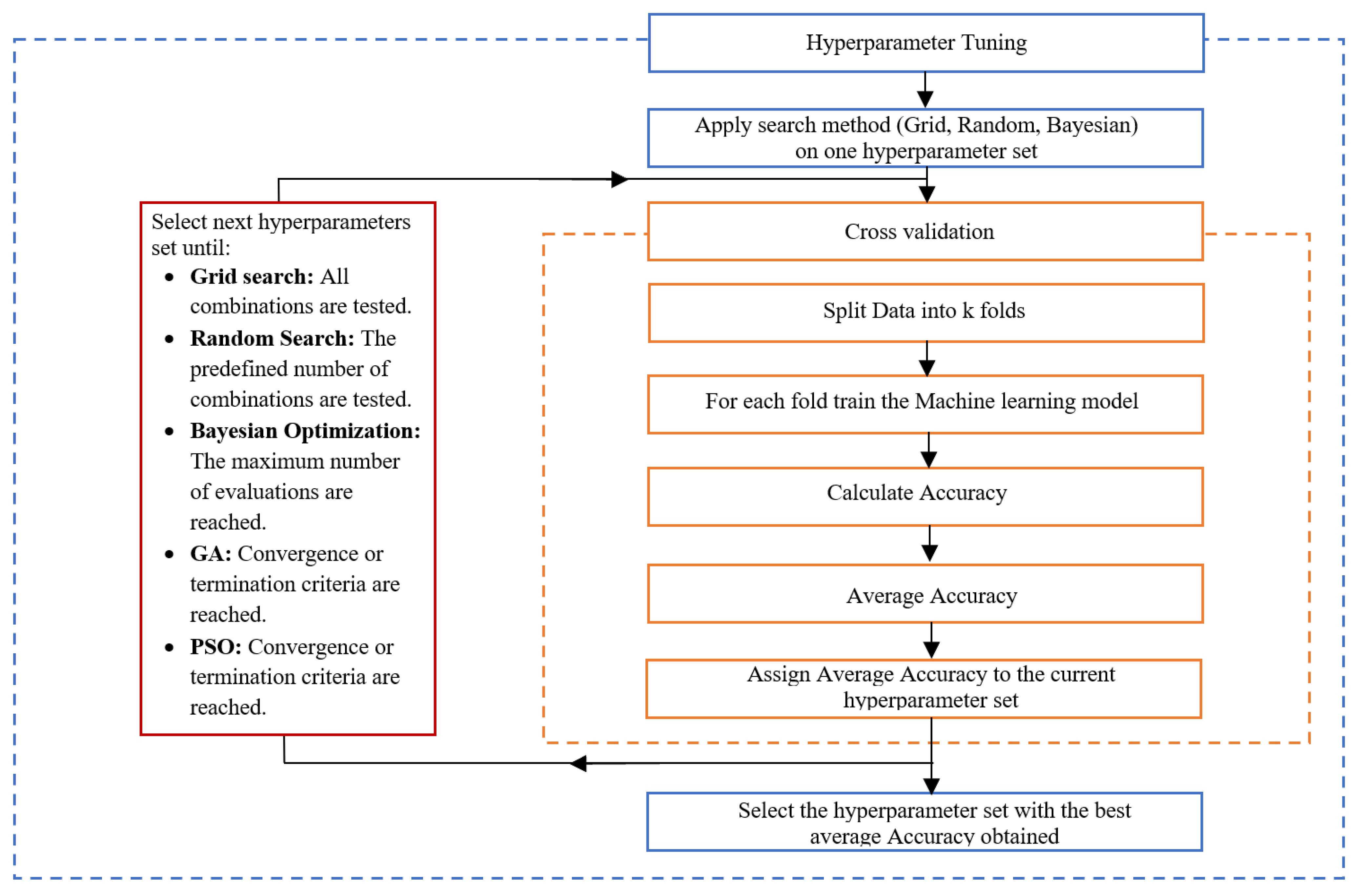
3. Hyperparameter Tuning
3.1. Grid Search
3.2. Random Search
3.3. Bayesian Optimization
3.4. Genetic Algorithm
3.5. Particle Swarm Optimization
4. Proposed Architecture for Arabic Sentiment Analysis
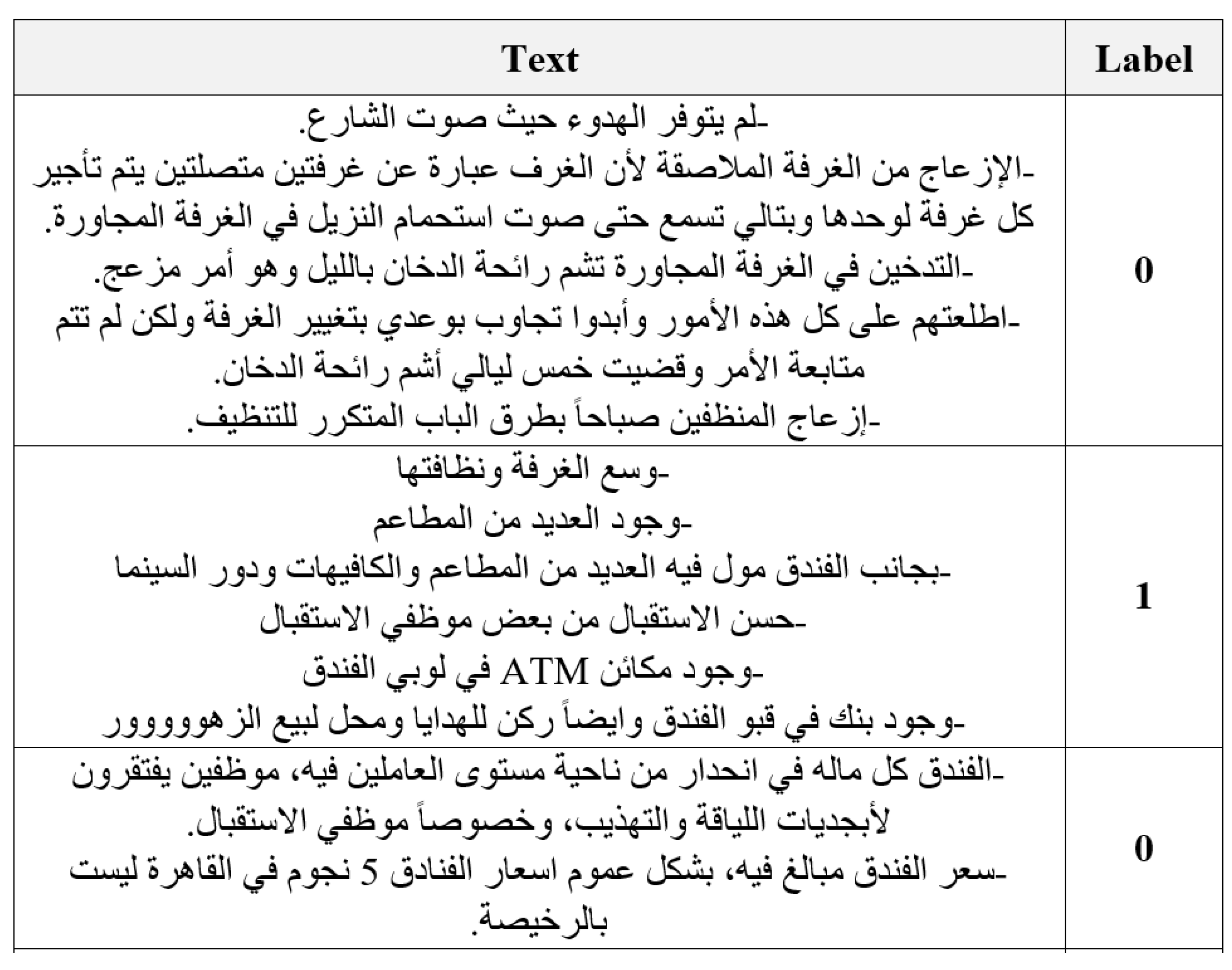
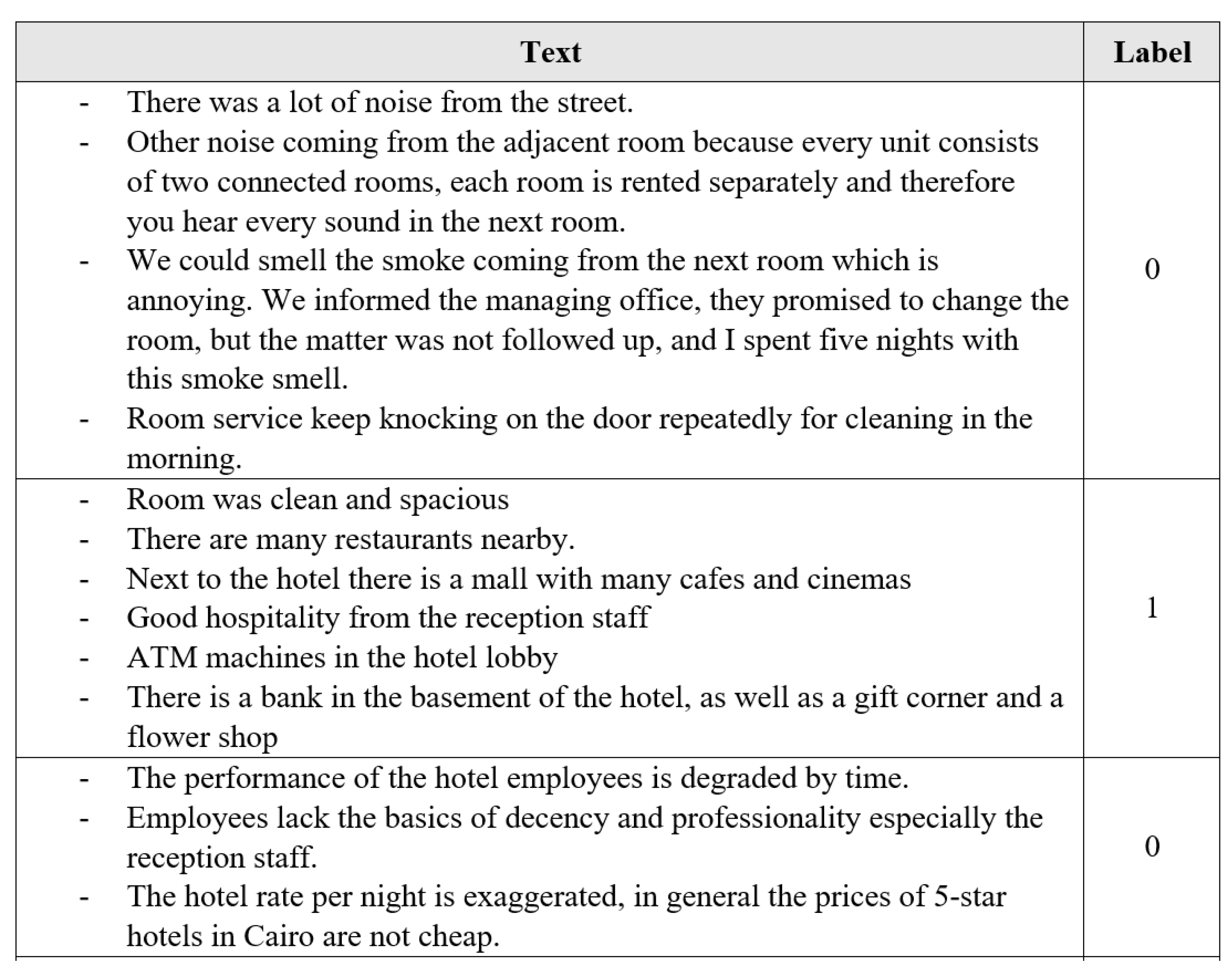
4.1. Data Collection
4.2. Cleaning and Annotation
4.3. Preprocessing
- Normalization: Normalization converts all possible conjugations of a specific word to its standard form. Our normalizer has been fed with a predefined set of rules to provide a standardized form of the collected Arabic reviews. For example, the normalizer removes unnecessary characters such as punctuation, numbers, non-Arabic characters, and special characters. It also removes repeated letters, usually used to express certain impressions, such as exaggeration or affirmation, and replaces this repetition with a single occurrence of the character.
- Stop Word Removal: Stop words are frequently used words that appear in a text but are not semantically related to the context in which they exist. These words can be removed from the text without affecting the classification task’s performance.
- Stemming: Stemming is the process of returning a word to its stem. Stemming trims words by reducing all forms of the word (i.e., adjectives, adverbs, etc.) to its origin base. Many Arabic words have the same stem. Hence, all such words are replaced with one word. This technique has a large impact on improving the efficiency of text categorization.
4.4. Feature Extraction
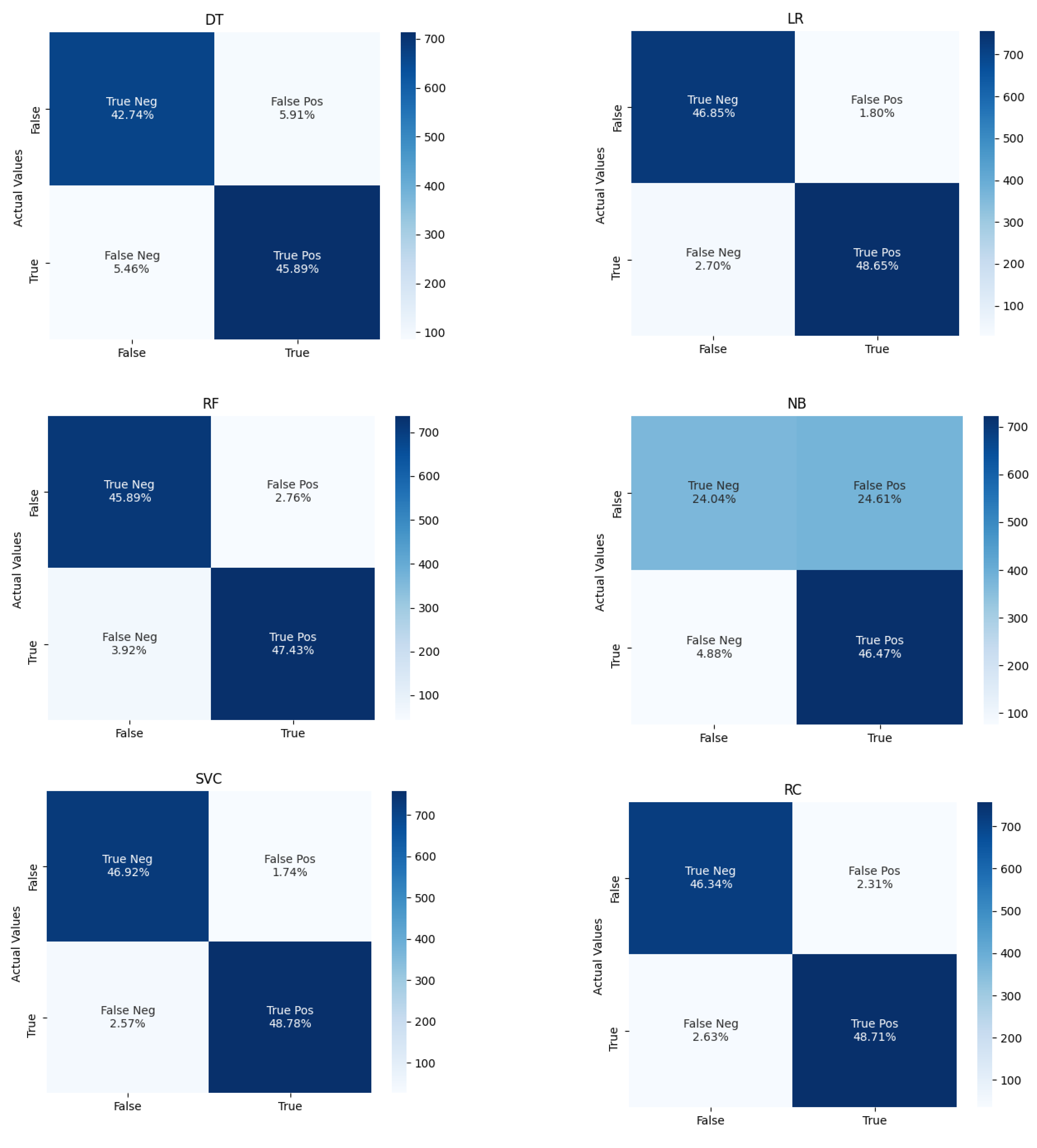
4.5. Training and Testing Classifiers
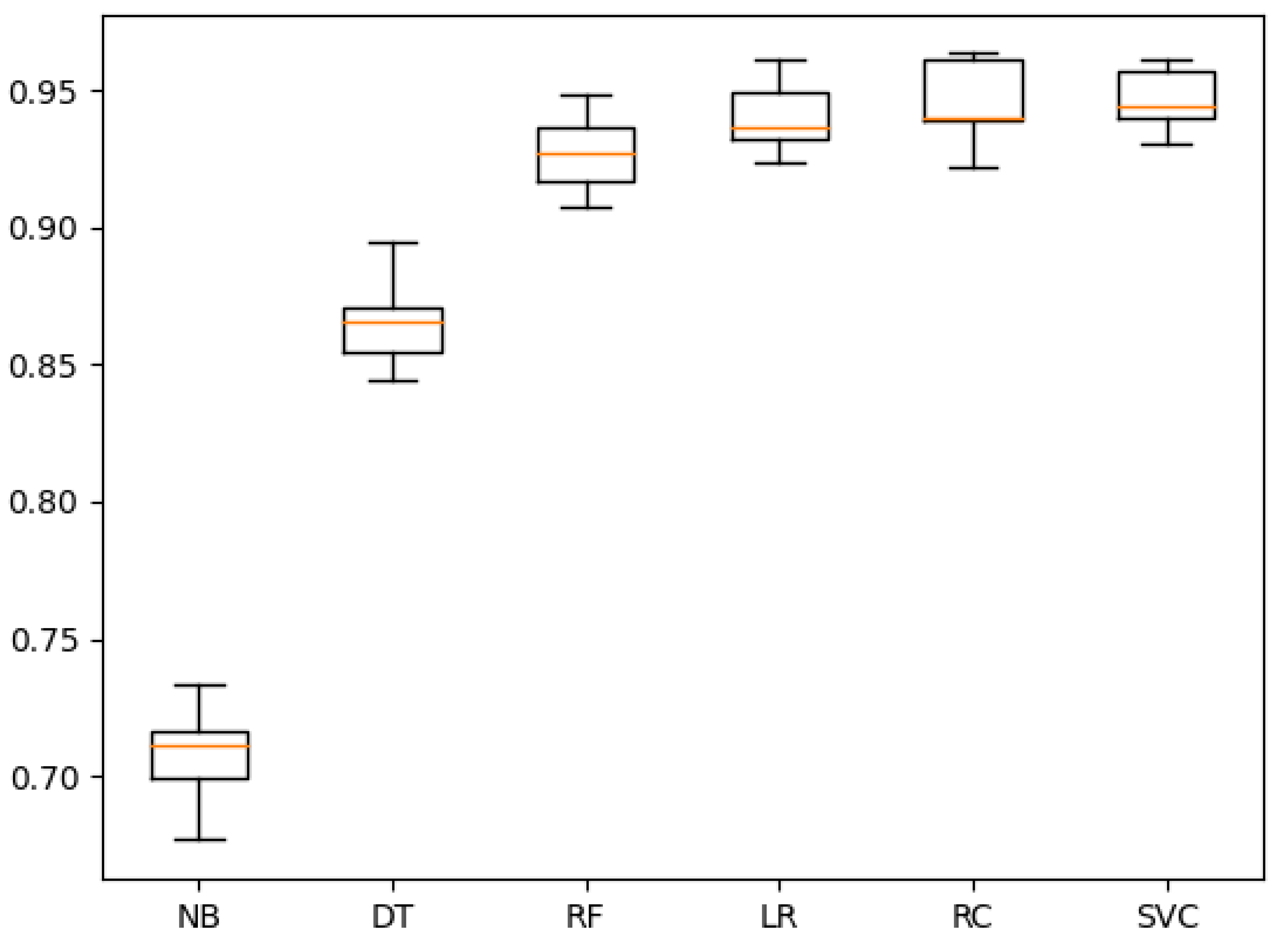
5. Experimental Results
5.1. Using Default Hyperparameters
5.2. Using Hyperparameter Tuning Techniques
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Buccafurri, F.; Lax, G.; Nicolazzo, S.; Nocera, A. Comparing Twitter and Facebook User Behavior. Comput. Hum. Behav. 2015, 52, 87–95. [Google Scholar] [CrossRef]
- Madhyastha, H.V.; Radwan, A.A.; Omara, F.; Mahmoud, T.M.; Elgeldawi, E. Pinterest Attraction between Users and Spammers. Int. J. Comput. Sci. Eng. Inf. Technol. Res. 2014, 4, 63–72. [Google Scholar]
- Elgeldawi, E.; Radwan, A.A.; Omara, F.; Mahmoud, T.M.; Madhyastha, H.V. Detection and Characterization of Fake Accounts on the Pinterest Social Networks. Int. J. Comput. Netw. Wirel. Mob. Commun. 2014, 4, 21–28. [Google Scholar]
- Bacanli, S.; Cimen, F.; Elgeldawi, E.; Turgut, D. Placement of Package Delivery Center for UAVs with Machine Learning. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021. [Google Scholar]
- de la Torre, R.; Corlu, C.G.; Faulin, J.; Onggo, B.S.; Juan, A.A. Simulation, Optimization, and Machine Learning in Sustainable Transportation Systems: Models and Applications. Sustainability 2021, 13, 1551. [Google Scholar] [CrossRef]
- Sayed, A.A.; Elgeldawi, E.; Zaki, A.M.; Galal, A.R. Sentiment Analysis for Arabic Reviews using Machine Learning Classification Algorithms. In Proceedings of the 2020 International Conference on Innovative Trends in Communication and Computer Engineering (ITCE), Aswan, Egypt, 8–9 February 2020; pp. 56–63. [Google Scholar]
- Sayed, A.; Abdallah, M.M.; Zaki, A.; Ahmed, A.A. Big Data analysis using a metaheuristic algorithm: Twitter as Case Study. In Proceedings of the 2020 International Conference on Innovative Trends in Communication and Computer Engineering (ITCE), Aswan, Egypt, 8–9 February 2020; pp. 20–26. [Google Scholar]
- Girgis, M.R.; Elgeldawi, E.; Gamal, R.M. A Comparative Study of Various Deep Learning Architectures for 8-state Protein Secondary Structures Prediction. In Proceedings of the International Conference on Advanced Intelligent Systems and Informatics 2020; Springer International Publishing: Cairo, Egypt, 2021; pp. 501–513. [Google Scholar]
- Shekar, B.H.; Dagnew, G. Grid Search-Based Hyperparameter Tuning and Classification of Microarray Cancer Data. In Proceedings of the 2019 Second International Conference on Advanced Computational and Communication Paradigms (ICACCP), Gangtok, India, 25–28 February 2019; pp. 1–8. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Liashchynskyi, P.; Liashchynskyi, P. Grid Search, Random Search, Genetic Algorithm: A Big Comparison for NAS. arXiv 2019, arXiv:abs/1912.06059. [Google Scholar]
- Villalobos-Arias, L.; Quesada-López, C.; Guevara-Coto, J.; Martínez, A.; Jenkins, M. Evaluating Hyper-Parameter Tuning Using Random Search in Support Vector Machines for Software Effort Estimation. In Proceedings of the PROMISE’20: 16th International Conference on Predictive Models and Data Analytics in Software Engineering, Virtual Event, Association for Computing Machinery, New York, NY, USA, 8–9 November 2020; pp. 31–40. [Google Scholar]
- Andonie, R.; Florea, A.C. Weighted Random Search for CNN Hyperparameter Optimization. Int. J. Comput. Commun. Control 2020, 15. [Google Scholar] [CrossRef] [Green Version]
- Probst, P.; Boulesteix, A.; Bischl, B. Tunability: Importance of Hyperparameters of Machine Learning Algorithms. J. Mach. Learn. Res. 2019, 20, 53:1–53:32. [Google Scholar]
- Syarif, I.; Prugel-Bennett, A.; Wills, G. SVM parameter optimization using grid search and genetic algorithm to improve classification performance. Telecommun. Comput. Electron. Control 2016, 14, 1502. [Google Scholar] [CrossRef]
- Wicaksono, A.S.; Supianto, A.F. Hyper Parameter Optimization using Genetic Algorithm on Machine Learning Methods for Online News Popularity Prediction. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 263–267. [Google Scholar] [CrossRef]
- Martínez-Cámara, E.; Barroso, N.R.; Moya, A.R.; Fernández, J.A.; Romero, E.; Herrera, F. Deep Learning Hyper-parameter Tuning for Sentiment Analysis in Twitter based on Evolutionary Algorithms. In Proceedings of the 2019 Federated Conference on Computer Science and Information Systems (FedCSIS), Leipzig, Germany, 1–4 September 2019; pp. 255–264. [Google Scholar]
- Alayba, A.M.; Palade, V.; England, M.; Iqbal, R. Improving Sentiment Analysis in Arabic Using Word Representation. In Proceedings of the 2018 IEEE 2nd International Workshop on Arabic and Derived Script Analysis and Recognition (ASAR), London, UK, 12–14 March 2018; pp. 13–18. [Google Scholar]
- Al-Twairesh, N.; Al-Negheimish, H. Surface and Deep Features Ensemble for Sentiment Analysis of Arabic Tweets. IEEE Access 2019, 7, 84122–84131. [Google Scholar] [CrossRef]
- Duwairi, R.; Qarqaz, I. Arabic Sentiment Analysis Using Supervised Classification. In Proceedings of the 2014 International Conference on Future Internet of Things and Cloud, Barcelona, Spain, 27–29 August 2014; pp. 579–583. [Google Scholar]
- Duwairi, R.; El-Orfali, M. A study of the effects of preprocessing strategies on sentiment analysis for Arabic text. J. Inf. Sci. 2014, 40, 501–513. [Google Scholar] [CrossRef] [Green Version]
- Štrimaitis, R.; Stefanovič, P.; Ramanauskaitė, S.; Slotkienė, A. Financial Context News Sentiment Analysis for the Lithuanian Language. Appl. Sci. 2021, 11, 4443. [Google Scholar] [CrossRef]
- Siji George, C.G.; Sumathi, B. Genetic Algorithm Based Hybrid Model Of Convolutional Neural Network And Random Forest Classifier For Sentiment Classification. Turk. J. Comput. Math. Educ. 2021, 12, 3216–3223. [Google Scholar]
- Pouransari, H.; Ghili, S. Deep learning for sentiment analysis of movie reviews. CS224N Proj. 2014, 1–8. [Google Scholar]
- Boudad, N.; Faizi, R.; Oulad Haj Thami, R.; Chiheb, R. Sentiment analysis in Arabic: A review of the literature. Ain Shams Eng. J. 2018, 9, 2479–2490. [Google Scholar] [CrossRef]
- Rahab, H.; Zitouni, A.; Djoudi, M. SIAAC: Sentiment Polarity Identification on Arabic Algerian Newspaper Comments. In Proceedings of the Computational Methods in Systems and Software Applied Computational (CoMeSySo 2017); Springer: Cham, Switzerland, 2017; pp. 139–149. [Google Scholar]
- Lorenzo, P.R.; Nalepa, J.; Kawulok, M.; Ramos, L.; Ranilla, J. Particle swarm optimization for hyper-parameter selection in deep neural networks. In Proceedings of the Genetic and Evolutionary Computation Conference, Berlin, Germany, 15–19 July 2017. [Google Scholar]
- Witt, C. Worst-Case and Average-Case Approximations by Simple Randomized Search Heuristics; Springer: Berlin/Heidelberg, Germany, 2005; pp. 44–56. [Google Scholar]
- Nguyen, V. Bayesian Optimization for Accelerating Hyper-Parameter Tuning. In Proceedings of the 2019 IEEE Second International Conference on Artificial Intelligence and Knowledge Engineering (AIKE), Sardinia, Italy, 3–5 June 2019; pp. 302–305. [Google Scholar]
- Hensman, J.; Fusi, N.; Lawrence, N. Gaussian processes for big data. In Proceedings of the 29th Conference on Uncertainty in Artificial Intelligence, Bellevue, WA, USA, 11–13 July 2013; pp. 282–290. [Google Scholar]
- Man, K.; Tang, K.; Kwong, S. Genetic algorithms: Concepts and applications [in engineering design]. IEEE Trans. Ind. Electron. 1996, 43, 519–534. [Google Scholar] [CrossRef]
- Friedrich, T.; Kötzing, T.; Krejca, M.S.; Sutton, A.M. The Compact Genetic Algorithm is Efficient Under Extreme Gaussian Noise. IEEE Trans. Evol. Comput. 2017, 21, 477–490. [Google Scholar] [CrossRef]
- Itano, F.; de Abreu de Sousa, M.A.; Del-Moral-Hernandez, E. Extending MLP ANN hyper-parameters Optimization by using Genetic Algorithm. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Srinivas, M.; Patnaik, L. Adaptive probabilities of crossover and mutation in genetic algorithms. IEEE Trans. Syst. Man Cybern. 1994, 24, 656–667. [Google Scholar] [CrossRef] [Green Version]
- Smullen, D.; Gillett, J.; Heron, J.; Rahnamayan, S. Genetic algorithm with self-adaptive mutation controlled by chromosome similarity. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 504–511. [Google Scholar]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Lobo, F.; Goldberg, D.; Pelikan, M. Time Complexity of genetic algorithms on exponentially scaled problems. In Proceedings of the GECCO Genetic and Evolutionary Computation Conference, Las Vegas, NV, USA, 10–12 July 2000. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Parameter selection in particle swarm optimization. In Evolutionary Programming VII; Porto, V.W., Saravanan, N., Waagen, D., Eiben, A.E., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 591–600. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Chuan, L.; Quanyuan, F. The Standard Particle Swarm Optimization Algorithm Convergence Analysis and Parameter Selection. In Proceedings of the Third International Conference on Natural Computation (ICNC 2007), Haikou, China, 24–27 August 2007; Volume 3, pp. 823–826. [Google Scholar]
- Xiaojing, Y.; Qingju, J.; Xinke, L. Center Particle Swarm Optimization Algorithm. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019; pp. 2084–2087. [Google Scholar]
- Yan, X.H.; He, F.Z.; Chen, Y.L. A Novel Hardware/Software Partitioning Method Based on Position Disturbed Particle Swarm Optimization with Invasive Weed Optimization. J. Comput. Sci. Technol. 2017, 32, 340–355. [Google Scholar] [CrossRef]
- Rauf, H.T.; Shoaib, U.; Lali, M.I.; Alhaisoni, M.; Irfan, M.N.; Khan, M.A. Particle Swarm Optimization With Probability Sequence for Global Optimization. IEEE Access 2020, 8, 110535–110549. [Google Scholar] [CrossRef]
- RASC. Reviews Sentiment Analysis Corpus (RSAC). 2019. Available online: https://github.com/asooft/Sentiment-Analysis-Hotel-Reviews-Dataset (accessed on 7 October 2021).
- Dreiseitl, S.; Ohno-Machado, L. Logistic regression and artificial neural network classification models: A methodology review. J. Biomed. Inform. 2002, 35, 352–359. [Google Scholar] [CrossRef] [Green Version]
- Raschka, S. Model Evaluation, Model Selection, and Algorithm Selection in Machine Learning. arXiv 2018, arXiv:abs/1811.12808. [Google Scholar]
- Han, K.X.; Chien, W.; Chiu, C.C.; Cheng, Y.T. Application of Support Vector Machine (SVM) in the Sentiment Analysis of Twitter DataSet. Appl. Sci. 2020, 10, 1125. [Google Scholar] [CrossRef] [Green Version]
- Gonçalves, P.; Araújo, M.; Benevenuto, F.; Cha, M. Comparing and combining sentiment analysis methods. arXiv 2013, arXiv:abs/1406.0032. [Google Scholar]
- Scikit Learn. Machine Learning in Python. 2020. Available online: https://scikit-learn.org/ (accessed on 7 October 2021).







| HP Approach | Complexity | Enable Parallelization | Easy Initialization |
|---|---|---|---|
| Grid | - | 🗸 | |
| Random | 🗸 | 🗸 | |
| Bayesian | - | 🗸 | |
| PSO | 🗸 | - | |
| GA | - | 🗸 |
| HP Approach | Accuracy | Best Hyperparameters |
|---|---|---|
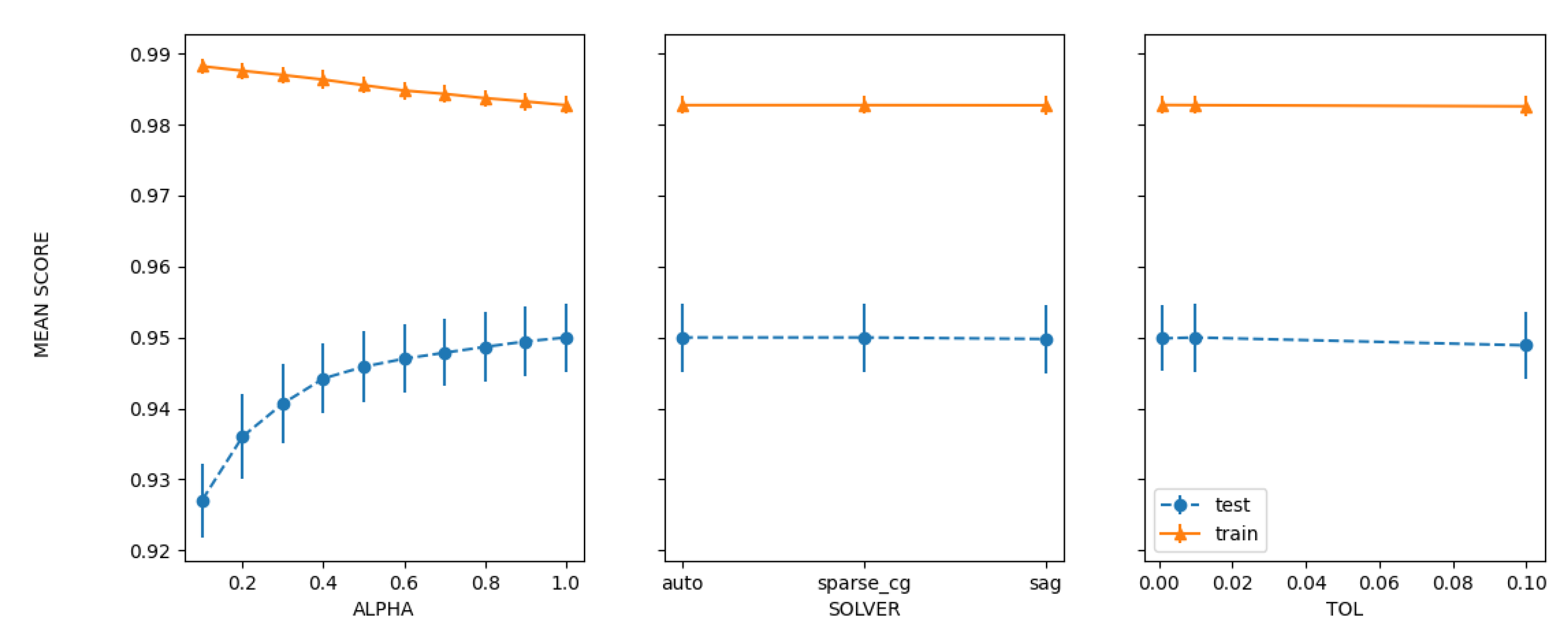
| Grid | 95.2178 | ‘alpha’: 1.0, ‘copyX’: True, ‘fitintercept’: True, ‘normalize’: False, ‘solver’: ‘auto’, ‘tol’: 0.001 |
| Random | 95.1279 | ‘tol’: 0.001, ‘solver’: ‘auto’, ‘normalize’: False, ‘fitintercept’: True, ‘copyX’: False, ‘alpha’: 0.9 |
| Bayesian | 95.1022 | ‘alpha’: 1.0, ‘copyX’: True, ‘fitintercept’: False, ‘normalize’: True, ‘solver’: ‘lsqr’, ‘tol’: 0.001 |
| PSO | 94.5494 | ‘alpha’: 0.807, ‘tol’: 0.0559 |
| GA | 94.5751 | ‘alpha’: 1, ‘solver’: ‘auto’, ‘fitintercept’: ‘False’, ‘normalize’: ‘True’, ‘copyX’: ‘False’, ‘tol’: 0.001 |
| HP Approach | Accuracy | Best Hyperparameters |
|---|---|---|
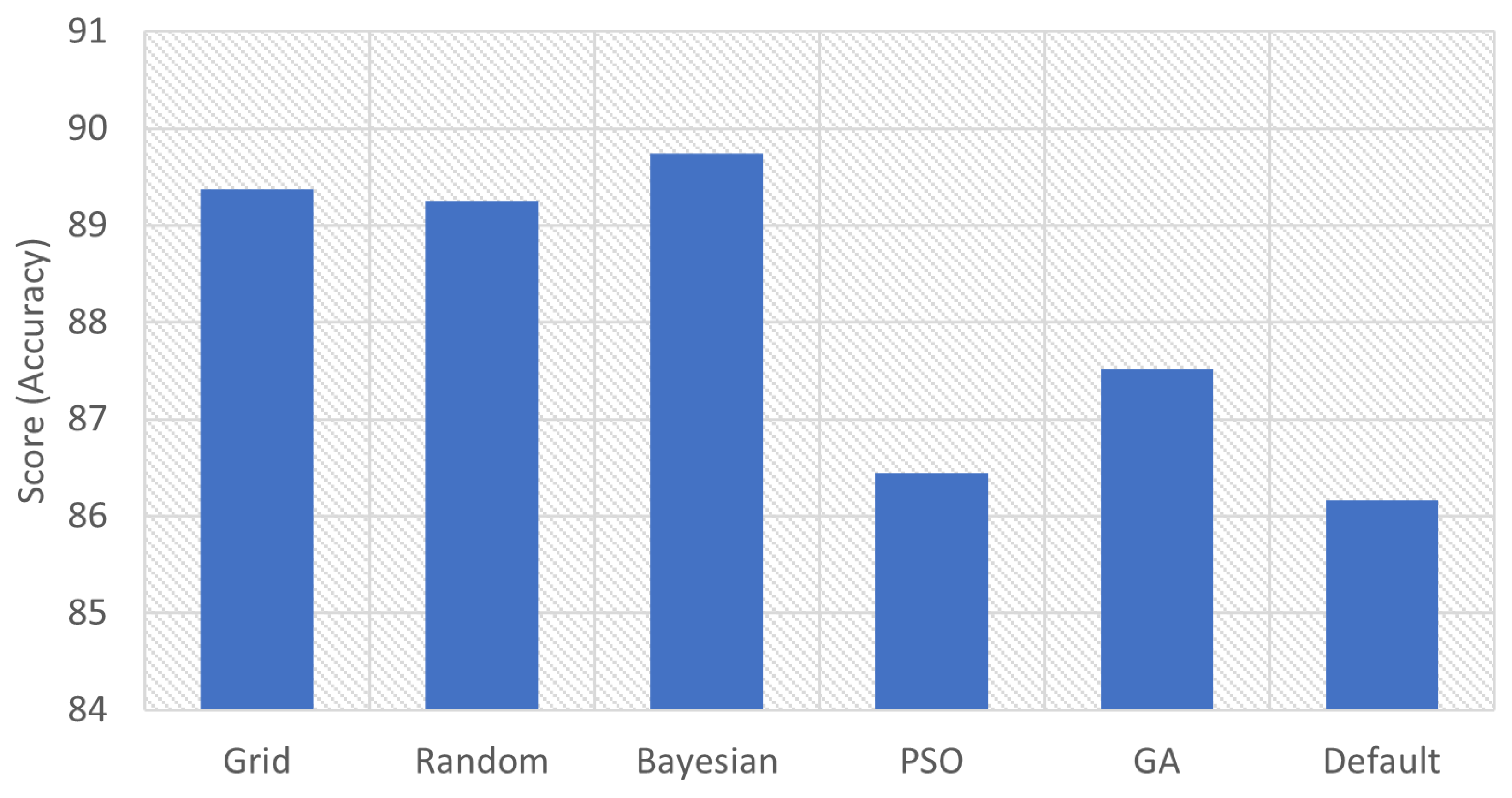
| Grid | 89.3773 | ‘criterion’: ‘entropy’, ‘splitter’: ‘random’ |
| Random | 89.253 | ‘splitter’: ‘random’, ‘criterion’: ‘entropy’ |
| Bayesian | 89.7459 | ‘criterion’: ‘entropy’, ‘splitter’: ‘random’ |
| PSO | 86.4421 | ‘splitter’: ‘random’, ‘criterion’: ‘entropy’ |
| GA | 87.5176 | ‘criterion’: ‘entropy’, ‘splitter’: ‘random’ |
| HP Approach | Accuracy | Best Hyperparameters |
|---|---|---|
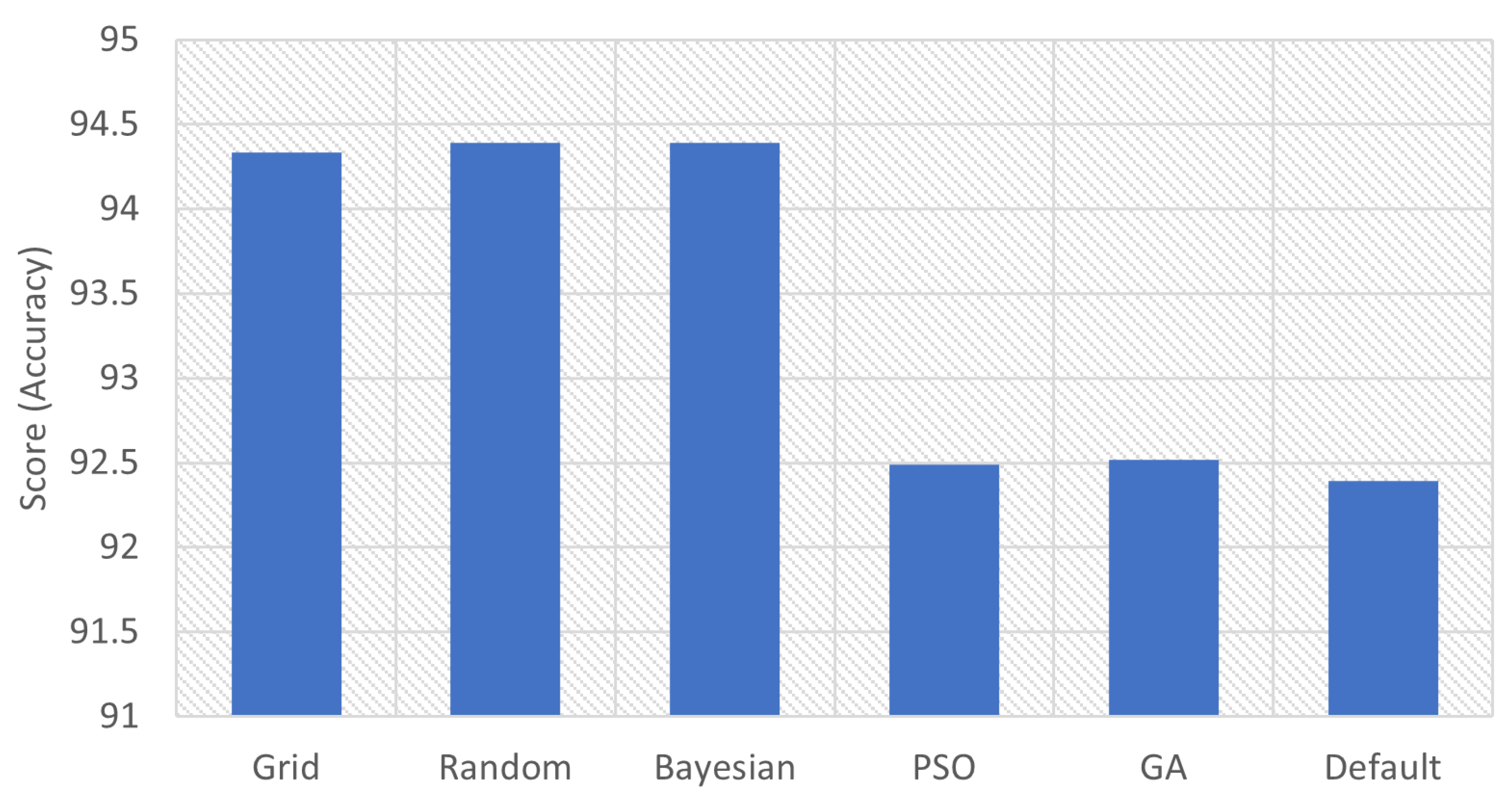
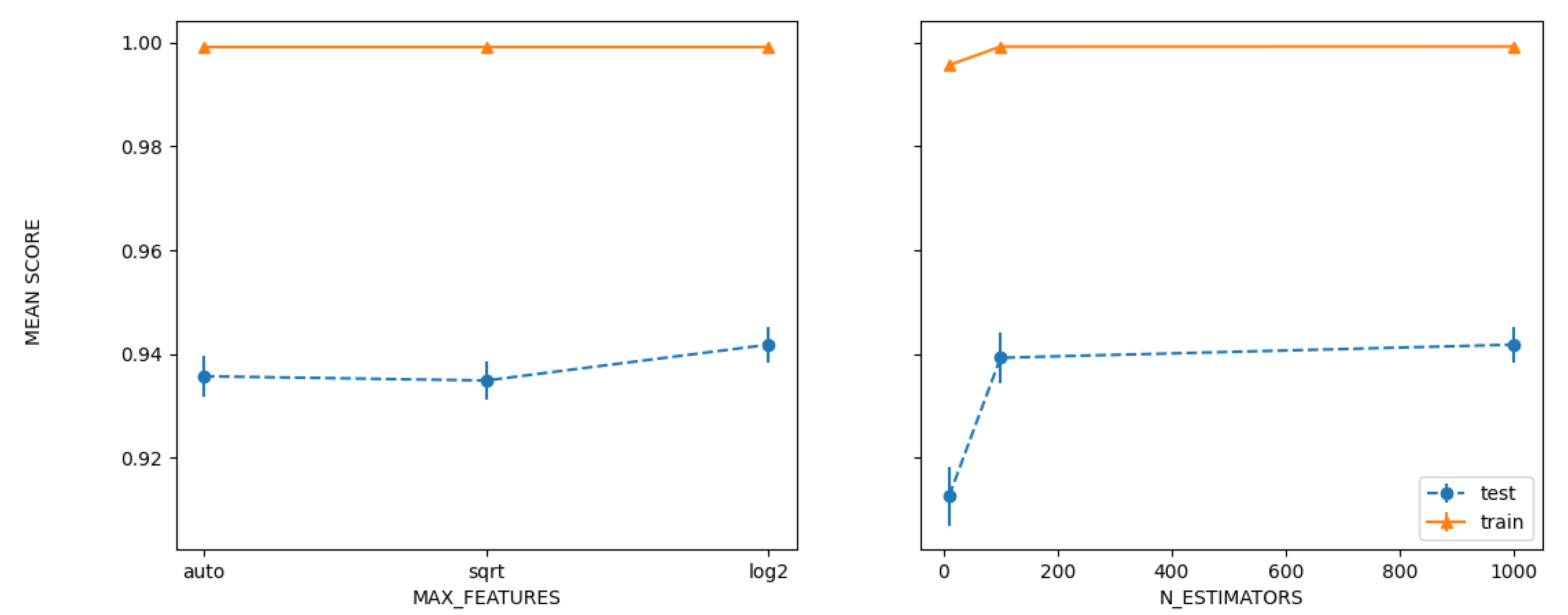
| Grid | 94.335 | ‘maxfeatures’: ‘log2’, ‘nestimators’: 1000 |
| Random | 94.3907 | ‘nestimators’: 1000, ‘maxfeatures’: ‘log2’ |
| Bayesian | 94.3907 | ‘nestimators’: 1000, ‘maxfeatures’: ‘log2’ |
| PSO | 92.4869 | ‘maxfeatures’: ‘log2’, ‘nestimators’: 1000 |
| GA | 92.5183 | ‘nestimators’: ‘log2’, ‘maxfeatures’: 63, ‘maxdepth’: 48, ‘minsamplessplit’: 6, ‘minsamplesleaf’: 1, ‘criterion’: ‘entropy’ |
| HP Approach | Accuracy | Best Hyperparameters |
|---|---|---|
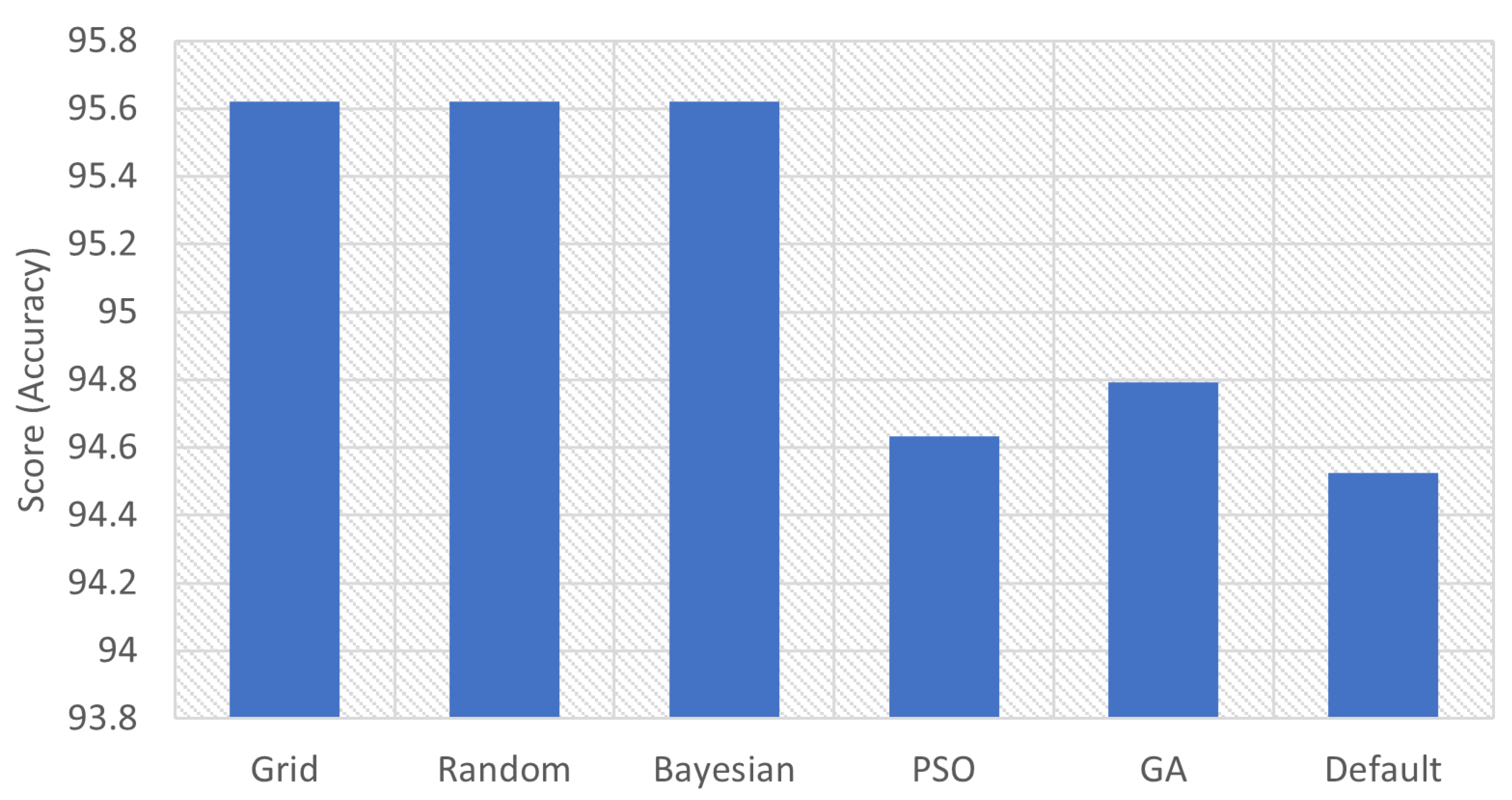
| Grid | 95.6206 | ‘C’: 1.0, ‘gamma’: ‘scale’, ‘kernel’: ‘rbf’ |
| Random | 95.6206 | ‘kernel’: ‘rbf’, ‘gamma’: ‘scale’, ‘C’: 1.0 |
| Bayesian | 95.6208 | ‘C’: 1.0, ‘gamma’: ‘scale’, ‘kernel’: ‘rbf’ |
| PSO | 94.6337 | ‘C’: 1.64, ‘kernel’: ‘rbf’, ‘gamma’: ‘scale’ |
| GA | 94.7936 | ‘C’: 1.65, ‘kernel’: ‘rbf’, ‘gamma’: ‘scale’ |
| HP Approach | Accuracy | Best Hyperparameters |
|---|---|---|
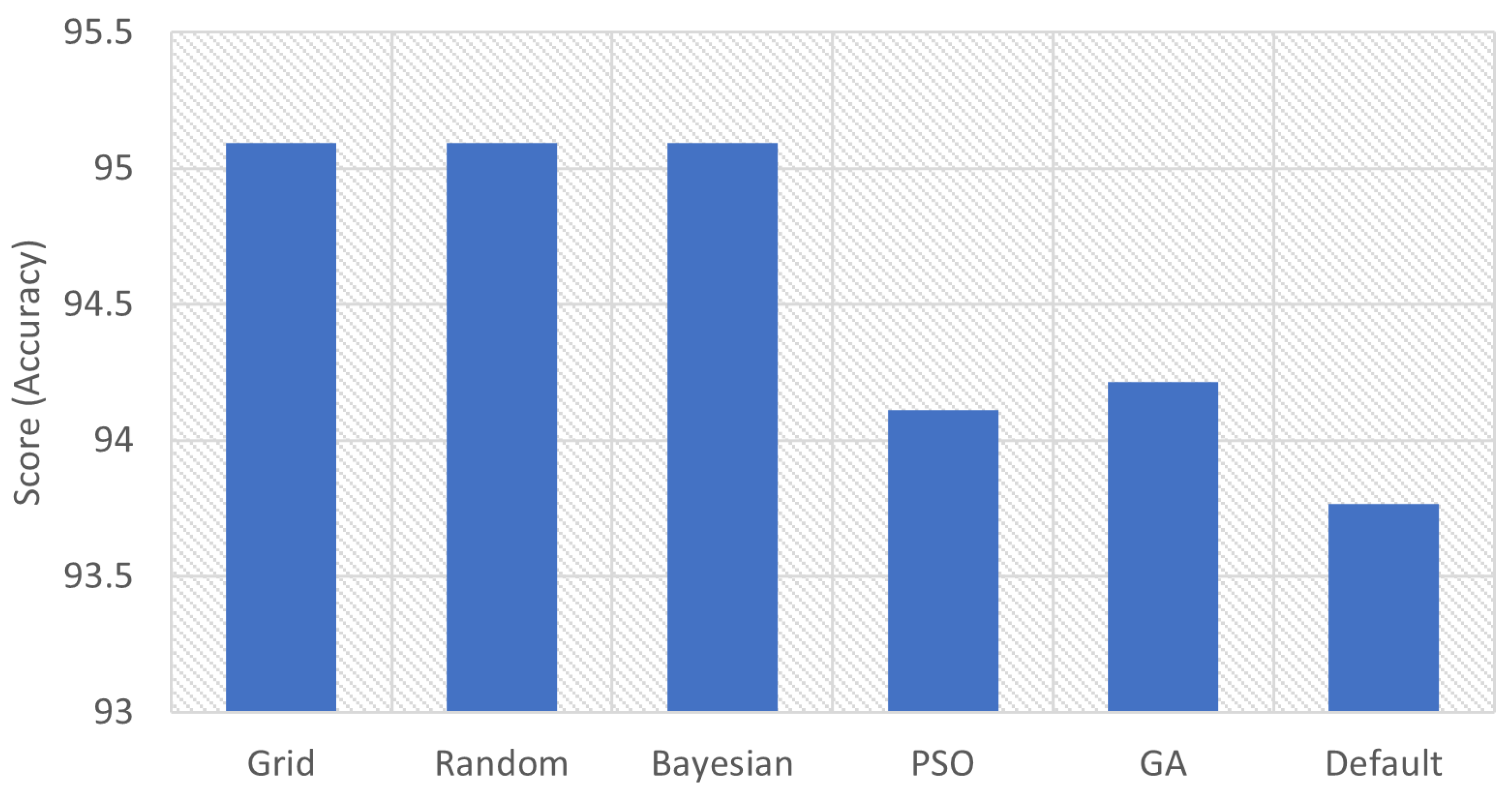
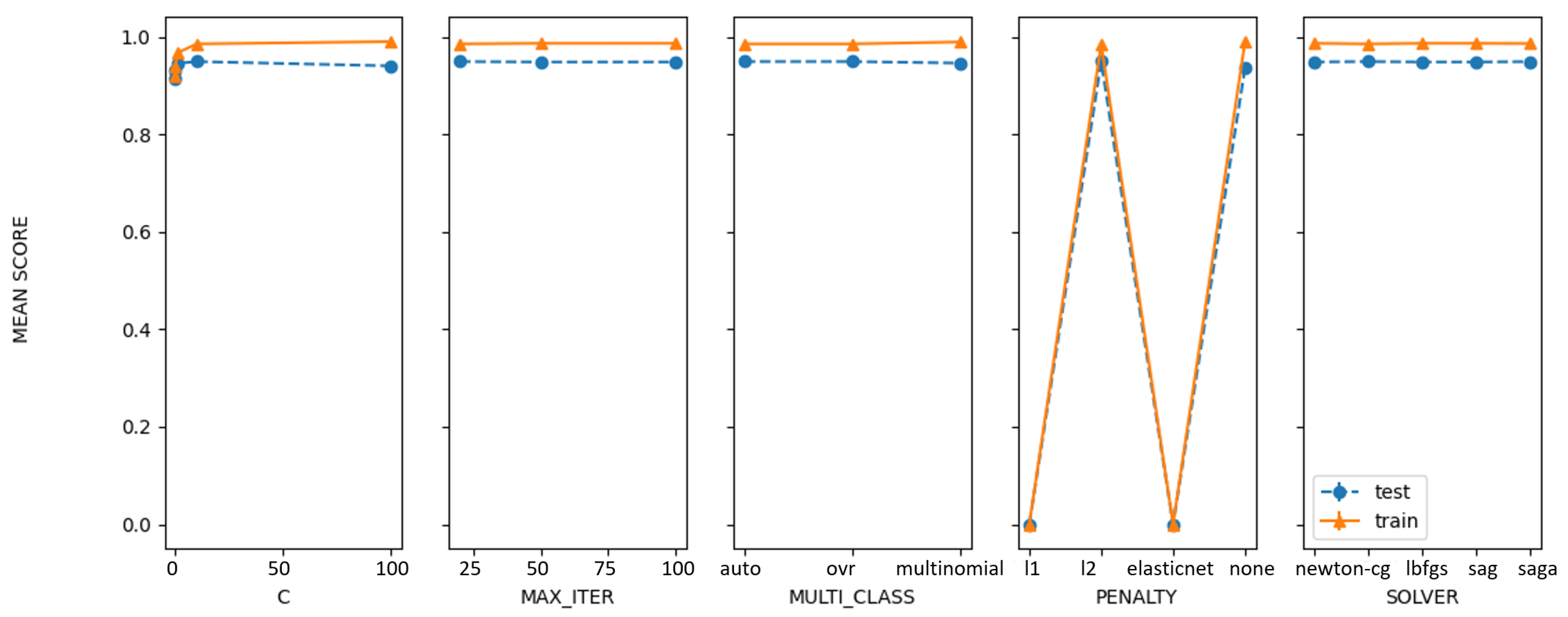
| Grid | 95.0936 | ‘C’: 10, ‘max_iter’: 20, ‘multi_class’: ‘ovr’, ‘penalty’: ‘l2’, ‘solver’: ‘saga’ |
| Random | 95.0936 | ‘solver’: ‘saga’, ‘penalty’: ‘l2’, ‘multi_class’: ‘auto’, ‘max_iter’: 100, ‘C’: 10 |
| Bayesian | 95.0938 | ‘C’: 10, ‘max_iter’: 20, ‘multi_class’: ‘ovr’, ‘penalty’: ‘l2’, ‘solver’: ‘saga’ |
| PSO | 94.1123 | ‘solver’: ‘liblinear’, ‘penalty’: ‘l2’, ‘multi_class’: ‘auto’, ‘max_iter’: 30.0634765625 |
| GA | 94.2152 | ‘solver’: ‘newton-cg’, ‘penalty’: ‘l2’, ‘multi_class’: ‘multinomial’, ‘max_iter’: 20 |
| HP Approach | Accuracy | Best Hyperparameters |
|---|---|---|
| Grid | 71.4402 | ‘varsmoothing’: |
| Random | 71.4402 | ‘varsmoothing’: |
| Bayesian | 71.4402 | ‘varsmoothing’: |
| PSO | 78.3005 | ‘varsmoothing’: |
| GA | 78.3005 | ‘varsmoothing’: 0.0001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elgeldawi, E.; Sayed, A.; Galal, A.R.; Zaki, A.M. Hyperparameter Tuning for Machine Learning Algorithms Used for Arabic Sentiment Analysis. Informatics 2021, 8, 79. https://doi.org/10.3390/informatics8040079
Elgeldawi E, Sayed A, Galal AR, Zaki AM. Hyperparameter Tuning for Machine Learning Algorithms Used for Arabic Sentiment Analysis. Informatics. 2021; 8(4):79. https://doi.org/10.3390/informatics8040079
Chicago/Turabian StyleElgeldawi, Enas, Awny Sayed, Ahmed R. Galal, and Alaa M. Zaki. 2021. "Hyperparameter Tuning for Machine Learning Algorithms Used for Arabic Sentiment Analysis" Informatics 8, no. 4: 79. https://doi.org/10.3390/informatics8040079
APA StyleElgeldawi, E., Sayed, A., Galal, A. R., & Zaki, A. M. (2021). Hyperparameter Tuning for Machine Learning Algorithms Used for Arabic Sentiment Analysis. Informatics, 8(4), 79. https://doi.org/10.3390/informatics8040079







