Abstract
There have been many machine learning-based studies to forecast stock price trends. These studies attempted to extract input features mostly from the price information with little focus on the trading volume information. In addition, modeling parameters to specify a learning problem have not been intensively investigated. We herein develop an improved method by handling those limitations. Specifically, we generated input variables by considering both price and volume information with even weight. We also defined three modeling parameters: the input and the target window sizes and the profit threshold. These specify the input and target variables, between which the underlying functions are learned by multilayer perceptrons and support vector machines. We tested our approach over six stocks and 15 years and compared with the expected performance over all considered parameter specifications. Our approach dramatically improved the prediction accuracy over the expected performance. In addition, our approach was shown to be stably more profitable than both the expected performance and the buy-and-hold strategy. On the other hand, the performance was degraded when the input variables generated from the trading volume were excluded from learning. All these results validate the importance of the volume and the modeling parameters in stock trading prediction.
1. Introduction
Investors are increasingly interested in developing a stock trading system incorporating artificial intelligence methods. In particular, many studies have sought to forecast stock price trends, which is a challenge because of the nonlinearity and volatility of stock markets [1]. The stock price prediction models are classified into fundamental analysis-based and technical analysis-based approaches. The former approach usually uses a company’s intrinsic financial information such as earnings, capital, sakes, share, and its relationship with other companies. The latter approach uses historical data of stock prices and/or the trading volume to generate technical indicators for prediction [2,3]. In this study, we consider a daily stock prediction problem for which a technical analysis-based approach is appropriate.
Many technical variables have been devised using moving averages, exponential smoothing, linear regression statistical methods, and so on [4]. For example, the weighted average of past price values was modeled to predict a short-term fluctuation of a given price by assuming that the data follow some historical pattern [5,6]. Moreover, machine learning methods have been extensively employed in stock prediction problems. For example, multilayer perceptrons (MLPs) have been applied to predict various stocks such as the daily New York Stock Exchange [7], daily Deutscher Aktienindex stock [8], intraday option contracts on the Financial Times Stock Exchange 100 Index (FTSE100) [9], S&P 500 future index price [10], Hong Kong Hang Seng stock index [11] and S&P 500 along with NASDAQ-100 index [12]. Support vector machines (SVMs) were also widely applied. For example, they were used to predict five future contracts collated from the Chicago Mercantile Market [13] and to extract rules for the first-day return of US stock market initial public offerings (IPOs) [14]. Another study compared the efficiency of stock forecasting between SVMs and MLPs [15]. Although these previous studies were successfully applied, two issues deserve further discussion: the type of input variables and the modeling parameters for learning. Regarding the former, it is important to construct the most informative input variables for a successful forecasting model. In fact, most input variables in previous studies have been generated from closing, opening, highest, or lowest price data. For example, moving averages [16], the relative strength index [17], golden cross and dead cross [18], stochastics [19] and many other technical indicators have been devised for use in stock prices. Meanwhile, the trading volume has been less emphasized in creating technical indicators. Although it was often considered for generation of input variables, it was relatively less focused than the price information. For example, 4%, 13% and 14% out of the total input variables were derived from the trading volume information in [6,17,20] whereas 96%, 87%, and 86%, respectively, were derived from the price information. Considering that the trading volume is known to be informative in explaining the status of a stock market [6,21], there is room to make greater use of the trading volume for input variables in stock price prediction. The latter issue is about the modeling parameters in a learning stage. Specially, we focus on three parameters: the number of past days to be considered for input variables, the maximum number of future days for a long position, and the minimum profit rate by trading. These parameters might be critical for an optimal trading strategy because they can modify the problem formulation and the degree of difficulty in learning. The parameters, however, were chosen by trial and error or even specified at random in previous studies. For example, the number of past days was fixed to five in the KOSPI 200 prediction [22], one in the National Stock Exchange (NSE) India prediction [23], and 30 in Shanghai Stock Exchange Composite Index prediction [24]. Optimal modeling parameter values can improve prediction performance by making the learning problem easier to learn.
In this paper, we designed a stock trading method to properly resolve these issues. We generated a same number of input variables from both price and volume information. We also optimized three modeling parameters of the input window size, the target window size, and the profit threshold parameters through a grid search. In addition, we employed two well-known learning algorithms for stock prediction, MLPs and SVMs. This paper is organized as follows. In the next section, we introduce the background of the daily stock trading problem. In Section 3 and Section 4, we propose our approach and show the experimental results, respectively. We offer discussion and conclusions in the last section.
2. Backgrounds
2.1. Daily Stock Trading
There can be various stock-trading schemes such as intraday, daily, weekly, or monthly trading, depending on the trading time intervals. In this paper, we consider a daily trading scheme because it was most frequently handled in previous studies [25]. A typical formulation for this problem is to approximate an underlying function for a target variable and a set of input variables at day as follows:
2.2. Related Studies
Many machine learning methods such as MLPs and SVMs have been used to solve the function approximation problem of optimal stock trading. In addition, a variety of target and input variables were modeled. For example, the authors in a previous study defined the target variable as [17], where represents the closing price at day , (i.e., a daily change rate of a closing price), and generated a total of 75 input variables from various technical indicators such as the moving average, relative strength index, and rate of change. We note that 65 and 10 input variables among them were based on the stock price and trading volume data, respectively. They showed a notable prediction accuracy for over 36 companies in the Dow Jones and Nasdaq for 13 years using a hybrid genetic algorithm combined with MLPs. In another study [5], the target variable was defined as , where means the -day exponential moving average at day , and the moving average was used to generate input variables such as . This model was trained by SVMs to predict five future contracts in the Chicago Mercantile Market, and a relatively good prediction was achieved. Another study investigated the usefulness of MLPs on predicting the closing price of Petroleo Brasileiro company’s stock by varying the window size [26], and a hybrid MLP combined with the wavelet method was tried to predict Shenzhen Composite Index [27].
We note that most variables in previous studies were created based on price information, and the trading volume information was less considered. In fact, some studies found a relationship between the trading volume and price variations. For example, Mubarik and Javid showed statistical relations among the trading volume, the returns, and the volatility in the Pakistan stock market [28]. Kanas and Yannopoulos found that trading volume can be a determinant factor for long-term forecasting [29,30]. It is better to explain the market return by investigating the dynamics of both the price and the trading volume than by focusing only on the closing price and its technical indicators. A previous study showed that a larger price movement was associated with a higher subsequent volume through analysis of the daily S&P 500 index from 1928–1987 [7]. Another study showed the monthly trading volume was strongly related to the future stock price movement [6]. Taken together, the trading volume can be an important and informative factor for input variable generation.
3. Our Proposed Method
In this section, we explain our proposed method for optimal stock trading based on neural networks.
3.1. Problem Formulation
In this paper, we also consider the approximation problem described in Section 2.1. However, we properly modify it as , where is a target vector and is a mapping, so that they can represent multiple neurons in the output layer of the neural networks. Let and be the closing price and the trading volume, respectively, at day , and define as follows:
where is a parameter of the input window size that denotes the number of past days to be considered for the input variables, and is a normalized trading volume defined as . In other words, determines the time window size of the training samples, and eventually includes information on the closing price and trading volume of the most recent days as of day . In this paper, can range from 1 to 10. We note that we constructed the same number of volume-specific input variables as the price-specific input variables to utilize the informative power of the trading volume. The target variable is represented by a vector of two Boolean values so that they can interact with two output neurons in our neural networks. Specifically, we defined it as follows:
where is a parameter of the target window size that denotes the maximum number of future days for a long position, and is a parameter of the profit-threshold that denotes the minimum profit rate for a feasible transaction. Then, indicates that the closing price goes up over percent within the forthcoming days. In other words, we could have an opportunity to gain a profit of at least percent if we bought the stock at the closing price of day . In this paper, ranges from 5 to 20 with a 5-day interval, and ranges from 0.020 to 0.070 with a 0.005 interval. As a result, we defined three modelling parameters and considered a total of 440 parameter combinations for optimal learning. We note that each specification of the parameters represents a different problem to learn.
Once a parameter combination is specified and a learning task is completed by MLPs or SVMs, we obtain an approximated function , which is interpreted as generating a trading signal as follows:
where and denote the first and the second element of , respectively.
3.2. Overall Framework
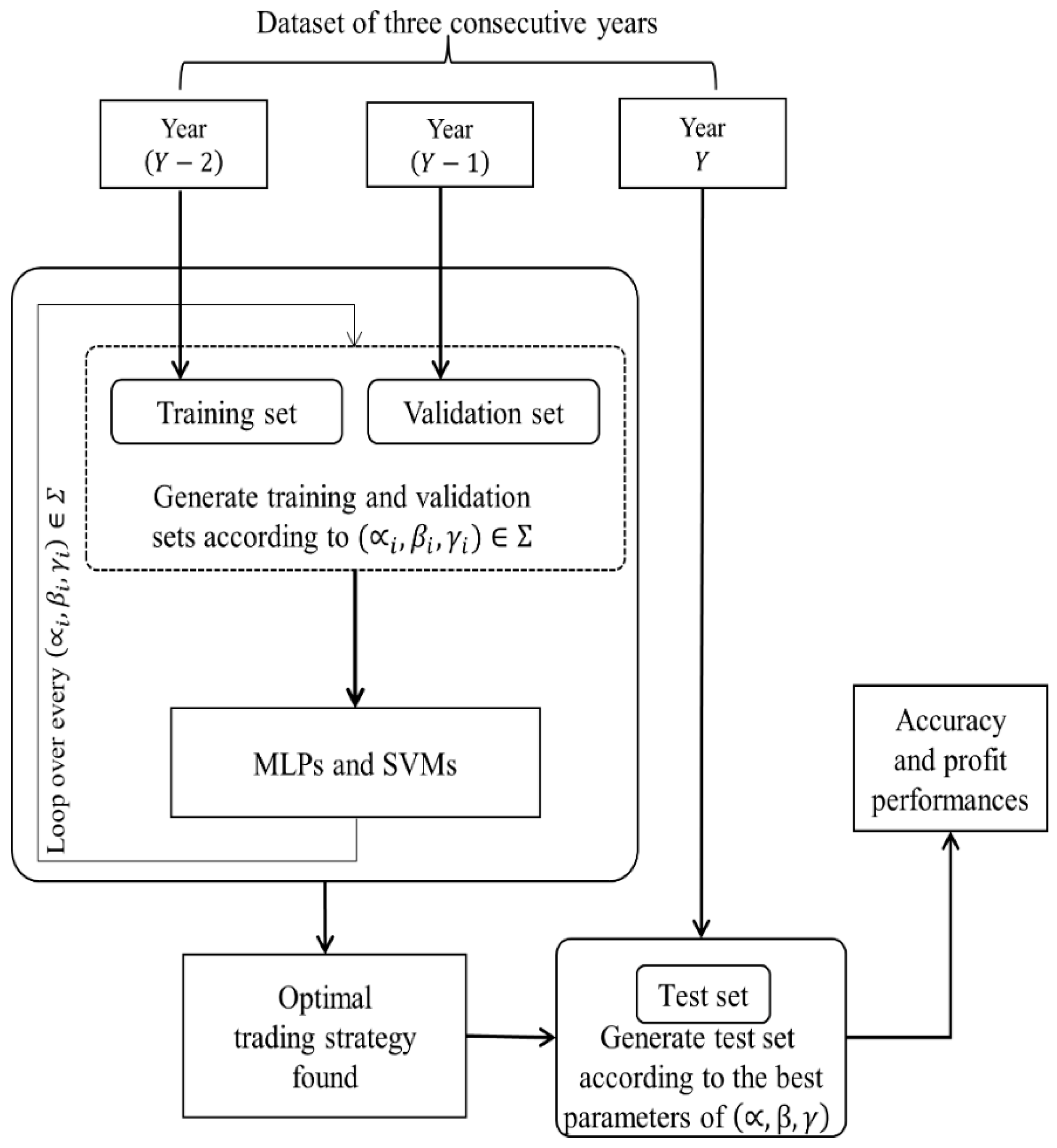
Figure 1 shows the overall framework of our approach. To test year , two previous consecutive years are used as training and validation sets, respectively. As explained in Section 3.1, the input and target variables are generated according to a specified modeling parameter combination . Then, the MLPs and SVMs learn the function approximation problem, and the performance is assessed by the validation year’s dataset. The best solution is chosen among the 440 model parameter combinations. The accuracy and the profit over the test year are evaluated.
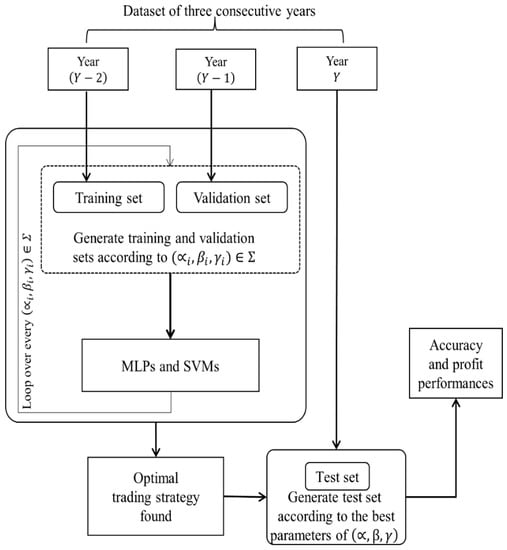
Figure 1.
Overall framework of our method.
3.3. Performace Evaluation
As we mentioned, the trading performance is evaluated based on two measures, the accuracy and the trading profit.
3.3.1. Accuracy
The accuracy is the ratio of correct prediction by comparing the target and the predicted Boolean vectors, and , respectively, during the testing year as follows:
where is the number of days and is an indicator function that returns 1 if the condition is true or 0 otherwise.
3.3.2. Trading Profit
To see if a trading strategy based on the neural network prediction can be profitable, we simulated a realistic trading task to compute a profit or loss. Let be the predicted results. To evaluate the trading profit, we define a transaction period represented by a pair of dates, as follows:
For convenience, is assumed. By these definitions, is the earliest day when the buy signal is generated since the last transaction ended, and is the day to sell the stock bought on day considering the deadline and the profit-threshold parameter (). Then, represents the -th trading transaction where the stock is bought and sold on days and , respectively (We note that ). The final trading profit for the test year is calculated by accumulating the profits over all transactions as follows:
where denotes the number of occurred transactions and is the transaction cost, which was set to 0.025% in this study. By considering the transaction fee, the profit measure can represent a more realistic trading gain or loss.
4. Experimental Results
We implemented our method by using the LibSVM (https://www.csie.ntu.edu.tw/~cjlin/libsvm/) and scikit-learn (http://scikit-learn.org/) libraries. In this study, MLPs consist of a single input, hidden neurons, and an output layer. The number of input neurons depends on the specified value of the input window size parameter , and the number of hidden neurons was fixed to 16 through trial and error. In addition, the number of output neurons was two. MLPs are learned by the backpropagation algorithm with a learning rate of 0.025 and a momentum rate of 0.9. The sigmoid function is chosen as a transfer function. In the SVMs, the penalty parameter of the error term, the kernel coefficient parameter, and the degree of the polynomial kernel were set to 100, 1.0, and 2, respectively.
4.1. Datasets
In this study, we tested our approach with six stocks: Hang Seng Index (HSI), NASDAQ Composite Index (NASDAQ), Financial Times Stock Exchange 100 Index (FTSE), Nikkei 225 Index (NIKKEI), Swiss Market Index (SMI), and Google (GOOGLE). We collected their daily closing prices and trading volumes from January 1999 to December 2015. Therefore, the test year varies from 2001 to 2015, as explained in Section 3.2. For each test year and each stock, we considered 440 combinations of the three modelling parameters . Thus, our method learned a total of 39,600 datasets (=6 stocks × 15 test years × 440).
4.2. Performance Analysis
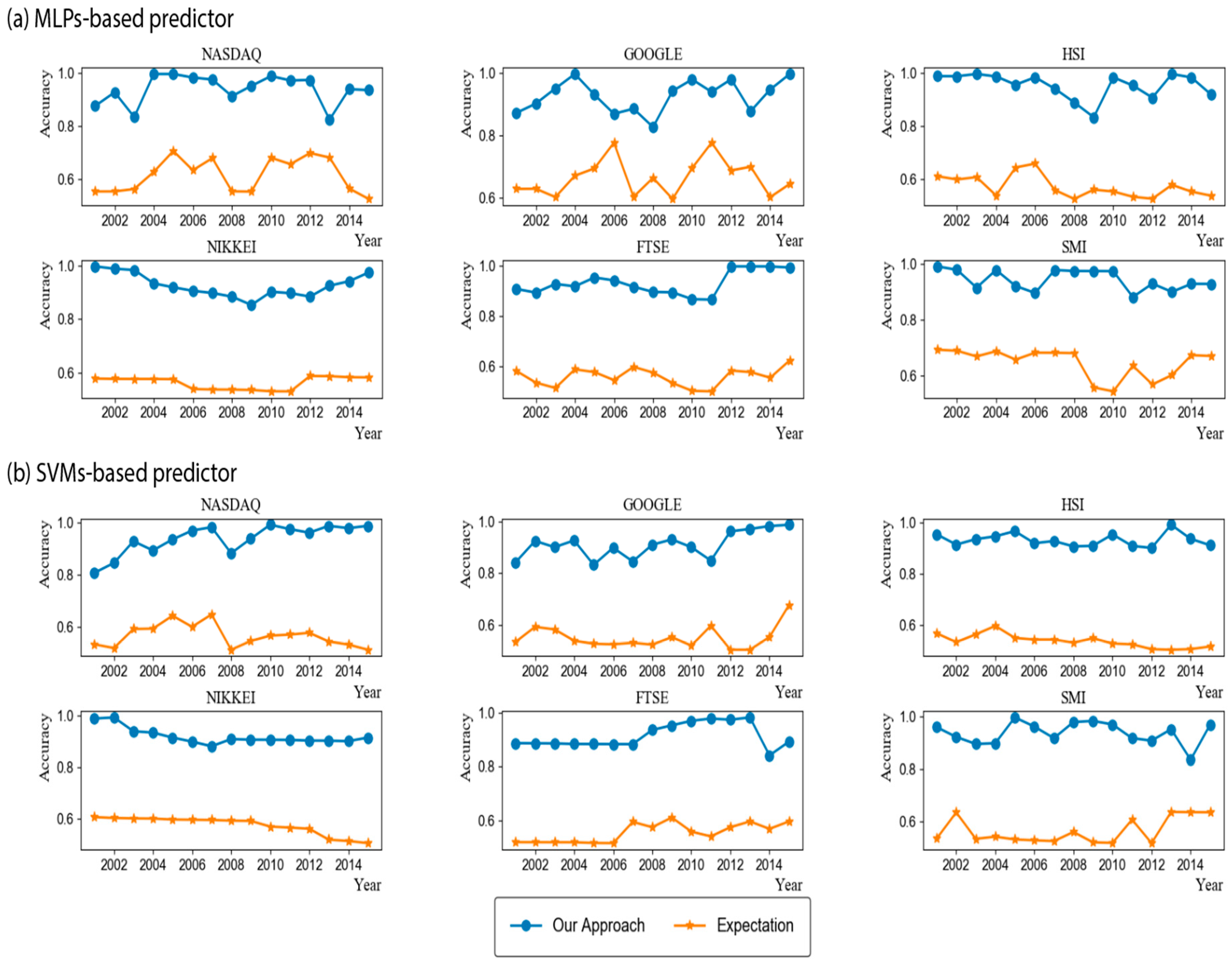
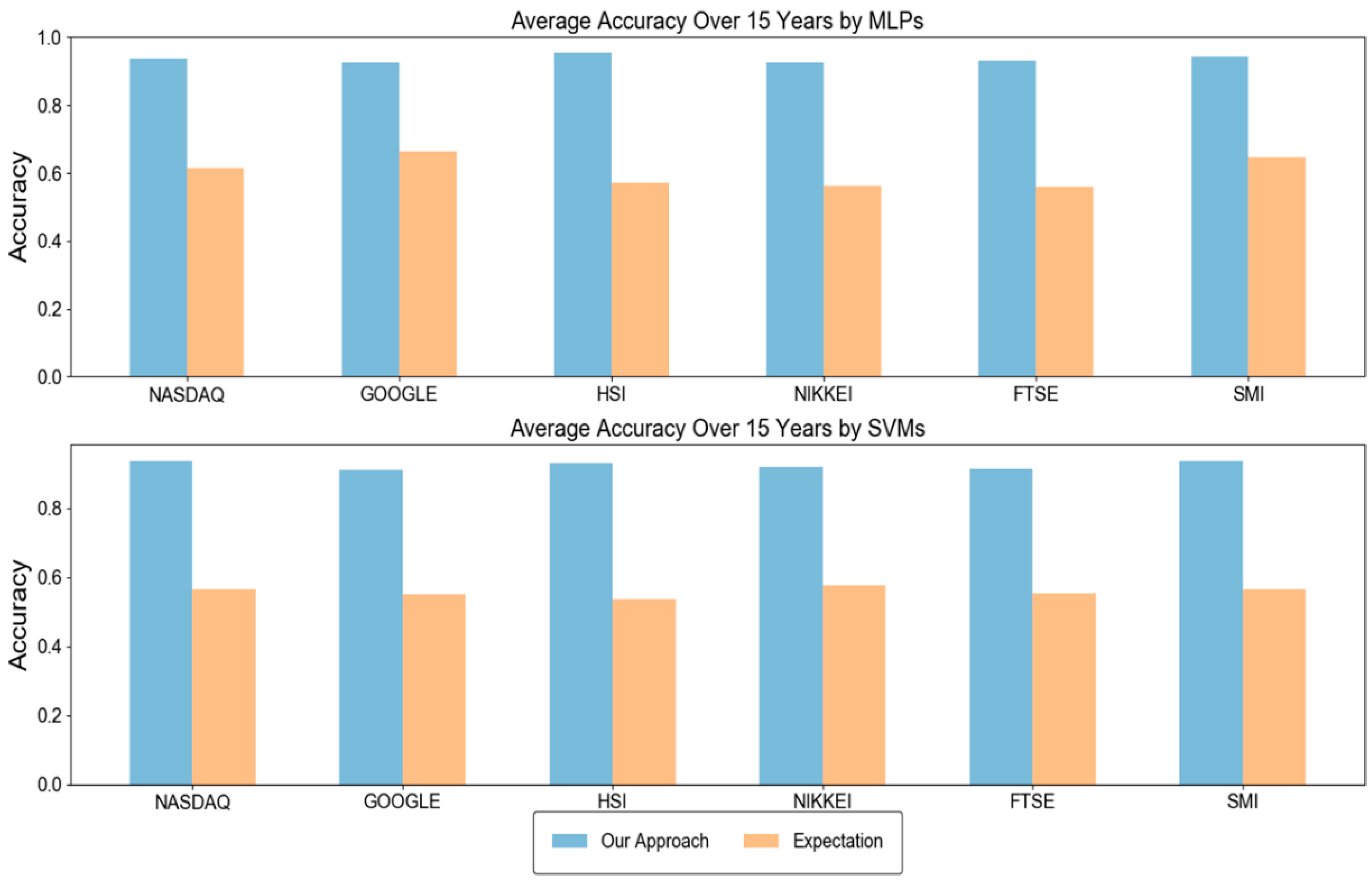
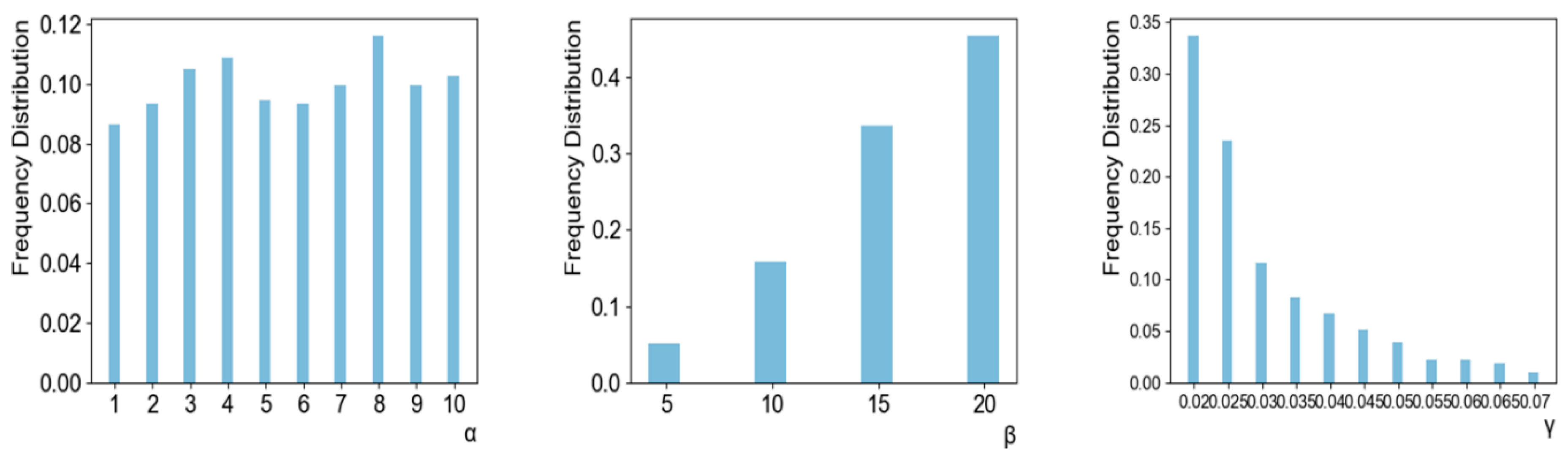
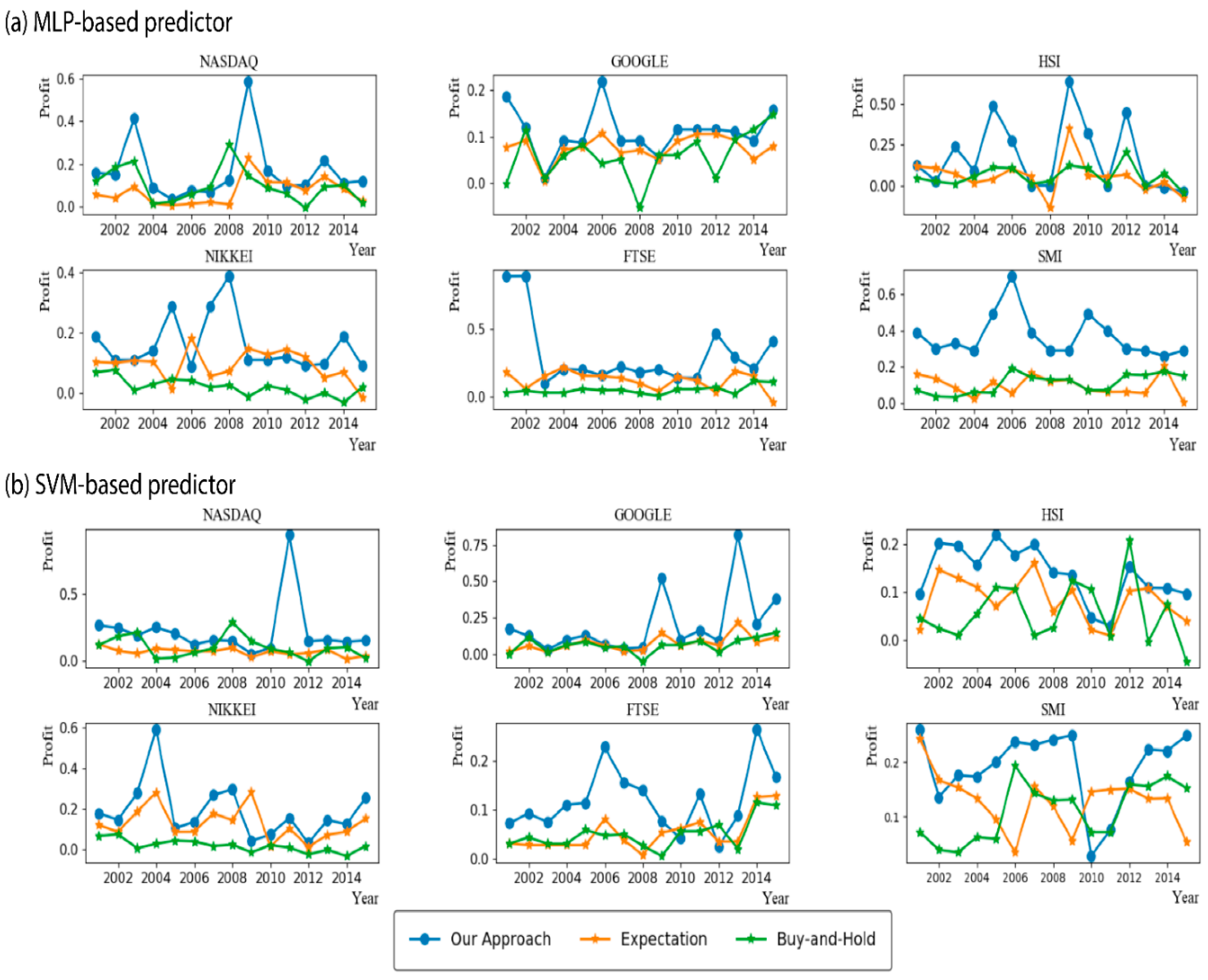
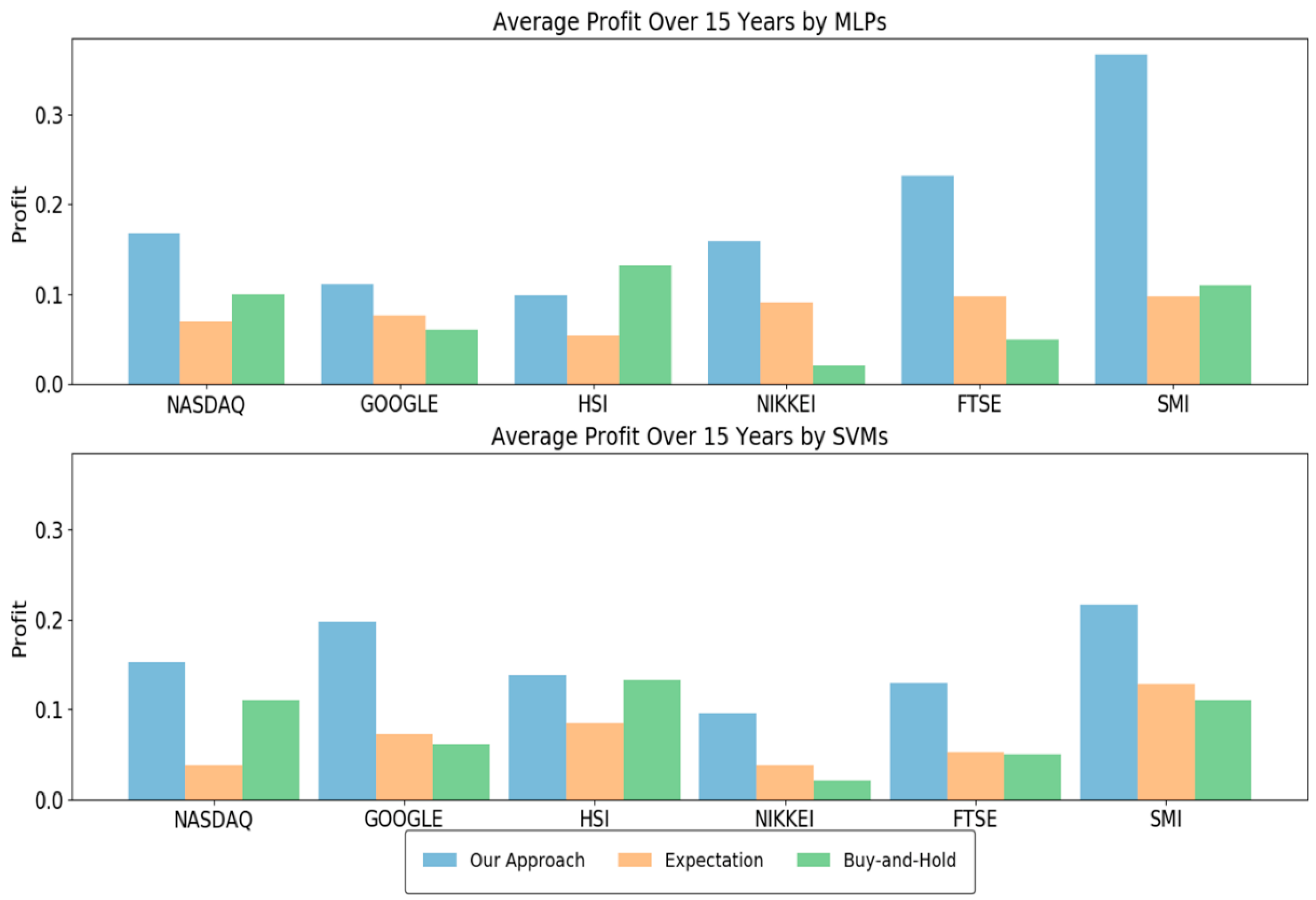
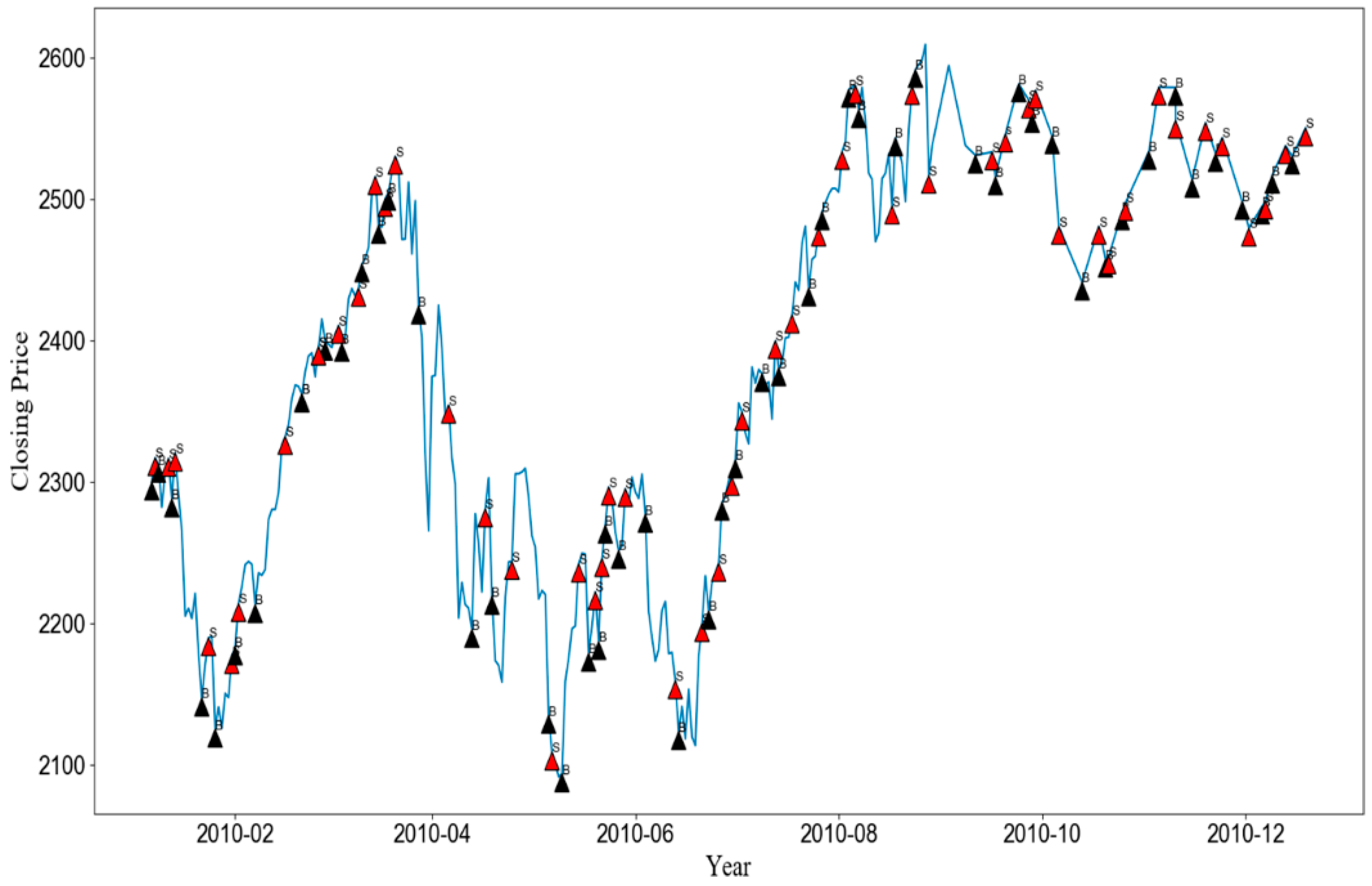
As explained in Section 3.2, our approach optimizes three modelling parameters through a grid search. To show the importance of optimal parameters, we compared the accuracy of our approach and the expected accuracy over all considered parameter combinations. In other words, the expected accuracy means the average accuracy of the networks each of which were trained with 440 different modeling parameters. We note that the best modeling parameter in our approach is chosen based on the validation set, not the test set. Thus, it is not guaranteed that our approach is always better than the expected accuracy. Figure 2 shows the results when MLPs and SVMs are used as the learning algorithm. As shown in the figure, our approach showed significantly higher accuracies than the expected accuracy, irrespective of the stock type and the test year. In addition, the numbers of test years in which the accuracy of our approach with MLPs was higher than 0.9 were 12, 9, 13, 10, 10, and 13 out of 15 years in NASDAQ, GOOGLE, HSI, NIKKEI, FTSE, and SMI, respectively. The corresponding numbers when using SVMs were 11, 10, 15, 12, 6, and 12 years in NASDAQ, GOOGLE, HSI, NIKKEI, FTSE, and SMI, respectively. For simplicity, we depicted the average accuracy over 15 test years in Figure 3. The average accuracy (0.939) of our approach with MLPs over 15 test years was higher than that (0.615) of the expected value by about 0.324 in the case of NASDAQ. The accuracy improvements of other stocks by our approach with MLPs were 0.270, 0.382, 0.361, 0.369, and 0.297 in the cases of GOOGLE, HSI, NIKKEI, FTSE, and SMI, respectively. The values when using SVMs were 0.373, 0.360, 0.395, 0.342, 0.361, and 0.372 in NASDAQ, GOOGLE, HSI, NIKKEI, FTSE, and SMI, respectively. These results validate the necessity of optimizing the modeling parameters, which results in dramatical improvements of the prediction accuracy. In addition, we examined the distributions of the optimal , , and values found over a total of 180 (=6 stocks × 15 test years × 2 learning methods) experiments (Figure 4). As shown in the figure, they were variant according to the datasets, which explains the importance of optimizing the modeling parameters. We further examined the performance with respect to the trading profit. In addition to the comparison with the expected profit over all combinations of modeling parameters, we examined the trading profit according to the buy-and-hold strategy, where the trader buys and sells stocks at the closing price of the first day and the last day of the test year, respectively. Figure 5 shows the results when the MLPs and SVMs are used as a learning algorithm, and Figure 6 shows the average trading profit over 15 years. As shown in these figures, our approach exhibited significantly higher profit than both the expected value and the buy-and-hold strategy. Specifically, the profit improvement of our method over the expectation ranged from 0.03 to 0.27 in the MLP-based prediction and from 0.07 to 0.13 in the SVM-based prediction. In addition, the improvement over the buy-and-hold strategy ranged from 0.04 to 0.21 in the MLP-based prediction and from 0.05 to 0.108 in the SVM-based prediction. These results imply that our method can be an efficient trading strategy for considerable and stable profit. Figure 7 shows an example result of the detailed trading transactions that took place when our method with MLPs predicted NASDAQ in 2010. The best modeling parameter was found to be . The red (“B”) and blue (“S”) triangles represent the buy and sell actions, respectively, and a transaction consists of a pair of consecutive buy and sell actions. As shown in the figure, a total of 53 transactions occurred, and there were 44 profitable cases.
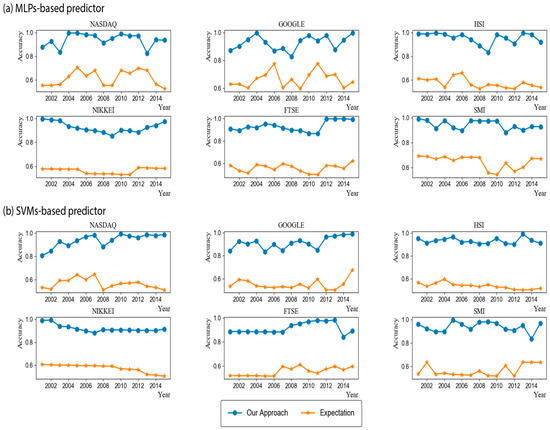
Figure 2.
Accuracy comparison. (a) Accuracy comparison by Multilayer Perceptron (MLP)-based predictor; (b) Accuracy comparison by Support Vector Machine (SVM)-based predictor.
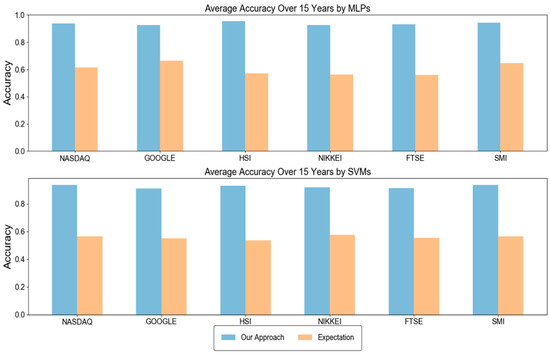
Figure 3.
Average accuracy comparison over 15 years.
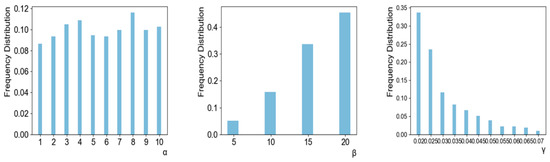
Figure 4.
Frequency distributions of the best , , and values found in experiments.
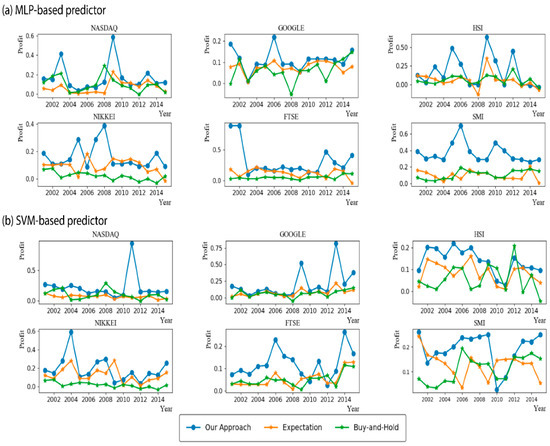
Figure 5.
Profit comparison. (a) Profit comparison by MLP-based predictor; (b) Profit comparison by SVM-based predictor.
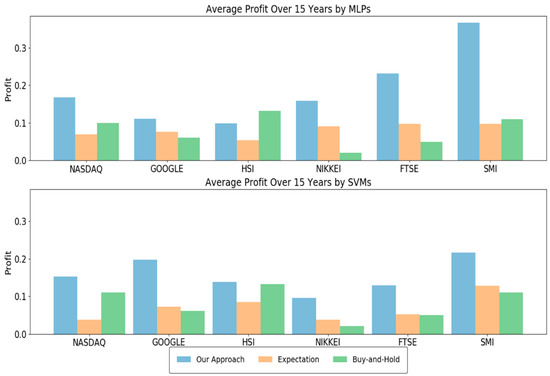
Figure 6.
Average profit comparison over 15 years.
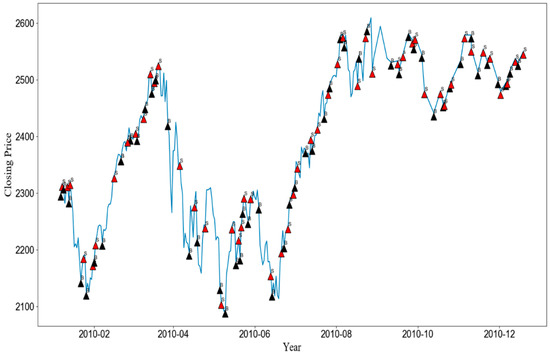
Figure 7.
An example of detail transaction by our method. “B” and “S” denote the buy and sell actions, respectively.
4.3. Usefulness of Trading Volume Information
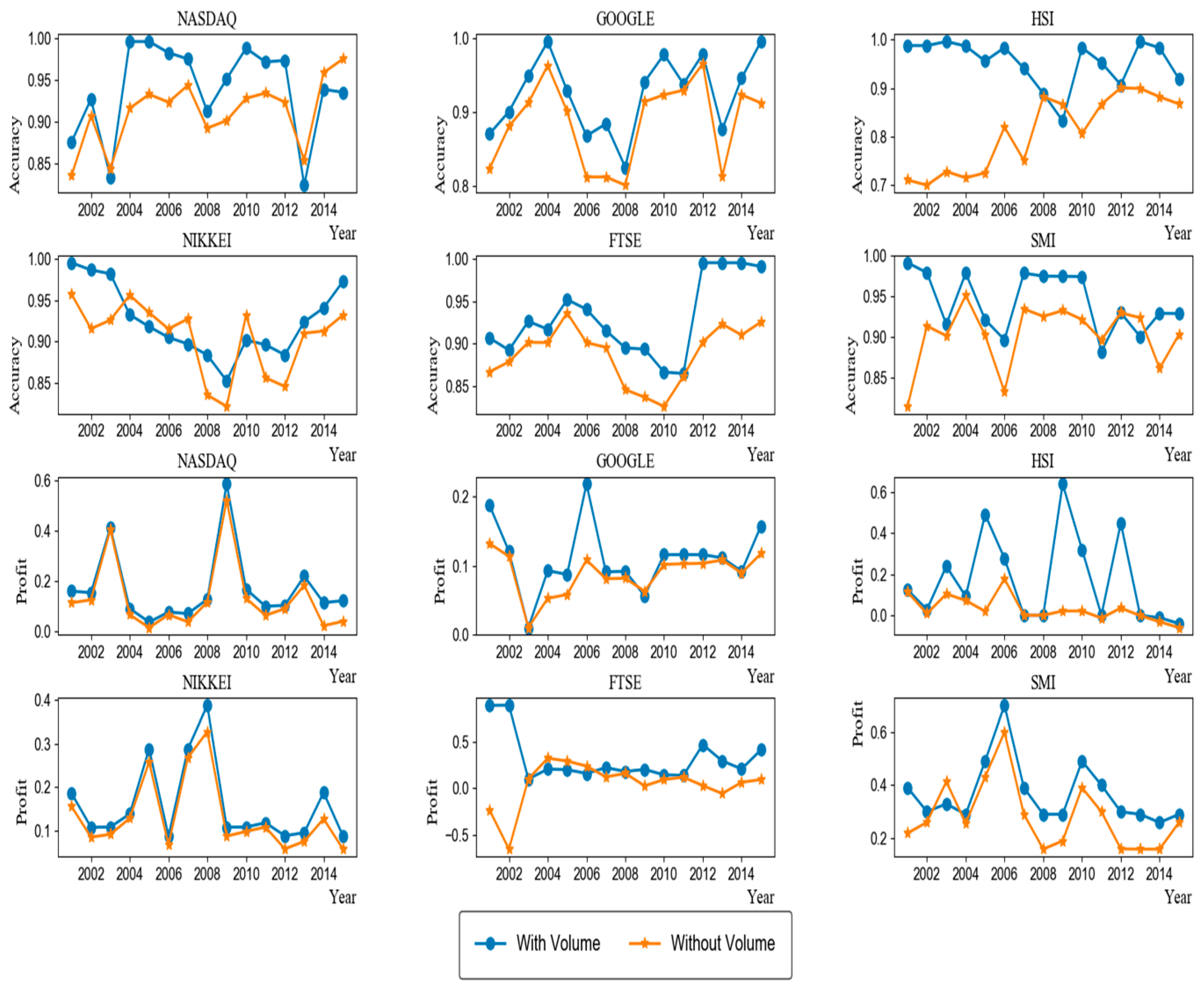
As explained in Section 3.2, we constructed , consisting of the same number of price-base and volume-based input variables. To investigate the importance of the trading volume information in prediction, we compared the performance of our original model and that of a variant model where the volume-based input variables were excluded from . We tested the accuracy and the profit using the MLP learning algorithm (Figure 8). As shown in the figure, our original model showed higher accuracy than did the variant model. In terms of accuracy, our original model was better and worse than the variant model by at least 0.08% in 70 and 20 cases among a total of 90 cases, respectively. With respect to the profit, our original model outperformed and underperformed the variant model by at least 0.01 in 78 and 12 cases respectively. Taken together, the volume data are considerably useful in improving performance.
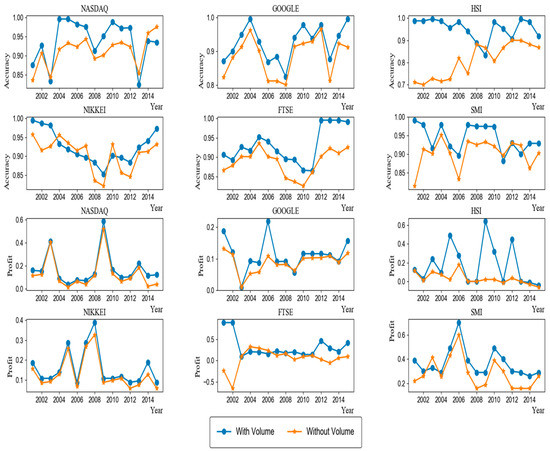
Figure 8.
Comparison of the performance between our model and other models without volume input data for the MLPs learning method.
5. Conclusions
In this paper, we proposed a new method for optimal daily stock trading. We used both the closing price and the trading volume to generate input variables. It is notable that they were considered with the same proportion in generating input variables, unlike most previous studies where the closing price was more intensively utilized. In addition, we defined three modelling parameters: the input window size, the target window size, and the profit threshold. The first parameter determines the number of input variables, and the second and third specify the target variable. We also would like to note that their impacts on performances were not clearly reported so far because they were simply set by trial-and-error in most previous studies. To resolve this parameterized function approximation problem, we applied SVMs and MLPs. We tested our model with six stocks for 15 years from 2001–2015; the model showed considerably high accuracy and profit. This successful performance explains the usefulness of the trading volume and the validation of the modeling parameters. Future studies will include the investigation of more complicated indicators that can be derived from either price of volume data. In addition, we will apply our method to the prediction of other financial markets such as interest rate, exchange rate and cryptocurrency.
Author Contributions
Conceived and designed the experiments: Y.-K.K. Performed the experiments: T.-A.D. Analyzed the data: T.-A.D. Wrote the paper: T.-A.D. and Y.-K.K.
Funding
This work was supported by National IT Industry Promotion Agency (NIPA) grant funded by the Korean government (MSIP) (S1106-16-1002, Development of smart RMS software for ship maintenance-based fault predictive diagnostics).
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Abhyankar, A.; Copeland, L.S.; Wong, W. Uncovering Nonlinear Structure in Real-Time Stock-Market Indexes: The S&P 500, the DAX, the Nikkei 225, and the FTSE-100. J. Bus. Econ. Stat. 1997, 15, 1–14. [Google Scholar]
- He, Y.; Fataliyev, K.; Wang, L. Feature selection for stock market analysis. In International Conference on Neural Information Processing; Springer: Berlin, Germany, 2013. [Google Scholar]
- Pring, M.J. Martin Pring’s Introduction to Technical Analysis; McGraw Hill Professional: New York, NY, USA, 2015. [Google Scholar]
- Kotler, P. Marketing Decision Making: A Model Building Approach; Holt, Rinehart and Winston: New York, NY, USA, 1971. [Google Scholar]
- Chen, J.; Hong, H.; Stein, J.C. Forecasting crashes: Trading volume, past returns, and conditional skewness in stock prices. J. Financ. Econ. 2001, 61, 345–381. [Google Scholar] [CrossRef]
- Yu, L.; Chen, H.; Wang, S.; Lai, K.K. Evolving least squares support vector machines for stock market trend mining. IEEE Trans. Evolut. Comput. 2009, 13, 87–102. [Google Scholar]
- Gallant, A.R.; Rossi, P.E.; Tauchen, G. Stock prices and volume. Rev. Financ. Stud. 1992, 5, 199–242. [Google Scholar] [CrossRef]
- Pacelli, V.; Bevilacqua, V.; Azzollini, M. An artificial neural network model to forecast exchange rates. J. Intell. Learn. Syst. Appl. 2011, 3, 57–69. [Google Scholar] [CrossRef]
- Tino, P.; Schittenkopf, C.; Dorffner, G. Financial volatility trading using recurrent neural networks. IEEE Trans. Neural Netw. 2001, 12, 865–874. [Google Scholar] [CrossRef] [PubMed]
- Hamid, S.A.; Iqbal, Z. Using neural networks for forecasting volatility of S&P 500 Index futures prices. J. Bus. Res. 2004, 57, 1116–1125. [Google Scholar]
- Zhu, M.; Wang, L. Intelligent trading using support vector regression and multilayer perceptrons optimized with genetic algorithms. In Proceedings of the IEEE 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010. [Google Scholar]
- Gupta, S.; Wang, L. Stock forecasting with feedforward neural networks and gradual data sub-sampling. Aust. J. Intell. Inf. Process. Syst. 2010, 11, 14–17. [Google Scholar]
- Cao, L.-J.; Tay, F.E.H. Support vector machine with adaptive parameters in financial time series forecasting. IEEE Trans. Neural Netw. 2003, 14, 1506–1518. [Google Scholar] [CrossRef] [PubMed]
- Mitsdorffer, R.; Diederich, J. Prediction of first-day returns of initial public offering in the US stock market using rule extraction from support vector machines. In Rule Extraction from Support Vector Machines; Springer: Berlin, Germany, 2008; pp. 185–203. [Google Scholar]
- Hussain, M.; Wajid, S.K.; Elzaart, A.; Berbar, M. A comparison of SVM kernel functions for breast cancer detection. In Proceedings of the IEEE 2011 Eighth International Conference on Computer Graphics, Imaging and Visualization (CGIV), Singapore, 17–19 August 2011. [Google Scholar]
- Kwon, Y.-K.; Moon, B.-R. Daily stock prediction using neuro-genetic hybrids. In Genetic and Evolutionary Computation—GECCO 2003; Springer: Berlin, Germany, 2003. [Google Scholar]
- Kwon, Y.-K.; Moon, B.-R. A hybrid neurogenetic approach for stock forecasting. IEEE Trans. Neural Netw. 2007, 18, 851–864. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Yang, Z.; Song, Y. Intelligent stock trading system based on improved technical analysis and Echo State Network. Expert Syst. Appl. 2011, 38, 11347–11354. [Google Scholar] [CrossRef]
- Kim, K.-J. Financial time series forecasting using support vector machines. Neurocomputing 2003, 55, 307–319. [Google Scholar] [CrossRef]
- Chang, P.-C.; Liu, C.-H.; Lin, J.-L.; Fan, C.-Y.; Ng, C.S.P. A neural network with a case based dynamic window for stock trading prediction. Expert Syst. Appl. 2009, 36, 6889–6898. [Google Scholar] [CrossRef]
- Fang, Y.; Fataliyev, K.; Wang, L.; Fu, X.; Wang, Y. Improving the genetic-algorithm-optimized wavelet neural network for stock market prediction. In Proceedings of the IEEE 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014. [Google Scholar]
- Roh, T.H. Forecasting the volatility of stock price index. Expert Syst. Appl. 2007, 33, 916–922. [Google Scholar]
- Bhat, A.A.; Kamath, S.S. Automated stock price prediction and trading framework for Nifty intraday trading. In Proceedings of the IEEE 2013 Fourth International Conference on Computing, Communications and Networking Technologies (ICCCNT), Tiruchengode, India, 4–6 July 2013. [Google Scholar]
- Dong, G.; Fataliyev, K.; Wang, L. One-step and multi-step ahead stock prediction using backpropagation neural networks. In Proceedings of the IEEE 2013 9th International Conference on Information, Communications and Signal Processing (ICICS), Tainan, Taiwan, 10–13 December 2013. [Google Scholar]
- Mittermayer, M.-A. Forecasting intraday stock price trends with text mining techniques. In Proceedings of the IEEE 37th Annual Hawaii International Conference on System Sciences, Big Island, HI, USA, 5–8 January 2004. [Google Scholar]
- de Oliveira, F.A.; Zárate, L.E.; de Azevedo Reis, M.; Nobre, C.N. The use of artificial neural networks in the analysis and prediction of stock prices. In Proceedings of the 2011 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Anchorage, AK, USA, 9–12 October 2011. [Google Scholar]
- Wang, L. Wavelet neural networks for stock trading and prediction. In Proceedings of the SPIE Defense, Security, and Sensing, Baltimore, MD, USA, 29 April–3 May 2013; Volume 29. [Google Scholar]
- Mubarik, F.; Javid, A. Relationship between stock return, trading volume and volatility: Evidence from Pakistani stock market. Asia Pac. J. Financ. Bank. Res. 2009, 3, 3. [Google Scholar]
- Kanas, A.; Yannopoulos, A. Comparing linear and nonlinear forecasts for stock returns. Int. Rev. Econ. Financ. 2001, 10, 383–398. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, H.; Xu, L.; Li, H. Predicting stock index increments by neural networks: The role of trading volume under different horizons. Expert Syst. Appl. 2008, 34, 3043–3054. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).