Tourist Flow Prediction Based on GA-ACO-BP Neural Network Model
Abstract
1. Introduction
- To address the limitations of previous studies that relied too heavily on historical tourist flow data, we introduced multiple influencing factors, including holiday types, climate comfort, and search popularity index on online map platforms, in addition to historical data such as yesterday’s tourist flow, the previous day’s tourist flow, and tourist flow during the same period last year, to assess tourist travel intentions and improve the accuracy of tourist flow predictions.
- To address the issue of BP neural networks easily falling into local optima and affecting prediction accuracy, we introduce a genetic algorithm (GA) to optimize the initial weights and thresholds of BP neural networks. GA has good global search capabilities and can effectively solve the problem of BP neural networks easily falling into local optima, improving the prediction accuracy and training convergence stability of the model.
- To address the issue of low local convergence efficiency in GA when optimizing BP neural networks, we further introduce the ant colony optimization algorithm (ACO) to improve real-time prediction performance. ACO accelerates the model’s convergence speed in local regions by simulating the transmission and accumulation of pheromones to guide weight adjustment paths. Additionally, using GA’s optimization results as ACO’s initial solution to initialize pheromone distribution helps overcome the issue of slow global search speed in the early stages of ACO due to insufficient pheromones.
2. Materials and Methods
2.1. Data Collection
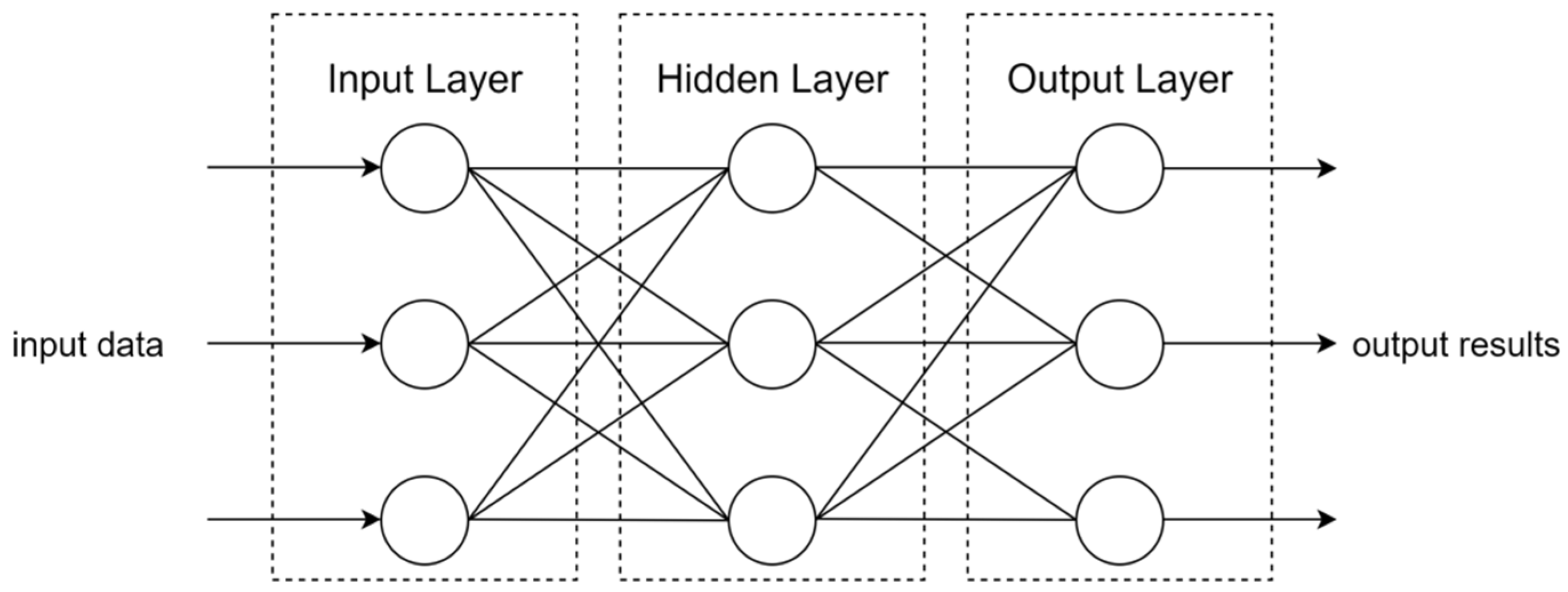
2.2. BP Neural Network Model
2.3. Improvements to the BP Model
2.3.1. Introduction of Genetic Algorithms
- 1.
- Initialize the population. Randomly generate an initial population of individuals. For each individual, use a linear interpolation function to generate a real number gene vector within a given data selection range as a chromosome of the GA. Use real number encoding to ensure that chromosomes can be directly mapped to the parameters of the BP neural network, thereby improving search efficiency and accuracy.
- 2.
- Evaluate individual fitness. Based on the optimized parameters of the BP neural network, assign the chromosomes generated in step 1 as the weights and thresholds of the network, and train using the training sample set. Then, calculate the sum of squared training errors to evaluate the fitness of each individual. If the fitness of the individual meets the termination condition, output the optimal solution. Otherwise, continue with the next step of genetic operation.
- 3.
- Perform individual selection operations based on the roulette wheel method using fitness ratios. The selection probability of each individual is related to its fitness, and the specific calculation method is shown in Formula (4):
- 4.
- Perform crossover operations. Crossover operations involve crossing genes at random positions on the chromosomes of two individuals to generate new offspring individuals. For example, the crossover operations for gene and gene at position are shown in Formula (5):
- 5.
- Perform mutation operations. Mutation operations adjust specific genes of individuals to enhance the global search capability of the algorithm. For example, select the jth gene of the ith individual for mutation operations. The specific calculation method is shown in Formula (6):
- 6.
- Select the individual with the optimal fitness as the optimal solution of GA and use the chromosome of that individual as the initial weight and threshold of the BP neural network.
2.3.2. Introduction of Ant Colony Optimization Algorithm
- Initialize pheromone distribution and ant colony parameters. We treat the weights and thresholds in the BP neural network as nodes on the ant colony search path, and the pheromone concentration is used to represent the importance of the corresponding path. Randomly initialize the pheromone concentration on the path, and set the number of ants, pheromone evaporation rate, and maximum number of iterations according to the problem scale while determining the initial distribution position of the ants.
- Selecting paths and constructing candidate solutions. During the search process, ants use a probability transfer mechanism to determine their next move based on the pheromone concentration and heuristic information on the current path, gradually constructing candidate solutions. The path selection probability formula is as follows:
- 3.
- Update pheromones. Update the pheromone distribution along the search paths of all ants based on their search paths. Pheromones along shorter paths are enhanced to guide more ants toward that path. At the same time, pheromones along the path also evaporate over time to prevent the algorithm from getting stuck in a local optimum. The pheromone update formula is shown in Formula (9), and the pheromone evaporation formula is shown in Formula (10):
- 4.
- Determine whether the termination conditions are met, such as reaching the maximum number of iterations or the error of the solution being less than the preset target. If the termination conditions are met, end the search process. Otherwise, jump to step 2.
- 5.
- Output the optimal solution. Select the path with the highest pheromone concentration as the currently found global optimal solution and use its corresponding weight and threshold as the initial parameters of the BP neural network.
2.3.3. GA-ACO-BP Neural Network Model
3. Results
3.1. Experimental Environment and Training Parameters
3.2. Evaluation Criteria
3.3. Comparative Experiment of Hidden Layer Nodes in BP Neural Networks
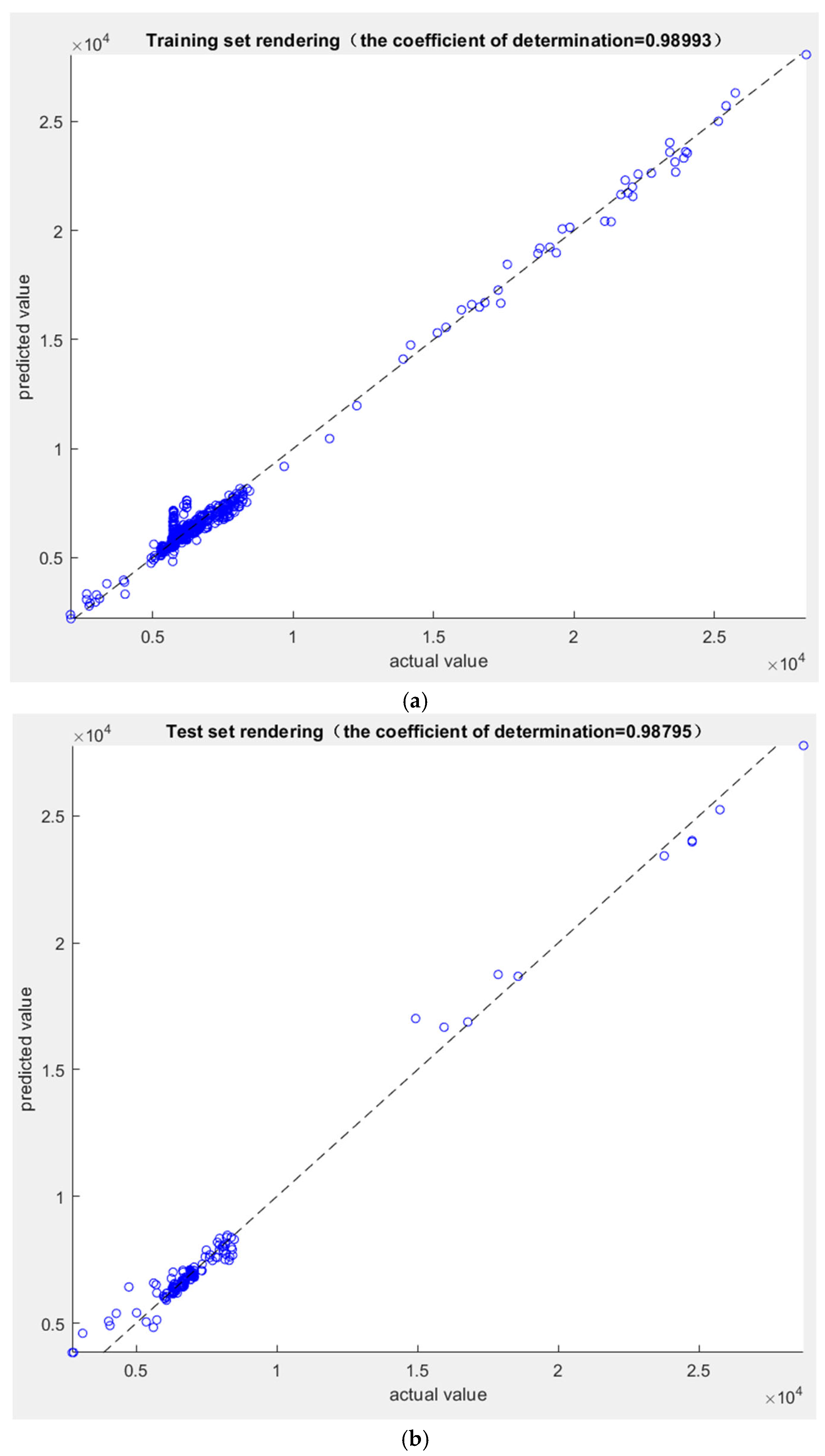
3.4. Tourist Flow Prediction Results of the GA-ACO-BP Model
3.5. Comparative Experiments of Different Prediction Models
3.6. Ablation Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Wang, Q.; Zhang, L.; Cai, D. Big data in China tourism research: A systematic review of publications from English journals. J. China Tour. Res. 2022, 18, 453–471. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Yang, Y.; Tan, Y.; Geng, T.; Wang, S. Short-and long-term prediction and determinant analysis of tourism flow networks: A novel steady-state Markov chain method. Tour. Manag. 2025, 109, 105139. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Fan, L.; Shi, S.; Zhang, T.; Qi, M. Research on the prediction of dangerous goods accidents during highway transportation based on the ARMA model. J. Loss Prev. Process Ind. 2021, 72, 104583. [Google Scholar] [CrossRef] [PubMed]
- Alabdulrazzaq, H.; Alenezi, M.N.; Rawajfih, Y.; Alghannam, B.A.; Al-Hassan, A.A.; Al-Anzi, F.S. On the accuracy of ARIMA based prediction of COVID-19 spread. Results Phys. 2021, 27, 104509. [Google Scholar] [CrossRef] [PubMed]
- Law, R. Back-propagation learning in improving the accuracy of neural network-based tourism demand forecasting. Tour. Manag. 2000, 21, 331–340. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Li, Y.; Cao, H. Prediction for tourism flow based on LSTM neural network. Procedia Comput. Sci. 2018, 129, 277–283. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Chen, Q.; Li, W.; Zhao, J. The use of LS-SVM for short-term passenger flow prediction. Transport 2011, 26, 5–10. [Google Scholar] [CrossRef]
- Suykens, J.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Liu, L.; Chen, R. A novel passenger flow prediction model using deep learning methods. Transp. Res. Part C Emerg. Technol. 2017, 84, 74–91. [Google Scholar] [CrossRef]
- Sze, V.; Chen, Y.; Yang, T.; Emer, J. Efficient processing of deep neural networks: A tutorial and survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef]
- Hu, H.-X.; Hu, Q.; Tan, G.; Zhang, Y.; Lin, Z.-Z. A Multi-Layer Model Based on Transformer and Deep Learning for Traffic Flow Prediction. IEEE Trans. Intell. Transp. Syst. 2023, 25, 443–451. [Google Scholar] [CrossRef]
- Lin, T.; Wang, Y.; Liu, X.; Qiu, X. A Survey of Transformers. AI Open 2022, 3, 111–132. [Google Scholar] [CrossRef]
- Li, K.; Lu, W.; Liang, C.; Wang, B. Intelligence in tourism management: A hybrid FOA-BP method on daily tourism demand forecasting with web search data. Mathematics 2019, 7, 531. [Google Scholar] [CrossRef]
- Pan, Q.; Sang, H.; Duan, J.; Gao, L. An improved fruit fly optimization algorithm for continuous function optimization problems. Knowl.-Based Syst. 2014, 62, 69–83. [Google Scholar] [CrossRef]
- Li, K.; Liang, C.; Lu, W.; Li, C.; Zhao, S.; Wang, B. Forecasting of short-term daily tourist flow based on seasonal clustering method and PSO-LSSVM. ISPRS Int. J. Geo-Inf. 2020, 9, 676. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Wang, K.; Ma, C.; Qiao, Y.; Lu, X.; Hao, W.; Dong, S. A Hybrid Deep Learning Model with 1DCNN-LSTM-Attention Networks for Short-Term Traffic Flow Prediction. Phys. A Stat. Mech. Appl. 2021, 583, 126293. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of Deep Learning: Concepts, CNN Architectures, Challenges, Applications, Future Directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.; Rui, H.; Liang, C.; Jiang, L.; Zhao, S.; Li, K. A Method Based on GA-CNN-LSTM for Daily Tourist Flow Prediction at Scenic Spots. Entropy 2020, 22, 261. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Siami-Namin, A. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 3285–3292. [Google Scholar] [CrossRef]
- Wen, X.; Li, W. Time series prediction based on LSTM-attention-LSTM model. IEEE Access 2023, 11, 48322–48331. [Google Scholar] [CrossRef]
- Adankon, M.; Cheriet, M. Model selection for the LS-SVM. Application to handwriting recognition. Pattern Recognit. 2009, 42, 3264–3270. [Google Scholar] [CrossRef]
- Shahani, N.; Zheng, X. Predicting backbreak due to blasting using LSSVM optimized by metaheuristic algorithms. Environ. Earth Sci. 2025, 84, 156. [Google Scholar] [CrossRef]
- Hu, C.; Zhao, F. Improved methods of BP neural network algorithm and its limitation. In Proceedings of the 2010 International Forum on Information Technology and Applications, Kunming, China, 16–18 July 2010; Volume 1, pp. 11–14. [Google Scholar] [CrossRef]
- Holland, J. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Jiang, C. Research on optimizing multimodal transport path under the schedule limitation based on genetic algorithm. J. Phys. Conf. Ser. 2022, 2258, 012014. [Google Scholar] [CrossRef]
- Beg, A.; Islam, M. Advantages and limitations of genetic algorithms for clustering records. In Proceedings of the 2016 IEEE 11th Conference on Industrial Electronics and Applications (ICIEA), Hefei, China, 5–7 June 2016; pp. 2478–2483. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stützle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2007, 1, 28–39. [Google Scholar] [CrossRef]
- Blum, C. Ant colony optimization: Introduction and recent trends. Phys. Life Rev. 2005, 2, 353–373. [Google Scholar] [CrossRef]
- Yang, J.; Zhuang, Y. An improved ant colony optimization algorithm for solving a complex combinatorial optimization problem. Appl. Soft Comput. 2010, 10, 653–660. [Google Scholar] [CrossRef]
- Panda, S.; Panda, G. Performance evaluation of a new BP algorithm for a modified artificial neural network. Neural Process. Lett. 2020, 51, 1869–1889. [Google Scholar] [CrossRef]
- Huang, G.; Zhu, Q.; Siew, C. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Zhang, Y.; Cui, N.; Feng, Y.; Gong, D.; Hu, X. Comparison of BP, PSO-BP and statistical models for predicting daily global solar radiation in arid Northwest China. Comput. Electron. Agric. 2019, 164, 104905. [Google Scholar] [CrossRef]








| Model | Parameter Name | Parameter Value |
|---|---|---|
| Learning rate | 0.01 | |
| BP | Target training error | 0.0001 |
| Maximum number of iterations | 1000 | |
| Population size | 20 | |
| GA | Cross probability | 0.8 |
| Mutation probability | 0.1 | |
| Maximum number of generations | 50 | |
| Ant population size | 20 | |
| Pheromone factor | 2 | |
| ACO | Heuristic function factor | 3 |
| Pheromone evaporation rate | 0.5 | |
| Maximum number of iterations | 50 |
| Model | MAPE (%) | RMSE | MAE | R2 |
|---|---|---|---|---|
| BP | 5.21 | 670.38 | 381.71 | 0.97005 |
| LSSVM | 4.46 | 498.92 | 302.50 | 0.98341 |
| LSTM | 4.65 | 493.62 | 306.83 | 0.98376 |
| ELM | 5.54 | 640.18 | 377.50 | 0.97269 |
| PSO-BP | 4.18 | 481.19 | 280.42 | 0.98457 |
| GA-ACO-BP | 4.09 | 426.34 | 258.80 | 0.98795 |
| Model | MAPE (%) | RMSE | MAE | R2 |
|---|---|---|---|---|
| BP | 5.21 | 670.38 | 381.71 | 0.97005 |
| GA-BP | 4.42 | 473.27 | 303.12 | 0.98515 |
| ACO-BP | 4.17 | 442.43 | 284.91 | 0.98691 |
| GA-ACO-BP | 4.09 | 426.34 | 258.80 | 0.98795 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Cheng, Y.; Dong, M.; Xie, X. Tourist Flow Prediction Based on GA-ACO-BP Neural Network Model. Informatics 2025, 12, 89. https://doi.org/10.3390/informatics12030089
Yang X, Cheng Y, Dong M, Xie X. Tourist Flow Prediction Based on GA-ACO-BP Neural Network Model. Informatics. 2025; 12(3):89. https://doi.org/10.3390/informatics12030089
Chicago/Turabian StyleYang, Xiang, Yongliang Cheng, Minggang Dong, and Xiaolan Xie. 2025. "Tourist Flow Prediction Based on GA-ACO-BP Neural Network Model" Informatics 12, no. 3: 89. https://doi.org/10.3390/informatics12030089
APA StyleYang, X., Cheng, Y., Dong, M., & Xie, X. (2025). Tourist Flow Prediction Based on GA-ACO-BP Neural Network Model. Informatics, 12(3), 89. https://doi.org/10.3390/informatics12030089







