Abstract
Decentralized finance (DeFi) has exploded in popularity with a billion-dollar market cap. While uncollateralized lending, known as a flash loan, emerged from DeFi, it has become a primary tool used by attackers to drain investment tokens from DeFi networks. The existing countermeasures seem practical, but no comprehensive quantitative analysis framework was available to test them. This paper proposes the Flash loan Attack Analysis (FAA) framework, which aids security practitioners in understanding the DeFi system’s effects on preventative methods when various factors change. The quantitative predictions can help security professionals in identifying hidden dangers and more efficiently adopting countermeasure strategies. The simulation predicts that the existing strategy, fair reserves, can fully protect the platform in a typical market environment; however, in a highly volatile market where the token price drops by 60% in a single hour, it will be broken, causing more than $8 million in damage.
1. Introduction
Blockchain technology has enabled the emergence of new financial markets and instruments, so-called decentralized finance (DeFi) [1]. As opposed to traditional financial markets, DeFi removes intermediaries from most parts of the transactions [2]. In particular, DeFi has demonstrated several advantages in terms of decentralization, and censorship resistance; it also provides liquidity for long-tailed assets through automated market makers, such as the ubiquitous constant function market makers [3]. Hence, DeFi grew rapidly between 2021 and 2022, with approximately $220 billion in total value locked (TVL) [4]. This growth indicates its potential to control a sizable transaction volume of global finance in the future.
One of the new concepts that has emerged from blockchain-based financial markets is an uncollateralized lending service known as a flash loan [5], in which a borrower can take out cryptocurrency loans without providing any collateral and repay the loan with interest in the same transaction as the loan origination. These activities need to be bundled into the transaction to ensure the atomicity property; therefore, the lender’s profit is guaranteed, or the transaction is canceled. Usually, a flash loan is used to swap loan collateral asset types or pursue arbitrage opportunities with minimal capital outlay; also, the flash loan service is popular among decentralized exchange (DEX) platforms. For instance, one could borrow USDT from a flash loan provider and exchange it for ETH on a market at a discount rate. The borrower then sells that ETH at a premium rate in another market to obtain more USDT. The flash loan protocol requires the borrower to repay USDT with a small fee. The remaining USDT becomes borrower’s profit. All steps are executed in one transaction.
Although DeFi brings new opportunities to the financial market, many exploitations have emerged, especially attacks related to flash loans that allow malicious traders to manipulate markets by using uncollateralized loans. Warp Finance and Ecosystem report significant assets lost due to flash loan attacks. Notable examples include the loss of $7.8 million DAI from the Warp Finance attack [6] and $0.53 million in damage from the Dopple Finance hack [7]. Generally, after a postmortem, remediation methods will be proposed to prevent future attacks. For instance, the Alpha Finance lead developer [8] reveals that the attacker in the Warp Finance exploit used the LP token value calculation vulnerability. Since the reserved amount used is in real-time, it can be manipulated, allowing the attacker to change the reserved amount by exploiting the flash loan service. In response, Alpha Finance proposed a prevention solution by introducing the time-weighted-average reserve (TWAR), so-called “fair reserves”. This method calculates the LP token price based on the average amount of tokens in the Alpha Finance pool [8]. On the other hand, after the Warp Finance postmortem [7], the time-weighted average price (TWAP) [9] was proposed to protect against flash loan attacks. The TWAP is calculated by dividing the total value of all trades made within the specified time period by the total volume of those trades. The TWAP method thwarts attackers from the Warp Finance; however, solutions such as the fair reserves model are ad hoc and require highly specialized experts in the DeFi and blockchain system to create. Moreover, debugging the distributed system is complicated, and the number of field experts is limited. An exploited platform loses not only equity but also the project’s credibility. Therefore, intensive validation is required to minimize vulnerabilities in the system. Despite the high demand for a solution to this issue, the number of articles related to smart contract model validation remains very limited.
Therefore, this paper proposes a novel Flash loan Attack Analysis (FAA) framework to help providers analyze DeFi attacks and validate mitigation solutions based on a mathematical simulation. The simulation is not only efficient at revealing hidden risks but also cost effective. The Warp Finance attack [6] was used to validate the mathematical models of the proposed framework, specifically, by using the Ethereum blockchain data snapshot at block number 11,473,329, which was the time of attack. Thus, the FAA simulation is compatible with real-world blockchain data. Moreover, by using attack flow data from a previous incident, FAA can validate the efficiency of mitigation models used by the prevention protocols. Specifically, we conducted analyses of existing risk mitigation (e.g., the fair reserve model [8]) to determine its efficiency. The fair reserves model was defined as a mathematical plugin for our proposed model to analyze the damage from the incident after the fair reserves were applied. Finally, we conducted complete quantitative analyses that will assist experts in comparing the effectiveness of different prevention models and discovering the hidden risks of each solution. Specifically, when the FAA framework is successfully applied, a risk report on the protocol can be generated. Here, the report contains results from the mitigation test, the internal parameter test, and the external parameter test. Hence, a DeFi developer or expert could adjust and re-evaluate the prevention model to minimize the risks of the system accordingly.
Our framework is designed for assessing and delineating the DEX platform that utilizes flash loans without restrictions. It is not suitable for the DEX platform that bans flash loans or imposes some kinds of flash loan attack protections (more details in Section 5). Additionally, this framework can only apply to the DEX platform, which retrieves the on-chain data (transactions from the blockchain). In contrast, it is not suitable for the platform that takes off-chain data (the value outside of the blockchain).
To the best of our knowledge, there is no similar DeFi risk assessment framework that specifically analyzes price manipulation attacks with flash loans. Thus, it is safe to state that the proposed framework is a novel work in this area. The approach can be specifically used for the flash loan price manipulation attack. We design the framework using the complex Warp Finance exploit case and make it broad enough to cover other flash loan price attack cases.
This work emphasizes the design of the smart contract code that is secured from a flash loan attack. Our contributions are as follows:
- (i)
- We proposed the FAA framework that allows security researchers to simulate attacks in different environments and a suitable and versatile risk countermeasure for the DeFi platform (see details in Section 3.1 and Section 3.2).
- (ii)
- We analyzed the efficiency of the existing fair reserves model by determining the potential damage prevented by the model in many circumstances. The report from the proposed FAA framework provides insight validation of the fair reserves protocol. It is crucial to ensure that the model is well validated before applying it to prevent potential damage (details are given in Section 3.3).
- (iii)
- We conducted simulations on flash loan sizes, collateral ratios, and market conditions to predict the degree of damage on the DeFi platform. Our analyses unveil the strengths and weaknesses of the existing TWAP and fair reserves models with respect to various internal and external conditions. Details of the analyses are discussed in Section 3.4 and Section 3.5, while our insights are presented in Section 4.
- (iv)
- We suggested a holistic prevention approach, which consists of the top six (6) best countermeasures to flash loan attacks (Section 5).
This work is organized as follows. Section 2 reviews blockchain and DeFi, the benefits of flash loans, exploit cases, and prevention methods. Section 3 describes the FAA framework and demonstrates the application of the framework with the Warp Finance exploit. The case is analyzed in many respects, including mitigation tests, internal parameter tests, and external parameter tests. Section 4 presents our insights from the analyses. Section 5 discusses the experimental results and demonstrates additional prevention methods. Finally, the work is concluded in Section 6.
2. Related Work
2.1. Blockchain, DeFi, and Smart Contract
Blockchain technology can be applied in various domains such as logistic [10], voting [11], and payment [12]. In addition, it generates innovation, especially in a financial domain. It eliminates several operating costs in the centralized financial system. Hence, the blockchain led to the emergence of DeFi, which comprises various financial services [13], such as stable coins, lending, borrowing, exchange, lottery, crowdfunding, etc. Specifically, a smart contract [2] is one of the key technologies that eliminate several operating costs required by the centralized financial system. Additionally, the smart contract is a crucial mechanism used to guarantee the integrity of a review platform [14,15].
The new ecosystem attracts many investors, as it is easier to transfer digital assets represented by tokens among user while users’ privacy is preserved [16]. As reported by Gua and Liang [17], DeFi yields a significant profit over traditional finance (TradFi) in 2016.
2.1.1. DeFi Vulnerability
Indeed, all investment opportunities come with risks. Particularly, several kinds of platform vulnerabilities. DeFi vulnerabilities can take many different forms and can have various motivations, but some common categories of DeFi attacks include:
- (i)
- Price manipulation: These attacks involve the use of flash loans [18] or oracle [19] to manipulate the prices of assets on a DeFi platform and potentially profit from the price changes.
- (ii)
- Data leakage: The sensitive data are exposed from phishing [20,21] or hacking [22]. These attacks involve the use of fake websites or other methods to trick users into revealing sensitive information, such as their private keys, which can then be used to steal their funds.
- (iii)
- Smart contract exploits: These attacks take advantage of vulnerabilities in the smart contracts that underlie DeFi platforms, allowing attackers to steal or redirect funds. For instance, the smart contract weakness classification (SWC) [23], reentrancy attack [24], front-running attack [25], and rug pull scam [26].
Interestingly, although DeFi protocols must be audited before they can be used, most of them are still compromised by attackers [22,27,28,29,30,31,32]. This indicates that smart contract verification cannot guarantee platform security. Moreover, when the code of the smart contract is upgraded, new vulnerabilities might appear.
2.1.2. Defi Risk Assessment Framework
In response to various DeFi vulnerabilities, many risk assessment frameworks have been proposed. For instance, Songsom et al. [23] proposed an algorithm to efficiently detect vulnerabilities from smart contract codes. Pengcheng Xia et al. [33], on the other hand, devised a machine learning model that automatically labels the scam from Uniswap V2 transactions history. Later, Mazorra et al. [26] proposed a framework to predict the malicious movements from ongoing trading activities. Since the flash loan attack is a different kind of vulnerability, our proposed work is complementary to these approaches.
There are many cases of rug pulls in DeFi that cannot be prevented using the time-weighted average price solution. However, this research only focuses on non-rug pull cases.
2.2. Flash Loans
A flash loan [34] is an uncollateralized and unsecured loan that must be repaid within a single blockchain transaction, guaranteed by a smart contract. The smart contract can execute any arbitrary code after borrowing to ensure that the funds are returned within the scope of the same transaction [5]. If the debt is not repaid within one transaction, the smart contract will revert all the buy/sell activities, meaning that it is as if the loan had never occurred. Various DeFi platforms provide flash loan services, such as dYdX [35], Uniswap [36], and Aave [37], which is one of the first DeFi platforms for flash loans. Flash loans currently have four main use cases.
2.2.1. Arbitrageur
DeFi economics [38,39,40] explores how individuals, businesses, and stakeholders exchange or distribute tokens at reasonable prices considering demand and supply. Arbitrageurs seek to buy tokens at a low price and sell them back at a higher price. Hence, the arbitrage mechanism helps to decrease the price gap between different DeFi platforms and increases market efficiency.
On the other hand, greedy arbitrageurs could manipulate the token price by using a large amount of funding, particularly by exploiting the flash loan service. If they do not have enough tokens in their wallets, flash loans will be used to borrow from a flash loan provider (e.g., Aave [37]) to leverage their trading position sizes and gain more profit.
2.2.2. Collateral Swap
A collateral swap describes the swapping of the collateral backing the user’s loan for another type of collateral. Cryptocurrency traders swap collateral when they expect the value of the swapping currency to decrease in the future. When they return the collateral, the actual value will be lower than the initial value, which is beneficial. For instance, consider that deposits an amount of ETH as collateral to borrow DAI and then wishes to swap collateral from ETH to BAT. However, he or she does not have enough DAI to get ETH back. One way to overcome this issue is to use a flash loan, borrowing DAI from a flash loan provider for a closing position by repaying DAI and receiving ETH back. Then, he or she swaps ETH to BAT using any DeFi swap provider (e.g., Uniswap [41]). Finally, he or she deposits BAT, borrows DAI again, and eventually returns DAI to the flash loan provider. All these steps need to be in a single transaction. Some DeFi lending platforms offer token borrowing with collateral, e.g., MakerDAO [42].
2.2.3. Self-Liquidation
When traders hold their trading position near liquidation, a flash loan can be used for self-liquidation when the price falls. For example, we can obtain DAI from a flash loan to close a DAI dept position. Then, we unlock ETH and swap it for DAI and repay DAI to the flash loan, receiving the rest of the ETH back [34].
2.2.4. Lower Transaction Fees
Since flash loans need to combine several financial transactions into a single transaction, the transaction fees are potentially lower than paying each transaction cost separately [34]. Therefore, some traders use flash loans to earn profit from the lower transaction fees.
2.3. Flash Loan Attacks
Although a flash loan can be helpful, as previously described with several use cases, it can augment a token economic exploit, especially price manipulation as known as a flash loan attack. The flash loan attack is a type of attack on a DeFi platform that involves the use of flash loans. In the flash loan attack, an attacker borrows a large amount of cryptocurrency through a flash loan, and then uses the borrowed funds to manipulate the prices of certain assets on the platform. For example, the attacker might use the borrowed funds to artificially inflate the price of a particular asset, and then sell the asset at the inflated price in order to profit. Flash loan attacks can be particularly damaging to DeFi platforms, as they can disrupt the normal functioning of the platform and potentially lead to losses for other users. Flash loan attacks can also be difficult to detect and prevent, as they often involve complex financial transactions that are executed very quickly.
As discussed previously, an arbitrageur’s objective is to augment price gaps in DeFi liquidity pools [43]. Here, liquidity provider pool size and trading volumes impact the profit (i.e., price differences) that the arbitrageur can obtain. Unfortunately, a malicious arbitrageur could exploit the flash loan service to manipulate market prices before arbitraging. Price manipulation is exemplified in the bitcoin ecosystem [44] by pump and dump schemes [27,28,29]. These schemes artificially pump up asset values to sell a position previously acquired at a better price.
Although many DeFi platforms advertise no fund risk, smart contract bugs, or operational security exploits, they have lost considerable funds because they lack price manipulation protection. As a result, several platforms have lost a large amount of liquidity. For instance, Bzx lost approximately $900K to supercharge financial attacks over a long weekend in the US [22,30,31]. Harvest finance [45] lost 33.8 M in October 2020. In the same year, an attacker used the Curve Finance Y pool [32] to swap funds and stretch stable coin prices out of proportion. Recently, $90 million was taken from the most popular lending and borrowing pool, compound [46]. A Flashot article [18] illustrates a snapshot from the DeFi attack using flash loans, where the attacker intertwines asset flows with smart contracts to manipulate the market price and thus benefit. New flash loan exploit cases occur frequently. Hence, it is essential to understand and learn prevention methods to secure the DeFi world.
Additionally, other security vulnerabilities are based on the smart contract layer, apart from common vulnerabilities. Although most vulnerabilities can be protected by using prevention techniques recommended by well-known security auditors, many smart contract developers may be unaware of these issues.
2.4. Flash Loan Attack Prevention
Despite the high number of attack incidents discussed in the last section, only a limited number of attack prevention and countermeasure approaches are presented in the literature. One high impact incident was the Warp Finance attack [6], which caused up to $8 million worth of damage. Although the TWAP solution [9] has been introduced to prevent future damage, the researchers have not analyzed the level of damage, especially in some specific cases (e.g., changing input sizes, collateral factors, and price fluctuation).
Another major incident was the Dopple Finance attack that cost the firm up to more than half a million dollars [7]. Although Dopple Finance used the TWAP oracle, it was still attacked by flash loans due to incorrect TWAP implementation. The TWAP implementation in Dopple used a spot price instead of a cumulative price which is more stable and resistant to price manipulation. In addition, Visor Finance was recently attacked by a flash loan attack twice in as many days [45,47].
Qin et al. [19] investigate flash loan attacks by describing attack parameter optimization, quantifying the opportunity loss, and identifying the impact of transaction atomicity on arbitrage. They also suggest that pump and arbitrage cases can be used to explain attacker behaviors.
Although previous usage analysis [6] and postmortems [7] of existing attacks are presented, none of these works compare fair reserve and TWAP, which are the primary flash loan prevention approaches. The best practice to protect flash loans is always using TWAP and never using spot prices from DEX. Fair reserve and modified TWAP were recently proposed after the postmortem from Warp Finance; therefore, this work proposes a damage analysis model and illustrates the application of the proposed model to the Warp Finance case.
3. A Novel DeFi Attack Risk Analysis Framework
This section presents a novel Flash loan Attack Analysis (FAA) framework for analyzing the DeFi protocol risks following an attack flow and validating the efficiency of various mitigation models.
As depicted in Figure 1, the FAA framework consists of five main processes. (Section 3.1) Damage model formulation: this process converts attack steps (e.g., flowchart, transaction steps, or text description) to a damage model. Additionally, it defines a core sub-model, which is a plugin of the damage model. The core submodel represents a mitigation model, such as the LP token price calculation in the Warp Finance case. (Section 3.2) Damage model validation: the damage model is validated using the blockchain data snapshot when the system was under attack. (Section 3.3) Mitigation test: the mitigation model is plugged into the core submodel. Then, it is tested using the same blockchain data snapshot as in the previous step. The output from this process provides quantitative results indicating the efficiency of the particular attack prevention techniques. Here, the outcome is vital to measure the efficiency of the prevention techniques. As some prevention methods can protect platforms in specific cases only, the next processes are necessary for uncovering hidden risks. (Section 3.4) Internal parameter test: the internal parameters are the parameters of the protocols that can be adjusted, such as the collateral ratio, slippage tolerance, liquidation, and incentive values. In this process, protocol parameters are dynamically adjusted to test the damage and mitigation models. (Section 3.5) External parameter test: the external parameters refer to values that do not depend on the protocol, such as token prices, market conditions, and trading volumes. The impacts of external parameters are derived from the actual blockchain data. To uncover hidden risks, damage models are simulated under the conditions of internal and external parameters, and a risk report of the protocol is generated based on variations of the parameters. The risk report consists of system damages and prevention quantity under the internal and external parameters. As a result, developers can simulate the damage and protection level of the prevention strategy based on various internal and external parameter settings; hence, the DeFi protection can be maximized. The detailed steps of the process are described in the following sections.
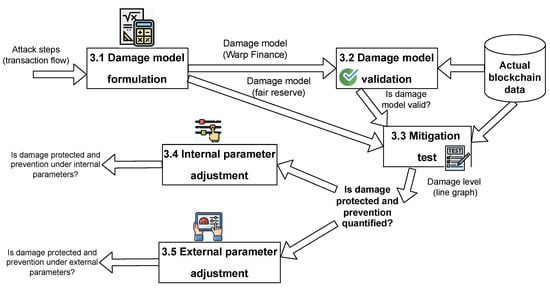
Figure 1.
System overview of the FAA framework.
3.1. Damage Model Formulation
This process is necessary to enable an insightful DeFi risk analysis because it provides a mathematical model for analyzing the damage from an attack based on different parameters. The damage model’s inputs are a sequence of actions and asset properties (the so-called attack flow); an output of the damage model is a mathematical model.
Our proposed FAA framework is developed based on data from the Warp Finance attack [6]. However, the damage model is generic for flash loan attacks on any DeFi platform as the mathematical equations define relationships between all the related parameters.
In the Warp Finance incident, the attacker conducted multiple attack steps to exploit the platform and steal tokens as illustrated in Figure 2. We walk through the exploit steps and formulate the mathematical model based on attacker’s actions. The following form the attack flow in the Warp Finance case:
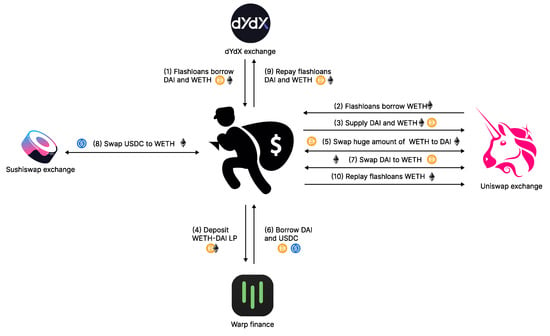
Figure 2.
Warp finance attack steps.
- (i)
- The attacker used flash loans to borrow DAI from dYdX solo margin pools. The amount of the borrowed DAI is denoted as .
- (ii)
- WETH is borrowed from the Uniswap and dYdX solo margin pools using flash loans. Let denote the maximum amount of WETH the attacker can borrow.
- (iii)
- DAI and WETH were supplied to Uniswap’s WETH-DAI pool to mint WETH-DAI LP tokens, which would be used as collateral for borrowing tokens from Warp Finance. Note that the values of the supplied DAI and WETH must be equal. Let and denote the amount of DAI and WETH in the pool, respectively.
- (iv)
- The attacker supplied all DAI () and the equivalent WETH () to the pool:The minted LP token amount (D), where represents the total supply of WETH-DAI tokens before supplying, is determined by the following equation:After adding liquidity, the pool reserved, and the total LP token supply was changed as follows:
- (v)
- Since the exploitation occurred while Warp finance was using their equation, the LP token price () was calculated using TWAP and real-time reserves, where and denote DAI and WETH TWAP, respectively:According to the report [6], the root cause of the exploitation related to the LP token price () calculation. Hence, we define the LP token price model (i.e., Equation (7)) as the core submodel, which is to be used in the upcoming steps.All the minted WETH-DAI LP tokens (D) were supplied to Warp Finance as collateral. LP token value in USD is denoted as (). The attacker was able to borrow tokens from Warp Finance. The borrowing limit (B) is the deposited LP token value divided by 1.5, which is the constant collateral value defined by the Warp Finance protocol.
- (vi)
- The attacker swapped the remaining WETH () for DAI () using the Uniswap WETH-DAI pool,Since the token swapping fee is 0.3%, is multiplied by 0.997. Thus, the trading output can be determined as:This step was the core of the attack as the attacker was able to substantially increase the amount of WETH (i.e., the expensive token) in the pool. The reserve amount changed dramatically after the trade:
- (vii)
- At this stage, the changing of real-time reserves causes LP token price updates. The manipulated LP token price is denoted as .The changing of LP token price affects borrow limit value. The manipulated borrow limit () is determined as follows:
- (viii)
- The attacker borrowed as much DAI as possible from the DAI Warp vault (). DAI was the priority borrowed token because the attacker could swap WETH back at a lower rate in the manipulated WETH-DAI pool. USDC () was borrowed as the secondary token after the vaults were emptied of DAI. The actual borrowed amounts ( and ) are thus determined by the minimum value between the borrowing limit and the available liquidity in the vaults:
- (ix)
- To accomplish the exploit, the attacker had to repay all flash loan positions, particularly, and . As the attacker received DAI from the first swap () and borrowing (), he or she could spare DAI for flash loan repayment. However, he or she did not have WETH. Hence, he or she swapped all the remaining DAI for WETH from the manipulated WETH-DAI pool. Here, we can calculate and as:As the WETH that was swapped for DAI was insufficient for repayment, the attacker used all the borrowed USDC to buy WETH from the Sushiswap WETH-USDC pool. Therefore,
- (x)
- This exploit damaged Warp Finance because the attacker borrowed more tokens than the proper limit. When the excess amount borrowed was sufficient for flash loan repayment plus the borrowing fee, the attack was considered successful. The damage from the attack can be evaluated by the number of tokens the attacker received after the success of the transaction. We therefore can calculate the value of tokens stolen from the platform (denoted ) as follows:
The next process in formulating the damage model is to define a core submodel, which is a plugin of this damage model (i.e., Equation (7)). During the analysis, several core submodels will be applied with the damage model. Since the main vulnerability is related to the LP token price calculation, the core submodel for this case is the LP token price model. In this work, two LP token price models are compared: the Warp Finance and fair reserves models.
3.1.1. Warp Finance Model
Warp Finance prevents LP token price manipulation by using Uniswap Oracle TWAP instead of relying on the real-time price, calculated from reserve tokens. However, there is no time-weighted-average reserve (TWAR) available on Uniswap Oracle [48]. Thus, it used the real-time reserve amount, which was the leading cause of the exploitation. According to Equation (7), the LP token price () can be calculated by incorporating the real-time reserve amount ( and ), the TWAP in USDC ( and ) and the total supply of LP tokens ().
Although the TWAP price is not affected by short term trade, the reserve amount changes with every trade. This factor is the main vulnerability, where attackers could increase the reserve of the expensive side token with a substantial trade on Uniswap. As a result, the LP token price dramatically increases, and attackers can borrow tokens beyond the proper borrow limit.
3.1.2. Fair Reserves Model
After the exploitation took place, the head developer of Alpha Finance demonstrated an idea to minimize damage. He proposed a fair reserve price calculation. It provides time-weighted-average reserves (TWARs), which are derived from the TWAP [49].
The constant product (k) is the product of a pair of reserves ( and ). It remains the same value during trades to keep the preserved fraction. In actual execution, the constant product changes slightly every trade due to the trading fee; however, it is negligible because the fee is very small. The k value will only change after liquidity is added. The real-time reserves and the TWARs calculate the same k value as shown in Equation (22) below.
Token prices ( and ) can be determined by the fraction of their reserves. TWAR values can be used to calculate the TWAP similarly to the real-time values:
From Equation (22), we obtain TWAR values from the following equations:
substitute Equation (24) into Equation (23):
substituting Equation (25) into Equation (23) yields:
The TWARs can be applied to the LP price calculation as follows:
The fair reserve LP token price model is promising as robust defense against price manipulation in a short period because it is independent of the real-time reserve values. While the k and values are real-time adjustable, they are fractional and have similar growth rates. As such, they are protected against manipulation.
3.2. Damage Model Validation
In this step, a damage model is evaluated to ensure the correctness of the analysis. This step uses the damage model formulated in Section 3.1 as an input. The model’s correctness is identified by comparing the actual case damage to the calculated damage.
We fetched the baseline data from block number 11,473,329 of the Ethereum blockchain, which was the moment before the attack occurred [50]. We forked the Ethereum main network state at the particular block by using the Hardhat [51] and Ethers [52] modules. The retrieved blockchain states are displayed in Table 1.

Table 1.
States of Ethereum blockchain number 11,473,329 (just before the attack).
With the baseline variables in Table 1, the models in Section 3.1.1 and Section 3.1.2 can be executed and compared with the actual case. The damage model constructed in Section 3.1 takes inputs ( and c) from the attack flow. Let denote the output, which is the damage to the DeFi platform. We substitute actual blockchain states into the damage model in Equation (20). We obtain the result shown in Table 2, column Standard.

Table 2.
Warp Finance damage model evaluation.
The result indicates that the damage calculated from the model matches the damage from the blockchain history. Specifically, the predicted value exactly matches the actual damage from the Warp Finance attack case [6]. Therefore, the damage model is valid.
3.3. Mitigation Strategies Evaluation
This stage verifies the mitigation model, which in this case is fair reserves (see Section 3.1.2). In terms of risk reduction efficiency, the mitigation model is assessed and compared to the damage model (i.e., the Warp Finance model in Section 3.1.1). This step’s inputs are all variables in Table 1, with the predicted damage in Table 2, column Fair reserves as the output.
The mitigation model for the Warp Finance attack case is the fair reserves model. We replace it with the damage model in the LP token price calculation section (i.e., the core submodel in Equation (7)). The same blockchain states from Table 1 are substituted into the derived Equation (20). The fair reserves model validation result is shown in Table 2, column Fair reserves. The predicted damage () is zero (0) when the fair reserves model is used to calculate the LP token price at the time of attack. Despite token prices being manipulated with flash loans, the platform remains safe. Hence, the fair reserves model is an effective measure against the Warp Finance exploit.
Furthermore, we study how the amount of input tokens affects the exploit damage . Here, we conducted an experiment on the variation of and the effect on the predicted damage. Figure 3 depicts the predicted system damage against the flash loan amount ranging from 0 to 500,000.00 WETH. The positive damage indicates the number of tokens that attackers drain from the platform. On the other hand, a negative value implies that the platform does not lose tokens. In fact, a negative value indicates the buffer distance that the damage caused by the attack will not impact the system. This does not mean that attackers lose tokens equal to the negative magnitude.
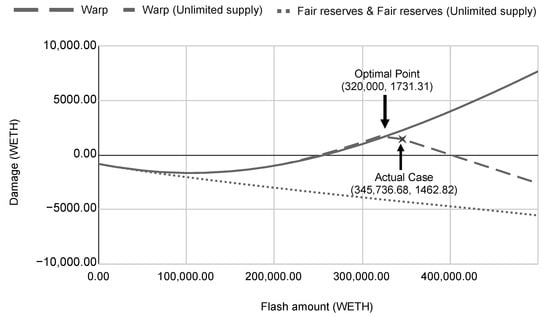
Figure 3.
Dynamic flash loan size analysis.
Considering the unlimited supply scenario of the Warp Finance case, the damage depends linearly on the flash loan size. When the platform reserves are limited, the flash loan amount does not always correlate with the damage. There is an optimal point that the attacker needs to consider before executing an attack. In the real-world incident, the attacker stole 1462.82 WETH from the platform by applying 345,736.68 flash loaned WETH, which was close to the optimal point. The flash loan amount in the real case was well calculated by the attacker, as the actual damage is close to the optimal point (see Figure 3).
While the size of the flash loan could damage Warp Finance, it does not impact the system with a fair reserves scheme. This is because the fair reserves model does not allow the price of the LP token to be changed within the same block time. As a result, increasing the flash loan size does not work under the fair reserves model.
3.4. Internal Parameter Test
Analyzing one specific case is insufficient to conclude on the effectiveness of a prevention approach. Several adjustable internal parameters of the platform, such as the collateral ratio, slippage tolerance, and liquidation incentives, could also be used to limit the potential damage caused by attackers. Moreover, some fixed parameters could be replaced with dynamic values to be more flexible in real-world situations. Hence, this step investigates the dynamics of the internal parameters to discover potential risks. Indeed, applying the proper settings can limit the potential damage caused by attackers. In this process, the proposed damage models are used as inputs, and the output demonstrates the correlation between the particular parameters and the platform risk.
First, in the Warp Finance protocol, the collateral ratio (C) is a value that can be changed internally. It relates to the user token borrowing limit (B). The limit directly correlates with the number of tokens (D) stolen from the platform. Hence, adjusting the collateral ratio will also decrease the damage from an exploit, as it limits the liquidity drained by attackers. When the collateral factor is dynamic, the borrowing limit is determined as follows:
When applying the Warp Finance LP token price model to the dynamic collateral ratio model, the borrowing limit will be
Additionally, Equation (29) can be applied to the fair reserves model. The borrowing limit with a fair reserve and an adjustable collateral ratio is
The above submodels in Equations (30) and (31) are plugged into the proposed damage model in Section 3.1 and the mitigation model in Section 3.3. We apply the actual blockchain states in these models and let the collateral ratio be an adjustable value.
Figure 4 depicts the relationship between the collateral ratio and damage from the attack. Adjusting the collateral ratio can change the number of tokens drained from the platform and thus potentially prevent exploit damage. In particular, increasing the collateral ratio will minimize the damage because it reduces the assets drained from the platform. However, the collateral ratio adjustment introduces a significant drawback. It reduces the utility of the platform. Generic users could borrow fewer tokens while depositing the same amount of collateral. While increasing the collateral ratio could gradually reduce the exploit damage, it requires the user to pay more collateral to borrow the same amount of tokens. Hence, the platform will become less attractive. Therefore, increasing the collateral ratio to prevent an attack is not a feasible method.
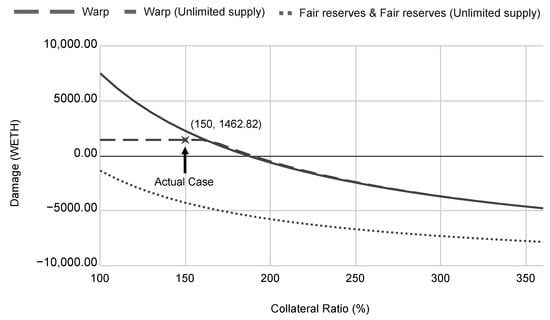
Figure 4.
Dynamic collateral ratio analysis.
3.5. External Parameter Test
Apart from the internal parameters, there are many uncontrollable external parameters of the ecosystem, for instance, token prices, trading volumes, and market conditions. These variables should also be considered as potential risks. To minimize platform risks, these values must also be analyzed.
In this process, the DeFi security practitioner will simulate blockchain states to analyze the impacts of those states on the platform risks. Considering the Warp Finance platform, the most relevant external parameter is market conditions. The platform is affected when the token price moves rapidly, i.e., a fluctuating market. In particular, if the period used to calculate the time-weighted-average value is too long, it could cause a large price difference from the real-time values. This could cause errors in some financial transactions.
Since the time-weighted-average values accumulate historical data, they reflect market conditions more slowly than the real-time data. There might be some cases where the difference between the real-time price and the TWAP is large enough to be exploited. Therefore, we propose models to analyze the degree of damage under any market conditions.
First, we need to simulate market conditions under which the real-time price and TWAP are different. Let denote the price difference, and let define a real-time price under any market conditions. Therefore,
.
Token reserves are the only primitive variables that cause price changes. Therefore, they must be derived to enable price fluctuation analysis under any market conditions. Here, the derived reserve values () can be obtained from the constant product equation:
The derived price can also be calculated in the same way as TWARs and real-time reserves:
finding :
substituting yields:
finding :
After obtaining the derived reserve values, we can apply them to all models that we wish to analyze under various market conditions. The model is validated to ensure the correctness of the outcome. Therefore, we compare the derived reserves with the actual reserves at a target price. The model is valid when the two values are equal. From the actual data, the differences between the real-time price and TWAP are:
Then, we apply the price differences to the model to find the reserve value:
According to the actual case in Table 1: , there were 90,409.01 WETH in the DAI-WETH Uniswap pool. This is slightly different from 90,211.72882, which was the simulated value . Here, the degree of difference is 0.2186%. This was because the TWAP was fetched from the USDC-WETH pool, but the simulated reserve amount was related to the DAI-WETH pool. As mentioned in Section 3.2, the simulated value must be the same as the actual value. However, there was no TWAP for the DAI-WETH pool. Thus, we used the USDC-WETH pool to simulate DAI-WETH reserves. Considering the degree of difference, the simulation result is acceptable.
However, price fluctuations influence the exploit damage. When token prices change rapidly, the margin between the real-time value and time-weighted-average value increases. A large price gap might cause vulnerabilities in platforms that rely on TWAP.
Figure 5 demonstrates that the exploit damage varies under different market conditions. The Warp Finance exploit case relies on the WETH price from two different sources, i.e., the real-time price and the TWAP. In our analysis, we simulated market conditions based on the difference between price sources, namely, and . Negative delta values represent the bear market condition, where the WETH prices drop dramatically in a short period of time. The real-time price is lower than the TWAP in a bear market. In contrast, the bull market condition occurs when the token price drastically rises. The real-time price is higher than the TWAP.
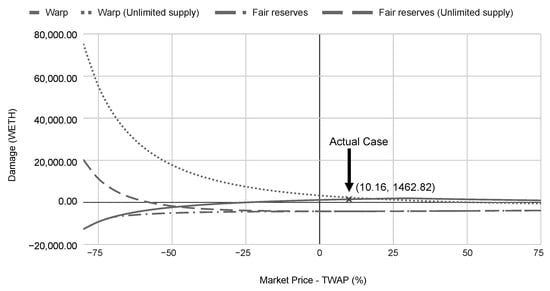
Figure 5.
Dynamic market condition.
Market fluctuations potentially damage in both the Warp Finance model and the fair reserves model. According to our simulations, the exploit damage is expanded when the WETH price dramatically falls, i.e., the negative x-axis in Figure 5. A bear market supports attackers in leveraging TWAP WETH to borrow stable coins from the platform and use them to buy back WETH at a discount rate, i.e., the real-time price. Thus, they obtain extra WETH after the flash loan repayment. When the market crashes, attackers can drain assets from the platform without price manipulation. As a result, the fair reserves model, which can protect against short term price manipulation, cannot prevent damage in this case.
As shown in Figure 5, the attack damage mostly occurs in unlimited supply cases. There are many external conditions that attenuate exploit damage in limited supply cases, such as limited borrowing amounts, slippages, and price impacts. However, it is difficult to find such a vulnerability, which requires the WETH price to decrease by at least 60% before the TWAP updates (i.e., 1 h in the Warp Finance case). In fact, the causes of the market crash, for example, rug pull [26], failure of the project, and hacking, are significant. Moreover, attackers will face challenges, such as, a high transaction fee or a quick recovery of the market price difference. Specifically, if they attempt to attack the platform, the blockchain traffic will be congested. Hence, the fee becomes more expensive. Moreover, when there is a price difference between markets, arbitrageurs will quickly recover the price difference between the two platforms. Hence, it is difficult for attackers to exploit in extreme market conditions. However, our best practice suggestion is to prepare for such cases.
4. Our Insights
This paper provides insight into possible exploit damage, which can be used to evaluate prevention methods. Specifically, for the case of Warp Finance, the fair reserve model was proposed to prevent flash loan attacks. Model valuation can be accomplished by considering the damage it can prevent. The fair reserves model can protect 1462.82 WETH in damage from the Warp Finance platform exploit. The protected values are expanded under increased supplies. This means that the model should be evaluated on at least 1462.82 WETH and can be scaled up with the project supply.
The results from Section 3.3–Section 3.5 indicate that the Warp Finance LP token price model fails to protect the exploit in most circumstances. Specifically, the damage increases in the size of flash loans. Raising the collateral ratio can limit the exploit damage, but it affects the general applications of the platform. The damage is much expanded in a bear market, which exhibits a price between real-time price and TWAP.
On the other hand, the fair reserves model is a promising solution that can completely protect against the exploit damage under normal market conditions. Attackers cannot cause damage to the platform regardless of flash loan sizes. However, in an extreme downtrend (i.e., token prices fall by at least 60% in one hour), exploit damage exists under the fair reserves model. It is a rare case but should be considered to cover all risk factors in the platform. After applying the FAA framework, we found a risk that has not been mentioned in any media. We suggest a workaround to address this issue by adding an instant oracle update when token prices drastically change. Moreover, there are several methods to respond to flash loan attacks, such as delay requirements, sanity checks, limited minting, using distributed price sources, and complying with TWAP best practices. The trade-offs of these methods will be discussed in the following section.
5. Flash Loan Countermeasures
This section suggests six (6) flash loan countermeasures for protecting the DeFi system against adversaries. These techniques can also be applied and tested with the FAA framework proposed in Section 3 to harden the security of the DeFi platform. We incorporate existing solutions with lessons learned from several analyses conducted in this research to suggest the best practice for the DeFi developer and researcher, as detailed below.
5.1. TWAP Update Threshold Technique
The fair reserves model could protect against all damages in a normal market. However, according to our analysis in Section 3.5, the fair reserves model is still vulnerable in an extreme downtrend. When the real-time price falls and TWAP does not update, there is a price gap that allows traders to borrow many tokens from the platform and spend them at a premium price. This could cause damage to the platform. There is a workaround to prevent rapid market fluctuation, specifically, defining a price change threshold to trigger TWAP updating. This method will balance the real-time price and the TWAP and prevent damage in extreme market conditions.
5.2. Delay Requirement Technique
This countermeasure could disrupt a flash loan attack, as all internal transactions must be completed within a time block to satisfy flash loan execution [5]. As a result, flash loan attacks are completely blocked from the system. Therefore, this strategy is unsuitable for any flash loan service. However, this method cannot protect against damage if the attacker spends his or her own tokens attacking the platform.
Note that, this solution does not completely ban the flash loan functionality. If the DEX wants to provide a flash loan service, it can enable the flash loan. The implementation of the delay solution will only block the “in-bound” flash loan from outside the DEX, whereas the “out-bound” flash loan from the DEX to other platforms will still be available. Hence, this solution allows DEX to block the flash loan from high-risk schemes.
5.3. Sanity Check Technique
With the atomic characteristic of a blockchain transaction, all state changes can be reverted if they do not meet a specific condition. Here, a sanity check technique is used to validate any state before and after an activity. A check statement [53] can be included at the end of a transaction to prevent an anomaly. For instance, the LP token price can be recorded at the beginning of the transaction and checked if it changes excessively at the end of that transaction.
5.4. Minting Limit Technique
A minting limit can be implemented in a smart contract. It restricts the maximum flash loan volume per day to reduce risk from flash loan attacks. However, the daily minting limits may cause a development team to pay more attention to the system every day. Therefore, they can be extended to limit minting by phase.
Phase minting separates minting into phases. For example, let us set the phase minting limit to 10 K, 20 K, and 100 K. When LP tokens nearly reach the minting limit at each phase, the system will go to the next phase or the minting limit will be increased by using votes from a system that has governance tokens. In addition, the phased minting limit usually includes a time lock [54] to be more transparent and secure.
5.5. Multiple Price Source Technique
In many cases, platforms that obtain token prices from an oracle are still vulnerable to price manipulation attacks. A single price source, especially an automated market maker (AMM) price oracle [48], might be insufficient to protect against price manipulation. Hence, using more than one price source makes the system more difficult and expensive to manipulate. The price sources should be curated from different points [55].
5.6. Suggested Practice for TWAP Implementation
Although the concept of TWAP seems to be sufficient to prevent price manipulation from the rapid change of the token price, an incident related to the improper implementation of the TWAP technique can still be seen. For instance, a report in [7] indicates that the root cause of the Dopple Finance attack was due to improper TWAP implementation in which the platform obtained only a few data points from an oracle. Hence, the attacker can easily manipulate the token price within only one update. In addition to the number of data points, the updating interval should also be considered carefully. Specifically, the too-short period might not prevent price manipulation efficiently, whereas the too-long period could cause a price inefficiency issue. Here, our proposed FFA framework can be used to do quantitative analysis to estimate the best parameter settings, e.g., the number of data points from an oracle and the optimal period to consider.
6. Conclusions
This paper proposes the FAA framework for conducting an insightful analysis of DeFi exploits. Our framework was used to analyze the famous Warp Finance exploit. It allows us to determine the damage while varying many internal and external factors, including dynamic flash loan sizes, the adjustable collateral ratio, and market fluctuations. We have presented an insightful analysis of the Warp Finance and fair reserves LP token price prevention methods. Our analysis indicated that the Warp Finance LP token price model failed to prevent exploitation in most circumstances; specifically, the damage increases with the size of flash loans. Although the fair reserves model was a promising solution, in an extreme market downtrend (i.e., token prices fall by at least 60% in an hour), exploit damage was still predicted. Many scenarios presented in this paper reveal the shortcomings of existing prevention solutions for the DeFi ecosystem, especially against flash loan attacks. In future work, we plan to test our framework on a broader number of cases, such as Dopple Finance.
Author Contributions
W.W.: Conceptualization, methodology, validation, investigation, resource, data curation, writing—review and editing, supervising, project administration, and funding acquisition. T.K.: Conceptualization, methodology, software, validation, investigation, data curation, writing—original draft, and visualization. T.A.: Conceptualization, validation, investigation, visualization, and supervision. J.S.: Writing—Review and Editing and supervision. E.S.: Writing—Review and Editing. P.B.: Writing—Review and Editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by National Science, Research and Innovation Fund (NSRF) and Prince of Songkla University (Grant No. COC6601136S) and College of Computing, Prince of Songkla University (Grant No. COC6304156S).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| USDT/USDC | US Dollars pegged, an asset-backed cryptocurrency stablecoin. USDT and USDC |
| are managed by Tether company limited, Hong Kong and Centre consortium, | |
| respectively [56]. | |
| ETH | Ether, an unstable token for the Ethereum chain [57]. |
| WETH | Wrapped Ether is an ERC-20 token that represents a wrapped version of |
| Ethereum [57]. | |
| DAI | A stable token whose value is kept close to one USD using a smart contract |
| system [42]. | |
| LP | A token from a liquidity provider, which is given to users who loan their tokens |
| to a liquidity pool [37]. | |
| DEX | Decentralized exchange, a marketplace where transactions occur directly between |
| crypto traders [40]. | |
| TWAP | Time Weighted Average Price, the average price of an asset over a specific period |
| of time [9]. | |
| TWAR | Time-Weighted-Average Reserve, the average amount of tokens in a pool of the |
| platform [8]. |
References
- Tolmach, P.; Li, Y.; Lin, S.W.; Liu, Y. Formal analysis of composable DeFi protocols. In Proceedings of the International Conference on Financial Cryptography and Data Security, Virtual Event, 1–5 March 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 149–161. [Google Scholar]
- Böhme, R.; Christin, N.; Edelman, B.; Moore, T. Bitcoin: Economics, technology, and governance. J. Econ. Perspect. 2015, 29, 213–238. [Google Scholar] [CrossRef]
- Angeris, G.; Kao, H.T.; Chiang, R.; Noyes, C.; Chitra, T. An Analysis of Uniswap markets. Cryptoecon. Syst. 2021, 1, 1–30. [Google Scholar] [CrossRef]
- Khan, R. Crypto Banking and Decentralized Finance—A New Frontier in Financial Services. 2022. Available online: https://www.forbes.com/sites/roomykhan/2022/04/11/crypto-banking-and-decentralized-finance–a-new-frontier-in-financial-services/?sh=66f1b5391b6d (accessed on 30 April 2022).
- Wang, D.; Wu, S.; Lin, Z.; Wu, L.; Yuan, X.; Zhou, Y.; Wang, H.; Ren, K. Towards a first step to understand flash loan and its applications in DeFi ecosystem. In Proceedings of the Ninth International Workshop on Security in Blockchain and Cloud Computing, Virtual Event, Hong Kong, 7 June 2021; pp. 23–28. [Google Scholar]
- Warp Finance. Warp Finance. 2020. Available online: https://warpfinance.medium.com/warp-finance-exploit-summary-recovery-of-funds-5b8fe4a11898 (accessed on 12 September 2021).
- Dopple; Twindex Team. Twindex Post-Mortem—Following an Incident on 2 OCT 2021. 2021. Available online: https://dopple-ecosystem.medium.com/twindex-post-mortem-following-an-incident-on-2-oct-2021-76ded3a5538a (accessed on 12 April 2021).
- Pitimanaaree, N. Fair Uniswap’s LP Token Pricing. 2020. Available online: https://blog.alphaventuredao.io/fair-lp-token-pricing/ (accessed on 27 December 2021).
- Shao, T. A Guide on Uniswap v3 TWAP Oracle. 2021. Available online: https://medium.com/blockchain-development-notes/a-guide-on-uniswap-v3-twap-oracle-2aa74a4a97c5 (accessed on 12 April 2021).
- Chukleang, T.; Jandaeng, C. Security Enhancement in Smart Logistics with Blockchain Technology: A Home Delivery Use Case. Informatics 2022, 9, 70. [Google Scholar] [CrossRef]
- Daramola, O.; Thebus, D. Architecture-centric evaluation of blockchain-based smart contract e-voting for national elections. Informatics 2020, 7, 16. [Google Scholar] [CrossRef]
- Nanayakkara, S.; Perera, S.; Senaratne, S.; Weerasuriya, G.T.; Bandara, H.M.N.D. Blockchain and smart contracts: A solution for payment issues in construction supply chains. Informatics 2021, 8, 36. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, Z.Z. Analysis and outlook of applications of blockchain technology to equity crowdfunding in China. Financ. Innov. 2016, 2, 29. [Google Scholar] [CrossRef]
- Karode, T.; Werapun, W.; Arpornthip, T. Blockchain-based global travel review framework. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 90–99. [Google Scholar] [CrossRef]
- Karode, T.; Werapun, W. Robustness against fraudulent activities of a blockchain-based online review system. Peer-to-Peer Netw. Appl. 2022, 15, 92–106. [Google Scholar] [CrossRef]
- Werapun, W.; Arpornthip, T.; Sangiamkul, E.; Wetprasit, R.; Karode, T. A Blockchain-based Renewable Energy Investment Management Platform: Decentralized Sustainable Development (DeSDev). J. Comput. Sci. 2020, 16, 1657–1668. [Google Scholar] [CrossRef]
- Guo, Y.; Liang, C. Blockchain application and outlook in the banking industry. Financ. Innov. 2016, 2, 24. [Google Scholar] [CrossRef]
- Cao, Y.; Zou, C.; Cheng, X. Flashot: A snapshot of flash loan attack on DeFi ecosystem. arXiv 2021, arXiv:2102.00626. [Google Scholar]
- Qin, K.; Zhou, L.; Livshits, B.; Gervais, A. Attacking the defi ecosystem with flash loans for fun and profit. In Proceedings of the International Conference on Financial Cryptography and Data Security, Virtual Event, 1–5 March 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 3–32. [Google Scholar]
- Holub, A.; O’Connor, J. COINHOARDER: Tracking a ukrainian bitcoin phishing ring DNS style. In Proceedings of the 2018 APWG Symposium on Electronic Crime Research (eCrime), San Diego, CA, USA, 15–17 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- PancakeSwap. DNS Incident Recap. 2021. Available online: https://medium.com/pancakeswap/dns-incident-recap-36a183a2aee6 (accessed on 19 March 2021).
- Russo, C. Arbs Exploit DeFi to Make $900k in Seconds; Provoke Soul-Searching in the Process. 2020. Available online: https://newsletter.thedefiant.io/p/arbs-exploit-defi-to-make-900k-in (accessed on 12 July 2021).
- Songsom, N.; Werapun, W.; Suaboot, J.; Rattanavipanon, N. The SWC-Based Security Analysis Tool for Smart Contract Vulnerability Detection. In Proceedings of the 6th IEEE International Conference on Information Technology (InCIT) 2022, Nonthaburi, Thailand, 10–11 November 2022; pp. 1–6. [Google Scholar]
- Cecchetti, E.; Yao, S.; Ni, H.; Myers, A.C. Compositional security for reentrant applications. In Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 24–27 May 2021; pp. 1249–1267. [Google Scholar]
- Daian, P.; Goldfeder, S.; Kell, T.; Li, Y.; Zhao, X.; Bentov, I.; Breidenbach, L.; Juels, A. Flash boys 2.0: Frontrunning, transaction reordering, and consensus instability in decentralized exchanges. arXiv 2019, arXiv:1904.05234. [Google Scholar]
- Mazorra, B.; Adan, V.; Daza, V. Do Not Rug on Me: Zero-Dimensional Scam Detection. Cryptology ePrint Archive, Paper 2022/350. 2022. Available online: https://eprint.iacr.org/2022/350 (accessed on 20 December 2022).
- Hamrick, J.; Rouhi, F.; Mukherjee, A.; Feder, A.; Gandal, N.; Moore, T.; Vasek, M. The Economics of Cryptocurrency Pump and Dump Schemes. Available at SSRN 3310307. 2018. Available online: https://tylermoore.utulsa.edu/weis19pump.pdf (accessed on 1 May 2021).
- Kamps, J.; Kleinberg, B. To the moon: Defining and detecting cryptocurrency pump-and-dumps. Crime Sci. 2018, 7, 18. [Google Scholar] [CrossRef]
- Xu, J.; Livshits, B. The Anatomy of a Cryptocurrency Pump-and-Dump Scheme. In Proceedings of the 28th USENIX Security Symposium (USENIX Security 19), Santa Clara, CA, USA, 14–16 August 2019; pp. 1609–1625. [Google Scholar]
- Russo, C. bZx Hacked for $8M after Security-Focused Relaunch. 2020. Available online: https://thedefiant.io/bzx-hacked-for-8m-after-security-focused-relaunch/ (accessed on 10 January 2021).
- Gudgeon, L.; Perez, D.; Harz, D.; Livshits, B.; Gervais, A. The decentralized financial crisis. In Proceedings of the 2020 IEEE Crypto Valley Conference on Blockchain Technology (CVCBT), Rotkreuz, Switzerland, 11–12 June 2020; pp. 1–15. [Google Scholar]
- Stevens, R. After DeFi Lost $100 Million to Flash Loan Attacks, Curve Pushes Chainlink. 2020. Available online: https://decrypt.co/49758/after-100-million-lost-to-flash-loan-attacks-curve-pushes-chainlink (accessed on 12 July 2021).
- Xia, P.; Gao, B.; Su, W.; Yu, Z.; Luo, X.; Zhang, C.; Xiao, X.; Xu, G. Demystifying Scam Tokens on Uniswap Decentralized Exchange. arXiv 2021, arXiv:2109.00229. [Google Scholar]
- Gronde, F. Flash Loans and Decentralized Lending Protocols: An In-Depth Analysis. Master’s Thesis, Center for Innovative Finance, University of Basel, Basel, Switzerland, 2012. [Google Scholar]
- Gudgeon, L.; Werner, S.; Perez, D.; Knottenbelt, W.J. Defi protocols for loanable funds: Interest rates, liquidity and market efficiency. In Proceedings of the 2nd ACM Conference on Advances in Financial Technologies, Zurich, Switzerland, 21–23 October 2020; pp. 92–112. [Google Scholar]
- Xia, P.; Wang, H.; Gao, B.; Su, W.; Yu, Z.; Luo, X.; Zhang, C.; Xiao, X.; Xu, G. Trade or Trick? Detecting and Characterizing Scam Tokens on Uniswap Decentralized Exchange. Proc. ACM Meas. Anal. Comput. Syst. 2021, 5, 1–26. [Google Scholar] [CrossRef]
- Avara UI Labs Ltd. Aave—Open Source Liquidity Protocol. 2021. Available online: https://docs.aave.com/hub/ (accessed on 12 December 2021).
- Bai, S.; Robinson, F. Automated Triangular Arbitrage: A Trading Algorithm for Foreign Exchange on a Cryptocurrency Market. 2019. Available online: https://www.diva-portal.org/smash/get/diva2:1322682/FULLTEXT02 (accessed on 10 February 2020).
- Bell, P. Arbitrage Trading Strategy in Gold Futures. 2019. Available online: https://mpra.ub.uni-muenchen.de/id/eprint/96124 (accessed on 12 January 2020).
- Boonpeam, N.; Werapun, W.; Karode, T. The arbitrage system on decentralized exchanges. In Proceedings of the 2021 18th IEEE International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Chiang Mai, Thailand, 19–22 May 2021; pp. 768–771. [Google Scholar]
- Uniswap Labs. Uniswap Protocol. 2021. Available online: https://uniswap.org/ (accessed on 12 December 2021).
- Makerdao.com. The Maker Protocol: MakerDAO’s Multi-Collateral Dai (MCD) System. 2021. Available online: https://makerdao.com/whitepaper/White%20Paper%20-The%20Maker%20Protocol_%20MakerDAO%E2%80%99s%20Multi-Collateral%20Dai%20(MCD)%20System-FINAL-%20021720.pdf (accessed on 12 December 2021).
- Gandal, N.; Hamrick, J.; Moore, T.; Oberman, T. Price manipulation in the Bitcoin ecosystem. J. Monet. Econ. 2018, 95, 86–96. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A peer-to-peer electronic cash system. 2008. Available online: https://www.debr.io/article/21260-bitcoin-a-peer-to-peer-electronic-cash-system (accessed on 6 April 2021).
- Harvest Finance. Harvest Flashloan Economic Attack Post-Mortem. 2020. Available online: https://medium.com/harvest-finance/harvest-flashloan-economic-attack-post-mortem-3cf900d65217 (accessed on 12 April 2021).
- Sigalos, M. DeFi Bug Accidentally Gives $90 Million to Users, Founder Begs Them to Return It. 2021. Available online: https://www.cnbc.com/2021/10/01/defi-protocol-compound-mistakenly-gives-away-millions-to-users.html (accessed on 4 December 2021).
- Zafar, T. Visor Finance Suffers Another DeFi Hack as Losses Mount Up to $8.2M. 2021. Available online: https://finance.yahoo.com/news/visor-finance-suffers-another-defi-094645929.html (accessed on 2 February 2022).
- Uniswap Labs. Uniswap Oracle. 2021. Available online: https://docs.uniswap.org/concepts/protocol/oracle (accessed on 29 December 2021).
- Julien, B. Warp Finance—Rekt. 2020. Available online: https://rekt.news/warp-finance-rekt/ (accessed on 17 December 2021).
- Ethtx.info. Ethtx.info Analysis 0x8bb8dc5c7c830bac85fa48acad250. 2021. Available online: https://ethtx.info/mainnet/0x8bb8dc5c7c830bac85fa48acad2505e9300a91c3ff239c9517d0cae33b595090/ (accessed on 20 December 2021).
- Nomic Foundation. Hardhat|Ethereum Development. 2020. Available online: https://hardhat.org/ (accessed on 27 December 2021).
- Etherscan. Ethereum (ETH) Blockchain Explorer. 2020. Available online: https://etherscan.io/ (accessed on 27 December 2021).
- Li, Y.; Liu, H.; Yang, Z.; Wang, B.; Ren, Q.; Wang, L.; Chen, B. Protect Your Smart Contract Against Unfair Payment. In Proceedings of the 2020 International Symposium on Reliable Distributed Systems (SRDS), Shanghai, China, 21–24 September 2020; pp. 61–70. [Google Scholar] [CrossRef]
- Lai, W.J.; Hsueh, C.W.; Wu, J.L. A Fully Decentralized Time-Lock Encryption System on Blockchain. In Proceedings of the 2019 IEEE International Conference on Blockchain (Blockchain), Atlanta, GA, USA, 14–17 July 2019; pp. 302–307. [Google Scholar] [CrossRef]
- Breidenbach, L.; Cachin, C.; Coventry, A.; Juels, A.; Miller, A. Chainlink Off-Chain Reporting Protocol. 2021. Available online: https://research.chain.link/ocr.pdf (accessed on 24 December 2021).
- Thanh, B.N.; Hong, T.N.V.; Pham, H.; Cong, T.N.; Anh, T.P.T. Are the stabilities of stablecoins connected? J. Ind. Bus. Econ. 2022, 1–11. [Google Scholar] [CrossRef]
- Vujičić, D.; Jagodić, D.; Ranđić, S. Blockchain technology, bitcoin, and Ethereum: A brief overview. In Proceedings of the 2018 17th IEEE International Symposium Infoteh-Jahorina (Infoteh), East Sarajevo, Bosnia and Herzegovina, 21–23 March 2018; pp. 1–6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).