Coherent Mortality Forecasting for Less Developed Countries †
Abstract
:1. Introduction
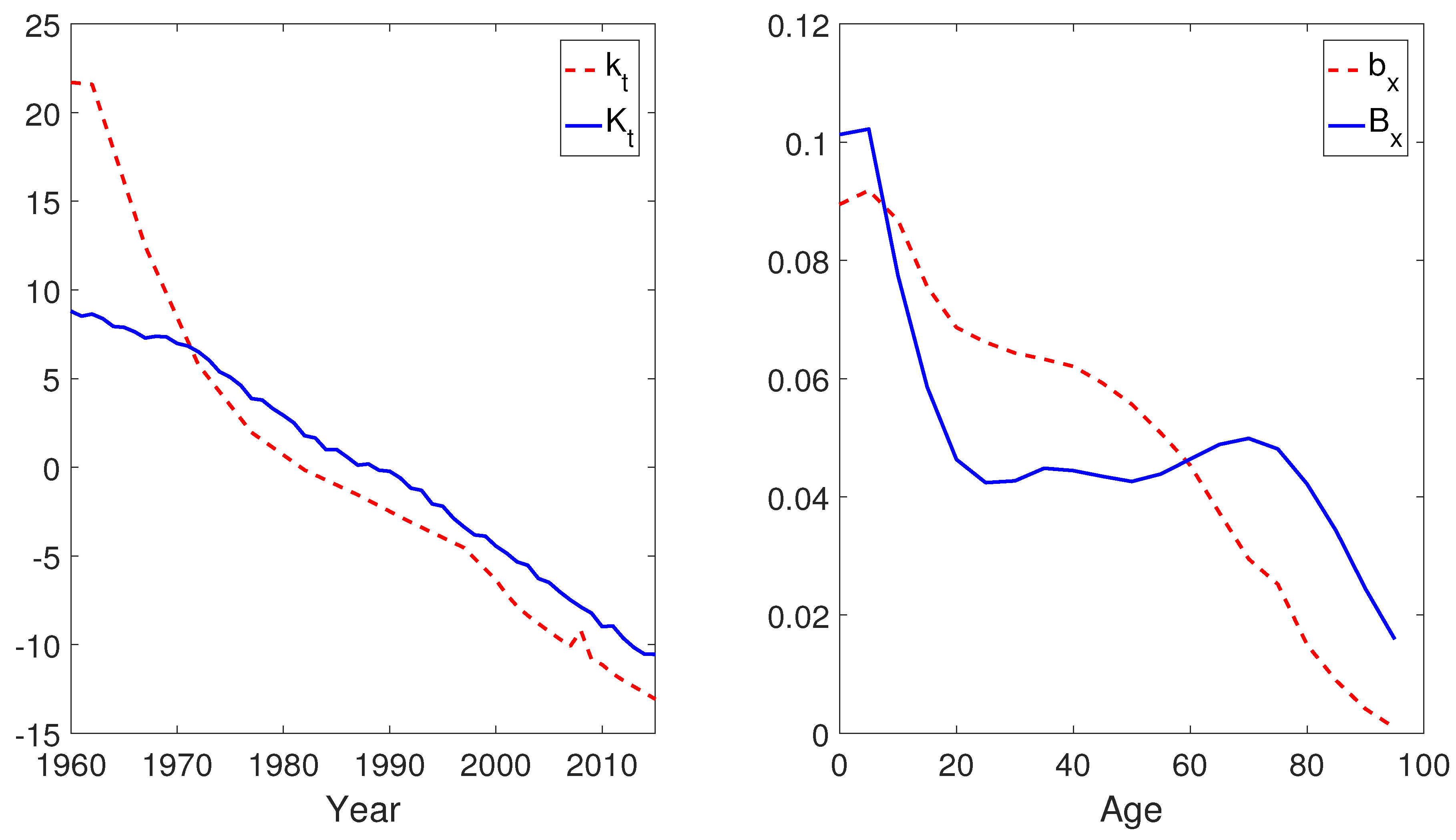
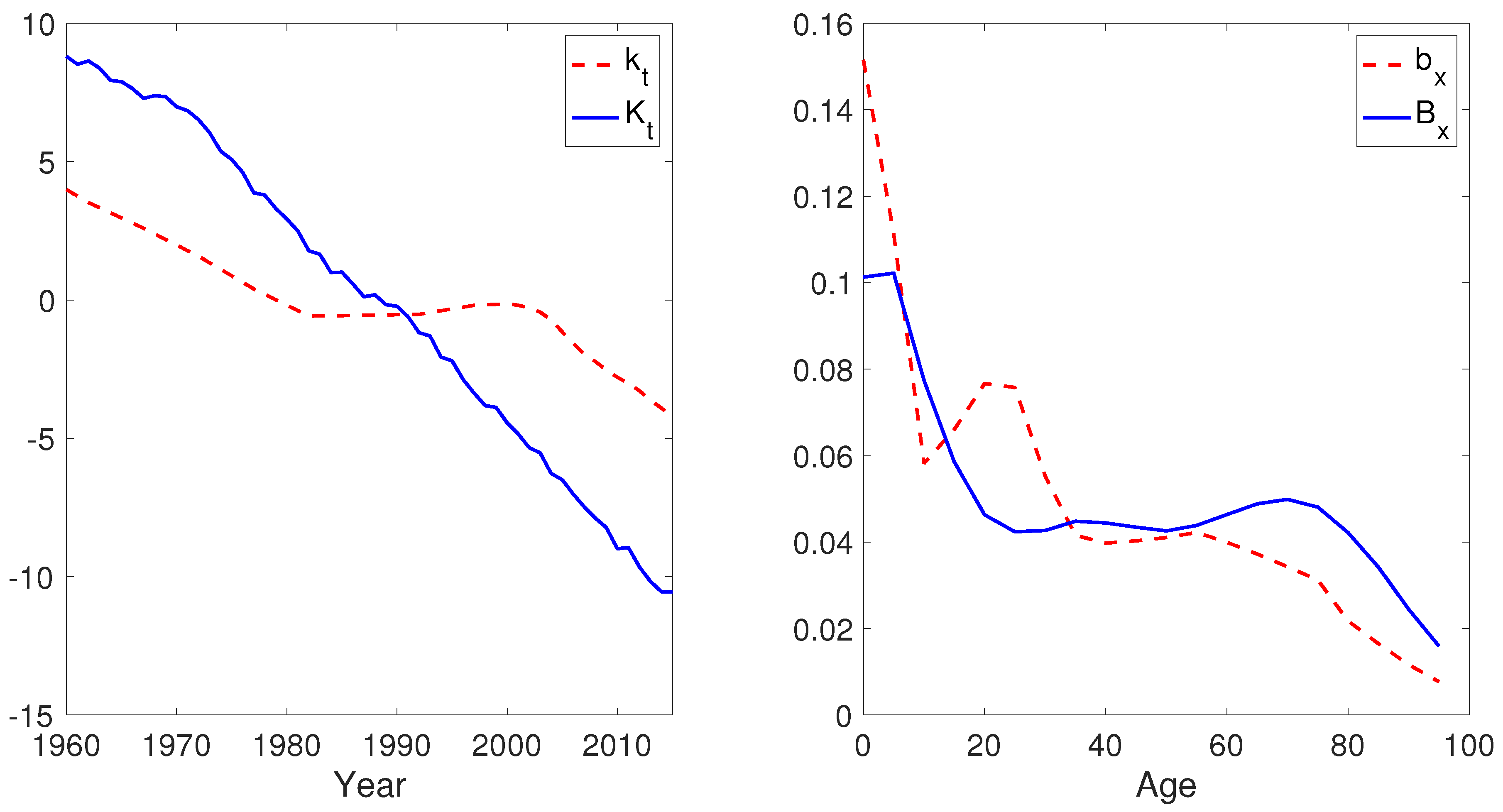
2. The Mortality Models
3. The Rotation Algorithm
3.1. Rotating the Age and Period Effects for Mortality Projections
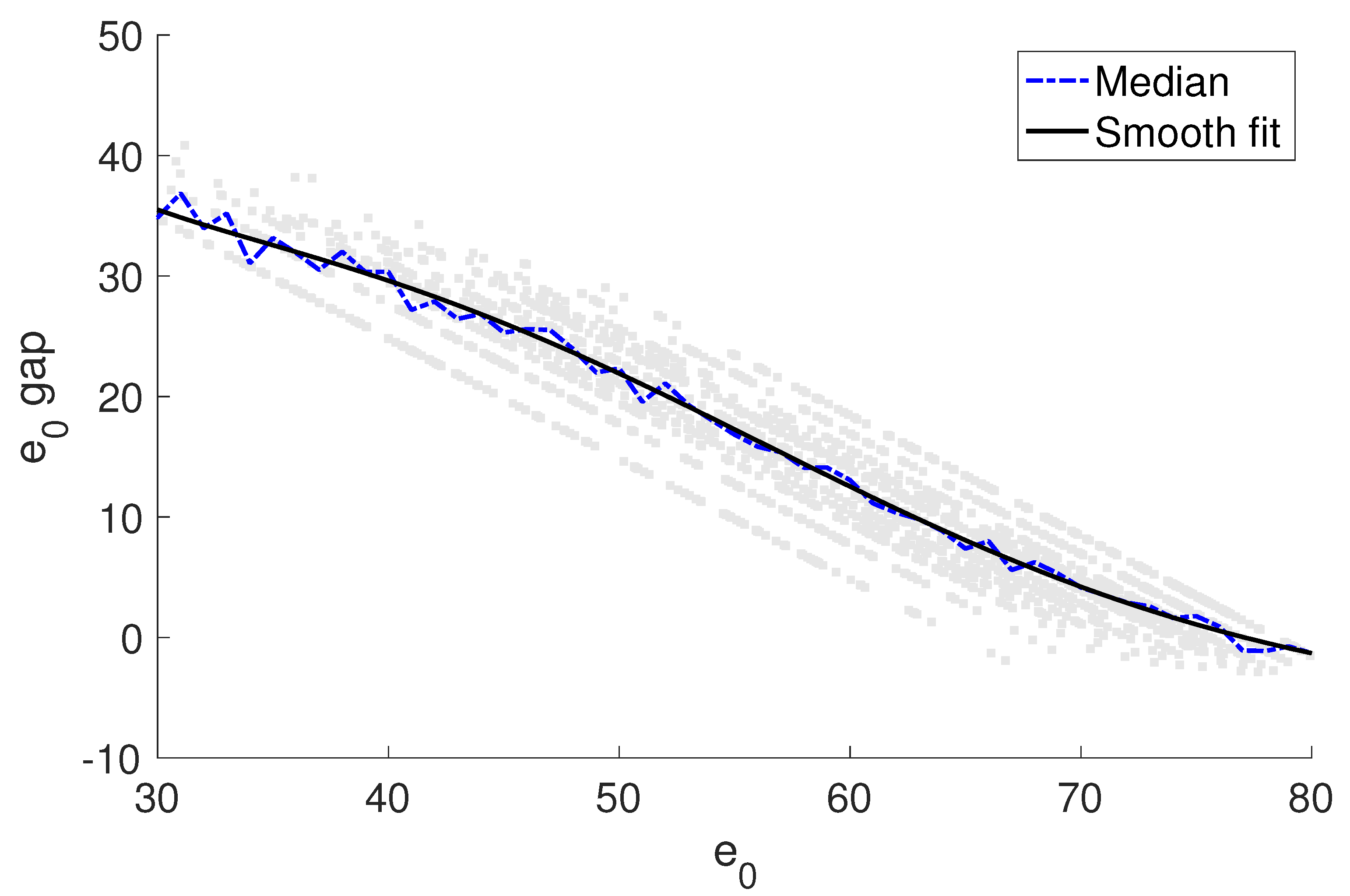
3.2. Determining the Weight Parameter
4. Empirical Analysis
4.1. Mortality Data
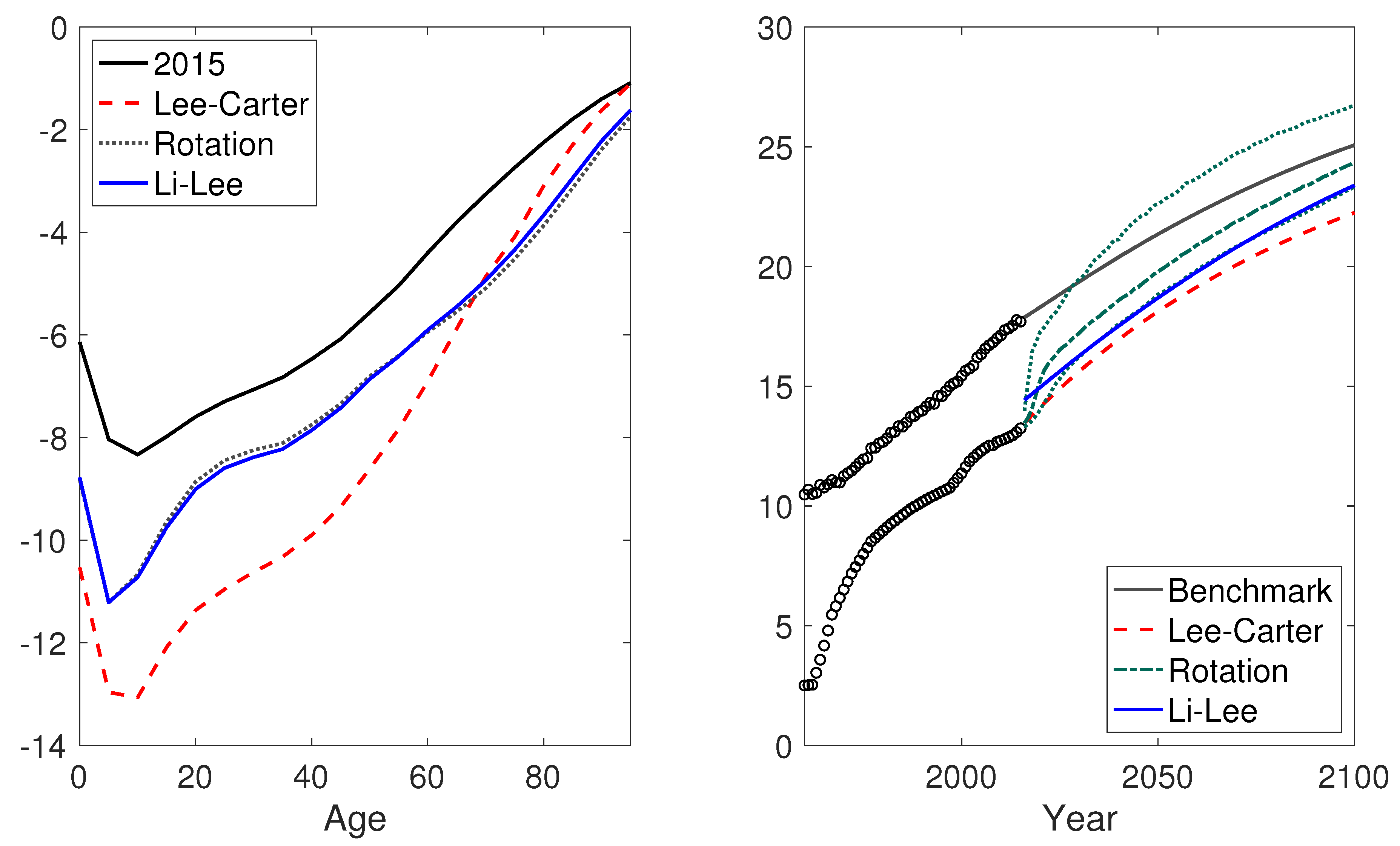
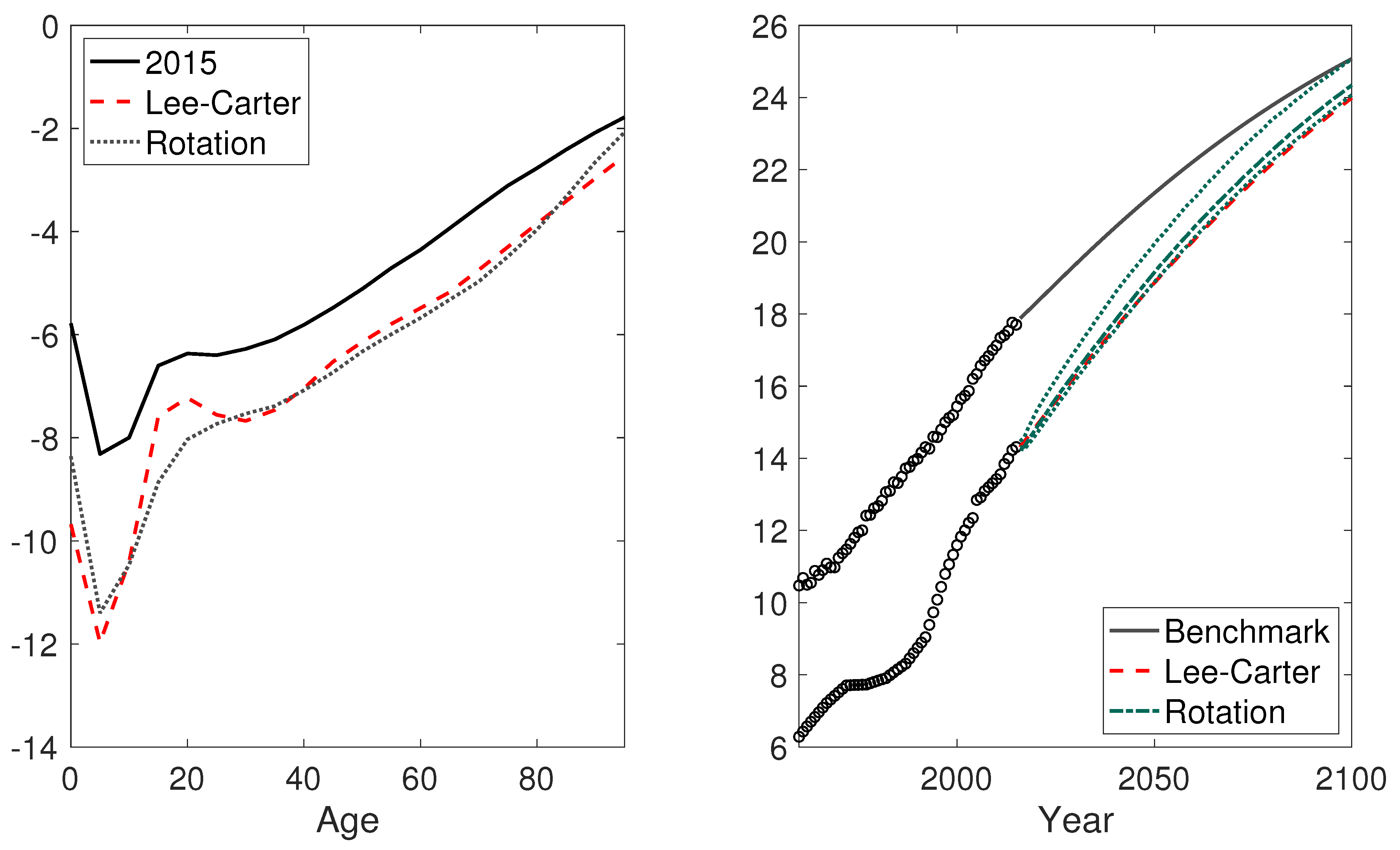
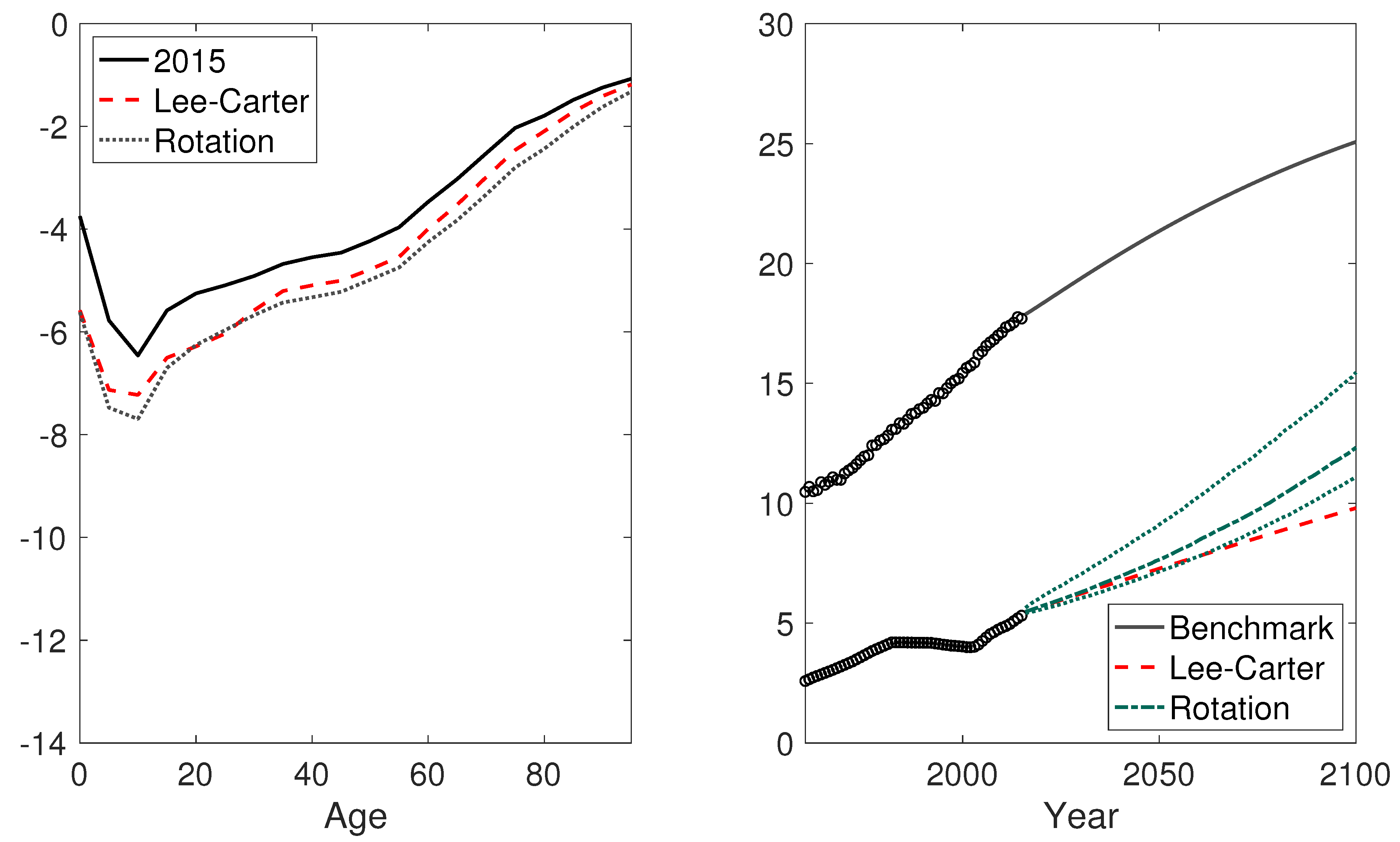
4.2. Empirical Results
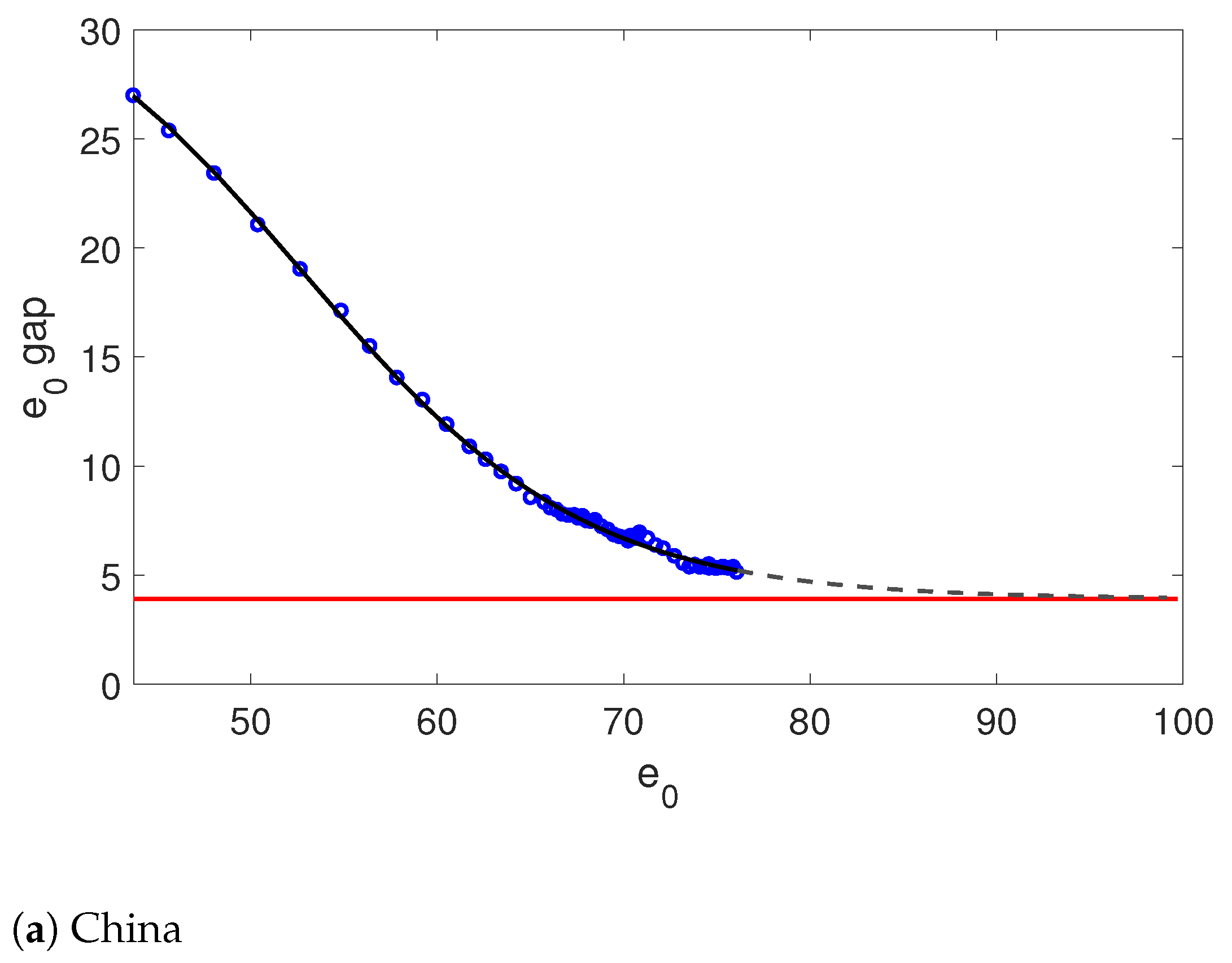
4.2.1. China
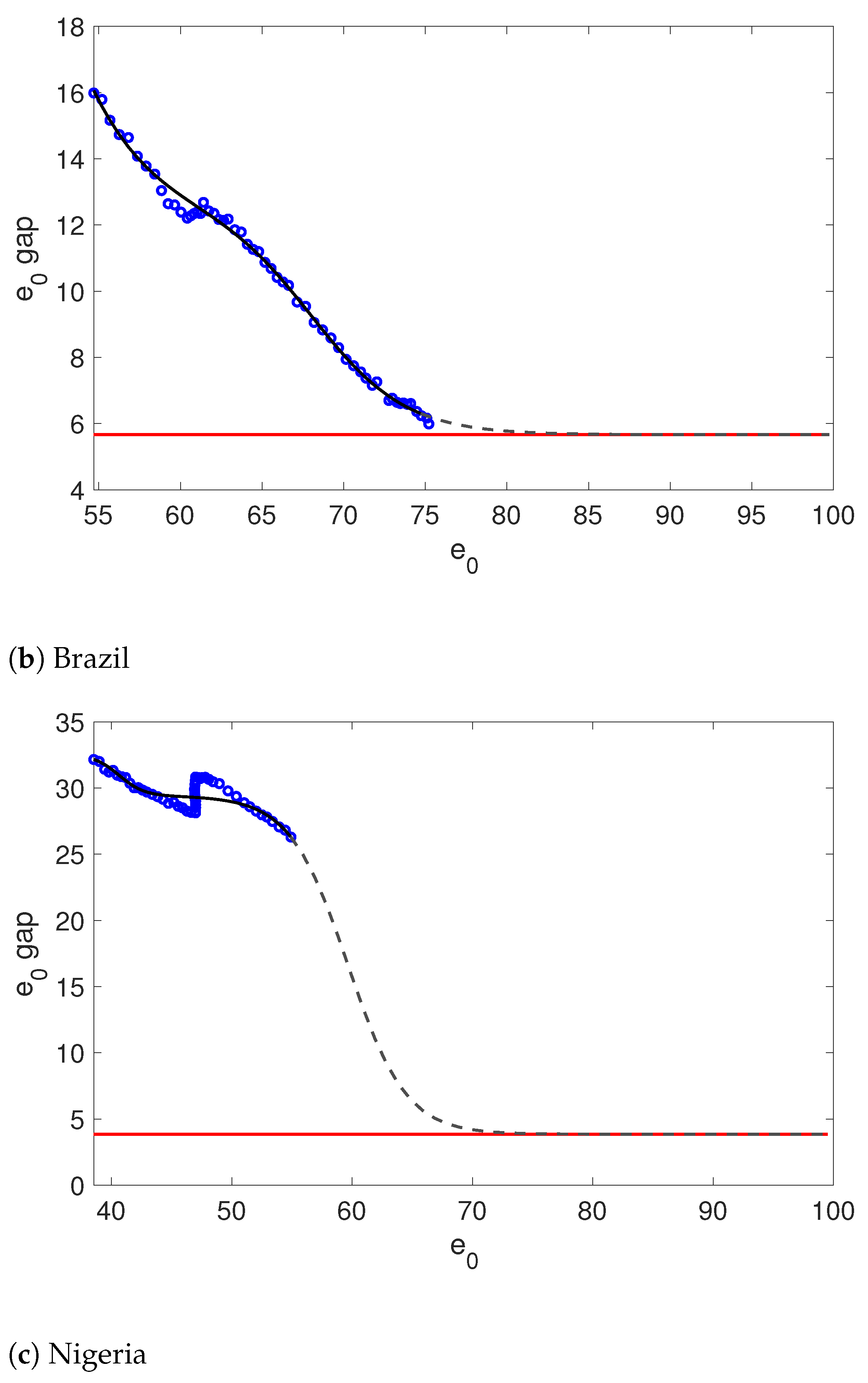
4.2.2. Brazil
4.2.3. Nigeria
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Variables of the Lee–Carter model: | |
| Log central mortality rate at age x in year t | |
| The average mortality level at each age x | |
| The mortality index at time t | |
| The age-specific sensitivity of to changes in | |
| The normal error term in the process | |
| The normal error term in the process | |
| Additional variables of the Li–Lee models | |
| Age effect of the common factor | |
| Period effect of the common factor | |
| The normal error term in the common factor | |
| The age-specific sensitivity of log central mortality rate to the population-specific index | |
Appendix A. Optimal Logistic Function
| AIC | ||
| Country | Single logistic | Double logistic |
| China | −21.32 | −16.23 |
| Brazil | 40.68 | −13.75 |
| Nigeria | 154.14 | 140.36 |
| BIC | ||
| Country | Single logistic | Double logistic |
| China | −13.22 | |
| Brazil | 48.79 | 0.43 |
| Nigeria | 162.24 | 154.54 |
Appendix B. The Weight Parameter of the Rotation Algorithm
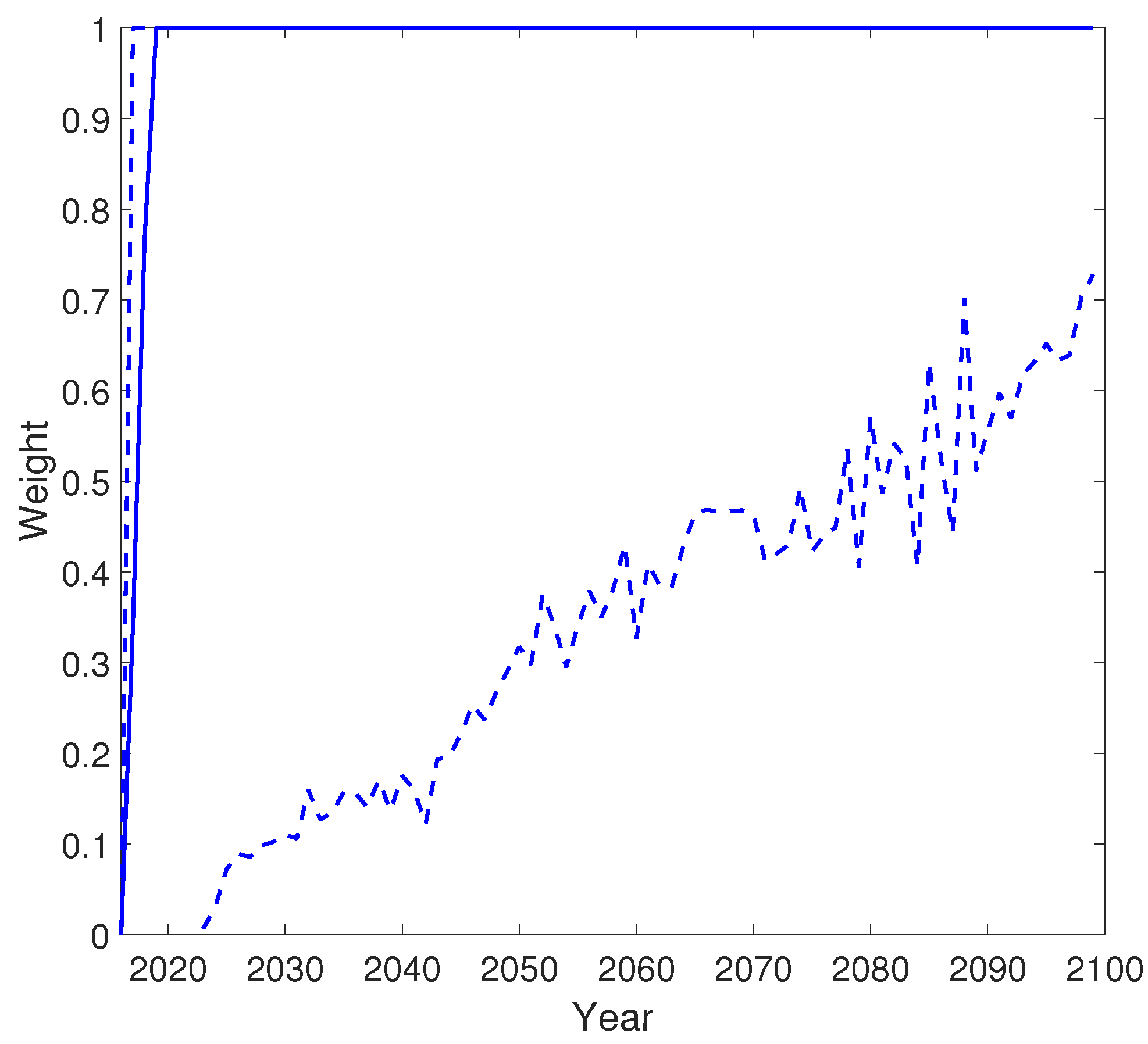
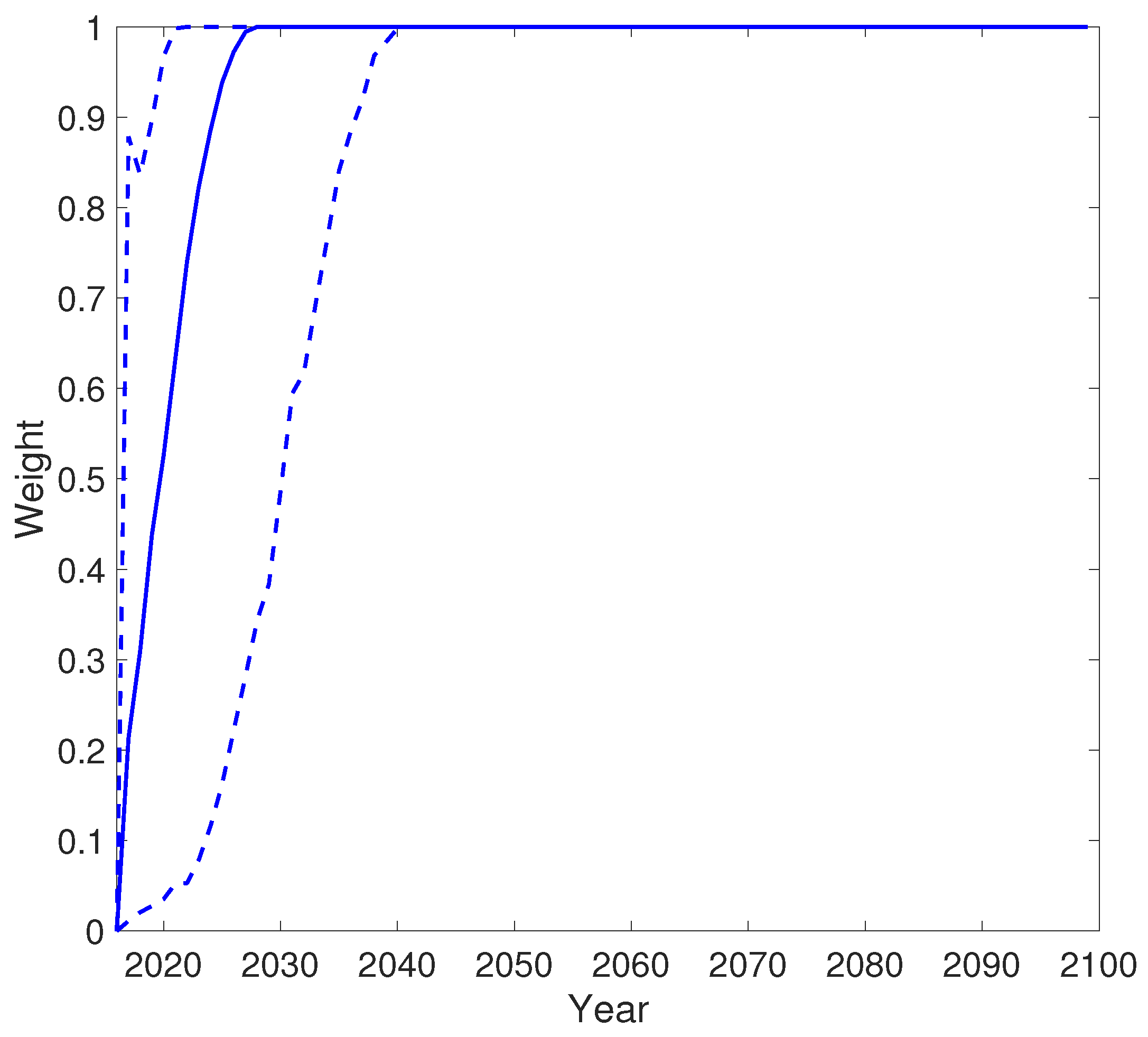

Appendix C. The Projected Life Expectancy at Birth
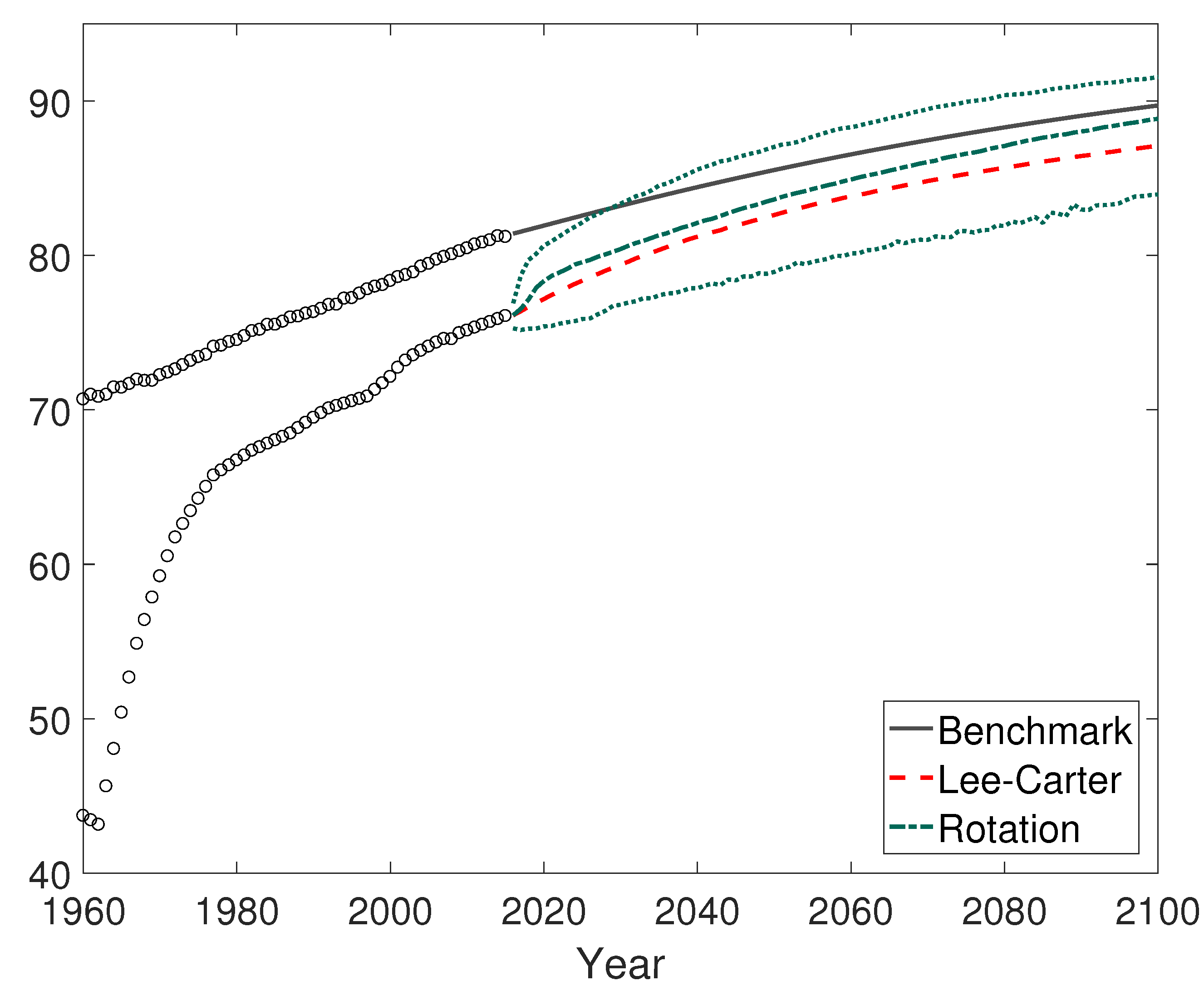


| 1 | The United Nations defines the less developed countries/regions as all regions of Africa, Asia (except Japan), Latin America and the Caribbean plus Melanesia, Micronesia and Polynesia, and the more developed countries/regions as all regions in Europe, Northern America, Australia, New Zealand, and Japan. For ease of exposition, we will use the word “country” to refer to any country or region. |
| 2 | The age-specific death rates are calculated using data from the 2017 revision of the World Population Prospects by the United Nations. The ranking is based on population statistics as of 1 June 2018. Source: https://www.census.gov/popclock/print.php?component=counter (accessed on 14 August 2021). |
| 3 | Besides these two models, there are many other linear extrapolation models consistent with our rotation algorithm, such as Cairns et al. (2006) and Hyndman and Ullah (2007), as well as Li et al. (2021) for a single population and Dowd et al. (2011), Hyndman et al. (2013), Li et al. (2019), Li and Lu (2018, 2019) for multiple populations. For summaries of linear extrapolation models, we refer to Booth et al. (2002), Cairns et al. (2011), and Li and Hardy (2011). |
| 4 | When convergence is achieved, the improvement rates of the logarithm of the age-specific mortality rates are the same between the modeled country and the benchmark countries. However, this does not necessarily lead to the same improvement rate of the life expectancy, due to Jensen’s inequality. |
| 5 | The data were collected from the 2017 revision of the World Population Prospects. We excluded 9 less developed countries/regions with life expectancy higher than 80 in 2010–2015, such as Hong Kong, Macao, and Singapore. The benchmark life expectancy was calculated using 10 more developed countries: Germany, Denmark, Finland, France, The Netherlands, Switzerland, Sweden, the UK, the US, and Japan. |
| 6 | The United Nations uses a simplified version of Equation (14) where is set to 0. |
| 7 | Source: http://www.mortality.org/ (accessed on 14 August 2021). |
| 8 | UN Source: http://www.un.org/en/development/desa/population/ (accessed on 14 August 2021). WHO Source: http://apps.who.int/gho/data/view.main.60340?lang=en (accessed on 14 August 2021). |
| 9 | Source: http://www.mortality.org/ (accessed on 14 August 2021). |
| 10 | UN Source: http://www.un.org/en/development/desa/population/ (accessed on 14 August 2021). WHO Source: http://apps.who.int/gho/data/view.main.60340?lang=en (accessed on 14 August 2021). |
References
- Abegunde, Dele O., Colin D. Mathers, Taghreed Adam, Monica Ortegon, and Kathleen Strong. 2007. The burden and costs of chronic diseases in low-income and middle-income countries. The Lancet 370: 1929–38. [Google Scholar] [CrossRef]
- Andreev, Kirill, and James Vaupel. 2006. Forecasts of cohort mortality after age 50. In Max Planck Institute for Demographic Research Working Paper. Rostock: Max Planck Institute for Demographic Research, vol. 12. [Google Scholar]
- Austin, Kelly, and Laura McKinney. 2012. Disease, war, hunger, and deprivation: A cross-national investigation of the determinants of life expectancy in less-developed and sub-saharan african nations. Sociological Perspectives 55: 421–47. [Google Scholar] [CrossRef]
- Booth, Heather, John Maindonald, and Len Smith. 2002. Applying Lee-Carter under conditions of variable mortality decline. Population Studies 56: 325–36. [Google Scholar] [CrossRef]
- Cairns, Andrew, David Blake, and Kevin Dowd. 2006. A two-factor model for stochastic mortality with parameter uncertainty: Theory and calibration. Journal of Risk and Insurance 73: 687–718. [Google Scholar] [CrossRef]
- Cairns, Andrew, David Blake, Kevin Dowd, Guy Coughlan, David Epstein, and Marwa Khalaf-Allah. 2011. Mortality Density Forecasts: An Analysis of Six Stochastic Mortality Models. Insurance: Mathematics and Economics 48: 355–67. [Google Scholar] [CrossRef] [Green Version]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, David Epstein, Alen Ong, and Igor Balevich. 2009. A quantitative comparison of stochastic mortality models using data from england and wales and the united states. North American Actuarial Journal 13: 1–35. [Google Scholar] [CrossRef]
- Castanheira, Helena, François Pelletier, and Igor Ribeiro. 2017. A Sensitivity Analysis of the Bayesian Framework for Projecting Life Expectancy at Birth. In UN Population Division. Technical Paper. New York: United Nations, No. 7. [Google Scholar]
- Chen, An, Hong Li, and Mark Schultze. 2021. Tail index-linked annuity: A longevity risk sharing retirement plan. Scandinavian Actuarial Journal. [Google Scholar] [CrossRef]
- CMI. 2009. Continuous Mortality Investigation: A Prototype Mortality Projections Model: Part Two—Detailed Analysis. Working Paper. London: Institute and Faculty of Actuaries, No. 39. [Google Scholar]
- Dowd, Kevin, Andrew Cairns, David Blake, Guy Coughlan, and Marwa Khalaf-Allah. 2011. A gravity model of mortality rates for two related populations. North American Actuarial Journal 15: 334–56. [Google Scholar] [CrossRef] [Green Version]
- Fogel, Robert. 2004. The Escape from Hunger and Premature Death, 1700–2100: Europe, America, and the Third World. Cambridge: Cambridge University Press, vol. 38. [Google Scholar]
- Hensher, Martin, Max Price, and Sarah Adomakoh. 2017. Disease Control Priorities in Developing Countries. Oxford: Oxford University Press. [Google Scholar]
- Huang, Fei, and Bridget Browne. 2017. Mortality forecasting using a modified continuous mortality investigation mortality projections model for china i: Methodology and country-level results. Annals of Actuarial Science 11: 20–45. [Google Scholar] [CrossRef]
- Hyndman, Rob J., Heather Booth, and Farah Yasmeen. 2013. Coherent mortality forecasting: The product-ratio method with functional time series models. Demography 50: 261–83. [Google Scholar] [CrossRef] [Green Version]
- Hyndman, Rob J., and Md Shahid Ullah. 2007. Robust forecasting of mortality and fertility rates: A functional data approach. Computational Statistics & Data Analysis 51: 4942–56. [Google Scholar]
- Jeuland, Marc A., David E. Fuente, Semra Ozdemir, Maura C. Allaire, and Dale Whittington. 2013. The long-term dynamics of mortality benefits from improved water and sanitation in less developed countries. PLoS ONE 8: e74804. [Google Scholar] [CrossRef] [Green Version]
- Lee, Ronald, and Timothy Miller. 2001. Evaluating the performance of the lee-carter method for forecasting mortality. Demography 38: 537–49. [Google Scholar] [CrossRef]
- Lee, Ronald, and Lawrence R. Carter. 1992. Modeling and forecasting US mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar]
- Li, Hong. 2018. Dynamic hedging of longevity risk: The effect of trading frequency. ASTIN Bulletin: The Journal of the IAA 48: 197–232. [Google Scholar] [CrossRef]
- Li, Hong, Anja De Waegenaere, and Bertrand Melenberg. 2015. The choice of sample size for mortality forecasting: A bayesian learning approach. Insurance: Mathematics and Economics 63: 153–68. [Google Scholar] [CrossRef]
- Li, Hong, Anja De Waegenaere, and Bertrand Melenberg. 2017. Robust mean–variance hedging of longevity risk. Journal of Risk and Insurance 84: 459–75. [Google Scholar] [CrossRef]
- Li, Han, Hong Li, Yang Lu, and Anastasios Panagiotelis. 2019. A forecast reconciliation approach to cause-of-death mortality modeling. Insurance: Mathematics and Economics 86: 122–33. [Google Scholar] [CrossRef]
- Li, Hong, and Johnny S. H. Li. 2017. Optimizing the Lee-Carter Approach in the Presence of Structural Changes in Time and Age Patterns of Mortality Improvements. Demography 54: 1073–95. [Google Scholar] [CrossRef] [PubMed]
- Li, Hong, and Yang Lu. 2017. Coherent forecasting of mortality rates: A sparse vector-autoregression approach. ASTIN Bulletin: The Journal of the IAA 47: 563–600. [Google Scholar] [CrossRef]
- Li, Hong, and Yang Lu. 2018. A bayesian non-parametric model for small population mortality. Scandinavian Actuarial Journal 2018: 605–28. [Google Scholar] [CrossRef]
- Li, Hong, and Yang Lu. 2019. Modeling cause-of-death mortality using hierarchical archimedean copula. Scandinavian Actuarial Journal 2019: 247–72. [Google Scholar] [CrossRef]
- Li, Hong, Yang Lu, and Pintao Lyu. 2018. Modeling and forecasting chinese population dynamics in a multi-population context. In SOA Research Reports. Schaumburg: Society of Actuaries. [Google Scholar]
- Li, Hong, and Yanlin Shi. 2021a. Forecasting mortality with international linkages: A global vector-autoregression approach. Insurance: Mathematics and Economics 100: 59–75. [Google Scholar] [CrossRef]
- Li, Hong, and Yanlin Shi. 2021b. Mortality forecasting with an age-coherent sparse var model. Risks 9: 35. [Google Scholar] [CrossRef]
- Li, Hong, Ken Seng Tan, Shripad Tuljapurkar, and Wenjun Zhu. 2021. Gompertz law revisited: Forecasting mortality with a multi-factor exponential model. Insurance: Mathematics and Economics 99: 268–81. [Google Scholar] [CrossRef]
- Li, Johnny S. H., and Mary Hardy. 2011. Measuring basis risk in longevity hedges. North American Actuarial Journal 15: 177–200. [Google Scholar] [CrossRef]
- Li, Nan, and Ronald D. Lee. 2005. Coherent mortality forecasts for a group of populations: An extension of the Lee-Carter method. Demography 42: 575–94. [Google Scholar] [CrossRef] [Green Version]
- Li, Nan, Ronald Lee, and Patrick Gerland. 2013. Extending the Lee-Carter method to model the rotation of age patterns of mortality decline for long-term projections. Demography 50: 2037–51. [Google Scholar] [CrossRef] [Green Version]
- Lin, Ro-Ting, Ya-Mei Chen, Lung-Chang Chien, and Chang-Chuan Chan. 2012. Political and social determinants of life expectancy in less developed countries: A longitudinal study. BMC Public Health 12: 85. [Google Scholar] [CrossRef] [Green Version]
- Lutz, Wolfgang, Warren Sanderson, and Sergei Scherbov. 2008. The coming acceleration of global population ageing. Nature 451: 716. [Google Scholar] [CrossRef]
- Mensah, George A., Gina S. Wei, Paul D. Sorlie, Lawrence J. Fine, Yves Rosenberg, Peter G. Kaufmann, Michael E. Mussolino, Lucy L. Hsu, Ebyan Addou, Michael M. Engelgau, and et al. 2017. Decline in cardiovascular mortality: Possible causes and implications. Circulation Research 120: 366–80. [Google Scholar] [CrossRef] [PubMed]
- Müller, Olaf, and Michael Krawinkel. 2005. Malnutrition and health in developing countries. Canadian Medical Association Journal 173: 279–86. [Google Scholar] [CrossRef] [Green Version]
- Peto, Richard, J. Boreham, Alan D. Lopez, Michael Thun, and Clark Heath. 1992. Mortality from tobacco in developed countries: Indirect estimation from national vital statistics. The Lancet 339: 1268–78. [Google Scholar] [CrossRef]
- Raftery, Adrian E., Jennifer L. Chunn, Patrick Gerland, and Hana Ševčíková. 2013. Bayesian probabilistic projections of life expectancy for all countries. Demography 50: 777–801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Renshaw, Arthur E., and Steven Haberman. 2006. A cohort-based extension to the lee–carter model for mortality reduction factors. Insurance: Mathematics and Economics 38: 556–70. [Google Scholar] [CrossRef]
- Riley, James. C. 2001. Rising Life Expectancy: A Global History. Cambridge: Cambridge University Press. [Google Scholar]
- Torri, Tiziana, and James W. Vaupel. 2012. Forecasting life expectancy in an international context. International Journal of Forecasting 28: 519–31. [Google Scholar] [CrossRef]
- Tuljapurkar, Shripad, Nan Li, and Carl Boe. 2000. A universal pattern of mortality decline in the G7 countries. Nature 405: 789. [Google Scholar] [CrossRef]
- United Nations. 2017. World Population Prospects: The 2017 Revision. New York: United Nations. [Google Scholar]
- Viner, Russell, Carolyn Coffey, Colin Mathers, Paul Bloem, Anthony Costello, John Santelli, and George Patton. 2011. 50-year mortality trends in children and young people: A study of 50 low-income, middle-income, and high-income countries. The Lancet 377: 1162–74. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Lu, Y.; Lyu, P. Coherent Mortality Forecasting for Less Developed Countries. Risks 2021, 9, 151. https://doi.org/10.3390/risks9090151
Li H, Lu Y, Lyu P. Coherent Mortality Forecasting for Less Developed Countries. Risks. 2021; 9(9):151. https://doi.org/10.3390/risks9090151
Chicago/Turabian StyleLi, Hong, Yang Lu, and Pintao Lyu. 2021. "Coherent Mortality Forecasting for Less Developed Countries" Risks 9, no. 9: 151. https://doi.org/10.3390/risks9090151
APA StyleLi, H., Lu, Y., & Lyu, P. (2021). Coherent Mortality Forecasting for Less Developed Countries. Risks, 9(9), 151. https://doi.org/10.3390/risks9090151







