Adapting the Default Weighted Survival Analysis Modelling Approach to Model IFRS 9 LGD
Abstract
1. Introduction
1.1. Background
1.2. IFRS 9 Concepts
2. Modelling Methodology: Default Weighted Survival Analysis
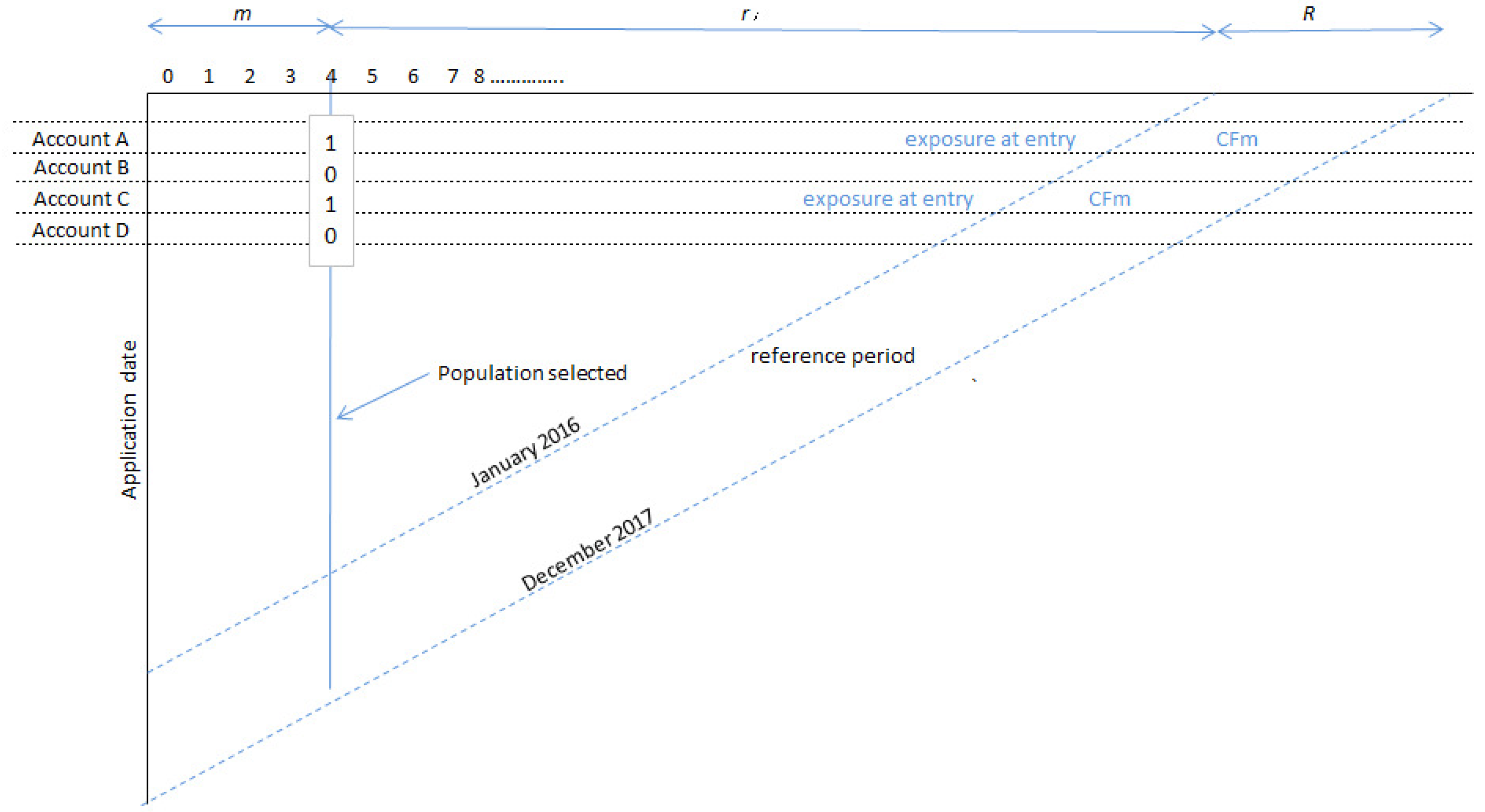
2.1. From Basel to IFRS 9 DWSA
2.2. Macro-Economic Adjustments
3. Case Study Data Description
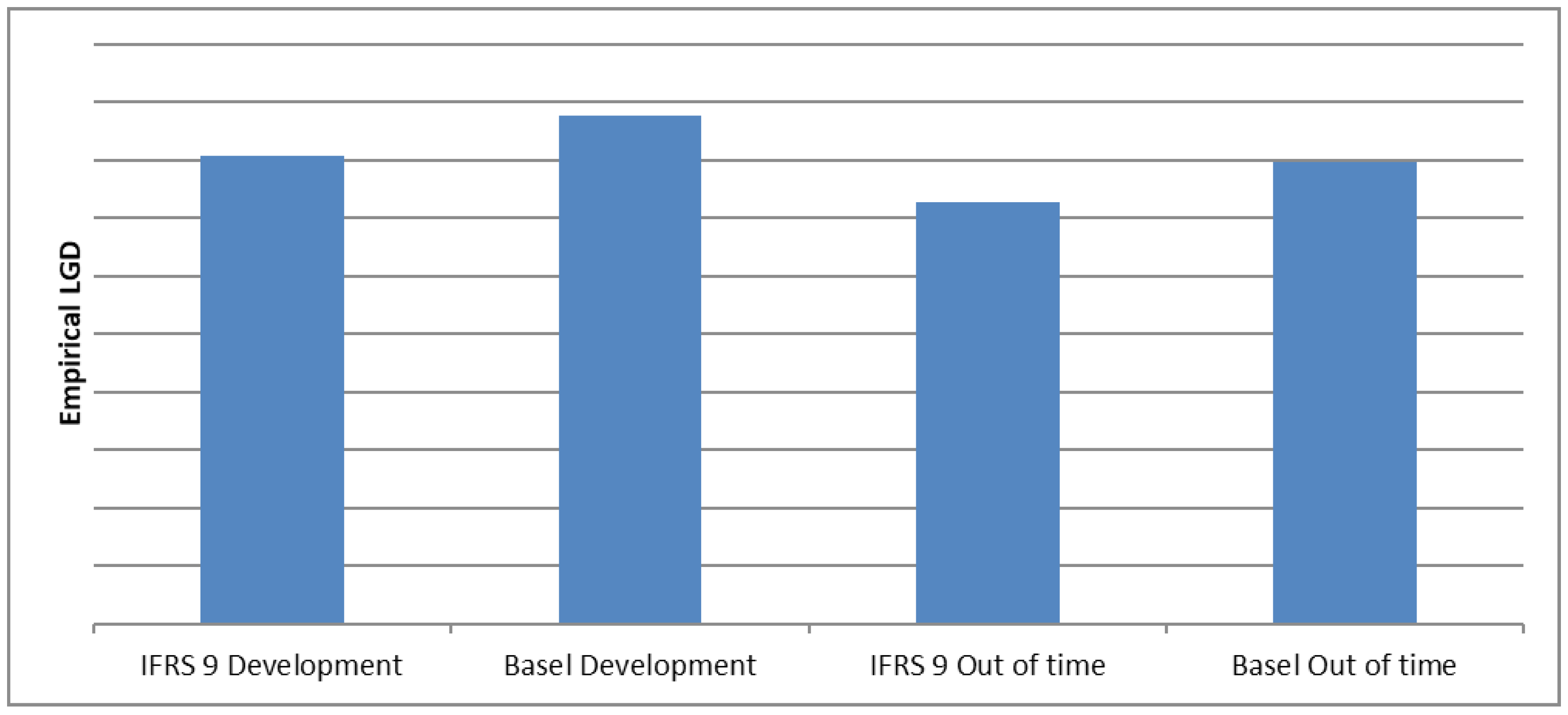
3.1. Empirical LGD
3.2. Macro-Economic Variables
- The consumer price index (CPI) is the increase in the level of prices of a representative basket of goods purchased by consumers and households. This measures how much purchasing power in a country is eroded by price increases.
- The ratio of debt to disposable household income (DDHI) is a measure that indicates the ability of households to repay their debts. This measure is derived by dividing total monthly household debt by monthly income.
- The debt service ratio (DSR) is the proportion of household income that is spent on covering existing debt agreements.
- The M3 money supply is the money supply in circulation and indicates a country’s liquid money supply.
- The gross domestic product (GDP) is an indication of the total local production of the economy.
- The nominal house price index (NHPI) is an index of the average house price level, without adjusting for inflation.
- The real house price index (RHPI) is an index measuring the average house price level, which adjusts for inflation.
- The prime interest rate is the rate at which the banks of South Africa lend money to customers.
- Debt affordability is the ratio of government debt relative to the resources available for repaying that debt.
- The leading indicator is a forecast of the general health of the South African economy.
- Rand dollar exchange rate is the price of one dollar in rand terms.
- Liquidity spread is the premium that flows to a party willing to provide liquidity to a party that is demanding it.
4. Results
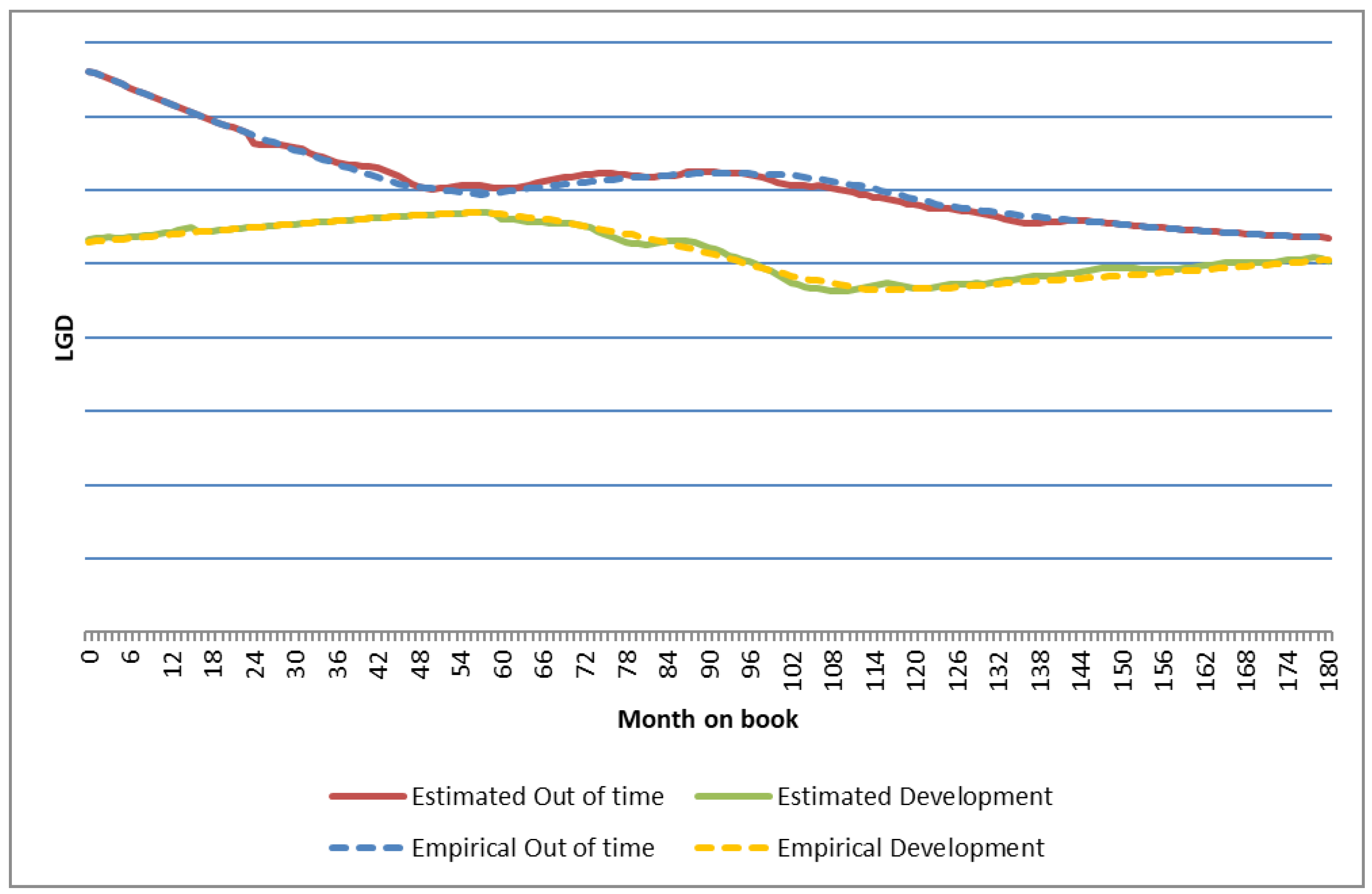
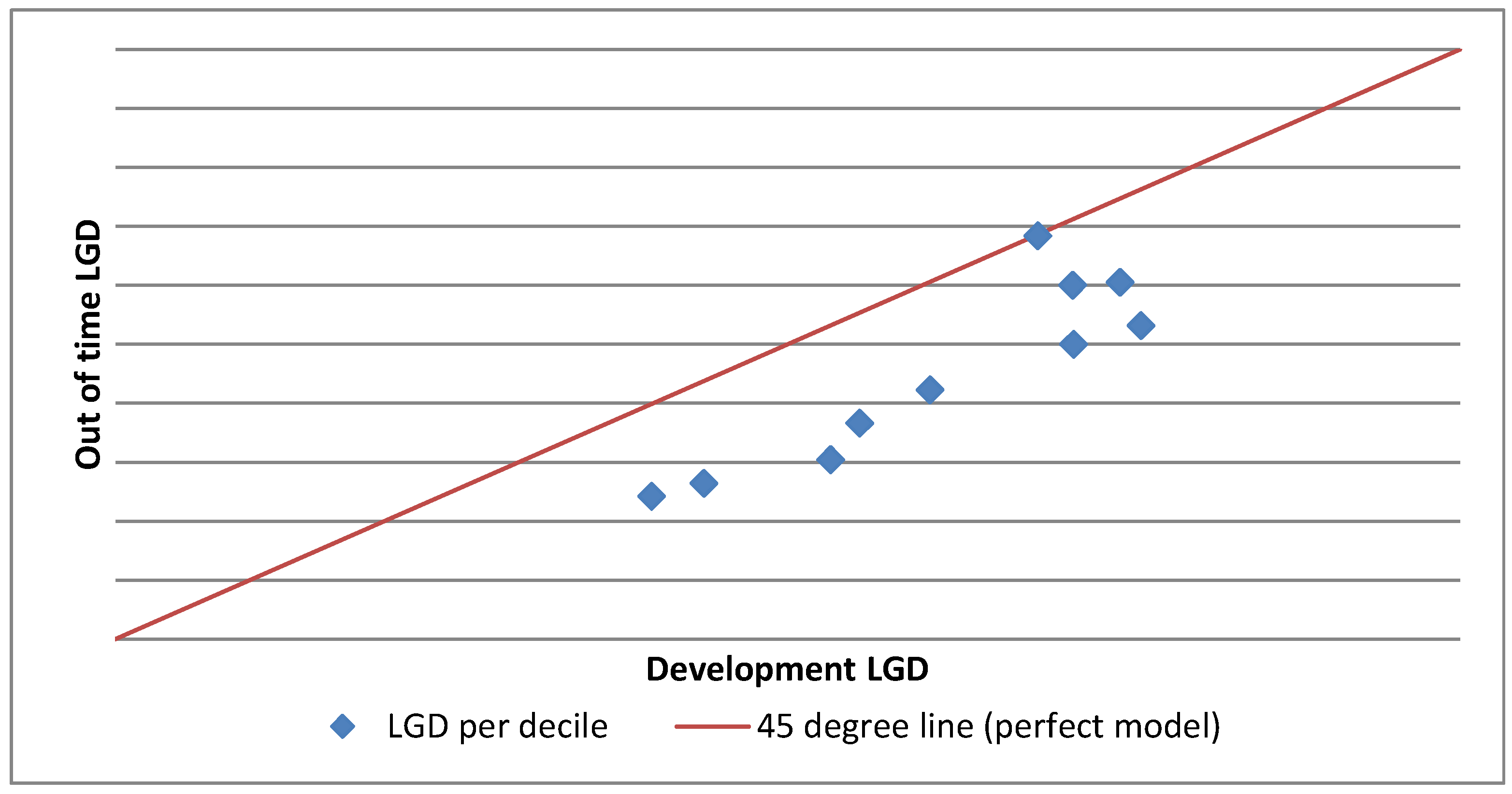
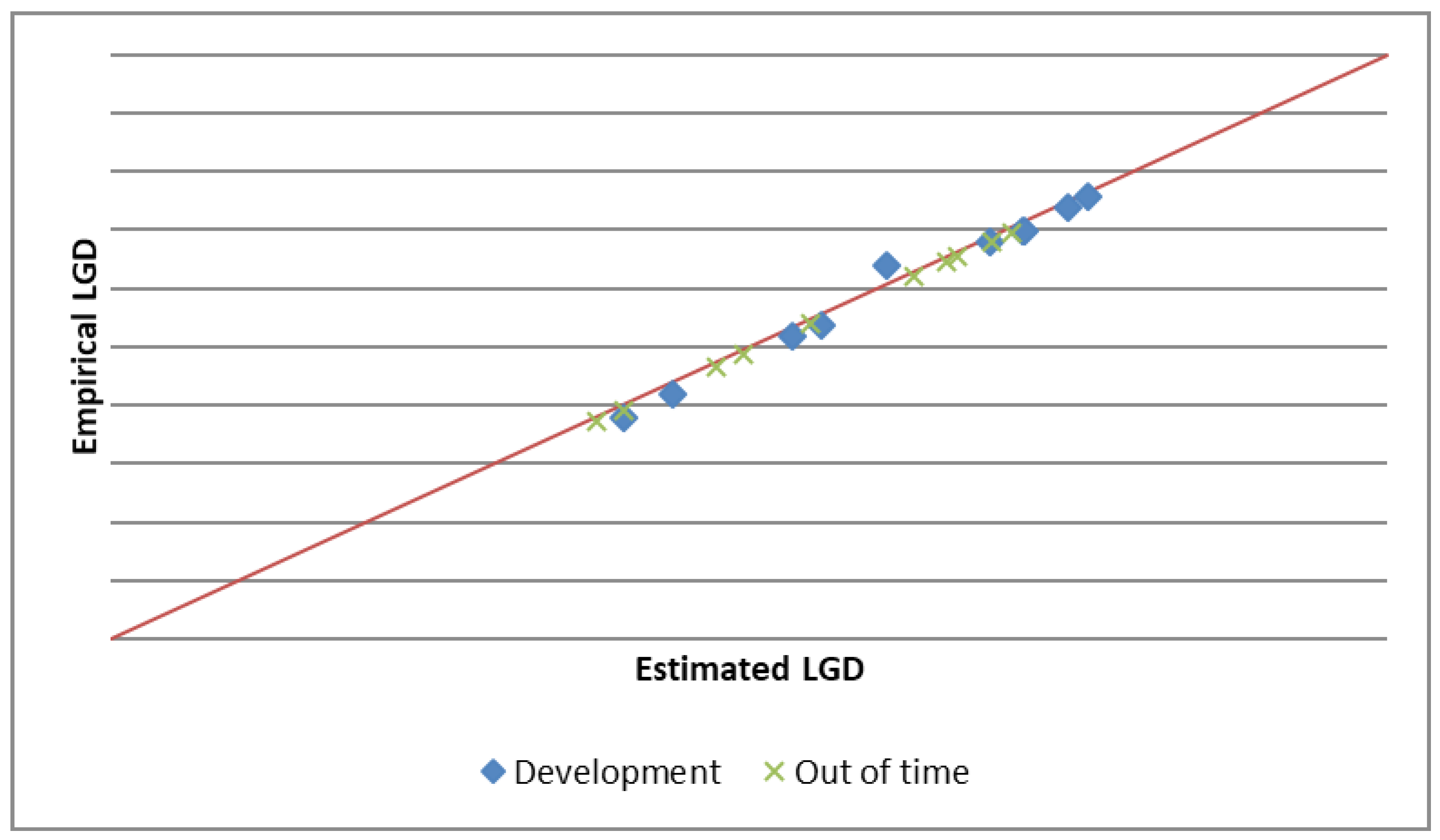
4.1. IFRS 9 LGD Model
4.2. Macro-Economic Model (ECM)
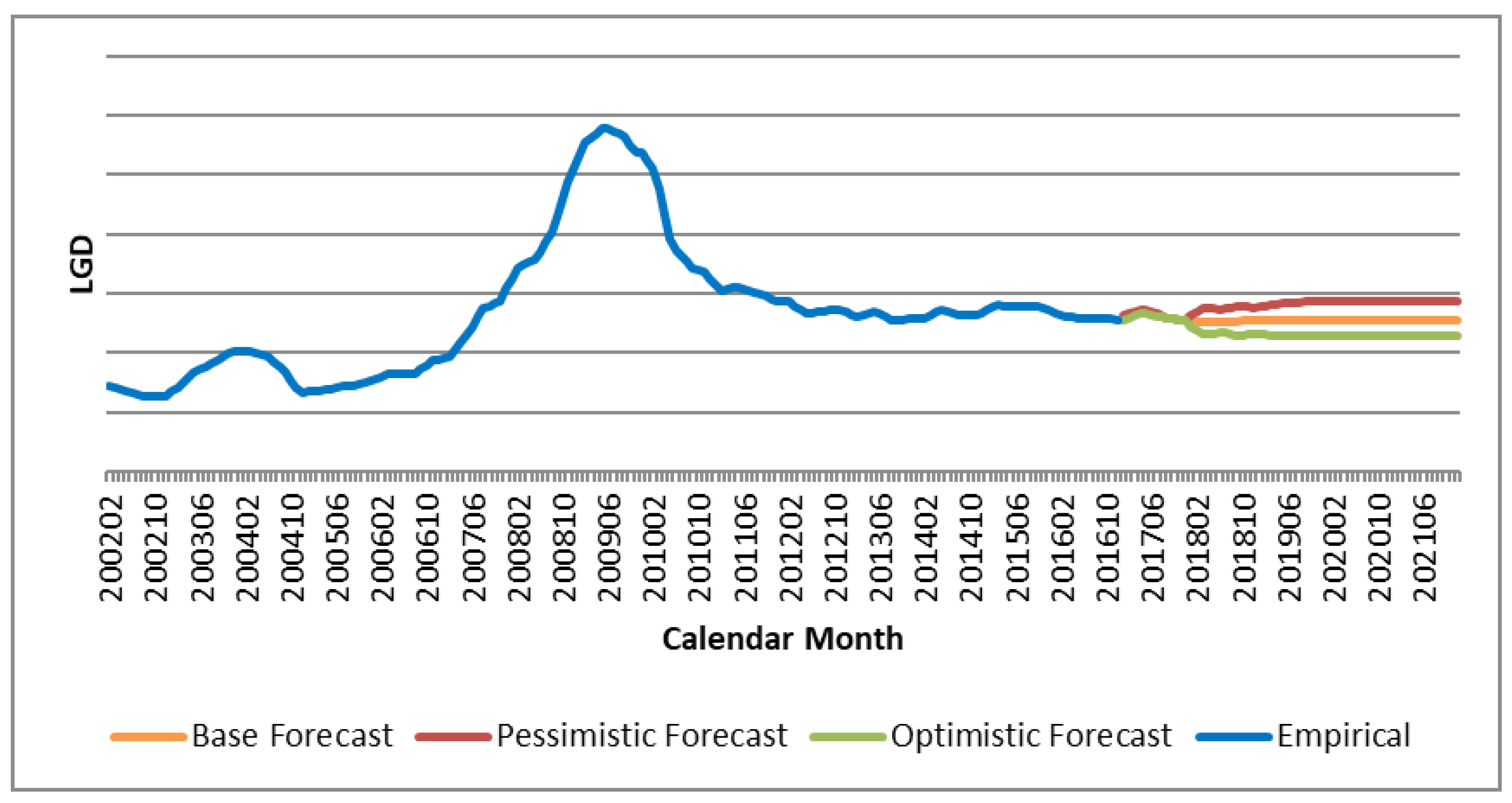
4.3. Macro-Economic Scenarios
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Aptivaa. 2016a. Building Blocks of Impairment Modeling (Issue 02). Available online: https://www.academia.edu/30200858/Building_Blocks_of_Impairment_Modeling (accessed on 4 March 2020).
- Aptivaa. 2016b. Cash Shortfall and LGD Two Sides of the Same Coin. Available online: http://www.aptivaa.com/blog/cash-shortfall-lgd-two-sides-of-the-same-coin/ (accessed on 4 March 2020).
- Baesens, Bart, Daniel Rösch, and Harald Scheule. 2016. Credit Risk Analytics. Hoboken: John Wiley & Sons, Inc. [Google Scholar] [CrossRef]
- Basel Committee on Banking Supervision (BCBS). 2015. Guidance on Accounting for Expected Credit Losses. Technical Report. Basel: Bank of International Settlement (BIS). [Google Scholar]
- Bastos, Joao A. 2010. Forecasting bank loans loss given default. Journal of Banking and Finance 34: 2510–17. [Google Scholar] [CrossRef]
- Beerbaum, Dirk. 2015. Significant increase in credit risk according to IFRS 9: Implications for financial institutions. International Journal of Economics & Management Sciences 4: 1–3. [Google Scholar] [CrossRef]
- Black, Barnaby, Glenn Levine, and Juan M. Licari. 2015. Probability-Weighted Outcomes Under IFRS 9—A Macroeconomic Approach. Moody’s Analytics, Risk Perspective, The Convergence of Risk, Finance and Accounting VII. Available online: https://www.moodysanalytics.com/risk-perspectives-magazine/risk-finance-accounting-converge-ifrs9/spotlight-ifrs-9/probability-weighted-outcomes-under-ifrs-9 (accessed on 20 March 2020).
- Braun, Christian. 2004. The prediction error of the chain ladder method applied to correlated run-off triangles. ASTIN Bulletin 34: 399–423. [Google Scholar] [CrossRef]
- Breed, Douw Gerbrand, Tanja Verster, Wd Schutte, and Naeem Siddiqi. 2019. Developing an impairment loss given default model using weighted logistic regression illustrated on a secured retail bank portfolio. Risks 7: 123. [Google Scholar] [CrossRef]
- Brown, Iain L. J. 2014. Developing Credit Risk Models Using SAS Enterprise Miner and SAS/STAT: Theory and Applications. Cary: SAS INST. [Google Scholar]
- Chawla, Gaurav, Lawrence R. Forest, and Scott D. Aguais. 2016. Point-in-time (PIT) LGD and EAD models for IFRS 9, CECL and stress testing. Journal of Risk Management in Financial Institutions 9: 249–63. [Google Scholar]
- Engle, Robert F., and Clive W. J. Granger. 1987. Cointegration and error-correction: Representation, estimation, and testing. Econometrica 55: 251–76. [Google Scholar] [CrossRef]
- European Banking Authority (EBA). 2016. Consultation Paper eba/cp/2016/10: Draft Guidelines on Credit Institutions: Credit Risk Management Practices and Accounting for Expected Credit Losses. Technical Report. La Défense: European Banking Authority (EBA). [Google Scholar]
- Global Public Policy Committee (GPPC). 2016. The Implementation of IFRS 9 Impairment Requirements by Banks. Available online: https://www2.deloitte.com/content/dam/Deloitte/global/Documents/Financial-Services/gx-fsi-gppc-ifrs-9-implementation-considerations.pdf (accessed on 10 April 2020).
- Gomez, Victor. 2019. Linear Time Series with MATLAB and OCTAVE. Statistics and Computing. Berlin/Heidelberg: Springer. [Google Scholar]
- Granger, Clive W. J. 1981. Some properties of time series data and their use in econometric model specification. Journal of Econometrics 16: 121–30. [Google Scholar] [CrossRef]
- Grzybowska, Urszula, and Marek Karwański. 2019. Application of machine learning method under IFRS 9 approach to LGD modeling. Acta Physica Polonica A 138: 116–22. [Google Scholar] [CrossRef]
- IFRS Foundation. 2014. IFRS 9 Financial Instruments. Technical Report. London: IFRS Foundation. [Google Scholar]
- Joubert, Morne, Tanja Verster, and Helgard Raubenheimer. 2020. Default weighted survival analysis to directly model loss given default. South African Statistical Journal 54: 173–202. [Google Scholar] [CrossRef]
- Krüger, Steffen, Toni Oehme, Daniel Rösch, and Harald Scheule. 2018. A copula sample selection model for predicting multi-year LGDs and lifetime expected losses. Journal of Empirical Finance 47: 246–62. [Google Scholar] [CrossRef]
- Miller, Rupert G. 2011. Survival Analysis. Hoboken: John Wiley & Sons, Inc. [Google Scholar]
- Mills, E. D. 2013. Adjusting for Covariates in Zero-Inflflated Gamma and Zero-Inflflatedlog-Normal Models for Semicontinuous Data. Ph.D. thesis, University of Iowa, Iowa City, IA, USA. [Google Scholar] [CrossRef]
- Miu, Peter, and Bogie Ozdemir. 2017. Adapting the basel ii advanced internal ratings based models for international financial reporting standard 9. Journal of Credit Risk 13: 53–83. [Google Scholar] [CrossRef]
- Mohamed, Ismail. 2009a. Simulating Time Series Analysis Using SAS-Part II Cointegration. Available online: http://support.sas.com/resources/papers/proceedings09/204-2009.pdf (accessed on 9 August 2020).
- Mohamed, Ismail. 2009b. Simulating Time Series Testing Using SAS-Part I the Augmented Dickey-Fuller (ADF) Test. Available online: http://support.sas.com/resources/papers/proceedings09/205-2009.pdf (accessed on 9 August 2020).
- Mohamed, I. 2010. Simulating Time Series Analysis Using SAS Part III: Error Correction Model (ECM). NorthEast SAS Users Group Proceedings. Available online: ttps://www.lexjansen.com/nesug/nesug10/po/po20.pdf (accessed on 9 August 2020).
- Nedbank. 2019. Pillar 3 Risk and Capital Management Report for the Year Ended 31 December 2019. Technical Report. Sandton: Nedbank. [Google Scholar]
- Novotny-Farkas, Zoltan. 2016. The Significance of IFRS 9 for Financial Stability and Supervisory Rules. Directorate-General for Internal Policies of the Union (European Parliment Economic and Scientific Policy), IP/A/ECON/2015-14/PE563.461. Luxembourg: Publications Office of the EU. [Google Scholar] [CrossRef]
- Schutte, Willem Daniel, Tanja Verster, Derek Doody, Helgard Raubenheimer, and Peet Jacobus Coetzee. 2020. A proposed benchmark model using a modularised approach to calculate IFRS 9 expected credit loss. Cogent Economics & Finance 8: 1735681. [Google Scholar] [CrossRef]
- Siddiqi, Naeem. 2017. Intelligent Credit Scoring: Building and Implementing Better Credit Risk Scorecards. Hoboken: John Wiley & Sons, Inc. [Google Scholar]
- Sigrist, F., and W. A. Stahel. 2011. Using the censored gamma distribution for modeling fractional response variables with an application to loss given default. ASTIN Bulletin 41: 673–710. [Google Scholar] [CrossRef]
- Smuts, Marius, and James S. Allison. 2020. An overview of survival analysis with an application in the credit risk environment. Orion 36: 89–110. [Google Scholar]
- Taylor, Jeremy. 2003. Risk-grading philosophy: Through the cycle versus point in time. The Risk Management Association Journal, 32–39. Available online: https://cms.rmau.org/uploadedFiles/Credit_Risk/Library/RMA_Journal/Risk_Ratings/Risk-Grading%20Philosophy_%20Through%20the%20Cycle%20versus%20Point%20in%20Time.pdf (accessed on 5 September 2020).
- Tong, E. N. C., C. Mues, and L. Thomas. 2013. A zero-adjusted gamma model for mortgage loan loss given default. International Journal of Forecasting 29: 548–62. [Google Scholar] [CrossRef]
- Tsay, Ruey S. 2014. Multivariate Time Series Analysis with R and Financial Applications. Hoboken: Wiley. [Google Scholar]
- Witzany, Jiri, Michal Rychnovsky, and Pavel Charamza. 2012. Survival analysis in LGD modelling. European Financial and Accounting Journal 7: 6–27. [Google Scholar] [CrossRef]

| Macro-Economic Variable | t-Value - No Differencing | t-Value - First Difference | t-Value - Error |
|---|---|---|---|
| CPI | −1.74 | −3.96 | −4.29 |
| DDHI | −2.23 | −5.84 | −5.78 |
| debt affordability | −1.26 | −5.75 | −6.58 |
| DSR | −1.22 | −5.44 | −3.97 |
| GDP | −2.97 | −4.24 | −5.86 |
| leading indicator | −0.44 | −4.45 | −5.48 |
| liquidity spread | −0.72 | −4.78 | −451 |
| M3 money supply | −0.71 | −4.74 | −4.85 |
| NHPI | −1.92 | −6.49 | −4.82 |
| prime interest rate | −1.87 | −5.26 | −5.36 |
| rand dollar exchange rate | −2.32 | −4.23 | −4.34 |
| RHPI | −0.93 | −5.39 | −5.51 |
| Parameter Estimates | ||||
|---|---|---|---|---|
| Variable | Intercept | GDP | DDHI | Prime |
| Lag used | - | Lag 3 | Lag 8 | Lag 7 |
| VIF | 2.44 | 1.02 | 2.42 |
| Parameter Estimates | |||
|---|---|---|---|
| Variable | Intercept | Leading indicator | Debt affordability |
| Lag used | - | Lag 1 | Lag 5 |
| VIF | 1.37 | 1.59 |
| Base Scenario | Pessimistic Scenario | Optimistic Scenario | |
|---|---|---|---|
| Probability of scenario occurring | 40% | 30% | 30% |
| % IFRS 9 LGD change from base | - | −4.03% | 5.17% |
| % IFRS 9 PD change from base | - | −2.07% | 3.29% |
| % ECL change from base | - | −3.27% | 4.39% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joubert, M.; Verster, T.; Raubenheimer, H.; Schutte, W.D. Adapting the Default Weighted Survival Analysis Modelling Approach to Model IFRS 9 LGD. Risks 2021, 9, 103. https://doi.org/10.3390/risks9060103
Joubert M, Verster T, Raubenheimer H, Schutte WD. Adapting the Default Weighted Survival Analysis Modelling Approach to Model IFRS 9 LGD. Risks. 2021; 9(6):103. https://doi.org/10.3390/risks9060103
Chicago/Turabian StyleJoubert, Morne, Tanja Verster, Helgard Raubenheimer, and Willem D. Schutte. 2021. "Adapting the Default Weighted Survival Analysis Modelling Approach to Model IFRS 9 LGD" Risks 9, no. 6: 103. https://doi.org/10.3390/risks9060103
APA StyleJoubert, M., Verster, T., Raubenheimer, H., & Schutte, W. D. (2021). Adapting the Default Weighted Survival Analysis Modelling Approach to Model IFRS 9 LGD. Risks, 9(6), 103. https://doi.org/10.3390/risks9060103






