1. Introduction
Longevity risk, the possibility that individuals die much later than the theoretical average, is covered by a range of insurance products. A primary example is lifetime annuities, which pay a guaranteed income even if individuals live longer than expected and exhaust their own savings. Measuring longevity risk in lifespan products of this type requires establishing assumptions or, at least, choosing a specific loss variable and a concrete risk measure, such as value-at-risk (VaR).
Here, we propose a flexible nonparametric estimator that is used to measure longevity risk with the (extreme) quantile of the age-at-death distribution. Our nonparametric approach is a generalization of the proposal by
Alemany et al. (
2013) that was based on only two given transformations.
Alemany et al. (
2013) proposed the transformed kernel estimation of the cumulative distribution function and the quantile. In order to transform the data, a parametric distribution function was proposed and then the bias and variance of the transformed kernel estimator were obtained. The general result established that with the transformed kernel estimation approach, the variance of the estimator diminishes at the cost of increasing its bias.
Alemany et al. (
2013) argued that, since the transformed variable follows a uniform distribution, then boundary bias emerges naturally. To reduce the bias, they proposed a second transformation based on the inverse Beta distribution. However, they did not study how this second transformation affects the bias and variance of the transformed kernel estimator. Here, we start from the initial results by
Alemany et al. (
2013) and analyze the role of the second transformation. Furthermore, we have deduced the properties of the estimator and have proved that the second transformation can increase or decrease the bias associated with the first transformation that will be able to be selected between alternative families of distributions. We argue that by doing so, we are able to reduce the model selection problem and, thus, eliminate the need to choose a specific parametric model which may be too restrictive for older ages, that is, “rare longevity events” corresponding to individuals that live much longer than the rest.
In
Section 2, the literature on longevity risk is gathered. In
Section 3, the estimator of the conditional quantile and its properties are shown. In
Section 4, we describe our proposed transformed kernel estimator of the cumulative distribution function and present interesting findings about its performance and about the smoothing parameter. Additionally, basic notions about the empirical distribution and kernel estimation are outlined. In
Section 5, we estimate conditional quantiles for each of the years in the period 2011–2017 for the population aged 65 and over and apply these results to split the price of an annuity into two segments: that is, the price up to the longevity risk age and the price beyond that age. By so doing, we express the age risk measure in terms of an annuity price in monetary units. Our conclusions are outlined in
Section 6. Proofs of the asymptotic properties of our estimator and the results of a simulation study analyzing finite sample properties are presented in the Appendix, along with a table showing the results of the application to the pricing of a single annuity.
2. Longevity Risk
Longevity risk, as a broad concept, has been widely studied at the aggregate level and has been associated with the forecasting of such demographic variables as life expectancy and mortality.
Stallard (
2006) differentiated between aggregate and individual longevity risk and proposed approaching the latter using individual survival functions, given a set of covariates related to the factors that affect mortality and life expectancy; however, implementing this proposal is far from straightforward as individual information on habits and health is generally unavailable.
Denuit (
2009) proposed estimating aggregate longevity risk from an extreme quantile of the life expectancy distribution which can be deduced from the Lee–Carter model (see
Lee and Carter 1992).
Basellini and Camarda (
2019) proposed a parametric model to forecast the age-at-death of the adult population in Japan, considering ages from 30 to 110 and beyond. More recently, using compositional data,
Shang and Haberman (
2020) forecast the whole age-at-death distribution and used these results to obtain the
t year survival probabilities at age
x (
), as well as evaluating the “single-premium temporary immediate annuity”. Here, we show that, using the forecast distribution, our nonparametric estimator can also be used to obtain a smooth estimation of these probabilities. In short, all these perspectives, in estimating longevity risk for populations at retirement age, convey just how important it is for public and private institutions alike to establish reserves for lifetime contracts and guarantee the sustainability of public and private pensions, and other health and long-term care systems.
Unlike the studies cited above, our aim is to obtain a longevity risk measure that can be expressed as a value in years and which corresponds to an advanced age, above which the probability of death is low or very low. In line with our definition, the higher this “longevity risk age” value, the greater the risk, since it can be interpreted directly as an age that a given fraction of individuals will survive. For example, if our quantile level is fixed at 99% and the measure of longevity risk equals 101 years, then this means that 1% of the population will survive beyond the age of 101.
Typically, the number of observations in this range of older ages is small and disperse, i.e., we have very few data. To address this, we propose an estimator for this extreme quantile that adapts to a situation in which statistical information is scarce in the right tail of the distribution. It should be noted, at this point, that in finance and insurance, the notion of the extreme quantile and VaR are used interchangeably.
Chen and Cummins (
2010) argued that some events can be extremely rare and extreme value distributions are necessary to model the improvement in mortality rates. However, the use of these distributions on the whole domain of the variable to estimate the VaR of the age-at-death distribution can give longevity risk values of over 150 years. An alternative is to focus on the extreme ages to fit the shape of the tail of the distribution based on the Generalized Pareto Distribution (GPD).
Coles et al. (
2001) described the semiparametric method based on the Mean Residual Life plot to obtain a threshold and then estimate shape and scale parameters for the GPD. However, catastrophic events can cause major changes in the shape of the age-at-death distribution, so that distributions that have provided a good fit over a long period of time stop doing so. An example is found in the current COVID pandemic. The proposed nonparametric estimator can easily be adapted to changing longevity scenarios.
Based on the shape parameter of the GPD,
Rootzén and Zholud (
2017) analysed if age-at-death could be a limit or not (see
Rootzén and Zholud 2018, for discussion). Here compare results obtained with semiparametric GPD for extreme ages, the Gompertz distribution, the generalized Gompertz distribution and our proposal to estimate extreme quantiles. We think that a nonparametric approach constitutes a suitable alternative; yet, given the small number of advanced ages observed, the direct implementation of basic nonparametric methods may not be efficient. Thus, we develop a procedure based on both parametric and kernel estimation methods to evaluate longevity risk using the cumulative distribution function of the age-at-death variable. We show that our proposal improves the inefficiency of using the empirical distribution or the classical kernel estimator, while coping with the bias of choosing possibly inadequate parametric distributions.
Specifically, we employ the conditional quantile because we estimate longevity risk from an extreme quantile of the age-at-death variable for a given population that has already survived to age
a. This is the most common situation in the case of insurance products covering lifetime resources after retirement, which usually means after the age of 65.
Stallard (
2006) explained that at the individual level “longevity risk refers to the possibility of living longer than assumed in financial planning for the retirement of a single individual”. It is upon this idea that the conditional extreme quantile is based. Conditional extreme quantiles are convenient to evaluate the effect of longevity risk on the unitary price of a lifetime and temporary annuities, where the former consider individuals throughout their lifespan for the probabilities that, at a certain age, they live
more years and the latter depend on a threshold (the maturity) from which the probability of living is assumed to be zero (see
Bowers et al. 1997;
Dickson et al. 1997, for a review in relation to life insurance). As we show in the last section of this paper, relating maturity to the conditional extreme quantile allows us to quantify and interpret longevity risk in lifetime annuities.
We illustrate the methodology with official micro-data containing the dates of birth and death of the deceased population in Spain between 2011 and 2017. The study is conducted differentiating by gender. In general, women have greater longevity than men, although these differences may disappear with age in some countries. For example, drawing on data from England and Wales,
Mayhew and Smith (
2014) showed that the gap between the life expectancy of men and women tends to close. Earlier, basing their arguments on reliability theory,
Gavrilov and Gavrilova (
2001) explained why relative differences in the mortality rates of populations within the same species and, hence, differences in their life expectancies, tend to disappear with age. From an empirical perspective,
Waldron (
1993),
Gjonça et al. (
2005) and
Glei and Hirouchi (
2007) analyse the gender gap between life expectancies in different periods. These authors show that there are countries in which the gender longevity gap narrowed and others in which it widened, depending on the period under analysis (see also
Mayhew and Smith 2011). The results presented here focus on Spain’s older population from 2011 to 2017 and show that the gap between male and female longevity risk exists and does not fade until a very advanced age is reached.
3. The Conditional Quantile and Longevity Risk
Let
X be a continuous random variable with probability density function (pdf)
and cumulative distribution function (cdf)
. In this paper,
X refers to the age-at-death of an individual in a given population. In such cases,
X takes positive values. Given a subpopulation with an age of death equal to or greater than
a, we propose a longevity risk measure obtained from the truncated cdf, which is equal to the conditional quantile (CQ) and is defined as:
where
a is a threshold and
is the conditional confidence level. The truncated cdf is:
To estimate the CQ defined in (
1) the theoretical truncated cdf needs to be replaced by an estimator. Given that we need to focus on the quantile at confidence level
, with this aim in mind, we can relate the probability associated with the truncated cdf with the probability associated with the untruncated cdf:
Thus, from expression (
3) and given a known confidence level
:
where
. In addition to this empirical approach, alternative kernel estimators (KEs) of
p are analysed, with the aim of finding the simplest and most efficient proposal.
To obtain the CQ, our strategy involves estimating , calculating the unconditional probability p, and deriving the quantile using the untruncated cdf. In practice, since , this requires estimating an extreme quantile. Furthermore, this strategy is easily applicable if, as we propose in this paper, the quantile estimator is obtained by inverting an estimator of the cdf.
Proposition 1. The expected value of is:and the variance is:where and are those of the corresponding nonparametric estimator. The proof of Proposition 1 is in
Appendix A. This proposition shows how the bias and variance of
are proportional to those of the estimator used for the unconditional cdf evaluated at
a,
.
Furthermore, given the properties of the KE (which we show in the following section), as
, then
and, asymptotically,
and, therefore,
is normally distributed (see, for example,
Reiss 1981).
The CQ provides us with a value of the age-at-death from which there is a probability that this age is higher. This allows us to evaluate the risk for a life insurance product, with a confidence level , once a given age has been reached.
4. Estimators of the Unconditional cdf
Let
be a sample of independent and identically distributed data observations of the continuous random variable
X with cdf
. Now, we summarise the main properties associated with the empirical distribution and the KE. The empirical distribution is:
where
is an indicator function that takes a value of 1 if the condition between parentheses is true and 0 otherwise. The bias of
is zero and its variance is:
We note that the empirical distribution is only defined in the observed values in the sample.
The usual expression for the KE of a cdf is (see
Azzalini 1981;
Reiss 1981, for a first deffinition):
where the function
K is a cdf associated with a kernel pdf
k. Examples of such functions are the Epanechnikov and the Gaussian kernels (
Silverman 1986). The parameter
, known as the bandwidth or smoothing parameter, controls the smoothness of the estimation. Thus, the higher the value of
b, the smoother the resulting function. However, obtaining an optimal value for this smoothing parameter is one of the greatest difficulties posed by kernel estimation.
Note that the classical kernel estimation of cdf defined in (
8) bears many similarities to the expression of the well-known empirical distribution in (
6). In (
8),
has to be replaced by
to obtain (
6). Focusing on the second-order properties, it has already been noted by
Reiss (
1981) and
Azzalini (
1981) that, when
as
,
is continuous and
exists, the asymptotic bias and variance of (
8) are (see also
Hill 1985):
and
The KE of the cdf has less variance than that of the empirical distribution, but it has some bias which tends to zero as .
When the distribution is right-skewed, at the extreme quantile with p near 1 the variance of the KE tends to the variance of the empirical quantile.
Let
be a continuous and monotonic non-decreasing transformation,
is the transformed random variable and
,
, are the transformed data, the TKE of
is:
In practice, the estimator defined in (
11) consists of transforming the data and obtaining the KE of the transformed variable. The smoothing parameter in the TKE is the same as that in the KE of the cdf associated with the transformed data. To calculate the KE, we need to determine the kernel function
K and the value of the smoothing parameter
b. For the former, we use the Epanechnikov kernel (
), although alternative kernels, such as the Gaussian, hardly affect the estimator properties. In the case of the latter, there are alternative methods that can be employed to calculate the smoothing parameter
b. For instance, cross-validation and plug-in methods are common (see, for example,
Altman and Léger 1995;
Bowman et al. 1998). However, they require considerable computational effort in large data sets and do not perform particularly well when there are parts of the distribution domain for which data are scarce.
Assume that
is continuous and that its first two derivatives exist. Then, from Theorem 1 in (
Alemany et al. 2013), it follows that (
indicates first derivative):
and
where
is an asymptotic term that tends to zero with its argument.
If
when
, then the TKE in (
11) is a consistent estimator of
. Furthermore, in the case where
,
and
, then the bias of TKE (
12) is zero.
If the transformed random variable
Y follows a Uniform
distribution then
and, therefore, any results based on a second-order approach like (
12) and (
13) cannot be obtained. We propose to choose
T so that the distribution of the transformed variable is different from the Uniform
distribution and so that it can be easily estimated using the KE.
Alemany et al. (
2013), following (
Bolancé et al. 2008;
Buch-Larsen et al. 2005), propose using a first transformation equal to the modified Champernowne distribution (see
Buch-Larsen et al. 2005) and a second transformation equal to the inverse of a given
distribution.
The proposal of (
Alemany et al. 2013) is presented as a particular case of the TKE with double transformation. However, these authors do not analyze the influence of the second
transformation on the resulting estimation. Here we generalize this TKE and obtain the theoretical properties of this new estimator of the cdf. These new results are shown below.
The procedure is based on the expression of bias of the KE shown below in (
9) which squared and integrated is:
Expression (
14) depends on the shape of the density through
.
Terrell (
1990) proved that the density that minimises this integral belongs to the Beta distribution family with pdf (see
Johnson et al. 1995):
where
is a location parameter,
is a scale parameter,
and
are shape parameters,
and
is Euler’s Gamma function.
Terrell (
1990) proved that the pdf expressed in (
15) with
,
and
is equal to the
which takes the smallest value of
among all the distributions with domain
and the same variance; therefore, given
b and
k, it takes the smallest value of the integrated bias defined in (
14). Previously,
Terrell and Scott (
1985) deduced that when
,
,
the density minimises
for all distributions with a domain
and the same variance.
Definition 1. Let be a first transformation coinciding with a cdf and be the cdf of the second transformation; then the Beta Transformed Kernel Estimator (BTKE) of the original cdf is defined as:where the cdf associated with the is: The BTKE has suitable properties to estimate the extreme quantile because, among other characteristics (see
Bolancé et al. 2020), as we describe in
Section 4.1, an optimal smoothing parameter based on the
distribution can be found.
Theorem 1, whose proof is given in
Appendix A, gives expressions for the asymptotic bias and variance of the BTKE in (
16).
Theorem 1. Let be the true pdf that is continuous and has at least one continuous derivative, be a cdf with continuous pdf and at least two continuous non-null derivatives and, for , be the pdf of defined in (17), then the asymptotic bias of BTKE of the true cdf is:and its variance is: From the results of Theorem 1, we can analyze the bias and variance of the BTKE and obtain Proposition 2, whose proof is direct and, hence, is not given.
Proposition 2. If the generating process or the distribution of the data is known and the first transformation can be estimated so that or, at the point evaluated x, and , the bias of the BTKE for a given smoothing parameter b and kernel k is:and the variance is: From Proposition 2, we can see that in the best case our estimation has some bias that tends to zero as
; however, this bias can be compensated by a low variance, especially in the most extreme quantiles. Alternatively,
Swanepoel and Van Graan (
2005) and
Alemany et al. (
2013) proved that the TKE is unbiased when
; so, given the difficulties associated with the kernel estimation of the Uniform
distribution function, the TKE based on a parametric or nonparametric cdf transformation cannot be used to estimate extreme CQs.
If the first transformation
is not equal to the true
or, at the extreme quantile evaluated,
,
and
, we obtain that the sign of the bias in (
19) depends on:
For extreme quantiles, the value of (
22) will be positive or negative depending on whether the distribution used as the first transformation has a heavier or lighter tail than the true distribution. In this way we obtain two different results:
For the variance, if is the cdf of a lighter tailed distribution than , so and the variance of BTKE will be smaller than the variance of KE. Alternatively, if is the cdf of a heavier tailed distribution than , so and the result will depend on this quotient, the less it is the greater the variance is.
4.1. Smoothing Parameter of BTKE
If we assume
, the transformed data in the BTKE follow the
distribution; then, the optimal bandwidth can be obtained by minimizing the asymptotic MSE, that is equal to the sum of the variance and the squared bias of the KE of the transformed variable, eliminating the asymptotic order terms:
The resulting smoothing parameter is:
where
is absolute value.
The smoothing parameter
in expression (
24) minimises the
of the BTKE of the quantile
if the true cdf fulfills
. However, if
then, as we show in Remark 1, the bandwidth expressed in (
24) could be lower or higher than the optimal.
Remark 1. Let M be the cdf and the optimal bandwidth when and let be the pth quantile of the random variable X, then:
If T is heavier tailed than then , and .
If is heavier tailed than T then , and .
A higher provides a higher estimated quantile and vice versa. In practice, Remark 1 implies that the difference between and T increases the bias when and increases the variance when , although both tend to zero as .
In
Appendix B, we present a simulation study comparing the
of the estimated
based on the empirical distribution, the KE and the BTKE. We simulated alternative distributions with different tail shapes: a long-tail with an exponential and subexponential decrease (Weibull and Lognormal, respectively) and a heavy tail with a power decrease (Pareto).
5. Data Analysis
We analyze the longevity risk of the population aged over 65 in Spain from 2011 to 2017. For this population, we fit the distribution of the age-at-death in months and we estimate extreme quantiles and conditional extreme quantiles with , and , which we also denominate as VaR at confidence level. Since we have a large number of observations, we can estimate quantiles based on the BTKE with very close to 1 quite accurately.
The data were provided by the Spanish National Institute of Statistics (INE—Instituto Nacional de Estadística) and contain information about the gender, the year and month of birth and the year and month of death of the population aged over 65. The information available allows us to obtain the age-at-death in months but, for ease of interpretation, the results are shown in years.
In
Table 1 we present the mortality rates and the basic descriptive statistics for the population aged over 65, differentiated by gender. It is can be seen that, in aggregate terms, for all years, female mortality rates are lower than those for men and, inversely, the average age-at-death for women is higher. However, if we focus on the maximum age-at-death values, the results are not so clear.
The first step in calculating the longevity risk is to fit alternative parametric distributions to our data. We obtain results for Lognormal, Weibull, Gamma, Generalised Pareto Distribution (GPD) and modified Champernowne, the best fit being provided by this last distribution. Not to confuse the reader, the parameters associated with the first transformation cdf, are not shown here, they are available from the authors. We observe that the three parameters of the modified Champernowne distribution endow this model with more flexibility near the minimum age (65 years) and in the tail of the distribution. However, if we use this distribution to estimate the CQs, in the more extreme cases, we obtain highly unlikely ages-at-death of over 150 years. For this reason, we use the BTKE to correct these unlikely values.
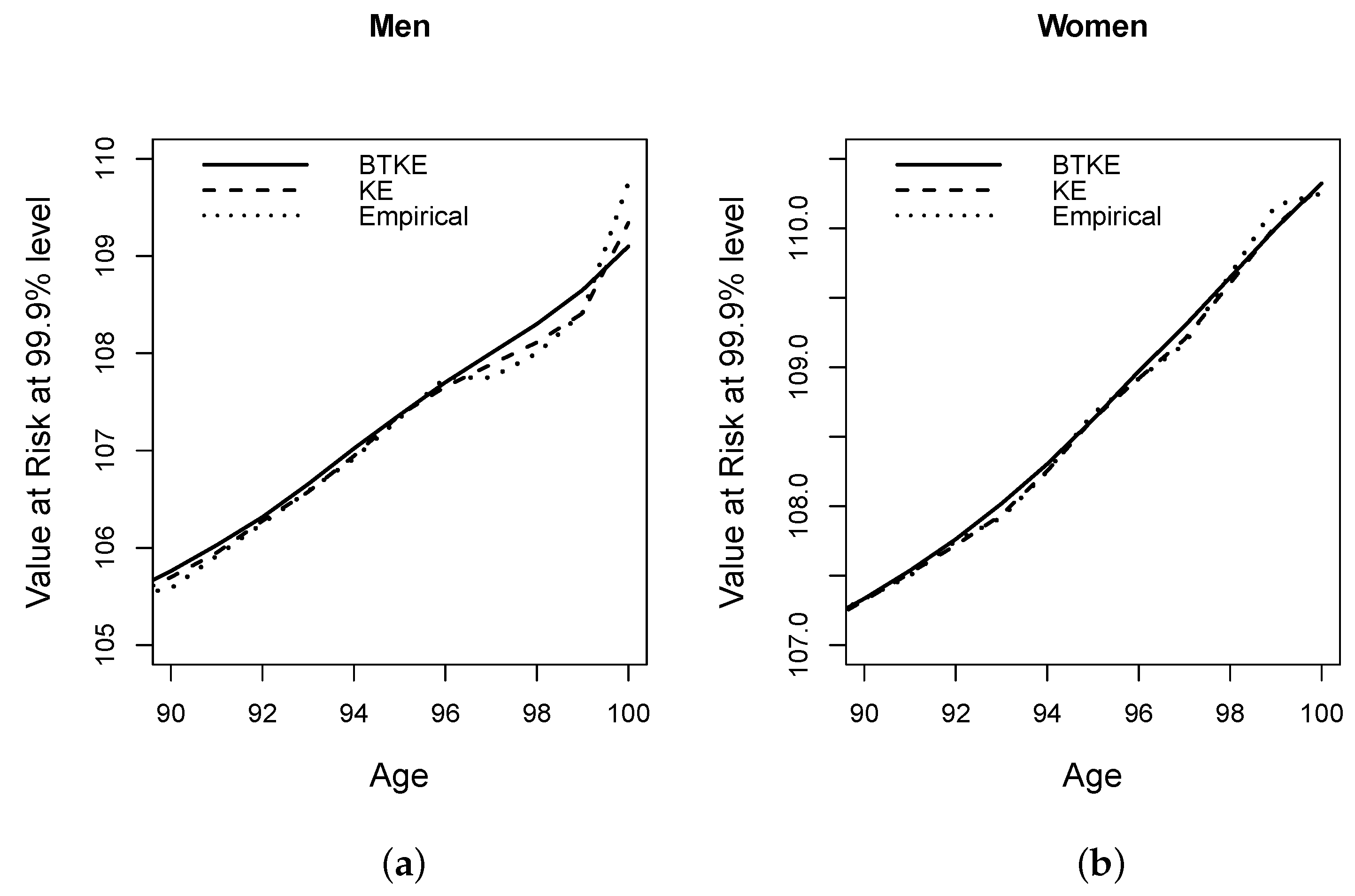
By way of illustration, and using the data analyzed for the year 2015, considering that we have more than 170,000 data items for men and women, in
Figure 1 we plot the CQs at the 99.9% level that were estimated using the empirical distribution, the KE and the BTKE.
Figure 1 emphasises the smoothed behavior of the estimation based on the BTKE compared to the respective shapes of those based on the empirical distribution and the KE, which are more strongly influenced by the scarce data observed for the largest values of the variable; this captures, perfectly, how the variance of the BTKE is lower than that of the KE, which is very similar to the variance of the empirical distribution.
The Gompertz and the Gompertz-
G distributions (see
Alizadeh et al. 2017) improve the fit of the modified Champernowne, the improvement is greater for Gompertz-
G. The Gompertz has traditionally been used in demography for fitting age-at-death distributions (see, for example,
Preston et al. 2001); the Gompertz-
G is a generalization where a first cdf
G is applied to the data. A particular case is
G equal to the log-logistic distribution. In fact, the modified Champernowne distribution defined in expression (
A1) with
is the log-logistic distribution. Therefore, there is a parallelism between our BTKE and the Gompertz-
G distribution; both start from similar cdf transformations.
Using the inverse of the estimated cdf, given a probability
, we have estimated the VaR for a grid of values for
a between the ages of 65 and 100 and at 99,
and
confidence levels, for each year from 2011 to 2017. To compare the results obtained with the BTKE, we consider GPD using the semiparametric estimates described in (
Coles et al. 2001), we also consider Gompertz and Gompertz-
G, with parameters estimated by maximum likelihood To carry on this comparison, we estimate
and we obtain its empirical significance level, which should be similar to the theoretical
. The quotients between the empirical vs. the theoretical significance levels are shown in
Table A4 and
Table A5 of
Appendix C. The results in
Table A4 indicate that the BTKE provides the best fit. Results with GPD do not provide good fits. Some years the shape parameter takes a negative value (2013, 2014 and 2015 for men and 2011, 2012 and 2015 for women). In the other years, the parameter is positive although lower than
. In general, the GPD procedure tends to underestimate the conditional quantiles more extreme (quotients greater than 1). In contrast, in
Table A5 we show as the Gompertz distribution under-estimates the longevity risk (quotients greater than 1) while the Gompertz-
G distribution greatly over-estimates the risk in most cases for men (quotients lower than 1) and provides highly unstable results for women. Some values of the quotient are equal to zero. They are obtained with the BTKE and the Gompertz-
G parametric distribution and they indicate that there are no observations larger than the estimated
. With BTKE this only occurs in the most extreme quantiles for men, i.e., in years 2012, 2013 and 2014, when
and confidence level 0.999. With Gompertz-
G this also occurs for men but in lower confidence levels.
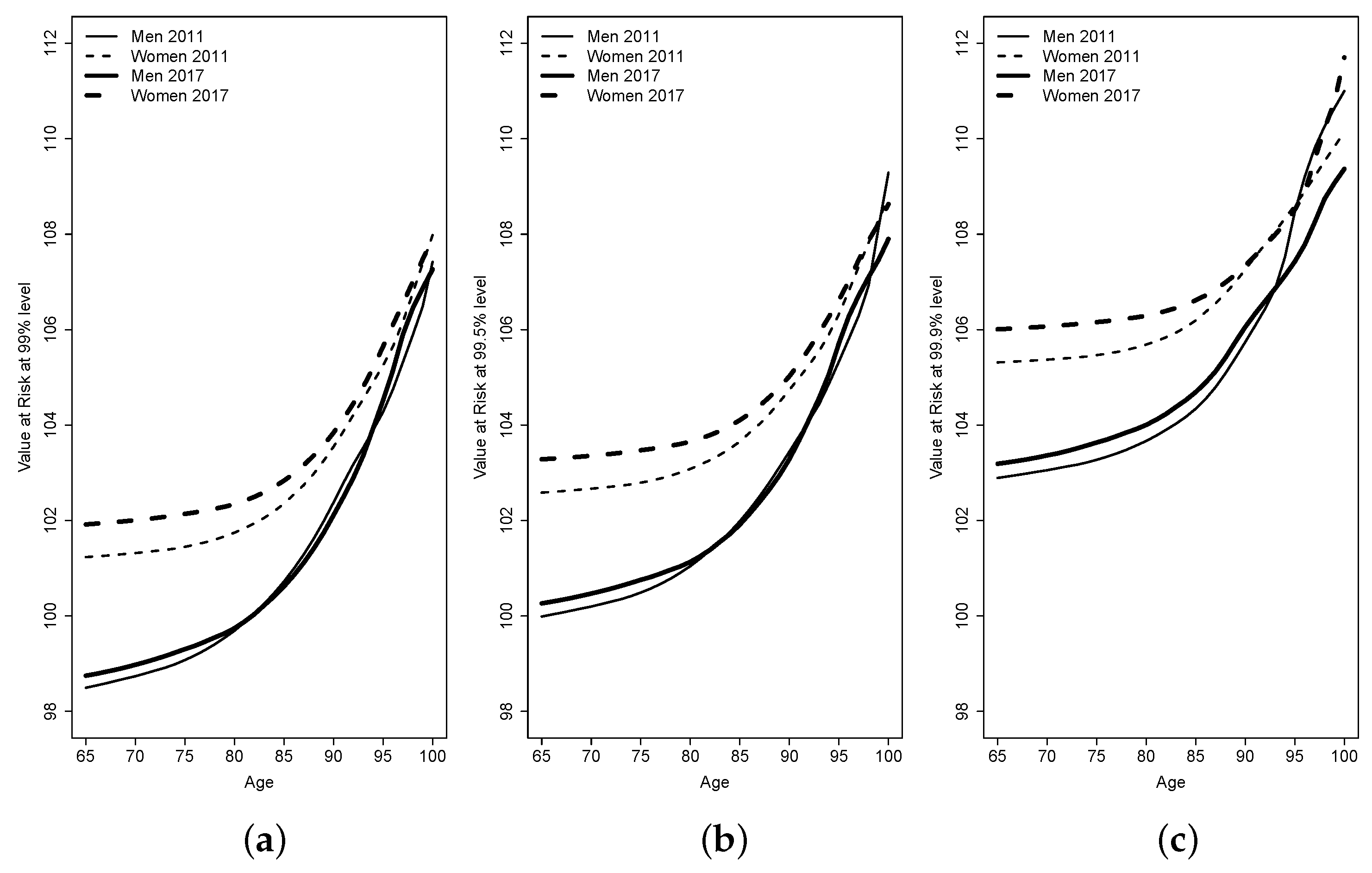
A summary of the
obtained with the BTKE is shown in
Figure 2 and in
Table 2 and
Table 3. Specifically, in
Figure 2 we plot these VaRs between 2011 and 2017, differentiating by gender. In general, we observe that the VaR has a slight tendency to increase over the years, disappearing for men beyond age 80, approximately, at confidence levels
and
, and beyond age 90 at confidence level
. Furthermore, CQ for women are higher than for men in almost all values of
a and
, although these differences tend to narrow with increasing age. In order to analyse the statistical significance of these differences during the period 2011–2017, in
Table 2 and
Table 3 we present the results for
with the bootstrap confidence intervals (CIs) at
based on a Normal distribution. We generate 1000 bootstrap samples with replacement and test how the estimated values in this sample follow a Normal distribution.
Focusing on
Table 2 and
Table 3, where we show the estimated
, differences between men and women are observed in all cases, except for the most extreme age and quantile, i.e.,
and
.
To analyze how the longevity risk increases for men and women the year 2011 is taken as our reference. Specifically, for each value of
a and
, we compare the upper limits of that year with the lower limits of the other years. In this way, we can determine whether or not the CIs overlap and, thus, conclude whether the VaR increases with respect to 2011 (no overlap of CIs) or not (overlap of CIs). In
Table 2 and
Table 3, some of the
values corresponding to the intervals do not overlap and they indicate that the longevity risk increases more quickly for women than it does for men during the period under consideration (2011–2017).
Application to the Annuity Longevity Risk
The actuarial present value of a lifetime annuity for a person of age
a is:
where
measures the probability of an individual of age
a surviving
t time longer,
r is the risk-free rate and
is the financial discount. We know that the value of
can be expressed as a function of the age-at-death distribution
(see
Preston et al. 2001, pp. 53–54):
So, with the BTKE we can obtain smoothed and consistent estimations of
and, therefore, calculate the value of single the premium expressed in (
25). In
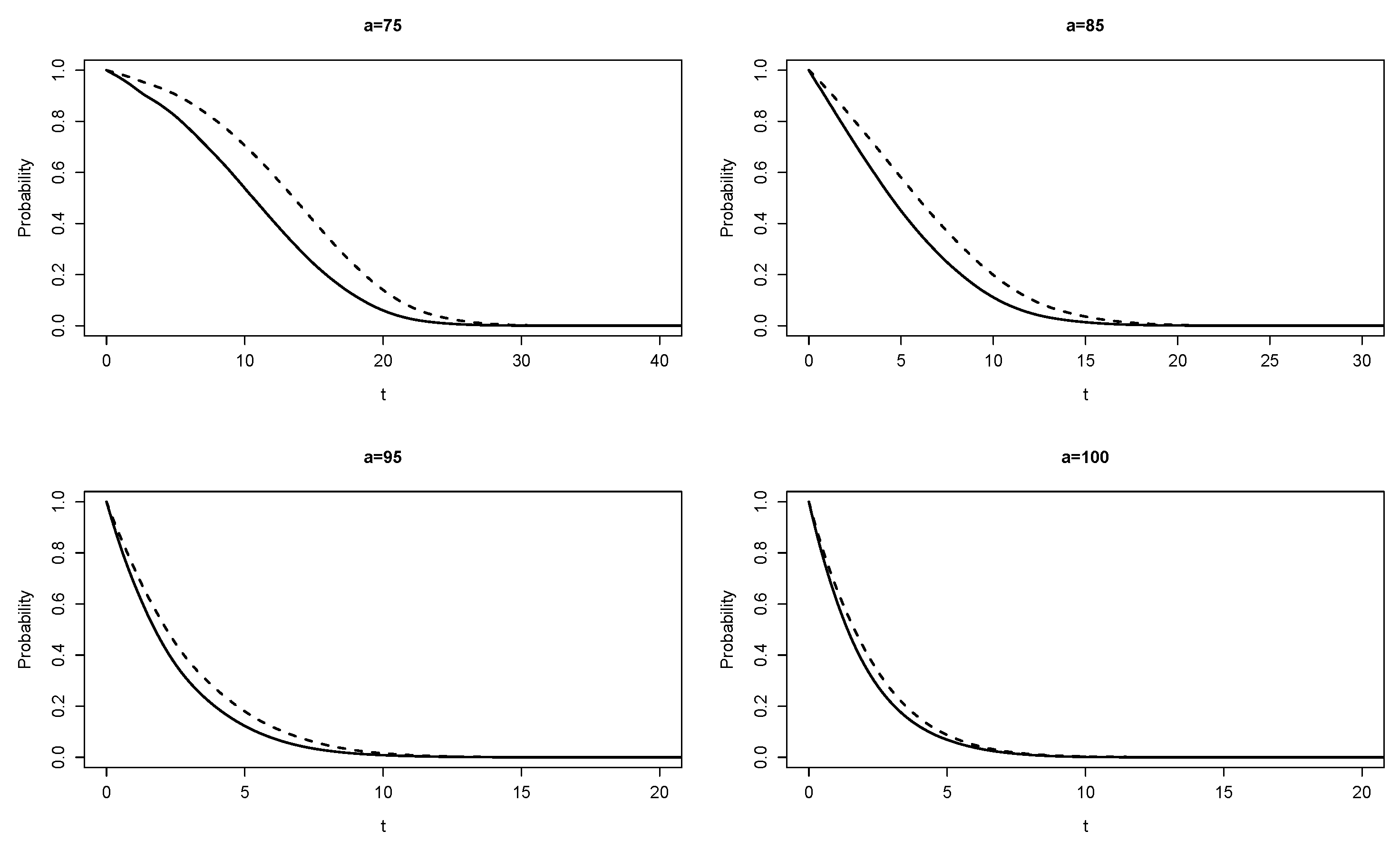
Figure 3, we show these estimated probabilities for
with the data for 2017. The values of
calculated using these estimated
and with
are shown in
Table 4.
As an alternative to the lifetime annuities, the temporary annuities (see
Shang and Haberman 2020, for the justification for this type of financial contract) depend on a given maturity or a given age from which the probability of living is assumed to be zero and which we call
w, being, a priori, the same for men and women (see
Chen et al. 2018, for an example of an application in solvency risk). So, in the integral expressed in (
25) we can finally replace the
∞ by
.
Usually, the value of
w is determined by the mortality rate or its projection. It normally corresponds to an age at which all individuals have died. Considering that longevity risk is the estimated CQ
at a given confidence level near 1, the integral (
25) can be divided into two parts, from 0 to
and from longevity risk
to
∞, i.e.,
Expression (
26) is convenient because it splits the lifetime annuity into two segments; only a
fraction of the participants will reach age
(we call this term “tail premium”), while a
fraction will not reach this age. For example, for age 75 with
, in
Table 2 we observe that for men
and the single premium in
Table 4 is split as
; for women
and this separation is
. These results indicate that when considering longevity risk, the maturity for women should be longer than for men and, on the contrary, the tail premium should be lower. The reason is that the tail premium starts later for women than it does for men and, therefore, covers a shorter period with higher mortality rates. The opposite is true for men, i.e., maturity should be shorter and the tail premium should be higher.
Table A6 in
Appendix D shows the results of the split premiums for each age (
a) and quantile level
.
Our approach helps identify the tail in terms of a percent of the whole distribution. An alternative approach would be to fix the advanced age, i.e., 100 years and estimate the proportion of cases above this bound or the annuity from this age. The difference between our method and this alternative is that, when age is fixed, the size of the tails are not comparable.
6. Conclusions
We have shown the utility of the kernel estimator for estimating longevity risk. Specifically, we have demonstrated that the beta transformed kernel estimator allows us to estimate conditional extreme quantiles efficiently when using a large database. Moreover, this estimator can be easily implemented with real or projected data. Finally, we obtained smoothed nonparametric estimations of the .
Using the BTKE, we have estimated longevity risk using the conditional extreme quantile of the age-at-death and we conclude that it is higher for women than it is for men in almost all the cases analyzed ( and ) in Spain. Furthermore, the longevity risk age increases across the period 2011–2017, especially in the case of women.
The method presented in this paper cannot be used with incomplete cohort data, because information on all ages of death is needed. Longevity cohort analysis, with still-living individuals, would require projections of mortality and, therefore, a parametric or a model approach would be better than the model-free kernels.
In short, here, we have proposed a way to measure longevity risk in insurance portfolios. This can be achieved by splitting the unitary lifetime annuity according to a conditional extreme quantile of the age-at-death distribution in the portfolio that is associated with the fact that individuals may reach a certain age with a low probability.
As a potential future research outline, it would be interesting to consider conventional risk factors as the alcohol consumption status or smoking status, alongside health issues (for example, diabetes or cardiac risk). The proposed methodology standardizes longevity risk comparison for annuity portfolios in insurance companies.