Abstract
The growing trend in the number and severity of auto insurance claims creates a need for new methods to efficiently handle these claims. Machine learning (ML) is one of the methods that solves this problem. As car insurers aim to improve their customer service, these companies have started adopting and applying ML to enhance the interpretation and comprehension of their data for efficiency, thus improving their customer service through a better understanding of their needs. This study considers how automotive insurance providers incorporate machinery learning in their company, and explores how ML models can apply to insurance big data. We utilize various ML methods, such as logistic regression, XGBoost, random forest, decision trees, naïve Bayes, and K-NN, to predict claim occurrence. Furthermore, we evaluate and compare these models’ performances. The results showed that RF is better than other methods with the accuracy, kappa, and AUC values of 0.8677, 0.7117, and 0.840, respectively.
1. Introduction
The insurance industry’s current challenges are its transformation into a new level of digital applications and the use of machine learning (ML) techniques. There are two groups in the insurance industry: life insurance and non-life insurance. This study considers non-life insurance, particularly auto insurance. Vehicle owners seek out automotive insurance companies for insurance so that, in the unfortunate event of an accident, they can mitigate the costs involved with coverage for the property (damage or theft to a car), liability (legal responsibility to others for the medical or property costs), and medical (treating injuries). Insurance claims occur when the policyholder (the customer) creates a formal request to an insurer for coverage or compensation for an accident. The insurance company must validate this request and then decide whether to issue payment to the policyholder. Several factors determine automotive insurance quotes1. These factors can establish how much a driver will pay for their insurance contract. A common example of these factors is credit history. Research suggests that individuals with lower credit scores are more likely to file claims and potentially commit fraud or miss payments, thus providing a large financial problem for the insurance company. Another essential example can be the driver’s location. Studies have revealed that densely populated areas with much congestion tend to experience more frequently occurring accidents, leading to many claims in this area. This can significantly raise the price of insurance for the customer. However, it is unfair for a good driver to pay more just because of where they live; this creates a problem for the client, because if the insurance price is raised, he may not be able to afford it, which subsequently affects the insurance firm by losing these clients. Considering these factors and their impacts on the insurance firm, this creates a problem, where there is a need for an efficient method to determine the risk a driver poses to insurance companies. Thus, these companies will adjust the insurance prices fairly to a driver’s ability and relevant personal information, making automotive insurance more accessible to clients. The forecast for claims occurrence will support the modification of insurance quotes based on the client’s ability. If a client has a good driving record, it would be unreasonable for a client with a poor driving background to pay a similar insurance premium. Therefore, the model should show which clients are unlikely to make claims, decrease their insurance cost, and raise the insurance cost for those who are likely to make a claim. Thus, more insurance companies want to have an insurance premium that is appropriate for each customer. This kind of premium is very relevant in regulatory and business terms. For the regulatory level, it is the best way to avoid discrimination and provide fair prices, and, for the business level, it gives calculations with flexibility, simplicity, and precision, allowing them to respond to any circumstance and control any loss.
According to the Insurance Information Institute report, the claims frequency, amount of claims per car, and claim severity are on the rise, e.g., accident claim severity increased by 35% for US car insurance between 2010 and 2019. The average US car insurance expenditure increased from USD $78,665 in 2009 to USD $100,458 in 20172. This increase indicates that a quicker and more efficient system for filing auto insurance claims is needed to follow the growing trends in claim severity and frequency. These facts make auto insurance pricing studies more meaningful and essential.
In the insurance industry, it is essential to set the product’s price before knowing its cost. This reality makes the process of rate-making more critical and significant. Insurance firms must predict how many claims are going to occur and the severity of these claims to enable insurers to set a fair price for their insurance products accordingly. In other words, claim prediction in the auto insurance sector is the cornerstone of premium estimates. Furthermore, it is crucial in the insurance sector to plan the correct insurance policy for each prospective policyholder. Failure to foresee auto insurance claims with accuracy would raise the insurance policy’s cost for the excellent client and lower the bad client’s price of the policy. This is referred to as pay-as-you-drive, and this strategy is an alternate mechanism for pricing premiums based on the customer’s personal driving behavior. The importance of pay-as-you-drive insurance policies was highlighted by Hultkrantz et al. (2012), as they enable the insurers to personalize the insurance costs for each client, thus the premium rate will be fair. Several studies have been done to personalize the premium estimate, such as Guillen et al. (2019) and Roel et al. (2017), they demonstrated the possible benefits of analyzing information from telematics when determining premiums for auto insurance. The predictive capacity of covariates obtained from telematics vehicle driving data was investigated by Gao and Wüthrich (2018) and Gao et al. (2019) using the speed–acceleration heatmaps suggested by Wüthrich (2017).
Prediction accuracy enables the insurance industry to adjust its premiums better, and makes car insurance coverage more affordable for more drivers. Currently, many insurance companies are using ML methods instead of a conventional approach, which offers a more comprehensive way of producing a more reliable and representative outcome. A new study related to artificial intelligence and business profit margins was conducted by McKinsey & Company (Columbus 2017). They showed that the businesses that have completely embraced artificial intelligence projects have generated a higher profit margin of 3% to 15%. However, selecting a suitable ML predictive model has yet to be fully addressed. In this study, we investigate more powerful ML techniques to make an accurate prediction for claims occurrence by analyzing the big dataset given by Porto Seguro, a large automotive company based in Brazil3, and we apply the ML methods in the dataset, such as logistic regression, XGBoost, random forest, decision trees, naïve Bayes, and K-NN. We also evaluate and compare the performance of these models.
This paper’s main objective is to create an ML algorithm that accurately predicts claims occurrence. Thus, the model must effectively consider consumer details, such as the type of vehicle or the car’s cost, that differ among the clients. The model’s results (and provided that the forecast is accurate) confirmed that car insurance firms will make insurance coverage more available to more clients.
2. Related Work
There is a lot of motivation for automotive insurance companies to implement machine learning algorithms in their business, as they are used for driver performance monitoring and insurance market analytics. Several papers have discussed the issue of prediction in the insurance sector by using ML models, such as Smith et al. (2000), who tested several machine learning models, like the decision tree and neural networks, to assess whether the policyholder submits a claim or not and addressed the effect that the case study will have on the insurance company. Weerasinghe and Wijegunasekara (2016) compared three ML methods for predicting claims severity. Their findings showed that the best predictor was the neural networks. Another example of a similar and satisfactory solution to the same problem is the thesis “Research on Probability-based Learning Application on Car Insurance Data” (Jing et al. 2018). They used only a Bayesian network to classify either a claim or no claim, and Kowshalya and Nandhini (2018), in order to predict fraudulent claims and calculate insurance premium amounts for various clients according to their personal information, used ML techniques; three classifiers were used to predict fraudulent claims, and these classifiers were random forest, J48, and naïve Bayes algorithms. The findings indicated that random forests outperform the remaining techniques. This paper does not involve forecasting insurance claims, but focuses on fraudulent claims. Additionally, an example of insurance market analytics is a model that predicts claim severity virtually, as well as the funds needed to repair vehicle damage (Dewi et al. 2019). This example represents how insurance providers look into many different forms of applying machine learning to their customer data. In the work that proposed a system (Singh et al. 2019), this system takes photos of the damaged vehicle as inputs. It generates specific information, such as the cost of repair used, to determine an insurance claim’s cost. Therefore, this paper does not involve the prediction of insurance claims occurrence, but was focused on estimating the repair cost (Stucki 2019). This study aims to provide an accurate method for insurance companies to predict whether the customer relationship with the insurer will be renewed or not after the first period that the consumer acquires new insurance, such as a vehicle, life, or property insurance; this study forecasts the potential turnover of the customer, and five classifiers were used. These classifiers are algorithms for LR, RF, KNN, AB, and ANN. This study showed that the best performing model was random forests. Pesantez-Narvaez et al. (2019) use two competing methods, XGBoost and logistic regression, to predict the frequency of motor insurance claims. This study shows that the XGBoost model is slightly better than logistic regression; however, they used a database comprised of only 2767 observations. Furthermore, a model for predicting insurance claims was developed (Abdelhadi et al. 2020); they built four classifiers to predict the claims, including XGBoost, J48, ANN, and naïve Bayes algorithms. The XGBoost model performed the best among the four models, and they used a database comprised of 30,240 observations.
All of the above studies considered neither big volume nor missing value issues. Therefore, in this paper, we focus on examining the machine learning methods that are the most suitable method for claim prediction with big training data and many missing values. Therefore, this study will have more variety in combining models for an accurate claim prediction, looking for the alternative and more complex machine learning model to predict the probability of claims occurring in the next year by using a real database provided by Porto Seguro company. Furthermore, from the above studies, we can say that some of the previous recent studies that applied some machine learning models in the insurance industry show that the XGBoost model is the best model for classification in the insurance industry (Pesantez-Narvaez et al. 2019; Abdelhadi et al. 2020). They used a database comprised of 2767 and 30,240 observations, respectively, while (Jing et al. 2018) shows that the naïve Bayes is an effective model for claims occurrence prediction. In our paper, we use big data that contained almost a million and a half (1,488,028) observations with 59 variables, and our results show that XGBoost is a useful model. Still, our results also show that RF and the decision tree (C50) is significantly better than XGBoost. Our results also show that the naïve Bayes is the worst model for predicting claims occurrence among all eight classification models used in this study. On the other hand, our results are consistent with a recent study (Dewi et al. 2019). The difference between this study and our study is that our study focuses on predicting the probability of claim occurrence, compared to predicting the cost of a claim and the funds required for the claim damage when the claim occurred. Their results are consistent with ours, showing that the random forest has the higher accuracy, and can be applied whether in cases of prediction of claim severity, as the results of their study shows, or in claim occurrence prediction, as our study shows. These results confirm the scalability of the random forest. Hence, the random forest model can be used to solve big data problems related to data volume. The results of the literature review have been summarized in Table 1.

Table 1.
Different studies for using ML models in the insurance industry to get a representative overview.
Table 1 is a chronological table that shows different studies for using ML models in the insurance industry, where LR is a logistic regression model, GAMS is a generalized additive model, RF is a random forest model, KNN is a K-nearest neighbor model, NN is a neural network model, DT is a decision tree, AB is an AdaBoost model, MLP is a multi-layer perceptron model, SGB is a stochastic gradient boosting model, SVM is a support vector machine model, MSE is the mean square error, and RMSE is the root mean square error.
3. Background
To understand the problem, it is essential to understand the insurance claims forecast, big data, ML, and classification. We explore the following terms.
The vast amount of data to determine the probability of claims occurrence makes a claim prediction issue require big data models. Thus, there is a need for an effective approach and a more reliable ML model to assess the danger that the driver poses to the insurance provider and the probability of filing a claim in the coming year, a model that can read and interpret vast databases containing thousands of consumer details provided by the Porto Seguro insurance company.
Porto Seguro is one of the biggest car and homeowner insurance firms in Brazil. Porto Seguro claims that their automotive division’s mission is to customize insurance quotes based on the driver’s ability. They believe that effective techniques can be applied for more accurate results to predict claims occurrence in the coming year. Thus, they provided the dataset containing 59 variables with 1,488,028 observations4. These observations include customer information that the company collected over several years.
3.1. Machine Learning
Machine learning is an area of computer science research that is gradually being adopted in data analysis, and it has gained high demand in the last decade (Géron 2019). Its rapid dissemination is due to the rapid growth of data generated from many sources and the vast quantities of data stored in databases. It enables individuals and organizations to understand their datasets in more detail. Forbes’s research has also indicated that one in ten companies now uses ten or more AI applications: 21% of the applications are based on fraud detection, 26% on process optimization, and 12% on opinion mining (Columbus 2018). Machine learning extends artificial intelligence, and can help machines develop their expertise by learning from the data and defining models with the minimum human involvement, and, through logic and conditions, a prediction can be made using learning algorithms (Goodfellow et al. 2016).
There is a significant number of applications for machine learning in industries available, including predictive models for online shopping, fraud detection in banks, or even spam filtering in email inboxes (Schmidt et al. 2019). However, the underlying principle behind these implementations is that the model must generalize well to generate reliable forecasts (Gonçalves et al. 2012). Machine learning aims primarily to discover models and patterns in data and use them to predict future outcomes (D’Angelo et al. 2017). One of the key aims of most research in artificial intelligence (AI) and big data analytics areas is learning complex trends, features, and relationships from vast data volumes. The basis for the application of AI in information discovery applications is machine learning and data mining based approaches. The essence of the intelligent machine’s learning method is the comparison between the objective to be achieved and the result derived by the machine state. In many research fields, this method has proved to be successful (D’Angelo et al. 2020), including in analysis of the insurance industry (Jing et al. 2018; Pesantez-Narvaez et al. 2019; Dewi et al. 2019; Abdelhadi et al. 2020). The generic machine learning algorithm will receive input data and split this data into two sets, the first called the training and the second called the test dataset. The model trained through training data is set to make predictions and determine the model’s ability to generalize to external data. The model evaluates the test data to determine if it predicts correctly.
3.2. Machine Learning Approach to Predict a Driver’s Risk
The prediction of the claims is intended to predict it the insured will file a claim or not. Let = {0,1} be the output possible, with 0,1 being categorical values that reflect that the client ‘will not file a claim’ or ‘will file a claim’, respectively.
The purpose of this machine learning model is to predict the probability of claim occurrence. This algorithm is modeled on data representing a customer that has (a) made a claim or (b) not made a claim. Therefore, the problem can be identified as a binary classification, where a claim is a 1 and no claim made is a 0 (Kotsiantis et al. 2006). Different classification algorithms can be used. Some of them perform better, and others perform worse, given the data state (Kotsiantis et al. 2007).
where X is a collection of instances xi that represents all of the known information of the i-th policyholder.
Pr(Y = 0|X = xi),
Pr(Y = 1|X = xi)
3.3. Classifiers
3.3.1. Regression Analysis
Linear regression is used to estimate the linear relationship between a variable of response (target) and a set of predictor variables. However, linear regression is not suitable when the target variable is binary (Sabbeh 2018). For the binary-dependent variables, logistic regression (LR) is a suitable model for evaluating regression. LR is a statistical analysis used to describe how a binary target variable is connected to various independent features. It has many similarities with linear regression.
LR is a multivariable learning algorithm for dichotomous results. It is a classification method with the best performance for models with two outputs, e.g., yes/no decision-making (Musa 2013). Therefore, it is suitable for predicting a vehicle insurance claim with two variables (claim or no claim). LR is similar to linear regression by its functionality. However, linear regression provides a continuous output compared to the categorical output we desire in the binary target variable. LR performs with a single output variable, yi, where i = {1, ... n}, and each yi can hold one of two values, 0 or 1 (but not both). This follows the Bernoulli probability density function, as in the following equation:
This takes the value 1 when the probability is , and 0 when the probability is 1 − ; the interest in this is when = 1 with an interesting probability . The classifier will then produce the output of the predicted label; is equal to 1 if it is greater than or equal to its threshold (by default, 0.5) (Musa 2013).
3.3.2. Decision Tree
A decision tree is a supervised learning approach used to solve classification and regression issues, but it is mostly used to solve classification issues. It is a classifier organized by the tree structure, where the internal nodes are the data variables, the branches are the decision rules, and each node is the output. It consists of two nodes. One of them is a decision node used for decision-making, and it has various branches. The second node is a leaf node, which represents the result of these decisions.
Decision trees provide many advantages, but usually do not perform predictively compared to more complex algorithms. However, there are strong ensemble algorithms, such as random forests and gradient boosters, that are developed intelligently by combining several decision trees. There are also different DTs models: CART, C4.5, C5.0, and more (Song and Ying 2015).
Figure 1 shows the structure of a general decision tree.
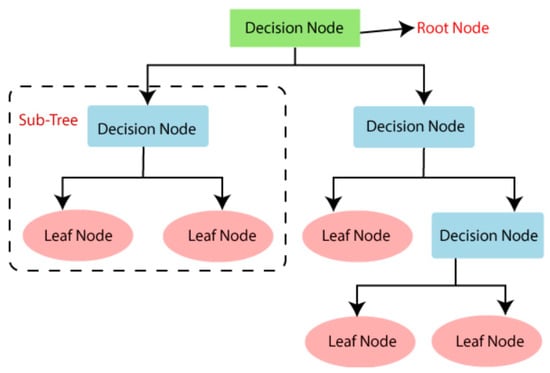
Figure 1.
Structure of a general decision tree.
3.3.3. XGBoost
XGBoost is a novel approach proposed by Chen and Guestrin to raise the gradient tree (Chen and Guestrin 2016). It uses various decision trees to predict a result. Figure 2 shows the methodology of the XGBoost model. XGBoost stands for extreme gradient boosting. A regression and classification problem learning technique optimizes a series of weak prediction models to construct a precise and accurate predictor. It is a desirable model, because it can boost weak learners (Zhou 2012). Furthermore, it can improve the insurance risk classifier’s performance by combining multiple models. Some studies showed that the XGBoost model is the best model for the prediction of claims occurrence with a small dataset (Pesantez-Narvaez et al. 2019).
Figure 2.
XGBoost methodology.
3.3.4. Random Forest
Random forests reflect a shift to the bagged decision trees that create a broad number of de-correlated trees so that predictive efficiency can be improved further. They are a very popular “off-the-box” or “off-the-shelf” learning algorithm with good predictive performance and relatively few hyper-parameters. There are many random forest implementations, however, the Leo Breiman algorithm (Breiman 2001) is widely authoritative. Random forests create a predictive value as a result of the regression of individual trees. It resolves to over-fit (Kayri et al. 2017). A random forest model can be expressed as follows:
where g is the final model, i.e., the sum of all models. Each model f(x) is a decision tree.
3.3.5. K-Nearest Neighbor
K-nearest neighbor is based on supervised learning techniques. It is considered one of the most straightforward ML models. K-NN assumes the comparison between the available data and the new data; it includes the new data in the category nearest to the classes available. It can be used for classification regression, but it is mainly used for classification. It is also known as a lazy model (Cunningham and Delany 2020), since it does not learn from the training dataset instantly. K-NN modes only store the dataset through training; when K-NN receives new data, it classifies this new data to the nearest available category based on the training data stored in the K-NN model. It can also be inefficient computationally. However, K-NNs have succeeded in several market problems (Mccord and Chuah 2011; Jiang et al. 2012).
3.3.6. Naïve Bayes
Naïve Bayes shows that the naïve Bayesian network can have good predictive performance compared to other classifiers, such as neural networks or decision trees (Friedman et al. 1997). From the training data, naïve Bayes classifiers learn each attribute Ai’s conditional probability on the class label C. For classification, the Bayes rule is applied to calculate the probability of C on the attribute instance Ai, …, An. The class that will be predicted is the class with the highest probability. For feasibility, the classifier operates under the assumption that all attributes Ai are conditionally independent given the value of class C. Figure 3 shows the methodology of the Naïve Bayes model.
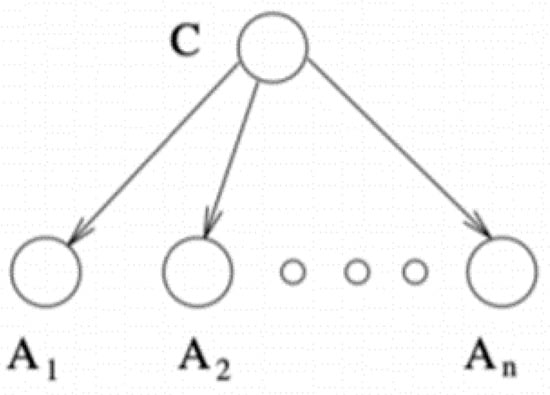
Figure 3.
Naïve Bayes network structure.
Because all attributes are processed independently, the performance can be surprising. This is because it ignores potentially significant correlations between features.
4. Evaluation Models (Prediction Performance)
There are several metrics to evaluate a classifier model and examine how well the model fits a dataset and its performance on the unseen data (Hossin and Sulaiman 2015). Accuracy alone for a classification problem cannot always be reliable, because it can provide bias for a majority class giving high accuracy and weak accuracy for the minority class, making it less informative for predictions, especially in the case of imbalanced data (Ganganwar 2012). Car insurance claims are an excellent example of imbalanced data, because the majority of policyholders do not make a claim. Therefore, if accuracy is used, there would be a bias toward a no claim class. Thus, we use other measures, such as kappa, F-measure, and the area under the curve (AUC). To understand how accuracy works, it is important to understand firstly how a confusion matrix works.
4.1. Confusion Matrix
A confusion matrix is used for binary classification problems. It is a beneficial method to distinguish which class outputs were predicted correctly or not. As shown in Table 2, the rows represent the predicted class, while the columns represent the actual class (Hossin and Sulaiman 2015). In the matrix, TP and TN represent the quantity of correctly classified positive and negative instances, whereas FP and FN represent incorrectly classified positive and negative samples, respectively.

Table 2.
Confusion matrix.
In car insurance claims, true positive would represent no claim made, and true negative would represent a claim.
4.2. Kappa Statistics
Kappa statistics significantly measure besides the accuracy, because it considers the probability of a correct prediction in both classes 0 and 1. Kappa is essential for datasets with extreme class imbalance, such as auto insurance claims, since a classifier can achieve high precision by merely guessing the most common class.
4.3. Sensitivity and Specificity
The sensitivity (true positive rate) evaluates the ratio of positive classified examples correctly by comparing the predicted positive class with the actual positive, while the specificity (true negative rate) evaluates the ratio of negative classified examples correctly by comparing the predicted negative class with the actual negative.
4.4. Precision and Recall
The precision metric is used to measure how trustworthy the class is classified, and if it belongs to the right class. Another useful metric is recall, which is used to measure how well the fraction of a positive class becomes correctly classified; this essentially shows how well the model can detect the class type (Hossin and Sulaiman 2015).
4.5. The F-Measure
The F-measure is a measure of model performance that combines precision and recall into a single number known as the F-measure (also called the F1 score or the F-score). The following is the formula for the F-measure:
Additionally, the area under the receiver operator characteristics (ROC) curve (AUC) is needed, since there is a weakness in accuracy, precision, and recall, because they are not as robust to the change of class distribution; a popularly used ranking evaluation technique is to use the AUC metric, otherwise known as the receiver operating characteristic (ROC) or the global classifier performance metric, since all different classification schemes are measured to compare overall performance (Wu and Flach 2005). If the test set were to change its distribution of positive and negative instances, the previous metrics might not perform as well as when they were previously tested. However, the ROC curve is insensitive to the change in the proportion of positive and negative instances and class distribution (Bradley 1997).
5. Dataset
In this study, we analyze a dataset given by Porto Seguro, a large Brazilian automotive company. Due to the privacy of this dataset, the database is kept safe and confidential, and the clients’ personal information is encrypted5. Some data, like categorical data, can be found in dataset columns. For example, ps car 04 cat may provide a general indication of planned car data (e.g., car type or car use), but for protective purposes, it is not specified.
It is necessary to understand how the datasets were structured before changing the dataset to construct the ML model. Our set of big data consists of 59 variables and 1,488,028 rows, and every row contains the personal details of a different single client. A data description has also been issued that contains essential data on the already processed data preparation. The key points to be noted are:
- Values of −1 indicate that the feature was missing from the observation.
- Feature names include the bin for binary features and cat for categorical features.
- ○
- Binary data has two possible values, 0 or 1.
- ○
- Categorical data (one of many possible values) have been processed into a value range for its lowest and highest value, respectively.
- Features are either continuous or ordinal.
- ○
- The value range appears as a range that has used feature scaling; therefore, feature scaling is not required.
- Features belonging to similar groupings are tagged as ind, reg, car, and calc.
- ○
- ind refers to a customer’s personal information, such as their name.
- ○
- reg refers to a customer’s region or location information.
- ○
- calc is Porto Seguro’s calculated features.
6. Proposed Model
In this paper, we developed a model to predict the occurrence of car insurance claims by applying ML techniques. And the stages of preparing the proposed model shown in Figure 4.
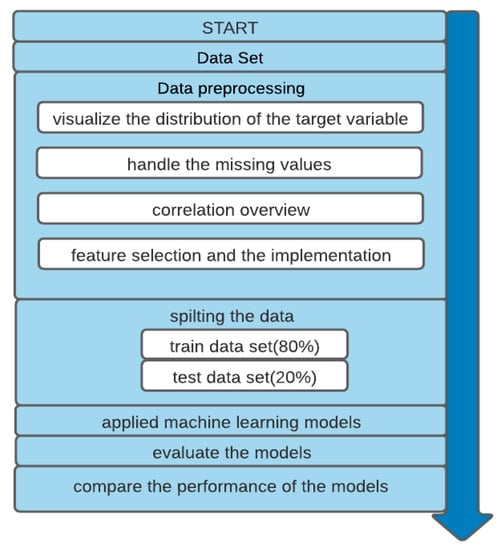
Figure 4.
Overall structure of the proposed model.
6.1. Data Preprocessing
The dataset consists of 59 variables. Each of these attributes has its relation to the insurance claims occurrence, which is our dependent target variable. The data is checked and modified to apply the data to the ML algorithms efficiently. We begin by considering the variable answer (dependent), target, then, all missing values are cleaned, as we shall see in Section 6.1.1 and Section 6.1.2.
6.1.1. Claims Occurrence Variable
Our target column is a binary variable that contains two classes (1,0), 1 if a claim has occurred and a 0 if a claim has not occurred. Figure 5 shows the distribution of 1 and 0 for the target column.
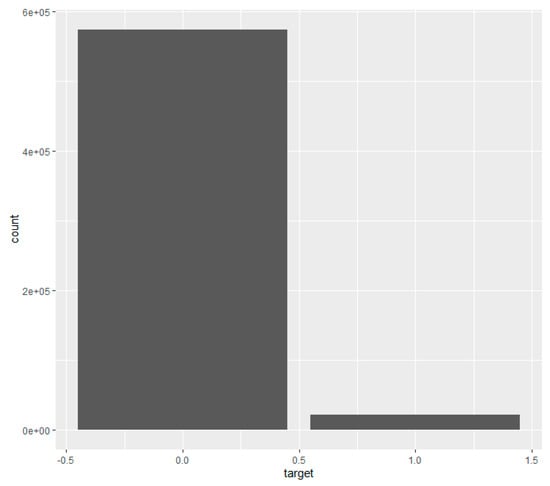
Figure 5.
Histogram of the distribution of target values.
The figure shows that the target variable is heavily imbalanced, with class 0 having 0.963% observations and class 1 having only 0.037% observations.
An algorithm for ML does not perform efficiently for imbalanced data. Thus, we applied the oversampling. Oversampling means that there are more representations of class 1, so the probability of class 1 increases. Figure 6 represents a binary target variable distribution after applying a random oversample using the ROSE library.
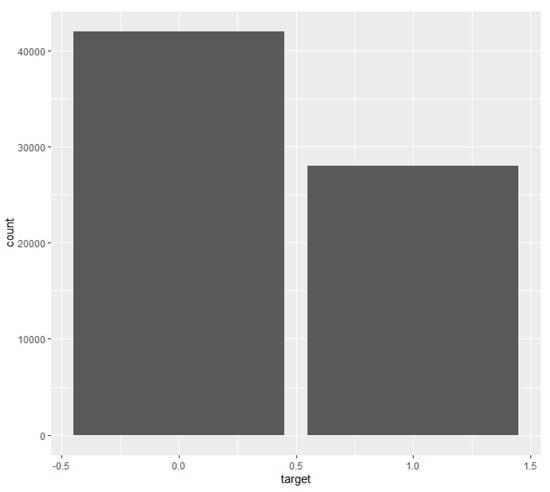
Figure 6.
Histogram of the balanced distribution of target values after using the ROSE package in R.
We balanced the given data using the function ROSE from a library called ROSE. The ROSE package is an R package. In the presence of imbalanced classes, it offers functions to deal with binary classification issues. According to ROSE, synthetic balanced samples are produced (Lunardon et al. 2014). Functions are also given that apply more conventional remedies to the class imbalance. Balanced samples are generated by random oversampling of minority examples, under-sampling of majority examples, or over- and under-sampling combinations.
6.1.2. Details on Missing Values
Before presenting our analysis, we will briefly examine different combinations of missing values in the data. In the following plot, the frequency of missing values per feature is shown in the top bar plot. Thus, the more red rectangles a feature has, the more missing values.
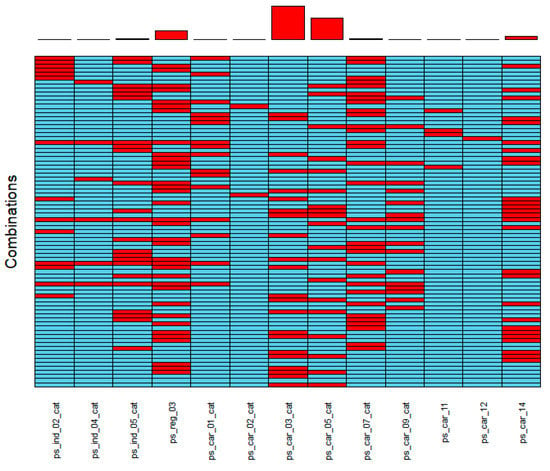
Figure 7.
Missing values in our data.
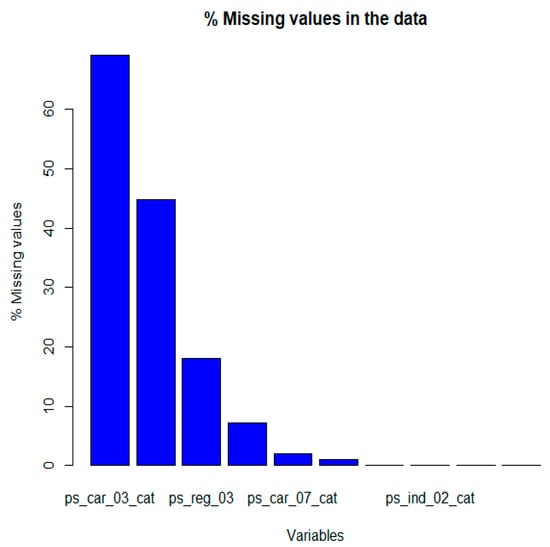
Figure 8.
Missing values in our data.
- The features of ps_car_03_cat and ps_car_05_cat have the largest number of missing values. They also share numerous instances where missing values occur in both for the same row.
- Some features share many missing value rows with other features, for instance, ps_reg_03. Other features have few missing values, like ps_car_12, ps_car_11, and ps_car_02.cat.
- We find that about 2.4% of the values are missing in total in each of the train and test datasets.
- From this figure, the features have a large proportion of missing values, being roughly 70% for ps_car_03_cat and 45% for ps_car_05_cat; therefore, these features are not that reliable, as there are too few values to represent the feature’s true meaning. Assigning new values that are missing to each customer record for these features may also not convey the feature’s purpose and negatively impact the learning algorithm’s performance. Due to these reasons, the features have been dropped and removed from the datasets.
- After we drop ps_car_03_cat and ps_car_05_cat, the features missing values in datasets become 0.18 instead of 2.4. The missing values for the rest of the variables are replaced such that missing values in every categorical and binary variable are replaced by the mode of the column values. In contrast, missing values in every continuous variable are replaced by the mean of the column values. This is because categorical data works well using the mode, and continuous data works well using the mean. Both methods are also quick and straightforward for inputting values (Badr 2019).
6.1.3. Correlation Overview
As previously shown, some feature selections have been processed, eliminating the ps car 03 cat and ps car 05 cat features, because they had too many missing values, and they will not be useful to an algorithm. At this point, it is essential to visualize and classify the features that are more useful using the Pearson correlation coefficient, as shown in Figure 9.
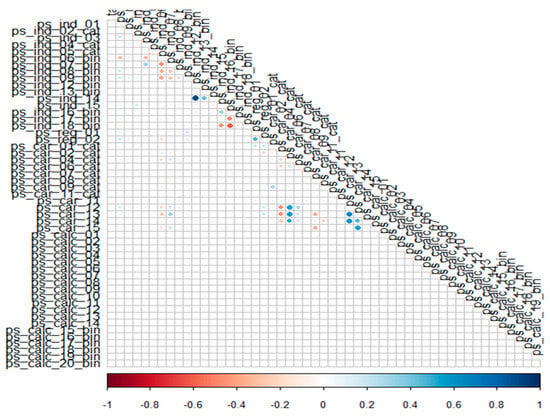
Figure 9.
Correlation matrix of all data features.
These results showed that all calc variables do not correlate well with other variables. Despite other features with a relatively poor relationship with the target variable, the calc variables do not correlate with the target variable. This is important, since the target variable dictates whether a claim occurs or not, so a specific correlation may occur. Due to this, the calc features for the datasets are dropped. We conducted a Pearson correlation, but did so after removing calc features; Figure 10 shows the Correlation matrix of data features after we drop calc features.
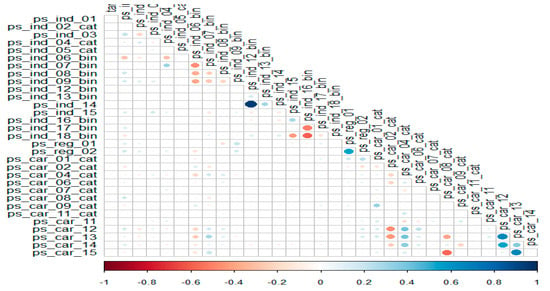
Figure 10.
Correlation matrix of data features after we drop calc features.
6.1.4. Hyper-Parameter Optimization
Grid searches were conducted to find hyper-parameters that would yield optimal performance for the models. A 10-fold cross-validation technique was used based on accuracy as an evaluation metric. Table 3 shows the hyper-parameter tuning on the models used in this paper.

Table 3.
The hyper-parameter tuning on the models used in this paper, where mtry is the number of randomly selected predictors, model is the model type, trials is the number of boosting iterations, eta is the learning rate, max_depth is the max tree depth, colsample_bytree is the subsample ratio of columns, nrounds is the number of boosting iterations, subsample is the subsample percentage, gamma is the minimum loss reduction, C is the confidence threshold, M is the minimum instances per leaf, K is the number of neighbors, cp is the complexity parameter, Laplace is the Laplace correction, adjust is the bandwidth adjustment, and usekernel is the distribution type.
6.1.5. Features Selection and Implementation
In this study, we used the Porto Seguro dataset. The study aims to predict the occurrence of claims using various ML models.
The dataset contains 59 variables and 1,488,028 observations. Every observation includes the personal details of a different single client, but we dropped the id, ps_car_03_cat, and ps_car_05_cat variables, since they had many missing values, and we dropped all of the calc variables, since they did not correlate with any other variables or with the target binary variable. Thus, we have a dataset containing 35 variables.
The dataset is separated into two parts; the first part is called the training data, and the second part is called the test data. The training data make up about 80% of the total data used, and the rest is for test data. These models are trained with the training data and evaluated with the test data (Grosan and Abraham 2011; Kansara et al. 2018; Yerpude 2020).
For this study, R x64 4.0.2 is used for implementing the models. For classification, we used accuracy, error rate, kappa, sensitivity, specificity, precision, F1, and AUC as measures of evaluation.
7. Results
This section analyzes the results obtained from each classification and compares the results to determine the best model with a highly accurate prediction. Every model used in this study was evaluated according to a confusion matrix, precision, recall, F1-score, and AUC; then, we compared all classifier models to explain why RF was selected as the best classifier (see Table 4).

Table 4.
Model performance.
Table 4 presents the evaluation of all classifiers of ML used in this study. The range of accuracy values for all ML models was between 60.56% and 86.77%. RF was the best model, with a high accuracy of 86.77% and a kappa coefficient of 0.7117. The results showed that RF was most likely to solve claim prediction problems correctly. The C50 model achieved good classification, with an accuracy of 79.13%. Naïve Bayes showed the lowest accuracy of 60.56% and a kappa coefficient of 0.1526.
From the table, we obtain that RF had the highest sensitivity, which means that 97.17% of the samples detected as positive were actually positive. The specificity for the RF model explains that 71% of the true negative samples were correctly classified.
Figure 11 shows the comparison between the techniques on various performance measures. It shows that, according to the accuracy and error rate, the best model was RF and the worst was naïve Bayes. The best model was RF and the worst was CART according to kappa; the best model was RF and the worst was naïve Bayes according to sensitivity. According to specificity, the best model was RF and the worst was CART; according to precision, the best model was RF and the worst was LR; according to recall, the best model was RF and the worst was CART; according to F1, the best model was RF and the worst was CART; and, according to AUC, the best model was RF and the worst was CART. Thus, we obtained that RF showed the best performance.
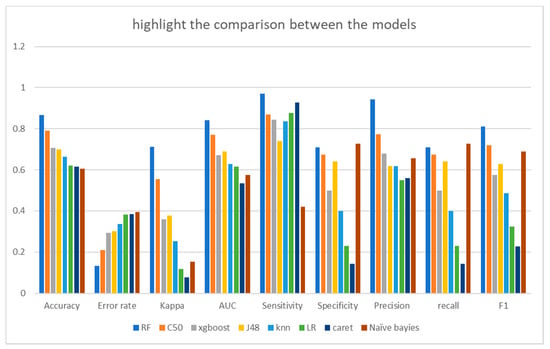
Figure 11.
Comparison between the models.
The ROC curves are shown in Figure 12. ROC offered the overall performance variable of the classification as its threshold for discrimination (Ariana et al. 2006). The AUC is known as the general quality index of the classifiers. The value of 1 for the AUC means a perfect classifier, while 0.5 means a random classifier. Based on the AUC comparison of the classifiers, the RF score was 0.840, which was the best, followed by C50 (0.769), J48 (0.689), and XGBoost (0.671). These findings suggest that RF, C50, J48, and XGBoost had satisfactory performance (AUC > 0.65), whereas naïve Bayes and CART had poor performance.
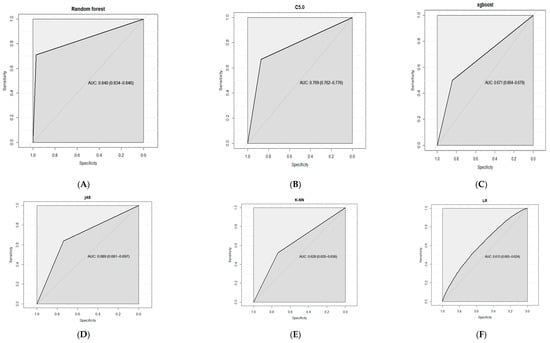

Figure 12.
ROC and calculated AUC obtained for the classifier models of (A) RF, (B) C50, (C) XGBoost, (D) J48, (E) K-NN, (F) LR, (G) caret, and (H) naïve Bayes.
Variable Importance
Variable importance is a technique that tests the contribution of each independent variable to the outcome prediction. The variable importance for all data features is shown in Figure 13 It starts with the most influential variables and ends with the variable with the smallest effects (Kuhn and Johnson 2013).
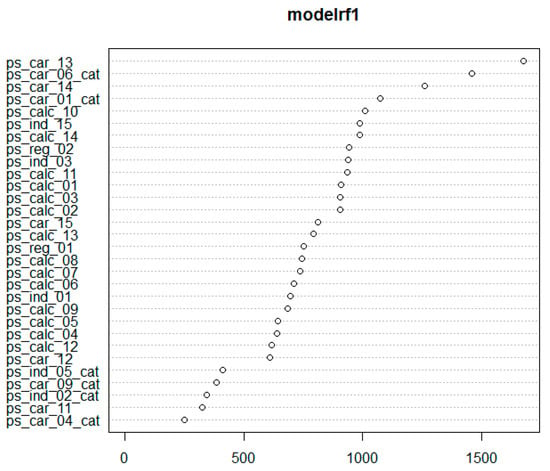
Figure 13.
The rank of features by importance based on the random forest algorithm.
8. Conclusions
There is a significant role in insurance risk management played by the emergence of big data and data science methods, such as ML models. In this study, we showed that data quality checks are necessary to omit redundant variables in the preparation and cleaning process, and how to handle an imbalanced dataset to prevent bias to a majority class.
Applying ML analytics in insurance is the same as in other industries—to optimize marketing strategies, improve the business, enhance the income, and reduce costs. This paper presented several ML techniques to efficiently analyze insurance claim prediction and compare their performances using various metrics. We proposed a solution using ML models to predict claim occurrence in the next year and to adjust the insurance prices fairly to the client’s ability, and used relevant personal information. Thus, insurance companies can make automotive insurance more accessible to more clients through a model that creates an accurate prediction. The accuracy of the prediction of claims can have a significant effect on the real economy. It is essential to routinely and consistently train workers in this new area to adapt and use these new techniques properly. Therefore, regulators and policymakers must make fast decisions to monitor the use of data science techniques, maximizing efficiency and understanding some of these algorithms’ limits.
We suggested that the performance metrics should not be limited to one criterion, such as the AUC (Kenett and Salini 2011). Thus, we used nine performance metrics to increase the modeling process transparency, because regulators will need to ensure the transparency of decision-making algorithms to prevent discrimination and a potentially harmful effect on the business.
The results of this paper show, firstly, that claim issues in the insurance company could be predicted using ML methods with relatively good performance and accuracy. Secondly, according to the results drawn from Table 4, it would seem that both RF and C50 are good performing models, but RF is the best; this is because it has the best performance measures. From the classifier models’ results, it is fair to say that the random forest model met the functional and non-functional requirements in the best detail. This is because it could classify the class 0 results accurately (97.17%). Although there was a range of incorrectly classified class 1 results, it predicted a good quantity of this class with accuracy (71%). It is essential to factor in that the datasets provided were very noisy and imbalanced.
Comparison of the models’ results showed that the random forest model is the most reliable among all eight models. The random forest model also showed promising results. It appears to classify and distinguish classes much better than the other models. This gave the RF model the upper hand in making it more robust and able to generalize as the best prediction model.
Future Research
It would be useful to see comparative studies for other ML and deep learning models using this dataset; it also would be worth performing this analysis with another insurance branch to conclude whether random forests still have the best predictive output or not.
Author Contributions
Methodology, M.H.; Supervision, R.M.; Writing—original draft, M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abdelhadi, Shady, Khaled Elbahnasy, and Mohamed Abdelsalam. 2020. A proposed model to predict auto insurance claims using machine learning techniques. Journal of Theoretical and Applied Information Technology 98: 3428–3437. [Google Scholar]
- Ariana, Diwan, Daniel E. Guyer, and Bim Shrestha. 2006. Integrating multispectral reflectance and fluorescence imaging for defect detection on apples. Computers and Electronics in Agriculture 50: 148–61. [Google Scholar] [CrossRef]
- Badr, W. 2019. Different Ways to Compensate for Missing Values in a Dataset (Data Imputation with Examples). Available online: https://towardsdatascience.com/6-different-ways-to-compensate-formissing-values-data-imputation-with-examples-6022d9ca0779 (accessed on 17 October 2019).
- Bradley, Andrew P. 1997. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognition 30: 1145–59. [Google Scholar] [CrossRef]
- Breiman, Leo. 2001. Random forests. Machine Learning 45: 5–32. [Google Scholar] [CrossRef]
- Chen, Tianqi, and Carlos Guestrin. 2016. XGBoost: A scalable tree boosting system. Paper presented at the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, August 13–17. [Google Scholar]
- Columbus, Louis. 2017. McKinsey’s State of Machine Learning and AI, 2017. Forbes. Available online: https://www.forbes.com/sites/louiscolumbus/2017/07/09/mckinseys-state-of-machine-learning-and-ai-2017 (accessed on 17 December 2020).
- Columbus, Louis. 2018. Roundup of Machine Learning Forecasts and Market Estimates, 2018. Forbes Contrib. Available online: https://www.forbes.com/sites/louiscolumbus/2018/02/18/roundup-of-machine-learning-forecasts-and-marketestimates-2018 (accessed on 17 December 2020).
- Cunningham, Padraig, and Sarah Jane Delany. 2020. k-Nearest Neighbour Classifiers–. arXiv arXiv:2004.04523. [Google Scholar]
- D’Angelo, Gianni, Massimo Tipaldi, Luigi Glielmo, and Salvatore Rampone. 2017. Spacecraft Autonomy Modeled via Markov Decision Process and Associative Rule-Based Machine Learning. Paper presented at 2017 IEEE International Workshop on Metrology for Aerospace (MetroAeroSpace), Padua, Italy, June 21–23; pp. 324–29. [Google Scholar]
- D’Angelo, Gianni, Massimo Ficco, and Francesco Palmieri. 2020. Malware detection in mobile environments based on Autoencoders and API-images. Journal of Parallel and Distributed Computing 137: 26–33. [Google Scholar] [CrossRef]
- Dewi, Kartika Chandra, Hendri Murfi, and Sarini Abdullah. 2019. Analysis Accuracy of Random forest Model for Big Data—A Case Study of Claim Severity Prediction in Car Insurance. Paper presented at 2019 5th International Conference on Science in Information Technology (ICSITech), Yogyakarta, Indonesia, October 23–24; pp. 60–65. [Google Scholar]
- Fang, Kuangnan, Yefei Jiang, and Malin Song. 2016. Customer profitability forecasting using Big Data analytics: A case study of the insurance industry. Computers & Industrial Engineering 101: 554–64. [Google Scholar]
- Friedman, Nir, Dan Geiger, and Moises Goldszmidt. 1997. Bayesian network classifiers. Machine Learning 29: 131–63. [Google Scholar] [CrossRef]
- Ganganwar, Vaishali. 2012. An overview of classification algorithms for imbalanced datasets. International Journal of Emerging Technology and Advanced Engineering 2: 42–47. [Google Scholar]
- Gao, Guangyuan, and Mario V. Wüthrich. 2018. Feature extraction from telematics car driving heatmaps. European Actuarial Journal 8: 383–406. [Google Scholar] [CrossRef]
- Gao, Guangyuan, Shengwang Meng, and Mario V. Wüthrich. 2019. Claims frequency modeling using telematics car driving data. Scandinavian Actuarial Journal 2019: 143–62. [Google Scholar] [CrossRef]
- Géron, Aurélien. 2019. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems. Newton: O’Reilly Media. [Google Scholar]
- Gonçalves, Ivo, Sara Silva, Joana B. Melo, and João MB Carreiras. 2012. Random sampling technique for overfitting control in genetic programming. In European Conference on Genetic Programming. Berlin and Heidelberg: Springer, pp. 218–29. [Google Scholar]
- Goodfellow, Ian, Yoshua Bengio, and Aaron Courville. 2016. Machine learning basics. Deep Learning 1: 98–164. [Google Scholar]
- Grosan, C., and A. Abraham. 2011. Intelligent Systems. Berlin: Springer. [Google Scholar]
- Guillen, Montserrat, Jens Perch Nielsen, Mercedes Ayuso, and Ana M. Pérez-Marín. 2019. The use of telematics devices to improve automobile insurance rates. Risk Analysis 39: 662–72. [Google Scholar] [CrossRef]
- Günther, Clara-Cecilie, Ingunn Fride Tvete, Kjersti Aas, Geir Inge Sandnes, and Ørnulf Borgan. 2014. Modelling and predicting customer churn from an insurance company. Scandinavian Actuarial Journal 2014: 58–71. [Google Scholar] [CrossRef]
- Hossin, Mohammad, and M. N. Sulaiman. 2015. A review on evaluation metrics for data classification evaluations. International Journal of Data Mining & Knowledge Management Process 5: 1. [Google Scholar]
- Hultkrantz, Lars, Jan-Eric Nilsson, and Sara Arvidsson. 2012. Voluntary internalization of speeding externalities with vehicle insurance. Transportation Research Part A: Policy and Practice 46: 926–37. [Google Scholar] [CrossRef]
- Jiang, Shengyi, Guansong Pang, Meiling Wu, and Limin Kuang. 2012. An improved K-nearest-neighbor algorithm for text categorization. Expert Systems with Applications 39: 1503–9. [Google Scholar] [CrossRef]
- Jing, Longhao, Wenjing Zhao, Karthik Sharma, and Runhua Feng. 2018. Research on Probability-based Learning Application on Car Insurance Data. In 2017 4th International Conference on Machinery, Materials and Computer (MACMC 2017). Amsterdam: Atlantis Press. [Google Scholar]
- Kansara, Dhvani, Rashika Singh, Deep Sanghvi, and Pratik Kanani. 2018. Improving Accuracy of Real Estate Valuation Using Stacked Regression. Int. J. Eng. Dev. Res. (IJEDR) 6: 571–77. [Google Scholar]
- Kayri, Murat, Ismail Kayri, and Muhsin Tunay Gencoglu. 2017. The performance comparison of multiple linear regression, random forest and artificial neural network by using photovoltaic and atmospheric data. Paper presented at 2017 14th International Conference on Engineering of Modern Electric Systems (EMES), Oradea, Romania, June 1–2; pp. 1–4. [Google Scholar]
- Kenett, Ron S., and Silvia Salini. 2011. Modern analysis of customer satisfaction surveys: Comparison of models and integrated analysis. Applied Stochastic Models in Business and Industry 27: 465–75. [Google Scholar] [CrossRef]
- Kotsiantis, Sotiris B., Ioannis D. Zaharakis, and Panayiotis E. Pintelas. 2006. Machine learning: A review of classification and combining techniques. Artificial Intelligence Review 26: 159–90. [Google Scholar] [CrossRef]
- Kotsiantis, Sotiris B., I. Zaharakis, and P. Pintelas. 2007. Supervised machine learning: A review of classification techniques. Emerging Artificial Intelligence Applications in Computer Engineering 160: 3–24. [Google Scholar]
- Kowshalya, G., and M. Nandhini. 2018. Predicting fraudulent claims in automobile insurance. Proceedings of the 2018 Second International Conference on Inventive Communication and Computational Technologies (ICICCT), Coimbatore, India, April 20–21; pp. 1338–43. [Google Scholar]
- Kuhn, Max, and Kjell Johnson. 2013. Applied Predictive Modeling. New York: Springer, vol. 26. [Google Scholar]
- Lunardon, Nicola, Giovanna Menardi, and Nicola Torelli. 2014. ROSE: A Package for Binary Imbalanced Learning. R Journal 6: 79–89. [Google Scholar] [CrossRef]
- Mau, Stefan, Irena Pletikosa, and Joël Wagner. 2018. Forecasting the next likely purchase events of insurance customers: A case study on the value of data-rich multichannel environments. International Journal of Bank Marketing 36: 6. [Google Scholar] [CrossRef]
- Mccord, Michael, and M. Chuah. 2011. Spam detection on twitter using traditional classifiers. In International Conference on Autonomic and Trusted Computing. Berlin and Heidelberg: Springer, pp. 175–86. [Google Scholar]
- Musa, Abdallah Bashir. 2013. Comparative study on classification performance between support vector machine and logistic regression. International Journal of Machine Learning and Cybernetics 4: 13–24. [Google Scholar] [CrossRef]
- Pesantez-Narvaez, Jessica, Montserrat Guillen, and Manuela Alcañiz. 2019. Predicting motor insurance claims using telematics data—XGBoost versus logistic regression. Risks 7: 70. [Google Scholar] [CrossRef]
- Roel, Verbelen, Katrien Antonio, and Gerda Claeskens. 2017. Unraveling the predictive power of telematics data in car insurance pricing. Journal of the Royal Statistical Society SSRN. , 2872112. [Google Scholar] [CrossRef]
- Sabbeh, Sahar F. 2018. Machine-learning techniques for customer retention: A comparative study. International Journal of Advanced Computer Science and Applications 9: 273–81. [Google Scholar]
- Schmidt, Jonathan, Mário R. G. Marques, Silvana Botti, and Miguel A. L. Marques. 2019. Recent advances and applications of machine learning in solid-state materials science. npj Computational Materials 5: 1–36. [Google Scholar] [CrossRef]
- Singh, Ranjodh, Meghna P. Ayyar, Tata Venkata Sri Pavan, Sandeep Gosain, and Rajiv Ratn Shah. 2019. Automating Car Insurance Claims Using Deep Learning Techniques. Paper presented at 2019 IEEE Fifth International Conference on Multimedia Big Data (BigMM), Singapore, September 11–13; pp. 199–207. [Google Scholar]
- Smith, Kate A., Robert J. Willis, and Malcolm Brooks. 2000. An analysis of customer retention and insurance claim patterns using data mining: A case study. Journal of the Operational Research Society 51: 532–41. [Google Scholar] [CrossRef]
- Song, Yan Yan, and L. U. Ying. 2015. Decision tree methods: Applications for classification and prediction. Shanghai Archives of Psychiatry 27: 130. [Google Scholar] [PubMed]
- Stucki, Oskar. 2019. Predicting the Customer Churn with Machine Learning Methods: Case: Private Insurance Customer Data. Master’s dissertation, LUT University, Lappeenranta, Finland. [Google Scholar]
- Subudhi, Sharmila, and Suvasini Panigrahi. 2017. Use of optimized Fuzzy C-Means clustering and supervised classifiers for automobile insurance fraud detection. Journal of King Saud University-Computer and Information Sciences 32: 568–75. [Google Scholar] [CrossRef]
- Weerasinghe, K. P. M. L. P., and M. C. Wijegunasekara. 2016. A comparative study of data mining algorithms in the prediction of auto insurance claims. European International Journal of Science and Technology 5: 47–54. [Google Scholar]
- Wu, Shaomin, and Peter Flach. 2005. A scored AUC metric for classifier evaluation and selection. Paper presented at Second Workshop on ROC Analysis in ML, Bonn, Germany, August 11. [Google Scholar]
- Wüthrich, Mario V. 2017. Covariate selection from telematics car driving data. European Actuarial Journal 7: 89–108. [Google Scholar] [CrossRef]
- Yerpude, Prajakta. 2020. Predictive Modelling of Crime Dataset Using Data Mining. International Journal of Data Mining & Knowledge Management Process (IJDKP) 7: 4. [Google Scholar]
- Zhou, Zhi Hua. 2012. Ensemble Methods: Foundations and Algorithms. Boca Raton: CRC Press. [Google Scholar]
| 1 | https://www.insure.com/car-insurance/ (accessed on 21 December 2020). |
| 2 | https://www.iii.org/fact-statistic/facts-statistics-auto-insurance (accessed on 19 December 2020). |
| 3 | https://www.kaggle.com/alinecristini/atividade2portoseguro (accessed on 15 December 2020). |
| 4 | https://www.kaggle.com/c/porto-seguro-safe-driverprediction/overview (accessed on 15 December 2020). |
| 5 | https://www.kaggle.com/c/porto-seguro-safe-driver-prediction/data (accessed on 15 December 2020). |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).