Hedging Effectiveness of Commodity Futures Contracts to Minimize Price Risk: Empirical Evidence from the Italian Field Crop Sector
Abstract
:1. Introduction
2. Hedging with Futures Contracts
3. Materials and Methods
3.1. Dataset and Hedging Horizon
3.2. Determination of the Optimal Hedging Ratio
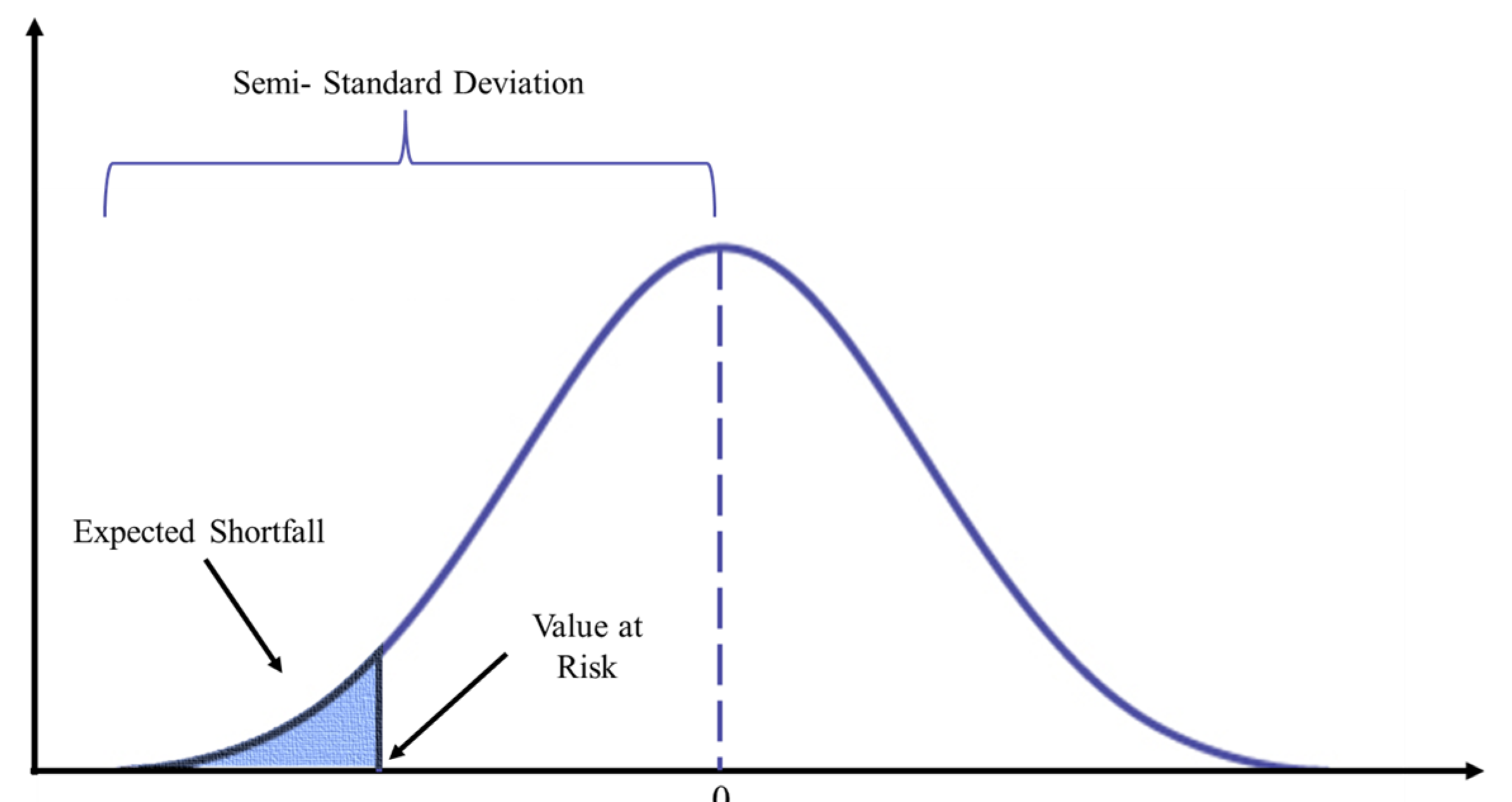
3.3. Hedging Effectiveness
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Models Specification
| 1 | A long position refers to a farmer that owns a commodity or a futures contract, a short position refers to a farmer that has to buy a commodity or a futures contract. |
| 2 | https://www.agerborsamerci.it (accessed on 17 November 2021). |
| 3 | https://www.cmegroup.com (accessed on 17 November 2021). |
| 4 | https://www.euronext.com (accessed on 17 November 2021). |
References
- Antón, Jesús, Shingo Kimura, Jussi Lankoski, and Andrea Cattaneo. 2012. A comparative study of risk management in agriculture under climate change. In OECD Food, Agriculture and Fisheries Working Papers. No. 58. Paris: OECD Publishing. [Google Scholar] [CrossRef]
- Baffes, John, and Tassos Haniotis. 2016. What explains agricultural price movements? Journal of Agricultural Economics 673: 706–21. [Google Scholar] [CrossRef]
- Bekkerman, Anton. 2011. Time-varying hedge ratios in linked agricultural markets. Agricultural Finance Review 71: 179–200. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1990. Modelling the coherence in short-run nominal exchange rates: A multivariate generalized ARCH model. The Review of Economics and Statistics 72: 498–505. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Robert F. Engle, and Jeffrey M. Wooldridge. 1988. A capital asset pricing model with time-varying covariances. Journal of Political Economy 96: 116–31. [Google Scholar] [CrossRef]
- Brooks, Chris, and James Chong. 2001. The cross-currency hedging performance of implied versus statistical forecasting models. Journal of Futures Markets 21: 1043–69. [Google Scholar] [CrossRef] [Green Version]
- Butterworth, Darren, and Phil Holmes. 2001. The hedging effectiveness of stock index futures: Evidence for the FTSE-100 and FTSE-Mid250 indexes traded in the UK. Applied Financial Economics 11: 57–68. [Google Scholar] [CrossRef]
- Candila, Vincenzo, and Salvatore Farace. 2018. On the volatility spillover between agricultural commodities and Latin American stock markets. Risks 6: 116. [Google Scholar] [CrossRef] [Green Version]
- Carter, Colin A. 1984. An evaluation of pricing performance and hedging effectiveness of the barley futures market. Western Journal of Agricultural Economics 9: 1–13. [Google Scholar]
- Chang, Chiao-Yi, Jing-Yi Lai, and I-Yuan Chuang. 2010. Futures hedging effectiveness under the segmentation of bear/bull energy markets. Energy Economics 32: 442–49. [Google Scholar] [CrossRef]
- Chang, Chia-Lin, Lydia González-Serrano, and Juan-Angel Jimenez-Martin. 2013. Currency hedging strategies using dynamic multivariate GARCH. Mathematics and Computers in Simulation 94: 164–82. [Google Scholar] [CrossRef] [Green Version]
- Chen, Sheng-Syan, Cheng-Few Lee, and Keshab Shrestha. 2003. Futures hedge ratios: A review. The Quarterly Review of Economics and Finance 43: 433–65. [Google Scholar] [CrossRef]
- Coletta, Attilio, Elisa Giampietri, Fabio Gaetano Santeramo, Simone Severini, and Samuele Trestini. 2018. A preliminary test on risk and ambiguity attitudes, and time preferences in decisions under uncertainty: Towards a better explanation of participation in crop insurance schemes. Bio-Based and Applied Economics 7: 265–77. [Google Scholar]
- Conforti, Piero. 2004. Price transmission in selected agricultural markets. In FAO Commodity and Trade Policy Research Working Paper 7. Rome: FAO. [Google Scholar]
- Conlon, Thomas, John Cotter, and Ramazan Gençay. 2016. Commodity futures hedging, risk aversion and the hedging horizon. The European Journal of Finance 22: 1534–60. [Google Scholar] [CrossRef]
- Dahlgran, Roger A. 2005. Transaction frequency and hedging in commodity processing. Journal of Agricultural and Resource Economics 30: 411–30. [Google Scholar]
- De Castro, Paolo, Jorgelina Di Pasquale, and Felice Adinolfi. 2012. Quale ruolo per la politica agricola europea in un’era d’instabilità dei mercati? Economia Agro-Alimentare 14: 235–48. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar] [CrossRef]
- Dowd, Kevin. 2007. Measuring Market Risk, 2nd ed. Chichester: John Wiley and Sons. [Google Scholar]
- Ederington, Louis H. 1979. The hedging performance of the new futures markets. Journal of Finance 34: 157–70. [Google Scholar] [CrossRef]
- Elleby, Christian, Ignacio Pérez Domínguez, Marcel Adenauer, and Giampiero Genovese. 2020. Impacts of the COVID-19 pandemic on the global agricultural markets. Environmental and Resource Economics. 76: 1067–79. [Google Scholar] [CrossRef]
- European Parliament Research Service’s Briefing (EPRS). 2016. Price Volatility in Agricultural Markets Risk Management and Other Tools. Available online: http://www.europarl.europa.eu/RegData/etudes/BRIE/2016/586609/EPRS_BRI(2016)586609_EN.pdf (accessed on 17 November 2021).
- Esposti, Roberto, and Giulia Listorti. 2013. Agricultural price transmission across space and commodities during price bubbles. Agricultural Economics 44: 125–39. [Google Scholar] [CrossRef] [Green Version]
- Ezeaku, Hillary C., Simplice A. Asongu, and Joseph Nnanna. 2021. Volatility of international commodity prices in times of COVID-19: Effects of oil supply and global demand shocks. The Extractive Industries and Society 8: 257–70. [Google Scholar] [CrossRef]
- Frascarelli, Angelo, Simone Del Sarto, and Giada Mastandrea. 2021. A New Tool for Covering Risk in Agriculture: The Revenue Insurance Policy. Risks 9: 131. [Google Scholar] [CrossRef]
- Giampietri, Elisa, Xiaohua Yu, and Samuele Trestini. 2020. The role of trust and perceived barriers on farmer’s intention to adopt risk management tools. Bio-Based and Applied Economics Journal 9: 1–24. [Google Scholar] [CrossRef]
- Harčariková, Monika. 2018. Managing price risk in the corn market using option strategies. Acta Universitatis Agriculturae et Silviculturae Mendelianae Brunensis 66: 767–79. [Google Scholar] [CrossRef] [Green Version]
- Höhler, Julia, and Alfons O. Lansink. 2021. Measuring the impact of COVID-19 on stock prices and profits in the food supply chain. Agribusiness 37: 171–86. [Google Scholar] [CrossRef] [PubMed]
- Hull, John C. 2008. Options, Futures, and Other Derivatives, 7th ed. Hoboken: Pearson Prentice Hall. [Google Scholar]
- Johnson, Leland L. 1960. The theory of hedging and speculation in commodity futures. Review of Economic Studies 27: 139–51. [Google Scholar] [CrossRef]
- Jorion, Philippe. 2006. Value at Risk: The New Benchmark for Managing Financial Risk, 3rd ed. New York: McGraw-Hill. [Google Scholar]
- Juhl, Ted, Ira G. Kawaller, and Paul D. Koch. 2012. The effect of the hedge horizon on optimal hedge size and effectiveness when prices are cointegrated. Journal of Futures Markets 32: 837–76. [Google Scholar] [CrossRef]
- Lence, Sergio H. 1995. The economic value of minimum-variance hedges. American Journal of Agricultural Economics 77: 353–64. [Google Scholar] [CrossRef]
- Lien, Donald, Y. K. Tse, and Albert Tsui. 2002. Evaluating the hedging performance of the constant-correlation GARCH model. Applied Financial Economics 12: 791–98. [Google Scholar] [CrossRef]
- Luo, Qunying, Karl Behrendt, and Michael Bange. 2017. Economics and risk of adaptation options in the Australian cotton industry. Agricultural Systems 150: 46–53. [Google Scholar] [CrossRef]
- Markowitz, Harry M. 1952. Portfolio Selection: Efficient Diversification of Investment. Cowles Foundation Monograph #16. New York: Wiley. [Google Scholar]
- McKenzie, Andrew M., and Navinderpal Singh. 2011. Hedging effectiveness around US Department of Agriculture crop reports. Journal of Agricultural and Applied Economics 43: 1–18. [Google Scholar] [CrossRef] [Green Version]
- Michels, Marius, Johannes Möllmann, and Oliver Musshoff. 2019. Understanding the intention to use commodity futures contracts. Agricultural Finance Review 79: 582–97. [Google Scholar] [CrossRef]
- Misund, Bård, and Frank Asche. 2016. Hedging efficiency of Atlantic salmon futures. Aquaculture Economics & Management 20: 368–81. [Google Scholar] [CrossRef] [Green Version]
- Monjardino, Marta, Therese M. McBeath, Lisa E. Brennan, and Rick S. Llewellyn. 2013. Are farmers in low rainfall cropping regions under-fertilising with nitrogen? A risk analysis. Agricultural Systems 116: 37–51. [Google Scholar] [CrossRef]
- Moschini, Giancarlo, and David A. Hennessy. 2001. Uncertainty, risk aversion, and risk management for agricultural producers. Handbook of Agricultural Economics 1: 87–153. [Google Scholar] [CrossRef]
- OECD. 2020. OECD Policy Responses to Coronavirus (COVID-19) The Impact of COVID-19 on Agricultural Markets and GHG Emissions. Available online: https://www.oecd.org/coronavirus/policy-responses/the-impact-of-covid-19-on-agricultural-markets-and-ghg-emissions-57e5eb53/ (accessed on 17 November 2021).
- Phillips, Peter C. B., and Pierre Perron. 1988. Testing for a unit root in time series regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Rao, Vadhindran K. 2000. Preference-free optimal hedging using futures. Economics Letters 66: 223–28. [Google Scholar] [CrossRef]
- Revoredo-Giha, Cesar, and Marco Zuppiroli. 2013. Commodity futures markets: Are they an effective price risk management tool for the European wheat supply chain? Bio-Based and Applied Economics 2: 237–55. [Google Scholar] [CrossRef]
- Ricome, Aymeric, and Arnaud Reynaud. 2021. Marketing contract choices in agriculture: The role of price expectation and price risk management. Agricultural Economics. [Google Scholar] [CrossRef]
- Santeramo, Fabio G., Emilia Lamonaca, Francesco Contò, Gianluca Nardone, and Antonio Stasi. 2018. Drivers of grain price volatility: A cursory critical review. Agricultural Economics 64: 347–56. [Google Scholar] [CrossRef]
- Stefani, Gianluca, and Marco Tiberti. 2016. Multiperiod optimal hedging ratios: Methodological aspects and application to a wheat market. European Review of Agricultural Economics 43: 503–31. [Google Scholar] [CrossRef] [Green Version]
- Stein, Jerome L. 1976. The simultaneous determination of spot and futures prices. In The Economics of Futures Trading. London: Palgrave Macmillan, pp. 124–30. [Google Scholar] [CrossRef]
- Tangermann, Stefan. 2011. Policy Solutions to Agricultural Market Volatility: A Synthesis. Issue Paper No. 33. Geneva: International Centre for Trade and Sustainable Development, pp. 1–13. [Google Scholar]
- Trestini, Samuele, and Carlotta Penone. 2018. Transmission of futures prices to the Italian spot market: Are there opportunities to hedge corn price risk? Economia Agro-Alimentare 20: 193–204. [Google Scholar] [CrossRef]
- Trestini, Samuele, Elisa Giampietri, and Vasco Boatto. 2017a. Toward the implementation of the Income Stabilization Tool: An analysis of factors affecting the probability of farm income losses in Italy. New Medit 16: 24–30. [Google Scholar]
- Trestini, Samuele, Eugenio Pomarici, and Elisa Giampietri. 2017b. Around the economic sustainability of Italian viticulture: Do farm strategies tackle income risks? Calitatea 18: 461–67. [Google Scholar]
- United State Department of Agriculture (USDA). 2021. World Agricultural Supply and Demand Estimates (WASDE). World Agricultural Outlook Board (WAOB). June. Available online: https://usda.library.cornell.edu/concern/publications/3t945q76s?locale=en (accessed on 17 November 2021).
- Wilson, William W., William E. Nganje, and Robert Wagner. 2006. Hedging strategies for grain processors. Canadian Journal of Agricultural Economics/Revue Canadienne D’agroeconomie 54: 311–26. [Google Scholar] [CrossRef]
- Yang, Wenling, and David E. Allen. 2005. Multivariate GARCH hedge ratios and hedging effectiveness in Australian futures markets. Accounting Finance 45: 301–21. [Google Scholar] [CrossRef]
- Yang, Jian, and Titus O. Awokuse. 2003. Asset storability and hedging effectiveness in commodity futures markets. Applied Economics Letters 10: 487–91. [Google Scholar] [CrossRef]
- Zinnanti, Cinzia, Emanuele Schimmenti, Valeria Borsellino, Giulio Paolini, and Simone Severini. 2019. Economic performance and risk of farming systems specialized in perennial crops: An analysis of Italian hazelnut production. Agricultural Systems 17: 102645. [Google Scholar] [CrossRef]
- Zuppiroli, Marco, and Cesar Revoredo-Giha. 2016. Hedging effectiveness of European wheat futures markets: An application of multivariate GARCH models. International Journal of Applied Management Science 8: 132–48. [Google Scholar] [CrossRef]
| Time Horizon (n. of Weeks) | N. of Obs. | Mean | St. Dev. | Min | Max | ADF t-Stat | PP t-Stat | ||
|---|---|---|---|---|---|---|---|---|---|
| Italian spot | Soybean | 1 | 750 | 0.11 | 2.06 | −9.84 | 8.23 | −12.66 *** | −22.27 *** |
| 4 | 747 | 0.45 | 5.02 | −18.41 | 17.14 | −7.32 *** | −9.09 *** | ||
| 12 | 739 | 1.28 | 9.86 | −35.31 | 25.11 | −5.95 *** | −22.27 *** | ||
| 32 | 719 | 2.72 | 16.51 | −44.02 | 48.95 | −3.65 *** | −29.50 *** | ||
| Corn | 1 | 750 | 0.06 | 2.40 | −19.01 | 23.52 | −15.92 *** | −21.25 *** | |
| 4 | 747 | 0.24 | 5.87 | −27.52 | 26.44 | −10.29 *** | −9.01 *** | ||
| 12 | 739 | 0.59 | 11.57 | −50.94 | 38.26 | −5.63 *** | −4.80 *** | ||
| 32 | 719 | 1.00 | 19.65 | −60.50 | 44.58 | −3.19 * | −2.56 | ||
| Wheat | 1 | 750 | 0.04 | 1.53 | −8.61 | 12.40 | −9.26 *** | −19.96 *** | |
| 4 | 747 | 0.16 | 4.19 | −16.54 | 21.01 | −6.66 *** | −7.73 *** | ||
| 12 | 739 | 0.46 | 9.16 | −32.40 | 39.02 | −6.11 *** | −4.37 *** | ||
| 32 | 719 | 0.93 | 17.81 | −40.86 | 60.09 | −4.20 *** | −2.58 | ||
| CBOT | Soybean | 1 | 750 | 0.12 | 2.82 | −14.68 | 8.71 | −17.08 *** | −22.76 *** |
| 4 | 747 | 0.47 | 6.47 | −22.97 | 21.00 | −13.40 *** | −10.53 *** | ||
| 12 | 739 | 1.27 | 11.28 | −33.33 | 28.92 | −6.54 *** | −5.77 *** | ||
| 32 | 719 | 2.84 | 17.19 | −39.96 | 49.51 | −3.81 ** | −3.37 * | ||
| Corn | 1 | 750 | 0.09 | 3.42 | −21.72 | 12.90 | −17.83 *** | −22.63 *** | |
| 4 | 747 | 0.35 | 7.84 | −28.31 | 31.48 | −8.00 *** | −10.08 *** | ||
| 12 | 739 | 0.80 | 13.64 | −40.40 | 38.37 | −5.81 *** | −5.40 *** | ||
| 32 | 719 | 1.85 | 22.48 | −58.40 | 62.67 | −3.19 * | −2.91 | ||
| Wheat | 1 | 750 | 0.06 | 3.61 | −12.67 | 16.04 | −17.59 *** | −22.68 *** | |
| 4 | 747 | 0.27 | 8.19 | −30.00 | 35.96 | −8.32 *** | −10.28 *** | ||
| 12 | 739 | 0.72 | 13.30 | −45.99 | 44.79 | −7.06 *** | −6.13 *** | ||
| 32 | 719 | 1.48 | 20.73 | −65.11 | 61.88 | −4.46 *** | −4.10 *** | ||
| Euronext | Corn | 1 | 750 | 0.06 | 2.58 | −24.86 | 11.96 | −17.52 *** | −21.99 *** |
| 4 | 747 | 0.22 | 6.02 | −29.18 | 19.34 | −11.78 *** | −9.90 *** | ||
| 12 | 739 | 0.57 | 11.15 | −44.40 | 30.42 | −5.57 *** | −5.15 *** | ||
| 32 | 719 | 0.88 | 18.57 | −53.89 | 47.39 | −3.40 ** | −3.24 * | ||
| Wheat | 1 | 750 | 0.05 | 2.81 | −13.98 | 17.50 | −17.12 *** | −20.83 *** | |
| 4 | 747 | 0.21 | 6.85 | −26.71 | 33.40 | −7.38 *** | −9.32 *** | ||
| 12 | 739 | 0.63 | 12.68 | −43.56 | 56.67 | −6.39 *** | −5.48 *** | ||
| 32 | 719 | 1.32 | 22.42 | −68.81 | 72.90 | −3.72 ** | −3.27 * |
| Time Horizon (n. of Weeks) | γOLS | γGARCH | ||
|---|---|---|---|---|
| Italian spot-CBOT | Soybean | 1 | 0.449 | 0.461 |
| 4 | 0.565 | 0.586 | ||
| 12 | 0.710 | 0.730 | ||
| 32 | 0.864 | 0.809 | ||
| Corn | 1 | 0.140 | 0.130 | |
| 4 | 0.294 | 0.327 | ||
| 12 | 0.438 | 0.454 | ||
| 32 | 0.524 | 0.668 | ||
| Wheat | 1 | 0.093 | 0.094 | |
| 4 | 0.238 | 0.225 | ||
| 12 | 0.420 | 0.253[A] | ||
| 32 | 0.660 | 0.678 | ||
| Italian spot-Euronext | Corn | 1 | 0.304 | 0.263 |
| 4 | 0.652 | 0.651 | ||
| 12 | 0.866 | 0.809 | ||
| 32 | 0.952 | 0.966 | ||
| Wheat | 1 | 0.185 | 0.189 | |
| 4 | 0.370 | 0.361 | ||
| 12 | 0.540 | 0.565 | ||
| 32 | 0.689 | 0.706 |
| Time Horizon (n. of Weeks) | Variance | ||||
|---|---|---|---|---|---|
| γnaive | γOLS | γGARCH | |||
| Italian spot-CBOT | Soybean | 1 | −0.207 | 0.377 | 0.377 |
| 4 | 0.217 | 0.531 | 0.531 | ||
| 12 | 0.549 | 0.660 | 0.659 | ||
| 32 | 0.788 | 0.808 | 0.805 | ||
| Corn | 1 | −1.464 | 0.038 | 0.038 | |
| 4 | −0.761 | 0.145 | 0.143 | ||
| 12 | −0.178 | 0.264 | 0.264 | ||
| 32 | 0.051 | 0.353 | 0.324 | ||
| Wheat | 1 | −4.492 | 0.049 | 0.049 | |
| 4 | −1.998 | 0.218 | 0.217 | ||
| 12 | −0.334 | 0.372 | 0.314 | ||
| 32 | 0.433 | 0.591 | 0.590 | ||
| Italian spot-Euronext | Corn | 1 | −0.456 | 0.105 | 0.103 |
| 4 | 0.310 | 0.440 | 0.440 | ||
| 12 | 0.678 | 0.695 | 0.692 | ||
| 32 | 0.805 | 0.808 | 0.808 | ||
| Wheat | 1 | −2.097 | 0.116 | 0.116 | |
| 4 | −0.700 | 0.367 | 0.366 | ||
| 12 | 0.155 | 0.561 | 0.559 | ||
| 32 | 0.597 | 0.752 | 0.752 | ||
| Time Horizon (n. of Weeks) | SSD | VaR | ES | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| γnaive | γOLS | γGARCH | γnaive | γOLS | γGARCH | γnaive | γOLS | γGARCH | |||
| Italian spot-CBOT | Soybean | 1 | 0.219 | 0.415 | 0.419 | −0.043 | 0.247 | 0.242 | 0.013 | 0.209 | 0.210 |
| 4 | 0.339 | 0.536 | 0.537 | 0.231 | 0.370 | 0.377 | 0.148 | 0.303 | 0.306 | ||
| 12 | 0.472 | 0.547 | 0.545 | 0.147 | 0.321 | 0.296 | 0.254 | 0.324 | 0.322 | ||
| 32 | 0.688 | 0.722 | 0.726 | 0.431 | 0.517 | 0.541 | 0.483 | 0.510 | 0.514 | ||
| Corn | 1 | −0.565 | 0.190 | 0.192 | −0.970 | 0.046 | 0.047 | −0.499 | 0.027 | 0.026 | |
| 4 | −0.404 | 0.077 | 0.071 | −0.292 | 0.127 | 0.139 | −0.219 | 0.077 | 0.079 | ||
| 12 | 0.374 | 0.345 | 0.354 | −0.057 | 0.192 | 0.171 | 0.148 | 0.149 | 0.151 | ||
| 32 | 0.209 | 0.302 | 0.321 | −0.116 | 0.044 | 0.004 | 0.089 | 0.185 | 0.204 | ||
| Wheat | 1 | −2.001 | 0.403 | 0.404 | −2.072 | 0.013 | 0.013 | −1.385 | 0.034 | 0.034 | |
| 4 | −1.820 | 0.334 | 0.327 | −0.952 | 0.073 | 0.067 | −0.832 | 0.108 | 0.105 | ||
| 12 | −0.550 | 0.364 | 0.306 | −0.315 | 0.217 | 0.175 | −0.256 | 0.196 | 0.149 | ||
| 32 | 0.274 | 0.529 | 0.528 | 0.072 | 0.267 | 0.261 | 0.167 | 0.332 | 0.329 | ||
| Italian spot-Euronext | Corn | 1 | −0.039 | 0.213 | 0.216 | −0.255 | 0.096 | 0.089 | −0.132 | 0.068 | 0.062 |
| 4 | 0.334 | 0.372 | 0.372 | 0.188 | 0.287 | 0.287 | 0.179 | 0.243 | 0.243 | ||
| 12 | 0.803 | 0.782 | 0.765 | 0.444 | 0.432 | 0.412 | 0.525 | 0.505 | 0.488 | ||
| 32 | 0.878 | 0.871 | 0.874 | 0.567 | 0.555 | 0.554 | 0.644 | 0.632 | 0.636 | ||
| Wheat | 1 | −0.335 | 0.527 | 0.528 | −1.258 | 0.088 | 0.081 | −0.686 | 0.095 | 0.096 | |
| 4 | −0.010 | 0.622 | 0.620 | −0.426 | 0.159 | 0.160 | −0.323 | 0.204 | 0.203 | ||
| 12 | 0.334 | 0.620 | 0.619 | −0.105 | 0.263 | 0.241 | 0.007 | 0.272 | 0.270 | ||
| 32 | 0.490 | 0.590 | 0.590 | 0.238 | 0.391 | 0.381 | 0.283 | 0.409 | 0.409 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Penone, C.; Giampietri, E.; Trestini, S. Hedging Effectiveness of Commodity Futures Contracts to Minimize Price Risk: Empirical Evidence from the Italian Field Crop Sector. Risks 2021, 9, 213. https://doi.org/10.3390/risks9120213
Penone C, Giampietri E, Trestini S. Hedging Effectiveness of Commodity Futures Contracts to Minimize Price Risk: Empirical Evidence from the Italian Field Crop Sector. Risks. 2021; 9(12):213. https://doi.org/10.3390/risks9120213
Chicago/Turabian StylePenone, Carlotta, Elisa Giampietri, and Samuele Trestini. 2021. "Hedging Effectiveness of Commodity Futures Contracts to Minimize Price Risk: Empirical Evidence from the Italian Field Crop Sector" Risks 9, no. 12: 213. https://doi.org/10.3390/risks9120213
APA StylePenone, C., Giampietri, E., & Trestini, S. (2021). Hedging Effectiveness of Commodity Futures Contracts to Minimize Price Risk: Empirical Evidence from the Italian Field Crop Sector. Risks, 9(12), 213. https://doi.org/10.3390/risks9120213








