Parsimonious Predictive Mortality Modeling by Regularization and Cross-Validation with and without Covid-Type Effect †
Abstract
1. Introduction
- Standard mortality models have a large number of parameters (easily between 100 and 200 parameters) in comparison with the small number of observations (often around 2000). Regularization techniques allow us to obtain a parsimonious model with very few parameters.
- Model choice is often performed based on the Bayes information criterion (BIC), which measures the ability of the model to fit the historical data (in-sample criterion). Our method, based on cross-validation, will select the model which has the best performance in terms of predictions (out-of-sample criterion).
2. Notation and Data
- The mortality rate which represents the probability that an individual aged exactly x at time t dies in the following year, i.e., between t and , is given by
- If we treat the number of deaths as a random variable and the central exposure as fixed, then follows a Poisson distributionwhere , see Pitacco et al. (2009).
3. Standard Approach to Mortality Modeling
3.1. The General Structure of Mortality Models
- The static age function term which captures the average shape of the mortality curve.
- N period-age terms () which describe the mortality trends.
- The term represents the lifelong cohort effect of certain generations.
3.2. Estimation and Standard Model Choice Criterion
3.3. Forecasting
4. Regularized Mortality Modeling
4.1. Polynomial Representation of Mortality Models
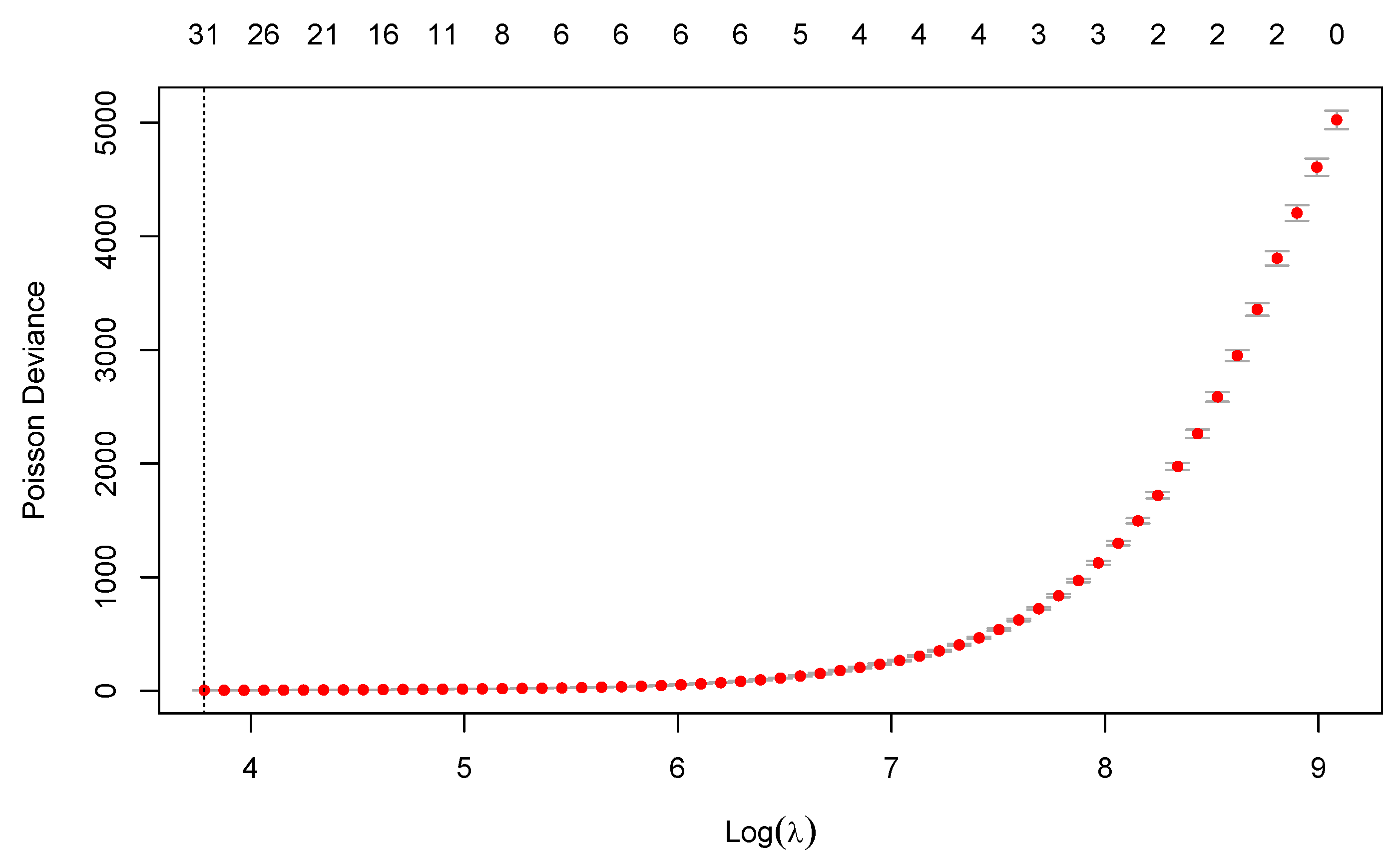
4.2. Estimation by Regularization and Cross-Validation
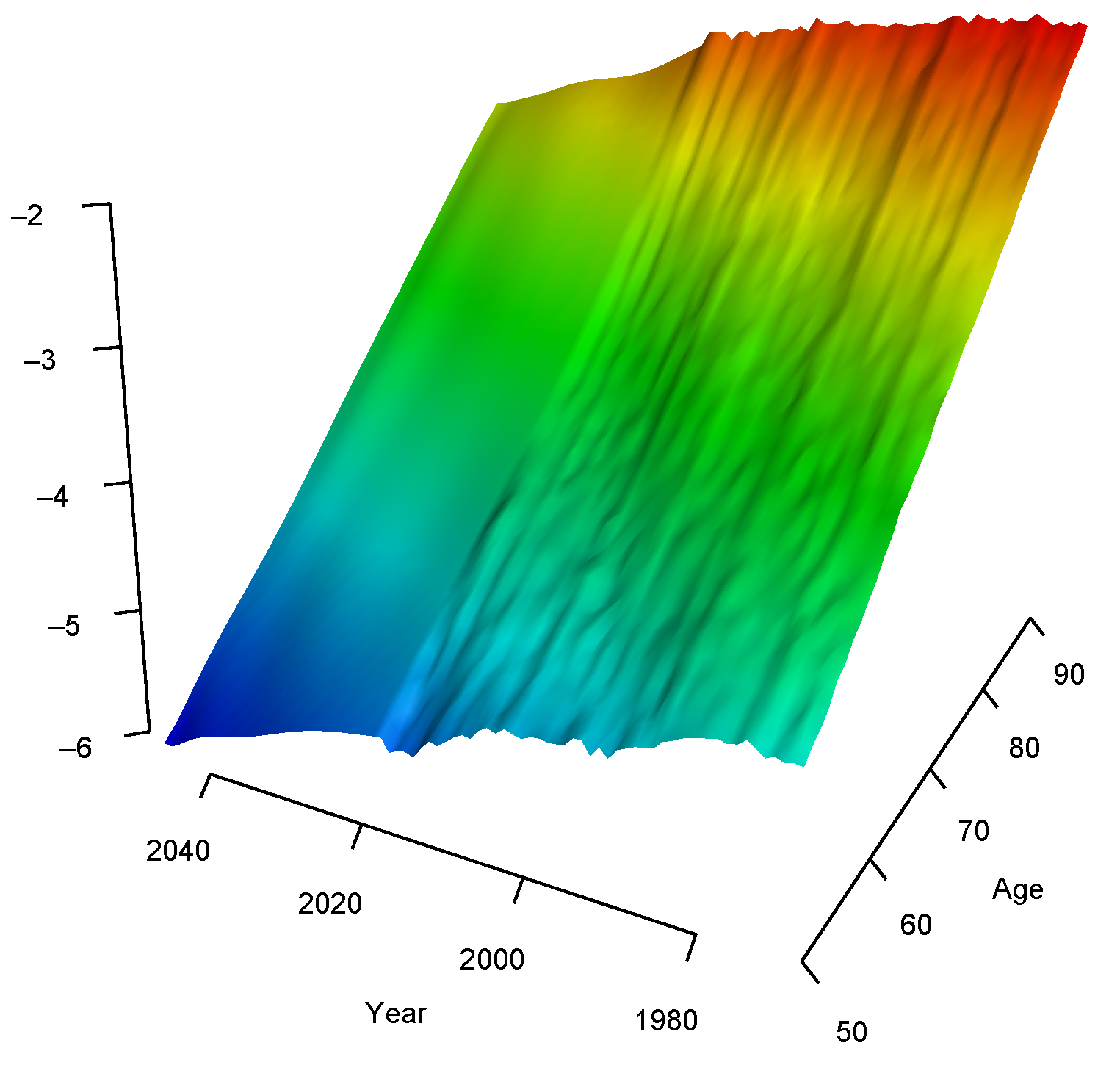
4.3. Forecasting
4.4. Effect of COVID-19
- During the year of the pandemic, , we assume that there is a death increase of :
- The next K years of the pandemic, , deaths and exposures are reduced to compensate the deaths of COVID-19:where is the number of years after the pandemic. Equations (8) reflect the idea that people who died from COVID-19 would have died in the next K years anyway. We note that we spread the deaths equally over the K years. To draw a parallel with the accelerated death models, measures the amplitude of the pandemic at age x and K measures the reach of the pandemic.
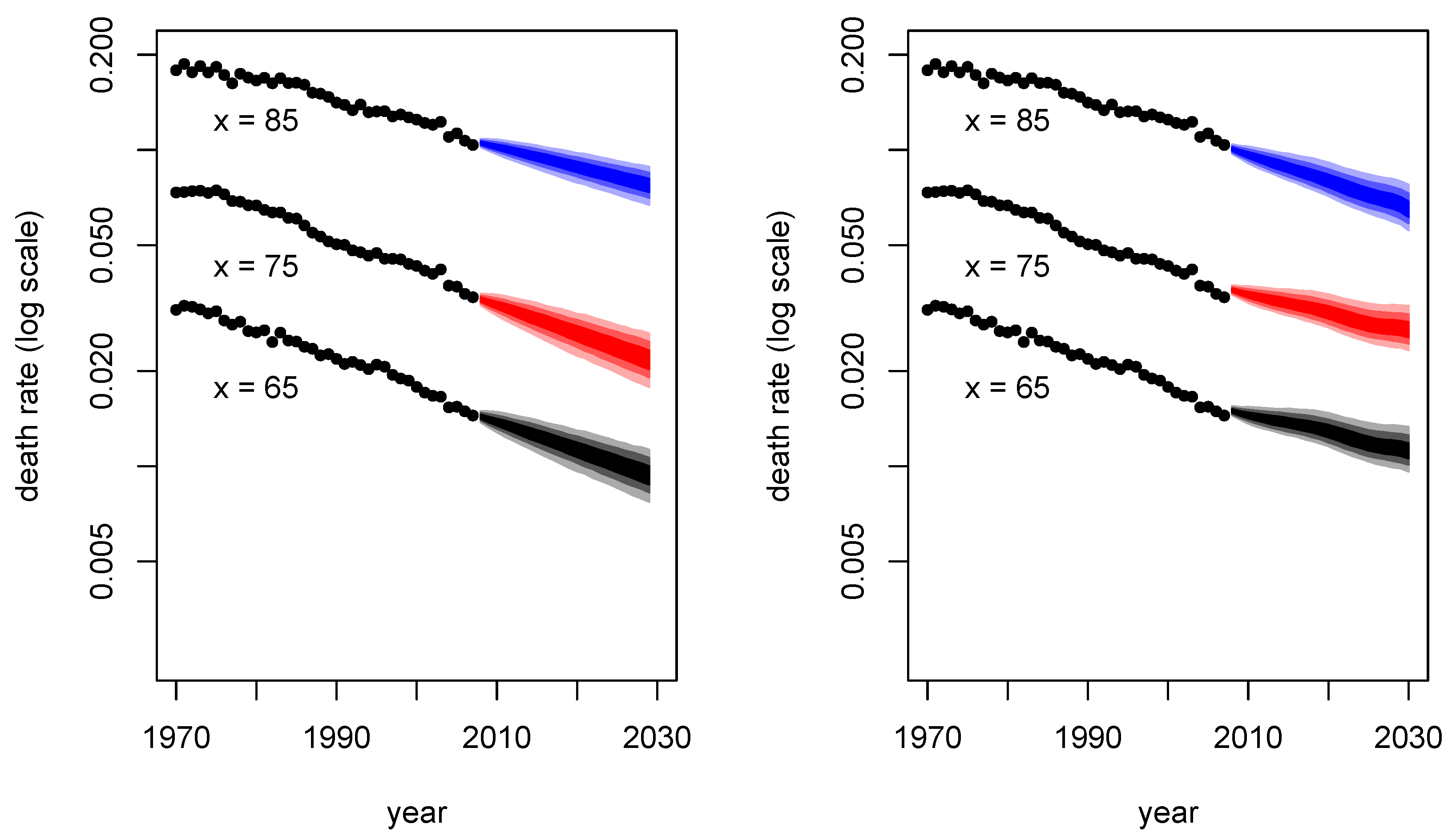
4.5. Model Uncertainty and Prediction Intervals
- In order to extract a period index, we assume that mortality rates improve at a general improvement rate per year:
- We estimate past improvement rates with the simple estimator:where and are the smoothed death rates.3
- We fit a random walk with drift (RWD) to past improvement rates: for .
- After the RWD fit, we can then obtain prediction intervals for future death rates:where and are the standard quantiles for the improvement rate for .
- Prediction intervals centered around the extrapolated central death rates can then be obtained with a shift of the mean:where is the mean of .
5. Numerical Analysis and Comparison of Models
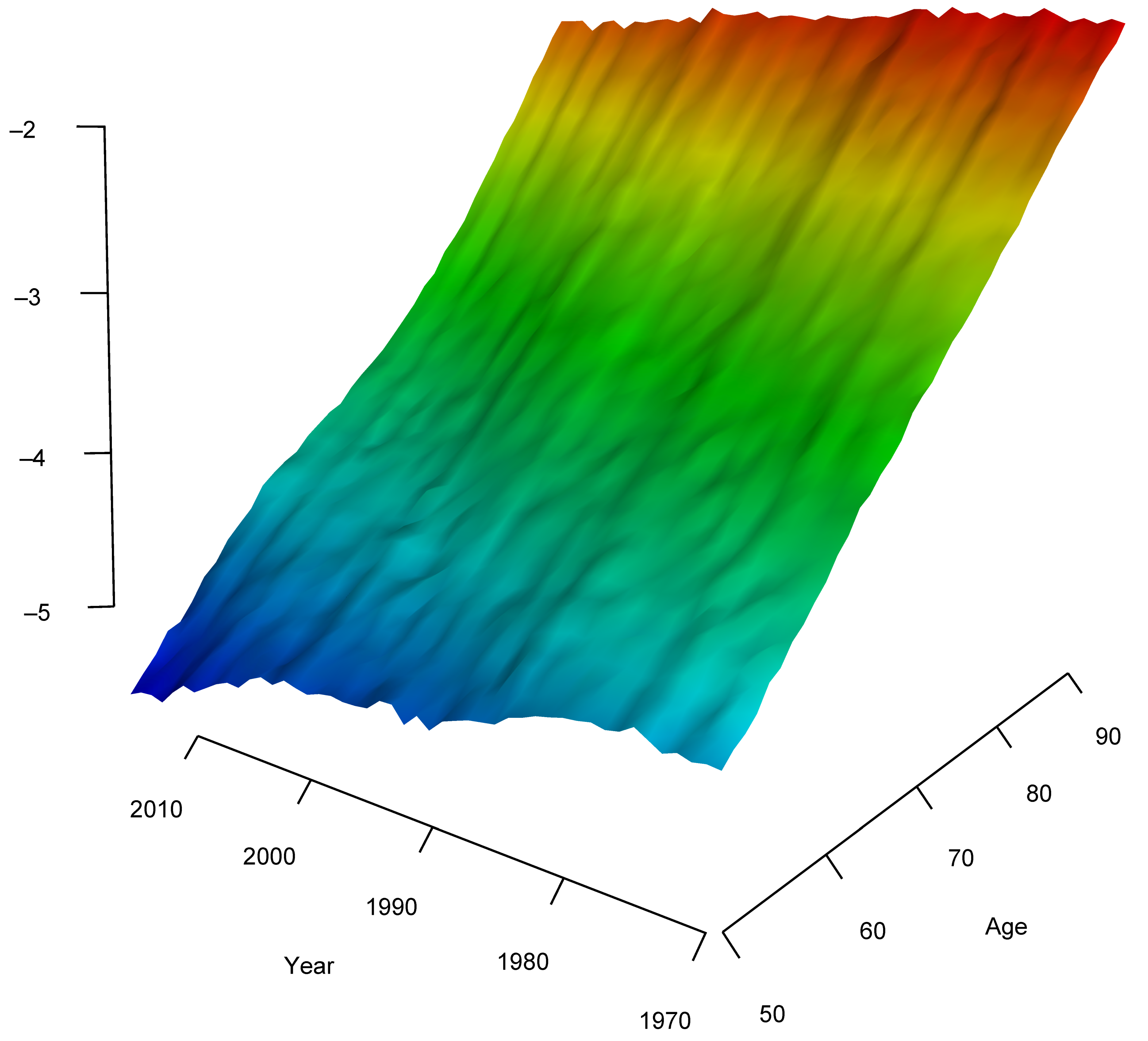
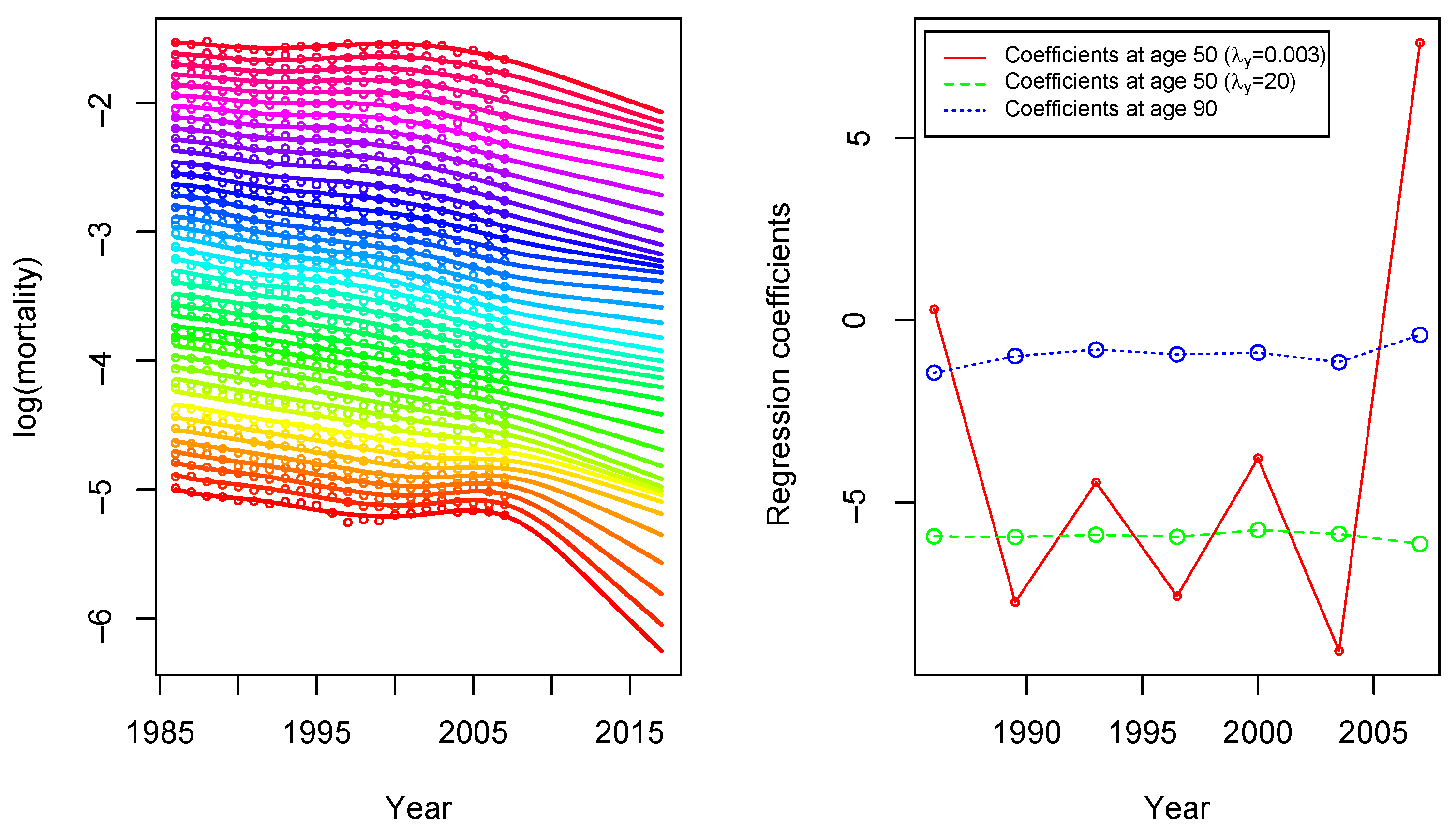
5.1. Smoothing and Forecasting Central Death Rates for France
5.2. Comparison with Standard Age-Period-Cohort Mortality Models
- The RH model is very sensitive to the fitted period. The model can go from the worst to the best model (cf. USA) and from the best to the worst model (cf. Belgium). Cairns et al. (2011) already pointed out that lack of robustness in this model as parameter estimates jump to a qualitatively different solution when we use more data.
- The regularized model and the Lee-Carter model appear to be reasonably robust relative to changes in the period of data used either in terms of MAE values or ranking positions. In particular, models without cohort effects tend to be more robust towards the sample data used as they do not require the projections of cohort terms.
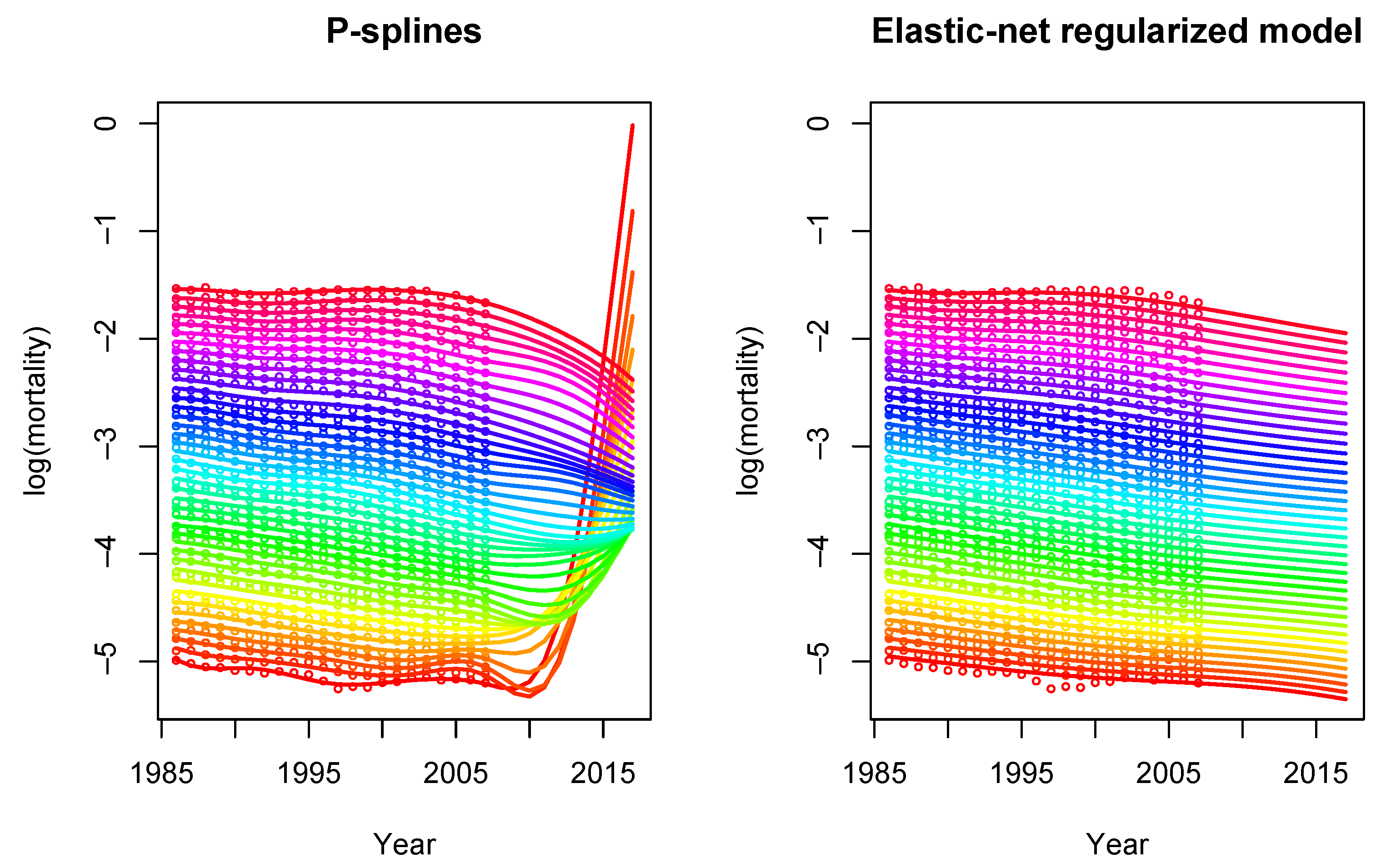
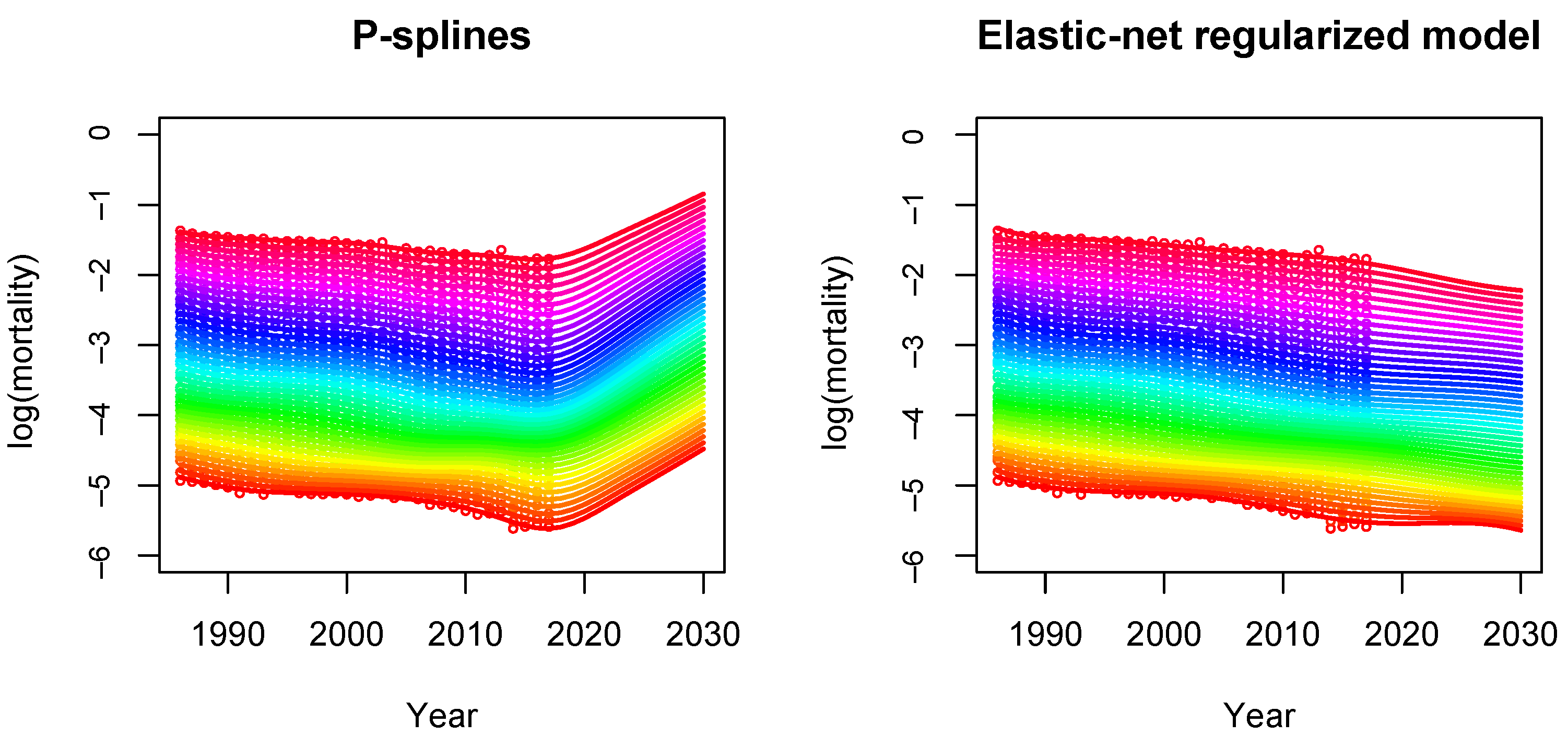
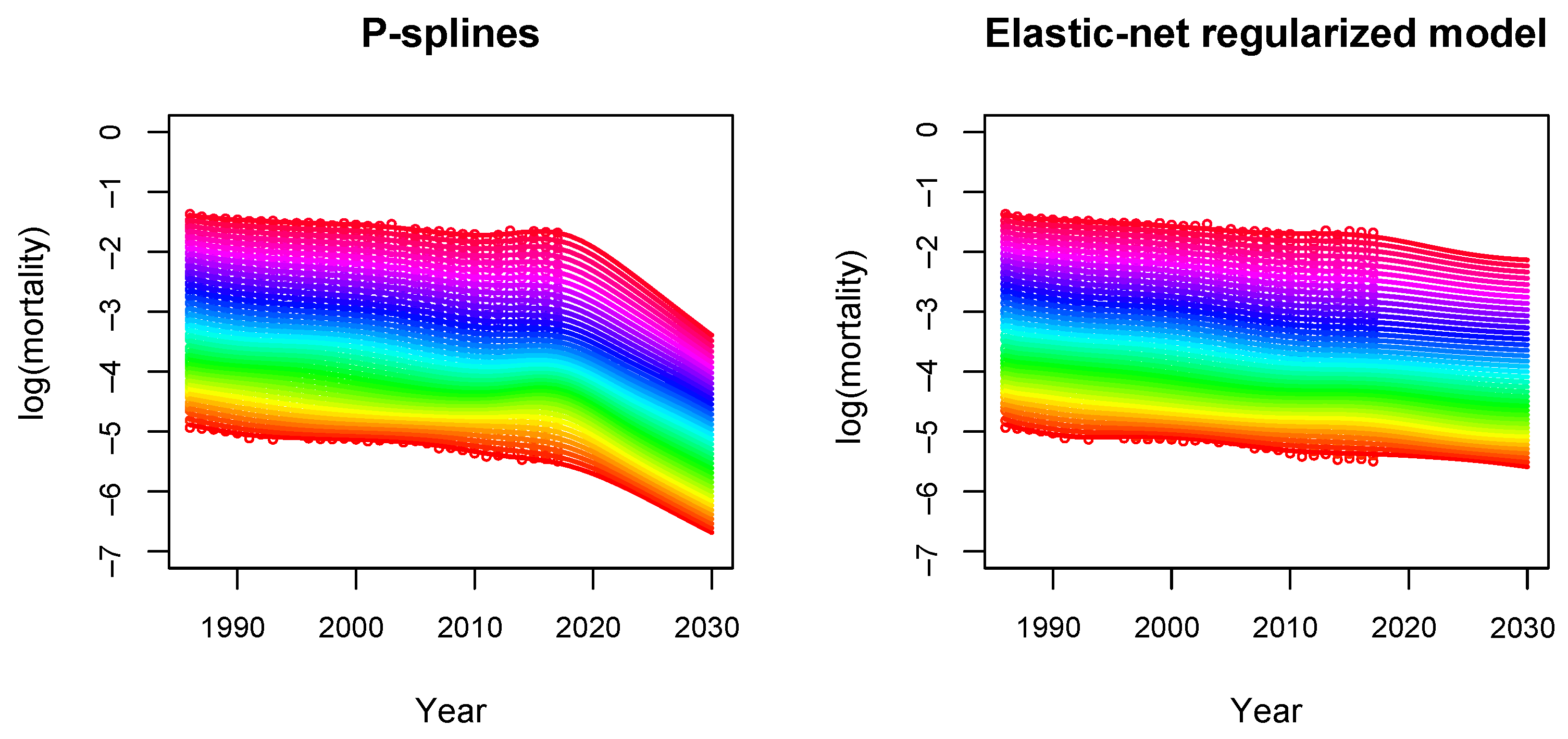
5.3. Comparison with the P-Spline Model
- The basis: In the P-spline model, the basis consists of cubic B-splines, which are bell-shaped curves composed of smoothly joined polynomial pieces of degree 3. By construction, B-splines are defined in a local manner, i.e. each B-spline is non-zero only in a certain neighborhood of the mortality surface. On the other hand, our regularized mortality model uses a global two-dimensional polynomial basis, see (6). More flexibility can be included either by increasing the number of knots in the B-spline approach or by increasing the degree order in the global polynomial basis.
- The penalty: To smooth the mortality surface and avoid overfitting, a penalty term on the regression coefficients is introduced. In the P-spline model, the following penalty matrix is defined:where and are the smoothing parameters in age and year, respectively, and and are second order difference matrices acting on the columns and rows of , respectively. Here, is the matrix of coefficients arranged in a matrix , where and are the dimensions of the bases spanning age and year, respectively. Smoothing parameters are chosen by minimizing the BIC. More details can be found in Currie et al. (2004).On the other hand, in our regularized model, the penalty term is given by the elastic-net regularization:where is the smoothing parameter and is the mixing parameter between the two types of penalization. An important difference is that both parameters are chosen in terms of prediction performance by cross-validation on out-of-sample data instead of in-sample criterion such as the BIC.
5.3.1. The Case of the Usa
5.3.2. The Case of COVID-19
5.4. Model Uncertainty and Prediction Intervals
6. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barrieu, Pauline, Harry Bensusan, Nicole El Karoui, Caroline Hillairet, Stéphane Loisel, Claudia Ravanelli, and Yahia Salhi. 2012. Understanding, modelling and managing longevity risk: Key issues and main challenges. Scandinavian Actuarial Journal 2012: 203–31. [Google Scholar] [CrossRef]
- Brouhns, Natacha, Michel Denuit, and Ingrid Van Keilegom. 2005. Bootstrapping the poisson log-bilinear model for mortality forecasting. Scandinavian Actuarial Journal 2005: 212–24. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, and Kevin Dowd. 2006. A two-factor model for stochastic mortality with parameter uncertainty: Theory and calibration. Journal of Risk and Insurance 73: 687–718. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, David Epstein, and Marwa Khalaf-Allah. 2011. Mortality density forecasts: An analysis of six stochastic mortality models. Insurance: Mathematics and Economics 48: 355–67. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, David Epstein, Alen Ong, and Igor Balevich. 2009. A quantitative comparison of stochastic mortality models using data from england and wales and the united states. North American Actuarial Journal 13: 1–35. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David P. Blake, Amy Kessler, and Marsha Kessler. 2020. The Impact of COVID-19 on Future Higher-Age Mortality. Available online: https://ssrn.com/abstract=3606988 (accessed on 19 May 2020).
- Camarda, Carlo G. 2012. Mortalitysmooth: An r package for smoothing poisson counts with p-splines. Journal of Statistical Software 50: 1–24. [Google Scholar] [CrossRef]
- Currie, Iain D. 2016. On fitting generalized linear and non-linear models of mortality. Scandinavian Actuarial Journal 2016: 356–83. [Google Scholar] [CrossRef]
- Currie, Iain D, Maria Durban, and Paul HC Eilers. 2004. Smoothing and forecasting mortality rates. Statistical Modelling 4: 279–98. [Google Scholar] [CrossRef]
- Doukhan, Paul, Denys Pommeret, Joseph Rynkiewicz, and Yahia Salhi. 2017. A class of random field memory models for mortality forecasting. Insurance: Mathematics and Economics 77: 97–110. [Google Scholar] [CrossRef]
- Doukhan, Paul, Joseph Rynkiewicz, and Yahia Salhi. 2020. Optimal Neighborhoods Selection for AR-ARCH Random Fields with Application to Mortality. Available online: https://hal.archives-ouvertes.fr/hal-02455803 (accessed on 1 November 2020).
- Friedman, Jerome, Trevor Hastie, and Rob Tibshirani. 2010. Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software 33: 1. [Google Scholar] [CrossRef]
- Guibert, Quentin, Olivier Lopez, and Pierrick Piette. 2019. Forecasting mortality rate improvements with a high-dimensional var. Insurance: Mathematics and Economics 88: 255–72. [Google Scholar] [CrossRef]
- Gylys, Rokas, and Jonas Šiaulys. 2020. Estimation of uncertainty in mortality projections using state-space lee-carter model. Mathematics 8: 1053. [Google Scholar] [CrossRef]
- Haberman, Steven, and Arthur Renshaw. 2011. A comparative study of parametric mortality projection models. Insurance: Mathematics and Economics 48: 35–55. [Google Scholar] [CrossRef]
- Hainaut, Donatien. 2012. Multidimensional lee–Carter model with switching mortality processes. Insurance: Mathematics and Economics 50: 236–46. [Google Scholar] [CrossRef]
- Human Mortality Database. 2019. University of California, Berkeley (Usa) and Max Planck Institute for Demographic Research (Germany). Available online: www.mortality.org (accessed on 18 June 2020).
- Hunt, Andrew, and David Blake. 2014. A general procedure for constructing mortality models. North American Actuarial Journal 18: 116–38. [Google Scholar] [CrossRef]
- Hunt, Andrew, and Andrés M Villegas. 2015. Robustness and convergence in the lee–carter model with cohort effects. Insurance: Mathematics and Economics 64: 186–202. [Google Scholar] [CrossRef]
- Koissi, Marie-Claire, Arnold F Shapiro, and Göran Högnäs. 2006. Evaluating and extending the lee–Carter model for mortality forecasting: Bootstrap confidence interval. Insurance: Mathematics and Economics 38: 1–20. [Google Scholar] [CrossRef]
- Kyung, Minjung, Jeff Gill, Malay Ghosh, and George Casella. 2010. Penalized regression, standard errors, and bayesian lassos. Bayesian Analysis 5: 369–411. [Google Scholar] [CrossRef]
- Lee, Ronald D., and Lawrence R. Carter. 1992. Modeling and forecasting us mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar]
- Lockhart, Richard, Jonathan Taylor, Ryan J. Tibshirani, and Robert Tibshirani. 2014. A significance test for the lasso. Annals of Statistics 42: 413. [Google Scholar] [CrossRef]
- Lovász, Enrico. 2011. Analysis of finnish and swedish mortality data with stochastic mortality models. European Actuarial Journal 1: 259–89. [Google Scholar] [CrossRef]
- Milidonis, Andreas, Yijia Lin, and Samuel H. Cox. 2011. Mortality regimes and pricing. North American Actuarial Journal 15: 266–89. [Google Scholar] [CrossRef]
- Millossovich, Pietro, Andrés M Villegas, and Vladimir K. Kaishev. 2018. Stmomo: An r package for stochastic mortality modelling. Journal of Statistical Software 84. [Google Scholar] [CrossRef]
- Pitacco, Ermanno, Michel Denuit, Steven Haberman, and Annamaria Olivieri. 2009. Modelling Longevity Dynamics for Pensions and Annuity Business. Oxford University Press: Oxford, UK. [Google Scholar]
- Renshaw, Arthur E., and Steven Haberman. 2006. A cohort-based extension to the lee–Carter model for mortality reduction factors. Insurance: Mathematics and Economics 38: 556–70. [Google Scholar] [CrossRef]
- Renshaw, Arthur E., and Steve Haberman. 2008. On simulation-based approaches to risk measurement in mortality with specific reference to poisson lee–Carter modelling. Insurance: Mathematics and Economics 42: 797–816. [Google Scholar] [CrossRef]
- Tibshirani, Ryan J., Alessandro Rinaldo, Rob Tibshirani, and Larry Wasserman. 2018. Uniform asymptotic inference and the bootstrap after model selection. The Annals of Statistics 46: 1255–87. [Google Scholar] [CrossRef]
- Zou, Hui, and Trevor Hastie. 2005. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 67: 301–20. [Google Scholar] [CrossRef]
| 1. | This type of analysis was for instance performed in Section 6.1.1. in Cairns et al. (2006) or Section 3.3 in Haberman and Renshaw (2011). |
| 2. | Moreover, we consider the orthogonal polynomial basis through the polym R function to ensure numerical stability. |
| 3. | The estimated improvement rate on crude death rates is very noisy. The use of smoothed death rates allows one to have a more regular pattern for the improvement rate. |
| 4. | Except Hong Kong, as data from Hong Kong are only available from 1986 onwards. |
| Mortality Model | Dynamics |
|---|---|
| Lee–Carter (LC) | |
| Cairns–Blake–Dowd (CBD) | |
| Age-Period-Cohort (APC) | |
| Renshaw–Haberman (RH) | |
| M7 |
| Mean Absolute Error (10-Year Forecast) | ||||||
|---|---|---|---|---|---|---|
| USA | UK | France | BEL | JAP | HKG | |
| LC | 0.00369 | 0.00225 | 0.00120 | 0.00246 | 0.00213 | 0.00265 |
| CBD | 0.00279 | 0.00205 | 0.00505 | 0.00388 | 0.00313 | 0.00261 |
| APC | 0.00161 | 0.00251 | 0.00206 | 0.00338 | 0.00250 | 0.00168 |
| RH | 0.00368 | 0.00463 | 0.00233 | 0.00308 | 0.00194 | 0.00275 |
| M7 | 0.00222 | 0.00152 | 0.00259 | 0.00200 | 0.00097 | 0.00143 |
| Reg | 0.00194 | 0.00212 | 0.00274 | 0.00244 | 0.00267 | 0.00214 |
| Mean Absolute Error (10-Year Forecast) | |||||
|---|---|---|---|---|---|
| USA | UK | France | BEL | JAP | |
| LC | 0.00432 | 0.00318 | 0.00147 | 0.00345 | 0.00213 |
| CBD | 0.00262 | 0.00193 | 0.00490 | 0.00335 | 0.00355 |
| APC | 0.00201 | 0.00265 | 0.00261 | 0.00370 | 0.00328 |
| RH | 0.00197 | 0.00313 | 0.00293 | 0.00622 | 0.00167 |
| M7 | 0.00407 | 0.00195 | 0.00227 | 0.00142 | 0.00298 |
| Reg | 0.00288 | 0.00307 | 0.00262 | 0.00287 | 0.00310 |
| Mean Absolute Error (10-Year Forecast) | ||||||
|---|---|---|---|---|---|---|
| USA | UK | France | BEL | JAP | HKG | |
| P-splines | 0.01405 | 0.00486 | 0.00232 | 0.00695 | 0.00384 | 0.00271 |
| Regularized | 0.00194 | 0.00212 | 0.00274 | 0.00244 | 0.00267 | 0.00214 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barigou, K.; Loisel, S.; Salhi, Y. Parsimonious Predictive Mortality Modeling by Regularization and Cross-Validation with and without Covid-Type Effect. Risks 2021, 9, 5. https://doi.org/10.3390/risks9010005
Barigou K, Loisel S, Salhi Y. Parsimonious Predictive Mortality Modeling by Regularization and Cross-Validation with and without Covid-Type Effect. Risks. 2021; 9(1):5. https://doi.org/10.3390/risks9010005
Chicago/Turabian StyleBarigou, Karim, Stéphane Loisel, and Yahia Salhi. 2021. "Parsimonious Predictive Mortality Modeling by Regularization and Cross-Validation with and without Covid-Type Effect" Risks 9, no. 1: 5. https://doi.org/10.3390/risks9010005
APA StyleBarigou, K., Loisel, S., & Salhi, Y. (2021). Parsimonious Predictive Mortality Modeling by Regularization and Cross-Validation with and without Covid-Type Effect. Risks, 9(1), 5. https://doi.org/10.3390/risks9010005






