Abstract
In this paper, we discuss a generalization of the collective risk model and of Panjer’s recursion. The model we consider consists of several business lines with dependent claim numbers. The distributions of the claim numbers are assumed to be Poisson mixture distributions. We let the claim causes have certain dependence structures and prove that Panjer’s recursion is also applicable by finding an appropriate equivalent representation of the claim numbers. These dependence structures are of a stochastic non-negative linear nature and may also produce negative correlations between the claim causes. The consideration of risk groups also includes dependence between claim sizes. Compounding the claim causes by common distributions also keeps Panjer’s recursion applicable.
1. Introduction
The aggregation of risks in a portfolio is an important component in both insurance mathematics and financial risk management such as credit risk, operational risk, and insurance risk. In the banking industry, risk management becomes more and more important with the introduction of the Basel II and Basel III accords. For this purpose, there are several portfolio risk models, the CreditRisk model (introduced by Credit Suisse First Boston (1997)) being a particular example with a lot of practical features. It does not require many assumptions and enables the recursive and exact computation of the loss distribution, i.e., it is not necessary to apply Monte Carlo methods that introduce a stochastic error. The collected contributions in Gundlach and Lehrbass (2004) offer a wide overview of CreditRisk and related results. However, a shortcoming of CreditRisk is the assumed independence of the default causes. Deshpande and Iyer (2009) also consider a dependence model for default causes in the usual CreditRisk model that comprises linear combinations of risk factors and is a generalization of Giese (2004). However, both models do not introduce negative correlation. Instead, we consider a more general linear dependence structure in an extension of the CreditRisk model that allows us to model negative correlation between default numbers and we can also comprise a stochastic component in the linear dependence. Moreover, we consider risk groups that model joint defaults (for both claim numbers and claim sizes).
Insurance companies have to comply with Solvency II requirements, and the model we consider is capable of aggregating and quantifying risks and can thus be used to determine the minimal capital requirements, which is the first pillar of Solvency II. There is also an increasing demand to reflect dependencies between the risks. Our model can be also used to aggregate operational risk.
In the (extended) CreditRisk model as in the collective risk model, it is necessary to calculate the distribution of a random sum. In risk management, the collective risk model is diversified into several risk clusters or lines of business and thus random sums where each claim number is driven by a claim cause. Thus, we consider a sum of several collective risk models. We should note that the term claim is used in an insurance context, whereas the term default is used in the credit risk context. We will use both notions interchangeably. Since we model claim numbers by Poisson mixture distributions, it is meaningful to speak of claim cause intensities as the claim causes are modelled by the mixing distributions (and accordingly default causes). Hence, we consider the random sum
where are independent sequences of independent and identically distributed random variables for each and are -valued random variables independent of .
For independent and independent that are independent of , Panjer’s recursion is the main mathematical tool to evaluate the distribution of the random sum in Equation (1). For the rest of this paper, we assume that are the natural numbers including zero, i.e., . The distribution of an -valued random variable N, denoted by , belongs to a Panjer class with and if and
Let be a sequence of -valued random variables. If and , then, according to (Hess et al. 2002, Corollary 4.3), the distribution is given by the recursion
for all with initial condition
which is the probability-generating function of the distribution of N at . The recursive evaluation of such compound distributions was introduced to actuarial science by Panjer (1981) and extended by Willmot and Panjer (1987). The distributions belonging to a Panjer class were identified by Sundt and Jewell (1981); Willmot (1988), and Hess et al. (2002). Gerhold et al. (2010) treat questions of numerical stability of Panjer’s recursion. Sundt and Vernic (2009) contributed extensively to this topic.
Note also that Panjer’s recursion can be generalized to multivariate claim sizes, cf. Sundt (1999), and the assumptions on the claim sizes can be weakened to exchangeability, cf. Hashorva (2011). Further details can be found in Rudolph (2014). For simplicity of the presentation, we concentrate on the dependence between the claim numbers and allow dependence between the individual losses only within risk groups, cf. Definition 2 below.
There are further approaches analyzing portfolio risk. The paper of Soltes and Danko (2017) proposes to create a portfolio with minimal risk. In Zoričák et al. (2019), we find an interesting approach to predict bankruptcy for imbalanced datasets by one-class classification methods. A general paper is proposed by Jajuga (2016) to introduce model risk in finance from an investor’s perspective, this is a complement to the modeling of risk in this paper. An analysis of real data with respect to dependencies and predictability of stock market returns is given in Fabiánová and Glova (2015).
The remainder of this paper is organized as follows: in Section 2, we introduce a non-negative linear dependence structure with a stochastic component of the claim cause intensities between risk factors and prove alternative representations of the claim numbers with the same joint distribution allowing for the application of Panjer’s recursion. It should be pointed out that this structure also allows for negative dependence, see Example 1. In addition, many models comprise dependence structures, but then the question arises how to calculate the distribution.
In Section 3, we consider a different dependence structure: we mix the default cause intensities with common mixture distributions by letting a parameter of the distribution be random. Then, we prove that an alternative representation with the same joint distribution exists that also allows for an application of Panjer’s recursion.
Finally, in Section 4, we conclude with some interesting examples that show that the choice of correlation and of the mixing distribution has an impact on the distribution of the total portfolio loss.
In the Appendix A, we recall some definitions and present a few useful results on compound and mixture distributions and the corresponding probability-generating functions. These results are important for the presentation of our results.
2. Construction of Dependent Claim Numbers by Linear Combinations
In this section, we present one of our major results. The starting point is the following. In an extension of the CreditRisk model to be found in Gerhold et al. (2010), the authors consider a random claim number , where, for each , the claim number has a Poisson mixture distribution and the mixing random variable is a gamma-distributed claim cause intensity . They only stipulate that the claim numbers are conditionally independent given . The conditional distribution of the random claim numbers given is assumed to satisfy
where . The claim cause intensities are assumed to be independent.
In contrast, we develop a generalization of this model by admitting dependence between risk group specific claim cause intensities. Dependent claim cause intensities provide the dependence structure. We construct dependence structures by linear combinations of several non-negative risk factors. These dependence structures are chosen stochastically allowing for risk groups. This means that risk clusters (or lines of business) within one risk group default together, i.e., the default of one risk cluster will immediately imply the default of all the other risks in this risk group. In this setting, we can also relax the assumption of gamma-distributed risk factors and consider -tempered -stable distributions too.
In the course of our considerations, we need the following definition of a multivariate Poisson distribution which is motivated in Lindskog and McNeil (2003) and can be also found in (Sundt and Vernic 2009, Chp. 20.1) with a different notation.
Definition 1.
Let , a collection of subsets of with , and Poisson parameters. For each , define the vector by
Let be independent random variables with for every . Then, the distribution of the -valued random vector
is called the m-variate Poisson distribution, we use the notation MPoisson().
This notation allows us to consider risk groups. In the credit risk interpretation, the obligors in a non-empty group default together with intensity , but independently of the other groups. An additional form of dependence of the claim numbers can come from the linear and stochastic dependence of the intensities, see Assumption 1 below.
Remark 1.
We consider individual claim sizes to take values in a vector space V. Throughout the paper, the reader may assume that V equals or a finite-dimensional Euclidean space and that . Figure 1 below is a numerical illustration with . However, unless specified otherwise, all theoretical results hold for a separable real Banach space V with topological dual .
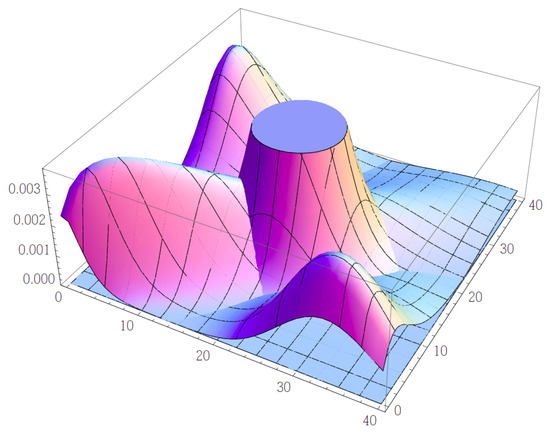
Figure 1.
Highly smoothed probability mass functions of the -valued portfolio loss corresponding to Figure 2 for the Poisson case (central truncated graph), the comonotone case (with a hump along the diagonal) and the case of (two symmetric humps near the corners). We take . The (group) claim sizes equal and in these cases, i.e., and .
Remark 2.
Multi-variate claim sizes have numerous applications, let us mention some examples:
- (a)
- A two-component model is of interest for budgeting purposes: The first component represents the loss payments in the current budget period, the second one the actuarial reserves for later claim payments.
- (b)
- In an insurance context, the components can represent different types of claim payments. For a portfolio of health insurance contracts, this can be costs of medical treatments and allowances for missing income of the insured. For a portfolio of personal liability or automobile collision insurances, these can be claims for bodily injuries and property damages.
- (c)
- For liquidity considerations, the components can refer to the time period when a claim occurs or a counterparty defaults. Furthermore, the size of the loss given default can depend on the time of the default, in particular when a loan or a mortgage is amortized during its life span and not at maturity.
- (d)
- In the context of stochastic claims reserving (see Wüthrich and Merz (2008) for a textbook presentation), the components can represent the development years. Here, the default probability (or intensity) refers to the claims originating from the initial insured period; the claims may be reported at a later year and payments may be spread out during the remaining years of the model.
Corresponding to Definition 1, we generalize the compound Poisson distribution (see Definition A1(b)) to the m-variate case.
Definition 2.
Suppose the random variable N has an m-variate Poisson distribution with representation (6). Let V be a vector space, and , where each is a probability distribution on such that for all where
Let be independent i.i.d. sequences of -valued random variables with for all independent of . Then, the distribution of
is called compound m-variate Poisson distribution .
Remark 3.
If and , i.e., the distribution concentrated in given by Equation (5), then . The distribution describes the random losses vector of the obligors in g defaulting together.
As a direct consequence of the stochastic representation in Equation (7), the independence of and the characteristic function for compound Poisson distributions, we obtain the following lemma.
Lemma 1.
The characteristic function of a random vector S with the compound m-variate Poisson distribution is given by
Remark 4.
For notational convenience, we write for and analogously for other distributions in the following.
To state the additivity of compound m-variate Poisson distributions in Lemma 2 below, the following notation is useful:
Definition 3.
Let be probability distributions on . Then, their convex combination with relative weights is a probability distribution on defined in terms of by
Remark 5.
If and if the joined support of the distributions is a finite or countably infinite set like , then can be computed in a numerically stable way by calculating, for each atom in the support, the convex combination of the corresponding probabilities of the atom.
Lemma 2.
Let and let for be independent random vectors with compound m-variate Poisson distributions according to Definition 2, where and . Then, with set of groups , intensities and group claim size distributions given by
respectively, where for .
Proof.
Using the independence of and Lemma 1, it follows with some rearrangement that
Using Definition 3, Equations (9) and Remark A1, the result follows. □
Remark 6.
Note that Lemma 2 implies the infinite divisibility of the compound m-variate Poisson distribution.
We now provide the conditional characteristic function of the distribution of a compound m-variate Poisson random vector that is mixed with a random vector of dependent intensities, whose components naturally have to be non-negative. For simplicity, we first introduce an assumption on the dependence scenario.
Assumption 1.
Let be an arbitrary finite set, , and assume with and . Let for and let J be a random variable with values in . Define the random matrix . Let be non-negative random variables and let be a non-negative constant. Define for .
Remark 7.
The random variable J can be interpreted as selecting a dependence scenario for claim cause intensities . Accordingly, the random variables can be interpreted as non-idiosyncratic risk factors, the constant as idiosyncratic “risk factor” or idiosyncratic component.
Lemma 3.
Let Assumption 1 be satisfied, let for and , and
Then, the characteristic function of the conditional distribution of the random vector S given satisfies
Proof.
As a consequence of Equation (10), the representation for in Assumption 1 and the characteristic function given in Lemma 1 the result follows. □
Remark 8.
Remark 9.
In Lemma 3, the non-negative parameters with and might look like redundant notation. However, when taking this framework as an extension of the CreditRisk model, these parameters are useful to control the expected value for since in the CreditRisk we have that only models the structure of dependence. The dependence of of is sustained to also have the possibility to model characteristics of scenarios.
Remark 10.
This model can be also considered over a time-horizon. Thus, it can be also used to model the impacts of one risk gradually spreading onto other risks. Therefore, we need to introduce sequences of independent i.i.d. sequences of -valued random variables with for all with and a risk group with respect to time. For each time step, we need to define corresponding risk groups to model a gradual spread. These risk groups need to be constructed according to potential distribution. A further result on such a multi-period model can be found in (Rudolph 2014, Lemma 6.21).
2.1. Alternative Representation
If we allow for dependent claim cause intensities and risk groups, the independence between the random sums for is lost, hence a convolution is not applicable. While the independence is also lost in our setting, it is nevertheless possible to find an adequate representation of the claim numbers with the same distribution such that a variant of Panjer’s recursion can be applied, as will be seen later. These claim cause intensities may be also considered as a multivariate gamma distribution. There are several approaches to construct multivariate gamma distributions, and one of them includes a linear dependence between the marginal distributions, cf. (Johnson et al. 2000, Chp. 48.3.4).
Based on Lemma 3, we derive a theorem that provides us with a general structure of a stochastically chosen non-negative linear dependence scenario:
Theorem 1.
Let the assumptions of Lemma 3 be satisfied. On the other hand, for every , consider independent sequences of i.i.d. random variables , independent of , such that, for all ,
where with satisfies the condition
for each , , and . Let be random variables conditionally independent given which satisfy
Assume further that and with are independent. Let be independent sequences for with identical distribution as for independent of all previous random variables. Finally, define the -valued random vector M by
Then, and have the same distribution.
Proof.
For the proof, we apply Remark A1. By Lemma 3, the characteristic function of the distribution of is given by Equation (11).
Now consider the characteristic function of the distribution of the random vector . By partitioning J, we get for all ,
Using the fact that the sequences and are i.i.d. and for independent of and for each and that has the distribution given in Equation (13) and thus applying the law of total probability, we observe that
Using the conditional independence of the random variables given for and Equation (15),
Remark 11.
The random sums for do not in general have a counting distribution in a Panjer class because the distributions of the random variables for and are not generally in a Panjer class.
Remark 12.
In the above theorem, the case for a and an has not been considered separately. If such a sum is zero, then it follows that . Hence, the corresponding term in the sum (16) can be omitted. Thus, the distribution of may be chosen arbitrarily.
Remark 13.
Of course, there are also other methods to construct dependence between claim cause intensities: Luo and Shevchenko (2010) propose in a bivariate set-up to model the dependence by a t-copula. They further use simulation and calibration methods. However, in such a case, recursion methods do not seem to be possible. In contrast, this is possible with our approach.
Remark 14.
Using this random and non-negative linear dependence and the concept of risk groups, we are able to compute the expectations and covariances for the claim cause intensities and hence claim numbers. Recall that for . Let J and be independent. We observe for
and, if the risk factors are in and uncorrelated,
Thus, we compute the covariance between and for
By the Poisson mixture distribution of the claim numbers given in Equation (12), the expectation of for is
For in , the variance of for is given by
and the covariance between and for with is
due to the conditional independence of the given and the conditional distribution of .
It might not be obvious from this remark how this construction may also provide negative dependence. This is different from other dependence modelling, since it usually only comprises positive dependence. We give the following example (see also Section 4.1 below).
Example 1.
Let Assumption 1 be satisfied and assume . Let and be two non-negative and non-degenerate risk factors, possibly dependent with unbounded support. Then, let and and for and . Consider a -valued random variable J independent of and
Then, the claim cause intensities are given by and . Thus,
because and J and are independent. Therefore, with this antithetic choice, we obtain negative correlation between the claim cause intensities since the expected values are positive. Let with be independent of and with . Consequently, the equivalent representations are given by Equation (16) with
because and are -degenerate distributions. Hence, the total loss is . If we assume to be gamma-distributed for , then we can apply a simplified version of Calculation Method 1 given below.
If we choose and for gamma-distributed and , it is possible to obtain every value in as correlation by an appropriate choice of the corresponding variances, see also (Schmock 2020, Example 6.38, Version March 25th 2020). In order to obtain perfect negative correlation, the risk factors need to have variance equal to zero, i.e., they have to be degenerate.
2.2. Evaluation of the Loss Distribution
In this section, we give an algorithm that shows how Panjer’s recursion is applicable in our model with the dependence structure given in this section. It might be suggested that the calculation of the distribution of the total loss arising from given in Equation (7) with conditional representation specified in Lemma 3 requires at least n convolutions (one for each risk factor). However, our algorithm, based on the ideas of (Gerhold et al. 2010, sct. 5.5), circumvents these convolutions by an iterated application of Panjer’s recursion (cf. Equations (23) and (26) below) and a convex combination (cf. Equation (24) below). In applications of the algorithm to gamma-distributed risk factors, we use the well-known fact that a negative binomial distribution is a compound Poisson distribution where the severity distribution is a logarithmic distribution, cf. also Ammeter (1948). The convex combination uses the fact that the convolution of compound Poisson distributions is again a compound Poisson distribution.
We now adapt the algorithm in (Gerhold et al. 2010, sct. 5.5) to the evaluation of the total loss in Equation (7).
Calculation Method 1.Consider the setting of Theorem 1 and assume in addition that are independent and have infinitely divisible distributions. Then, are independent for each . An application of Theorem 1 yields for the total loss given as the sum of the m components in Equation (7):
where with as well as with and are independent sequences of i.i.d. -valued random vectors with corresponding distribution . To calculate the distribution of the right-hand side of Equation (20) , we start with the inner sum and define the distributions of the group losses by
where . If the components of are independent, then can be computed by convolution. For certain classes of multivariate distributions (like the multivariate logarithmic or negative multinomial distribution), the distribution of the sum of its components is known in closed form. In any case, we assume that is known or can be computed for every . Since the risk group g in the inner sum of the right-hand side of Equation (20) is selected with probability determined by Equation (14), we obtain the discrete mixture distribution
for each and , see Definition 3.
By (Sundt and Vernic 2009, Corollary 4.1) and the infinite divisibility of the distributions of , the random variable with conditional distribution specified in Equation (15) has a compound Poisson distribution, cf. Definition A1(b), hence there exist a Poisson intensity and a distribution on such that for every and ; see Section 2.3 below for more details and examples. Define the compound distribution
see Definition A1(a). If is a Panjer distribution and is concentrated on , then can be evaluated with Panjer’s recursion, which is numerically stable in many cases, cf. (Gerhold et al. 2010, Theorem 4.5). For each , define the discrete mixture distribution
and the Poisson intensity
Then,
The final step is to calculate the discrete mixture distribution
2.3. Examples for Distributions of the Risk Factors
2.3.1. Gamma Distribution
Remark 15.
As a specific case in Calculation Method 1, fix a risk factor and assume that has a gamma distribution, so with shape parameter and rate parameter . Define, for ,
2.3.2. Generalized Tempered Stable Distribution
We consider another and more general case as usual in the CreditRisk model that has already been considered in Gerhold et al. (2010). We allow one or several of the risk factors to have a -tempered -stable distribution instead of a gamma distribution. This is a very flexible family of distributions and also allows for modelling of heavy tails. Stable distributions are denoted by with , scale parameter , skewness parameter and shift parameter , cf. e.g., (Samorodnitsky and Taqqu 1994, p. 9). If , , and , then the support of is on the non-negative real line (cf. (Samorodnitsky and Taqqu 1994, p. 15)). We can generalize such a distribution by a change of measure of as in (Gerhold et al. 2010, sct. 5.3) by introducing additionally a tempering parameter and and to obtain the distribution function
In case , this is a -tempered -stable distribution (cf. (Rosiński 2007, Theorem 4.1)).
In this context, it is interesting to introduce the notation of the extended negative binomial distribution, cf. (Hess et al. 2002, p. 287):
Definition 4.
Let , , and . A random variable N has the extended negative binomial distribution if for and
where the generalized binomial coefficient is given by
The probability-generating function of this distribution for the important case is given by
cf. e.g., (Gerhold et al. 2010, eq. (2.3) with an adjustment to our notation.
Remark 16.
As another case in Calculation Method 1, fix a risk factor and assume that has a τ-tempered α-stable distribution, i.e., . Then, the distribution of the random variables for in Equation (15) can be written as a compound Poisson distribution and the application of (Gerhold et al. 2010, Lemma 5.10) provides a means of converting this distribution into a random sum with distributions in a Panjer class, namely
where
with parameters
and
Then, Panjer’s recursion can be applied using (Gerhold et al. 2010, Theorem 4.5 and Algorithm 5.12) to this random sum. Altogether, Calculation Method 1 can be applied.
Remark 17.
In case the distribution of the risk factors is given in Equation (30) with , it is possible to apply (Gerhold et al. 2010, Algorithm 5.18).
3. Dependent Claim Numbers by Continuous Mixtures
In Section 2, we constructed dependence between the group-specific claim cause intensities by random non-negative linear combinations of the risk factors and by joint claims within risk groups. Now, we construct dependence between the risk factors by continuous mixture distributions. By choosing and A the identity matrix, we can have this type of dependence directly. We turn one parameter of the distributions of the risk factors into a random variable, and, if it appears in several risk factors, we obtain dependence. As in Section 2, the independence between the components of the sum S given in Equation (7) is lost and there is also a need for an alternative to convolutions. Hence, we establish an alternative representation of the claim numbers with equal joint distribution if the claim cause intensities have either a gamma distribution or a -tempered -stable distribution.
3.1. Continuous Compounding
In this subsection, we mix the risk factors with random variables that do not themselves have a mixture distribution. We consider a rather general result on mixture distributions to construct dependent claim numbers. As in the previous section, we let the group-specific claim cause intensities be random and non-negatively linearly dependent.
Theorem 2.
Let Assumption 1 be satisfied. Let be strictly positive random variables. Let for all and for all and . Then, we define two -valued random vectors S and M as follows:
- (a)
- Let be random variables with conditional gamma distributions, conditionally independent given and let their shape parameters be randomized, i.e., for eachThen, let
- (b)
- For each , consider random variables , which are conditionally independent given , such that for eachwith given by Equation (28) and a random variable independent of such thatLet with be independent double-indexed sequences independent of , consisting of i.i.d. random vectors such that forwith as in Theorem 1. Let further with be independent sequences, independent of , consisting of i.i.d. random variables such thatcf. Definition A3. Let be independent double-indexed sequences for with identical distribution given by for independent of all previous random variables. Define the random vector M by
Then, and have the same distribution.
Remark 18.
We consider the same stochastic representation as in Remark 8 except for the conditional distribution of , which is given by
with as in Assumption A1.
Remark 19.
In setting (b) of Theorem 2, note that by Lemma A2 with and in that framework
but the representation (38) is more convenient for Algorithm 2 below.
Proof.
We apply Remark A1. Fix , . Let . First, we compute the characteristic function at of the distribution of . By an analogous argumentation as in the proof of Lemma 3, we obtain
Conditioning on , using the conditional independence of given and using Equation (33) and the Laplace transform of the gamma distribution yields
Now, consider the characteristic function at of the distribution of the random vector . Using the definition of M and partitioning J, we obtain
For each , using the fact that , , and for are i.i.d., independent, and independent of and that and are independent of gives
Conditioning on , using the conditional independence of given , the independence of of for each , and using Equations (34) and (35) provides
with
and for
where is the probability-generating function of the distribution of . By Equation (36) and the law of total probability, we obtain for
and by Equation (37) for
and for
In case for some with , it follows that , and we have
If , this implies , and we have
Altogether, we obtain
which completes the proof. □
Remark 20.
If for has a beta distribution, then the distribution of for and is a Poisson-beta distribution, also known as a general Waring distribution. (Hesselager 1996, Theorem 1, Example 3) provides a recursive algorithm for a compound distribution with such a counting distribution. Finally, an n-fold convolution becomes necessary. In this case, should be independent.
Now, we formulate a similar but different result to Theorem 2. Here, we consider -tempered -stable distributions as distributions for the claim cause intensities.
Lemma 4.
Let Assumption 1 be satisfied. Let be non-negative random variables and a non-negative constant and , and for each and for each and . Then, we define the two -valued random vectors S and M as follows:
- (a)
- Let be a non-negative constant and let be random variables with conditional τ-tempered α-stable distributions, conditionally independent given and let their parameters be random, i.e., for eachLet for . Then, let
- (b)
- For each , consider random variables which are conditionally independent given such that for eachwhere is given by Equation (31), and for each a random variable , which is independent of such thatLet further with be independent sequences independent of , consisting of i.i.d. random variables such thatfor where is given by Equation (32), and let . Let with be independent double-indexed sequences independent of and for , consisting of i.i.d. random variables such thatwith and satisfies . Let be independent double-indexed sequences for with identical distribution given by for independent of all previous random variables. Define the random vector M by
Then, and have the same distribution.
Remark 21.
We consider the same stochastic representation as in Remark 8 except for the conditional distribution of , which is given by
with as in Assumption A1.
Proof.
We apply Remark A1. Fix , . Let . First, we compute the characteristic function at of the distribution of . By an analogous argumentation as in the proof of Lemma 3, we obtain
Conditioning on , using the conditional independence of given and Equation (41) (and hence (Gerhold et al. 2010, eq. (5.25)) provides
Now consider the characteristic function at of the distribution of the random vector . Using the definition of M and partitioning J yields
For each , using that , , and are i.i.d. and independent of the random variables and and that are independent of and , we observe
By Equation (45) and due to the law of total probability, we obtain
Conditioning on , using the conditional independence of the random variables given and the independence of of for each and using Equations (42) and (43) yields
with
where we have used already Equation (44) for and simplified the term, and for
where denotes the probability-generating function of the distribution of . If for some , then, by Equation (44), and hence
Unfortunately, due to the parameter for , it is not possible to choose, as before, the random variables with a gamma distribution or a -tempered -stable distribution. By (Steutel and van Harn 2004, Example VI.12.8), is not even infinitely divisible if is gamma-distributed. It is only known that powers of -tempered -stable distributed random variables (then the distribution of is by (Steutel and van Harn 2004, Proposition VI.5.7) and (Steutel and van Harn 2004, Proposition VI.5.26) a generalized gamma convolution) are infinitely divisible if , cf. (Steutel and van Harn 2004, Theorem VI.5.18) and (Steutel and van Harn 2004, Proposition VI.5.19(i). If , then is only infinitely divisible if the corresponding characteristic function has no zeros (cf. (Lukacs 1970, Theorem 8.4.1)). Hence, we need to assume that has a gamma distribution or a -tempered -stable distribution.
3.2. Evaluation of the Loss Distribution
In a constellation such as in Theorem 2, the evaluation of the distribution of the random sum S is an adaptation of the algorithm in (Gerhold et al. 2010, sct. 5.5) under certain assumptions and slighty different from the other dependence scenario.
Calculation Method 2.Consider the setting of Theorem 2. In addition, assume that the random variables are independent. Furthermore, similar to the approach of (Giese 2004, sct. 10.2), assume that with shape parameter and rate parameter for every . We apply Theorem 2 and obtain for the total loss given as in Equation (7):
where with and with and are independent sequences of i.i.d. -valued random vectors with corresponding distribution . To calculate the distribution of the right-hand side of Equation (47), first define the group loss distribution by Equation (21) and then the discrete mixture distributions by the right-hand side of Equation (22) for each and .
In contrast to Calculation Method 1, the next step is to compute, for each , the compound logarithmic distribution
If the support of is contained in , then Panjer’s algorithm is applicable and numerically stable because Panjer for the case .
Let
Since have gamma distributions, it follows from Lemma A1 (with and in that framework) that
Hence, we can proceed as in Calculation Method 1, where we have to replace Equation (23) by
and then use Equations (24)–(27).
Remark 22.
It should be pointed out that the random variables need not be independent. This is crucial for the construction of dependence. For instance, we could let be independent random variables and a non-negative constant. Define another random matrix with an arbitrary finite set and for and K a -valued random variable. Then, let . Then, an application of Theorem 1 should be inserted because are not independent.
Remark 23.
The algorithms do not only work this way if and , respectively, are gamma-distributed. They also work if or have a τ-tempered α-stable distribution. By an application of (Gerhold et al. 2010, Lemma 5.10), the severity distribution of the corresponding compound Poisson distribution of with parameters given in 16 is an extended negative binomial distribution. Thus, apply (Gerhold et al. 2010, Algorithm 5.12). A special case of this class of distributions is e.g., the inverse Gaussian distribution, which has also been described in (Sundt and Vernic 2009, p. 91). (Gerhold et al. 2010, Example 5.21) also present how to evaluate such a distribution.
Remark 24.
Using the convex combination for the evaluation of the portfolio distribution provides a claim size with a logarithmic distribution that might require high computational effort in the evaluation of Panjer’s recursion. This convex combination also requires a high computational effort in the evaluation of Panjer’s recursion with the Poisson distribution. However, this approach is preferable since the evaluation of Panjer’s recursion for a negative binomial distribution followed by several convolutions clearly demands more resources.
4. Numerical Illustration
In this section, we give examples of the impacts of different dependence structures in our model on the distribution of the portfolio loss. More precisely, this means we consider the impacts of different correlations. We will see that, given certain constraints originating from the extended CreditRisk model, the resulting distributions differ significantly.
4.1. Dependence Modelling with Two Gamma-Distributed Risk Factors
We give an example of the application of Calculation Method 1 that implements the dependence structures given in Theorem 1. We consider four cases of dependence structures, and we use the following assumptions and parameters: in each case, we consider two independent and gamma-distributed risk factors, i.e., with , hence and for . We consider two lines of business, meaning that , and we simplify notation by writing and instead of and . A further constraint of our example is that the claim cause intensities satisfy for in each case of correlation. In each of these four cases, the distribution of the random sum from Equation (20) can be determined explicitly by computing the characteristic functions.
- (a)
- Positively correlated claim cause intensities: Take , omit the index j, let , take any , and defineBy Equation (17),and . Hence, depending on , the correlationcan take every value in . Similar to Equation (11) using Equation (21), we obtain for everywith claim size distribution , see Definition 3. Using Definition A1(d) and Equation (A2), we see that is the convolution of the two compound negative binomial distributions
- (b)
- Independent claim cause intensities: Take in Case (a), hence .
- (c)
- Comonotone claim cause intensities: Take in Case (a). Then, the convolution is not necessary and is a compound negative binomial distribution.
- (d)
- Negatively correlated claim cause intensities (cf. Example 1): We choose two dependence scenarios, i.e., , and let J be a random variable independent of such that and . Let for . With define for as well asHence, is a mixture ofandeach of which is a convolution of a compound Poisson distribution with a compound negative binomial distributions. Note that, forhencewhere the last two equations can also be derived from Equation (17). To get for such that and according to Equation (51) have the same expectations as in the previous cases, we can can take any and and define and , or we can take any and and define , and .
Remark 25.
In the case of independent, identically gamma-distributed risk factors and , meaning that , (we will drop these indices), we can not only have the same expectation but also the same variance of and in Cases (b), (c) and (d): Due to Equation (48), in Cases (b) and (c). Due to Equation (52) with the choice , and as discussed above,
in Case (d). The quadratic equation has the solutions
If , then and the solution cannot be used. If , then . However, for all , hence always works. Thus, given , one or two choices for the matrices and in Equation (50) are determined.
For the numerical example in the setting of Remark 25, see Figure 1 and Figure 2, we specify the remaining parameters as follows: we choose the risk factors such that and , e.g., . In addition, we take . Thus, the two sets of parameters for the matrices and in Equation (50) are given by
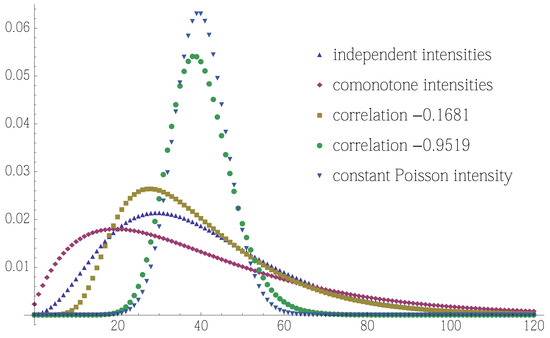
Figure 2.
Probability mass functions of the -valued portfolio loss for different dependence structures for the two claim cause intensities and satisfying and as discussed in Section 4.1. We take . The claim size equals 1 in all cases, i.e., . For comparison, also the case , yielding a Poisson distribution with expectation 40, is shown.
As a sanity check, Equation (48) for as well as Equation (52) for the above parameter sets give for . Equation (49) for gives , and by Equations (52) and (53) for the above parameters,
As Poisson parameters for Figure 1 and Figure 2, we choose for ; for the distribution of the (group) claim sizes, cf. Equation (21), we take and in Figure 1, and in Figure 2.
An application of Theorem 1 gives us an equivalent representation such that we can apply Algorithm 1. For a better comparison, we put the probability mass functions into one graph, see Figure 2 with the first 120 values. We see interesting differences between the probability mass functions. Taking the probability mass function with independent claim cause intensities as an initial point of comparison, we observe that the probability mass function for negatively correlated claim cause intensities is a bit less, and, much less, respectively, light-tailed with a (much) taller maximum, whereas the probability mass function for comonotone, i.e., positively correlated claim cause intensities has a mass with a smaller maximum. We also observe that the probability mass function for the claim cause intensities with positive correlation has a heavier tail than the other probability mass functions.
4.2. Dependence Modelling with Two -Tempered -stable-Distributed Risk Factors
For an illustration of Calculation Method 1 that implements the dependence structures given in Theorem 1, here with respect to Remark 16, we consider two risk factors meaning . This implies that the considered risk factors have a -tempered -stable distribution, i.e., with . Following the notation of Remark 16, we need to compute a Panjer’s recursion for an extended negative binomial distribution, followed by a computation of Panjer’s recursion for a Poisson distribution and finally the distribution of a discrete mixture distribution.
We consider three different dependence structures: independent risk factors, positively correlated risk factors, and negatively correlated risk factors. We use the following assumptions and parameters: in each case, we consider two independent and -tempered -stable-distributed risk factors, i.e., with , and . We consider two lines of business, meaning that , and we simplify notation by writing and instead of and . The remaining parameters are chosen as follows: , , and for and . Furthermore, we let .
For the case of independent risk factors we take and
and for the case of positive correlation, also with , we choose
In the case of negative correlation, we need two matrices:
and
The distribution of the required random variable J is . For simplicity, we choose a degenerate distribution of the claim sizes . The result of the computation is depicted in Figure 3.
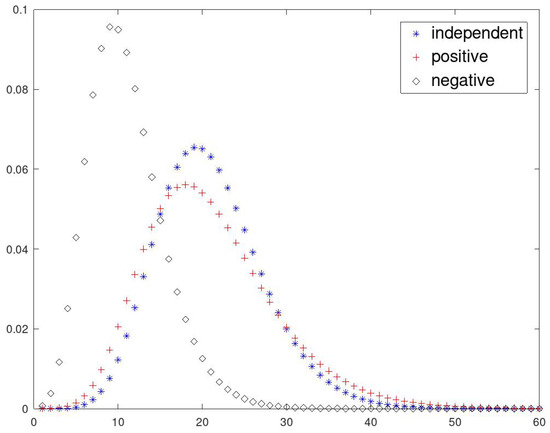
Figure 3.
Probability mass functions of the -valued portfolio loss for different dependence structures for the two claim cause intensities and . We take . The claim size equals 1 in all cases, i.e., .
4.3. Dependence Modeling with Three Gamma-Distributed Risk Factors
In this example, we extend the setting of the previous subsection and also apply Calculation Method 1. We want to study the impacts of the comonotone and two negative correlation structures between the claim cause intensities and compare with the case of independence. In each one of the four dependence structures, we consider three independent, gamma-distributed risk factors, i.e., with , hence and for . We again consider lines of business, but we allow for simultaneous claims in both of them, meaning that . For comparison of the different dependence cases in our example, we impose the constraint that the claim cause intensities always satisfy
- (a)
- Three positively correlated claim cause intensities: Take , omit the index j, let , take any with , and definewith the convention that .
- (b)
- Independent claim cause intensities: Take in Case (a).
- (c)
- Comonotone claim cause intensities: Take and in Case (a).
- (d)
- Positive correlation between the individual claim cause intensities and , and both of them negatively correlated to the joined claim cause intensity : We take two dependence scenarios, i.e., , and let J be a random variable independent of such that and . Let for and . With , we define , for as well asThen, for and . To satisfy the conditions in Equation (56), we need again that for as in Case (d) of Section 4.1.
In the case of independent, identically gamma-distributed risk factors we can, in addition to the same expectations, also have the same variances of , and in Cases (b), (c) and (d) above; for details, see Remark 25.
For the numerical illustration in Figure 4 and the comparison with Figure 2, we take and independent with . Furthermore, we take for and . For , we get claims in both business lines simultaneously, hence each business line gets 20 claims in expectation, which corresponds to the numerical example of the previous subsection. In Case (d), we take and , as in (54), hence the correlation for is given by the right-hand side of Equation (55).
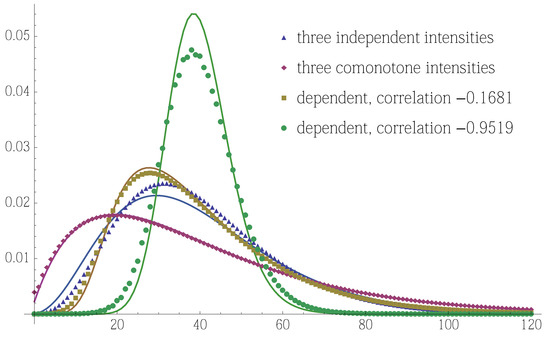
Figure 4.
Probability mass functions of the portfolio loss for four different dependence structures for the three claim cause intensities , and satisfying and for all as discussed in Section 4.3. The group claim size, cf. Equation (21), equals 1 for and 2 for , i.e., and . The given correlation refers to for , see the right-hand side of Equation (55). For comparison with Section 4.1, the corresponding probability mass functions from Figure 2 are indicated as solid lines.
4.4. Dependence Modelling with Two Risk Factors and Mixture
For an illustration of Calculation Method 2, we choose the following contraints. Consider the conditions of Theorem 2. We assume two risk factors and a gamma-distributed random variable T with with and . Since such a single mixture distribution introduces a very strong measure of dependence, it is not useful to consider also negative correlation. For negative correlation, refer to (Rudolph 2014, Remark 4.11). For instance, an antithetic choice would suffice. Thus, it is sufficient to let and we define . The distribution of the conditionally independent risk factors is given by
We consider two dependence matrices: For a case, we call independent (since we do not impose further dependence)
and another case that imposes further (very strong) dependence
For simplicity, we choose a degenerate distribution of the claim sizes . We let , and for . Furthermore, we choose and and . The result of the computation is shown in Figure 5.
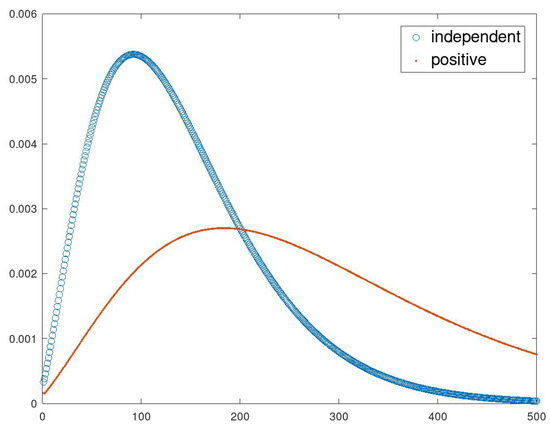
Figure 5.
Probability mass functions of the -valued portfolio loss for different dependence structures for the two claim cause intensities and satisfying . We take . The claim size equals 1 in all cases, i.e., .
Author Contributions
Supervision, U.S.; writing–original draft preparation, C.R.; writing–review and editing, C.R. and U.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the Christian Doppler Research Association (CDG). The authors gratefully acknowledge the fruitful collaboration and support by UniCredit Bank Austria, Austrian Federal Financing Agency, COR & FJA (now msg life) and Österreichische Kontrollbank through CDG and the Christian Doppler Laboratory for Portfolio Risk Management (PRisMa Lab). The second author also gratefully acknowledges financial support from funds of the Österreichische Nationalbank (Anniversary Fund, project number 16549).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this appendix, we provide for further reference some general representations of distributions when compounded or mixed that we needed in the preceding sections. Additionally, we introduce a dependence scenario between claim cause intensities and prove a corresponding formula for the probability-generating function of the distributions of Poisson mixture vectors.
Remark A1.
A probability-generating function uniquely determines a distribution, cf. (Kallenberg 2002, Theorem 5.3). The result is proven for characteristic functions but carries over to probability-generating functions. If V is a separable Banach space, see (Ledoux and Talagrand 1991, p. 39).
Definition A1
(Notation for compound distributions). Let N be an -valued random variable and an i.i.d. sequence of random variables, independent of N. Let and F denote the distributions of N and , respectively.
- (a)
- Let the distribution of the random sum be .
- (b)
- If N has a Poisson distribution with expectation , then S has a compound Poisson distribution and we write .
- (c)
- If N has a logarithmic distribution with parameter , cf. Definition A3, then S has a compound logarithmic distribution and we write .
- (d)
- If N has a negative binomial distribution with parameters and , cf. Definition A2, then S has a compound negative binomial distribution and we write .
Results pointing out the relation between a compound Poisson distribution and a Poisson mixture distribution are already well known. It is interesting to consider compound distributions with negative binomial distributions instead. For this purpose, we give a definition of the negative multinomial distribution, cf. (Sibuya et al. 1964, sct. 2), which is a multivariate generalization of the negative binomial distribution.
Definition A2.
A random vector has an m-variate negative multinomial distribution with parameters and with if
for all . Denote this distribution on by . In the case , we write . Note that .
According to (Wishart 1949, eq. (2.1), the corresponding probability-generating function is
defined for all with . For further reading on the negative multinomial distribution, we refer to Sibuya et al. (1964); Wishart (1949), or (Johnson et al. 1997, Chp. 36). This negative multinomial distribution can be also seen as a generalization in the sense of a generalization of the geometric distribution, see also Mai et al. (2013).
The following lemma generalizes the fact that a Poisson-gamma mixture is a negative binomial distribution and will be useful for further applications. It also generalizes (Sibuya et al. 1964, sct. 3.b) by allowing T to be random.
Lemma A1.
Let and . Let T be a strictly positive random variable and let Λ be a random variable such that . Let be a random vector with conditionally independent components given such that
Then, with for every .
Proof.
Apply Remark A1 and compute the probability-generating function of the conditional distribution of N given T. Conditioning on and using the conditional independence of given and the conditional distribution of N given yields for
A further result also exists on mixtures of the negative multinomial distribution. It is a generalization of a result that can be found in (Sibuya et al. 1964, sct. 3.d). Let us first introduce a generalization of the logarithmic distribution to multivariate dimensions taken from (Sibuya et al. 1964, sct. 3.d).
Definition A3.
Let with . A random vector has a multivariate logarithmic distribution if
where . We denote this distribution by . In the case , we just write and define .
According to (Sibuya et al. 1964, eq. (3.2), its probability-generating function is given by
Then, the aforementioned generalization is the following. It is a generalization of (Schröter 1995, p. 95/96) and a special case of it with and can be also found in Ammeter (1948).
Lemma A2.
Let , and with . Let T be a strictly positive random variable and let N be a random variable such that
Let be a sequence independent of , consisting of i.i.d. m-dimensional random vectors with . Define . Then,
Proof.
Using Remark A1, we prove the claim by considering the probability-generating function of the conditional distribution of S given T for with
The sequence is i.i.d. and independent of . Hence, using also Equation (A4), we observe
Using Equation (A5) and a simplification provide
which completes the proof. □
References
- Ammeter, Hans. 1948. A generalization of the collective theory of risk in regard to fluctuating basic-probabilities. Scandinavian Actuarial Journal 31: 171–98. [Google Scholar] [CrossRef]
- Credit Suisse First Boston. 1997. CreditRisk+: A Credit Risk Management Framework. Available online: http://www.csfb.com/institutional/research/assets/creditrisk.pdf (accessed on 15 April 2014).
- Deshpande, Amogh, and Srikanth K. Iyer. 2009. The CreditRisk+ model with general sector correlations. Central European Journal of Operations Research 17: 219–28. [Google Scholar] [CrossRef]
- Fabiánová, Lucia, and Jozef Glova. 2015. Dependency and predictability of stock market returns: An empirical study of German capital market. Journal of Applied Economic Sciences 10: 1020–22. [Google Scholar]
- Gerhold, Stefan, Uwe Schmock, and Richard Warnung. 2010. A generalization of Panjer’s recursion and numerically stable risk aggregation. Finance and Stochastics 14: 81–128. [Google Scholar] [CrossRef]
- Giese, Götz. 2004. Dependent risk factors. In CreditRisk+ in the Banking Industry. Berlin: Springer, pp. 153–66. [Google Scholar]
- Gundlach, Matthias, and Frank Lehrbass. 2004. CreditRisk+ in the Banking Industry. Berlin: Springer. [Google Scholar]
- Hashorva, Enkelejd. 2011. A convolution identity for exchangeable risks. Albanian Journal of Mathematics 5: 41–43. [Google Scholar]
- Hess, Klaus Th., Anett Liewald, and Klaus D. Schmidt. 2002. An extension of Panjer’s recursion. ASTIN Bulletin: The Journal of the IAA 32: 283–97. [Google Scholar] [CrossRef]
- Hesselager, Ole. 1996. A recursive procedure for calculation of some mixed compound Poisson distributions. Scandinavian Actuarial Journal 1996: 54–63. [Google Scholar] [CrossRef]
- Jajuga, Krzysztof. 2016. Model risk in finance—Investor perspective. Transformations in Business and Economics 15: 289–304. [Google Scholar]
- Johnson, Norman Lloyd, Samuel Kotz, and Narayanaswamy Balakrishnan. 1997. Discrete Multivariate Distributions. New York: John Wiley & Sons Inc. [Google Scholar]
- Johnson, Norman Lloyd, Samuel Kotz, and Narayanaswamy Balakrishnan. 2000. Continuous Multivariate Distributions. In Models and Applications, 2nd ed. New York: Wiley-Interscience, vol. 1. [Google Scholar]
- Kallenberg, Olav. 2002. Foundations of Modern Probability, 2nd ed. New York: Springer. [Google Scholar]
- Ledoux, Michel, and Michel Talagrand. 1991. Probability in Banach Spaces. Berlin: Springer. [Google Scholar]
- Lindskog, Filip, and Alexander J. McNeil. 2003. Common Poisson shock models: Applications to insurance and credit risk modelling. ASTIN Bulletin: The Journal of the IAA 33: 209–38. [Google Scholar] [CrossRef][Green Version]
- Lukacs, Eugene. 1970. Characteristic Functions, 2nd ed. New York: Hafner Publishing Co. [Google Scholar]
- Luo, Xiaolin, and Pavel V. Shevchenko. 2010. The t-copula with multiple parameters of degrees of freedom: Bivariate characteristics and application to risk management. Quantitative Finance 10: 1039–54. [Google Scholar] [CrossRef]
- Mai, Jan-Frederik, Matthias Scherer, and Natalia Shenkman. 2013. Multivariate geometric distributions, (logarithmically) monotone sequences, and infinitely divisible laws. Journal of Multivariate Analysis 115: 457–80. [Google Scholar] [CrossRef]
- Panjer, Harry H. 1981. Recursive evaluation of a family of compound distributions. ASTIN Bulletin: The Journal of the IAA 12: 22–26. [Google Scholar] [CrossRef]
- Rosiński, Jan. 2007. Tempering stable processes. Stochastic Processes and Their Applications 117: 677–707. [Google Scholar] [CrossRef]
- Rudolph, Cordelia. 2014. A Generalization of Panjer’s Recursion for Dependent Claim Numbers and an Approximation of Poisson Mixture Models. Ph.D. Thesis, Vienna University of Technology, Vienna, Austria. [Google Scholar]
- Samorodnitsky, Gennady, and M. S. Taqqu. 1994. Stable Non-Gaussian Random Processes. Stochastic Models with Infinite Variance. New York: Chapman & Hall. [Google Scholar]
- Schmock, Uwe. 2020. Modelling Dependent Credit Risks with Extensions of CreditRisk+ and Application to Operational Risk. Lecture Notes. Vienna: Vienna University of Technology. [Google Scholar]
- Schröter, Klaus Jürgen. 1995. Verfahren zur Approximation der Gesamtschadenverteilung. Karlsruhe: Verlag Versicherungswirtschaft. [Google Scholar]
- Sibuya, Masaaki, Isao Yoshimura, and Ryoichi Shimizu. 1964. Negative multinomial distribution. Annals of the Institute of Statistical Mathematics 16: 409–26. [Google Scholar] [CrossRef]
- Soltes, Vincent, and Jakub Danko. 2017. Proposal of creation of a portfolio with minimal risk. Investment Management and Financial Innovations 14: 107–15. [Google Scholar] [CrossRef][Green Version]
- Steutel, Fred W., and Klaas van Harn. 2004. Infinite Divisibility of Probability Distributions on the Real Line. New York: Marcel Dekker Inc., vol. 259. [Google Scholar]
- Sundt, Bjørn. 1999. On multivariate Panjer recursions. ASTIN Bulletin: The Journal of the IAA 29: 29–45. [Google Scholar] [CrossRef]
- Sundt, Bjørn, and William S. Jewell. 1981. Further results on recursive evaluation of compound distributions. ASTIN Bulletin: The Journal of the IAA 12: 27–39. [Google Scholar] [CrossRef]
- Sundt, Bjørn, and Raluca Vernic. 2009. Recursions for Convolutions and Compound Distributions with Insurance Applications. Berlin: Springer. [Google Scholar]
- Willmot, Gordon E. 1988. Sundt and Jewell’s familiy of discrete distributions. ASTIN Bulletin: The Journal of the IAA 18: 17–29. [Google Scholar] [CrossRef]
- Willmot, Gordon E., and Harry H. Panjer. 1987. Difference equation approaches in evaluation of compound distributions. Insurance: Mathematics and Economics 6: 43–56. [Google Scholar] [CrossRef]
- Wishart, John. 1949. Cumulants of multivariate multinomial distributions. Biometrika 36: 47–58. [Google Scholar] [CrossRef]
- Wüthrich, Mario V., and Michael Merz. 2008. Stochastic Claims Reserving Methods in Insurance. Chichester: John Wiley & Sons Inc. [Google Scholar]
- Zoričák, Martin, Peter Gnip, Peter Drotár, and Vladimír Gazda. 2019. Bankruptcy prediction for small- and medium-sized companies using severely imbalanced datasets. Economic Modelling 84: 165–76. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).