Conditional Variance Forecasts for Long-Term Stock Returns
Abstract
1. Introduction
2. A Framework for Conditional Variance Prediction
2.1. One-Year Predictions
2.2. Longer-Horizon Predictions
2.3. Alternative Ways in Estimating the Conditional Variance Function
2.4. The Validation Criterion for the Choice of Smoothing Parameters and Model Selection
2.5. A Bootstrap-Test: No Predictability vs. Predictability of the Conditional Variance
3. Empirical Application: Conditional Variance Prediction for Stock Returns in Excess of Different Benchmarks
3.1. The Data
3.2. Single Benchmarking Approach
3.3. Full Benchmarking Approach
3.4. Real-Income Long-Term Pension Prediction
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Heiko Ebens. 2001. The distribution of realized stock return volatility. Journal of Finacial Economics 61: 43–76. [Google Scholar] [CrossRef]
- Burman, Prabir, Edmond Chow, and Deborah Nolan. 1994. A cross-validatory method for dependent data. Biometrika 81: 351–58. [Google Scholar] [CrossRef]
- Chen, Qingqing, and Yongmiao Hong. 2010. Predictability of Equity Returns Over Different Time Horizons: A Nonparametric Approach. Working Paper. Ithaca: Cornell University/Department of Economics. [Google Scholar]
- Cheng, Tingting, Jiti Gao, and Oliver Linton. 2019. Nonparametric Predictive Regressions for Stock Return Predictions. Cambridge Working Papers in Economics: 1932. Cambridge: Faculty of Economics, University of Cambridge. [Google Scholar]
- Christoffersen, Peter F., and Francis X. Diebold. 2000. How relevant is volatility forecasting for financial risk management? Review of Economics and Statistics 82: 12–22. [Google Scholar] [CrossRef]
- Chu, C. K., and J. S. Marron. 1991. Comparison of two bandwidth selectors with dependent errors. The Annals of Statistics 19: 1906–18. [Google Scholar] [CrossRef]
- De Brabanter, Kris, Jos De Brabanter, Johan A.K. Suykens, and Bart De Moor. 2011. Kernel regression in the presence of correlated errors. Journal of Machine Learning Research 12: 1955–76. [Google Scholar]
- Fan, Jianqing, and Qiwei Yao. 1998. Efficient estimation of conditional variance functions in stochastic regression. Biometrika 85: 645–60. [Google Scholar] [CrossRef]
- Galbraith, John W. 2003. Content horizons for univariate time-series forecasts. International Journal of Forecasting 19: 43–55. [Google Scholar] [CrossRef]
- Galbraith, John W., and Turgut Kisinbay. 2005. Content horizons for conditional variance forecasts. International Journal of Forecasting 21: 249–60. [Google Scholar] [CrossRef]
- Geller, Juliane, and Michael H. Neumann. 2018. Improved local polynomial estimation in time series regression. Journal of Nonparametric Statistics 30: 1–27. [Google Scholar] [CrossRef]
- Gerrard, Russell, Munir Hiabu, Ioannis Kyriakou, and Jens Perch Nielsen. 2019a. Communication and personal selection of pension saver’s financial risk. European Journal of Operational Research 274: 1102–11. [Google Scholar] [CrossRef]
- Gerrard, Russell, Munir Hiabu, Ioannis Kyriakou, and Jens Perch Nielsen. 2019b. Self-selection and risk sharing in a modern world of life-long annuities. British Actuarial Journal 23: e30. [Google Scholar] [CrossRef]
- Gerrard, Russell, Munir Hiabu, Jens Perch Nielsen, and Peter Vodicka. 2019c. Long-Term Real Dynamic Investment Planning. Working Paper. London: Cass Business School. [Google Scholar]
- Geweke, John F. 1996. Monte carlo simulation and numerical integration. In Handbook of Computational Economics. Edited by Hans M. Amman, David A. Kendrick and John Rust. Amsterdam: Elsevier, vol. I, pp. 731–800. [Google Scholar]
- Glad, Ingrid K. 1998. Parametrically guided non-parametric regression. Scandinavian Journal of Statistics 25: 649–68. [Google Scholar] [CrossRef]
- Gonzales-Manteiga, Wenceslao, and Rosa M. Crujeiras. 2013. An updated review of goodness-of-fit tests for regression models. Test 22: 361–411. [Google Scholar] [CrossRef]
- Härdle, Wolfgang K., and Enno Mammen. 1993. Comparing nonparametric versus parametric regression fits. Annals of Statistics 21: 1926–47. [Google Scholar] [CrossRef]
- Härdle, Wolfgang K., and Alexandre B. Tsybakov. 1997. Local polynomial estimators of the volatility function in nonparametric autoregression. Journal of Econometrics 81: 223–42. [Google Scholar] [CrossRef]
- Kim, Tong Suk, and Edward Omberg. 1996. Dynamic nonmyopic portfolio behavior. The Review of Financial Studies 9: 141–61. [Google Scholar] [CrossRef]
- Kothari, S. P., Jonathan Lewellen, and Jerold B. Warner. 2006. Stock returns, aggregate earnings surprises, and behavioral finance. Journal of Financial Economics 79: 537–68. [Google Scholar] [CrossRef]
- Kreiss, Jens-Peter, Michael H. Neumann, and Qiwei Yao. 2008. Bootstrap tests for simple structures in nonparametric time series regression. Statistics and Its Interfaces 1: 367–80. [Google Scholar] [CrossRef]
- Kyriakou, Ioannis, Parastoo Mousavi, Jens Perch Nielsen, and Michael Scholz. 2019a. Forecasting benchmarks of long-term stock returns via machine learning. Annals of Operations Research. [Google Scholar] [CrossRef]
- Kyriakou, Ioannis, Parastoo Mousavi, Jens Perch Nielsen, and Michael Scholz. 2019b. Machine Learning for Forecasting Excess Stock Returns—The Five-year View. Graz Economics Papers 2019-06. Graz: University of Graz, Departmemt of Economics. [Google Scholar]
- Lettau, Martin, and Stijn Van Nieuwerburgh. 2008. Reconciling the return predictability evidence. Review of Financial Studies 21: 1607–52. [Google Scholar] [CrossRef]
- Linton, Oliver, and Benoit Perron. 2003. The shape of the risk premium: Evidence from a semiparametric generalized autoregressive conditional heteroscedasticity model. Journal of Business & Economic Statistics 21: 354–67. [Google Scholar]
- Linton, Oliver B., and Yang Yan. 2011. Semi- and nonparametric arch processes. Journal of Probability and Statistics 2011: 906212. [Google Scholar] [CrossRef]
- Linton, Oliver B., and Enno Mammen. 2008. Nonparametric transformation to white noise. Journal of Econometrics 142: 241–64. [Google Scholar] [CrossRef]
- Merton, Robert C. 1973. An intertemporal capital asset pricing model. Econometrica 41: 867–87. [Google Scholar] [CrossRef]
- Merton, Robert C. 2014. The crisis in retirement planning. Harvard Business Review 92: 43–50. [Google Scholar]
- Mishra, Santosh, Liangjun Su, and Aman Ullah. 2010. Semiparametric estimator of time series conditional variance. Journal of Business & Economic Statistics 28: 256–74. [Google Scholar]
- Munk, Claus, and Jesper Rangvid. 2018. New assumptions of a pension forecast model: Background, level and consequences for individuals forecasted pension. Finans/Invest 6: 6–14. [Google Scholar]
- Nielsen, Jens Perch, and Stefan Sperlich. 2003. Prediction of stock returns: A new way to look at it. ASTIN Bulletin 33: 399–417. [Google Scholar] [CrossRef]
- Opsomer, Jean, Yuedong Wang, and Yuhong Yang. 2001. Nonparametric regression with correlated errors. Statistical Science 16: 134–53. [Google Scholar]
- Pagan, Adrian R., and Yong-Sik Hong. 1991. Nonparametric estimation and the risk premium. In Nonparametric and Semiparametric Methods in Econometrics and Statistics. Edited by William A. Barnett, James Powell and George E. Tauchen. Cambridge: Cambridge University Press, pp. 51–76. [Google Scholar]
- Pagan, Adrian R., and Aman Ullah. 1988. The econometric analysis of models with risk terms. Journal of Applied Econometrics 3: 87–105. [Google Scholar] [CrossRef]
- Politis, Dimitris N., and Joseph P. Romano. 1994. The stationary bootstrap. Journal of the American Statistical Association 89: 1303–13. [Google Scholar] [CrossRef]
- Rapach, David, and Guofu Zhou. 2013. Forecasting stock returns. In Handbook of Economic Forecasting. Edited by Graham Elliott and Allan Timmerman. Amsterdam: Elsevier, vol. 2A, pp. 328–83. [Google Scholar]
- Scholz, Michael, Jens Perch Nielsen, and Stefan Sperlich. 2015. Nonparametric prediction of stock returns based on yearly data: The long-term view. Insurance: Mathematics and Economics 65: 143–55. [Google Scholar] [CrossRef]
- Scholz, Michael, Stefan Sperlich, and Jens Perch Nielsen. 2016. Nonparametric long term prediction of stock returns with generated bond yields. Insurance: Mathematics and Economics 69: 82–96. [Google Scholar] [CrossRef]
- Shiller, Robert J. 1989. Market Volatility. Cambridge: MIT Press. [Google Scholar]
- Su, Liangjun, and Aman Ullah. 2006. More efficient estimation in nonparametric regression with nonparametric autocorrelated errors. Econometric Theory 22: 98–126. [Google Scholar] [CrossRef]
- Wang, Lie, Lawrence D. Brown, T. Tony Cai, and Michael Levine. 2008. Effect of mean on variance function estimation in nonparametric regression. The Annals of Statistics 36: 646–64. [Google Scholar] [CrossRef]
- Wang, WenWu, and Ping Yu. 2017. Asymptotically optimal differenced estimators of error variance in nonparametric regression. Computational Statistics and Data Analysis 105: 125–43. [Google Scholar] [CrossRef]
- Welch, Ivo, and Amit Goyal. 2008. A comprehensive look at the empirical performance of equity premium prediction. Review of Financial Studies 21: 1455–508. [Google Scholar] [CrossRef]
- Xiao, Zhijie, Oliver B. Linton, Raymond J. Carroll, and Enno Mammen. 2003. More efficient local polynomial estimation in nonparametric regression with autocorrelated errors. Journal of the American Statistical Association 98: 980–92. [Google Scholar] [CrossRef]
- Xu, Ke Li, and Peter C. B. Phillips. 2011. Tilted nonparametric estimation of volatility functions with empirical applications. Journal of Business & Economic Statistics 29: 518–28. [Google Scholar]
- Yu, Keming, and M.C. Jones. 2004. Likelihood-based local linear estimation of the conditional variance function. Journal of the American Statistical Association 99: 139–44. [Google Scholar] [CrossRef]
- Ziegelmann, Flavio A. 2002. Nonparametric estimation of volatility functions: The local exponential estimator. Econometric Theory 18: 985–91. [Google Scholar] [CrossRef]
| 1 | Our methodology of validating a fully nonparametric structure can be viewed as one of the simplest and therefore also most transparent version of machine learning; see Section 2 of Kyriakou et al. (2019a) for more details justifying the label machine learning for our approach. |
| 2 | Note that the use of a different ML method would come with the cost of losing interpretability, smoothness, or flexibility due to restrictions on the functional form. A comparison of different ML techniques in finding that one which gives the best predictions, wins an investment horse-race out-of-sample, or being the most robust method over different periods is out of the scope of our work. |
| 3 | The choice of the one-year horizon is related to the frequency of the data. In contrast, the five-year horizon is arbitrary but is intended to be a starting point for actuarial long-term models for real-income savings. Other horizons and related questions remain for future research. |
| 4 | Note that the set of explanatory variables in (2) could be different or overlapping for the mean and variance function. |
| 5 | For a description and statistical properties of the local-linear smoother, see, for example, Section 2.3 in Kyriakou et al. (2019b). Note further that the smoothing parameters h and g are separately chosen in each step. |
| 6 | Our flexible location-scale model in (5), could be easily extended to time-lags of higher order. However, in the empirical application in Section 3, we see that, for example, for real-earnings—the main driver of real-returns—an AR1-type model is ideally suited. This is in line with findings from Kothari et al. (2006). Note further that one might expect risk and return to be somehow related (see, for example, Merton 1973). The parametric GARCH-in-Mean process captures this idea (Linton and Yan 2011). However, the inclusion of an interaction of mean and variance in a fully nonparametric fashion is out of the scope of this paper. To our knowledge, only semiparametric versions where either the mean or variance function is modeled parametrically can be found in the literature, see, for example, Pagan and Hong (1991); Pagan and Ullah (1988); Linton and Perron (2003). |
| 7 | For possible solutions to the problem of autocorrelation, see, for example, Xiao et al. (2003); Su and Ullah (2006); Linton and Mammen (2008), or more recently Geller and Neumann (2018). The implementation and analysis of these techniques remain for future research. In our approach, we account for autocorrelation in the validation criterion with a leave-k-out strategy, where ; see Section 2.4. |
| 8 | It does not estimate the volatility function as efficiently as if the true mean were known. |
| 9 | Examples of these variants are: (i) Applying a local-linear kernel smoother in both stages (Fan and Yao 1998). The result is again not necessarily nonnegative but asymptotically fully adaptive to the unknown mean function. (ii) Using the local exponential estimator to ensure nonnegativity (Ziegelmann 2002). (iii) Implementing a combined estimator (a multiplicative bias reduction technique), where a parametric guide captures some roughness features of the unknown variance function (Glad 1998; Mishra et al. 2010). (iv) Utilising a re-weighted local constant estimator maximising the empirical likelihood such that it becomes a bias-reducing moment restriction (Xu and Phillips 2011). |
| 10 | Those results are available upon request by the authors. |
| 11 | There is also a lack of studies using the difference-sequence method in a random design and in multivariate problems as in our case. |
| 12 | Model selection in the sense of composition of the set of explanatory variables. |
| 13 | The symbol denotes the indicator function of an appropriate condition A, i.e., it is one when A is true and zero otherwise. |
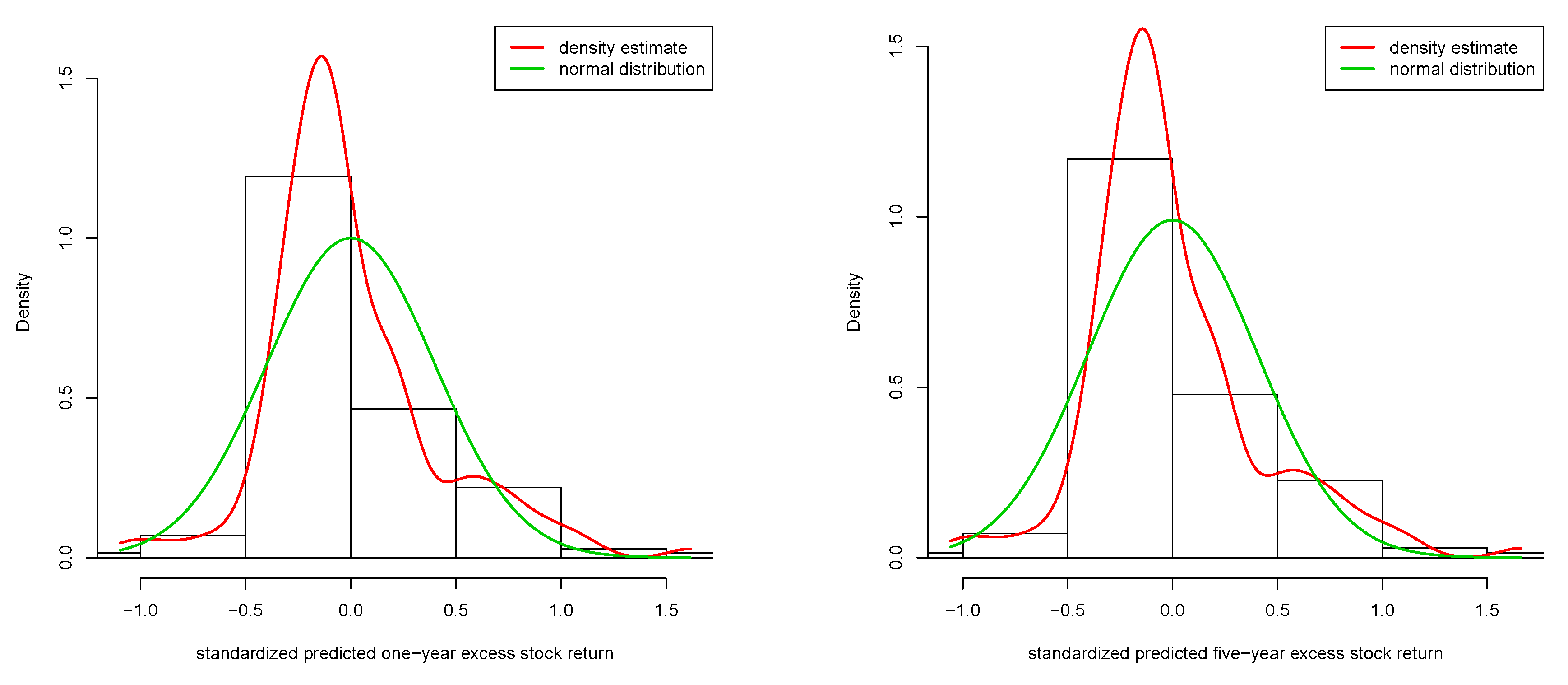
| 14 | The tests were conducted with 1000 repetitions at the 5% significance level for a selected number of cases. We do not present the p-values of the tests to save space. The results are available upon request by the authors. |
| 15 | Note that until now we have used the same set of covariates in both steps of our analysis to reduce the overwhelming number of models. It is also clear that not all combinations of variables are practically relevant. Now, we relax this restriction for the model with the highest predictive power for the returns. |
| 16 | Table 6 and Table 7 also present the results for the short- and long-term interest benchmarks and . However, it is again hard to find predictability at all in these cases. Note that the benchmark using the earnings-by-price variable is not applicable since it matches the covariate and the benchmark in the first step. |
| 17 | Here, we use the Sharpe-ratio for the comparison. From Table 1, we get and divide it either by 18.05% or by 16.91%. We obtain 0.355 and 0.379, which corresponds to a difference of 2.4% points. |
| 18 | Here, we use again the Sharpe-ratio for the comparison. From Table 1, we get and divide it either by 36.42% or by 34.08%. We obtain 0.888 and 0.949, which corresponds to a difference of 6.1% points. |
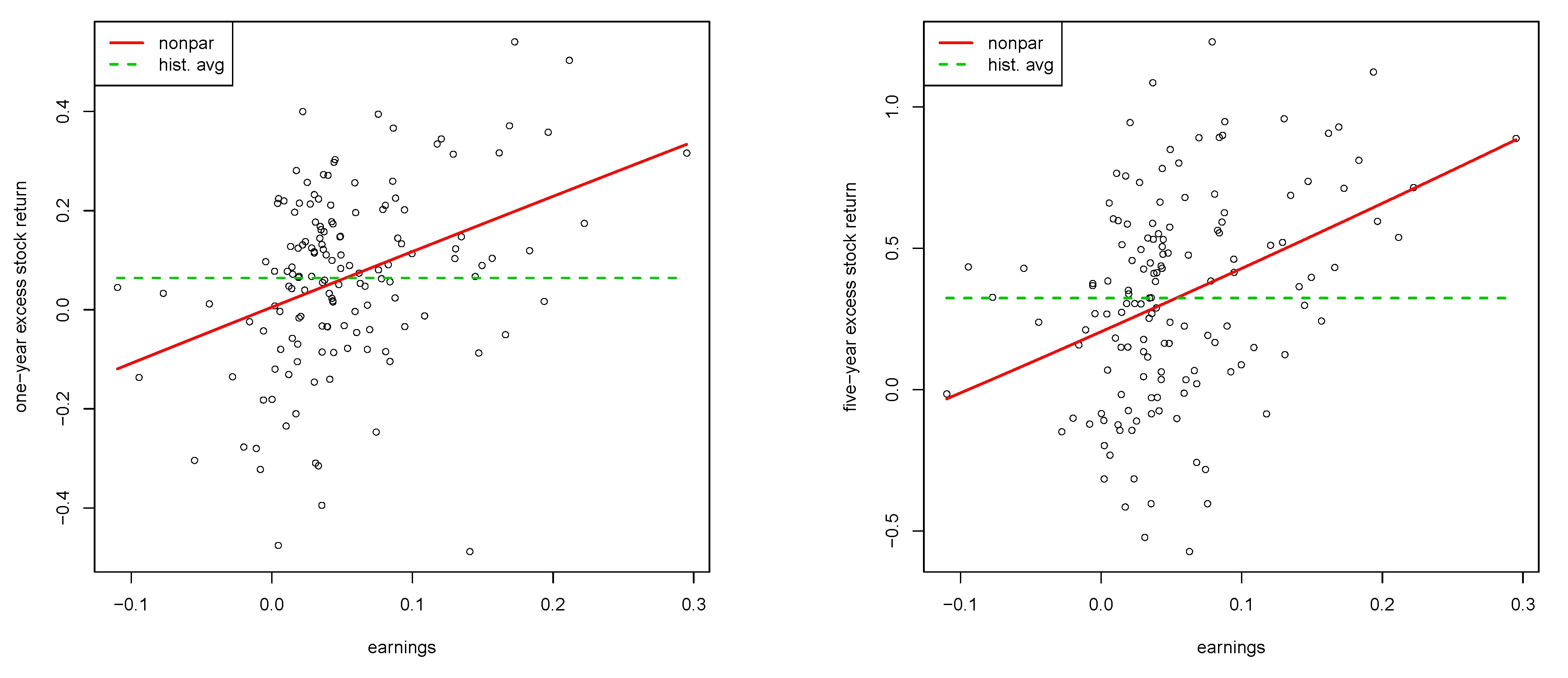
| 19 | The estimated coefficient is significant at the 0.1%-level (with a corresponding standard error of 0.08), the residual standard error of the regression is 0.0572, and its has a value of 0.357. |
| 20 | The following values are used for the calculation of the current real earnings-by-price: , , . |
| Max | Min | Mean | Sd | Skew | Exc. kurt | |
|---|---|---|---|---|---|---|
| S&P stock price index P | 2789.80 | 3.25 | 277.58 | 558.13 | 2.43 | 5.50 |
| Dividend accruing to index D | 53.75 | 0.18 | 6.04 | 10.56 | 2.45 | 6.00 |
| Earnings accruing to index E | 132.39 | 0.16 | 13.96 | 26.31 | 2.43 | 5.35 |
| Dividend-by-price d | 9.88 | 1.17 | 4.31 | 1.71 | 0.46 | 0.25 |
| Earnings-by-price e | 17.75 | 1.72 | 7.28 | 2.75 | 1.05 | 1.39 |
| Short-term interest rate r | 14.93 | 0.07 | 3.97 | 2.50 | 0.96 | 2.34 |
| Long-term interest rate l | 14.59 | 1.88 | 4.53 | 2.27 | 1.81 | 3.63 |
| Inflation | 20.69 | −15.65 | 2.23 | 5.96 | 0.26 | 1.60 |
| Spread s | 3.64 | −3.71 | 0.56 | 1.32 | −0.05 | 0.02 |
| One-year excess stock returns | 42.39 | −58.26 | 4.58 | 17.28 | −0.57 | 0.68 |
| One-year excess stock returns | 54.04 | −48.81 | 6.41 | 18.05 | −0.40 | 0.64 |
| Five-year excess stock returns | 107.27 | −78.54 | 23.49 | 36.69 | −0.14 | −0.37 |
| Five-year excess stock returns | 122.96 | −57.34 | 32.34 | 36.42 | −0.05 | −0.40 |
| Benchmark | Explanatory Variable(s) | ||||||
|---|---|---|---|---|---|---|---|
| d | e | r | l | s | |||
| Short-term rate | 2.2 | −1.1 | −0.6 | −0.3 | 0.3 | −1.2 | −0.1 |
| Long-term rate | 2.4 | −1.2 | −0.6 | 0.3 | 0.6 | −1.4 | −0.1 |
| Earnings-by-price | 1.5 | −1.3 | −0.7 | −0.1 | 0.5 | −1.4 | 0.1 |
| Inflation | 0.2 | 0.1 | −1.3 | −0.4 | 0.5 | −1.2 | −0.6 |
| Short-term rate | 2.4 | 1.9 | 1.1 | 2.2 | 0.1 | 0.3 | |
| Long-term rate | 1.5 | 1.4 | 1.1 | 2.1 | −0.2 | 0.1 | |
| Earnings-by-price | 1.6 | 1.4 | 0.9 | 2.0 | −0.2 | 0.1 | |
| Inflation | −1.0 | −1.1 | −0.6 | 0.6 | −2.1 | −1.0 | |
| Short-term rate | −2.1 | −1.5 | −0.8 | −2.4 | −1.5 | ||
| Long-term rate | −2.0 | −1.1 | −0.6 | −2.2 | −1.5 | ||
| Earnings-by-price | −1.9 | −1.4 | −0.7 | −2.3 | −1.5 | ||
| Inflation | −0.4 | −1.0 | −0.2 | −2.3 | −1.3 | ||
| Short-term rate | −1.0 | −0.4 | −2.3 | −0.8 | |||
| Long-term rate | −0.6 | −0.2 | −2.2 | −0.8 | |||
| Earnings-by-price | −1.0 | −0.2 | −2.2 | −0.8 | |||
| Inflation | −1.7 | −0.9 | −2.2 | −1.6 | |||
| Short-term rate | 1.3 | −1.5 | 1.4 | ||||
| Long-term rate | 1.3 | −1.0 | 1.4 | ||||
| Earnings-by-price | 1.4 | −1.5 | 1.6 | ||||
| Inflation | 1.3 | −1.5 | 1.2 | ||||
| Short-term rate | −1.2 | 1.4 | |||||
| Long-term rate | −0.9 | 1.4 | |||||
| Earnings-by-price | −1.0 | 1.6 | |||||
| Inflation | −0.9 | 1.3 | |||||
| Short-term rate | 0.2 | ||||||
| Long-term rate | 0.2 | ||||||
| Earnings-by-price | −0.6 | ||||||
| Inflation | −0.1 | ||||||
| Benchmark | Explanatory Variable(s) | ||||||
|---|---|---|---|---|---|---|---|
| d | e | r | l | s | |||
| Short-term rate | 0.6 | −1.7 | −1.7 | −1.2 | −1.0 | −2.0 | −3.0 |
| Long-term rate | 0.0 | −1.5 | −1.3 | −1.2 | −1.1 | −1.2 | −2.7 |
| Earnings-by-price | 0.8 | −1.8 | −1.1 | −1.8 | −2.7 | −0.3 | −3.8 |
| Inflation | −1.0 | −3.8 | −4.7 | −0.7 | −1.5 | 1.4 | 0.5 |
| Short-term rate | −2.8 | −2.5 | −1.7 | −1.7 | −1.7 | −3.9 | |
| Long-term rate | −2.5 | −2.1 | −1.6 | −1.8 | −1.2 | −3.4 | |
| Earnings-by-price | −2.3 | −2.1 | −1.2 | −4.1 | 0.4 | −3.4 | |
| Inflation | −5.1 | −4.7 | −1.5 | −2.6 | 0.4 | −0.9 | |
| Short-term rate | −3.6 | −3.1 | −2.2 | −2.8 | −4.1 | ||
| Long-term rate | −3.1 | −3.2 | −2.7 | −2.3 | −4.3 | ||
| Earnings-by-price | −4.1 | −4.0 | −5.3 | −2.3 | −4.9 | ||
| Inflation | −5.2 | −5.0 | −8.9 | −2.5 | −3.2 | ||
| Short-term rate | −3.3 | −3.3 | −3.5 | −4.9 | |||
| Long-term rate | −2.8 | −3.3 | −2.9 | −4.9 | |||
| Earnings-by-price | −4.5 | −5.5 | −2.7 | −6.5 | |||
| Inflation | −8.5 | −7.8 | −4.9 | −6.4 | |||
| Short-term rate | −3.8 | −1.7 | −3.9 | ||||
| Long-term rate | −4.1 | −1.3 | −4.2 | ||||
| Earnings-by-price | −5.3 | −1.9 | −5.4 | ||||
| Inflation | −3.9 | 0.3 | −1.9 | ||||
| Short-term rate | −1.7 | −3.9 | |||||
| Long-term rate | −1.3 | −4.2 | |||||
| Earnings-by-price | −2.6 | −5.4 | |||||
| Inflation | −1.2 | −1.8 | |||||
| Short-term rate | −4.4 | ||||||
| Long-term rate | −3.5 | ||||||
| Earnings-by-price | −4.8 | ||||||
| Inflation | −0.1 | ||||||
| Benchmark | Explanatory Variable(s) | ||||||
|---|---|---|---|---|---|---|---|
| Short-term rate | 2.2 | −0.3 | 0.7 | – | −0.2 | 0.1 | −0.2 |
| Long-term rate | 2.4 | 0.2 | −0.5 | −0.1 | – | −0.2 | −0.1 |
| Earnings-by-price | 1.5 | −0.2 | – | 0.6 | −0.2 | −0.7 | 0.0 |
| Inflation | 0.2 | −0.9 | −1.2 | −0.3 | −0.2 | – | −0.7 |
| Short-term rate | 0.8 | 0.7 | – | 0.2 | 0.1 | 0.2 | |
| Long-term rate | 1.3 | 3.0 | 0.1 | – | −0.3 | 0.1 | |
| Earnings-by-price | 0.2 | – | 0.7 | 2.5 | 0.0 | 0.1 | |
| Inflation | −3.1 | −1.4 | −1.5 | −1.9 | – | −1.0 | |
| Short-term rate | −1.3 | – | 0.9 | 0.0 | 0.9 | ||
| Long-term rate | −1.0 | 0.9 | – | −0.7 | 0.9 | ||
| Earnings-by-price | – | −0.3 | −0.8 | −1.8 | 0.4 | ||
| Inflation | −1.9 | 0.7 | 1.6 | – | −0.7 | ||
| Short-term rate | – | −0.4 | −2.6 | −0.4 | |||
| Long-term rate | −0.6 | – | −2.5 | −0.6 | |||
| Earnings-by-price | – | – | – | – | |||
| Inflation | −1.6 | −1.5 | – | −1.6 | |||
| Short-term rate | – | – | – | ||||
| Long-term rate | – | −1.2 | – | ||||
| Earnings-by-price | −0.5 | −2.1 | −0.3 | ||||
| Inflation | −1.9 | – | −1.6 | ||||
| Short-term rate | −1.4 | – | |||||
| Long-term rate | – | – | |||||
| Earnings-by-price | −2.5 | −0.5 | |||||
| Inflation | – | −1.7 | |||||
| Short-term rate | −1.4 | ||||||
| Long-term rate | −1.2 | ||||||
| Earnings-by-price | −1.6 | ||||||
| Inflation | – | ||||||
| Benchmark | Explanatory Variable(s) | ||||||
|---|---|---|---|---|---|---|---|
| Short-term rate | 0.6 | −2.2 | −3.2 | – | −3.1 | −3.2 | −3.1 |
| Long-term rate | 0.0 | −3.4 | −2.8 | −2.8 | – | −1.3 | −2.8 |
| Earnings-by-price | 0.8 | 1.8 | – | −2.3 | −3.2 | 0.6 | −3.8 |
| Inflation | −1.0 | 1.6 | 0.3 | 0.6 | 1.6 | – | 0.3 |
| Short-term rate | −2.1 | −4.3 | – | −4.0 | −1.2 | −4.0 | |
| Long-term rate | −3.8 | −3.2 | −3.6 | – | −1.1 | −3.6 | |
| Earnings-by-price | 1.1 | – | −2.8 | −3.8 | −0.5 | −3.4 | |
| Inflation | 0.3 | −0.8 | −0.3 | 0.4 | – | −1.0 | |
| Short-term rate | −3.7 | – | −5.4 | −2.1 | −5.4 | ||
| Long-term rate | −4.2 | −5.8 | – | −3.3 | −5.8 | ||
| Earnings-by-price | – | −0.4 | −2.6 | 0.3 | −3.3 | ||
| Inflation | −4.3 | −0.2 | −0.8 | – | −0.8 | ||
| Short-term rate | – | −5.9 | −4.9 | −5.9 | |||
| Long-term rate | −6.1 | – | −4.1 | −6.1 | |||
| Earnings-by-price | – | – | – | – | |||
| Inflation | −4.8 | −4.1 | – | −2.1 | |||
| Short-term rate | – | – | – | ||||
| Long-term rate | – | −2.3 | – | ||||
| Earnings-by-price | −6.3 | −3.2 | −6.1 | ||||
| Inflation | −1.0 | – | 0.5 | ||||
| Short-term rate | −3.4 | – | |||||
| Long-term rate | – | – | |||||
| Earnings-by-price | −3.6 | −6.2 | |||||
| Inflation | – | 0.5 | |||||
| Short-term rate | −3.4 | ||||||
| Long-term rate | −2.3 | ||||||
| Earnings-by-price | −4.6 | ||||||
| Inflation | – | ||||||
| Benchmark | Explanatory Variable(s) | ||||||
|---|---|---|---|---|---|---|---|
| Short-term rate | 1.0 | 0.3 | 0.7 | – | 0.1 | −0.4 | 0.1 |
| Long-term rate | 1.4 | 0.1 | −0.5 | 0.9 | – | −0.1 | 0.9 |
| Inflation | 0.4 | −0.6 | −1.2 | −0.4 | −0.1 | – | 0.8 |
| Short-term rate | 0.6 | 0.7 | – | 0.2 | −0.5 | 0.2 | |
| Long-term rate | 0.7 | 2.0 | 0.7 | – | −0.6 | 0.7 | |
| Inflation | −1.7 | −1.6 | −1.5 | −1.7 | – | −0.4 | |
| Short-term rate | 0.0 | – | −0.5 | −0.4 | −0.5 | ||
| Long-term rate | −1.0 | 0.3 | – | −1.4 | 0.3 | ||
| Inflation | −1.9 | 2.9 | 2.0 | – | 1.5 | ||
| Short-term rate | – | 0.5 | −2.2 | 0.5 | |||
| Long-term rate | −0.7 | – | −2.5 | −0.7 | |||
| Inflation | −0.9 | −1.7 | – | −0.3 | |||
| Short-term rate | – | – | – | ||||
| Long-term rate | – | −0.4 | – | ||||
| Inflation | −0.5 | – | 0.7 | ||||
| Short-term rate | 0.1 | – | |||||
| Long-term rate | – | – | |||||
| Inflation | – | −0.2 | |||||
| Short-term rate | 0.1 | ||||||
| Long-term rate | −0.4 | ||||||
| Inflation | – | ||||||
| Benchmark | Explanatory Variable(s) | ||||||
|---|---|---|---|---|---|---|---|
| Short-term rate | 0.1 | −1.8 | −3.2 | – | −4.5 | −2.5 | −4.5 |
| Long-term rate | 0.6 | −3.9 | −2.8 | −4.2 | – | −1.1 | −4.2 |
| Inflation | 0.0 | −0.1 | 0.3 | −0.4 | −0.1 | – | −2.6 |
| Short-term rate | −1.7 | −4.6 | – | −5.7 | −3.7 | −5.7 | |
| Long-term rate | −4.5 | −4.5 | −4.2 | – | −2.5 | −4.2 | |
| Inflation | −1.9 | −1.8 | −1.9 | −1.7 | – | −3.9 | |
| Short-term rate | −6.2 | – | −7.1 | −4.3 | −7.1 | ||
| Long-term rate | −4.5 | −7.9 | – | −5.2 | −7.9 | ||
| Inflation | −3.9 | −2.1 | −3.2 | – | −2.8 | ||
| Short-term rate | – | −8.1 | −5.8 | −8.1 | |||
| Long-term rate | −6.6 | – | −4.9 | −6.6 | |||
| Inflation | −2.8 | −3.4 | – | −2.6 | |||
| Short-term rate | – | – | – | ||||
| Long-term rate | – | −5.7 | – | ||||
| Inflation | −3.0 | – | −3.1 | ||||
| Short-term rate | −6.5 | – | |||||
| Long-term rate | – | – | |||||
| Inflation | – | −3.0 | |||||
| Short-term rate | −6.5 | ||||||
| Long-term rate | −5.7 | ||||||
| Inflation | – | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mammen, E.; Nielsen, J.P.; Scholz, M.; Sperlich, S. Conditional Variance Forecasts for Long-Term Stock Returns. Risks 2019, 7, 113. https://doi.org/10.3390/risks7040113
Mammen E, Nielsen JP, Scholz M, Sperlich S. Conditional Variance Forecasts for Long-Term Stock Returns. Risks. 2019; 7(4):113. https://doi.org/10.3390/risks7040113
Chicago/Turabian StyleMammen, Enno, Jens Perch Nielsen, Michael Scholz, and Stefan Sperlich. 2019. "Conditional Variance Forecasts for Long-Term Stock Returns" Risks 7, no. 4: 113. https://doi.org/10.3390/risks7040113
APA StyleMammen, E., Nielsen, J. P., Scholz, M., & Sperlich, S. (2019). Conditional Variance Forecasts for Long-Term Stock Returns. Risks, 7(4), 113. https://doi.org/10.3390/risks7040113





