A Generalised CIR Process with Externally-Exciting and Self-Exciting Jumps and Its Applications in Insurance and Finance
Abstract
1. Introduction
2. Mathematical Background
- is the initial value at time ;
- is the constant mean-reversion level;
- is the constant mean-reversion rate;
- is the constant that governs the volatility;
- is a standard Brownian motion;
- are the sizes of externally-exciting jumps, a sequence of i.i.d. positive r.v.s with distribution function , occurring at the corresponding random times following a Poisson process of constant rate ;
- are the sizes of self-exciting jumps, a sequence of i.i.d. positive r.v.s with distribution function , occurring at the corresponding random times , and this point process has a stochastic intensity linearly dependent on , i.e.,and
- the sequences , , and are assumed to be independent of each other.
- The first two terms correspond to the classical square-root process (Feller 1951) or CIR process (Cox et al. 1985).
- The third term corresponds to the impact of exogenous shocks.
- The last term corresponds to the impact of past exogenous shocks acting on the future intensity, and this term corresponds to the self-exciting component in a generalised Hawkes framework.
3. Distributional Properties
- Under the condition of , we havethen, is a strictly decreasing function of . Thus, we have for , since ; there is one unique positive solution to for , and for .
- As should be approachable to zero, we assume , we have and , then, Equation Equation (10) can be written asIntegrate both sides from time 0 to with the initial condition , then we haveDefine the function on the left-hand side asthen, we have ; it is obvious that when .
- By convergence test, we haveObviously, , then,thus when . Therefore, is a well defined (strictly increasing) function and its inverse function exists.
- The unique solution is found by . Hence, .
- Now, is determined byBy the change of variable we have , and
- Finally, substitute and into Equation (8) and the result follows.
4. Applications
4.1. An Application in Insurance: Insurance Premium Calculation
- If there are no self-exciting jumps and no diffusion in Equation (12), it becomes a simple Poisson shot-noise process, denoted by , i.e.,This process has been used for actuarial applications as a discounted aggregate loss process, see Jang (2004, 2007) and Jang and Krvavych (2004). If we assume (often implicitly) that interest rate is zero, i.e., , it becomes a simple compound Poisson process .
- If we replace by and set in Equation (12) and , then we have a process ofwith the SDERemark 1.This shot-noise self-exciting jump process in Equation (15) may be interpreted in the context of non-life insurance. A single event (e.g., natural catastrophe) may induce losses for a line of business. Each loss may produce a cluster of losses according to a branching structure (Dassios and Zhao 2011). Both losses are accumulated on a constant risk-free force of interest rate δ.
- In contrast, now let us consider a stochastic interest rate to the aggregate loss amounts up to time t, denoted by , as it is not deterministic in practice. Thus, if we replace by in Equation (12), then we can extend our study from Equations (15) and (16) toRemark 2.This shot-noise self-exciting jump-diffusion process in Equation (17) may be also interpreted in the context of non-life insurance. Similarly, a single event (e.g., a natural catastrophe) may induce losses for a line of business. Compared with Equation (16), both losses are accumulated on a stochastic force of interest rate. The proposed model captures the effect of sudden intensity increases due to external events, together with the accumulation of losses on a stochastic interest rate. Hence, it does have a potential interest in the insurance field.
4.1.1. Expectation of Loss Process
4.1.2. Variance of Loss Process
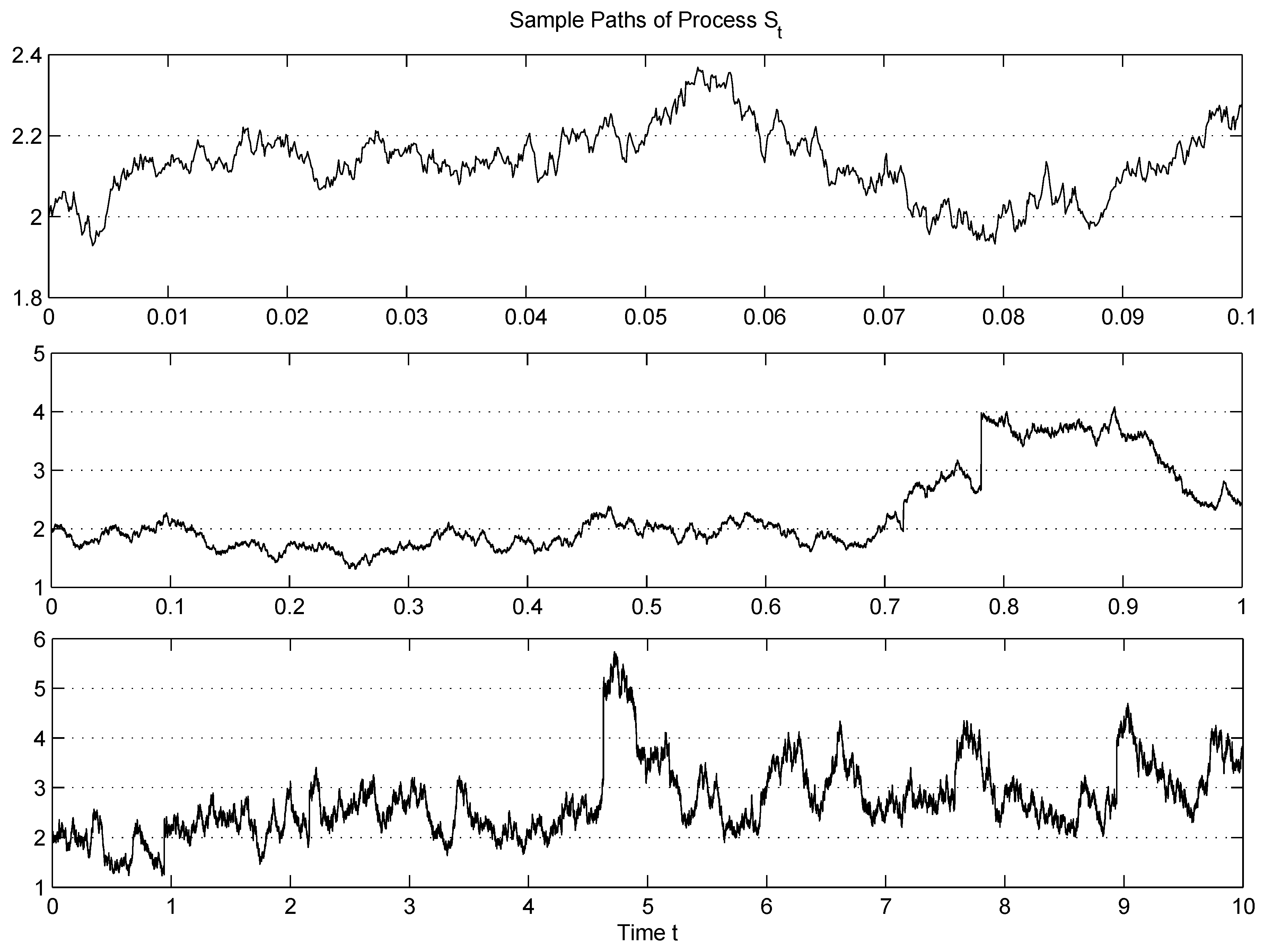
4.1.3. Numerical Examples
4.2. An Application in Finance: Default-Free Bond Pricing
Numerical Examples
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof for Proposition 1
References
- Adamopoulos, L. 1976. Cluster models for earthquakes: Regional comparisons. Journal of the International Association for Mathematical Geology 8: 463–75. [Google Scholar] [CrossRef]
- Aït-Sahalia, Yacine, Julio Cacho-Diaz, and Roger J. A. Laeven. 2015. Modeling financial contagion using mutually exciting jump processes. Journal of Financial Economics 117: 585–606. [Google Scholar] [CrossRef]
- Aït-Sahalia, Yacine, Roger J. A. Laeven, and Loriana Pelizzon. 2014. Mutual excitation in Eurozone sovereign CDS. Journal of Econometrics 183: 151–67. [Google Scholar] [CrossRef]
- Bacry, Emmanuel, Sylvain Delattre, Marc Hoffmann, and Jean-François Muzy. 2013. Modelling microstructure noise with mutually exciting point processes. Quantitative Finance 13: 65–77. [Google Scholar] [CrossRef]
- Bauwens, Luc, and Nikolaus Hautsch. 2009. Modelling financial high frequency data using point processes. In Handbook of Financial Time Series. Edited by Torben G. Andersen, Richard A. Davis, Jens-Peter Kreiß and Thomas Mikosc. Berlin: Springer, pp. 953–79. [Google Scholar]
- Boumezoued, Alexandre. 2016. Population viewpoint on Hawkes processes. Advances in Applied Probability 48: 463–80. [Google Scholar] [CrossRef]
- Bowsher, Clive G. 2007. Modelling security market events in continuous time: Intensity based, multivariate point process models. Journal of Econometrics 141: 876–912. [Google Scholar] [CrossRef]
- Brémaud, Pierre, and Laurent Massoulié. 1996. Stability of nonlinear Hawkes processes. Annals of Probability 24: 1563–88. [Google Scholar]
- Brémaud, Pierre, and Laurent Massoulié. 2001. Hawkes branching point processes without ancestors. Journal of Applied Probability 38: 122–35. [Google Scholar] [CrossRef]
- Brémaud, Pierre, and Laurent Massoulié. 2002. Power spectra of general shot noises and Hawkes point processes with a random excitation. Advances in Applied Probability 34: 205–22. [Google Scholar] [CrossRef]
- Bühlmann, Hans. 1970. Mathematical Methods in Risk Theory. Berlin: Springer-Verlag. [Google Scholar]
- Chavez-Demoulin, Valerie, Anthony C. Davison, and Alexander J. McNeil. 2005. Estimating value-at-risk: A point process approach. Quantitative Finance 5: 227–34. [Google Scholar] [CrossRef]
- Cox, John C., Jonathan E. Ingersoll, Jr., and Stephen A. Ross. 1985. A theory of the term structure of interest rates. Econometrica 53: 385–407. [Google Scholar] [CrossRef]
- Dassios, Angelos, and Paul Embrechts. 1989. Martingales and insurance risk. Stochastic Models 5: 181–217. [Google Scholar] [CrossRef]
- Dassios, Angelos, and Ji-Wook Jang. 2003. Pricing of catastrophe reinsurance and derivatives using the Cox process with shot noise intensity. Finance and Stochastics 7: 73–95. [Google Scholar] [CrossRef]
- Dassios, Angelos, and Hongbiao Zhao. 2011. A dynamic contagion process. Advances in Applied Probability 43: 814–46. [Google Scholar] [CrossRef]
- Dassios, Angelos, and Hongbiao Zhao. 2012. Ruin by dynamic contagion claims. Insurance: Mathematics and Economics 51: 93–106. [Google Scholar] [CrossRef]
- Dassios, Angelos, and Hongbiao Zhao. 2017a. A generalised contagion process with an application to credit risk. International Journal of Theoretical and Applied Finance 20: 1–33. [Google Scholar] [CrossRef]
- Dassios, Angelos, and Hongbiao Zhao. 2017b. Efficient simulation of clustering jumps with CIR intensity. Operations Research 65: 1494–515. [Google Scholar] [CrossRef]
- Duffie, Darrell, Damir Filipović, and Walter Schachermayer. 2003. Affine processes and applications in finance. Annals of Applied Probability 13: 984–1053. [Google Scholar]
- Duffie, Darrell, Jun Pan, and Kenneth Singleton. 2000. Transform analysis and asset pricing for affine jump-diffusions. Econometrica 68: 1343–76. [Google Scholar] [CrossRef]
- Embrechts, Paul, Thomas Liniger, and Lu Lin. 2011. Multivariate Hawkes processes: An application to financial data. Journal of Applied Probability 48A: 367–78. [Google Scholar]
- Errais, Eymen, Kay Giesecke, and Lisa R. Goldberg. 2010. Affine point processes and portfolio credit risk. SIAM Journal on Financial Mathematics 1: 642–65. [Google Scholar] [CrossRef]
- Feller, William. 1951. Two singular diffusion problems. Annals of Mathematics 54: 173–82. [Google Scholar] [CrossRef]
- Gerber, Hans U. 1979. An Introduction to Mathematical Risk Theory. Philadelphia: S.S. Huebner Foundation for Insurance Education. [Google Scholar]
- Goovaerts, Marc J., Florent De Vylder, and Jean Haezendonck. 1984. Insurance Premiums. Amsterdam: North-Holland. [Google Scholar]
- Hawkes, Alan G. 1971a. Point spectra of some mutually exciting point processes. Journal of the Royal Statistical Society. Series B (Methodological) 33: 438–43. [Google Scholar] [CrossRef]
- Hawkes, Alan G. 1971b. Spectra of some self-exciting and mutually exciting point processes. Biometrika 58: 83–90. [Google Scholar] [CrossRef]
- Hawkes, Alan G., and David Oakes. 1974. A cluster process representation of a self-exciting process. Journal of Applied Probability 11: 493–503. [Google Scholar] [CrossRef]
- Jaisson, Thibault, and Mathieu Rosenbaum. 2015. Limit theorems for nearly unstable Hawkes processes. Annals of Applied Probability 25: 600–31. [Google Scholar] [CrossRef]
- Jang, Ji-Wook. 2004. Martingale approach for moments of discounted aggregate claims. Journal of Risk and Insurance 71: 201–11. [Google Scholar] [CrossRef]
- Jang, Ji-Wook. 2007. Jump diffusion processes and their applications in insurance and finance. Insurance: Mathematics and Economics 41: 62–70. [Google Scholar] [CrossRef]
- Jang, Jiwook, and Angelos Dassios. 2013. A bivariate shot noise self-exciting process for insurance. Insurance: Mathematics and Economics 53: 524–32. [Google Scholar] [CrossRef]
- Jang, Ji-Wook, and Yuriy Krvavych. 2004. Arbitrage-free premium calculation for extreme losses using the shot noise process and the Esscher transform. Insurance: Mathematics and Economics 35: 97–111. [Google Scholar] [CrossRef]
- Lando, David. 2004. Credit Risk Modeling: Theory and Applications. Princeton: Princeton University Press. [Google Scholar]
- Léveillé, Ghislain, and José Garrido. 2001. Moments of compound renewal sums with discounted claims. Insurance: Mathematics and Economics 28: 217–31. [Google Scholar]
- Ogata, Yosihiko. 1988. Statistical models for earthquake occurrences and residual analysis for point processes. Journal of the American Statistical Association 83: 9–27. [Google Scholar] [CrossRef]
- Ozaki, Tohru. 1979. Maximum likelihood estimation of Hawkes’ self-exciting point processes. Annals of the Institute of Statistical Mathematics 31: 145–55. [Google Scholar] [CrossRef]
- Stabile, Gabriele, and Giovanni Luca Torrisi. 2010. Risk processes with non-stationary Hawkes claims arrivals. Methodology and Computing in Applied Probability 12: 415–29. [Google Scholar] [CrossRef]
- Vere-Jones, D. 1975. Stochastic models for earthquake sequences. Geophysical Journal International 42: 811–26. [Google Scholar] [CrossRef]
- Vere-Jones, D. 1978. Earthquake prediction—A statistician’s view. Journal of Physics of the Earth 26: 129–46. [Google Scholar] [CrossRef]
- Vere-Jones, D., and T. Ozaki. 1982. Some examples of statistical estimation applied to earthquake data. Annals of the Institute of Statistical Mathematics 34: 189–207. [Google Scholar] [CrossRef]
- Zhu, Lingjiong. 2013a. Central limit theorem for nonlinear Hawkes processes. Journal of Applied Probability 50: 760–71. [Google Scholar] [CrossRef]
- Zhu, Lingjiong. 2013b. Ruin probabilities for risk processes with non-stationary arrivals and subexponential claims. Insurance: Mathematics and Economics 53: 544–50. [Google Scholar] [CrossRef]
- Zhu, Lingjiong. 2014. Limit theorems for a Cox-Ingersoll-Ross process with Hawkes jumps. Journal of Applied Probability 51: 699–712. [Google Scholar] [CrossRef]
- Zhu, Lingjiong. 2015. Large deviations for Markovian nonlinear Hawkes processes. Annals of Applied Probability 25: 548–81. [Google Scholar] [CrossRef]
| 1 | A Markovian Hawkes process is the one with exponential fertility rate. |
| 2 | A similar setup as Equation (2) for constructing dependency between the interest rate and default rate was presented in Lando (2004, p. 123). |
| Equation (18) | 24.28 | |
| , if there are no self-exciting jumps | Equation (19) | 6.18 |
| , if we only consider self-exciting jumps | Equation (20) | 7.77 |
| Equation (21) | 620.77 | |
| , if there are no self-exciting jumps | Equation (22) | 14.22 |
| , if we only consider self-exciting jumps | Equation (23) | 230.81 |
| (21) | (24) | ||
|---|---|---|---|
| 0.0 | 567.88 | 567.88 | 0.00 |
| 0.5 | 581.10 | 567.88 | 13.22 |
| 0.6 | 586.92 | 567.88 | 19.04 |
| 0.7 | 593.80 | 567.88 | 25.92 |
| 0.8 | 601.73 | 567.88 | 33.85 |
| 0.9 | 610.72 | 567.88 | 42.84 |
| 1.0 | 620.77 | 567.88 | 52.89 |
| (19) | (22) | (20) | (23) | (21) | (24) | |
|---|---|---|---|---|---|---|
| 10.00 | 6.18 | 14.22 | 1.16 | 1.28 | 15.91 | 11.75 |
| 5.00 | 6.18 | 14.22 | 1.28 | 1.58 | 18.03 | 13.35 |
| 1.00 | 6.18 | 14.22 | 2.86 | 15.17 | 72.77 | 59.89 |
| 0.50 | 6.18 | 14.22 | 7.77 | 230.81 | 620.77 | 567.88 |
| 0.25 | 6.18 | 14.22 | 57.40 | 26,376.00 | 46,440.00 | 45,156.00 |
| Equation (26) | 0.9419 | |
| , if there are no self-exciting jumps | Equation (27) | 0.9423 |
| , if we only consider self-exciting jumps | Equation (28) | 0.9552 |
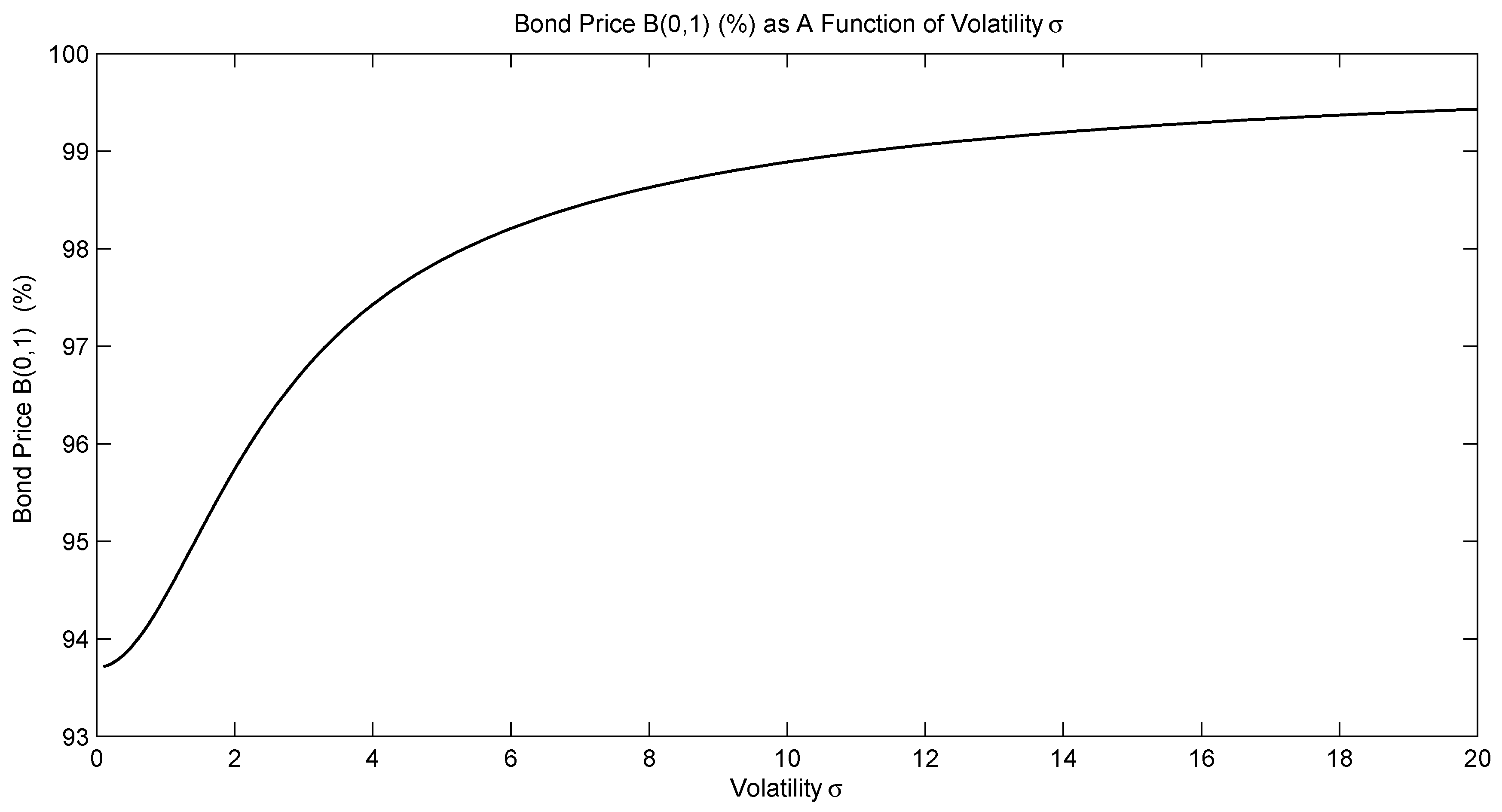
| 0.01 | 0.9368 |
| 0.1 | 0.9369 |
| 0.5 | 0.9389 |
| 0.8 | 0.9419 |
| 10 | 0.9889 |
| ∞ | 1 |
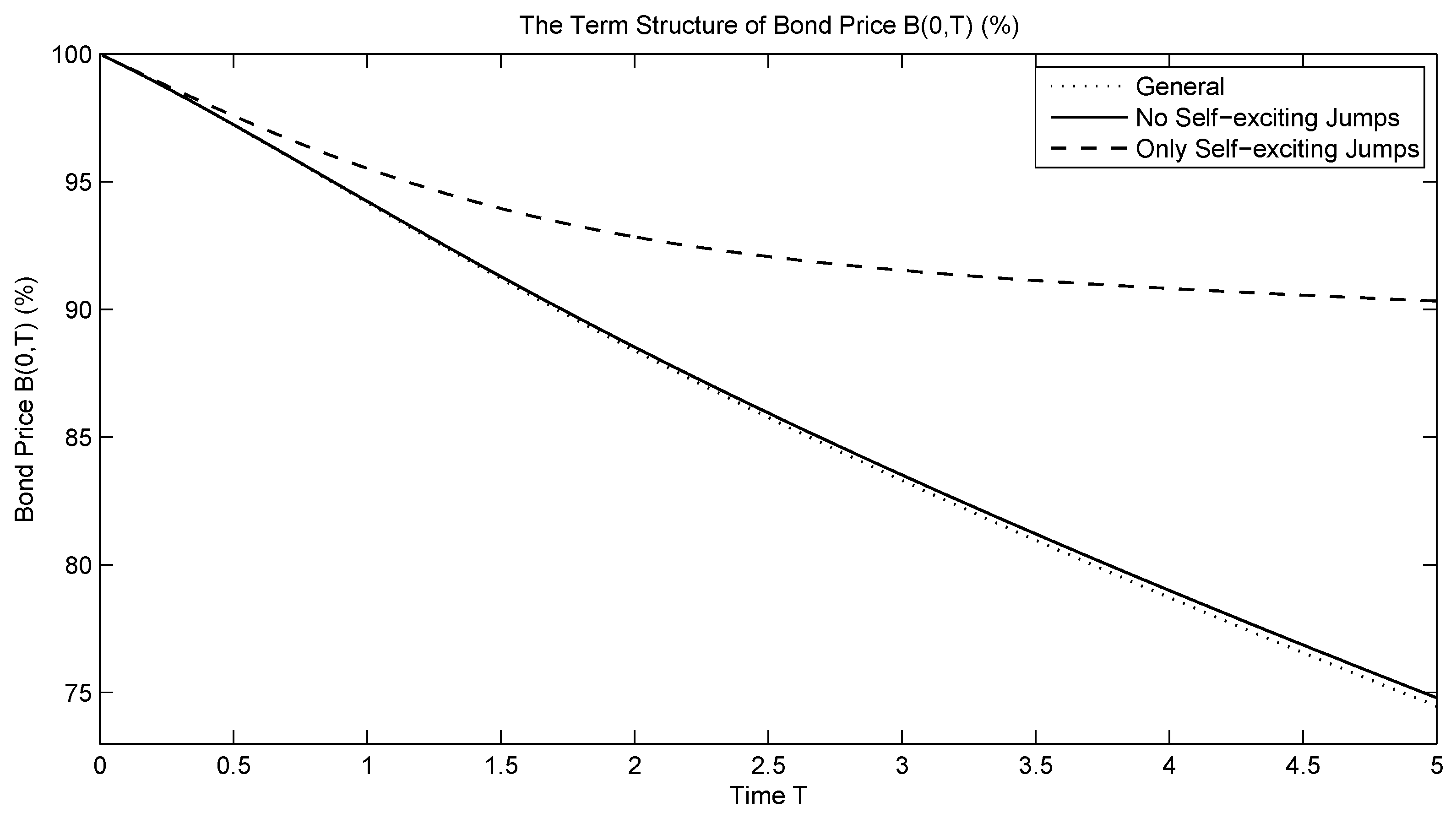
| (26) | (27) | |
|---|---|---|
| ∞ | 0.955201 | 0.955585 |
| 100 | 0.941880 | 0.942340 |
| 90 | 0.940422 | 0.940889 |
| 70 | 0.936278 | 0.936768 |
| 50 | 0.928904 | 0.929434 |
| 30 | 0.912734 | 0.912116 |
| 5 | 0.742420 | 0.743715 |
| 1 | 0.391674 | 0.393072 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dassios, A.; Jang, J.; Zhao, H. A Generalised CIR Process with Externally-Exciting and Self-Exciting Jumps and Its Applications in Insurance and Finance. Risks 2019, 7, 103. https://doi.org/10.3390/risks7040103
Dassios A, Jang J, Zhao H. A Generalised CIR Process with Externally-Exciting and Self-Exciting Jumps and Its Applications in Insurance and Finance. Risks. 2019; 7(4):103. https://doi.org/10.3390/risks7040103
Chicago/Turabian StyleDassios, Angelos, Jiwook Jang, and Hongbiao Zhao. 2019. "A Generalised CIR Process with Externally-Exciting and Self-Exciting Jumps and Its Applications in Insurance and Finance" Risks 7, no. 4: 103. https://doi.org/10.3390/risks7040103
APA StyleDassios, A., Jang, J., & Zhao, H. (2019). A Generalised CIR Process with Externally-Exciting and Self-Exciting Jumps and Its Applications in Insurance and Finance. Risks, 7(4), 103. https://doi.org/10.3390/risks7040103






