1. Introduction
Since their launch, credit default swaps (CDS) have been a frequent research topic. Researchers apply methods similar to those for other types of securities—such as stocks—to the empirical analysis of CDS spreads. Their purposes vary, including detecting the information content of these securities (
Blanco et al. 2005), assessing the risks of individual firms or sovereign countries (
Acharya et al. 2014), and finding the determinants of CDS spreads (
Galil et al. 2014).
However, unlike stock prices, whose values come from the values of the underlying entities, CDS spread values are derived from the risks of the reference entities and are typically between 0 and 1. As stocks and CDS are intrinsically different concepts, we cannot assume they have the same dynamic properties.
In addition, CDS spreads for large banks are an important input for calculating financial systemic risk, as shown by
Huang et al. (
2009,
2012a,
2012b). Thus, the dynamics of CDS spreads can provide some insight into the dynamics of overall financial systemic risk.
Given the intrinsically different natures of stocks and CDS, as well as the importance of CDS in both empirical research and systemic risk analysis, a rigorous time-series analysis of CDS spreads is needed. Different time-series tests have been developed in the literature, and many papers have applied them to studying the time-series properties of various macroeconomic or financial data. For example,
Kwiatkowski et al. (
1992) studied the unit root property of 14 annual time series of U.S. macroeconomics and stock price data.
Ng and Perron (
2001) tested the unit root hypothesis for inflation data from the G-7 countries.
Engle and Granger (
1987) used cointegration tests to show that consumption and income as well as long- and short-term interest rates are cointegrated, while wages and prices as well as nominal GNP and the nominal money measures of M1 and M3 are not. However, up to now, no study has been devoted to analyzing the time-series properties of CDS spreads.
The goal of this paper is to fill such a gap in the literature by providing a rigorous time-series analysis of CDS spreads. Specifically, we apply the augmented Dickey–Fuller, Phillips–Perron, Kwiatkowski–Phillips–Schmidt–Shin, and Ng–Perron tests to study the unit root property of CDS spreads, and we use the Phillips–Ouliaris–Hansen tests to determine whether they are cointegrated. The empirical sample consists of daily CDS spreads of six large U.S. banks that have been designated as global systemically important financial institutions (G-SIFIs). The sample period is from 2001 to 2018. The main findings of this paper are that it is log, not raw, CDS spreads that are unit root processes, and that the log CDS spreads of large U.S. banks are cointegrated. These findings imply that, even though the risks of individual banks may deviate from each other in the short run, there is a long-run relation that ties them together.
2. Data
For any given firm, there are multiple CDS contracts being traded at the same time. The sample CDS data in this paper are from the most actively traded U.S. CDS contracts—five-year maturity, senior unsecured (SNRFOR) tier, ex-restructuring (XR) document clause, and U.S. dollar denomination. As the transaction prices for CDS contracts are proprietary information, we use the publicly available daily CDS quote data provided by Markit.
The sample reference entities consist of six large U.S. banks: Bank of America (BAC), Citigroup (C), Goldman Sachs (GS), J.P. Morgan Chase (JPM), Morgan Stanley (MS), and Wells Fargo (WFC). These banks are chosen for three reasons. First, they are the reference entities of the first traded corporate CDS contracts since the launch of CDS trading in the early 2000s. Thus, their CDS spread time series are among the longest available, which facilitates the unit root study. Second, since the beginning of CDS trading, the CDS contracts of these banks are almost always among the top 10 most-traded CDS contracts, which ensures that their spreads capture risk accurately. Third, these six banks are also among the earliest U.S. financial institutions that were designated as G-SIFIs by the Financial Stability Board. Thus, the joint study of these reference entities can provide useful insight into overall U.S. financial systemic risk.
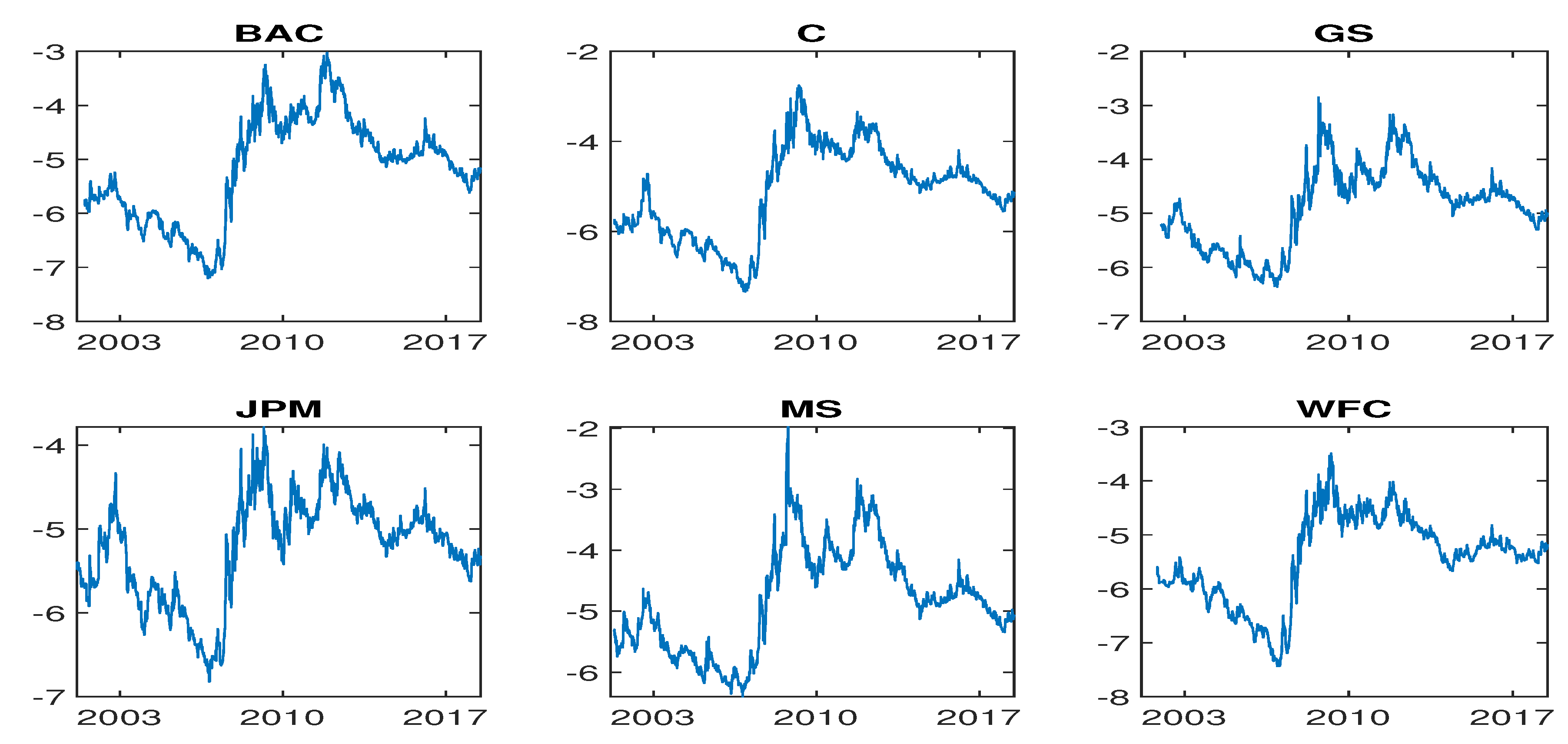
Figure 1, which plots the daily log CDS spreads of these sample banks from 2001 or 2002 (depending on the bank) to 29 June 2018, suggests that the CDS spread time series may not be covariance stationary.
The nonstationary feature can be revealed by some basic sample statistics.
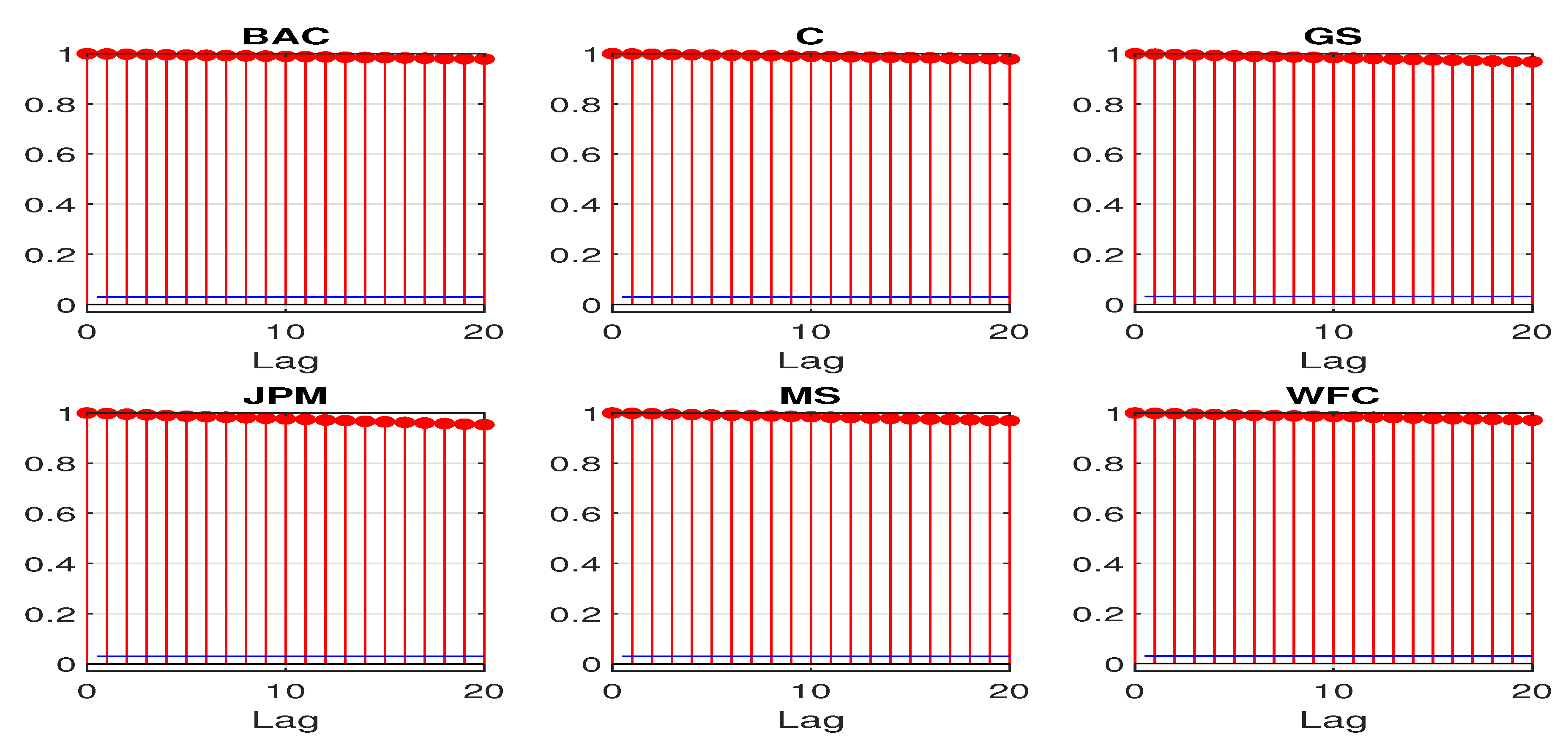
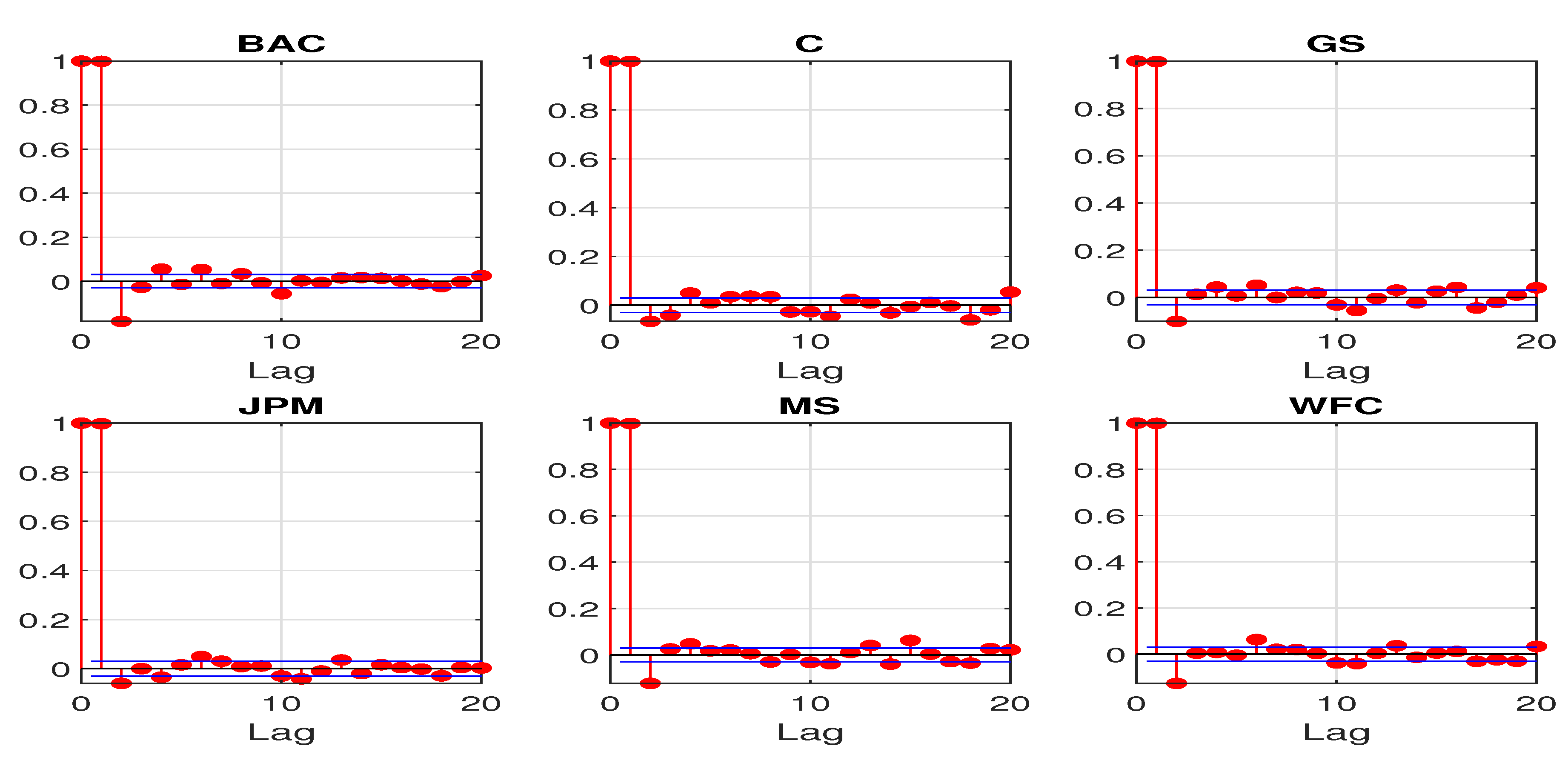
Figure 2 and
Figure 3 plot the first 20 sample autocorrelations and partial autocorrelations of the log CDS spreads. The sample autocorrelations for all the sample banks remain close to 1 even at lag 20. The sample partial autocorrelations at lag 1 are also almost 1 for all the sample banks. The above statistics all suggest a potential unit root for the daily log CDS spreads.
3. Covariance Stationary versus Unit Root
All of these tests depend on whether there is a time trend in the tested time series
, where
can be either raw or log CDS spreads.
Figure 1 shows a small positive upward trend in our CDS data, likely due to the market’s underestimation of the credit risk before the financial crisis and the subsequent correction. Thus, a time trend is included in the regression
The null hypothesis of a unit root is , and the alternative hypothesis is .
To allow for potential serial correlations in
of Equation (
1), we first implement the augmented Dickey–Fuller (ADF) tests based on the following autoregressive (AR) regression:
where
. The number of AR lags
p is determined by starting with a large lag (for example, 30), performing a
t test that
, and, if it is not rejected, then successively performing an
F test that
until
is rejected for some
l. Then, the recommended number of AR lags is
.
The ADF test statistics are computed as follows:
where
,
, and
are the ordinary least squares (OLS) estimates of the corresponding population parameters. The simulated critical values of these tests for the sample sizes of 4000 and 5000 (as our empirical sample sizes are in this range) and 100,000 Monte Carlo repetitions are reported in the top of
Table 1 in the “
” and “
t” rows.
The computed ADF
and
t values in the bottom of
Table 1 for the log CDS spreads show that the null hypothesis of a unit root (
) cannot be rejected even at the 15% significance level for the six sample banks, while it is marginally rejected for Morgan Stanley at the 10% level by the ADF
test.
The complete null hypothesis
can be tested by a standard
F test formula, but its asymptotic distribution is nonstandard. We report the simulated critical values in the “
F” rows and the computed test statistics in the “
F” columns in
Table 1. The “
F” test results show that the null hypothesis of a unit root for the log or raw CDS spreads cannot be rejected at the 10% significance level.
The PP tests are the nonparametric counterpart to the parametric ADF tests. Moreover, the PP tests directly account for the potential serial correlations in the residual
, thus the AR regression takes the simple form of Equation (
1). A summary of the PP test formulae is available in the work of
Hamilton (
1994) and reproduced in
Appendix A.1. The truncation parameter is set at
for the sample size
T between 4000 and 5000.
The PP test results in
Table 1 are very similar to, but sharper than, the ADF test results. The null hypothesis of a unit root for the log CDS spreads cannot be rejected even at the 15% significance level for the six sample banks. In contrast, for the raw CDS spreads, the null hypothesis is rejected at the 5% significance level for Goldman Sachs, J.P. Morgan Chase, and Wells Fargo, and at the 1% level for Morgan Stanley.
Kwiatkowski et al. (
1992) noted that the above ADF and PP tests for the null hypothesis of a unit root may have low powers when
is less than, but very close to, 1; thus, they suggested flipping the null and alternative hypotheses. As our ADF and PP tests do not reject the null of a unit root for log CDS spreads, we implement the KPSS test to confirm their unit root property. The KPSS test is essentially an upper-tail Lagrange Multiplier (LM) test. We follow the setup in (
Kwiatkowski et al. 1992) that has a time trend and summarize the related formulae in
Appendix A.2. The lag truncation parameter is set at
.
As the asymptotic distribution for the KPSS test is nonstandard, we simulate LM critical values from its asymptotic distribution
, where
is the second-level Brownian bridge given by
where
is a standard Brownian motion. In the numerical simulations, we approximate
by partial sums of
random variables with 4000 and 5000 steps for the corresponding sample sizes. The number of Monte Carlo repetitions is 100,000. Comparing the computed LM test values with the simulated critical values in
Table 1, the null hypothesis of covariance stationarity is rejected for both the log and raw CDS spreads at the 1% significance level. This unit root finding for CDS spreads is very similar to the unit root finding for U.S. stock prices in (
Kwiatkowski et al. 1992), even though the CDS data frequency in this paper is daily while their stock data frequency is annual, and even though the CDS data in this paper cover the most recent period (2001–2018) while their stock data end in 1970. Moreover, we study both the raw and log CDS spreads, while
Kwiatkowski et al. (
1992) used the raw stock prices.
The above results of the ADF, PP, and KPSS tests show clear evidence of unit root for the log CDS spreads, but the evidence is mixed for the raw CDS spreads.
Schwert (
2002) found that if the data generation process has an moving average (MA) component—for example,
—and the MA parameter
is close to negative 1, then the ADF and PP tests tend to over-reject the null hypothesis of a unit root.
Perron and Ng (
1996) (PN) proposed modified PP tests to mitigate this size distortion problem. In addition, as an alternative to the above KPSS test to solve the low-power problem,
Elliott et al. (
1996) (ERS) proposed an efficient version of the ADF t-statistic and called it the DF-GLS (generalized least squares) test. Combining ERS’s GLS detrending procedure and PN’s modified PP tests,
Ng and Perron (
2001) (NP) created the efficient modified PP tests, called
, for both good size and good power properties.
1 They also proposed modified information criteria to select the optimal truncation lag parameter.
Appendix A.3 summarizes the technical details of NP’s
test procedure.
To confirm the above findings of the ADF, PP, and KPSS tests, we run NP’s
tests on the same log and raw CDS spread data. The top of
Table 2 reports the critical values simulated from the asymptotic distributions of the
tests, as summarized in
Appendix A.3, for the setup of a unit root process with a drift. The Brownian motion in the asymptotic distributions is approximated by partial sums of
random variables with 4000 and 5000 steps for the corresponding sample sizes. The number of Monte Carlo repetitions is 100,000. The bottom of
Table 2 reports the computed test statistics and the associated optimal truncation lag parameter
k set to minimize the modified Akaike information criterion (MAIC) developed in (
Ng and Perron 2001).
The
test values in the bottom of
Table 2 for the log CDS spreads show that the null hypothesis of a unit root cannot be rejected at the 10% significance level for the six sample banks. In comparison, the evidence for the raw CDS spreads is relatively mixed. The unit root null hypothesis cannot be rejected at the 10% level for Bank of America, Citigroup, and Goldman Sachs; it can be marginally rejected at the 10% level for J.P. Morgan Chase and for Wells Fargo by
and
; and it can be rejected at the 5% level for Morgan Stanley. Indeed, the mixed evidence for the raw CDS spreads is very similar to the mixed findings in (
Ng and Perron 2001) for the inflation rate data from the G-7 countries between 1960:Q2 and 1997:Q2. Thus, the clear unit root evidence for the log CDS spreads and the mixed evidence for the raw CDS spreads revealed by the
tests confirm the above findings by the ADF, PP, and KPSS tests.
In summary, whether the tests are parametric or nonparametric, whether the null hypothesis is unit root or covariance stationary, and whether the original or modified tests are used, the empirical evidence shows that it is log, not raw, CDS spreads that are unit root processes. The unit root property of log CDS spreads implies that the efficient market hypothesis holds for the CDS market: it is hard for investors to beat the CDS market. The best predictor for the log CDS spread tomorrow is the log CDS spread today. Meanwhile, the first difference of log CDS spreads, not raw CDS spreads, is just the return of holding a CDS contract, if we treat CDS spreads as the prices for the CDS contract. The unit root property of log CDS spreads thus implies that CDS returns are covariance stationary.
4. Cointegration
As all of the sample entities are U.S. G-SIFI banks
2, whether their CDS spreads are cointegrated has implications for overall financial systemic risk. Thus, we conduct the Phillips–Ouliaris–Hansen cointegration tests on the six sample banks. Given the log CDS spreads of each pair of banks,
and
, we run the following OLS regression:
Then, we calculate the ADF and PP tests on the time series of residuals
, with the setup of no constant term in the OLS regression:
If the null hypothesis that is a unit root process is rejected, then and are cointegrated.
As the ADF and PP tests are based on the estimated residuals
, instead of the original data,
Phillips and Ouliaris (
1990) show that their asymptotic distributions are different from those in the univariate unit root tests. Moreover, according to the results of
Section 3, the true process for individual log CDS spreads is a random walk with a drift:
Hansen (
1992) noted that the asymptotic results change when a drift is included in the true process. Thus, we simulate the new critical values for the setup of a constant term and one explanatory variable in the estimated cointegrating regression (Equation (
6)), the true process of a random walk with a drift for individual time series (Equation (
7)), and the sample sizes of 4000 and 5000, respectively. The top of
Table 3 reports the simulated critical values based on 100,000 Monte Carlo repetitions, and the bottom of
Table 3 reports the computed
(lower triangles) and
t (upper triangles) values.
The ADF tests in
Table 3 reject the null hypothesis that
has a unit root at the 5% significance level for most pairs of sample banks, except for the BAC-C and BAC-WFC pairs. However, the PP
and
t tests for all pairs of sample banks are significant at the 5% or even 1% level.
Phillips and Ouliaris (
1990) noticed that the ADF
t and PP
tests have slower rates of divergence under the alternative hypothesis of cointegration, thus, in large samples such as those in this study, the PP
t test has better power properties. Thus, the significant results in the upper triangle of the PP tests panel are relatively more reliable, and we conclude that the daily log CDS spreads of large U.S. banks are generally cointegrated. This cointegration relation among log CDS spreads is very similar to the cointegration finding in (
Engle and Granger 1987) for another pair of financial time series: long- and short-term interest rates.
The cointegration among the log CDS spreads of large U.S. banks means that, even though the risks of individual banks may deviate from each other in the short run, there is a long-run relation that ties their risks together. Thus, for portfolio diversification, investors should hold more securities than simply a basket of CDS contracts referring to large U.S. banks to reduce the effect of their common long-run risks. Moreover, foreign investors may face additional layers of risks when trading CDS contracts. As the most actively traded U.S. CDS contracts are denominated in U.S. dollars, foreign investors, unless they have cash flows in U.S. dollars, have to face either the exchange rate risk when converting their local currencies to U.S. dollars in order to trade these liquid CDS contracts, or the liquidity risk when trading the CDS contracts denominated in their local currencies as these CDS contracts are much less actively traded.
5. Conclusions
This paper conducts a rigorous time-series analysis of single-name CDS spreads. To study the univariate unit root property, we apply the ADF, PP, KPSS, and NP tests. To study the multivariate cointegration relationship, we apply the Phillips–Ouliaris–Hansen cointegration tests. The empirical sample consists of six U.S. G-SIFI banks for the period from 2001 to 2018. The main empirical findings are that it is log, not raw, CDS spreads that are clearly unit root processes. Moreover, the log CDS spreads of the U.S. G-SIFI banks are cointegrated, pointing to a long-run relation that ties together the risks of these banks.
The above empirical findings provide some practical guidance for both empirical CDS analysis and financial systemic risk analysis. First, in terms of empirical analysis, as raw CDS spreads do not clearly exhibit either covariance stationarity or a unit root pattern, we should take the logarithm of raw CDS spreads before putting them in regressions. Moreover, as log CDS spreads have a unit root, we may need to take the first difference if we run regressions on a bank’s CDS and other variables of interest to avoid the potential spurious regression problem. However, as the log CDS spreads of large U.S. banks are cointegrated, if we analyze these banks jointly, then error correction representation (
Engle and Granger 1987) is the right way to go, because, if we take the first difference in the joint analysis, we are going to lose the long-run trend that ties together these banks. Second, in terms of financial system risk, as the CDS spreads of these G-SIFI banks are an important driving force for U.S. financial systemic risk, the persistence of their CDS spreads implies that financial systemic risk is also persistent, even if it is not a unit root process. This is similar to other risk measures, such as conditional volatility or correlations. The long-run trend that ties together these banks implies that, in the long run, the risks of these banks will move together with overall financial systemic risk.
Consequently, there are at least two policy implications. First, in monitoring systemic risk, policymakers should focus on long-run trends rather than short-run fluctuations of individual CDS spreads. Second, in controlling systemic risk, policy measures that reduce the long-run risks of individual banks, such as stress testing and capital buffers, are helpful in mitigating overall systemic risk.