Logarithmic Asymptotics for Probability of Component-Wise Ruin in a Two-Dimensional Brownian Model

Abstract

We consider a two-dimensional ruin problem where the surplus process of business lines is modelled by a two-dimensional correlated Brownian motion with drift. We study the ruin function $P\left(u\right)$ for the component-wise ruin (that is both business lines are ruined in an infinite-time horizon), where u is the same initial capital for each line. We measure the goodness of the business by analysing the adjustment coefficient, that is the limit of $-lnP\left(u\right)/u$ as u tends to infinity, which depends essentially on the correlation $\rho$ of the two surplus processes. In order to work out the adjustment coefficient we solve a two-layer optimization problem.

1. Introduction

In classical risk theory, the surplus process of an insurance company is modelled by the compound Poisson risk model. For both applied and theoretical investigations, calculation of ruin probabilities for such model is of particular interest. In order to avoid technical calculations, diffusion approximation is often considered e.g., (Asmussen and Albrecher 2010; Grandell 1991; Iglehart 1969; Klugman et al. 2012), which results in tractable approximations for the interested finite-time or infinite-time ruin probabilities. The basic premise for the approximation is to let the number of claims grow in a unit time interval and to make the claim sizes smaller in such a way that the risk process converges to a Brownian motion with drift. Precisely, the Brownian motion risk process is defined by

$$\begin{array}{c}\hfill R\left(t\right)=x+pt-\sigma B\left(t\right),t\ge 0,\end{array}$$

where $x>0$ is the initial capital, $p>0$ is the net profit rate and $\sigma B\left(t\right)$ models the net loss process with $\sigma >0$ the volatility coefficient. Roughly speaking, $\sigma B\left(t\right)$ is an approximation of the total claim amount process by time t minus its expectation, the latter is usually called the pure premium amount and calculated to cover the average payments of claims. The net profit, also called safety loading, is the component which protects the company from large deviations of claims from the average and also allows an accumulation of capital. Ruin related problems for Brownian models have been well studied; see, for example, Asmussen and Albrecher (2010); Gerber and Shiu (2004).

In recent years, multi-dimensional risk models have been introduced to model the surplus of multiple business lines of an insurance company or the suplus of collaborating companies (e.g., insurance and reinsurance). We refer to Asmussen and Albrecher (2010) [Chapter XIII 9] and Avram and Loke (2018); Avram and Minca (2017); Avram et al. (2008a, 2008b); Albrecher et al. (2017); Azcue and Muler (2018); Azcue et al. (2019); Foss et al. (2017); Ji and Robert (2018) for relevant recent discussions. It is concluded in the literature that in comparison with the well-understood 1-dimensional risk models, study of multi-dimensional risk models is much more challenging. It was shown recently in Delsing et al. (2019) that multi-dimensional Brownian model can serve as approximation of a multi-dimensional classical risk model in a Markovian environment. Therefore, obtained results for multi-dimensional Brownian model can serve as approximations of the multi-dimensional classical risk models in a Markovian environment; ruin probability approximation has been used in the aforementioned paper. Actually, multi-dimensional Brownian models have drawn a lot of attention due to its tractability and practical relevancy.

A d-dimensional Brownian model can be defined in a matrix form as

$$\begin{array}{c}\hfill \mathit{R}\left(t\right)=\mathit{x}+\mathit{p}t-\mathit{X}\left(t\right),t\ge 0,\mathrm{with}\mathit{X}\left(t\right)=A\mathit{B}\left(t\right),\end{array}$$

where $\mathit{x}={(x_1,\cdots ,x_d)}^{\top },\mathit{p}={(p_1,\cdots ,p_d)}^{\top }\in {(0,\infty )}^d$ are, respectively, (column) vectors representing the initial capital and net profit rate, $A\in {\mathbb{R}}^{d\times d}$ is a non-singular matrix modelling dependence between different business lines and $\mathit{B}\left(t\right)={(B_1\left(t\right),\dots ,B_d\left(t\right))}^{\top },t\ge 0$ is a standard d-dimensional Brownian motion (BM) with independent coordinates. Here ⊤ is the transpose sign. In what follows, vectors are understood as column vectors written in bold letters.

Different types of ruin can be considered in multi-dimensional models, which are relevant to the probability that the surplus of one or more of the business lines drops below zero in a certain time interval $[0,T]$ with T either a finite constant or infinity. One of the commonly studied is the so-called simultaneous ruin probability defined as

$$Q_T\left(\mathit{x}\right):=\mathbb{P}\left\{{\exists }_{t\in [0,T]}\bigcap _{i=1}^d\{R_i\left(t\right)<0\}\right\},$$

which is the probability that at a certain time $t\in [0,T]$ all the surpluses become negative. Here for $T<\infty$, $Q_T\left(\mathit{x}\right)$ is called finite-time simultaneous ruin probability, and $Q_{\infty }\left(\mathit{x}\right)$ is called infinite-time simultaneous ruin probability. Simultaneous ruin probability, which is essentially the hitting probability of $\mathit{R}\left(t\right)$ to the orthant $\{\mathit{y}\in {\mathbb{R}}^d:y_i<0,i=1,\dots ,d\}$, has been discussed for multi-dimensional Brownian models in different contexts; see Dȩbicki et al. (2018); Garbit and Raschel (2014). In Garbit and Raschel (2014), for fixed $\mathit{x}$ the asymptotic behaviour of $Q_T\left(\mathit{x}\right)$ as $T\to \infty$ has been discussed. Whereas, in Dȩbicki et al. (2018), the asymptotic behaviour, as $u\to \infty$, of the infinite-time ruin probability $Q_{\infty }\left(\mathit{x}\right)$, with $\mathit{x}=\mathit{\alpha }u={({\alpha }_{1}u,{\alpha }_{2}u,\dots ,{\alpha }_{d}u)}^{\top },{\alpha }_i>0,1\le i\le d$ has been obtained. Note that it is common in risk theory to derive the later type of asymptotic results for ruin probabilities; see, for example, Avram et al. (2008a); Embrechts et al. (1997); Mikosch (2008).

Another type of ruin probability is the component-wise (or joint) ruin probability defined as

$$\begin{array}{c}\hfill P_T\left(\mathit{x}\right):=\mathbb{P}\left\{\bigcap _{i=1}^d\{{\exists }_{t\in [0,T]}{R}_i\left(t\right)<0\}\right\}=\mathbb{P}\left\{\bigcap _{i=1}^d\{\underset{t_i\in [0,T]}{sup}(X_i\left(t_i\right)-p_i{t}_i)>x_i\}\right\},\end{array}$$

(1)

which is the probability that all surpluses get below zero but possibly at different times. It is this possibility that makes the study of $P_T\left(\mathit{x}\right)$ more difficult.

The study of joint distribution of the extrema of multi-dimensional BM over finite-time interval has been proved to be important in quantitative finance; see, for example, He et al. (1998); Kou and Zhong (2016). We refer to Delsing et al. (2019) for a comprehensive summary of related results. Due to the complexity of the problem, two-dimensional case has been the focus in the literature and for this case some explicit formulas can be obtained by using a PDE approach. Of particular relevance to the ruin probability $P_T\left(\mathit{x}\right)$ is a result derived in He et al. (1998) which shows that

$$\begin{array}{c}\mathbb{P}\left\{\underset{t\in [0,T]}{sup}(X_1\left(t\right)-p_{1}t)\le x_1,\underset{s\in [0,T]}{sup}(X_2\left(s\right)-p_{2}s)\le x_2\right\}\hfill \\ =e^{a_1{x}_1+a_2{x}_2+bT}f(x_1,x_2,T),\hfill \end{array}$$

where $a_1,a_2,b$ are known constants and f is a function defined in terms of infinite-series, double-integral and Bessel function. Using the above formula one can derive an expression for $P_T\left(\mathit{x}\right)$ in two-dimensional case as follows

$$\begin{array}{ccc}\hfill P_T\left(\mathit{x}\right)& =& 1-\mathbb{P}\left\{\underset{t\in [0,T]}{sup}(X_1\left(t\right)-p_{1}t)\le x_1\right\}-\mathbb{P}\left\{\underset{s\in [0,T]}{sup}(X_2\left(s\right)-p_{2}s)\le x_2\right\}\hfill \\ & & +\mathbb{P}\left\{\underset{t\in [0,T]}{sup}(X_1\left(t\right)-p_{1}t)\le x_1,\underset{s\in [0,T]}{sup}(X_2\left(s\right)-p_{2}s)\le x_2\right\},\hfill \end{array}$$

(2)

where the expression for the distribution of single supremum is also known; see He et al. (1998). Note that even though we have obtained explicit expression of $P_T\left(\mathit{x}\right)$ in (2) for the two-dimensional case, it seems difficult to derive the explicit form of the corresponding infinite-time ruin probability $P_{\infty }\left(\mathit{x}\right)$ by simply putting $T\to \infty$ in (2).

By assuming $\mathit{x}=\mathit{\alpha }u={({\alpha }_{1}u,{\alpha }_{2}u,\dots ,{\alpha }_{d}u)}^{\top },{\alpha }_i>0,1\le i\le d$, we aim to analyse the asymptotic behaviour of the infinite-time ruin probability $P_{\infty }\left(\mathit{x}\right)$ as $u\to \infty$. Applying Theorem 1 in Dȩbicki et al. (2010) we arrive at the following logarithmic asymptotics

$$\begin{array}{ccc}\hfill -\frac{1}{u}ln{P}_{\infty }\left(\mathit{x}\right)& \sim & \frac{1}{2}\underset{\mathit{t}>\mathbf{0}}{inf}\underset{\mathit{v}\ge \alpha +\mathit{p}\mathit{t}}{inf}{\mathit{v}}^{\top }{\sum }_{\mathit{t}}^{-1}\mathit{v},\mathrm{as}u\to \infty \hfill \end{array}$$

(3)

provided ${\sum }_{\mathit{t}}$ is non-singular, where $\mathit{pt}:={(p_1{t}_1,\cdots ,p_d{t}_d)}^{\top }$, inequality of vectors are meant component-wise, and ${\sum }_{\mathit{t}}^{-1}$ is the inverse matrix of the covariance function ${\sum }_{\mathit{t}}$ of $(X_1\left(t_1\right),\cdots ,X_d\left(t_d\right))$, with $\mathit{t}={(t_1,\cdots ,t_d)}^{\top }$ and $\mathbf{0}={(0,\cdots ,0)}^{\top }\in {\mathbb{R}}^d$. Let us recall that conventionally for two given positive functions $f(·)$ and $h(·)$, we write $f\left(x\right)\sim h\left(x\right)$ if ${lim}_{x\to \infty }f\left(x\right)/h\left(x\right)=1$.

For more precise analysis on $P_{\infty }\left(\mathit{x}\right)$, it seems crucial to first solve the two-layer optimization problem in (3) and find the optimization points ${\mathit{t}}_0$. As it can be recognized in the following, when dealing with d-dimensional case with $d>2$ the calculations become highly nontrivial and complicated. Therefore, in this contribution we only discuss a tractable two-dimensional model and aim for an explicit logarithmic asymptotics by solving the minimization problem in (3).

In the classical ruin theory when analysing the compound Poisson model or Sparre Andersen model, the so-called adjustment coefficient is used as a measure of goodness; see, for example, Asmussen and Albrecher (2010) or Rolski et al. (2009). It is of interest to obtain the solution of the minimization problem in (3) from a practical point of view, as it can be seen as an analogue of the adjustment coefficient and thus we could get some insights about the risk that the company is facing. As discussed in Asmussen and Albrecher (2010) and Li et al. (2007) it is also of interest to know how the dependence between different risks influences the joint ruin probability, which can be easily analysed through the obtained logarithmic asymptotics; see Remark 2.

The rest of this paper is organised as follows. In Section 2, we formulate the two-dimensional Brownian model and give the main results of this paper. The main lines of proof with auxiliary lemmas are displayed in Section 3. In Section 4 we conclude the paper. All technical proofs of the lemmas in Section 3 are presented in Appendix A.

2. Model Formulation and Main Results

Due to the fact that component-wise ruin probability $P_{\infty }\left(\mathit{x}\right)$ does not change under scaling, we can simply assume that the volatility coefficient for all business lines is equal to 1. Furthermore, noting that the timelines for different business lines should be distinguished as shown in (1) and (3), we introduce a two-parameter extension of correlated two-dimensional BM defined as

$$\left(X_1\left(t\right),X_2\left(s\right)\right)=\left(B_1\left(t\right),\rho B_1\left(s\right)+\sqrt{1-{\rho }^2}{B}_2\left(s\right)\right),t,s\ge 0,$$

with $\rho \in (-1,1)$ and mutually independent Brownian motions $B_1,B_2$. We shall consider the following two dependent insurance risk processes

$$R_i\left(t\right)=u+{\mu }_{i}t-X_i\left(t\right),t\ge 0,i=1,2,$$

where ${\mu }_1,{\mu }_2>0$ are net profit rates, u is the initial capital (which is assumed to be the same for both business lines, as otherwise, the calculations become rather complicated). We shall assume without loss of generality that ${\mu }_1\le {\mu }_2$. Here, ${\mu }_i$ is different from $p_i$ (see (1)) in the sense that it corresponds to the (scaled) model with volatility coefficient standardized to be 1.

In this contribution, we shall focus on the logarithmic asymptotics of

$$\begin{array}{ccc}\hfill P\left(u\right):=P_{\infty }\left(u{(1,1)}^{\top }\right)& =& \mathbb{P}\left\{\{{\exists }_{t\ge 0}{R}_1\left(t\right)<0\}\cap \{{\exists }_{s\ge 0}{R}_2\left(s\right)<0\}\right\}\hfill \\ & =& \mathbb{P}\left\{\underset{t\ge 0}{sup}(X_1\left(t\right)-{\mu }_{1}t)>u,\underset{s\ge 0}{sup}(X_2\left(s\right)-{\mu }_{2}s)>u\right\},\mathrm{as}u\to \infty .\hfill \end{array}$$

(4)

Define

$$\begin{array}{c}\hfill {\widehat{\rho }}_1=\frac{{\mu }_1+{\mu }_2-\sqrt{{({\mu }_1+{\mu }_2)}^2-4{\mu }_1({\mu }_2-{\mu }_1)}}{4{\mu }_1}\in [0,\frac{1}{2}),{\widehat{\rho }}_2=\frac{{\mu }_1+{\mu }_2}{2{\mu }_2}\end{array}$$

(5)

and let

$$\begin{array}{c}\hfill t^{*}=t^{*}\left(\rho \right)=s^{*}=s^{*}\left(\rho \right):=\sqrt{\frac{2(1-\rho )}{{\mu }_1^2+{\mu }_2^2-2\rho {\mu }_1{\mu }_2}}.\end{array}$$

(6)

The following theorem constitutes the main result of this contribution.

Theorem 1.

For the joint infinite-time ruin probability (4) we have, as $u\to \infty$,

$$\begin{array}{c}\hfill -\frac{log\left(P\right(u\left)\right)}{u}\sim \left\{\begin{array}{cc}2({\mu }_2+(1-2\rho ){\mu }_1),\hfill & \mathit{if}-1<\rho \le {\widehat{\rho }}_1;\hfill \\ \frac{{\mu }_1+{\mu }_2+2/t^{*}}{1+\rho },\hfill & \mathit{if}{\widehat{\rho }}_1<\rho <{\widehat{\rho }}_2;\hfill \\ 2{\mu }_2,\hfill & \mathit{if}{\widehat{\rho }}_2\le \rho <1.\hfill \end{array}\right.\end{array}$$

Remark 2.

(a) Following the classical one-dimensional risk theory we can call quantities on the right hand side in Theorem 1 as adjustment coefficients. They serve sometimes as a measure of goodness for a risk business.

(b) One can easily check that adjustment coefficient as a function of ρ is continuous, strictly decreasing on $(-1,{\widehat{\rho }}_2]$ and it is constant, equal to $2{\mu }_2$ on $[{\widehat{\rho }}_2,1)$. This means that as the two lines of business becomes more positively correlated the risk of ruin becomes larger, which is consistent with the intuition.

Define

$$\begin{gathered} \begin{array}{c}\hfill g(t,s):={\displaystyle \underset{x\ge 1+{\mu }_{1}t \\ y\ge 1+{\mu }_{2}s}{inf}}(x,y){\sum }_{ts}^{-1}{(x,y)}^{\top },t,s>0,\end{array} \end{gathered}$$

(7)

where ${\sum }_{ts}^{-1}$ is the inverse matrix of ${\sum }_{ts}=\left(\begin{array}{cc}t& \rho t\wedge s\\ \rho t\wedge s& s\end{array}\right),$ with $t\wedge s=min(t,s)$ and $\rho \in (-1,1)$.

The proof of Theorem 1 follows from (3) which implies that the logarithmic asymptotics for $P\left(u\right)$ is of the form

$$\begin{array}{ccc}\hfill -\frac{1}{u}lnP\left(u\right)& \sim & \frac{g\left({\mathit{t}}_0\right)}{2},u\to \infty ,\hfill \end{array}$$

(8)

where

$$\begin{array}{c}\hfill g\left({\mathit{t}}_0\right)=\underset{(t,s)\in {(0,\infty )}^2}{inf}g(t,s),\end{array}$$

(9)

and Proposition 3 below, wherein we list dominating points ${\mathit{t}}_0$ that optimize the function g over ${(0,\infty )}^2$ and the corresponding optimal values $g\left({\mathit{t}}_0\right)$.

In order to solve the two-layer minimization problem in (9) (see also (7)) we define for $t,s>0$ the following functions:

$$\begin{array}{c}{g}_1\left(t\right)=\frac{{(1+{\mu }_{1}t)}^2}{t},g_2\left(s\right)=\frac{{(1+{\mu }_{2}s)}^2}{s},\hfill \\ g_3(t,s)=(1+{\mu }_{1}t,1+{\mu }_{2}s){\sum }_{ts}^{-1}{(1+{\mu }_{1}t,1+{\mu }_{2}s)}^{\top }.\hfill \end{array}$$

Since $t\wedge s$ appears in the above formula, we shall consider a partition of the quadrant ${(0,\infty )}^2$, namely

$$\begin{array}{c}\hfill {(0,\infty )}^2=A\cup L\cup B,A=\{s<t\},L=\{s=t\},B=\{s>t\}.\end{array}$$

(10)

For convenience we denote $\overline{A}=\{s\le t\}=A\cup L$ and $\overline{B}=\{s\ge t\}=B\cup L$. Hereafter, all sets are defined on ${(0,\infty )}^2$, so $(t,s)\in {(0,\infty )}^2$ will be omitted.

Note that $g_3(t,s)$ can be represented in the following form:

$$\begin{array}{ccc}\hfill g_3(t,s)& =& \left\{\begin{array}{cc}{g}_A(t,s):=\frac{{(1+{\mu }_{2}s)}^2}{s}+\frac{{((1+{\mu }_{1}t)-\rho (1+{\mu }_{2}s))}^2}{t-{\rho }^{2}s},& \mathrm{if}(t,s)\in \overline{A}\\ g_B(t,s):=\frac{{(1+{\mu }_{1}t)}^2}{t}+\frac{{((1+{\mu }_{2}s)-\rho (1+{\mu }_{1}t))}^2}{s-{\rho }^{2}t},& \mathrm{if}(t,s)\in \overline{B}.\end{array}\right.\hfill \end{array}$$

(11)

Denote further

$$\begin{array}{c}\hfill g_L\left(s\right):=g_A(s,s)=g_B(s,s)=\frac{{(1+{\mu }_{1}s)}^2+{(1+{\mu }_{2}s)}^2-2\rho (1+{\mu }_{1}s)(1+{\mu }_{2}s)}{(1-{\rho }^2)s},s>0.\end{array}$$

(12)

In the next proposition we identify the so-called dominating points, that is, points ${\mathit{t}}_0$ for which function defined in (7) achieves its minimum. This identification might also be useful for deriving a more subtle asymptotics for $P\left(u\right)$.

Notation:In the following, in order to keep the notation consistent, $\rho \le {\mu }_1/{\mu }_2$ is understood as $\rho <1$ if ${\mu }_1={\mu }_2.$

Proposition 3.

(i) 

Suppose that $-1<\rho <0$.

For ${\mu }_1<{\mu }_2$ we have

$$\begin{array}{c}\hfill g\left({\mathit{t}}_0\right)=g_A(t_A,s_A)=4({\mu }_2+(1-2\rho ){\mu }_1),\end{array}$$

where, $(t_A,s_A)=(t_A\left(\rho \right),s_A\left(\rho \right)):=\left(\frac{1-2\rho }{{\mu }_1},\frac{1}{{\mu }_2-2{\mu }_1\rho }\right)$ is the unique minimizer of $g(t,s),(t,s)\in {(0,\infty )}^2$.

For ${\mu }_1={\mu }_2=:\mu$ we have

$$\begin{array}{c}\hfill g\left({\mathit{t}}_0\right)=g_A(t_A,s_A)=g_B(t_B,s_B)=8(1-\rho )\mu ,\end{array}$$

where $(t_A,s_A)=\left(\frac{1-2\rho }{\mu },\frac{1}{(1-2\rho )\mu }\right)\in A,(t_B,s_B):=\left(\frac{1}{(1-2\rho )\mu },\frac{1-2\rho }{\mu }\right)\in B$ are the only two minimizers of $g(t,s),(t,s)\in {(0,\infty )}^2$.

(ii) 

Suppose that $0\le \rho <{\widehat{\rho }}_1$. We have

$$\begin{array}{c}\hfill g\left({\mathit{t}}_0\right)=g_A(t_A,s_A)=4({\mu }_2+(1-2\rho ){\mu }_1),\end{array}$$

where $(t_A,s_A)\in A$ is the unique minimizer of $g(t,s),(t,s)\in {(0,\infty )}^2$.

(iii) 

Suppose that $\rho ={\widehat{\rho }}_1$. We have

$$\begin{array}{c}\hfill g\left({\mathit{t}}_0\right)=g_A(t_A,s_A)=4({\mu }_2+(1-2\rho ){\mu }_1),\end{array}$$

where $(t_A,s_A)=(t_A\left({\widehat{\rho }}_1\right),s_A\left({\widehat{\rho }}_1\right))=(t^{*}\left({\widehat{\rho }}_1\right),s^{*}\left({\widehat{\rho }}_1\right))\in L$, is the unique minimizer of $g(t,s),(t,s)\in {(0,\infty )}^2$, with $(t^{*},s^{*})$ defined in (6).

(iv) 

Suppose that ${\widehat{\rho }}_1<\rho <{\widehat{\rho }}_2$. We have

$$\begin{array}{c}\hfill g\left({\mathit{t}}_0\right)=g_A(t^{*},s^{*})=g_L\left(t^{*}\right)=\frac{2}{1+\rho }({\mu }_1+{\mu }_2+2/t^{*}),\end{array}$$

where $(t^{*},s^{*})\in L$ is the unique minimizer of $g(t,s),(t,s)\in {(0,\infty )}^2$.

(v) 

Suppose that $\rho ={\widehat{\rho }}_2$. We have $t^{*}\left({\widehat{\rho }}_2\right)=s^{*}\left({\widehat{\rho }}_2\right)=1/{\mu }_2$ and

$$\begin{array}{c}\hfill g\left({\mathit{t}}_0\right)=g_A(1/{\mu }_2,1/{\mu }_2)=g_L(1/{\mu }_2)=g_2(1/{\mu }_2)=4{\mu }_2,\end{array}$$

where the minimum of $g(t,s),(t,s)\in {(0,\infty )}^2$ is attained at $(1/{\mu }_2,1/{\mu }_2)$, with $g_3(1/{\mu }_2,1/{\mu }_2)=g_2(1/{\mu }_2)$ and $1/{\mu }_2$ is the unique minimizer of $g_2\left(s\right),s\in (0,\infty )$.

(vi) 

Suppose that ${\widehat{\rho }}_2<\rho <1$. We have

$$\begin{array}{c}\hfill g\left({\mathit{t}}_0\right)=g_2(1/{\mu }_2)=4{\mu }_2,\end{array}$$

where the minimum of $g(t,s),(t,s)\in {(0,\infty )}^2$ is attained when $g(t,s)=g_2\left(s\right)$.

Remark 4.

In case that ${\mu }_1={\mu }_2$, we have ${\widehat{\rho }}_1=0,{\widehat{\rho }}_2=1$ and thus scenarios (ii) and (vi) do not apply.

3. Proofs of Main Results

As discussed in the previous section, Proposition 3 combined with (8), straightforwardly implies the thesis of Theorem 1. In what follows, we shall focus on the proof of Proposition 3, for which we need to find the dominating points ${\mathit{t}}_0$ by solving the two-layer minimization problem (9).

The solution of quadratic programming problem of the form (7) (inner minimization problem of (9)) has been well understood; for example, Hashorva (2005); Hashorva and Hüsler (2002) (see also Lemma 2.1 of Dȩbicki et al. (2018)). For completeness and for reference, we present below Lemma 2.1 of Dȩbicki et al. (2018) for the case where $d=2$.

We introduce some more notation. If $I\subset \{1,2\}$, then for a vector $\mathit{a}\in {\mathbb{R}}^2$ we denote by ${\mathit{a}}_I=(a_i,i\in I)$ a sub-block vector of $\mathit{a}$. Similarly, if further $J\subset \{1,2\}$, for a matrix $M={\left(m_{ij}\right)}_{i,j\in \{1,2\}}\in {\mathbb{R}}^{2\times 2}$ we denote by $M_{IJ}=M_{I,J}={\left(m_{ij}\right)}_{i\in I,j\in J}$ the sub-block matrix of M determined by I and J. Further, write $M_{II}^{-1}={\left(M_{II}\right)}^{-1}$ for the inverse matrix of $M_{II}$ whenever it exists.

Lemma 5.

Let $M\in {\mathbb{R}}^{2\times 2}$ be a positive definite matrix. If $\mathit{b}\in {\mathbb{R}}^2\backslash {(-\infty ,0]}^2$, then the quadratic programming problem

$$P_M\left(\mathit{b}\right):\mathit{Minimise}{\mathit{x}}^{\top }{M}^{-1}\mathit{x}\mathit{under}\mathit{the}\mathit{linear}\mathit{constraint}\mathit{x}\ge \mathit{b}$$

has a unique solution $\tilde{\mathit{b}}$ and there exists a unique non-empty index set $I\subseteq \{1,2\}$ such that

$$\begin{array}{cc}\hfill & {\tilde{\mathit{b}}}_I={\mathit{b}}_I\ne {\mathbf{0}}_I,M_{II}^{-1}{\mathit{b}}_I>{\mathbf{0}}_I,\hfill \\ \hfill \mathit{and}& \mathit{if}{I}^c=\{1,2\}\backslash I\ne \varnothing ,\mathit{then}{\tilde{\mathit{b}}}_{I^c}=M_{I^{c}I}{M}_{II}^{-1}{\mathit{b}}_I\ge {\mathit{b}}_{I^c}.\hfill \end{array}$$

Furthermore,

$$\begin{array}{ccc}\hfill \underset{\mathit{x}\ge \mathit{b}}{min}{\mathit{x}}^{\top }{M}^{-1}\mathit{x}& =& {\tilde{\mathit{b}}}^{\top }{M}^{-1}\tilde{\mathit{b}}={\mathit{b}}_I^{\top }{M}_{II}^{-1}{\mathit{b}}_I>0,\hfill \\ \hfill {\mathit{x}}^{\top }{M}^{-1}\tilde{\mathit{b}}& =& {\mathit{x}}_I^{\top }{M}_{II}^{-1}{\tilde{\mathit{b}}}_I={\mathit{x}}_I^{\top }{M}_{II}^{-1}{\mathit{b}}_I,\forall \mathit{x}\in {\mathbb{R}}^2.\hfill \end{array}$$

For the solution of the quadratic programming problem (7) a suitable representation for $g(t,s)$ is worked out in the following lemma.

For $1>\rho >{\mu }_1/{\mu }_2,$ let $D_2=\{(t,s):w_1\left(s\right)\le t\le f_1\left(s\right)\}$ and $D_1={(0,\infty )}^2\backslash D_2$, with boundary functions given by

$$\begin{array}{c}\hfill f_1\left(s\right)=\frac{\rho -1}{{\mu }_1}+\frac{\rho {\mu }_2}{{\mu }_1}s,w_1\left(s\right)=\frac{s}{\rho +(\rho {\mu }_2-{\mu }_1)s},s\ge 0,\end{array}$$

(13)

and the unique intersection point of $f_1\left(s\right),w_1\left(s\right),s\ge 0,$ given by

$$\begin{array}{c}\hfill s_1^{*}=s_1^{*}\left(\rho \right):=\frac{1-\rho }{\rho {\mu }_2-{\mu }_1},\end{array}$$

(14)

as depicted in Figure 1.

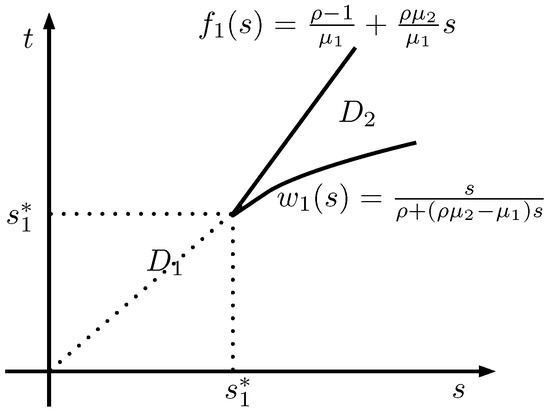
Figure 1. Partition of ${(0,\infty )}^2$ into $D_1,D_2$.

Lemma 6.

Let $g(t,s),t,s>0$ be given as in (7). We have:

(i) 

If $-1<\rho \le {\mu }_1/{\mu }_2,$ then

$$g(t,s)=g_3(t,s),(t,s)\in {(0,\infty )}^2.$$

(ii) 

If $1>\rho >{\mu }_1/{\mu }_2,$ then

$$g(t,s)=\left\{\begin{array}{cc}{g}_3(t,s),& \mathit{if}(t,s)\in D_1\\ g_2\left(s\right),& \mathit{if}(t,s)\in D_2.\end{array}\right.$$

Moreover, we have $g_3(f_1\left(s\right),s)=g_3(w_1\left(s\right),s)=g_2\left(s\right)$ for all $s\ge s_1^{*}$.

3.1. Proof of Proposition 3

We shall discuss in order the case when $-1<\rho <0$ and the case when $0\le \rho <1$ in the following two subsections. In both scenarios we shall first derive the minimizers of the function $g(t,s)$ on regions $\overline{A}$ and $\overline{B}$ (see (10)) separately and then look for a global minimizer by comparing the two minimum values. For clarity some scenarios are analysed in forms of lemmas.

3.1.1. Case $-1<\rho <0$

By Lemma 6, we have that

$$\begin{array}{c}\hfill g(t,s)=g_3(t,s),(t,s)\in {(0,\infty )}^2.\end{array}$$

We shall derive the minimizers of $g_3(t,s)$ on $\overline{A},\overline{B}$ separately.

Minimizers of $g_3(t,s)$ on $\overline{A}$. We have, for any fixed s,

$$\begin{array}{c}\hfill \frac{\partial g_3(t,s)}{\partial t}=\frac{\partial g_A(t,s)}{\partial t}=0\iff ({\mu }_{1}t+1-\rho -\rho {\mu }_{2}s)({\mu }_{1}t-(2{\mu }_1{\rho }^2-\rho {\mu }_2)s+\rho -1)=0,\end{array}$$

where the representation (11) is used. Two roots of the above equation are:

$$\begin{array}{c}\hfill t_1=t_1\left(s\right):=\frac{\rho -1+\rho {\mu }_{2}s}{{\mu }_1},t_2=t_2\left(s\right):=\frac{1-\rho +(2{\mu }_1{\rho }^2-\rho {\mu }_2)s}{{\mu }_1}.\end{array}$$

(15)

Note that, due to the form of the function $g_A(t,s)$ given in (11), for any fixed s, there exists a unique minimizer of $g_A(t,s)$ on $\overline{A}$ which is either an inner point $t_1$ or $t_2$ (the one that is larger than s), or a boundary point s. Next, we check if any of $t_i,i=1,2,$ is larger than s. Since $\rho <0$, $t_1<0<t_2$. So we check if $t_2>s$. It can be shown that

$$\begin{array}{c}\hfill t_2>s\iff ({\mu }_1+\rho {\mu }_2-2{\mu }_1{\rho }^2)s<1-\rho .\end{array}$$

(16)

Two scenarios ${\mu }_1+\rho {\mu }_2-2{\mu }_1{\rho }^2\le 0$ and ${\mu }_1+\rho {\mu }_2-2{\mu }_1{\rho }^2>0$ will be distinguished.

Scenario ${\mu }_1+\rho {\mu }_2-2{\mu }_1{\rho }^2\le 0$. We have from (16) that

$$t_1<0<s<t_2,$$

and thus

$$\underset{(t,s)\in \overline{A}}{inf}{g}_3(t,s)=\underset{s>0}{inf}{f}_A\left(s\right),$$

where

$$\begin{array}{c}\hfill f_A\left(s\right):=g_A(t_2\left(s\right),s)=\frac{{(1+{\mu }_{2}s)}^2}{s}+4{\mu }_1((1-\rho )+({\rho }^2{\mu }_1-\rho {\mu }_2)s).\end{array}$$

Next, since

$$\begin{array}{c}\hfill f_A^{\prime }\left(s\right)=0\iff s_A=s_A\left(\rho \right):=\frac{1}{|{\mu }_2-2\rho {\mu }_1|}=\frac{1}{{\mu }_2-2\rho {\mu }_1}>0,\end{array}$$

(17)

the unique minimizer of $g_3(t,s)$ on $\overline{A}$ is given by $(t_A,s_A)$ with

$$t_A:=t_2\left(s_A\right)=\frac{1-2\rho }{{\mu }_1}.$$

Scenario ${\mu }_1+\rho {\mu }_2-2{\mu }_1{\rho }^2>0$. We have from (16) that

$$\begin{array}{c}\hfill t_1<0<s<t_2\iff s<\frac{1-\rho }{{\mu }_1+\rho {\mu }_2-2{\mu }_1{\rho }^2}=\frac{1-\rho }{\rho ({\mu }_2-{\mu }_1\rho )+{\mu }_1(1-{\rho }^2)}=:s^{**}\left(\rho \right)=s^{**},\end{array}$$

(18)

and in this case,

$$\begin{array}{c}\hfill \underset{(t,s)\in \overline{A}}{inf}{g}_3(t,s)=min\left(\underset{0<s<s^{**}}{inf}{f}_A\left(s\right),\underset{s\ge s^{**}}{inf}{g}_L\left(s\right)\right),\end{array}$$

(19)

where $g_L\left(s\right)$ is given in (12). Note that

$$\begin{array}{c}\hfill g_L^{\prime }\left(s\right)=0\iff s^{*}=s^{*}\left(\rho \right)=\sqrt{\frac{2(1-\rho )}{{\mu }_1^2+{\mu }_2^2-2\rho {\mu }_1{\mu }_2}}.\end{array}$$

(20)

Next, for $-1<\rho <0$ we have that (recall $s^{**}$ given in (18))

$$\begin{array}{c}\hfill s^{**}\ge \frac{1-\rho }{{\mu }_1(1-{\rho }^2)}>\frac{1}{{\mu }_1}\ge \frac{1}{{\mu }_2}>s_A,s^{**}>\frac{1-\rho }{{\mu }_1}>s^{*}.\end{array}$$

Therefore, by (19) we conclude that the unique minimizer of $g_3(t,s)$ on $\overline{A}$ is again given by $(t_A,s_A)$. Consequently, for all $-1<\rho <0$, we have that the unique minimizer of $g_3(t,s)$ on $\overline{A}$ is given by $(t_A,s_A)$, and

$$\begin{array}{c}\hfill \underset{(t,s)\in \overline{A}}{inf}{g}_3(t,s)=g_A(t_A,s_A)=4({\mu }_2+(1-2\rho ){\mu }_1).\end{array}$$

(21)

Minimizers of $g_3(t,s)$ on $\overline{B}$. Similarly, we have, for any fixed t,

$$\begin{array}{c}\hfill \frac{\partial g_3(t,s)}{\partial s}=\frac{\partial g_B(t,s)}{\partial s}=0\iff ({\mu }_{2}s+1-\rho -\rho {\mu }_{1}t)({\mu }_{2}s-(2{\mu }_2{\rho }^2-\rho {\mu }_1)t+\rho -1)=0.\end{array}$$

Two roots of the above equation are:

$$\begin{array}{c}\hfill s_1=s_1\left(t\right):=\frac{\rho -1+\rho {\mu }_{1}t}{{\mu }_2},s_2=s_2\left(t\right):=\frac{1-\rho +(2{\mu }_2{\rho }^2-\rho {\mu }_1)t}{{\mu }_2}.\end{array}$$

(22)

Next, we check if any of $s_i,i=1,2,$ is greater than t. Again $s_1<0<s_2$ as $\rho <0$. So we check if $s_2>t$. It can be shown that

$$\begin{array}{c}\hfill s_2>t\iff ({\mu }_2+\rho {\mu }_1-2{\mu }_2{\rho }^2)t<1-\rho .\end{array}$$

(23)

Thus, for Scenario ${\mu }_2+\rho {\mu }_1-2{\mu }_2{\rho }^2\le 0$ we have that

$$s_1<0<t<s_2$$

and in this case

$$\underset{(t,s)\in \overline{B}}{inf}{g}_3(t,s)=\underset{t>0}{inf}{f}_B\left(t\right),$$

with

$$\begin{array}{c}\hfill f_B\left(t\right):=g_B(t,s_2\left(t\right))=\frac{{(1+{\mu }_{1}t)}^2}{t}+4{\mu }_2((1-\rho )+({\rho }^2{\mu }_2-\rho {\mu }_1)t).\end{array}$$

Next, note that

$$\begin{array}{c}\hfill f_B^{\prime }\left(t\right)=0\iff t_B=t_B\left(\rho \right):=\frac{1}{|{\mu }_1-2\rho {\mu }_2|}=\frac{1}{{\mu }_1-2\rho {\mu }_2}>0.\end{array}$$

(24)

Therefore, the unique minimizer of $g_3(t,s)$ on $\overline{B}$ is given by $(t_B,s_B)$ with

$$\begin{array}{c}\hfill s_B:=s_2\left(t_B\right)=\frac{1-2\rho }{{\mu }_2},\underset{(t,s)\in \overline{B}}{inf}{g}_3(t,s)=g_B(t_B,s_B)=4({\mu }_1+(1-2\rho ){\mu }_2).\end{array}$$

For Scenario ${\mu }_2+\rho {\mu }_1-2{\mu }_2{\rho }^2>0$ we have from (23) that

$$\begin{array}{c}\hfill s_1<0<t<s_2\iff t<\frac{1-\rho }{{\mu }_2+\rho {\mu }_1-2{\mu }_2{\rho }^2}=\frac{1-\rho }{\rho ({\mu }_1-\rho {\mu }_2)+{\mu }_2(1-{\rho }^2)}=:t^{**}\left(\rho \right)=t^{**}.\end{array}$$

(25)

In this case,

$$\begin{array}{c}\hfill \underset{(t,s)\in \overline{B}}{inf}{g}_3(t,s)=min\left(\underset{0<t<t^{**}}{inf}{f}_B\left(t\right),\underset{t\ge t^{**}}{inf}{g}_L\left(t\right)\right).\end{array}$$

Though it is not easy to determine explicitly the optimizer, we can conclude that the minimizer should be taken at $(t_B,s_B)$, $(t^{*},t^{*})$ or $(t^{**},t^{**})$, where $t^{*}=t^{*}\left(\rho \right)=s^{*}\left(\rho \right)$. Further, we have from the discussion in (19) that

$$g_A(t_A,s_A)<g_L\left(s^{*}\right)=g_L\left(t^{*}\right)=min(g_L(t^{*}),g_L(t^{**})),$$

and

$$g_B(t_B,s_B)=4({\mu }_1+(1-2\rho ){\mu }_2)\ge 4({\mu }_2+(1-2\rho ){\mu }_1)=g_A(t_A,s_A).$$

Combining the above discussions on $\overline{A},\overline{B}$, we conclude that Proposition 3 holds for $-1<\rho <0$.

3.1.2. Case $0\le \rho <1$

We shall derive the minimizers of $g(t,s)$ on $\overline{A},\overline{B}$ separately. We start with discussions on $\overline{B}$, for which we give the following lemma. Recall $t^{*}\left(\rho \right)=s^{*}\left(\rho \right)$ defined in (20) (see also (6)), $t_B\left(\rho \right)$ defined in (24), $t^{**}\left(\rho \right)$ defined in (25) and $s_1^{*}\left(\rho \right)$ defined in (14) for ${\mu }_1/{\mu }_2<\rho <1$. Note that where it applies, $1/0$ is understood as $+\infty$ and $1/\infty$ is understood as 0.

Lemma 7.

We have:

(a) 

The function $t^{*}\left(\rho \right)$ is a decreasing function on $[0,1]$ and both $t_B\left(\rho \right)$ and $s_1^{*}\left(\rho \right)$ are decreasing functions on $({\mu }_1/{\mu }_2,1)$.

(b) 

The function $t^{**}\left(\rho \right)$ decreases from $1/{\mu }_2$ at $\rho =0$ to some positive value and then increases to $1/{\mu }_2$ at ${\widehat{\rho }}_2$ (defined in (5)) and then increases to $+\infty$ at the root $\widehat{\rho }\in (0,1]$ of the equation ${\mu }_2+\rho {\mu }_1-2{\mu }_2{\rho }^2=0.$

(c) 

For $0\le \rho \le {\mu }_1/{\mu }_2$, we have

$$\begin{array}{c}\hfill t_B\left(\rho \right)\ge t^{**}\left(\rho \right),t^{*}\left(\rho \right)\ge t^{**}\left(\rho \right),\end{array}$$

where both equalities hold only when $\rho =0$ and ${\mu }_1={\mu }_2.$

(d) 

It holds that

$$\begin{array}{c}\hfill t^{*}\left({\widehat{\rho }}_2\right)=t_B\left({\widehat{\rho }}_2\right)=s_1^{*}\left({\widehat{\rho }}_2\right)=t^{**}\left({\widehat{\rho }}_2\right)=\frac{1}{{\mu }_2}.\end{array}$$

(26)

Moreover, for ${\mu }_1/{\mu }_2<\rho <1$ we have

(i) 

$t^{*}\left(\rho \right)<s_1^{*}\left(\rho \right)\mathit{for}\mathit{all}\rho \in ({\mu }_1/{\mu }_2,{\widehat{\rho }}_2),t^{*}\left(\rho \right)>s_1^{*}\left(\rho \right)\mathit{for}\mathit{all}\rho \in ({\widehat{\rho }}_2,1).$

(ii) 

$t_B\left(\rho \right)<s_1^{*}\left(\rho \right)\mathit{for}\mathit{all}\rho \in ({\mu }_1/{\mu }_2,{\widehat{\rho }}_2),t_B\left(\rho \right)>s_1^{*}\left(\rho \right)\mathit{for}\mathit{all}\rho \in ({\widehat{\rho }}_2,1).$

(iii) 

$t^{**}\left(\rho \right)<s_1^{*}\left(\rho \right)\mathit{for}\mathit{all}\rho \in ({\mu }_1/{\mu }_2,{\widehat{\rho }}_2),t^{**}\left(\rho \right)>s_1^{*}\left(\rho \right)\mathit{for}\mathit{all}\rho \in ({\widehat{\rho }}_2,\widehat{\rho }).$

(iv) 

$t^{**}\left(\rho \right)<t^{*}\left(\rho \right)\mathit{for}\mathit{all}\rho \in ({\mu }_1/{\mu }_2,{\widehat{\rho }}_2),t^{**}\left(\rho \right)>t^{*}\left(\rho \right)\mathit{for}\mathit{all}\rho \in ({\widehat{\rho }}_2,\widehat{\rho }).$

(v) 

$t^{**}\left(\rho \right)<t_B\left(\rho \right)\mathit{for}\mathit{all}\rho \in ({\mu }_1/{\mu }_2,{\widehat{\rho }}_2),t^{**}\left(\rho \right)>t_B\left(\rho \right)\mathit{for}\mathit{all}\rho \in ({\widehat{\rho }}_2,\widehat{\rho }).$

Recall that by definition $g_L\left(s\right)=g_A(s,s)=g_B(s,s),s>0$ (cf. (12)). For the minimum of $g(t,s)$ on $\overline{B}$ we have the following lemma.

Lemma 8.

We have

(i) 

If $0\le \rho <{\widehat{\rho }}_2$, then

$$\begin{array}{c}\hfill \underset{(t,s)\in \overline{B}}{inf}g(t,s)=g_L\left(t^{*}\right)=\frac{2}{1+\rho }({\mu }_1+{\mu }_2+2/t^{*}),\end{array}$$

where $(t^{*},t^{*})$ is the unique minimizer of $g(t,s)$ on $\overline{B}$.

(ii) 

If $\rho ={\widehat{\rho }}_2$, then $t^{*}\left({\widehat{\rho }}_2\right)=s^{*}\left({\widehat{\rho }}_2\right)=1/{\mu }_2$ and

$$\begin{array}{c}\hfill \underset{(t,s)\in \overline{B}}{inf}g(t,s)=g_L(1/{\mu }_2)=g_2(1/{\mu }_2)=4{\mu }_2,\end{array}$$

where the minimum of $g(t,s)$ on $\overline{B}$ is attained at $(1/{\mu }_2,1/{\mu }_2)$, with $g_3(1/{\mu }_2,1/{\mu }_2)=g_2(1/{\mu }_2)$ and $1/{\mu }_2$ is the unique minimizer of $g_2\left(s\right),s\in (0,\infty ).$

(iii) 

If ${\widehat{\rho }}_2<\rho <1$, then

$$\begin{array}{c}\hfill \underset{(t,s)\in \overline{B}}{inf}g(t,s)=\underset{(t,s)\in D_2}{inf}{g}_2\left(s\right)=g_2(1/{\mu }_2)=4{\mu }_2,\end{array}$$

where the minimum of $g(t,s)$ on $\overline{B}$ is attained when $g(t,s)=g_2\left(s\right)$ on $D_2$ (see Figure 1).

Next we consider the minimum of $g(t,s)$ on $\overline{A}$. Recall $s^{*}\left(\rho \right)$ defined in (20), $s_A\left(\rho \right)$ defined in (17) and $s^{**}\left(\rho \right)$ defined in (18). We first give the following lemma.

Lemma 9.

We have

(a) 

Both $s^{*}\left(\rho \right)$ and $s^{**}\left(\rho \right)$ are decreasing functions on $[0,1]$.

(b) 

That ${\widehat{\rho }}_1$ is the unique point on $[0,1)$ such that

$$\begin{array}{c}\hfill s_A\left({\widehat{\rho }}_1\right)=s^{**}\left({\widehat{\rho }}_1\right)=s^{*}\left({\widehat{\rho }}_1\right),\end{array}$$

and

(i) 

$s_A\left(\rho \right)<s^{**}\left(\rho \right)\mathit{for}\mathit{all}\rho \in [0,{\widehat{\rho }}_1),s_A\left(\rho \right)>s^{**}\left(\rho \right)\mathit{for}\mathit{all}\rho \in ({\widehat{\rho }}_1,1)$,

(ii) 

$s^{*}\left(\rho \right)<s^{**}\left(\rho \right)\mathit{for}\mathit{all}\rho \in [0,{\widehat{\rho }}_1),s^{*}\left(\rho \right)>s^{**}\left(\rho \right)\mathit{for}\mathit{all}\rho \in ({\widehat{\rho }}_1,1).$

(c) 

For all ${\mu }_1/{\mu }_2<\rho <1$, it holds that $s^{**}\left(\rho \right)<s_1^{*}\left(\rho \right)$.

For the minimum of $g(t,s)$ on $\overline{A}$ we have the following lemma.

Lemma 10.

We have

(i) 

If $0\le \rho <{\widehat{\rho }}_1$, then

$$\begin{array}{c}\hfill \underset{(t,s)\in \overline{A}}{inf}g(t,s)=g_A(t_A,s_A)=4({\mu }_2+(1-2\rho ){\mu }_1),\end{array}$$

where $(t_A,s_A)\in A$ is the unique minimizer of $g(t,s)$ on $\overline{A}$.

(ii) 

If $\rho ={\widehat{\rho }}_1$, then

$$\begin{array}{c}\hfill \underset{(t,s)\in \overline{A}}{inf}g(t,s)=g_A(t_A,s_A)=4({\mu }_2+(1-2\rho ){\mu }_1),\end{array}$$

where $(t_A,s_A)=(t^{*},s^{*})\in L$ is the unique minimizer of $g(t,s)$ on $\overline{A}$.

(iii) 

If ${\widehat{\rho }}_1<\rho <{\widehat{\rho }}_2$, then

$$\begin{array}{c}\hfill \underset{(t,s)\in \overline{A}}{inf}g(t,s)=g_L\left(s^{*}\right)=\frac{2}{1+\rho }({\mu }_1+{\mu }_2+2/s^{*}),\end{array}$$

where $(s^{*},s^{*})$ is the unique minimizer of $g(t,s)$ on $\overline{A}$.

(iv) 

If $\rho ={\widehat{\rho }}_2$, then $t^{*}\left({\widehat{\rho }}_2\right)=s^{*}\left({\widehat{\rho }}_2\right)=1/{\mu }_2$ and

$$\begin{array}{c}\hfill \underset{(t,s)\in \overline{A}}{inf}g(t,s)=g_L\left(s^{*}\right)=g_2(1/{\mu }_2)=4{\mu }_2,\end{array}$$

where the minimum of $g(t,s)$ on $\overline{A}$ is attained at $(1/{\mu }_2,1/{\mu }_2)$, with $g_3(1/{\mu }_2,1/{\mu }_2)=g_2(1/{\mu }_2)$.

(v) 

If ${\widehat{\rho }}_2<\rho <1$, then

$$\begin{array}{c}\hfill \underset{(t,s)\in \overline{A}}{inf}g(t,s)=g_2(1/{\mu }_2)=4{\mu }_2,\end{array}$$

where the minimum of $g(t,s)$ on $\overline{A}$ is attained when $g(t,s)=g_2\left(s\right)$ on $D_2$ (see Figure 1).

Consequently, combining the results in Lemma 8 and Lemma 10, we conclude that Proposition 3 holds for $0\le \rho <1$. Thus, the proof is complete.

4. Conclusions and Discussions

In the multi-dimensional risk theory, the so-called “ruin” can be defined in different manner. Motivated by diffusion approximation approach, in this paper we modelled the risk process via a multi-dimensional BM with drift. We analyzed the component-wise infinite-time ruin probability for dimension $d=2$ by solving a two-layer optimization problem, which by the use of Theorem 1 from Dȩbicki et al. (2010) led to the logarithmic asymptotics for $P\left(u\right)$ as $u\to \infty$, given by explicit form of the adjustment coefficient $\gamma =g\left({\mathit{t}}_0\right)/2$ (see (8)). An important tool here is Lemma 5 on the quadratic programming, cited from Hashorva (2005). In this way we were also able to identify the dominating points by careful analysis of different regimes for $\rho$ and specify three regimes with different formulas for $\gamma$ (see Theorem 1). An open and difficult problem is the derivation of exact asymptotics for $P\left(u\right)$ in (4), for which the problem of finding dominating points would be the first step. A refined double-sum method as in Dȩbicki et al. (2018) might be suitable for this purpose. A detailed analysis of the case for dimensions $d>2$ seems to be technically very complicated, even for getting the logarithmic asymptotics. We also note that a more natural problem of considering $R_i\left(t\right)={\alpha }_{i}u+{\mu }_{i}t-X_i\left(t\right)$, with general ${\alpha }_i>0,i=1,2$, leads to much more difficult technicalities with the analysis of $\gamma$.

Define the ruin time of component i, $1\le i\le d$, by $T_i=min\{t:R_i\left(t\right)<0\}$ and let $T_{\left(1\right)}\le T_{\left(2\right)}\le \dots \le T_{\left(d\right)}$ be the order statistics of ruin times. Then the component-wise infinite-time ruin probability is equivalent to $\mathbb{P}\left\{T_{\left(d\right)}<\infty \right\}$ while the ruin time of at least one business line is $T_{min}=T_{\left(1\right)}={min}_i{T}_i$. Other interesting problems like $\mathbb{P}\left\{T_{\left(j\right)}<\infty \right\}$ have not yet been analysed. For instance, it would be interesting for $d=3$ to study the case $T_{\left(2\right)}$. The general scheme on how to obtain logarithmic asymptotics for such problems was discussed in Dȩbicki et al. (2010).

Random vector $\overline{\mathit{X}}={({sup}_{t\ge 0}(X_1\left(t\right)-p_{1}t),\dots ,{sup}_{t\ge 0}(X_d\left(t\right)-p_{d}t))}^{\top }$ has exponential marginals and if it is not concentrated on a subspace of dimension less than d, it defines a multi-variate exponential distribution. In this paper for dimension $d=2$, we derived some asymptotic properties of such distribution. Little is known about properties of this multi-variate distriution and more studies on it would be of interest. For example a correlation structure of $\overline{\mathit{X}}$ is unknown. In particular, in the context of findings presented in this contribution, it would be interesting to find the correlation between ${sup}_{t\ge 0}(X_1\left(t\right)-{\mu }_{1}t)$ and ${sup}_{t\ge 0}(X_2\left(t\right)-{\mu }_{2}t)$.