Abstract
We propose an alternative approach to the modeling of the positive dependence between the probability of default and the loss given default in a portfolio of exposures, using a bivariate urn process. The model combines the power of Bayesian nonparametrics and statistical learning, allowing for the elicitation and the exploitation of experts’ judgements, and for the constant update of this information over time, every time new data are available. A real-world application on mortgages is described using the Single Family Loan-Level Dataset by Freddie Mac.
1. Introduction
The ambition of this paper is to present a new way of modeling the empirically-verified positive dependence between the Probability of Default (PD) and the Loss Given Default (LGD) using a Bayesian nonparametric approach, based on urns and beta-Stacy processes (Walker and Muliere 1997). The model is able to learn from the data, and it improves its performances over time, compatibly with the machine/deep learning paradigm. Similarly to the recent construction of Cheng and Cirillo (2018) for recovery times, this learning ability is mainly due to the underlying urn model.
The PD and the LGD are two fundamental quantities in modern credit risk management. The PD of a counterparty indicates the likelihood that such a counterparty defaults, thus not fulfilling its debt obligations. The LGD represents the percent loss. In terms of the notional value of the exposure known as the Exposure-at-Default or EAD, one actually experiences when a counterparty defaults and every possible recovery process is over. Within the Basel framework (BCBS 2000, 2011), a set of international standards developed by the Basel Committee on Banking Supervision (BCBS) to harmonize the banking sector and improve the way banks manage risk, the PD and the LGD are considered pivotal risk parameters for the quantification of the minimum capital requirements for credit risk. In particular, under the so-called Internal Rating-Based (IRB) approaches, both the PD and the LGD are inputs of the main formulas for the computation of the risk-weighted assets (BCBS 2005, 2006).
Surprisingly, in most theoretical models in the literature, and most of all in the formulas suggested by the BCBS, the PD and the LGD are assumed to be independent, even though several empirical studies have shown that there is a non-negligible positive dependence between them (Altman 2006; Altman et al. 2001; Frye 2005; Miu and Ozdemir 2006; Witzany 2011). Borrowing from the terminology developed in the field of credit valuation adjustment (CVA) (Hull 2015), this dependence is often referred to as wrong-way risk (WWR). Simply put, WWR is the risk that the possible loss generated by a counterparty increases with the deterioration of its creditworthiness. Ignoring this WWR can easily lead to an unreliable estimation of credit risk for a given counterparty (Witzany 2011).
The link between the PD and the LGD is particularly important when dealing with mortgages, as shown by the 2007–2008 financial crisis, which was triggered by an avalanche of defaults in the US subprime market (Eichengreen et al. 2012), with a consequent drop in estate prices, and thus in the recovery rates of the defaulted exposures (Hull 2015). The financial crisis was therefore one of the main drivers for the rising interest in the joint modeling of PD and LGD, something long ignored both in the academia and in the practice, including regulators. In the paper, we show how the model we propose can be used in the field of mortgages with a real-world application.
The first model implicitly dealing with the dependence between the PD and the LGD was Merton’s one. In his seminal work, Merton (1974) introduced the first structural model of default, developing what we can consider the Black and Scholes model for credit risk. In that model, the recovery rate (with ), conditionally on the credit event, follows a lognormal distribution (Resti and Sironi 2007), and it is negatively correlated with the PD. While not consistent with later empirical findings (Altman et al. 2005; Jones et al. 1984) on WWR, Merton’s model remained for long time the only model actually dealing with this problem.
Many models have been derived from Merton’s original construction, both in the academic and in the industrial literature, think for example of Geske (1977); Kim et al. (1993); Longstaff and Schwartz (1995); Nielsen et al. (2001) and Vasicek (1984). During the 1990s, on the wake of the—at the time—forthcoming financial regulations (Basel I and later Basel II), several new approaches were introduced, like the so-called reduced-form family (Duffie 1998; Duffie and Singleton 1999; Lando 1998) and the VaR (Value-at-Risk) methodology (JP Morgan 1997; Wilde 1997; Wilson 1998). However, and somehow surprisingly, the great majority of these models, while solving other problems of Merton’s original contribution—like the fact that default could only happen at predetermined times—often neglected the dependence between PD and LGD, sometimes even explicitly assuming independence, as in the Credit Risk Plus case (Wilde 1997), where LGD is mainly assumed deterministic.
In the new century, given the rising interest of regulators and investors, especially after the 2007 crisis, a lot of empirical research has definitely shown the positive dependence—in most cases, positive correlation, hence linear dependence–between PD and LGD. For example, Frye (2000) proposed a standard one-factor model, becoming a pivotal reference in the modeling of the WWR between PD and LGD. The paper focuses on the PD and the Market LGD of corporate bonds on a firm level, assuming dependence on a common systematic factor, plus some other independent idiosyncratic components to deal with marginal variability.
Witzany (2011) moved forward, proposing a two-factor model on retail data, looking at the overall economic environment as the source of dependence between PD and LGD. Then, for the LGD only, a second component accounts for the conditions of the economy during the workout process. Other meaningful constructions in the common factor framework are Hamerle et al. (2011) and Yao et al. (2017). The latter is also interesting for the literature review, together with Altman et al. (2005).
Using a two-state latent variable construction, Bruche and Gonzalez-Aguado (2010) introduced another valuable model. The time series of the latent variable is referred to as credit cycle, and it is represented by a simple Markov chain. Interestingly, this credit cycle variable proves to be able to better capture the time variation in the joint distribution of the PD and the LGD, with respect to observable macroeconomic factors.
Notwithstanding the importance of the topic, and despite the notable efforts cited above, it seems that there is still a lot to do in the modeling of the PD/LGD dependence, which remains a yet-to-be-developed part of credit risk management; see the discussions in Altman (2006) and Maio (2017), and the references therein.
Our contribution to this open problem is represented by the present paper, which finds its root in the recent literature about the use of urn models in credit risk management (Amerio et al. 2004; Cheng and Cirillo 2018; Cirillo et al. 2010; Peluso et al. 2015), and more in general in the Bayesian modeling of credit risk—see, for example, Baesens et al. (2016); Cerchiello and Giudici (2014); Giudici (2001); Giudici et al. (2003); McNeil and Wendin (2007).
For the reader’s convenience, we here summarise the main findings of the paper:
- An intuitive bivariate model is proposed for the joint modeling of PD and LGD. The construction exploits the power of Polya urns to generate a Bayesian nonparametric approach to wrong-way risk. The model can be interpreted as a mixture model, following the typical credit risk management classification (McNeil et al. 2015).
- The proposed model is able to combine prior beliefs with empirical evidence and, exploiting the reinforcement mechanism embedded in Polya urns, it learns, thus improving its performances over time.
- The ability of learning and improving gives the model a machine/deep learning flavour. However, differently from the common machine/deep learning approaches, the behavior of the new model can be controlled and studied in a rigorous way from a probabilistic point of view. In other words, the common “black box” argument (Knight 2017) of machine/deep learning does not apply.
- The possibility of eliciting an a priori allows for the exploitation of experts’ judgements, which can be extremely useful when dealing with rare events, historical bias and data problems in general (Cheng and Cirillo 2018; Derbyshire 2017; Shackle 1955).
- The model we propose can only deal with positive dependence. Given the empirical literature, this is not a problem in WWR modeling; however, it is important to be aware of this feature, if other applications are considered.
The paper develops as follows: Section 2 is devoted to the description of the theoretical framework and the introduction of all the necessary probabilistic tools. In Section 3, we briefly describe the Freddie Mac data we then use in Section 4, where we show how to use and the performances of the model, when studying the dependence between PD and LGD for residential US mortgages. Section 5 closes the paper.
2. Model
The main idea of the model we propose was first presented in Bulla (2005), in the field of survival analysis, and it is based on powerful tools of Bayesian nonparametrics, like the beta-Stacy process of Walker and Muliere (1997). Here, we give a different representation in terms of Reinforced Urn Processes (RUP), to bridge towards some recent papers in the credit risk management literature like Peluso et al. (2015) and Cheng and Cirillo (2018).
2.1. The Two-Color RUP
An RUP is a combinatorial stochastic process, first introduced in Muliere et al. (2000). It can be seen as a reinforced random walk over a state space of urns, and depending on how its parameters are specified, it can generate a large number of interesting models. Essential references on the topic are (Muliere et al. 2000, 2003) and Fortini and Petrone (2012). In this paper, we need to specify an RUP able to generate a discrete beta-Stacy process, a particular random distribution over the space of discrete distributions.
Definition 1
(Discrete beta-Stacy Process (Walker and Muliere 1997)). A random distribution function F is a beta-Stacy process with jumps at and parameters , if there exist mutually independent random variables , each beta distributed with parameters , such that the random mass assigned by F to , written , is given by .
Consider the set of the natural numbers , including zero. On each , place a Polya urn containing balls of two colors, say blue and red, and reinforcement equal to 1. A Polya urn is the prototype of urn with reinforcement: every time a ball is sampled, its color is recorded, and the ball is put back into the urn together with an extra ball (i.e., the reinforcement) of the same color (Mahmoud 2008). This mechanism clearly increases the probability of picking the sampled color again in the future. We assume that all urns contain at least a ball of each color, but their compositions can be actually different. As the only exception, the urn centered on 0, , only contains blue balls, so that red balls cannot be sampled.
Let represent time, which we take to be discrete. A two-color reinforced urn process is built as follows. Set and sample urn : given our assumptions, the only color we can pick is blue. Put the ball back into , add an extra blue ball, and set . Now, sample : this urn contains both blue and red balls. If the sampled ball is blue, put it back, add an extra blue ball and set . If the sampled balls is red, put it back in , add an extra red ball and set . In general, the value of will be decided by the sampling of the urn visited by . If a blue ball is selected at time , then , otherwise . Blue balls thus make the process go further in the exploration of the natural numbers, while every red ball makes the process restart from 0.
If one is interested in defining a two-color RUP only on a subset of , say , it is sufficient to set to zero the number of blue balls in all urns and so on. For the rest, the mechanism stays unchanged.
It is not difficult to verify that, if all urns , , contain a positive number of red balls, the process is recurrent, and it will visit 0 infinitely many times for .
A two-color recurrent RUP clearly generates sequences of nonnegative natural numbers, like the following
These sequences are easily split into blocks, each starting with 0, as in Equation (1). In terms of sampling, those 0s represent the times the process has been reset after the extraction of a red ball from the urn centered on the natural number preceding that 0. Notice that by construction no sequence can contain two contiguous 0s. In the example above, the process is reset to 0 after the sampling of in , in , and in . Muliere et al. (2000) have shown that the blocks–or the 0-blocks in their terminology–generated by a two-color RUP are exchangeable, and that their de Finetti measure is a beta-Stacy process.
Exchangeability means that, if we take the joint distribution of a certain number of blocks, this distribution is immune to a reshuffling of the blocks themselves, i.e., we can permute them, changing their order of appearance, and yet the probability of the sequence containing them will be the same; for instance in Equation (1). Notice that the exchangeability of the blocks does not imply the exchangeability of the single states visited; in fact, one can easily check that each block constitutes a Markov chain. This implies that the RUP can be seen as a mixture of Markov chains, while the sequence of visited states is partially exchangeable in the sense of Diaconis and Freedman (1980).
Given their exchangeability, de Finetti’s representation theorem guarantees that there exists a random distribution function F such that, given F, the blocks generated by the two-color RUP are i.i.d. with distribution F. Theorem 3.26 in Muliere et al. (2000) tells us that such a random distribution is a beta-Stacy process with parameters , where and are the initial numbers of red, respectively blue, balls in urn , prior to any sampling. In other words, with probability 1 and, for , the increment has the same distribution as , where is a sequence of independent random variables, such that . For a reader familiar with urn processes, each beta distributed is clearly the result of the corresponding Polya urn (Mahmoud 2008).
Let be the first m blocks generated by a two-color RUP . With , we indicate the last state visited by within block i. Coming back to Equation (1), we would have , and . Since the random variables are measurable functions of the exchangeable blocks, they are exchangeable as well, and their de Finetti measure is the same beta-Stacy governing . In what follows, a sequence is called LS (Last State) sequence. In terms of probabilities, for , one can easily observe that
and, for ,
while
where and . From Equations (3) and (4), we see that, every time it is reset to 0 creating a new block, an RUP remembers what happened in the past thanks to the Polya reinforcement mechanism of each visited urn. The process thus learns, combining its initial knowledge, as represented by the quantities , with the additional balls that are introduced in the system, to obtain the predictives in Equations (3) and (4).
Regarding the initial knowledge, notice that, when we choose the quantities and , for , from a Bayesian point of view, we are eliciting a prior. In fact, by setting
we are just requiring , so that the beta-Stacy process F–a random distribution on discrete distributions–is centered on the discrete distribution G, which we guess may correctly describe the phenomenon we are modeling. The quantity is called strength of belief, and it represents how confident we are in our a priori. Given a constant reinforcement, as the one we are using here (+1 ball of the same color), a reduces the speed of learning of the RUP, making the evidence emerging from sampling less relevant in updating the initial compositions. In other terms, helps in controlling the stickiness of to . For more details, we refer to (Muliere et al. 2000, 2003).
2.2. Modeling Dependence
Consider a portfolio containing m exposures. For , let and represent the PD, respectively the LGD, of the i-th counterparty, when discretised and transformed into levels, in a way similar to what Cheng and Cirillo (2018) propose in their work. In other terms, one can split the PD and the LGD into levels, such that for example indicates a PD or LGD of , something between 0% and 5%, a quantity in , and so on until the last level L. The levels do not need to correspond to equally spaced intervals, and this gives flexibility to the modeling. Clearly, the larger L, the finer the partition we obtain. As we will see in Section 4, convenient ways of defining levels are through quantiles, via rounding and, when available, thanks to experts’ judgements.
As observed in Altman et al. (2005), discretisation is a common and useful procedure in risk management, as it reduces the noise in the data. The unavoidable loss of information is more than compensated by the gain in interpretability, if levels are chosen in the correct way. From now on, the bivariate sequence is therefore our object of interest in studying the dependence between the PD and the LGD. Both and will take values in
Let , and be three independent LS sequences generated by three independent two-color RUPs , , . As we know, the sequence is exchangeable, and its de Finetti measure is a beta-Stacy process of parameters . Similarly, for and , we have with , and with .
Now, as in Bulla et al. (2007), let us assume that, for each exposure , we have
This construction builds a special dependence between the discretised PD and the discretised LGD: we are indeed assuming that, for each counterparty i, there exists a common factor influencing both, while and can be seen as idiosyncratic components. Observe that, conditionally on , and are clearly independent. Since both X and Y are between 0 and 100%1, the compositions of the urns defining the processes , , can be tuned so that it is not possible to observe values larger than 100%.
From Equation (6), we can derive important features of the model we are proposing. Since we can write , it is clear that we are assuming a linear dependence between and . This is compatible with several empirical findings, like Altman et al. (2005) or Miu and Ozdemir (2006).
Furthermore, given Equation (6) and the properties of the sequences , and , we can immediately observe that
where Var is the variance, Cov the covariance, , and similarly , . Therefore, with the bivariate urn construction, we can only model positive dependence. Again, this is totally in line with the purpose of our analysis—the study of wrong-way risk that, by definition, is a positive dependence between PD and LGD—and, with the empirical literature, as discussed in Section 1. However, it is important to stress that the model in Equation (6) cannot be used when negative dependence is possible.
Always from Equation (6), we can verify that the sequence is exchangeable2. This comes directly from the exchangeability of , and and the fact that is a measurable function of . An implicit assumption of our model is therefore that the m counterparties in are exchangeable. As observed in McNeil et al. (2015), exchangeability is a common assumption in credit risk, for it is seen as a relaxation of the stronger hypothesis of independence (think about Bernoulli mixtures and the beta-binomial model). All in all, what we ask is that the order in which we observe our counterparties is irrelevant to study the joint distribution of their PDs and LGDs, which is therefore immune to changes in the order of appearance of each exposure. Exchangeability and the fact that and are conditionally independent given suggest that the methodology we are proposing falls under the larger umbrella of mixture models (Duffie and Singleton 2003; McNeil et al. 2015).
Since is exchangeable, de Finetti’s representation theorem guarantees the existence of a bivariate random distribution , conditionally on which the couples are i.i.d. with distribution . The properties of have been studied in detail in Bulla (2005).
Let and be the marginal distributions of and . Clearly, we have
so that both and are convolutions of beta-Stacy processes. The dependence between X and Y, given and is thus simply
Furthermore, if P is the probability function corresponding to F, one has
Assume now that we have observed m exposures, and we have registered their actual PD and LGD, which we have discretised to get . The construction of Equation (6), together with the properties of the beta-Stacy processes involved, allows for a nice derivation of the predictive distribution for a new exposure , given the observed couples . This can be extremely useful in applications, when one is interested in making inference about the PD, the LGD and their relation.
In fact,
From a theoretical point of view, computing Equation (10) just requires counting the balls in the urns behind , and , and then to use formulas like those in Equations (2) and (3), something that for a small portfolio can be done explicitly. However, when m is large, it becomes numerically unfeasible to perform all those sums and products.
Luckily, developing an alternative Markov Chain Monte Carlo algorithm is simple and effective. It is sufficient to go through the following steps:
- (1)
- Given the observations and , the sequence is generated via a Gibbs sampling. The full conditional of , , is such thatSince is exchangeable, all the other full conditionals, , where , have an analogous form.
- (2)
- Once is obtained, compute and .
- (3)
- The quantities , , and are then sampled according to their beta-Stacy predictive distributions , , and as per Equation (3).
- (4)
- Finally, set and .
3. Data
We want to show the potentialities of the bivariate urn construction of Section 2 in modeling the dependence between PD and LGD in a large portfolio of residential mortgages. The data we use come from Maio (2017).
Maio’s dataset is the result of cleaning operations (treatment of NA’s, inconsistent data, etc.) on the well-known Single Family Loan-Level Dataset Sample by Freddie Mac, freely available online (Freddie Mac 2019a). Freddie Mac’s sample contains 50,000 observations per year over the period 1999–2017. Observations are randomly selected, on a yearly basis, from the much larger Single Family Loan-Level Dataset, covering approximately 26.6 million fixed-rate mortgages. Extensive documentation about Freddie Mac’s data collections can be found in Freddie Mac (2019b).
Maio’s dataset contains 383,465 loans over the period 2002–2016. Each loan is uniquely identified by an alphanumeric code, which can be used to match the data with the original Freddie Mac’s source.
For each loan, several interesting pieces of information are available, like its origination date, the loan age in months, the geographical location (ZIP code) within the US, the FICO score of the subscriber, the presence of some form of insurance, the loan to value, the combined loan to value, the debt-to-income ratio, and many others. In terms of credit performance, quantities like the unpaid principal balance and the delinquency status up to termination date are known. Clearly, termination can be due to several reasons, from voluntary prepayment to foreclosure, and this information is also recorded, following Freddie Mac (2019b). A loan is considered defaulted when it is delinquent for more than 180 days, even if it is later repurchased (Freddie Mac 2019c). In addition to the information also available in the Freddie Mac’s collection, Maio’s dataset is enriched with estimates of the PD and the LGD for each loan, obtained via survival analysis3. It is worth noticing that both the PD and the LGD are always contained in the interval .
If one considers the pooled data, the correlation between the PD and the LGD is 0.2556. The average PD is 0.0121 with a standard deviation of 0.0157, while, for LGD, we have 0.1494 and 0.0937, respectively. Regarding the minima and the maxima, we have and 0.3723 for PD, and 0 and 0.5361 for LGD.
In the parametric approach proposed by Maio (2017), the covariates which affect both the PD and LGD, possibly justifying their positive dependence, are the unpaid principal balance (UPB) and the debt-to-income ratio (DTI). Other covariates, from the age of the loan to the ZIP code, are then relevant in explaining the marginal behaviour of either the PD or the LGD. In modeling both the PD and the LGD, Maio (2017) proposes the use of two Weibull accelerated failure time (AFT) models, following a recent trend in modern credit risk management (Narain 1992). The dependence between PD and LGD is then modelled parametrically using copulas and a brand new approach involving a bivariate beta distribution. For more details, we refer to Maio (2017).
A correlation around 0.26 clearly indicates a positive dependence between PD and LGD, and it is in line with the empirical literature we have mentioned in Section 1. However, considering all mortgages together may not be the correct approach, as we are pooling together very different counterparties, possibly watering down more meaningful areas of dependence.
Given the richness of the dataset, there are many ways of disaggregating the data. For example, one can compute the correlation between PD and LGD for different FICO score classes. The FICO score, originally developed by the Fair Isaac Corporation (https://www.fico.com), is a leading credit score in the US, and one of the significant covariates for the estimation of PD in Maio’s survival model (Maio 2017). In the original Freddie Mac’s sample, it ranges from 301 to 850.
Following a common classification (Experian 2019), we can define five classes of creditworthiness: Very poor, for a FICO below 579; Fair, for 580–669; Good, for 670–739; Very good, for 740–799; and Exceptional, with a score above 800. Table 1 contains the number of loans in the different classes, the corresponding average PD and LGD, and naturally their correlation . As expected, the average PD is higher when the FICO score is lower, while the opposite is observable for the average LGD. This is probably due to the fact that, for less creditworthy counterparties, stronger insurances are generally required, as compensation for the higher risk of default. Moreover, in terms of recovery, in putting the collateral on the market, it is probably easier to sell a house with a lower value than a very expensive property, for which discounts on the price are quite common (Eichengreen et al. 2012). Interestingly, in disaggregating the data, we see that the PD–LGD correlation is always above 0.3, with the only exception being the most reliable FICO class (≈0.19).

Table 1.
Some descriptive information about the data used in the analysis. Loans are collected in terms of FICO score.
As an example, Figure 1 shows two plots of the relation between PD and LGD for the “Very poor” class. On the left, a simple scatter plot of PD vs. LGD. On the right, to deal with the large number of overlapping points, thus improving interpretability, we provide a hexagonal heatmap with counts. To obtain this plot, the plane is divided into regular hexagons (20 for each dimension), the number of cases in each hexagon is counted, and it is then mapped to a color scale. This second plot tells us that most of the PD–LGD couples lie in the square .
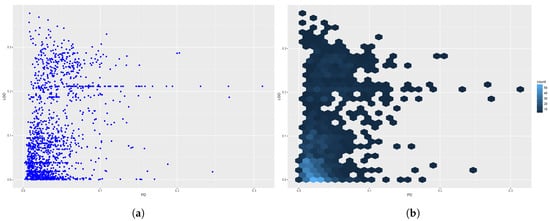
Figure 1.
Plots of PD vs. LGD for mortgages in the “Very poor” (FICO score below 579) class—on the left, a simple scatter plot; on the right, a hexagonal heatmap with counts. (a) scatter plot; (b) hexagonal heatmap.
In Figure 2, the two histograms of the marginal distributions of PD and LGD in the “Very poor” rating class are shown. While for PD the distribution is unimodal, for LGD, we can clearly see bimodality (a second bump is visible around 0.25). These behaviours are present among the different classes and at the pooled level.
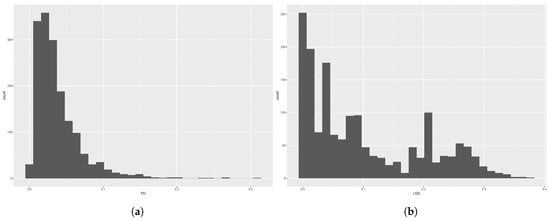
Figure 2.
Histograms of the marginal distributions of PD and LGD in the “Very poor” rating class. (a) PD; (b) LGD.
4. Results
In this section, we discuss the performances of the bivariate urn model on the mortgage data described in Section 3. For the sake of space, we show the results for “Very poor” and the “Exceptional” FICO score classes, as per Table 1.
In order to use the model, we need (1) to transform and discretise both the PD and the LGD into levels, and (2) to define an a priori for the different beta-Stacy processes involved in the construction of Equation (6).
The results we obtain are promising and suggest that the bivariate urn model can represent an interesting way of modeling PD and LGD dependence for banks and practitioners.
Please notice that our purpose is to show that the bivariate urn model actually works. The present section has no ambition of being a complete empirical study on the PD–LGD dependence in the Freddie Mac’s or Maio’s datasets.
4.1. Discretisation
In order to discretise the PD and LGD into X and Y, it is necessary to choose the appropriate levels . In the absence of specific ranges, possibly arising from a bank’s business practice or imposed by a regulator, a convenient way for defining the levels is through quantiles (Cheng and Cirillo 2018).
For example, let be the deciles for the quantity . We can set levels , where
Such a partition guarantees that each level, apart from , contains 10% of the values for both PD and LGD. Notice that the thresholds are not the same, for example, when focusing on the “Very poor” class, , while . A finer partition can be obtained by choosing other percentiles. Clearly, in using a similar approach, one should remember that she is imposing a uniform behaviour on X and Y, in a way similar to copulas (Nelsen 2006). However, differently from copulas, the dependence between X and Y is not restricted to any particular parametric form (the copula function): dependence will emerge from the combination of the a priori and the data.
Another simple way for defining levels is to round the raw observations to the nearest largest integer (ceiling) or to some other value. For instance, we can consider:
Even if it is not a strong requirement, given the meaning of the value 0 in an RUP (recall the 0-blocks), we recommend to use 0 as a special level, not mapping to an interval. Moreover, as already observed, equally-spaced intervals are easier to implement and often to interpret, but again this is not a necessity: levels can represent intervals of different sizes.
Notice that, if correctly applied, discretisation maintains the dependence structure between the variables. For the “Very poor” class, using the levels in Equation (11) in defining X and Y, we find that , in line with the value 0.3370 in Table 1. For the “Exceptional” group, using the levels in Equation (12), we obtain , still comparable.
In what follows, we discuss the results mainly using the levels in Equation (12). However, our findings are robust to different choices of the partition. In general, choosing a smaller number of levels improves fitting because the number of observations per level increases, reinforcing the Polya learning process, ceteris paribus. Moreover—and this is why partitions based on quantiles give nice performances—better results are obtained when intervals guarantee more or less the same number of observations per level.
Choosing a very large L may lead to the situation in which, for a specific level, no transition is observed, so that, for that level, no learning via reinforcement is possible, and, if our beliefs are wrong—or not meant to compensate some lack of information in the data—this naturally has an impact on the goodness of fit. Therefore, in choosing L, there is a trade-off between fitting and precision. The higher L, the lower the impact of discretisation and noise reduction.
The right way to define the number of levels is therefore to look for a compromise between precision, as required by internal procedures or the regulator, and the quantity and the quality of the empirical data. The more and the better the observations, the more precise the partition can be because the higher is the chance of not observing empty levels. In any case, each level should guarantee a minimum number of observations in order to fully exploit the Bayesian learning mechanism. To improve fitting, rarely visited levels should be aggregated. Once again, experts’ judgements could represent a possible solution. We refer to Cheng and Cirillo (2018) for further discussion on level setting.
4.2. Prior Elicitation
In order to use the bivariate urn model, it is necessary to elicit an a priori for all its components, namely , and . This is fundamental for any computation and to initialise the Markov Chain Monte Carlo algorithm discussed in Section 2.2.
Prior elicitation can be performed (1) in a completely subjective way, on the basis of one’s knowledge of the phenomenon under scrutiny, (2) by just looking at the data in a fully empirical approach, or (3) by combining data and beliefs, as suggested for example by Figini and Giudici (2011). In reality, a fully data-driven approach based on the sole use of the empirical distribution functions, as for example the one suggested in Cheng and Cirillo (2018), is not advisable for the bivariate urn construction. While there is no problem in observing X and Y, thus exploiting their empirical distributions for prior elicitation, it is not immediate to do the same for the unobserved quantity A, necessary to obtain both B and C. A possibility could be to use the empirical Kendall’s function (Genest and Rivest 1993), but then one would end up with a model not different from the standard empirical copula approach (Rueschendorf 2009), especially if the number of observations used for the definition of the a priori is large. A compromise could thus be to elicit a subjective prior for A only, and to combine this information with the empirical distributions of X and Y, in order to obtain B and C. As common in Bayesian nonparametrics (Hjort et al. 2010), no unique best way exists: everything depends on personal preferences—this is the unavoidable subjectivity of every statistical model (Galavotti 2001)—and on exogenous constraints that, in credit risk management, are usually represented by the actual regulatory framework (BCBS 2000; Hull 2015).
Recalling Equation (8), it seems natural to choose the prior for so that its variance coincides with the empirical covariance between X and Y. When looking at the “Very poor” and “Exceptional” classes, this covariance is approximately 3 (i.e., 2.7345 and 3.2066, respectively), using the levels in Equation (11). For the situation in Equation (12), conversely, we have a covariance of 10.28 for the “Very poor” class, and 1.46 for the other. Apart from the reasonable constraint on the variance, the choice of the distribution for A can be completely free.
Given the ranges of variation of X and Y, one can choose the appropriate supports for the three beta-Stacy processes. Considering the levels in Equation (11), for , and , it is not rational to choose priors putting a positive mass above 10. Being the levels defined via deciles, it is impossible to observe a level equal to 11 or more. Similarly, using the levels in Equation (12) and recalling Figure 1, where neither the PD nor the LGD reach values above 40% (0.4), once can decide not to allow large values of X and Y, initialising the RUP’s urns only until level 40.
Since we do not have any specific experts’ knowledge to exploit, we have tried different prior combinations. Here, we discuss two possibilities:
- Independent discrete uniforms for , and , where the range of variation for B and C is simply inherited from X and Y (but extra conditions can be applied, if needed), while for A the range is chosen to guarantee . For instance, if the covariance between X and Y is approximately 3, the interval guarantees that as well. We can simply use the formula for the variance of a discrete uniform, i.e.,
- Independent Poisson distributions, such that , while for B and C one sets and , where is the empirical mean of X. This guarantees, for example, that . Recall in fact that, in a Poisson random variable, the mean and the variance are both equal to the intensity parameter, and independent Poissons are closed under convolution. Given our data, where the empirical variances of X and Y are not at all equal to the empirical means, but definitely larger, the Poisson prior can be seen as an example of a wrong prior.
Notice that the possibility of eliciting an a priori is an extremely useful feature of every urn construction (Amerio et al. 2004; Cheng and Cirillo 2018; Cirillo et al. 2010). In fact, a good prior—when available—can compensate for the lack of information in the data, and it can effectively deal with extremes and rare events, a relevant problem in modern risk management (Calabrese and Giudici 2015; Hull 2015; Taleb 2007). For example, if an expert believes that her data under-represent a given phenomenon, like for example some unusual combinations of PD and LGD, she could easily solve the problem by choosing a prior putting a relevant mass on those combinations, so that the posterior distribution will always take into account the possibility of those events, at least remotely. This can clearly correct for the common problem of historical bias (Derbyshire 2017; Shackle 1955).
Once the priors have been decided, the urn compositions can be derived via Equation (5). Different values of have been tried in our experiments. Here, we discuss the cases and for all values of j. The former indicates a moderate trust in our a priori, while the latter shows a strong confidence in our beliefs. Cheng and Cirillo (2018) have observed that, in constructions involving the use of reinforced urn processes, if the number of observations used to train the model is large, then priors become asymptotically irrelevant, for the empirical data prevail. However, when the number of data points is not very large, having a strong prior does make a difference. Given the set cardinalities, we shall see that a strong prior has a clear impact for the “Very poor” rating class (“only” 1627 observations), while no appreciable effect is observable for the “Exceptional” one (32,403 data points).
As a final remark, it is worth noticing that one could take all the urns behind to be empty. This would correspond to assuming that no dependence is actually possible between PD and LGD, so that , and . As discussed in Bulla et al. (2007), it can be shown that, when A is degenerate on 0—and no learning on dependence is thus possible, given the infringement of Cromwell’s rule (Lindley 1991)—the bivariate urn model simply corresponds to playing with the bivariate empirical distribution and the bivariate Kaplan–Meier estimator. While certainly not useful to model a dependence we know is present, this possibility further props the flexibility of the bivariate urn model up.
4.3. Fitting
Figure 3 shows, for the exposures in the “Very Poor” group, the very good fitting performances of the model for the marginal distributions of X and Y, the discretised PD and LGD, respectively. Each subfigure shows the elicited prior, the empirical cumulative distribution function (ECDF) and the posterior, as obtained via learning and reinforcement. In the figure shown, the levels are given by Equation (12), while the priors are discrete uniforms with . Since the covariance between X and Y is 10.28, the discrete uniform on A is on . For both B and C, the support is . A two sample Kolmogorov–Smirnov (KS) test does not reject the null hypothesis of the same distribution between the ECDFs and the relative posteriors (p-values stably above ).
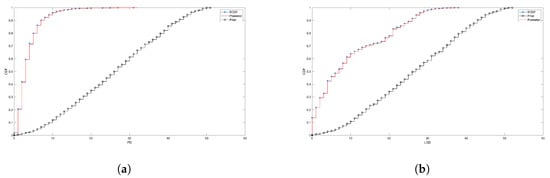
Figure 3.
Prior, posterior and ECDF for the discretised PD and LGD in the “Very poor” rating class, when priors are uniform and levels are like those in Equation (12). The strength of belief is always set to 1. (a) PD; (b) LGD.
It is worth noticing that, qualitatively, the results we discuss here are robust to different choices of the levels, until a sufficient number of observations is available for the update of the urns and hence learning, as already observed at the end of Section 4.1. For example, we have tested the partitions and : all findings were consistent with what we see in these pages. An example of partition that does not work is conversely the one based on increments equal to per level, which proves to be too fine, so that several urns are never updated and the posteriors do not pass the relative KS tests.
Figure 4 is generated in the same way as Figure 3. The only difference is that now , indicating a strong belief on the uniform priors. In this case, it is more difficult for the bivariate urn process to update the prior, and in fact the posterior distribution is not as close as before to the ECDF. The effect is more visible for PD than for LGD; however, in both cases, the KS test rejects the null (p-value 0.005 and 0.038). Please notice that this is not necessarily a problem, if one really believes that the available data do not contain all the necessary information, thus correcting for historical bias, or she wants to incorporate specific knowledge about future trends.
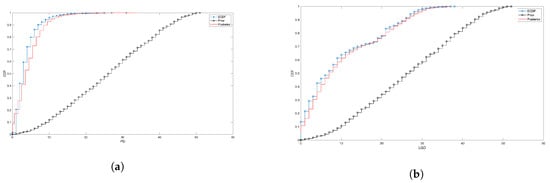
Figure 4.
Prior, posterior and ECDF for the discretised PD and LGD in the “Very poor” rating class, when priors are uniform and levels are like those in Equation (12). The strength of belief is always set to 100. (a) PD; (b) LGD.
As anticipated, the number of observations available in the data plays a major role in updating—and, in case of a wrongly elicited belief, correcting—the prior. Focusing on the PD, Figure 5 shows that, when the “Exceptional” rating class is considered, no big difference can be observed in the obtained posterior, no matter the strength of belief . In fact, for both cases, a KS test does not reject the null hypothesis with respect to the ECDF (p-values: and ). The reason is simple: with more than 30,000 observations, the model necessarily converges towards the ECDF, even if the prior distribution is clearly wrong and we put a strong belief on it (one needs to see some difference). Similar results hold for the LGD. In producing the figure, A has a uniform prior on , while B and C on .
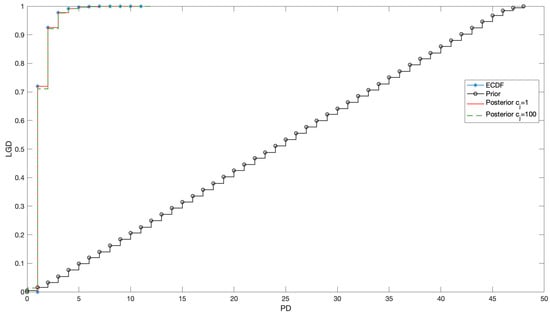
Figure 5.
Prior, posteriors ( and = 100) and ECDF for the discretised PD in the “Exceptional” rating class, when priors are uniform.
Figure 6 shows the bivariate distribution we obtain for the discretised PD and LGD for the “Very poor” FICO score group, when and we use the Poisson priors on the levels of Equation (12). Figure 7 shows the case . As one would expect, the strong prior provides a smoother joint distribution, while the weak one tends to make the empirical data prevail, with more peaks, bumps and holes. In Figure 8, the equivalent of Figure 6 is given for the “Exceptional” rating class.
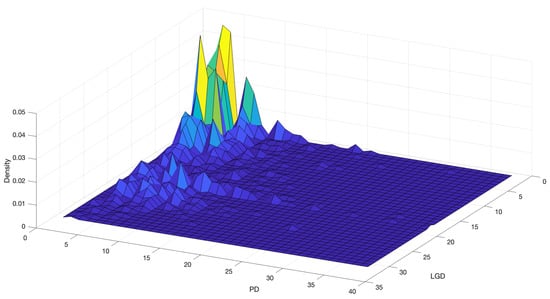
Figure 6.
Bivariate density distribution of PD and LGD in the “Very poor” rating class, with Poisson priors and strength of belief equal to 1.
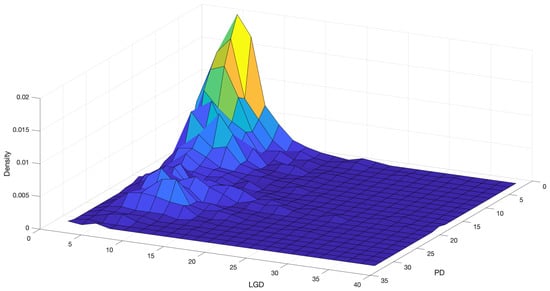
Figure 7.
Bivariate density distribution of PD and LGD in the “Very poor” rating class, with Poisson priors and strength of belief equal to 100.
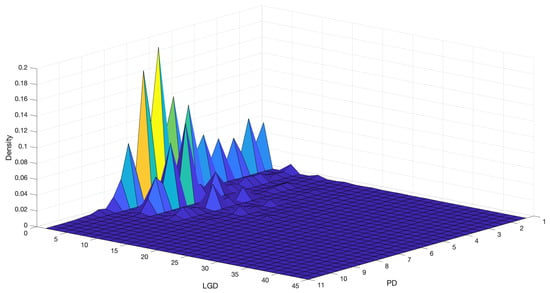
Figure 8.
Bivariate density distribution of PD and LGD in the “Exceptional” rating class, with Poisson priors and strength of belief equal to 1.
Regarding the numbers, all priors and level settings are able to model the dependence between X and Y. The correlation is properly captured (the way in which the prior on A is defined surely helps), as well as the mean and the variances of the marginals, especially when the strength of beliefs is small. The only problem is represented by the Poisson priors used on the “Very poor” class. In this case, the number of observations is not sufficient to correct the error induced by the initial use of a Poisson distribution, i.e., the same value for mean and variance, and the variance of both PD and LGD is underestimated, while the mean is correctly captured. In particular, while the estimated and actual means are and for X, and and for Y, in the case of the variances, the actual values and are definitely larger than the predicted ones, i.e., and . This is a clear signal that more data would be necessary to properly move away from the wrong prior beliefs, forgetting the Poisson nature.
In the case of Figure 6, the actual correlation is , and the model estimates . However, under Poisson priors with strong degrees of belief, a certain overestimation is observable for the “Very poor” rating group, in line with the underestimation of the variances.
The results we have just commented are all in sample: we have indeed used all the observations available to verify how the model fits the data, and no out of sample performance was checked. Using the Bayesian terminology of Jackman (2009) and Meng (1994), we have therefore performed a posterior consistency check.
Luckily, the out of sample validation of the bivariate urn model is equally satisfactory. To perform it, we have used the Freddie Mac’s sampling year to create two samples. The first one includes all the loans (362,104) sampled in the period 2002–2015 and we call it the training sample. The validation sample, conversely, includes all the loans sampled in 2016, for a total of 21,321 data points. The samples have then been split into FICO score groups, as before.
For the “Very Poor” class, Figure 9 shows the predictive distribution of the PD as obtained by training the bivariate urn construction (uniform priors) on the training sample (1590 loans) against the ECDF of the corresponding validation sample (37 loans). The fit is definitely acceptable, especially if we consider the difference in the sample sizes. The mean (level) of the predictive distribution is , while that of the validation sample is . The standard deviations are and . The median 3 in both cases. Regarding dependence, a correlation of is predicted by the model, while the realised one in the validation sample is smaller and equal to . This difference is probably due to the fact that in the validation set the PD never exceeds level 13, while in the training one the maximum level reached is 31. When the validation set is larger, as in the case of the “Exceptional” class, the dependence is better predicted: one has a correlation of against . Similar or better results are obtained for the other classes, using the different prior sets, once again with the only exception of the Poisson priors with a large strength of belief, when applied to the “Very poor” class. In Table 2, we show the PD and correlation results for all classes under uniform priors, while Table 3 deals with the LGD.
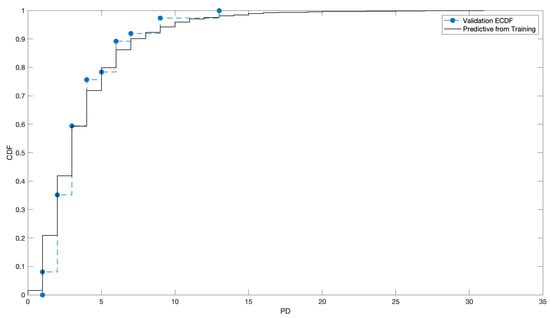
Figure 9.
Predictive distribution generated by the bivariate urn model for the “Very poor” class when trained on the training sample (1590 loans), against the empirical ECDF from the validation set (37 loans).

Table 2.
PD values (%) and correlation. Some descriptive descriptive statistics (mean, median, standard deviation, correlation for the joint) for the predictive distribution (P) and the validation set (V) for the different FICO classes, under uniform priors.

Table 3.
LGD values (%). Some descriptive descriptive statistics (mean, median, standard deviation) for the predictive distribution (P) and the validation set (V) for the different FICO classes, under uniform priors.
It is important to stress that this simple out of sample validation does not guarantee that the predictive distribution would be able to actually predict new data, in the case of a major change in the underlying phenomenon—something not observed in Maio’s dataset—like a structural break, to use the econometric jargon. This would be exactly the case in which the clever use of the prior distribution—in the form of expert prior knowledge—could contribute in obtaining a better fit.
4.4. What about the Crisis?
In line with findings in the literature (Eichengreen et al. 2012; Ivashina and Scharfstein 2010; Turlakov 2013; Witzany 2011), Maio’s dataset—as well as the original one by Freddie Mac—shows that the financial crisis of 2007–2008 had a clear impact on the dependence between PD and LGD. In particular, an increase in the strength of correlation is observable during the the crisis and in the years after. In fact, we can observe an overall value of 0.11 before 2008, which grows up to 0.24 in 2011 and remains pretty stable after. A compatible behavior is observed for the different FICO classes.
When evaluated in-sample, the bivariate urn model, given the large number of observations is always able to perform satisfactorily: this holds true for example when we restrict our attention on the intervals [2002–2007], [2007–2010] or [2010–2016]. Performances are conversely not good when the model trained on pre-crisis data is used to predict the post-crisis period, given the substantial difference in the strength of the dependence, which is persistently underestimated. Clearly, we are speaking about those situations in which the prior we elicited were not taking into consideration a strong increase in correlation. An ad hoc modification of the support of A could represent a viable solution, provided we could be aware of this ex ante, and not just ex post.
An interesting thing, worth mentioning, happens when we focus our attention on the loans originated (not defaulted) during the crisis and follow them. Here, the relation between PD and LGD tends to 0 or, for some FICO classes, it becomes slightly negative, probably because of the stricter selection the scared banks likely imposed on applicants, asking for more collateral and guarantees. While the model is still capable of dealing with no dependence, a negative correlation cannot be studied.
5. Conclusions
We have presented a bivariate urn construction to model the dependence between PD and LGD, also showing a promising application on mortgage data.
Exploiting the reinforcement mechanism of Polya urns and the conjugacy of beta-Stacy processes, the Bayesian nonparametric model we propose is able to combine experts’ judgements, in the form of a priori knowledge, with the empirical evidence coming from data, learning and improving its performances every time new information becomes available.
The possibility of using prior knowledge is an important feature of the Bayesian approach. In fact, it can compensate for the lack of information in the data with the beliefs of experienced professionals about possible trends and rare events. For rare events in particular, the possibility of eliciting an a priori on something rarely or never observed before can mitigate, at least partially, the relevant problem of historical bias (Derbyshire 2017; Shackle 1955; Taleb 2007).
One could argue that nothing guarantees the ability of eliciting a reliable a priori: experts could be easily wrong. The answer to such a relevant observation is that the bivariate urn model learns over time, at every interaction with actual data. A sufficient amount of data can easily compensate unrealistic beliefs. Moreover, as already observed in Cirillo et al. (2013), thanks to reinforcement, urns are able to learn hidden patterns in the data, casting light on previously ignored relations and features. Such a capability bridges towards the paradigm of machine/deep learning (Murphy 2012). However, differently from standard machine/deep learning techniques, the combinatorial stochastic nature of the bivariate urn model allows for a greater control of its probabilistic features. There is no black box (Knight 2017).
Clearly, if an a priori cannot be elicited nor is desired, one can still use the model in a totally data-driven way, building priors based on ECDFs (Cheng and Cirillo 2018). In such a case, however, the results of the bivariate urn construction would not substantially differ from those of a more standard empirical copula approach (Rueschendorf 2009), notwithstanding the difficulty of dealing with non-directly (fully) observable quantities like the joint factor A. More interesting can therefore be the “merging” methodology developed by Figini and Giudici (2011), in which the combination of quantitative and qualitative information can (at least partially) solve the lack of experts’ priors.
Furthermore, thanks to its nonparametric nature, the model we propose does not require the development of parametric assumptions, with the subsequent problem of choosing among them, as one should for instance do in using copulas (Nelsen 2006).
As observed in Section 2, an important limitation of the bivariate urn model is the possibility of only modeling positive linear dependence. Its use when dependence can be negative, or strongly nonlinear, is not advised. However, this seems not to be the case with mortgages, and PD/LGD in general.
Finally, the bivariate urn model can be computationally intensive. For large datasets and portfolios, a standard laptop may require from a few hours to a full day to obtain the posterior distribution. Clearly the quality of coding, which was not our main investigation path, has a big impact on the final performances.
Author Contributions
Conceptualization, P.C.; Data curation, D.C. and P.C.; Formal analysis, D.C. and P.C.; Investigation, D.C. and P.C.; Methodology, D.C. and P.C.; Supervision, P.C.; Visualization, P.C.; Writing the original draft, D.C. and P.C.; Review and editing, P.C. and D.C.
Funding
This research received no external funding.
Acknowledgments
The authors thank Vittorio Maio for sharing his data with them, and two anonymous referees for their suggestions and comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Altman, Edward I. 2006. Default Recovery Rates and LGD in Credit Risk Modeling and Practice: An Updated Review of the Literature and Empirical Evidence. New York University, Stern School of Business. [Google Scholar] [CrossRef]
- Altman, Edward I., Andrea Resti, and Andrea Sironi. 2001. Analyzing and Explaining Default Recovery Rates. A Report Submitted to the International Swaps & Derivatives Association. Available online: http://people.stern.nyu.edu/ealtman/Review1.pdf (accessed on 14 January 2019).
- Altman, Edward I., Brooks Brady, Andrea Resti, and Andrea Sironi. 2005. The Link between Default and Recovery Rates: Theory, Empirical Evidence, and Implications. The Journal of Business 78: 2203–27. [Google Scholar] [CrossRef]
- Amerio, Emanuele, Pietro Muliere, and Piercesare Secchi. 2004. Reinforced Urn Processes for Modeling Credit Default Distributions. International Journal of Theoretical and Applied Finance 7: 407–23. [Google Scholar] [CrossRef]
- Baesens, Bart, Daniel Roesch, and Harald Scheule. 2016. Credit Risk Analytics: Measurement Techniques, Applications, and Examples in SAS. Hoboken: Wiley. [Google Scholar]
- BCBS. 2000. Principles for the Management of Credit Risk. Available online: https://www.bis.org/publ/bcbs75.pdf (accessed on 10 March 2019).
- BCBS. 2005. An Explanatory Note on the Basel II IRB Risk Weight Functions. Available online: https://www.bis.org/bcbs/irbriskweight.pdf (accessed on 10 March 2019).
- BCBS. 2006. International Convergence of Capital Measurement and Capital Standards. Number 30 June. Basel: Bank for International Settlements, p. 285. [Google Scholar]
- BCBS. 2011. Basel III: A Global Regulatory Framework for More Resilient Banks and Banking Systems. Number 1 June. Basel: Bank for International Settlements, p. 69. [Google Scholar]
- Bruche, Max, and Carlos Gonzalez-Aguado. 2010. Recovery Rates, Default Probabilities, and the Credit Cycle. Journal of Banking & Finance 34: 754–64. [Google Scholar]
- Bulla, Paolo. 2005. Application of Reinforced Urn Processes to Survival Analysis. Ph.D. thesis, Bocconi University, Milan, Italy. [Google Scholar]
- Bulla, Paolo, Pietro Muliere, and Steven Walker. 2007. Bayesian Nonparametric Estimation of a Bivariate Survival Function. Statistica Sinica 17: 427–44. [Google Scholar]
- Calabrese, Raffaella, and Paolo Giudici. 2015. Estimating Bank Default with Generalised Extreme Value Regression Models. Journal of the Operational Research Society 28: 1–10. [Google Scholar] [CrossRef]
- Cerchiello, Paola, and Paolo Giudici. 2014. Bayesian Credit Rating Assessment. Communications in Statistics: Theory and Methods 111: 101–15. [Google Scholar]
- Cheng, Dan, and Pasquale Cirillo. 2018. A Reinforced Urn Process Modeling of Recovery Rates and Recovery Times. Journal of Banking & Finance 96: 1–17. [Google Scholar]
- Cirillo, Pasquale, Jürg Hüsler, and Pietro Muliere. 2010. A Nonparametric Urn-based Approach to Interacting Failing Systems with an Application to Credit Risk Modeling. International Journal of Theoretical and Applied Finance 41: 1–18. [Google Scholar] [CrossRef]
- Cirillo, Pasquale, Jürg Hüsler, and Pietro Muliere. 2013. Alarm Systems and Catastrophes from a Diverse Point of View. Methodology and Computing in Applied Probability 15: 821–39. [Google Scholar] [CrossRef]
- Derbyshire, James. 2017. The Siren Call of Probability: Dangers Associated with Using Probability for Consideration of the Future. Futures 88: 43–54. [Google Scholar] [CrossRef]
- Diaconis, Persi, and David Freedman. 1980. De Finetti’s Theorem for Markov Chains. The Annals of Probability 8: 115–30. [Google Scholar] [CrossRef]
- Duffie, Darrell. 1998. Defaultable Term Structure Models with Fractional Recovery of Par. Technical Report. Stanford: Graduate School of Business, Stanford University. [Google Scholar]
- Duffie, Darrell, and Kenneth J. Singleton. 1999. Modeling Term Structures of Defaultable Bonds. The Review of Financial Studies 12: 687–720. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Kenneth J. Singleton. 2003. Credit Risk. Cambridge: Cambridge University Press. [Google Scholar]
- Eichengreen, Barry, Ashoka Mody, Milan Nedeljkovic, and Lucio Sarno. 2012. How the Subprime Crisis Went Global: Evidence from Bank Credit Default Swap Spreads. Journal of International Money and Finance 31: 1299–318. [Google Scholar] [CrossRef]
- Experian. 2019. Blog: What Are the Different Credit Scoring Ranges? Available online: https://www.experian.com/blogs/ask-experian/infographic-what-are-the-different-scoring-ranges/ (accessed on 18 January 2019).
- Figini, Silvia, and Paolo Giudici. 2011. Statistical Merging of Rating Models. Journal of the Operational Research Society 62: 1067–74. [Google Scholar] [CrossRef]
- Fortini, Sandra, and Sonia Petrone. 2012. Hierarchical Reinforced Urn Processes. Statistics & Probability Letters 82: 1521–29. [Google Scholar]
- Freddie Mac. 2019a. Single Family Loan-Level Dataset; Freddie Mac. Available online: http://www.freddiemac.com/research/datasets/sf_loanlevel_dataset.page (accessed on 3 February 2019).
- Freddie Mac. 2019b. Single Family Loan-Level Dataset General User Guide; Freddie Mac. Available online: http://www.freddiemac.com/fmac-resources/research/pdf/user_guide.pdf (accessed on 3 February 2019).
- Freddie Mac. 2019c. Single Family Loan-Level Dataset Summary Statistics; Freddie Mac. Available online: http://www.freddiemac.com/fmac-resources/research/pdf/summary_statistics.pdf (accessed on 3 February 2019).
- Frye, Jon. 2000. Depressing Recoveries. Risk 13: 108–11. [Google Scholar]
- Frye, Jon. 2005. The Effects of Systematic Credit Risk: A False Sense of Security. In Recovery Risk. Edited by Edward Altman, Andrea Resti and Andrea Sironi. London: Risk Books, pp. 187–200. [Google Scholar]
- Galavotti, Maria Carla. 2001. Subjectivism, objectivism and objectivity in bruno de finetti’s bayesianism. In Foundations of Bayesianism. Edited by David Corfield and Jon Williamson. Dordrecht: Springer, pp. 161–74. [Google Scholar]
- Genest, Christian, and Louis-Paul Rivest. 1993. Statistical inference procedures for bivariate archimedean copulas. Journal of the American Statistical Association 88: 1034–43. [Google Scholar] [CrossRef]
- Geske, Robert. 1977. The Valuation of Corporate Liabilities as Compound Options. Journal of Financial and Quantitative Analysis 12: 541–52. [Google Scholar] [CrossRef]
- Giudici, Paolo. 2001. Bayesian Data Mining, with Application to Credit Scoring and Benchmarking. Applied Stochastic Models in Business and Industry 17: 69–81. [Google Scholar] [CrossRef]
- Giudici, Paolo, Pietro Muliere, and Maura Mezzetti. 2003. Mixtures of Dirichlet Process Priors for Variable Selection in Survival Analysis. Journal of Statistical Planning and Inference 17: 867–78. [Google Scholar]
- Hamerle, Alfred, Michael Knapp, and Nicole Wildenauer. 2011. Modelling Loss Given Default: A “Point in Time”-Approach. In The Basel II Risk Parameters: Estimation, Validation, Stress Testing—With Applications to Loan Risk Management. Edited by Bernd Engelmann and Robert Rauhmeier. Berlin: Springer, pp. 137–50. [Google Scholar]
- Hjort, Nils Lid, Chris Holmes, Peter Mueller, and Stephen G. Walker. 2010. Bayesian Nonparametrics. Cambridge: Cambridge University Press. [Google Scholar]
- Hull, John C. 2015. Risk Management and Financial Institutions, 4th ed. New York: Wiley. [Google Scholar]
- Ivashina, Victoria, and David Scharfstein. 2010. Bank lending during the financial crisis of 2008. Journal of Financial Economics 97: 319–38. [Google Scholar] [CrossRef]
- Jackman, Simon. 2009. Bayesian Analysis for the Social Sciences. New York: Wiley. [Google Scholar]
- Jones, Philip, Scott P. Mason, and Eric Rosenfeld. 1984. Contingent Claims Analysis of Corporate Capital Structures: An Empirical Investigation. The Journal of Finance 39: 611–25. [Google Scholar] [CrossRef]
- JP Morgan. 1997. Creditmetrics—Technical Document. Available online: http://www.defaultrisk.com/_pdf6j4/creditmetrics_techdoc.pdf (accessed on 3 February 2019).
- Kim, In Joon, Krishna Ramaswamy, and Suresh Sundaresan. 1993. Does Default Risk in Coupons Affect the Valuation of Corporate Bonds?: A Contingent Claims Model. Financial Management 22: 117–31. [Google Scholar] [CrossRef]
- Knight, Will. 2017. The Dark Secret at the Heart of AI. Technology Review 120: 54–63. [Google Scholar]
- Lando, David. 1998. On Cox Processes and Credit Risky Securities. Review of Derivatives Research 2: 99–120. [Google Scholar] [CrossRef]
- Lindley, Dennis. 1991. Making Decisions, 2nd ed. New York: Wiley. [Google Scholar]
- Longstaff, Francis A., and Eduardo S. Schwartz. 1995. A Simple Approach to Valuing Risky Fixed and Floating Rate Debt. The Journal of Finance 50: 789–819. [Google Scholar] [CrossRef]
- Mahmoud, Hosam. 2008. Polya Urn Models. Boca Raton: CRC Press. [Google Scholar]
- Maio, Vittorio. 2017. Modelling the Dependence between PD and LGD. A New Regulatory Capital Calculation with Empirical Analysis from the US Mortgage Market. Master’s thesis, Politecnico di Milano, Milano, Italy. Available online: https://www.politesi.polimi.it/handle/10589/137281 (accessed on 10 March 2019).
- McNeil, Alexander J., and Jonathan P. Wendin. 2007. Bayesian inference for generalized linear mixed models of portfolio credit risk. Journal of Empirical Finance 14: 131–49. [Google Scholar] [CrossRef]
- McNeil, Alexander J., Ruediger Frey, and Paul Embrechts. 2015. Quantitative Risk Management. Princeton: Princeton University Press. [Google Scholar]
- Meng, Xiao-Li. 1994. Multiple-Imputation Inferences with Uncongenial Sources of Input. Statistical Science 9: 538–58. [Google Scholar] [CrossRef]
- Merton, Robert C. 1974. On the Pricing of Corporate Debt: The Risk Structure of Interest Rates. The Journal of Finance 29: 449–70. [Google Scholar]
- Miu, Peter, and Bogie Ozdemir. 2006. Basel Requirement of Downturn LGD: Modeling and Estimating PD & LGD Correlations. Journal of Credit Risk 2: 43–68. [Google Scholar]
- Muliere, Pietro, Piercesare Secchi, and Stephen G Walker. 2000. Urn Schemes and Reinforced Random Walks. Stochastic Processes and their Applications 88: 59–78. [Google Scholar] [CrossRef]
- Muliere, Pietro, Piercesare Secchi, and Stephen G Walker. 2003. Reinforced Random Processes in Continuous Time. Stochastic Processes and Their Applications 104: 117–30. [Google Scholar] [CrossRef]
- Murphy, Kevin P. 2012. Machine Learning: A Probabilistic Perspective. Cambridge: The MIT Press. [Google Scholar]
- Narain, Bhavana. 1992. Survival Analysis and the Credit Granting Decision. In Credit Scoring and Credit Control. Edited by Lyn C. Thomas, David B. Edelman and Jonathan N. Crook. Oxford: Oxford University Press, pp. 109–21. [Google Scholar]
- Nelsen, Roger B. 2006. An Introduction to Copulas. New York: Springer. [Google Scholar]
- Nielsen, Lars Tyge, Jesus Saà-Requejo, and Pedro Santa-Clara. 2001. Default Risk and Interest Rate Risk: The Term Structure of Default Spreads. Paris: INSEAD. [Google Scholar]
- Peluso, Stefano, Antonietta Mira, and Pietro Muliere. 2015. Reinforced Urn Processes for Credit Risk Models. Journal of Econometrics 184: 1–12. [Google Scholar] [CrossRef]
- Resti, Andrea, and Andrea Sironi. 2007. Risk Management and Shareholders’ Value in Banking. New York: Wiley. [Google Scholar]
- Rueschendorf, Ludger. 2009. On the distributional transform, sklar’s theorem, and the empirical copula process. Journal of Statistical Planning and Inference 139: 3921–27. [Google Scholar] [CrossRef]
- Shackle, George Lennox Sharman. 1955. Uncertainty in Economics and Other Reflections. Cambridge: Cambridge University Press. [Google Scholar]
- Taleb, Nassim Nicholas. 2007. The Black Swan: The Impact of the Highly Improbable. New York: Random House. [Google Scholar]
- Turlakov, Mihail. 2013. Wrong-way risk, credit and funding. Risk 26: 69–71. [Google Scholar]
- Vasicek, Oldrich A. 1984. Credit Valuation. Available online: http://www.ressources-actuarielles.net/EXT/ISFA/1226.nsf/0/c181fb77ee99d464c125757a00505078/$FILE/Credit_Valuation.pdf (accessed on 10 March 2019).
- Walker, Stephen, and Pietro Muliere. 1997. Beta-Stacy Processes and a Generalization of the Pólya-Urn Scheme. The Annals of Statistics 25: 1762–80. [Google Scholar] [CrossRef]
- Wilde, Tom. 1997. CreditRisk+: A Credit Risk Management Framework. Technical Report. New York: Credit Suisse First, Boston. [Google Scholar]
- Wilson, Thomas C. 1998. Portfolio credit risk. Economic Policy Review 4: 71–82. [Google Scholar] [CrossRef]
- Witzany, Jiřì. 2011. A Two Factor Model for PD and LGD Correlation. Bulletin of the Czech Econometric Society 18. [Google Scholar] [CrossRef]
- Yao, Xiao, Jonathan Crook, and Galina Andreeva. 2017. Is It Obligor or Instrument That Explains Recovery Rate: Evidence from US Corporate Bond. Journal of Financial Stability 28: 1–15. [Google Scholar] [CrossRef]
- Zhang, Jie, and Lyn C. Thomas. 2012. Comparisons of Linear Regression and Survival Analysis Using Single and Mixture Distributions Approaches in Modelling LGD. International Journal of Forecasting 28: 204–15. [Google Scholar] [CrossRef]
| 1 | In reality, as observed in Zhang and Thomas (2012), the LGD can be slightly negative or slightly above 100% because of fees and interests; however, we exclude that situation here. In terms of applications, all negative values can be set to 0, and all values above 100 can be rounded to 100. |
| 2 | Please observe that exchangeability only applies among the couples , while within each couple there is a clear dependence, so that and are not exchangeable. |
| 3 | To avoid any copyright problem with Freddie Mac, which already freely shares its data online, from Maio’s dataset (here attached), we only provide the PD and the LGD estimates, together with the unique alphanumeric identifier. In this way, merging the data sources is straightforward. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).