Abstract
In the past two decades increasing computational power resulted in the development of more advanced claims reserving techniques, allowing the stochastic branch to overcome the deterministic methods, resulting in forecasts of enhanced quality. Hence, not only point estimates, but predictive distributions can be generated in order to forecast future claim amounts. The significant expansion in the variety of models requires the validation of these methods and the creation of supporting techniques for appropriate decision making. The present article compares and validates several existing and self-developed stochastic methods on actual data applying comparison measures in an algorithmic manner.
1. Introduction
Insurance and reinsurance institutions, particularly property and casualty insurers, put a considerable amount of effort into the understanding of outstanding claims reserves. These amount to the most material proportion of technical provisions, hence, their volume and uncertainty are critical to be controlled well by actuaries and management. Not only the measure and pattern of future cash outflows and metrics of associated risks play a role in the insurance business, but also management decisions are triggered by the outcome of calculations.
Scholars and industry professionals have been studying different estimation models in the past decades extensively. Interest in stochastic models has outgrown the interest in deterministic ones, shifting from simple point estimations to approximation of probability distributions, enabling the calculation of features of the examined object with more insight into the nature of the underlying phenomenon. The demand for forecasts embodied in distributional forms rather than point estimates has grown rapidly along with the growth of computational power, simultaneously allowing for the pragmatic implementation of Monte Carlo type algorithms. This increasing interest has emerged not only in insurance but in several other disciplines, such as meteorology or finance, demanding a more meaningful prediction of future outcomes. England and Verrall (2002); Wüthrich and Merz (2008) contain comprehensive overviews of reserving methods. In our view, the validation of the models on actual industrial data and the comparison of these models’ appropriateness is a crucial question. In spite of the relevance of model suitability, proportionally to the size of existing literature on models, even more attention has to be given to the substantiation of model quality and to the comparison of methodologies. Professionals who are offered countless different models need guidelines that can support an optimal selection. A more recent work, Meyers (2015) performs investigation on bootstrap and Bayesian models using publicly available claims data from American insurance companies. The work also proposes new methods practically solved through MCMC simulations.
A case study is performed in Wüthrich (2010) in order to analyse the accounting year effects in the triangles. This study compares Bayesian models with mean square error of prediction (MSEP) and deviance information criterion (DIC). Shi and Frees (2011) and Shi et al. (2012) provide another comparison alternative with QQ-plots and PP-plots. Nevertheless, the first one focusses on understanding the dependency among the triangles of different business lines with a copula regression model, and the second one describes retrospective tests on the models proposed. Even more focus is put on the validation of methods in Martínez-Miranda et al. (2013), evaluating which methodology should be preferred. Three methods, the double chain ladder, the Bornhuetter–Ferguson and the incurred double chain ladder methods are compared through two real data sets from property and casualty insurers, and the metrics used are call error, calendar year error and total error. Supported by real-life claims data, Tee et al. (2017) compares three models with different residual adjustments using the Dawid–Sebastiani scoring rule (DSS).
This paper analyses diverse stochastic claims reserving methods by means of several goodness-of-fit measures. In a game-theoretic interpretation of forecasts, it sets up a ranking framework selecting from competing models. Certainly, there is hardly any manner of ranking methodology which all actuaries would unanimously agree with, as a peremptory selector of the most proper prediction models. However, it is reasonable to define and observe the important characteristics of estimations, which put together may support the decision-making process and the validation of the applied methods. In the assessment of reserving models, there is a strong intention to promote measures originally used in stochastic forecasting. Another objective of the paper is to support the methodological background and perform assessments of diverse sets of models on actual data. Probability integral transform (PIT) provides more justification on the predictive distribution appropriateness, while the Kolmogorov–Smirnov or Cramér–von Mises statistics would fail to shed light on what exactly goes wrong with the hypothesis. Established scores compare and verify qualities of rival probabilistic forecasting models on the basis of estimation and real outcomes.
From the wide range of scoring rules, we apply the continuous ranked probability scores (CRPS) due to their flexible applicability on differing distributions, see Gneiting and Raftery (2007). Coverage shows the central prediction interval of a prediction given a real governing distribution. Sharpness, a related metric is the width as expected difference between lower and upper p-quantiles, the narrower the better expressed in payment, see Gneiting et al. (2007). Alternatively, sharpness is also called average width. For backtesting the stochastic reserving models we apply these five metrics on the full quadrangles, i.e., on the run-off tringles completed with the lower part. In several cases, when the prediction model is distribution-free, the empirical forecast has been drawn through bootstrapping. This makes an empirical predictive distribution uniformly available.
In order to measure according to real scenarios, the database published in Meyers and Shi (2011) has been used. Paid and incurred claims data originate from the National Association of Insurance Commissioners (NAIC), and contain tables for six different lines of business, encompassing (1) commercial auto and truck liability and medical, (2) medical malpractice, (3) private passenger auto liability and medical, (4) product liability, (5) workers’ compensation and (6) other liability. Lines of business are homogeneous groups of policies with identical coverage. Data are segmented into these clusters in order to avoid the amalgamation of claim payment run-offs with significantly different characteristics. Leong et al. (2014) evaluates backtesting on the referred data with respect to the application of bootstrap overdispersed Poisson model.
Simulations have been carried out with R, using packages ChainLadder Gesmann (2018) and rjags for the MCMC simulations. Besides the self-written program codes, scripts published in association with Meyers (2015) have been embedded into the calculations.
The primary objective of the present article is to support decision making among several available models applied on run-off triangles, by defining and calculating measures of the actual and predictive distributions. Given that actual distributions can hardly be extracted, we have used empirical distributions from real ultimate claims data.
To the authors’ knowledge, neither the credibility bootstrap method in Section 3.3, nor the collective semi-stochastic model in Section 3.5 have ever been discussed in peer-reviewed journals. Two of the models incorporate experience ratemaking from the claims history of an entire community of companies. One step further is exploiting collective data to improve individual (insurance company level) prediction reliabilities, requiring the coordination of regulatory authorities as data collectors and processors.
To summarise the novelties communicated by the present paper: (1) Metrics in actuarial reserving such as CRPS, coverage and sharpness of several models to analyse their performance and determine an order of appropriateness have been presented by Arató et al. (2017) on simulated data. Here we apply all the calculations on actual triangles from multiple risk groups. (2) PIT has already been applied by Meyers (2015) on stochastic models, here we continue presenting the calculations involving further methods not covered elsewhere (credibility bootstrap, bootstrap Munich, semi-stochastic). (3) Two new models are introduced, credibility bootstrap in Section 3.3 and collective semi-stochastic in Section 3.5. (4) We emphasise the importance of an algorithmic way of model selection from competing peers in Section 4. (5) Models based on internal information only (single triangle) are also compared with collective ones (multiple triangles and credibility), and the article intends to convey the potential of oversight data collection and possible application on multiple triangles. (6) Scripts published by Meyers (2015) are developed further with new code chunks and made available in the paper’s supplement.
The article is structured as follows: Section 2 contains the expository description of insurance data published by the NAIC and used for comparative analysis, consisting of observations of claims and premiums from hundreds of insurance institutions. Section 3 enumerates of methodologically distinct and diverse reserving models, a number of which are applied widely in the insurance industry. Having approached the original, claims reserving problem as a probabilistic forecast, Section 4 provides insight into five measures. The section includes the validation of individual models from the angle of the five indicators. Section 5 concludes the paper.
2. Data
Open source data enables the validation of methodologies on real loss figures. The National Association of Insurance Commissioners (NAIC) published data tables consisting of the names of insurance institutions, incurred and paid loss per accident year and per development year, and earned premiums per contract year. Meyers and Shi (2011) published these tables along with the article.
Historical values applied in the present paper concern the run-off triangles built up by paid and incurred losses. Six different lines of business can be distinguished; (1) commercial auto and truck liability and medical, (2) medical malpractice, (3) private passenger auto liability and medical, (4) product liability, (5) workers’ compensation and (6) other liability, with a variable number of corporations contributing to the data set. Business lines correspond to homogeneous segments of insurance portfolios, which are addressed separately for the reason that they generally show distinct run-off behaviour. Hence, clusters on the basis of coverage type are made in order not to amalgamate different run-off characteristics. Let one observation mean the loss triangle associated to one insurance company, see Table 1.

Table 1.
Number of observations (insurance institutions) in the data sets.
In fact, accident years cover a 10-year time span between 1988 and 1997, with a 10-year development lag for each accident year. In other words, not only the triangle values above (and including) the anti-diagonal are available (Table 2), but the entire rectangle in each case. From a validation perspective, it is crucial that the actual ultimate claim values, i.e., the lower triangles are known (Table 3).

Table 2.
Cumulative paid loss triangle observed in the past (commercial auto data set, group code 2712).

Table 3.
Cumulative paid loss triangle observed in the future (commercial auto data set, group code 2712).
Ultimate claim values range from zero to millions in extreme cases, see Table 4 for paid losses, implying magnitudinal diversity in the set of companies in terms of reserves. In fact, only few outliers can be found with negative total claims, which we consider the less reliable part of the data set. These instances have been taken out of the analysis. Hence, a natural and far not trivial question is whether or not to apply a normalisation on the run-off triangles, in order to make reserving models reasonably comparable with each other by mitigating the heterogeneity of the underlying figures. For instance, this can be achieved by multiplying each triangle by different constants to make ultimate reserves equal to a unit value. Several pitfalls accompany the scaling: applying a discrete model such as the overdispersed Poisson model (family) on triangles consisting of small numbers, the estimation will be useless if the Poisson parameter is close enough to zero to make future claim increments equal to zero with high probability. As a matter of fact, this issue can be remediated by choosing an appropriately large normalising constant. The standardisation of such overdispersed Poisson data has been extensively discussed in the past in connection with stochastic reserving. Each of the run-off triangle elements are normalised by a volume measure related to the accident year, i.e., each incremental or cumulative claim in row i is divided by a weight . This exposure volume can be the number of reported claims in accident year i, see Wüthrich (2003). Another convention is to choose the earned premium volume or the number of policies, see Shi and Frees (2011).

Table 4.
Ranges of paid losses per business line.
The second and more contradictory argument against scaling is embedded in the data: large companies likely provide more robust claim records than their smaller counterparts, i.e., it is rational to take them into account with larger weights, which is ensured by the larger reserve values. Hence, the question is whether to allow institutions to contribute to the total loss values according to their reserve volumes, or compose a democratic aggregate observation set with a similar contribution from each institution in terms of ultimate claim. An intermediate solution can be a nonconstant rescaling of data, which might be considered by the reader. In loss reserving calculations, the author in Shi (2015) applies normalisation in order to mitigate the heterogeneity of the data. Present calculations leave original figures as they are, as a consequence of our entirely arbitrary choice. Normalised calculations might be replicated easily based on the supplied scripts.
3. Claims Reserving Models
In this section five conceptually distinct modelling approaches are enumerated in claims reserving, where in some of the cases, the model refers to a method family rather than a single one. These are the (1) bootstrap models with Gamma and overdispersed Poisson background, (2) Bayesian models using MCMC techniques, (3) credibility models, including a newly introduced one combined with bootstrapping, (4) original Munich Chain Ladder and its bootstrapped modification and (5) a semi-stochastic model.
Notations the reader frequently encounters in this section are the following: I and J denote the number of occurrences and development years in the triangles (and quadrangles), i.e., they stand for the dimensions. Let and denote the incurred and paid triangles in Section 3.4. Avoid confusing the superscript in , which stands for ’Incurred’, with the I number of rows in the triangle. If the paid or incurred indicatives are not relevant from a technical perspective, they will not be marked. Superscript in connection with cumulative triangle element means that the value is related to company k. stands for the upper run-off triangle of the jth company, i.e., the claims data acquired until the time of reserve calculation.
3.1. Bootstrap Models
Bootstrapping in the mathematical sense has a proper literature and has been studied for almost four decades, well before applications in insurance emerged. The original introduction dates back to Efron (1979b, 1979a) as a generalisation of jackknife, enhancing the power of available sample by resampling. Introducing an application of bootstrapping in insurance, Ashe (1986) was among the first papers, estimating distribution error. Later, England and Verrall (1999) analyses the prediction error in conjunction with generalised linear models (GLMs) with bootstrapping, whilst Pinheiro et al. (2003) proposes an alternative bootstrap procedure to the previous one, using corrected residuals. The capability of error prediction was the primary feature of the concept which has driven the development of such models in the actuarial field. Contrary to the simple chain ladder model, it allows to capture the variability of the outcome. More recent achievements are Björkwall et al. (2009); Leong et al. (2014) and a more practical guide is Shapland (2016). Thus, models using bootstrapping have become widely applied in actuarial practice, and studied in numerous works. In this paper we apply the overdispersed Poisson and gamma bootstrap models. For more comprehensive works that describe the underlying GLM and residuals, the reader is advised to see England and Verrall (2002); Wüthrich and Merz (2008).
3.2. Bayesian Models Using MCMC
Two methods based on Markov Chain Monte Carlo simulation that follow a Bayesian concept are presented by Meyers (2015). The author made the self-prepared R codes public in order to facilitate the replication of results. These code chunks have been embedded into the set of codes supporting the analysis in the present article. Models with MCMC sampling are the most computation-intensive ones among the modelling principles the reader encounters here.
3.2.1. Correlated Chain Ladder Model
In the correlated chain ladder (CCL) model incurred claims are the basis of calculation, in the form of cumulative losses. The motivation is to address the possible underestimation of ultimate claim variability in the original Mack model Mack (1993). The underlying assumption is that the unknown losses are governed by the log-normal distribution. See Meyers (2015) for the detailed model assumptions.
3.2.2. Correlated Incremental Trend Model
The second model is built on the incremental paid loss amounts rather than the incurred claims, and has a distribution skewed to the right. For the introduction of skew-normal distribution see Frühwirth-Schnatter and Pyne (2010).
Meyers (2015) points to the issue that skew-normal distribution has a skewness of a truncated normal variable in the extreme case, which still may not reflect the real skewness stemming from the loss data, creating the demand for an even more skewed distribution to be applied instead of the truncated normal.
Note that another model in the referred monograph, called changing settlement rate model, may address the phenomenon of accelerating claim settlements, driven by technological changes.
3.3. Credibility Models
The present subsection contains the basic idea of credibility theory and its connection with claims reserving. By combining this idea with the methodology of bootstrapping, a new reserving model is introduced.
Papers Bühlmann (1967, 1969) contain the original concept of experience ratemaking. The core principle is to exploit the available information from sources outside of the sample, but somehow related to it, and combine the two data sets in order to get a more reliable approximation of unknown characteristics. Considering one business line, in order to create the claim forecast of one particular triangle, the other run-off triangles of the same group are also taken into account. From another angle, the model consists of 2 urns, where we pick the risk parameter from the first one, which determines the value sampled from the second urn. Shi and Hartman (2016) proposes credibility based stochastic reserving driven by the idea that data from peer counterparty insurers can lead to an improvement of prediction reliability.
To the analogy of the Mack Chain Ladder methodology Mack (1993), construct the following model assumptions in a Bayesian thinking.
Assumptions 1.
- (C 1)
- Let each unknown chain ladder factor be a positive random variable for , independent of for .
- (C 2)
- are conditionally independent of .
- (C 3)
- The conditional distribution of under the constraint depends only on . Furthermore, conditional expectation and variance areand
Recall from Bayesian statistics that for an arbitrary random variable and array of observations , the linear Bayesian estimator satisfies . Also recall from Gisler and Wüthrich (2008) the Definition 2 of the credibility based predictor and a relevant Theorem 3.
Definition 2.
The credibility based predictor of the ultimate claim given is
where
and , the subset of upper triangle information.
Given the multiplicative structure of the ultimate claim estimator it may not be appropriate to call it simply a credibility estimator, which is by definition a linear function of the observations, hence the credibility based appellation.
Theorem 3.
The credibility estimators of the development factors are given by
where , , , and . The latter two are the structural parameters (or credibility factors and their quotient, is the credibility coefficient).
For the mean square error of prediction it is also true that , see Definition 17.
Proof: See Gisler and Wüthrich (2008).
Data concerning the credibility factor in particular are not available in general. In the present article these parameters are approximated on the basis of claim triangles published by several companies.
From regulatory perspective it is extremely important to understand how the inflowing data can be exploited in order to support the insurance institutions with reliable information. Financial regulatory authorities tend to collect an increasing amount of detailed data for the purpose gaining insight into the insurance institutions’ solvency. In Europe, for instance, the European Insurance and Occupational Pensions Authority (EIOPA) shows guidance to local regulators and collects submissions of statistical and financial data from several countries. Besides transparency, the information enables the adequate support of corporations by providing them with processed data to their benefit. This is where credibility models have an untapped potential. The question whether or not to use collective experience to improve individual approximations is particularly relevant due to the fact that regulatory authorities collect vast amount of information from insurance companies. Thus, the processed data might be of value to share with the contributors, enabling more precise solvency evaluations.
Let stand for the cumulative payment or incurred claim value with occurrence year i and development year j with respect to company k. In general, for simplicity’s sake it is supposed that for each insurance institution the triangle dimensions are equal, moreover, . n denotes the number of companies observed in a homogeneous risk group and the dimension of the kth triangle. The parameter estimation of credibility factors is constructed in accordance with Section 4.8 in Bühlmann and Gisler (2006). Let index j be fixed and let be defined for each triangle as
Observe that
which implies that in line with Assumption 1. Hence, for each j, i.e., provides an unbiased estimator for . Taking the average of values for all the companies results in an unbiased estimator of :
It can also be shown with further calculations that is an unbiased estimator of :
with .
Parameter needs extra attention having observed that the estimator below can attain negative values, not only in an extremely theoretical sense, but on the real world trajectories, as well. For that reason, let the approximation be capped by 0 from below.
Furthermore, let the estimator of be
In the following model we assume the Pearson residuals, where increment stems from the cumulative values . Residuals are adjusted for bias correction by multiplying the Pearson residulals with a proportion of all the underlying data points and estimated parameters. This adjustment remains similar to the standard bootstrap method, as well as the scale parameter estimation.
Method 4 (Credibility Bootstrap).
- (Step 1)
- (Step 2)
- With respect to each company, exchange the chain ladder factors with the credibility chain ladder factors.
- (Step 3)
- Apply the bootstrap overdispersed Poisson model with the credibility chain ladder factors.
As an illustration of the outcome of the first two steps in the credibility bootstrap methodology, consider a few arbitrarily selected companies in one business line. The cumulative product of the development factors can be seen on Figure 1a for each, in the sense that the function value of the first year is equal to 1, and for year k ().
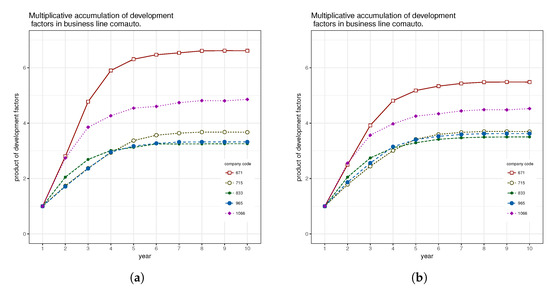
Figure 1.
Multiplicative accumulation of development factors (a) without and (b) with credibility adjustment.
Figure 1b presents the same institutions as the previous figure, but with credibility adjustment, i.e., instead of the original values, the developments in a similarly product based pattern. Observe the narrowing range of individual patterns.
3.4. Munich Chain Ladder Model
3.4.1. Original Model
Observe that all the reserving models enumerated so far are operated with one run-off triangle, be it either the paid or the incurred one. The question naturally arises why not to use both triangles at the same time, doubling the volume of the information and, hopefully upgrading the quality of prediction. Quarg and Mack (2004) introduced the Munich Chain Ladder (MCL) algorithm, which takes into account both paid and incurred cumulative data, assuming correlation between paid and incurred stemming from different accident years, but not in the same accident year for both. Here we only mention the model assumptions and notations.
Notation 5.
- 1.
- Let stand for the regular chain ladder development factors in the paid, and in the incurred triangle, where and . Let and , and , be the ratios of paid and incurred claims, or (P/I) and (I/P) ratios.
- 2.
- Let generated σ-fields and be the information acquired until development year k related to claims in accident year i. Let denote the combined knowledge .
Assumptions 6.
- (A)
- (Expectations) There exist positive development factors and such that and and . Furthermore, there exist and such that and .
- (B)
- (Variances) There exist non-negative constants and such that and and . Furthermore, there exist and such that and .
- (C)
- (Independence) Occurrence years are independent, i.e., setsare stochastically independent.
- (D)
- (Correlations) Generally, let denote the conditional residual of random variable ξ given σ-algebra . There exist and constants such that and . Rearranging the equations results in formsand
3.4.2. Bootstrapping the Munich Chain Ladder
In its original form the MCL method fails to establish distributions for ultimate paid or incurred claim values and thus to enable the analysis of their stochastic behaviour. Recalling the application of bootstrap techniques, Liu and Verrall (2010) suggests a plausible solution to generate random outcomes by drawing random samples from the four residual sets in the MCL procedure.
3.4.3. Applicability and Limitations
A practical drawback of the model which may materialise during reserve calculations is that variance parameters and can attain extremely low values or even zero. It means that their ratio can be a large number, which contributes to the conditional development factor, see Assumptions 6 (D), eventually resulting in unrealistic ultimate claims.
To give an example from the actually documented NAIC figures, see paid Table 5 and incurred Table 6 triangles from the commercial automobile insurance claims of a company.

Table 5.
Cumulative paid loss triangle observed in the past (commercial auto data set, group code 8079).

Table 6.
Cumulative incurred loss triangle observed in the past (commercial auto data set, group code 8079).
Evaluating the variance parameters defined in Assumptions 6 (B), it becomes clear that for higher js, and gets close to zero. The unbiased parameter estimators
and
may result in almost zero numbers due to the fact that as index j approaches J, each sum of the four estimators can be close or equal to zero, see Table 7. Thus, excessive fractions and yield degenerate MCL development factor estimations and , exceeding any upper bound.

Table 7.
Variance assumption parameters. (Observe that the parameters become zero for development steps 8 and 9).
Such estimators contribute to the approximate reserves on Table 8, see columns MCL paid and incurred. The astronomical values are the direct result of the parameter calculation according to the closed formulas in Equations (7) and (8). Hence, as an alternative, change and to zero in case they fall out of a pre-defined interval, which is in principle equivalent to applying simple chain ladder development factors assigned to the last few development years. This kind of truncation practice is followed in the present Bootstrap MCL calculations.

Table 8.
Paid and incurred estimates divided into accident years (bootstrapped MCL, original MCL and actual). Data used from commercial auto, group code 8079.
3.5. Semi-Stochastic Models
A family of models with the idea that the chain ladder factors are bootstrapped directly is presented in Faluközy et al. (2007).
Assumptions 7 (Base Semi-stochastic).
(1) Suppose that each subsequent cumulative claim has a multiplicative link to the previous one in development year j through a random variable . (2) Let random variables be mutually independent and governed by the discrete uniform distribution on the set
The expectation of each is , equal to the average of the set of values, making the model of the type ’link ratios with simple average’ method.
Method 8 (Base Semi-stochastic).
In other words, this base model creates alternative lower triangles by completing each row recursively, choosing from factors randomly and processing for . The ultimate claims are also random variables with parameters implied by the previous random recursion.
The expectation of the ultimate claim is .
Instead of addressing each triangle separately, consider the possibility of using other companies’ data from a corresponding product group. Being able to do so may either reflect the perspective of a regulatory organisation with collected data from insurance institutions, or data made publicly available voluntarily by the insurance institutions for collective improvement purposes. Eventually, the NAIC database is an example of the latter. The principle is similar to the above method, however, instead of sampling from in one stand-alone run-off triangle, the new version is as follows.
Assumptions 9 (Collective Semi-Stochastic).
(1’) As (1). (2’) random variables are discrete uniform on the set of development factors.
The assumption is similar to the one above Faluközy et al. (2007), however, now the cumulative claims are driven recursively by random variables stemming from an unknown distribution, identically distributed across the run-off triangles.
Method 10 (Collective Semi-stochastic).
- Step 1
- Calculate chain ladder link ratios for ; .
- Step 2
- For each j sample from with replacement; , where M stands for an arbitrarily large sample size. M equals to 5000 in the actual examples in Section 4.
- Step 3
- Perform the multiplication of last cumulative observations in order to get the randomly generated ultimate claims. For a fixed company, , .
4. Comparing Forecasts
Prediction of the uncertain future has been enjoying a growing interest in numerous disciplines in the past decades, let it be meteorology, financial risk management or actuarial sciences. The demand for forecasts embodied in distributional forms rather than point estimates has grown rapidly along with the growth of computational power, simultaneously allowing for the pragmatic implementation of Monte Carlo type algorithms.
The probabilistic forecast as distribution dates back at least to Dawid (1984), introducing the prequential principle. The term stems from the words probabilistic forecasting with sequential prediction, which refers to accumulating new observations from time to time, and implementing them into the subsequent days’ estimations. A game-theoretic interpretation of probabilistic forecasts in the context of meteorological applications (similarly to the previous one) is analysed in Gneiting et al. (2007), guiding through the predicting performance of a set of climatological experts. Observe the analogy between climate forecast experts and competing reserving methods. Both of these articles have a wide range of applicability going beyond meteorology, selecting the better performers from several rival models. Diebold et al. (1998) describes density forecast evaluation in a financial framework with example application of probability integral transform on real S&P500 return data. Purely from a conceptual perspective, market data between ’62 and ’78 are in-sample, whilst the ones between ’78 and ’95 are out-of-sample observations, splitting the set into these two parts in order to perform both a model estimation and an evalution of the forecast. Drawing parallels between this financial example and our claims reserving task, the in-sample can be considered as the upper and the out-of-sample as the lower run-off triangle.
In other words, when the insurer decides to involve all the past claim observations for the purpose of claims reserving, the figures by definition build up an upper triangle. For this reason, the usage of total quadrangles may seem to be counter-intuitive. However, in a longer run, the missing entries are filled and can be used for backtesting. New rows are unavoidably born at the same time with deficient elements on the right hand side of the row, which does not alter the fact that the older upper triangle is completed with a lower one. Depending on the total run-off period of the claims of a product, definite values become visible after 5 to 40 years, with the important discrepancy between the duration of fire (short) or liability (long) claims. Regulators of insurance practice tend to use complete claim data sets available to them, which can also mean the truncation of a large triangle on its south-west and north-east part, where the north-west part tends to 0 for the reason of run-off. In contrast to liability insurance with potentially long payout periods, in property insurance such as motor vehicle or homeowners insurance the run-off is not more than 3–4 years, allowing for a full quadrangle within 7 years of experience. Insurance companies do not usually have more triangles, apart from arranging the observations according to homogeneous risk groups, whilst regulators or oversight organisations do, see the example of NAIC. In the latter case it is of collective interest to use the triangles for some benefit of the participating insurance institutions. In addition, Arató et al. (2017) proposes a simulation-based technique to complete lower triangles, particularly for heavy-tailed risk groups.
There is hardly any manner of ranking two forecasts in a way that all actuaries would agree with. Certainly, in case the predicting distribution coincides with the real distribution governing the sample, that one is the preference above all. Provided that in real life modelling questions professionals lack this exact knowledge, it is justified to create a ranking framework, which takes into account not only the mean square error of the prediction, but also other features discussed in the coming subsections. It is essential to understand how to assess these measures on the basis of available data and how to build a decision making framework in an algorithmic manner. For the more explicit explanation of the algorithmic steps see Arató et al. (2017), however, the mechanism can be replicated on the basis of the present section.
Two out of the six sets of homogeneous risk groups available from NAIC are used to demonstrate results and draw conclusions. Commercial auto and private passenger auto liability data have been selected, justified by the higher sample size, 158 and 146 companies. Recall that the two samples still contain closely degenerate run-off triangles (almost all zero elements, for instance), which had to be sieved out in order to work with institutions where all the reserving models provide meaningful results. Thus sample sizes have been reduced to 71 and 73. The only exception is the Munich Chain Ladder method, which is applicable to even less claim histories and would have rarefied the observations substantially. In each calculation, the actual sizes are indicated. Furthermore, continuous ranked probability score, coverage and average width cannot be applied for the original MCL results.
4.1. Probability Integral Transform
Probability integral transform (PIT) can be traced back to the early papers Pearson (1933, 1938) published consecutively by father and son from the Pearson family, as well as to the short remarks of Rosenblatt (1952) on multidimensional transformation. Later, the concept emerges in Dawid (1984); Diebold et al. (1998); Gneiting et al. (2007). Statistical tests such as Kolmogorov–Smirnov or Cramér–von Mises decide whether or not to reject a certain distribution, however, they are deficient in suggesting what goes wrong with the hypothesis.
Suppose that an observation is governed by an absolutely continuous distribution , or density function . Placing the observation into the argument of its own distribution function results in a uniform random variable, i.e., or . Either be it one-dimensional or in higher dimension, this property will always be valid, except that in the latter case transformation has to be carried out with conditional distributions on the previous coordinates, see Rosenblatt (1952). Now let be the prediction given for . Regardless of the question whether the stochastic method has a distribution or it is distribution-free, the empirical predictive distribution can always be generated by drawing randomly or bootstrapping a sufficient amount of samples. For a fixed reserving method, each quadrangle is associated with one and the combination of these is used for backtesting. Coinciding with the real distribution has a necessary condition such that . In its analysis of ranking histograms Hamill (2001) introduced a counterexample with biased prediction and uniform PIT at the same time, disproving the uniform property as a satisfying condition. The paper highlights the possible fallacies and misinterpretations of qualities that the rank histogram ensembles may conceal.
Proceed to the implementation of the PIT concept into the claims reserving model framework. A certain set of companies related to one business line has n claims history quadrangles, e.g., the 132 institutions for workers’ compensation. Fix an arbitrary reserving model and perform the ultimate claim value estimation for each of the triangles, followed by the observation of actually occured total claims from the lower triangles. The latter stand for the realisation from the real unknown distribution, where the value is practically unknown for future estimation, but known for past data enabling validation. The result is n pair of values, determining the PIT values and hence, the histrogram. Should the set consist of an extremely low number of data points, then the application of a randomised PIT or a non-randomised uniform version of PIT is more proper, see Czado et al. (2009).
Generally, the deviation of the PIT histogram from uniformity reflects the dispersion of the predictive model. A ∩-shaped histogram can be translated as an overdispersed prediction with excessively wide prediction interval, i.e., overly heavy tailed distribution. By contrast, ∪-shaped PIT suggests that the prediction shall be underdispersed with narrow prediction interval, i.e., lighter tail than the underlying distribution would imply. In the latter case, variability of the real governing distribution exceeds the variability of the model, whilst it is the other way around in the former case. Going forward, real-life data and models result in a histogram of less pure shapes, which are combinations of the mentioned two instances: skewed ∩-shaped PIT or entirely biased towards 0 (or 1), for instance.
Each figure in the following subsections uses consistent abbreviations to indicate reserving methods, see Table 9.

Table 9.
Legends of reserving models.
Results of the two business lines on Figure 2 and Figure 3 suggest similar inferences. It becomes instantly obvious that none of the reserving models provide unbiased estimation of the ultimate claim. In fact, the question is what exactly goes wrong with each one of them.
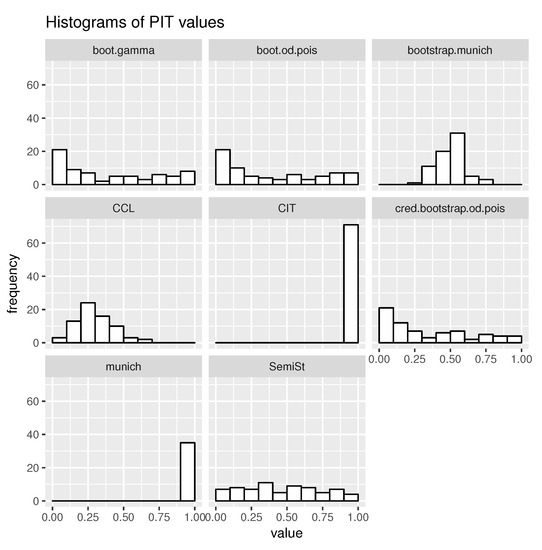
Figure 2.
Histograms of PIT values from the commercial auto data.
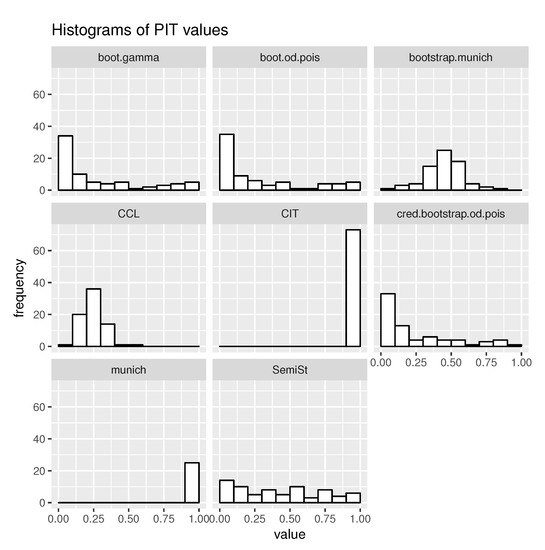
Figure 3.
Histograms of PIT values from the private passenger auto liability data.
The Munich chain ladder (MCL) is an odd one out, the only model discussed in the present article, which is not suitable for producing predictive distribution, and works only for a fraction of underlying run-off triangles, thus the lower amount of frequencies. Since MCL results in one single prediction, the frequencies are reflected on the MCL histograms. Besides, both related histograms prove that in each case, MCL consistently underestimated the actual outcome. The correlated incremental trend (CIT) model has a similar deficiency, resulting in underdispersed predictions with one-sided biasedness.
The bootstrapped version of MCL and correlated chain ladder (CCL) models are both on the overdispersed spectrum. The former tends to result in a symmetric PIT histogram, suggesting that the expected value of the ultimate claim forecast is close to the expectation from the real distribution, which implies a significant improvement compared to the original MCL. PIT values of CCL model are biased to the left, as a sign of underestimation of ultimate claims.
The third group having similar results consists of bootstrap gamma and overdispersed Poisson and credibility bootstrap overdispersed Poisson models, having ∪-shaped PIT, i.e., narrow prediction intervals. Furthermore, biasedness can be observed to the left, indicating an underestimation of the real ultimate claims. The collective semi-stochastic approach performs relatively well in terms of PIT uniformity. We may conclude that the latter four models have the best qualities from a PIT perspective.
4.2. Continuous Ranked Probability Score
Scores support the quality verification of probabilistic forecasts based on the distribution estimates and observed outcomes. There are scores with a wide spectrum of types used for both discrete and absolutely continuous distributions, such as Brier score, logarithmic score, spherical score, continuous ranked probability score, energy score, etc. For an extensive introduction see Gneiting and Raftery (2007), including a meteorological case study. In spite of the applicability in other disciplines, to our knowledge, scores have been researched to a limited extent in peer-reviewed journals in the context of technical reserving in insurance. A simulation-based methodology is constructed in Arató et al. (2017) for the selection from competing models. In the extension of regression models in non-life ratemaking to generalised additive models for location, scale, and shape (GAMLSS), Klein et al. (2014) compares various models through their score contributions. Brier score, logarithmic score, spherical score and deviance information criterion (DIC) is used for Poisson, zero-inflated Poisson and negative binomial assumptions, whilst CRPS is also calculated for three zero-adjusted models. Using a real-life data set, Tee et al. (2017) compares the overdispersed Poisson, gamma and log-normal models in the bootstrap framework and their residual adjustments using the Dawid-Sebastiani scoring rule (DSS). In modelling of claim severities and frequencies in automobile insurance Gschlössl and Czado (2007) considers scores for model comparison, which either apply or exclude spatial and certain claim number components.
Definition 11 (Score).
Generally, let be a real valued functional with the two possible exceptions of and , where stands for a family of probability measures and Ω for a sample space. The first argument can be interpreted as a prediction, whilst the second one as a realisation.
Definition 12 (Expected score).
Let the expected score be .
Without loss of generality, suppose that forecast is not worse than , if in expectation, where x is governed by probability measure Q. Let a scoring rule be proper if for family of distributions, see Bernardo (1979); Staël von Holstein (1970), for instance. Furthermore, let a scoring rule be strictly proper if if and only if .
Different distributions above are analogous to different forecasters, or using insurance claims prediction terminology, the competing models of reserving. Given that these models may either result in discrete or in absolutely continuous predictive distributions, it is of high practical relevance to select an appropriate score functional flexible enough to cope with both cases. The following scoring rule is more robust than the logarithmic or Brier scores, and requires practically no assumption with regards to the distribution observed, let it be either discrete or not.
Definition 13 (Continuous ranked probability score (CRPS)).
where indicator function equals 1 if and 0 otherwise.
Some of the articles define positive CRPS, however, here we will use its negative counterpart. CRPS can be considered as generalisation of the Brier score (BS); it is the integral of BS over the domain of all threshold values, see Hersbach (2000). In other words, there is a direct connection between the CRPS and an event-no-event score. Vice versa, the concept of energy score (ES) can be thought of as the generalisation of CRPS.
Definition 14 (Energy score).
with an arbitrary constant . Let X and be independent copies from probability distribution F. For , , see Székely and Rizzo (2005).
On a set of observations and corresponding predictive distributions, the goal is to maximise the mean score, resulting in a ranking of competing predictive models through maximising the expected utility:
Let stand for the empirical predictive distribution derived for company i on the basis of a fixed reserving model, where denotes the kth randomly generated total ultimate claim for company i (). We have seen in the discussion of PIT that distribution-free models can also be used to generate predictive distribution by bootstrapping. Furthermore, full quadrangles that contain actual ultimate claims enable backtesting. Analytical formulae can rarely be derived for CRPS, not to mention the practical models of claims prediction, although, it is feasible if the distribution F is normal, see Gneiting and Raftery (2007). A reasonable question is how sensitively the mean score is exposed to extremely inappropriate models, i.e., if the sample size is relatively small and an outstanding score value is involved. For that reason the complete scale of score outcomes is proposed to be analysed in the form of a boxplot, the plotted for the sake of better visual understanding, see Figure 4 and Figure 5. The higher the boxplot, the better the performance of forecast according to the scoring rule.
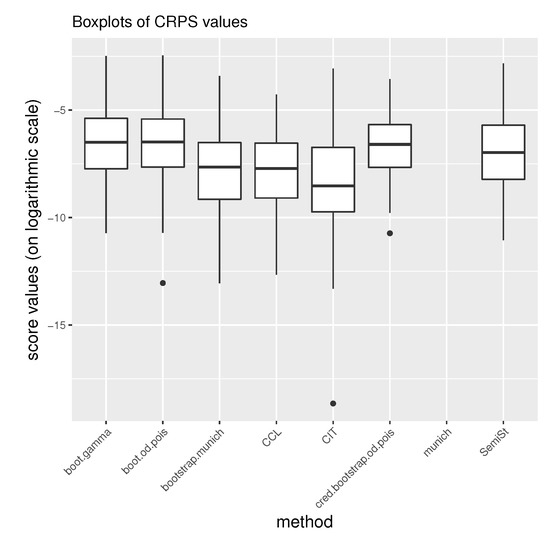
Figure 4.
Boxplots of CRPS values from the commercial auto data.
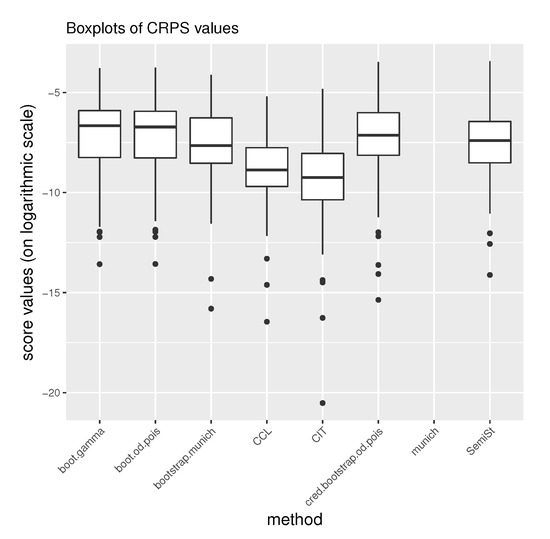
Figure 5.
Boxplots of CRPS values from the private passenger auto liability data.
CRPS is not defined in relation to the MCL model due to the lack of predictive distribution. On Table 10 and Table 11 the mean CRPS values are demonstrated, which determine the ranking of competing models. In order to see whether an extreme value has influenced the mean outcome (defined in Equation (9)), the median scores are added to the second column. Reserve calculations in accordance with the CIT model on both commercial and private passenger portfolios show scores of outstandingly large absolute value, implying that forecasts on some of the companies performed poorly.

Table 10.
Average and median CRPS values from the commercial auto data.

Table 11.
Average and median CRPS values from the private passenger auto liability data.
In the calculation on the commercial auto data, the best performing model has been the credibility bootstrap overdispersed Poisson one, using experience ratemaking, whilst applied on the private passenger auto data it has performed behind the other bootstrap methods. The semi-stochastic claims reserving technique becomes the third one applied on each of the data sets. Bootstrap MCL and CCL can be ranked behind these four models, and the CIT model yields significantly lower mean score values than the previous ones.
4.3. Coverage and Average Width
The intention of the following definition is to grasp the consistency between the probability of falling out of a given interval assuming a predictive distribution, and the real distribution. In other words, to find the likelihood that a random variable of measure Q coincides with a central predictive interval determined by F. Meteorology related discussion can be found in Baran et al. (2013). For an application from the financial sector see Christoffersen (1998), addressing conditional interval forecasts and asymmetric intervals, whilst the closest one to stochastic claims reserving can be found in Arató and Martinek (2015); Arató et al. (2017). Both on coverage and average width the most detailed study is believably provided by Gneiting et al. (2007).
Definition 15 (Coverage α).
Let Q stand for the probability measure governing the real distribution of the ultimate claim, and F the forecast distribution. is the central α prediction interval of F given Q.
The definition above results in the observations coinciding with the interval bounded by the lower and upper quantiles of the predictive distribution. In order to give the concept meaning in the context of run-off triangles and ultimate claims, conditional distributions have to be defined, given the upper tringles. Suppose that is an upper triangle associated with the jth company. Fix an arbitrary model discussed in Section 3, to be applied on each triangle for claim forecasting purposes. Let stand for the ultimate claim distribution resulted by the chosen model given , whilst is the actual conditional distribution. With the previous notations, the definition of coverage converts into
It is easy to see that if has identical distribution to , which means a perfect prediction, expression Equation (10) equals to for any value in . Now assume that the model determines the predictive distribution given in the form of a random sample for and arbitrarily large positive integer M. Let stand for the p-quantile of the empirical distribution determined by sample . For the central prediction interval’s approximation is , using for the notation of the indicator function of event A. That is given by generating an ultimate claim random sample on the basis of the fixed model, conditionally on for each . In order to achieve convergence, increase the sample size M arbitrarily large.
As an ancillary measure besides coverage, average width of prediction covers the expected difference between the lower and upper p-quantiles, a value expressed in actual payment. Alternatively it is called the sharpness of the predictive evaluation. The narrower the width, the better the prediction.
Definition 16 (Average width (sharpness)).
Let be the conditional probability measure of the ultimate claim based on a fixed model, provided that the upper triangle is . Suppose there is an underlying multivariate distribution governing upper triangle . The average width of the model is
Similarly to the practical evaluation of coverage, generate for each upper triangle a sufficiently large amount of random ultimate claim values, where M denotes an integer large enough. Hence, the sharpness of the model given the set of run-off triangle observations is .
In the calculations with NAIC data, each width in the average calculation formula above is normalised in every triangle with the realised incurred but not reported (IBNR) value. That normalising value stands for the lower triangle sum in case of an incremental point of view, or, in other words, the ultimate claim reduced by the payment already available in the upper triangle. Hence, it reflects the average span interval as a unit of realised IBNR value.
In the ideal case of coinciding predictive and actual probability measures , coverage equals to for any given . Table 12 and Table 13 calculated on the basis of two values prove that the applied models produce coverages that are far from ideal. The original MCL method does not have any coverage or average width output due to lack of predictive distribution. CIT and bootstrap MCL show the most inappropriate characteristics, in essence with degenerate coverages, either equal or close to 0 or 1. CCL performs better in the sense that the lower coverage is and in the two cases. The credibility bootstrap and original bootstrap gamma and overdispersed Poisson methods result in similar coverage and average width: Measures are balanced among these three models, and have the narrowest sharpness. The collective semi-stochastic method results in coverages closest to identity, however, at the cost of having wider average width values.

Table 12.
Coverage and average width from the commercial auto data.

Table 13.
Coverage and average width from the private passenger auto liability data.
4.4. Mean Square Error of Prediction
Measuring the expected squared distance between the predictor and the actual outcome has been part of the conventional way of actuarial reserving. We shall distinguish the conditional error given the upper triangle and the unconditional one. Eventually, in the judgment of the specific model, the unconditional version is assessed in order to measure the average performance of the model without constraining it on a fixed run-off triangle. Several articles break down the definition on occurrence years, i.e., inspecting real and estimated ultimate claims for occurrence year i, or the future (reserve) part of the claims real and . Without loss of generality, the definition in the present paper is formalised for total ultimate claims . For the sake of traceability, the definition contains the notation of ultimate claim for company i and ultimate claim prediction. Furthermore, stands for the -field generated by the upper triangle, as already used previously.
Definition 17 (Mean square error of prediction (MSEP)).
The conditional mean square error of prediction of estimator for given is
The unconditional MSEP is
It is easy to see that MSEP can be split into , where the first term is the variance of the process, whilst the second term reflects the estimation error. Similarly to the conditional version, . In conjunction with some of the parameteric models, MSEP can be derived in an analytical form, see Mack (1993) for the original Mack model and Buchwalder et al. (2006) in a time series method revisiting the result of the previous article.
Results calculated here differ from the original definition in the sense that each outcome is normalised by the ultimate reserve. The reason corresponds to the one discussed in Section 2, i.e., the magnitudinal discrepancies among the claims in distinct companies. Hence, instead of estimate . Draw a random sample from the distribution of determined by the forecasting model, and the real observed realisation of ; and .
Statement 18.
is an unbiased estimator of .
Proving the statement works by taking expectation
Finally, the MSEP estimator of the model, unconstrained on the upper triangle is the average of the elements calculated for each company i. However, should the mean be dominated by any extreme value, the median of conditional MSEPs is included in the calculation results. Observe the differing values on Table 14 and Table 15, supporting the actuary with insufficient background in order to determine reliable methods on the data sets. Extreme values may easily occur where very high squares are possible with a low probability. Taking exclusively the MSEP into account in model decisions is clearly not the proper way of ranking them and does not provide information concerning the appropriateness of predictive distribution.

Table 14.
Mean square error of prediction from the commercial auto data.

Table 15.
Mean square error of prediction from the private passenger auto liability data.
4.5. Ranking Algorithm
We summarise the algorithmic steps of the ranking framework. Suppose that the triangles stem from one homogeneous risk group.
- Stochastic forecast phase. For { bootstrap gamma, bootstrap ODP, …}, for {set of companies}, generate M ultimate claim values.Result: .
- Backtest phase. For , {set of companies} calculate PIT, CRPS, coverage, sharpness, MSEP from and real .Result: (a) , (b) , (c) , (d) , (e) .
- Ranking phase. Separate comparison of metrics (a)-(e). Combined comparison of metrics (f). (We assume to compare 7 stochastic methods, excluding MCL.)
- (a)
- Calculate the entropy of each set and order . Assign rank i to , the lower the rank the better the performance.
- (b)
- Calculate average CRPS and order . Assign rank i to .
- (c)
- Calculate coverage values and order for each p and assign rank i to . For each method, take the arithmetic average of the two ranks.
- (d)
- Calculate sharpness values and order for each p and assign rank i to . Similarly to coverage take the average of the two ranks for each method.
- (e)
- Calculate MSEP values and rank as for sharpness.
- (f)
- For { bootstrap gamma, bootstrap ODP, …} determine. Method k performs better than l if .
Observe that the metrics have identical weights in ranking, which is an arbitrary choice. These steps describe a combined ranking based on different characteristics. However, this ranking should not be applied without scrutinising PIT, CRPS, etc. separately in order to see the exact weakness of a reserving method. The ranking results per business line can be found on Table 16. Observe that in contrast to all other models, the bootstrap gamma one never ranked worse than 3.

Table 16.
Combined rankings of stochastic reserving methods per business line. (Excluding MCL.)
5. Conclusions
Rapidly increasing computational power has been generating a shift from deterministic claims reserving models to stochastic ones. Simultaneously, the validation of model appropriateness has to receive sufficient attention from researchers. In our view it is crucial to understand the performance of different methodologies for the calculation of remaining future payments in an insurance portfolio, and to compare them from several perspectives. We have interpreted claims reserving as a probabilistic forecast, as already done by other disciplines, such as meteorology or finance. Data sets of six business lines from American insurance institutions supported calculations in order to remain in contact with actual real-life claim outcomes.
Eight different models have been used with key parameter estimation details, out of which five principally different method families can be distinguished. Two of the models are first introduced in the present article, using not only the individual insurers’, but collective claims observations from other companies for calibration. See experience ratemaking embedded into the credibility bootstrap overdispersed Poisson model. Semi-stochastic and credibility bootstrap models have been among the best performing ones, however, results lack significant evidence that they would considerably outperform their regular bootstrap counterparts.
Goodness-of-fit measures describing the nature of predictive distribution are clearly more informative than exclusively observing the mean square error of the prediction. Probability integral transform is better than Kolmogorov–Smirnov or Cramér–von Mises in the sense that it highlights what goes wrong with the hypothesis. Continuous ranked probability scores can widely be applied on distributions with no constraint on absolute continuity, defining a ranking among competing models. Further characteristics such as coverage and sharpness explain the central prediction interval and its expected width. Models differ significantly in terms of these two metrics. Methodologies with bootstrapping have shown the best performance in general, along with the semi-stochastic model, calculated with two selected homogeneous risk groups from the NAIC data.
Supplementary Materials
The following are available at https://www.mdpi.com/2227-9091/7/2/62/s1.
Funding
This research received no external funding.
Acknowledgments
The author would like to thank the editor and the reviewers for their highly constructive observations. For his advice and useful discussions, special thanks to Miklós Arató.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arató, Miklós, and László Martinek. 2015. Comparison of reserving and spatial models in insurance. In Current Topics on Risk Analysis: ICRA6 and RISK 2015 Conference. Edited by Montserrat Guillén, Ángel A. Juan, Helena Ramalhinho, Isabel Serra and Carles Serrat. Barcelona: Fundación MAPFRE, pp. 71–78. [Google Scholar]
- Arató, Miklós, László Martinek, and Miklós Mályusz. 2017. Simulation based comparison of stochastic claims reserving models in general insurance. Studia Scientiarum Mathematicarum Hungarica 54: 241–75. [Google Scholar] [CrossRef]
- Ashe, Frank. 1986. An essay at measuring the variance of estimates of outstanding claim payments. Astin Bulletin 16: S99–S113. [Google Scholar] [CrossRef]
- Baran, Sándor, András Horányi, and Dóra Nemoda. 2013. Statistical post-processing of probabilistic wind speed forecasting in Hungary. Meteorologische Zeitschrift 22: 273–82. [Google Scholar] [CrossRef]
- Bernardo, José M. 1979. Expected information as expected utility. The Annals of Statistics 7: 686–90. [Google Scholar] [CrossRef]
- Björkwall, Susanna, Ola Hössjer, and Esbjörn Ohlsson. 2009. Non-parametric and parametric bootstrap techniques for age-to-age development factor methods in stochastic claims reserving. Scandinavian Actuarial Journal 4: 306–31. [Google Scholar] [CrossRef]
- Buchwalder, Markus, Hans Bühlmann, Michael Merz, and Mario V. Wüthrich. 2006. The mean square error of prediction in the chain ladder reserving method (mack and murphy revisited). Astin Bulletin 36: 521–42. [Google Scholar] [CrossRef]
- Bühlmann, Hans. 1967. Experience rating and credibility. Astin Bulletin 4: 199–207. [Google Scholar] [CrossRef]
- Bühlmann, Hans. 1969. Experience rating and credibility. Astin Bulletin 5: 157–65. [Google Scholar] [CrossRef]
- Bühlmann, Hans, and Alois Gisler. 2006. A Course in Credibility Theory and Its Applications. Berlin: Springer Science & Business Media. [Google Scholar] [CrossRef]
- Christoffersen, Peter F. 1998. Evaluating interval forecasts. International Economic Review 39: 841–62. [Google Scholar] [CrossRef]
- Czado, Claudia, Tilmann Gneiting, and Leonhard Held. 2009. Predictive model assessment for count data. Biometrics 65: 1254–61. [Google Scholar] [CrossRef]
- Dawid, Alexander Philip. 1984. Present position and potential developments: Some personal views: Statistical theory: The prequential approach. Journal of the Royal Statistical Society. Series A (General) 147: 278–92. [Google Scholar] [CrossRef]
- Diebold, Francis X., Todd A. Gunther, and Anthony S. Tay. 1998. Evaluating density forecasts with applications to financial risk management. International Economic Review 39: 863–83. [Google Scholar] [CrossRef]
- Efron, Bradley. 1979a. Bootstrap methods: Another look at the jackknife. The Annals of Statistics 7: 1–26. [Google Scholar] [CrossRef]
- Efron, Bradley. 1979b. Computers and the theory of statistics: Thinking the unthinkable. SIAM Review 21: 460–80. [Google Scholar] [CrossRef]
- England, Peter D., and Richard J. Verrall. 1999. Analytic and bootstrap estimates of prediction errors in claims reserving. Insurance: Mathematics and Economics 25: 281–93. [Google Scholar] [CrossRef]
- England, Peter D., and Richard J. Verrall. 2002. Stochastic claims reserving in general insurance. British Actuarial Journal 8: 443–518. [Google Scholar] [CrossRef]
- Faluközy, Tamás, Miklós Arató, and Ildikó I. Vitéz. 2007. Stochastic Models for Claims Reserving in Insurance Business. Singapore: World Scientific, pp. 102–13. [Google Scholar] [CrossRef]
- Frühwirth-Schnatter, Sylvia, and Saumyadipta Pyne. 2010. Bayesian inference for finite mixtures of univariate and multivariate skew-normal and skew-t distributions. Biostatistics 11: 317–36. [Google Scholar] [CrossRef]
- Gesmann, Markus. 2018. Statistical Methods and Models for Claims Reserving in General Insurance. Available online: https://cran.r-project.org/web/packages/ChainLadder/ChainLadder.pdf (accessed on 10 October 2018).
- Gisler, Alois, and Mario V. Wüthrich. 2008. Credibility for the chain ladder reserving method. Astin Bulletin 38: 565–600. [Google Scholar] [CrossRef]
- Gneiting, Tilmann, Fadoua Balabdaoui, and Adrian E. Raftery. 2007. Probabilistic forecasts, calibration and sharpness. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 69: 243–68. [Google Scholar] [CrossRef]
- Gneiting, Tilmann, and Adrian E. Raftery. 2007. Strictly proper scoring rules, prediction, and estimation. Journal of the American Statistical Association 102: 359–78. [Google Scholar] [CrossRef]
- Gschlössl, Susanne, and Claudia Czado. 2007. Spatial modelling of claim frequency and claim size in non-life insurance. Scandinavian Actuarial Journal 3: 202–25. [Google Scholar] [CrossRef]
- Hamill, Thomas M. 2001. Interpretation of rank histograms for verifying ensemble forecasts. Monthly Weather Review 129: 550–60. [Google Scholar] [CrossRef]
- Hersbach, Hans. 2000. Decomposition of the continuous ranked probability score for ensemble prediction systems. Weather and Forecasting 15: 559–70. [Google Scholar] [CrossRef]
- Klein, Nadja, Michel Denuit, Thomas Kneib, and Stefan Lang. 2014. Nonlife ratemaking and risk management with bayesian generalized additive models for location, scale, and shape. Insurance: Mathematics and Economics 55: 225–49. [Google Scholar] [CrossRef]
- Leong, Jessica (Weng Kah), Han Chen, and Shaun Wang. 2014. Back-testing the odp bootstrap of the paid chain-ladder model with actual historical claims data. Variance 8: 182–202. [Google Scholar]
- Liu, Huijuan, and Richard J. Verrall. 2010. Bootstrap estimation of the predictive distributions of reserves using paid and incurred claims. Variance 4: 121–35. [Google Scholar]
- Mack, Thomas. 1993. Distribution-free calculation of the standard error of chain ladder reserve estimates. ASTIN Bulletin—The Journal of the International Actuarial Association 23: 213–25. [Google Scholar] [CrossRef]
- Martínez-Miranda, Maria Dolores, Jens Perch Nielsen, and Richard Verrall. 2013. Double chain ladder and bornhuetter-ferguson. North American Actuarial Journal 17: 101–13. [Google Scholar] [CrossRef][Green Version]
- Meyers, Glenn. 2015. Stochastic Loss Reserving Using Bayesian Mcmc Models. CAS Monograph Series; New York: Casualty Actuarial Society. [Google Scholar]
- Meyers, Glenn, and Peng Shi. 2011. The retrospective testing of stochastic loss reserve models. Paper presented at Casualty Actuarial Society E-Forum, Philadelphia, PA, USA, June 5–7. [Google Scholar]
- Pearson, Egon S. 1938. The probability integral transformation for testing goodness of fit and combining independent tests of significance. Biometrika 30: 134–48. [Google Scholar] [CrossRef]
- Pearson, Karl. 1933. On a method of determining whether a sample of size n supposed to have been drawn from a parent population having a known probability integral has probably been drawn at random. Biometrika 25: 379–410. [Google Scholar] [CrossRef]
- Pinheiro, Paulo J. R., João Manuel Andrade e Silva, and Maria De Lourdes Centeno. 2003. Bootstrap methodology in claim reserving. The Journal of Risk and Insurance 70: 701–14. [Google Scholar] [CrossRef]
- Quarg, Gerhard, and Thomas Mack. 2004. Munich chain ladder. Blätter der DGVFM 26: 597–630. [Google Scholar] [CrossRef]
- Rosenblatt, Murray. 1952. Remarks on a multivariate transformation. The Annals of Mathematical Statistics 23: 470–72. [Google Scholar] [CrossRef]
- Shapland, Mark R. 2016. Using the odp bootstrap model: A practitioner’s guide. CAS Monograph Series Number 4; Arlington: Casualty Actuarial Society. [Google Scholar]
- Shi, Peng. 2015. A multivariate analysis of intercompany loss triangles. Journal of Risk and Insurance 84: 717–37. [Google Scholar] [CrossRef]
- Shi, Peng, Sanjib Basu, and Glenn G. Meyers. 2012. A bayesian log-normal model for multivariate loss reserving. North American Actuarial Journal 16: 29–51. [Google Scholar] [CrossRef]
- Shi, Peng, and Edward W. Frees. 2011. Dependent loss reserving using copulas. ASTIN Bulletin 41: 449–86. [Google Scholar] [CrossRef]
- Shi, Peng, and Brian M. Hartman. 2016. Credibility in loss reserving. North American Actuarial Journal 20: 114–32. [Google Scholar] [CrossRef]
- Staël von Holstein, Carl-Axel S. 1970. A family of strictly proper scoring rules which are sensitive to distance. Journal of Applied Meteorology 9: 360–64. [Google Scholar] [CrossRef]
- Székely, Gábor J., and Maria L. Rizzo. 2005. A new test for multivariate normality. Journal of Multivariate Analysis 93: 58–80. [Google Scholar] [CrossRef]
- Tee, Liivika, Meelis Käärik, and Rauno Viin. 2017. On comparison of stochastic reserving methods with bootstrapping. Risks 5: 2. [Google Scholar] [CrossRef]
- Wüthrich, Mario V. 2003. Claims reserving using tweedie’s compound poisson model. ASTIN Bulletin 33: 331–46. [Google Scholar] [CrossRef]
- Wüthrich, Mario V. 2010. Accounting year effects modeling in the stochastic chain ladder reserving method. North American Actuarial Journal 14: 235–55. [Google Scholar] [CrossRef]
- Wüthrich, Mario V., and Michael Merz. 2008. Stochastic Claims Reserving Methods in Insurance. Hoboken: John Wiley & Sons. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).