The Population Accuracy Index: A New Measure of Population Stability for Model Monitoring

Abstract

Risk models developed on one dataset are often applied to new data and, in such cases, it is prudent to check that the model is suitable for the new data. An important application is in the banking industry, where statistical models are applied to loans to determine provisions and capital requirements. These models are developed on historical data, and regulations require their monitoring to ensure they remain valid on current portfolios—often years since the models were developed. The Population Stability Index (PSI) is an industry standard to measure whether the distribution of the current data has shifted significantly from the distribution of data used to develop the model. This paper explores several disadvantages of the PSI and proposes the Prediction Accuracy Index (PAI) as an alternative. The superior properties and interpretation of the PAI are discussed and it is concluded that the PAI can more accurately summarise the level of population stability, helping risk analysts and managers determine whether the model remains fit-for-purpose.

1. Introduction

For banks, their loans are not only assets—as they are income producing—but also liabilities when customers default and do not repay their debt. In many jurisdictions, these liabilities are measured by procedures in regulations such as the Basel Accord (Basel Committee on Banking Supervision 2006) for capital and the International Financial Reporting Standards (IFRS 9) for provisioning (International Accounting Standards Board 2014). Capital is required in case of a severe economic downturn, while provisions reflect losses expected in current economic conditions. As these valuations form part of the value of the company, their accuracy is important to many stakeholders. These stakeholders include the bank itself (for example, to make profitable acquisition decisions for new loans); external auditors (who assess the accuracy and reliability of financial statements); regulators (who assess the sustainability of the bank); and investors (who rely on this information to make investment decisions).

Both the Basel Accord and the IFRS 9 adopt a standard approach of assessing risk of loans with three components: probability of default (PD), exposure at default (EAD), and loss given default (LGD). Thus, three models are required to respectively predict the likelihood of a loan defaulting (unable to make its contractual obligations, typically 90 days overdue in payments); the balance owing at the time of default; and the monetary loss to the bank in the case of default (expressed as a fraction of the EAD). Expected loss might be estimated with the product PD × EAD × LGD.

Model development in the banking industry is well covered in the literature (Siddiqi 2005) but an equally important regulated activity is the continual monitoring of whether the model remains suitable (fit-for-purpose). For example:

Banks that have adopted or are willing to adopt the Basel II A-IRB approach are required to put in place a regular cycle of model validation that should include at least monitoring of the model performance and stability, review of the model relationships, and testing of model outputs against outcomes (i.e., back testing).

Sabato (2010, p. 40)

and also:

Stability and performance (i.e., prediction accuracy) are extremely important as they provide information about the quality of the scoring models. As such, they should be tracked and analyzed at least on a monthly basis by banks, regardless of the validation exercise.

Sabato (2010, p. 40)

This aspect is typically performed internally and externally by bankers, auditors, and regulators. Monitoring is important because a model developed years earlier may no longer be fit-for-purpose for the current portfolio. One reason for this is the type of customers within the portfolio may differ from the types of customers available to develop the model.

Population stability refers to whether the characteristics of the portfolio (especially the distribution of explanatory variables) is changing over time. When this distribution changes (low population stability) there is more concern over whether the model is currently fit-for-purpose since the data used to develop the model differs from the data the model is being applied to. Applying the model to these new types of customers might involve extrapolation and hence lower confidence in model outputs.

There are other characteristics of a model that requires monitoring to ensure the model is fit-for-purpose. These include calibration (whether the model is unbiased) and discrimination (whether the model correctly ranks orders the loans from best to worst). While these measures are important, they require known outcomes. For example, a PD model predicting defaults in a one-year window must evaluate loans at least one year old to determine calibration and discrimination. Therefore, conclusions from these measures are at least one year out of date compared to the current portfolio.

Population stability is important as it requires no lag; it can be measured with the current portfolio since the outcome is not required. Therefore, it is important to monitor population stability to gain insights concerning whether the current portfolio (rather than the portfolio one year ago) is fit-for-purpose.

This paper focuses on the measurement of population stability, especially the Population Stability Index (PSI) which has become an industry standard. Deficiencies in the PSI are explored and an alternative that has superior properties and whose values are more directly interpretable is introduced. Statistical tests also exist to test the null hypothesis that the distribution of the development data and the distribution of the review data are equal. Examples include the Kolmogorov-Smirnov test for numerical data or a chi-squared test for categorical data. We do not consider these appropriate because they summarize the amount of evidence against the null hypothesis and are too reliant on sample size. In large samples, small and unimportant differences in the distributions can be statistically significant, while in small samples, large and important differences can be statistically insignificant. We therefore do not consider these further in this paper.

1.1. Models and Notation

Model development tasks are extensive and well covered in the literature, of which Siddiqi (2005) is particularly relevant to the banking industry. Briefly, empirical historical data is used to estimate relationships between an outcome (such as default in the case of a PD model) and explanatory variables (such as employment status of the customer). PD models typically estimate probabilities of default within one year, so for model development, explanatory variables must be at least one year old (so the outcome is known). The model development then looks for, and captures in mathematical form, relationships in the data between the explanatory variables and the outcome. For example, this may take the form of a logistic or probit regression model predicting default. This mathematical form often takes the form of a regression where some (possibly transformed) measure of the outcome equals

$${\beta }_0{x}_{i0}+{\beta }_1{x}_{i1}+\dots +{\beta }_k{x}_{ik}$$

(1)

where ${\beta }_0$ to ${\beta }_k$ are estimated coefficients and $x_{i0}$ to $x_{ik}$ are the values of the explanatory (numerical) variables for the $i$th observation (typically $x_{i0}$ is defined to always equal 1, in which case ${\beta }_0$ is an intercept). For example, a logistic regression used to predict default uses Equation (1) to predict the log-odds of default (defined as the natural logarithm of the ratio of the probability of default to the probability of not defaulting).

The explanatory variables have several basic types whose treatments are summarized here because these affect the details presented later (see Pyle (1999) for further details of these issues and treatments). In particular, variables might be categorical or numerical. Categorical variables (such as occupation category) take values from a list (such as trade, professional, retired, student, etc.) and typically have no natural ordering or numerical value. Modelling might create n − 1 (where n is the number of categories) dummy variables (taking numerical values of 0 or 1) or by numeration where a numerical value (the weight of evidence) is assigned to each category (Siddiqi 2005). For example, numerical values might be determined from the observed default rate within each category.

Numerical variables are defined in numerical terms. For example, the loan to value (LVR) ratio is defined as the value of the loan divided by the value of the asset securing the loan. Modelling might use this numerical value directly, after a simple numerical transformation (such as logarithms or Winsorizing) or by bucketing into a small number of categories (such as 0 to 0.5; 0.5 to 0.8; 0.8 to 1; and >1). Thus, bucketing transforms a numerical variable into a categorical variable (which in turn may be numerated with weight of evidence or dummy variables during model development). As expanded on below, this is a key issue not only because bucketing is a common practice in banking but because the PSI is only defined for categorical variables (or bucketed numerical variables).

1.2. The Population Stability Index (PSI)

The PSI is closely related to well-established entropy measures, and essentially is a symmetric measure of the difference between two statistical distributions. The index specifically called ‘Population stability index’ (PSI) is found in Karakoulas (2004), as a “diagnostic technique for monitoring shifts in characteristics distributions”. It is also described in Siddiqi (2005), who explains its use to either monitor overall population score stability (“System stability report”) or, as a likely follow-up, the stability of individual explanatory variables (“Characteristic analysis report”) in credit risk modelling scorecards for the banking industry. The same formulation has appeared in the statistical literature as the “J divergence” (Lin 1991, who in turn references Jeffreys 1946), and is closely related to the Jensen-Shannon divergence.

The formula for the PSI assumes there are K mutually exclusive categories, numbered 1 to K, with:

$$\mathrm{PSI}={{\displaystyle \sum }}_{i=1}^K(O_i-E_i)\times \ln \left(\frac{O_i}{E_i}\right)$$

(2)

where $O_i$ is the observed relative frequency of accounts in category $i$ at review; $E_i$ is the relative frequency of accounts in category $i$ at development (the review relative frequency is expected to be similar to the development relative frequency); $i$ is the category, taking values from 1 to K; and $\ln ()$ is the natural logarithm.

A PSI value of 0 implies the observed and expected distributions are identical with the PSI increasing in value as the two distributions diverge. Siddiqi (2005) interpreted PSI values as follows: less than 10% show no significant change; values between 10% and 25% show a small change requiring investigation; and values greater than 25% show a significant change. Note the PSI is large when a category has either the observed or expected relative frequency close to zero and is not defined if either relative frequency equals 0. Therefore, a limit argument suggests the PSI might be interpreted as having an infinite value when one of the relative frequencies equals zero.

The calculation of the PSI is illustrated with a hypothetical example in

Table 1. Calculation of the PSI (example 1).

Term	1	2	3	4	5	6	7	8	9	10	Total
$O_i$	21%	9%	7%	7%	6%	6%	7%	7%	9%	21%	100%
$E_i$	10%	10%	10%	10%	10%	10%	10%	10%	10%	10%	100%
$\left(O_i-E_i\right)\times \ln \left(\frac{O_i}{E_i}\right)$	0.082	0.001	0.011	0.011	0.020	0.020	0.011	0.011	0.001	0.082	0.25

. A PSI of 0.25 results primarily from the high observed frequencies of 21% in categories 1 and 10. Thus the interpretation recommended by Siddiqi (2005) suggests the distribution of the data has changed significantly from development to review.

Table 2. Calculation of the PSI (example 2).

Term	1	2	3	4	5	6	7	8	9	10	Total
$O_i$	3%	8%	11%	14%	15%	15%	14%	11%	8%	3%	100% 1
$E_i$	10%	10%	10%	10%	10%	10%	10%	10%	10%	10%	100%
$\left(O_i-E_i\right)\times \ln \left(\frac{O_i}{E_i}\right)$	0.084	0.004	0.001	0.013	0.020	0.020	0.013	0.001	0.004	0.084	0.25

¹ Observed values at review are rounded but sum to 100%.

shows the calculation of the PSI for a second hypothetical example that also results in a value of 0.25 for the PSI. The similar PSI values are interpreted to mean the deviations from development in the two examples are similar in magnitude.

The similar interpretations based on the PSI from these examples might be reasonable if the 10 categories represent categorical divisions, such as industry sector. However, this is questionable if the categories represent a division of a continuous scale used in model development. For example, the explanatory variable might be the loan to value (LVR) ratio: the value of the loan divided by the value of the asset securing the loan (a common and intuitive predictor of loss). This continuum is divided into 10 categories as this is required for calculation of the PSI (it may or may not have been a modelling choice). Failing to take this information into account and instead treating the categories as unordered can lead to misleading conclusions concerning whether the model remains fit-for-purpose.

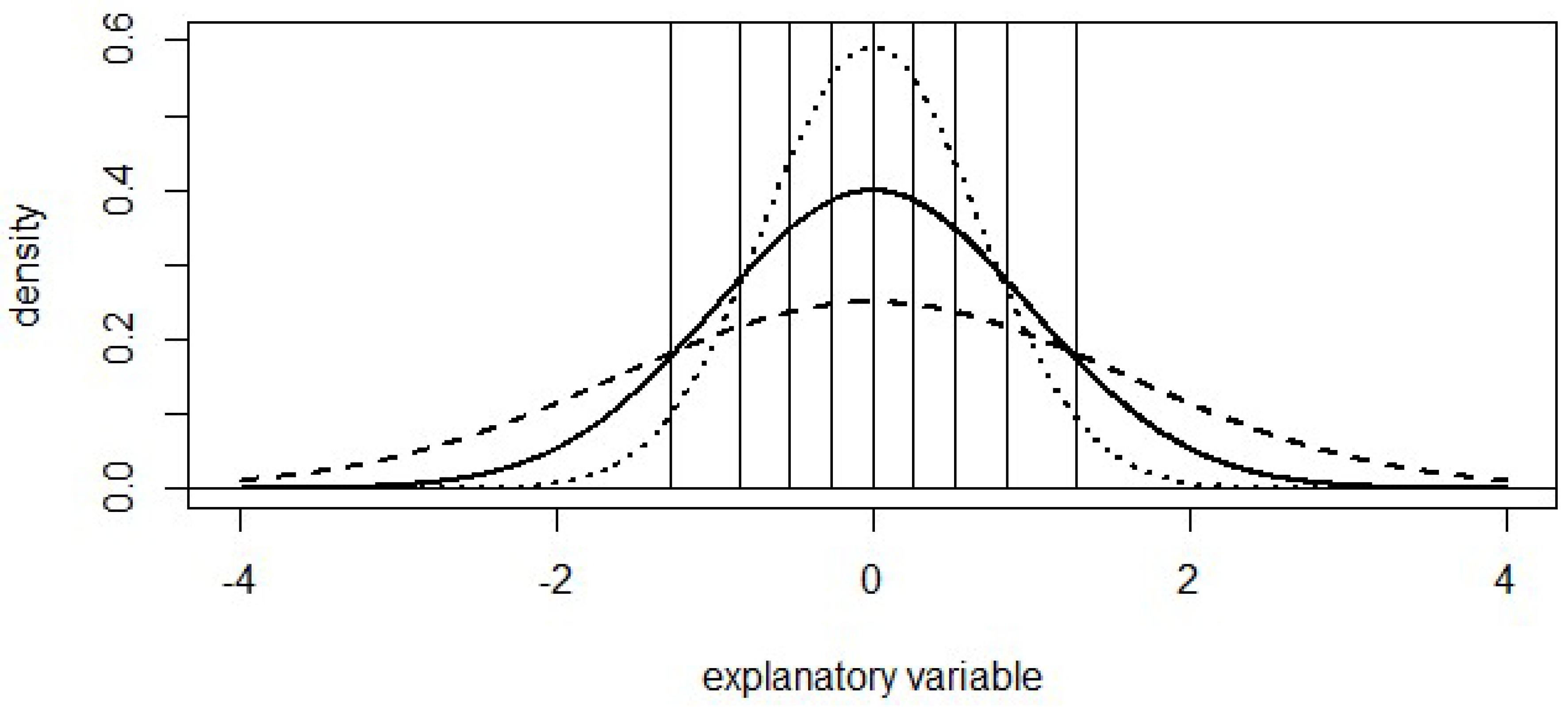
The categories in Table 1 and Table 2 were constructed from underlying development data with a standard normal distribution, with intervals defined to each capture 10% of the distribution: −infinity to −1.28; −1.28 to −0.84; −0.84 to −0.52, etc. The review data in Table 1 was also normally distributed, but with a standard deviation of 1.6 instead of 1, creating more observations in the extreme categories (below −1.28 and above 1.28 respectively). Observed frequencies were rounded to the nearest percent to ensure the calculations use the exact observed and expected values in Table 1. Similarly, the review data in Table 2 was constructed with a standard deviation of 0.674, creating less data in the extreme categories. This is illustrated in Figure 1. Note that the use of the normal distribution is not important here since bucketing is used to create 10 buckets of equal frequency.

Although the PSI value in Table 1 and Table 2 both equal 0.25, the extent to which the model is fit-for-purpose for the corresponding review data is not. In Table 1, the model is being applied to more extreme data than was available at development. Confidence that the data is suitable for this review data should be low; especially when the model is being extrapolated from development data to the more extreme review data. Not only will a small change in estimated coefficients have a larger impact on the predicted value for these observations, but we have less confidence in the validity of assumptions such as linearity of relationships between response and explanatory variables. In contrast, the review data in Table 2 suggests no extrapolation is involved. If the model was considered fit-for-purpose at development then this change in distribution gives no reason to suggest the model is no longer fit-for-purpose: if it was fit for standard normal data (95% of which is within −1.96 and +1.96) then it should be fit for the review data (95% of which is within −1.35 and +1.35). These examples illustrate how the PSI captures any differences between the development and review data rather than focussing on those differences that suggest the model is not fit for the purpose of estimation on the review data.

The PSI is typically calculated for each independent variable in the model. It can also be computed for variables not in the model, such as variables considered serious candidates during modelling. However, since a separate PSI value is obtained for each variable, this can result in numerous quantitative results when a single value summarizing stability is desirable. To avoid this issue of multiple values summarising population stability, the PSI can be computed on the model output (or score) instead. However, this requires placing the typically numeric model output into categories before calculation.

Finally, the value of the PSI can be influenced by the number and choice of categories. Too many categories and the PSI can detect minor differences in the distribution; too few categories and it may miss differences (for example, if two categories, one with a high frequency and one with a low frequency, are combined to form a single category). This can create interpretation issues as it is not always clear whether the categories used are determined a priori, or whether they are chosen to smooth out differences in the distributions. This is an important issue in practice as the categories for the PSI often have to be chosen after inspection of the data. In particular, the PSI has unreliable properties when frequencies for a category approach 0. Furthermore, due to the necessity to create categories for numerical variables, extreme outliers have minimal impact on the PSI even though they may have significant impact on model accuracy; if the model uses a numerical variable, then assessing population stability using a categorical (bucketed) version may not capture changes in stability appropriately.

2. The Prediction Accuracy Index (PAI)

The Prediction Accuracy Index (PAI) is defined as the average variance of the estimated mean response at review divided by the average variance of the estimated mean response at development. As with the PSI, in this definition it is the values of the explanatory variables (design space) that is important; the values of the response are irrelevant and not required. The PAI is high when: at review, the explanatory variables take values that result in a variance of the predicted response that is higher than the corresponding variance at development. The cases of a single numeric variable, multiple regression, and a categorical variable are considered in the following three sections. Note that these sections are presented for ordinary least squares regression where the response is normally distributed, however, the above definition of the PAI can be applied to any model (e.g., a neural network) where variances of estimated mean responses are available (by techniques such as bootstrapping if necessary). In particular, the results presented below are immediately applicable to logistic regression used to predict default if the predictions are taken to be the log-odds of default (see Equation (1)).

Unlike the PSI, which is defined on a scale with no obvious interpretation, the PAI measures the increase in the variance of estimated mean response since development. For example, a PAI value of 2 is directly interpretable as the variance of the predicted mean response at review is double the variance of the mean response at development (on average). It is recommended that PAI values are interpreted as follows: values less than 1.1 indicate no significant deterioration; values from 1.1 to 1.5 indicate a deterioration requiring further investigation; and values exceeding 1.5 indicate the predictive accuracy of the model has deteriorated significantly. Note that these guidelines are more stringent than the interpretations by Siddiqi (2005) for the PSI (note in Table 1 the PSI was 0.252, the boundary of a significant change, but the PAI equals 1.78, well above the recommended boundary of 1.5). These more stringent recommendations are based on several factors: a value of PAI equal to 1.5 corresponds to review data having a standard deviation of 1.4 times the standard deviation of development data (if distributions are normal), which is a significant increase; a PSI greater than 0.25 is rare; and since the PAI is more focussed on model predictive accuracy, it has more power at detecting deterioration in this important characteristic specific to the model.

2.1. Simple Regression

In the case of simple linear regression (Equation (1) with $k=1$ and $x_{i0}$ is defined to always equal 1), the variance of the estimated mean response when the explanatory variable $x_i$ is equal to $z$ is given by (Ramsey and Schafer 2002, p. 187):

$$\mathrm{MSE}\times \left(\frac{1}{n}+\frac{{\left(z-\overline{x}\right)}^2}{{{\displaystyle \sum }}^{}{\left(x_i-\overline{x}\right)}^2}\right)$$

(3)

where MSE is the mean squared error (of the residuals) from model development; $\overline{x}$ is the mean value of the explanatory variable $x$ at development; $n$ is the sample size at development; and the summation is over all values $x_i$ of the explanatory variable used during scorecard development. Note the average value of Equation (3), averaging over values of $z$ equal to the development data $x_i$, is equal to $\mathrm{MSE}\times 2/n$.

The PAI for simple linear regression equals Equation (3) averaged over all values of $z$ equal to the review data (denoted $r_j$; $j$ = 1 to $N$) divided by Equation (3) averaged over all values of $z$ equal to the development data (denoted $x_i$; $i$ = 1 to $n$):

$$\mathrm{PAI}=\frac{1}{2}\times \left(1+\frac{{{\displaystyle \sum }}_{j=1}^N{\left(r_j-\overline{x}\right)}^2/N}{{{\displaystyle \sum }}_{i=1}^n{\left(x_i-\overline{x}\right)}^2/n}\right)$$

(4)

Note that the sum of squares in both the numerator and the denominator are centred on the average of the explanatory variable in the development data (not the average of the review data).

Applying Equation (4) to the normally distributed review data in Table 1 gives a value for the PAI of 1.78. That is, the variance of the estimated mean response is, on average, 78% higher when calculated on the review data than when calculated on the development data. This is directly interpretable as the model being 78% less precise on the review data than on the development data. In contrast, the PAI equals 0.73 for the review data in Table 2, and hence the model is on average more accurate on the review data in Table 2 than it was on the development data. This is interpretable as the model being 27% more precise on the review data than on the development data.

2.2. Multiple Regression

In the case of a multiple regression model given by Equation (1), the estimated variance of the mean response when the explanatory variables $x_{i1}, x_{i2},\dots ,x_{ip}$ take values $z_{i1}, z_{i2},\dots ,z_{ip}$ is given by (Johnson and Wichern 2007, p. 378):

$$\mathrm{MSE}\times z_j^T{\left(X^{T}X\right)}^{–1}{z}_j$$

(5)

where $z_j^T=\left(z_{i1}, z_{i2},\dots ,z_{ip}\right)$ is the row vector of explanatory variables ($z_{i1}=1$ when an intercept is included); X is the matrix of explanatory variables at development; MSE is the mean squared error (of the residuals) from model development; T indicates transpose; and ${()}^{–1}$ denotes matrix inverse.

The columns of $X$ equal the values of the explanatory variables of the development data (the rows are similar to $z_j^T$ for each observation in the model development data). In practice, Equation (5) can be calculated with:

$$z_j^{T}V{z}_j$$

(6)

where $V=\mathrm{MSE}\times {\left(X^{T}X\right)}^{–1}$ is the variance-covariance matrix of the estimated regression coefficients $({\beta }_1,{\beta }_2,\dots ,{\beta }_p)$ and is available from most regression software.

The PAI for multiple regression is defined as the average of Equation (6) calculated at the values of the explanatory variables $z_j$ at review divided by the average of Equation (6) calculated at the values of the explanatory variables $z_j$ at development:

$$\mathrm{PAI}=\frac{{{\displaystyle \sum }}_{j=1}^N{r}_j^{T}V{r}_j/N}{{{\displaystyle \sum }}_{i=1}^n{x}_i^{T}V{x}_i/n}$$

(7)

where $r_j$ is the vector of explanatory variables for the $j$th observation of the review data ($j$ = 1 to $N$); $x_i$ is the vector of explanatory variables for the $i$th observation of the development data ($i$ = 1 to $n$).

The following sections apply this formula to the cases where a single categorical variable has more than two categories (requiring multiple regression with dummy variables to estimate the mean response for each category) and a multiple regression where the model contains several explanatory variables.

2.3. One Categorical Variable

Applying Equation (7) to a categorical variable requires the construction of dummy variables to model the differences between the categories; the multiple regression requires a number of parameters (including the intercept) equal to the number of categories. This results in the PAI taking the value of 1 for data in both Table 1 and Table 2. Indeed, for any distribution of review data across these 10 categories, the PAI will always equal 1 if the development data is equally distributed across the categories. This is because in this case the response can be measured with the same precision for each category; a shift in customers from one category at the time of development to another category at review has no impact on model precision if both categories were estimated with equal precision at development. The PSI does not share this property, instead, capturing the extent to which the distribution of the review data deviates from the equal frequency distribution at development.

This invariance property does not hold if the categories are not equally frequent at development. A shift in customers from one category at the time of development to another category at review will give a higher value for the PAI if the customers move into a category that, at development, had a lower frequency. To illustrate, if the roles of development and review data are reversed in the examples, so Table 2 now involves extrapolation (from 3% of development data to 10% review data in categories 1 and 10), the PAI is 1.60. The PAI for Table 1 with reversed data is 0.70. This asymmetry property of the PAI is arguably desirable as extrapolation and interpolation are not equivalent with regards to model accuracy. The PSI, however, was designed to possess this symmetry as there was no distinction between development and review in its conception (reversing the roles of review and development data gives the same value for the PSI).

3. The Multivariate Predictive Accuracy Index (MPAI)

The Multivariate Predictive Accuracy Index (MPAI) is defined as Equation (7) using all the explanatory variables in the model. While this is mathematically equivalent to the case of multiple regression, Equation (7), it is discussed separately in this section because considering all explanatory variables is important and not feasible with the PSI. The PSI cannot easily be applied to multivariate distributions of many variables because it requires categories, and ensuring there are enough categories to capture the multidimensional space typically results in too many categories, many of which will have frequencies of development or review data too close to zero.

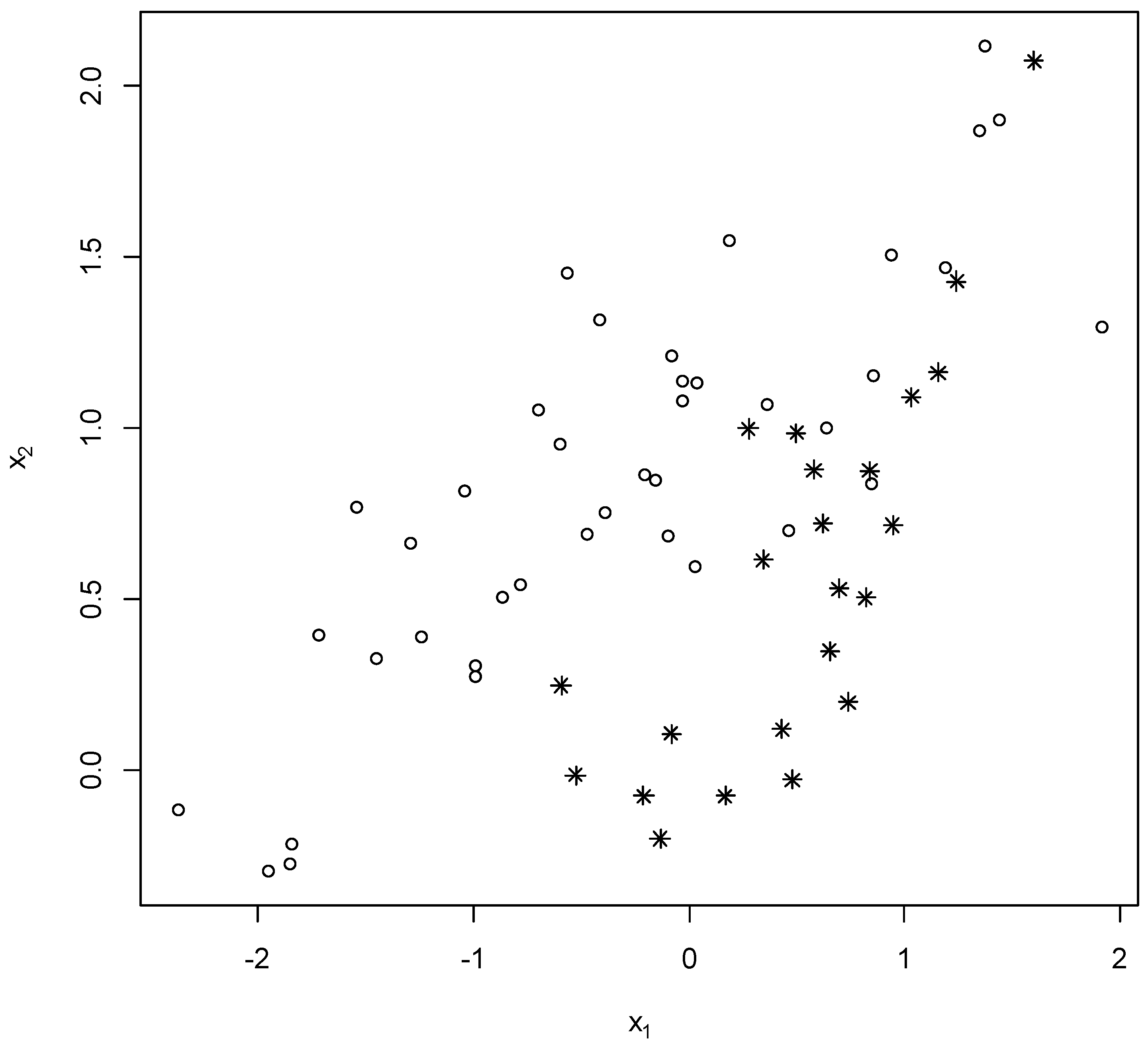
To illustrate the importance of the MPAI, consider a model with two explanatory variables that are positively correlated at development (circles) and at review (stars) in Figure 2. While the review data does not represent extreme variables for either variable (the most extreme observation for either variable is always in the development data), there is a visual pattern whereby the review data tends to be in the lower right corner (high $x_1$ and low $x_2$) where no development data exists. Thus, in a multivariate sense, extrapolation is involved with this data, and the model estimated using the development data may not be fit-for-purpose for the review data.

Applying the MPAI to the data in Figure 2 (three parameters are estimated; one for each of the two explanatory variables and one for the intercept) produces a PAI value of 5.43. This suggests the accuracy of the estimates have a variance at review that is over 5 times higher than the variance at development. The univariate PAI from Equation (4) are respectively 0.93 for variable $x_1$ and 1.02 for variable $x_2$ (similarly acceptable values are obtained with the PSI if reasonable categories are created). Thus, this multivariate PAI is a significant contribution in its own right as it enables deviations between the development and review multivariate distributions to be detected that univariate statistics may not1.

To avoid confusion, it is recommended that the term Multivariate Predictive Accuracy Index (MPAI) is used when all variables are included, and the term Univariate Predictive Accuracy Index (UPAI) is used when only one variable is included at a time. The term PAI can be used for either case. Note that the UPAI may involve multiple regression even though only one variable is considered; examples include the treatment of a categorical variable or when a quadratic term is included with a numerical variable to avoid making assumptions of linearity (as discussed in the next section).

4. Discussion

This paper considers the requirement of stability: that the data used to develop a model is representative of the data the model is currently applied to. The industry standard in banking to measure stability, the Population Stability Index (PSI), interprets this as the distribution of development data and the distribution of review data are similar. This paper introduces the Prediction Accuracy Index (PAI) which takes a different perspective on this requirement. The PAI requires the predictive ability of the model on current data is not significantly worse than the predictive ability at development. This perspective more suitably answers the key question of whether a model is still fit-for-purpose. Both indices only examine the distribution of the inputs to a model, so do not address concerns such as calibration or discrimination of the model. While calibration and discrimination are also important, they have the disadvantage that values of the response are required. This can make the model input data old; at least one year ago if an outcome such as default over a one-year outcome window is used. In contrast, the PAI and PSI can be calculated on the characteristics of today’s portfolio. This can provide an earlier warning that the model may no longer be suitable for the current customers. A high value of the PAI may therefore require consideration of overlays above model outputs to prudently provision for expected losses or capital, even if historical calibration and discrimination were considered satisfactory.

The negative consequences of using the PSI are illustrated with the example in Table 2. The PSI value of 0.25 is interpreted as a significant change that may lead banks to take action such as planning re-development of the model or applying an overlay to provisions or capital to account for this unjustified lack of confidence in model predictions. These actions can have severe consequences, including unnecessary expense re-developing a model that remains fit-for-purpose or sending inappropriate messages to investors. The PAI correctly recommends no such actions are required. Importantly, this phenomenon can easily occur because a new model declines high-risk customers that were previously accepted. Hence, we may expect some extreme customers that were present at development to be absent from the review data. That is, the fact that high-risk customers are less frequent in the review data compared to the development data is an expected outcome of a new model deployment and should not be interpreted, as the PSI does, as evidence that the model is no longer fit-for-purpose.

The PAI has several advantages over the PSI. First, the PAI measures the predictive accuracy of the model when applied to the review data rather than a generic difference in the distribution of review and development data. The PAI penalises a model when it is applied to review data beyond the boundary of development data (extrapolation), but not when the review data is more concentrated in the regions suited for the model. The latter is not uncommon; an example is when a new application scorecard replaces an old inferior application scorecard and thereby reduces the number of poor applications accepted. This can reduce the variation in the types of customers accepted without introducing customers that were not accepted previously (so no extrapolation is involved).

Second, the PAI is directly applicable to explanatory variables that are numeric or categorical (ordered or unordered). While the PAI could be applied to variables bucketed into categories (for example when the model applies this transformation of a numeric variable into a few categories), there is no need to do so. Applying the PAI to a raw, untransformed variable might also give important insights.

Third, the PAI does not suffer from calculation problems when categories have frequencies close to zero in either development or review data. Both will give an infinite value (or undefined value) for categorical data if a category has no observations at development but at least one observation at review, but, unless there is good reason to combine this category with another category, this conclusion is not unreasonable as the model cannot provide a prediction for such an observation. This issue does not arise when the PAI is applied to numeric variables.

Fourth, the PAI can be applied to many explanatory variables simultaneously, thus revealing the extent to which the review data involves extrapolation in a multivariate sense. This is arguably more important than assessing the univariate distributions of each variable one at a time. A common attempt to include multiple explanatory variables in the PSI is to use the model output (score) rather than the model inputs. This is similar to the simple linear regression case, Equation (4), as the score is typically a numerical value. In order to apply the PSI, the scores must first be assigned to categories. While this approach does take into account all explanatory variables, it has several of the above disadvantages: it requires creation of arbitrary categories; extreme scores will be placed into a category without taking into account how extreme they are (possible extrapolation); and the PSI considers these as unordered categories when the score is clearly ordered. If too many categories are used the PSI can be high due to a minor difference in frequencies and if too few categories are used important differences in the distributions are not captured. More significantly, the PSI only examines one dimension of the multivariate design space (the one defined by the model coefficients) but deviations in other directions are just as important from a model fit-for-purpose perspective.

Fifth, the PAI is directly applicable to most model structures. For example, regression models that include non-linear terms such as logarithmic transformations, quadratics or interactions between two variables are handled naturally by the MPAI. The PSI requires some manipulation of variables that may be unnatural, require careful thought, or have undesirable consequences. For example, it is difficult to interpret the PSI when applied to both a variable and its square in a quadratic regression model, and it is unclear how two variables involved in an interaction should be categorised for application of the PSI.

Sixth, the PAI can be applied without making any linearity assumptions considered appropriate at model development that may no longer be valid. For example, including the square of each numeric variable (as well as the variable itself) in the calculation of the PAI, even though the quadratic is not in the model, will estimate population stability that considers the possibility that relationships are non-linear. Due to the extra uncertainty of model predictions when the linearity assumption is relaxed and extrapolation is involved, this will increase the PAI when the review data has significant outliers compared to the development data.

While these points suggest the PAI has many advantages over the PSI, it also has characteristics that might be considered disadvantages if they are not taken into account. First, modelling often applies bucketing (or Winsorizing) of variables to remove the impact of extreme outliers. Similar actions should be considered when calculating the PAI as otherwise the PAI may be heavily influenced by a few extreme outliers. However, if it is desired to monitor the modelling decision to bucket or Winsorize, then we recommend calculating the PAI both with and without this action being applied to the data. Second, the MPAI may be inappropriate if too many explanatory variables are included due to the curse of dimensionality. For this reason, we recommend calculating the MPAI using only the variables in the model or using these and a few other variables considered important. These variables might be included because business experience suggests they might be important predictors and quadratic and interaction effects of variables. These additional variables should be included in the MPAI if it is desired to monitor the decision to include or exclude variables; a practice that has much to be recommended. The curse of dimensionality is not a suggestion that only variables in the model should be considered, but a warning against including all available modelling variables (including potentially all their squares, interactions, etc.) in the MPAI, as this will typically be a lot more than just a few times the number of variables included in the final model.

Third, it is important to remember the PSI and PAI measure subtly different ideas of stability. While the PSI measures any change in the distribution of explanatory variables, the PAI only measures how this change influences the predictive accuracy of the model. This was illustrated in the example in Table 2, where changes in the distribution of a categorical variable have no effect on the PAI if all the categories are equally frequent in the development data. We argue this is of more interest when monitoring the performance of a model. Nevertheless, the PSI can detect a change in the characteristics of customers that may be of interest for reasons other than whether the model remains fit-for-purpose.

It is recommended that the MPAI is used as the primary diagnostic for population stability. This provides a single value to measure population stability, and hence, more concise reporting than would be the case if a UPAI (or PSI) value was presented for each variable. UPAI values may add insights concerning which variables are responsible for instability should the MPAI indicate population stability is low. Following these guidelines will produce monitoring reports that more concisely and accurately assess whether a lack of population stability suggests the model under review is no longer fit-for-purpose.

5. Conclusions

The auditing and monitoring of models to assess whether they remain fit-for-purpose are important, and regulations within the banking industry make it clear this is essential to ensure banks, auditors, regulators, and investors have confidence in model outputs. The Population Stability Index is an industry standard to assess stability: whether the data the model is currently applied to differs from the data used to develop the model. This paper introduces the Prediction Accuracy Index which addresses many deficiencies in the PSI and assesses more precisely whether the model remains fit-for-purpose by considering when review data is inappropriate for the model, rather than just different to the development data. Adoption of the Prediction Accuracy Index as an industry standard will simplify reporting and improve confidence in the use of credit models.