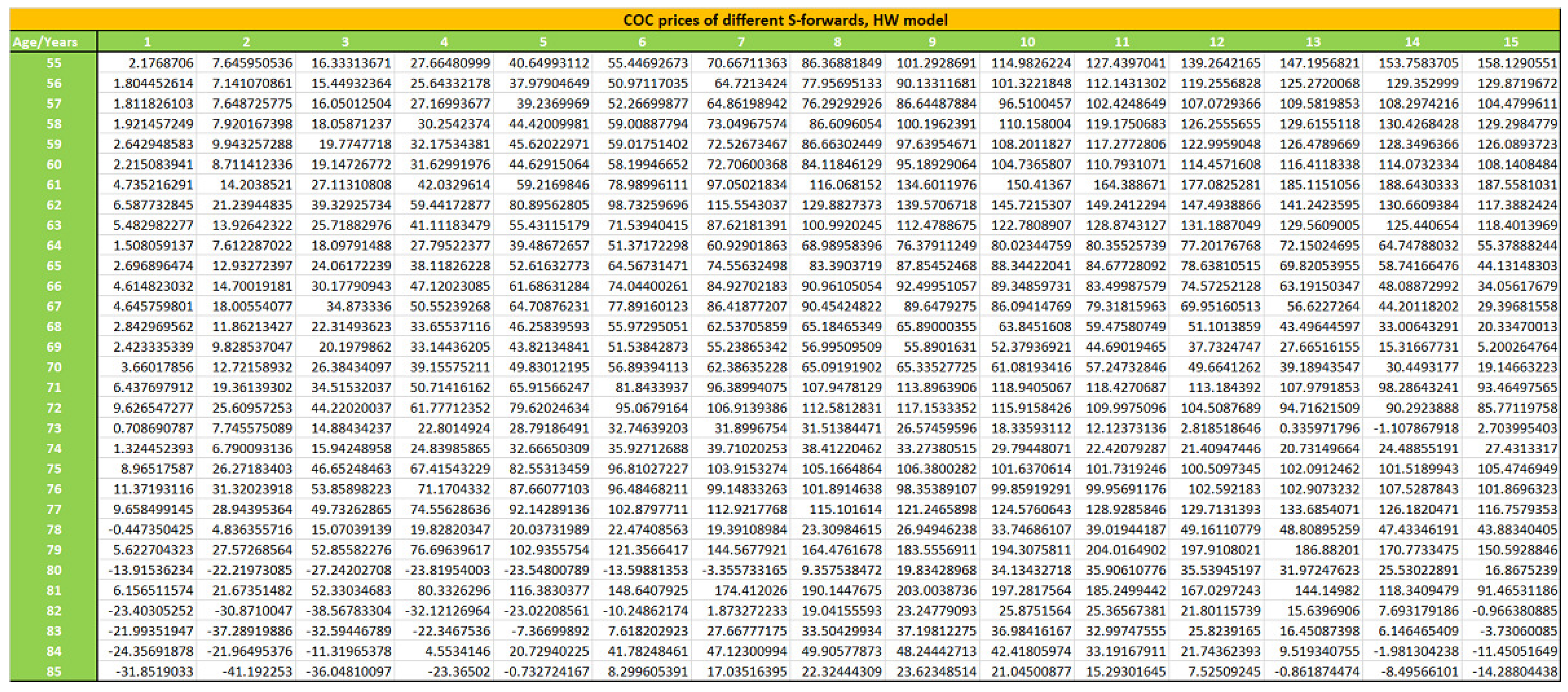
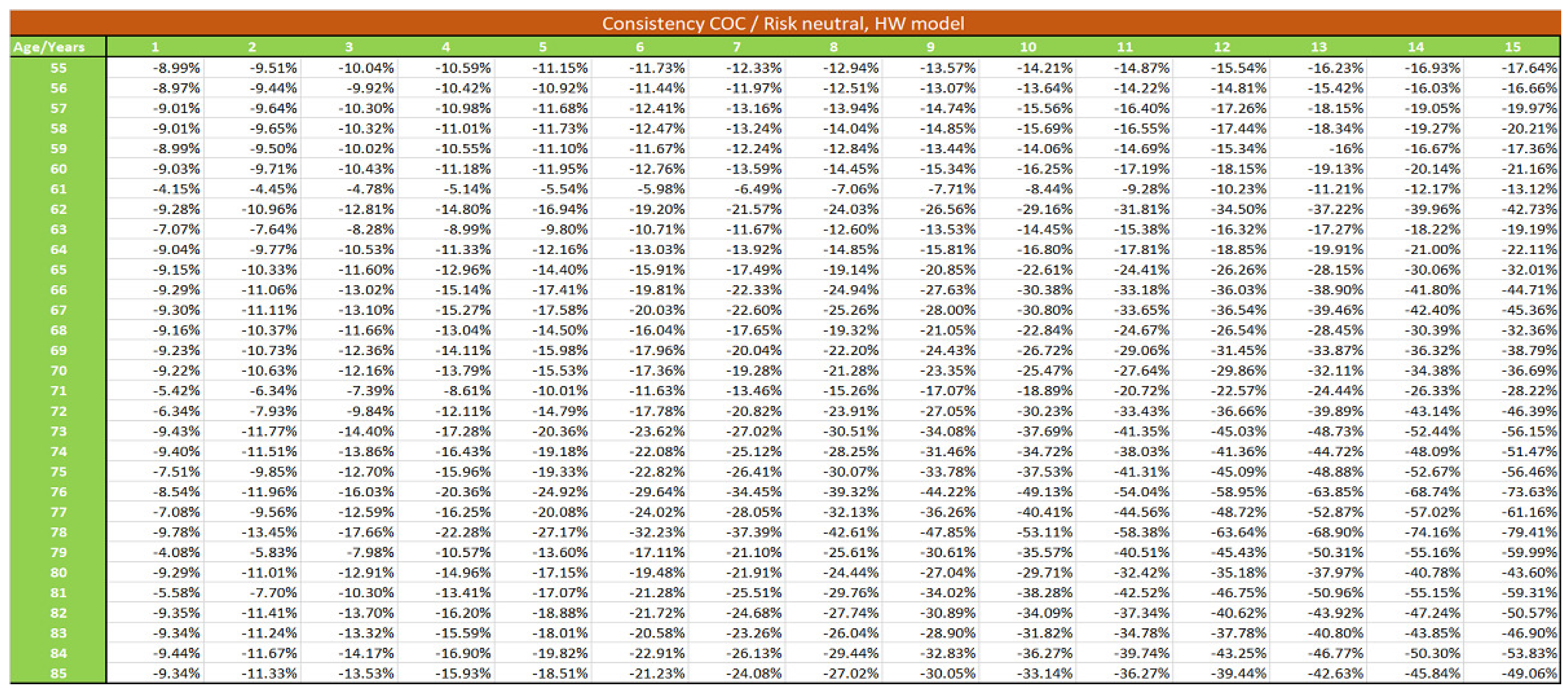
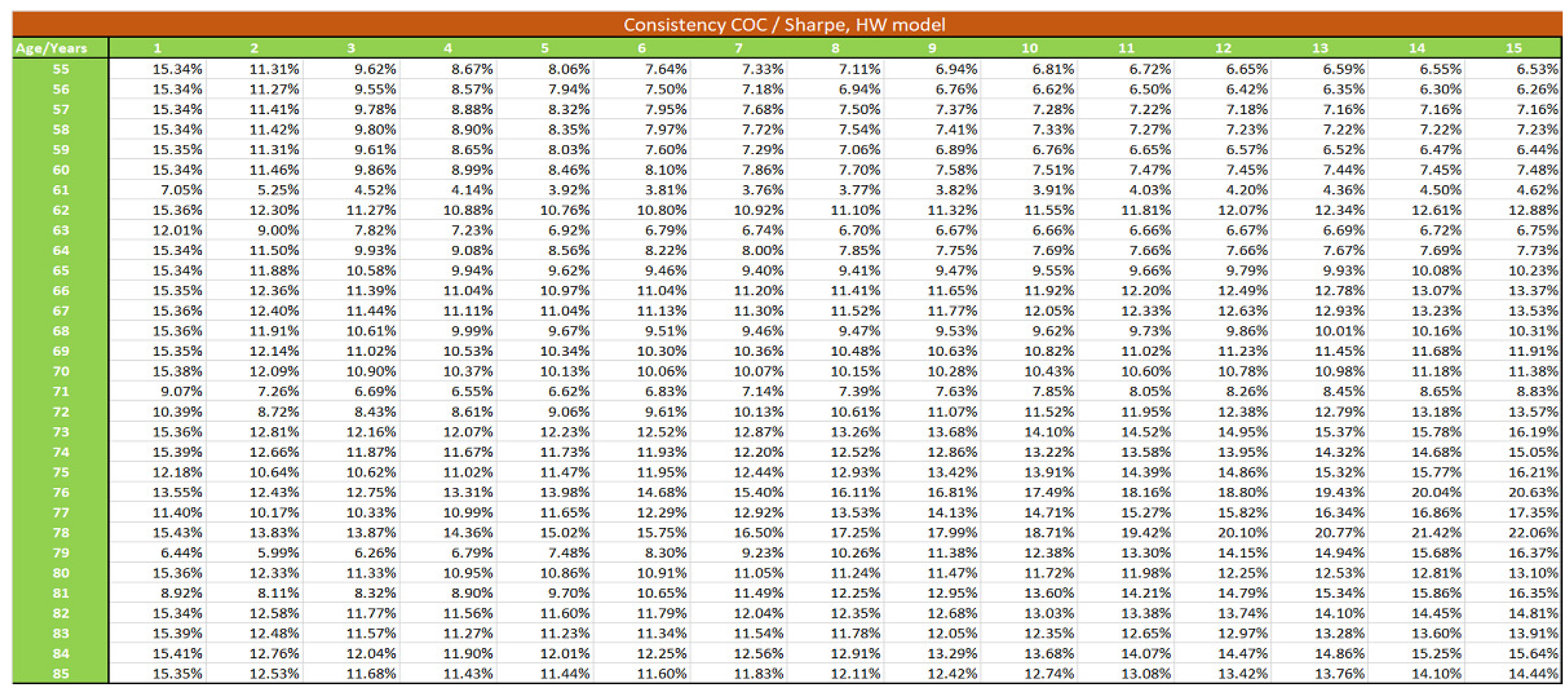
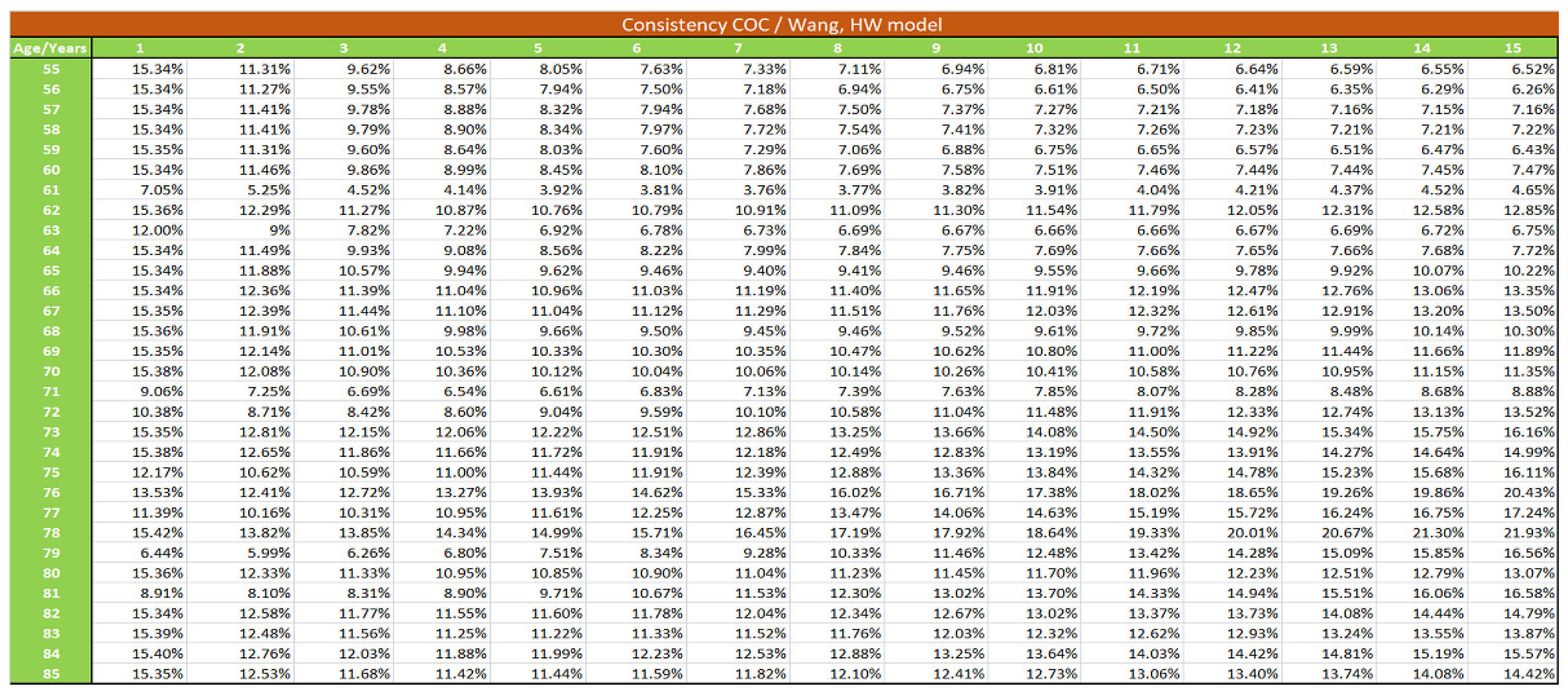
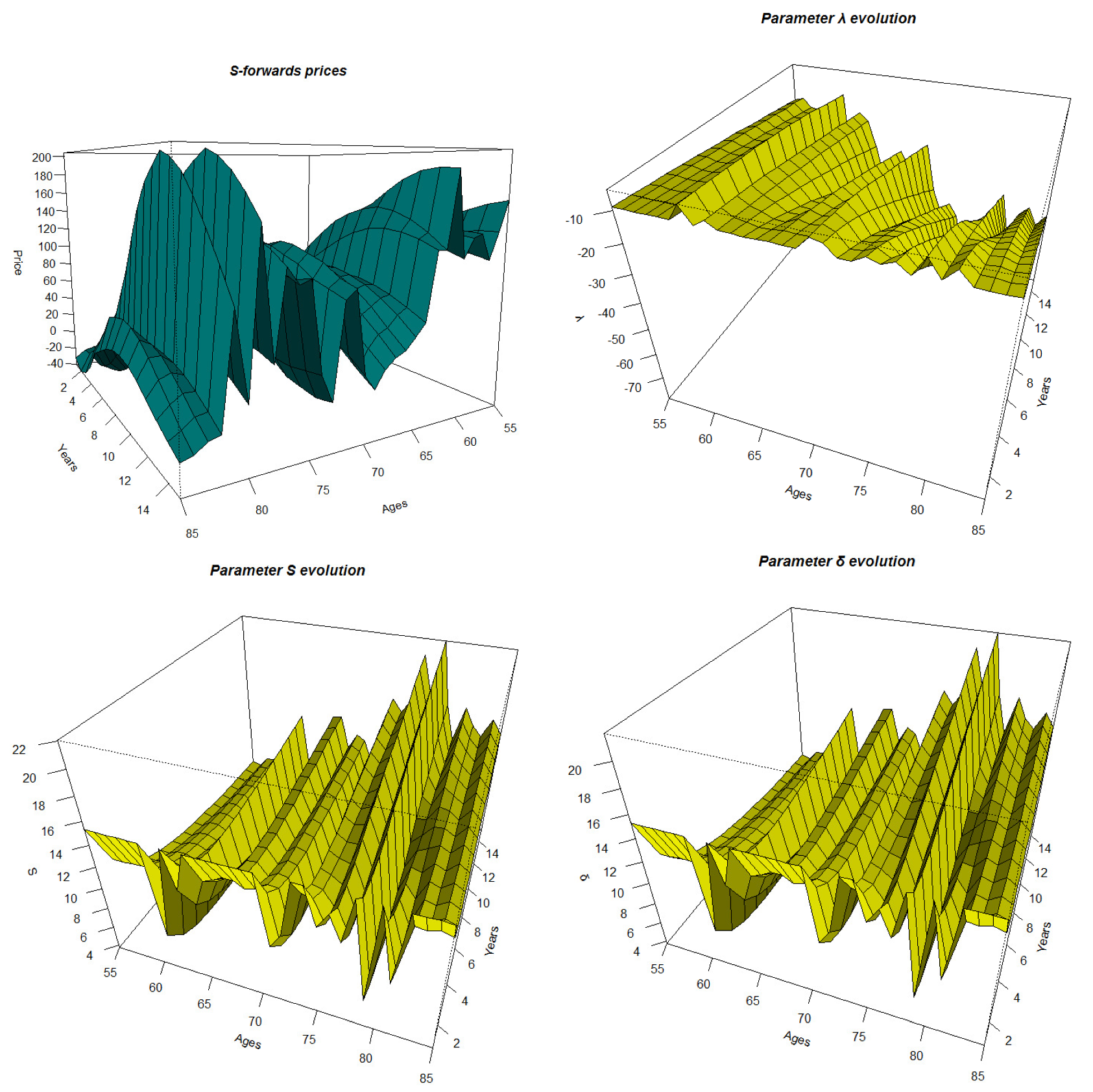
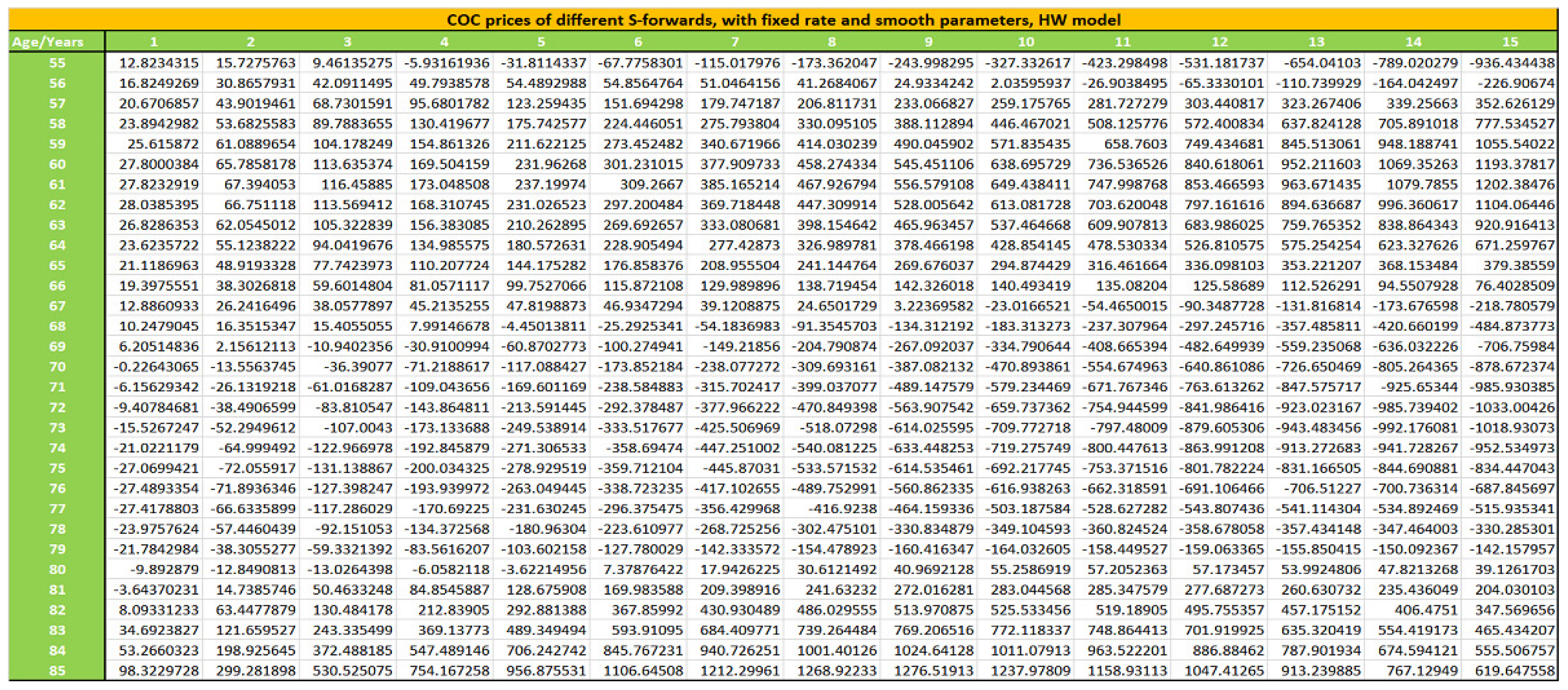
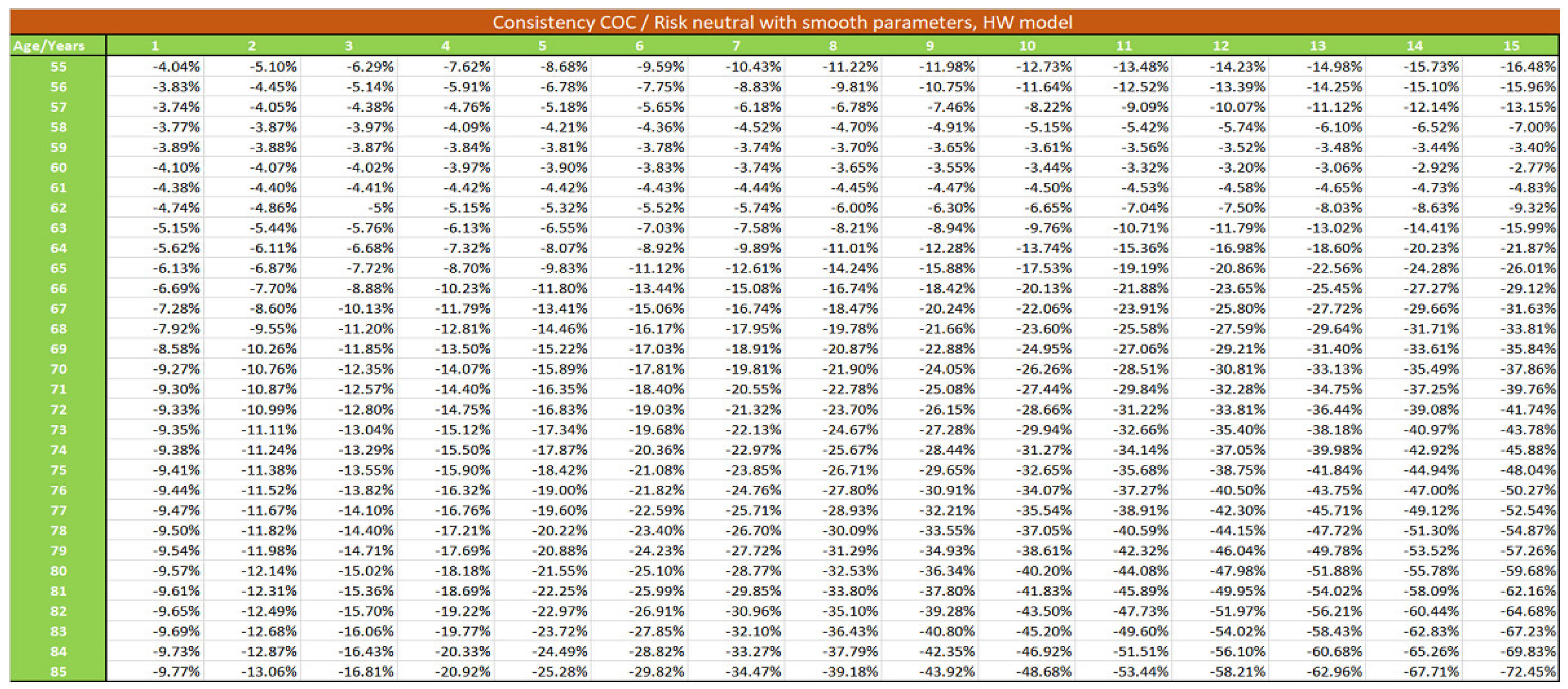
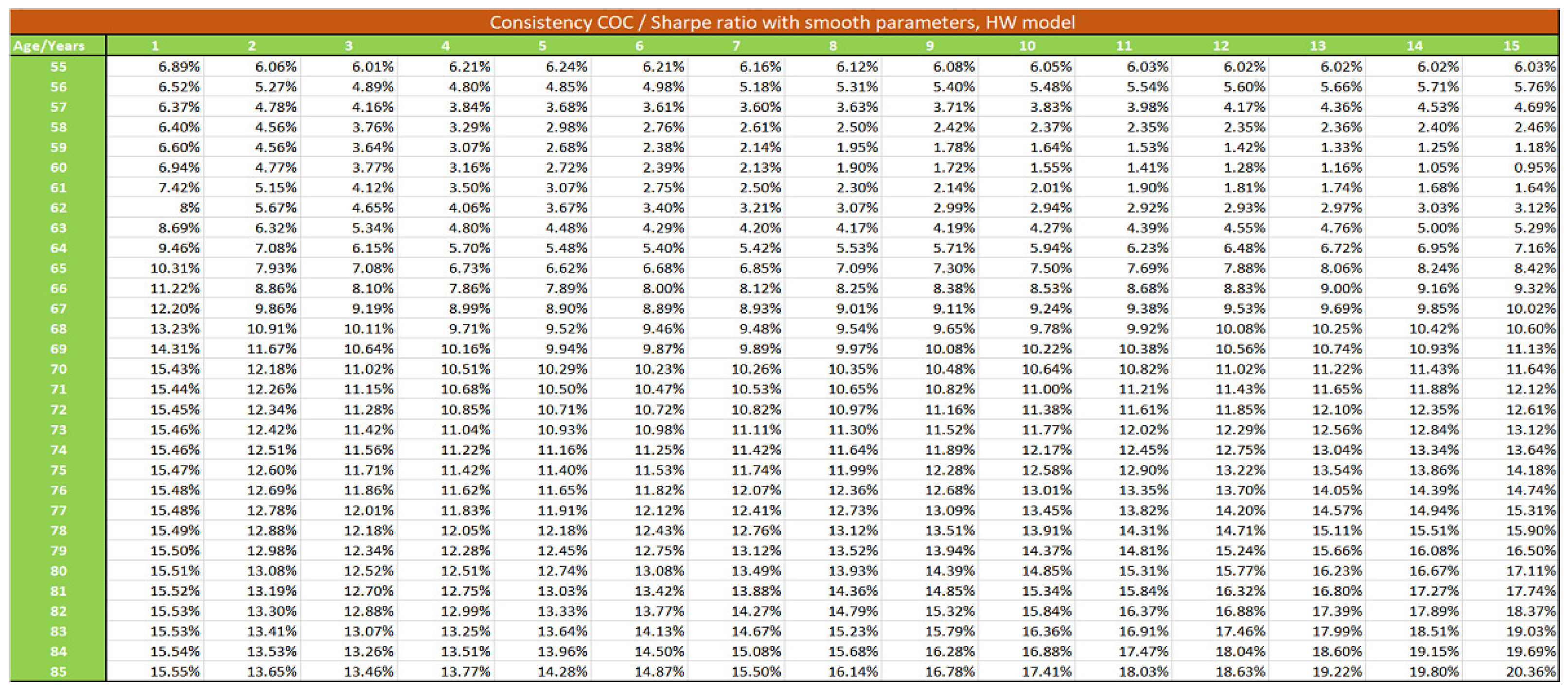
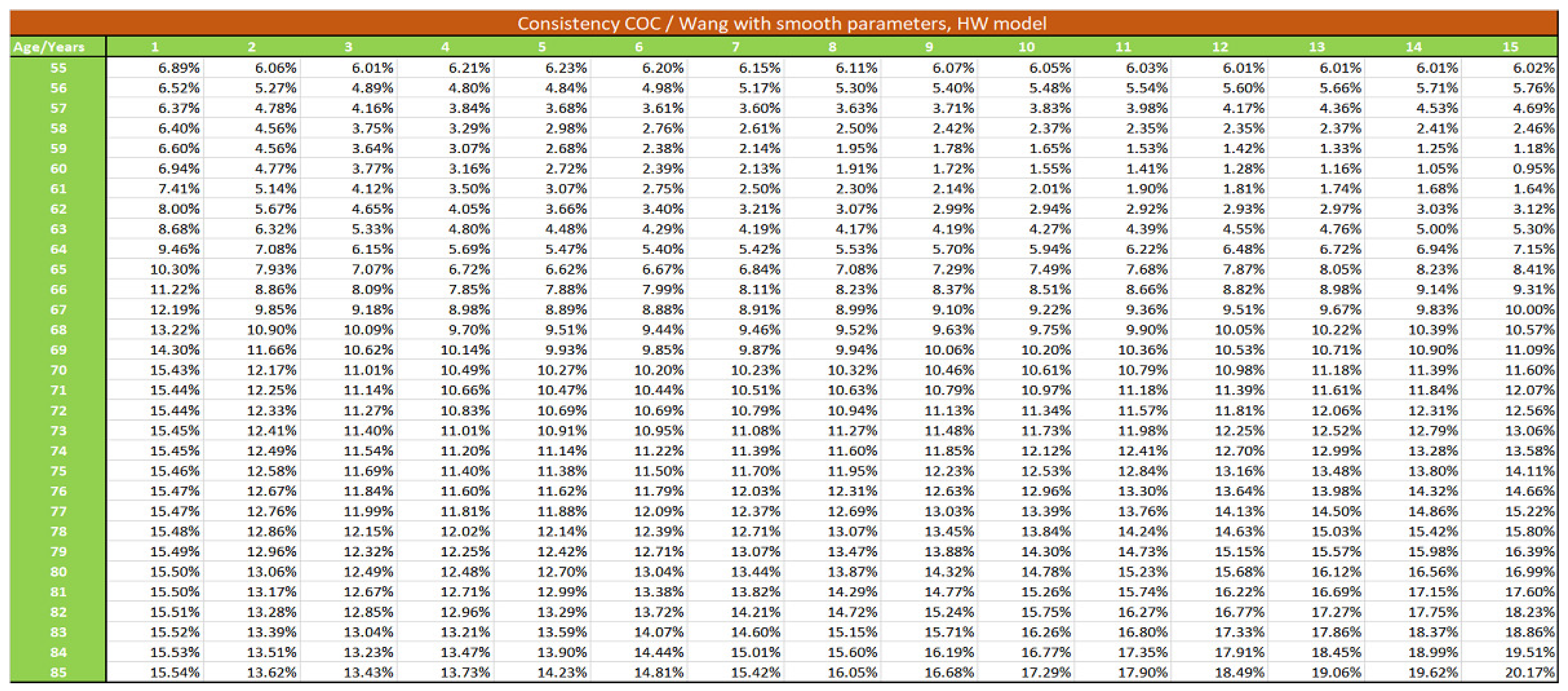
We develop in this section the pricing of the S-forward contract, following other alternative theoretical formulas to compare with formula (34):
2.4.1. Risk-Neutral Approach
The risk-neutral pricing is a technique widely used in quantitative finance to compute the values of derivatives, and could be adapted to price longevity-linked securities.
As discussed in some papers, (see for example (
Cairns et al. 2006b)), this approach is not ideal to price longevity derivatives as the longevity market is immature, and this method requires the availability of a considered amount of data. However, it is interesting to explore the risk-neutral pricing formula for comparison purpose.
Under the risk-neutral probability measure
, the price of an S-forward at time
t is given by:
where
is the market price of longevity risk.
We first consider the HW model to get an explicit expression of the S-forward price. We assume that follows the HW process given by (2).
Let’s introduce the market prices associated with longevity risk, and let .
We consider a model with a constant market price of risk
The SDE of the force of mortality under the risk-neutral measure becomes:
From Equation (
38), we see that a positive value of
would increase the drift of the force of mortality. To follow the same insurer’s logic, by overestimating the survival process expected value and underestimating the mortality, we have to choose a negative value for
.
Under the risk-neutral measure, the survival probability takes the form:
where
and
are given by:
Hence, the price of the S-forward at time
t with the risk-neutral approach is as follows:
CIR Model
Let us now assume that follows the CIR process given by (3).
We introduce the market prices associated with longevity risk,
Under the real-world probability measure is a Brownian motion with drift, and therefore is not a martingale. According to Girsanov’s theorem, is a standard Brownian motion under the risk-neutral measure .
The SDE of the force of mortality becomes:
The survival probability also takes the form:
We assume that the market price of longevity risk has the following classical form: with is a constant.
Equation (
42) then becomes:
The parameters
and
are given by:
with
.
Finally, the price is given by:
2.4.2. Wang Transform Approach
The Wang transform method is a distortion approach that is based on a distortion operator (
Leung et al. 2018). In the insurance context, this operator converts the best estimate of the survival index into its risk equivalent using a specific price of risk. This procedure was presented by (
Dowd et al. 2006) as a pricing method used in the pricing of several over-the-counter longevity swaps in practice, and used for instance by (
Denuit et al. 2007).
The Wang distortion risk measure is given by:
where
x is a continuous non-negative random variable.
is its decumulative function, and
is the distortion function assiciated with the distortion parameter
and given by:
where
is the cumulative standard normal distribution
The price of the S-forward at time
t is then given by:
HW Model
To obtain an explicit expression of the S-forward price with the HW model, we need to determine the formula of .
The Wang distortion of a log-normal distribution is still log-normal with a corrected drift parameter:
The price of S-forward with Wang approach at time t is finally given by:
CIR Model
Because of its complicated distribution, it is not easy to find an explicit formula for . Hence, we will need an SDE discretization scheme.
For the CIR model, the Euler discretization scheme is as follows:
In order to simulate the survival index , we will make a classical assumption often encountered in life insurance theory: we will suppose that the force of mortality is piecewise constant between each point computed by the above Euler discretization.
We will use an R numerical simulation to determine the price of the S-forward; the algorithm will be described in
Section 4.
2.4.3. The Sharpe Ratio Approach
The Sharpe ratio method was used for instance by (
Milevsky et al. 2005) and by (
Loeys et al. 2007) to price q-forwards. It is a standard deviation principle that does not use a transformation of survival probabilities.
In liquid financial markets, the Sharpe ratio provides a benchmark for the determination of risk premia. The Sharpe ratio is given by:
where
is the expected return of the portfolio,
is the risk free rate and
is the standard deviation of the portfolio return.
Using the analogy to the Sharpe ratio in financial market, the Sharpe ratio in the insurance context (
Barrieu and Veraart 2014) is equal to the excess payoff on the longevity-linked securities over its best estimate divided by its standard deviation:
According to this approach, the price of the S-forward is given by:
where
S is the chosen fixed Sharpe ratio, and
is the variance of the survival index.
HW Model
The variance of the survival process is as follows:
The price of the S-forward at time t is then given by:
CIR Model
and
are then given by:
with
and
can be solved numerically. The variance of the survival index under the real world probability is:
Finally, the price of the S-forward is as follows: