1. Introduction
The modern portfolio theory of
Markowitz (
1959) pioneered the quantitative analysis of financial economics. The most important idea proposed in this theory is that one should focus on the trade-off between expected return and the risk measured by the standard deviation. Mathematically, the modern portfolio theory leads to a quadratic optimization problem with linear constraints. Using this simple mathematical structure, Markowitz gave a complete characterization of the efficient frontier for trade-off of the return and risk. Tobin showed that the efficient portfolios are an affine function of the expected return
Tobin (
1958). Markowitz portfolio theory was later generalized by
Lintner (
1965),
Mossin (
1966),
Sharpe (
1964) and
Treynor (
1999) in the capital asset pricing model (CAPM) by involving a riskless bond. In the CAPM model, both the efficient frontier and the related efficient portfolios are affine in terms of the expected return (
Sharpe 1964;
Tobin 1958).
The nice structures of the solutions in the modern portfolio theory and the CAPM model afford many applications. For example, the CAPM model is designed to provide reasonable equilibrium prices for risky assets in the market place. Sharpe used the ratio of excess return to risk (called the Sharpe ratio) to provide a measurement for investment performance (
Sharpe 1966). In addition, the affine structure of the efficient portfolio in terms of the expected return leads to the concept of a market portfolio as well as the two fund theorem (
Tobin 1958) and the one fund theorem (
Sharpe 1964;
Tobin 1958). These results provided a theoretical foundation for passive investment strategies.
In many practical portfolio problems, however, one needs to consider more general pairs of reward and risk. For example, the growth portfolio theory can be viewed as maximizing the log utility of a portfolio. In order to address the issue that an optimal growth portfolio is usually too risky in practice, practitioners often have to impose additional restrictions on the risk (
MacLean et al. 2009;
Vince 2009;
Vince and Zhu 2015). In particular, current drawdown (
Maier-Paape 2016), maximum drawdown and its approximations (
De Prado et al. 2013;
Maier-Paape 2015;
Vince and Zhu 2015), deviation measure (
Rockafellar et al. 2006), as well as conditional value at risk (
Rockafellar and Uryasev 2000) and more abstract coherent risk measures (
Artzner et al. 1999) are widely used as risk measures in practice. Risk, as measured by such criteria, is reduced by diversification. Mathematically, it is to say these risk measures are convex. For these reasons, considering the trade-off between general risk measures and expected utilities are crucial in portfolio problems. In particular, including risk measures beyond positive homogeneous risk measures allows for measuring risk by drawdown (see
Maier-Paape and Zhu (
2017)), a concept to which many practitioners are sensitive.
The goal and main results of this paper are to extend the modern portfolio theory into a general framework under which one can analyze efficient portfolios that trade-off between a convex risk measure and a reward captured by a concave expected utility (see
Section 3). We phrase our primal problem as a convex portfolio optimization problem of minimizing a convex risk measure subject to the constraint that the expected utility of the portfolio is above a certain level. Thus, convex duality plays a crucial role and the structure of the solutions to both the primal and dual problems often have significant financial implications. We show that, in the space of risk measure and expected utility, efficient trade-off happens on an increasing concave curve (cf. Proposition 8 and Theorem 4). We also show that the efficient portfolios continuously depend on the level of the expected utility (see Theorem 5), and moreover, we can describe the curve of efficient portfolios quantitatively in a precise manner (cf. Proposition 9 and Corollary 2).
To avoid technical complications, we restrict our analysis to the practical case in which the status of an underlying economy is represented by a finite sample space. Under this restriction, the Markowitz modern portfolio theory and the capital asset pricing model are special cases of this general theory. Markowitz determines portfolios of purely risky assets which provide an efficient trade-off between expected return and risk measured by the standard deviation (or equivalently the variance). Mathematically, this is a class of convex programming problems of minimizing the standard deviation of the portfolio parameterized by the level of the expected returns. The capital asset pricing model, in essence, extends the Markowitz modern portfolio theory by including a riskless bond in the portfolio. We observe that the space of the risk-expected return is, in fact, the space corresponding to the dual of the Markowitz portfolio problem. The shape of the famous Markowitz bullet is a manifestation of the well known fact that the optimal value function of a convex programming problem is convex with respect to the level of constraint. As mentioned above, the Markowitz portfolio problem is a quadratic optimization problem with linear constraint. This special structure of the problem dictates the affine structure of the optimal portfolio as a function of the expected return (see Theorem 6). This affine structure leads to the important two fund theorem (cf. Theorem 7) that provides a theoretical foundation for the passive investment method. For the capital asset pricing model, such an affine structure appears in both the primal and dual representation of the solutions, which leads to the one fund theorem in the portfolio space and the capital market line in the dual space of risk-return trade-off (cf. Theorems 8 and 9).
The flexibility in choosing different risk measures allows us to extend the analysis of the essentially quadratic risk measure pioneered by Markowitz to a wider range. For example, when a deviation measure (
Rockafellar et al. 2006) is used as risk measure, which happens e.g., when an approximation of the current drawdown is considered (see
Maier-Paape and Zhu (
2017)), and the expected return is used to gauge the performance, we show that the affine structure of the efficient solution in the classical capital market pricing model is preserved (cf. Theorem 10 and Corollary 3), recovering and extending especially the results in
Rockafellar et al. (
2006). In particular, we can show that the condition in CAPM that ensures the existence of a market portfolio has a full generalization to portfolio problems with positive homogeneous risk measures (see Theorem 11). This is significant in that it shows that the passive investment strategy is justifiable in a wide range of settings.
The consideration of a general utility function, however, allows us to go beyond the “additive” performance measure in modern portfolio theory to a “multiplicative” one including cumulative returns when, for example, using the log utility. As a result, the growth optimal portfolio theory (
Lintner 1965) and the leverage space portfolio theory (
Vince 2009) can also be understood under our general framework. The optimal growth portfolio pursues to maximize the expected log utility that is equivalent to maximize the expected cumulative compound return. It is known that the growth optimal portfolio is usually too risky. Thus, practitioners often scale back the risky exposure from a growth optimal portfolio. In our general framework, we consider the portfolio that minimizes a risk measure given a fixed level of expected log utility. Under reasonable conditions, we show that such portfolios form a path parameterized by the level of expected log utility in the portfolio space that connects the optimal growth portfolio and the portfolio of a riskless bond (see Theorem 13). In general, for different risk measures, we will derive different paths. These paths provide justifications for risk reducing curves proposed in the leverage space portfolio theory (
Vince 2009). The dual problem projects the efficient trade-off path into a concave curve in the risk-expected log utility space parallel to the role of Markowitz bullet in the modern portfolio theory and the capital market line in the capital asset pricing model. Under reasonable assumptions, the efficient frontier for log utility is a bounded increasing concave curve. The lower left endpoint of the curve corresponds to the portfolio of pure riskless bond and the upper right endpoint corresponds to the growth optimal portfolio. The increasing nature of the curve tells us that the more risk we take, the more cumulative return we can expect. The concavity of the curve indicates, however, that, with the increase of the risk, the marginal increase of the expected cumulative return will decrease.
Markowitz portfolio theory essentially maximizes a linear expected utility while the growth optimal portfolio focuses on the log utility. Other utility functions were also considered in portfolio problems. Our general framework brings them together in a unified way. Besides unifying the several important results laid out above, the general framework, furthermore, has many new applications. In this first installment of the paper, we layout the framework, derive the theoretical results of crucial importance and illustrate them with a few examples. More specific results on drawdown risk measures will appear in
Maier-Paape and Zhu (
2017). We arrange the paper as follows: first, we discuss necessary preliminaries in the next section.
Section 3 is devoted to our main result: a framework to efficient trade-off between risk and utility of portfolios and its properties. In
Section 4, we give a unified treatment of Markowitz portfolio theory and capital asset pricing model using our framework.
Section 5 is devoted to a discussion of positive homogeneous risk measures under which the optimal trade-off portfolio possesses an affine structure. This situation fully generalizes Markowitz and CAPM theories and thus many of the conditions in
Section 4 find an analog in
Section 5.
Section 6 discusses growth optimal portfolio theory and leverage portfolio theory. We conclude in
Section 7 pointing to applications worthy of further investigation.
2. Preliminaries
2.1. A Portfolio Model
We consider a simple one period financial market model
S on an economy with finite states represented by a sample space
. We use a probability space
to represent the states of the economy and their corresponding probability of occurring, where
is the algebra of all subsets of
. The space of random variables on
is denoted
and it is used to represent the payoff of risky financial assets. Since the sample space
is finite,
is a finite dimensional vector space. We use
to represent of the cone of nonnegative random variables in
. Introducing the inner product
becomes a (finite dimensional) Hilbert space.
Definition 1. (Financial Market) We say that is a financial market in a one period economy provided that and . Here, represents a risk free bond with a positive return when . The rest of the components represent the price of the m-th risky financial asset at time t.
We will use the notation when we need to focus on the risky assets. We assume that is a constant vector representing the prices of the assets in this financial market at . The risk is modeled by assuming to be a nonnegative random vector on the probability space , that is . A portfolio is a column vector whose components represent the share of the m-th asset in the portfolio and is the portion of capital invested in asset m at time t. Hence, corresponds to the investment in the risk free bond and is the risky part.
Remark 1. Restricting to a finite sample space avoids the distraction of technical difficulties. This is also practical since, in the real world, one can only use a finite quantity of information. Furthermore, we restrict our presentation to the one period market model. However, more complex sample spaces and market models such as multi-period financial models should be treatable with a similar approach.
We often need to restrict the selection of portfolios. For example, in many applications, we consider only portfolios with unit initial cost, i.e., . The following definition makes this precise.
Definition 2. (Admissible Portfolio) We say that is a set of admissible portfolios provided that A is a nonempty closed and convex set. We say that A is a set of admissible portfolios with unit initial price provided that A is a closed convex subset of .
2.2. Convex Programming
The trade-off between convex risks and concave expected utilities yields essentially convex programming problems. For convenience of the reader, we collect notation and relevant results in convex analysis, which are important in the discussion below. We omit most of the proofs that can be found in
Borwein and Zhu (
2016);
Carr and Zhu (
forthcoming);
Rockafellar (
1970). Readers who know convex programming well can skip this section.
Let
X be a finite dimensional Banach space. Recall that a set
is convex if, for any
and
,
. For an extended valued function
, we define its domain by
and its epigraph by
We say f is lower semi-continuous if is a closed set. The following proposition characterizes an epigraph of a function.
Proposition 1. (Characterization of Epigraph)
Let F be a closed subset of such that for all . Then, F is the epigraph for a lower semi-continuous function , i.e., , if and only if Proof. The key is to observe that, for a set
F with the structure in (
1), a function
is well defined and then
holds. ☐
We say a function
f is convex if
is a convex set. Alternatively,
f is convex if and only if, for any
and
,
Consider
. We say
f is concave when
is convex and we say
f is upper semi-continuous if
is lower semi-continuous. Define the hypograph of a function
f by
Then, a symmetric version of Proposition 1 is
Proposition 2. (Characterization of Hypograph)
Let F be a closed subset of such that for all . Then, F is the hypograph of an upper semi-continuous function , i.e., , if and only ifMoreover, the function f can be defined by Remark 2. The value of the function f in Proposition 1 (Proposition 2) at a given point x cannot assume () and therefore .
Since utility functions are concave and risk measures are usually convex, the analysis of a general trade-off between utility and risk naturally leads to a convex programming problem. The general form of such convex programming problems is
where
f,
g and
h satisfy the following assumption.
Assumption 1. Assume that is a lower semi-continuous extended valued convex function, is a vector valued function with convex components, ≤ signifies componentwise minorization and is an affine mapping, for natural numbers . Moreover, at least one of the components of g has compact sublevel sets.
Convex programming problems have nice properties due to the convex structure. We briefly recall the pertinent results related to convex programming. First, the optimal value function
v is convex. This is a well-known result that can be found in standard books on convex analysis, e.g.,
Borwein and Zhu (
2005).
Proposition 3. (Convexity of Optimal Value Function)
Let f, g and h satisfy Assumption 1. Then, the optimal value function v in the convex programming problem (5) is convex and lower semi-continuous. By and large, there are two (equivalent) general approaches to help solving a convex programming problem: by using the related dual problem and by using Lagrange multipliers. The two methods are equivalent in the sense that a solution to the dual problem is exactly a Lagrange multiplier (see
Borwein and Zhu (
2016)). Using Lagrange multipliers is more accessible to practitioners outside the special area of convex analysis. We will take this approach. The Lagrange multipliers method tells us that, under mild assumptions, we can expect there exists a Lagrange multiplier
with
such that
is a solution to the convex programming problem (
5) if and only if it is a solution to the unconstrained problem of minimizing
The function is called the Lagrangian. To understand why and when a Lagrange multiplier exists, we need to recall the definition of the subdifferential.
Definition 3. (Subdifferential)
Let X be a finite dimensional Banach space and its dual space. The subdifferential of a lower semi-continuous convex function at is defined by Geometrically, an element of the subdifferential gives us the normal vector of a support hyperplane for the convex function at the relevant point. It turns out that Lagrange multipliers of problem (
5) are simply the negative of elements of the subdifferential of
v as summarized in the lemma below.
Theorem 1. (Lagrange Multiplier)
Let be the optimal value function of the constrained optimization problem (5) with and h satisfying Assumption 1. Suppose that, for fixed , and is a solution of (5). Then,- (i)
,
- (ii)
the Lagrangian defined in (6) attains a global minimum at , and - (iii)
λ satisfies the complementary slackness conditionwhere signifies the inner product.
Remark 3. By Theorem 1 Lagrange multipliers exist when (
5) has a solution
and
. Calculating
requires to know the value of
v in a neighborhood of
and is not realistic. Fortunately, the well-known Fenchel–Rockafellar theorem (see e.g.,
Borwein and Zhu (
2005)) tells us when
belongs to the relative interior of
, then
. This is a very useful sufficient condition. A particularly useful special case is the Slater condition (see also
Borwein and Zhu (
2005)): there exists
such that
. Under this condition,
holds.
3. Efficient Trade-Off between Risk and Utility
We consider the financial market described in Definition 1 and consider a set of admissible portfolios (see Definition 2). The payoff of each portfolio at time is . The merit of a portfolio x is often judged by its expected utility where u is an increasing concave utility function. The increasing property of u models the more payoff the better. The concavity reflects the fact that, with the increase of payoff, its marginal utility to an investor decreases. On the other hand, investors are often sensitive to the risk of a portfolio that can be gauged by a risk measure. Because diversification reduces risk, the risk measure should be a convex function.
3.1. Technical Assumptions
Some standard assumptions on the utility and risk functions are often needed in the more technical discussion below. We collect them here.
Assumption 2. (Conditions on Risk Measure) Consider a continuous risk function where A is a set of admissible portfolios according to Definition 2. We will often refer to some of the following assumptions:
- (r1)
(Riskless Asset Contributes No risk) The risk measure is a function of only the risky part of the portfolio, where .
- (r1n)
(Normalization) There is at least one portfolio of purely bonds in A. Furthermore, if and only if x contains only riskless bonds, i.e., for some .
- (r2)
(Diversification Reduces Risk) The risk function is convex.
- (r2s)
(Diversification Strictly Reduces Risk) The risk function is strictly convex.
- (r3)
(Positive homogeneous) For , .
- (r3s)
(Diversification Strictly Reduces Risk on Level Sets)
The risk function satisfies (r3) and, for all with and ,
Condition (r3) precludes (r2s). Thus, condition (r3s) serves as a replacement for (r2s) when the risk measure satisfies (r3). Moreover, we have the following useful result.
Lemma 1. Assuming a risk measure satisfies (r1), (r1n) and (r3s). Then,
- (a)
satisfies (r2), and
- (b)
satisfies (r1), (r1n) and (r2s).
Proof. Let
and
be given. If
and
lie on the same ray through
, say
for some
, then convexity of
there is clear due to (r3). For
and
not on the same ray and with
, defining
we have
and since
, by (r3s), we have
verifying (r2) for
since
depends only on
by (r1).
Clearly,
has the properties (r1) and (r1n). Squaring (
8), we derive
Furthermore, on rays due to (r3), we have and the strict convexity of there is clear as well. Hence, the square of the risk measure satisfies (r2s). ☐
Remark 4. (Deviation measure)
Our risk measure is described in terms of the portfolio. Assumptions (r1), (r1n), (r2) and (r3) are equivalent to the axioms of a deviation measure
in Rockafellar et al. (2006), which is described in terms of the random payoff variable generated by the portfolio. Assumption (r1) excludes the widely used coherent risk measure introduced in Artzner et al. (1999), which requires cash reserve, reduces risk. Assumption 3. (Conditions on Utility Function) Utility functions are upper semi-continuous functions on their domain and are usually assumed to satisfy some of the following properties:
- (u1)
(Profit Seeking) The utility function u is an increasing function.
- (u2)
(Diminishing Marginal Utility) The utility function u is concave.
- (u2s)
(Strict Diminishing Marginal Utility) The utility function u is strictly concave.
- (u3)
(Bankrupcy Forbidden) For , .
- (u4)
(Unlimited Growth) For , we have .
Another important condition that often appears in the financial literature is no arbitrage (see (
Carr and Zhu forthcoming, Definition 3.5)). In the sequel, it is also useful to have two other related concepts.
Definition 4. Consider a portfolio on the financial market .
- (a)
(No Nontrivial Riskless Portfolio)
We say a portfolio x is riskless
ifWe say the market has no nontrivial riskless portfolio
if there does not exist a riskless portfolio x with .- (b)
(No Arbitrage)
We say x is an arbitrage
if it is riskless and there exists some such thatWe say market has no arbitrage
if there does not exist any arbitrage portfolio.- (c)
(Nontrivial Bond Replicating Portfolio)
We say that is a nontrivial bond replicating portfolio
if and
An arbitrage is a way to make return above the risk free rate without taking any risk of losing money. If such an opportunity exists, then investors will try to take advantage of it. In this process, they will bid up the price of the risky assets and cause the arbitrage opportunity to disappear. For this reason, usually people assume a financial market does not contain any arbitrage. A trivial riskless portfolio of investing everything in the riskless asset always exists. A nontrivial riskless portfolio, however, is not to be expected and we will often use this assumption. It turns out that the difference between no nontrivial riskless portfolio and no arbitrage is exactly the existence of a nontrivial bond replicating portfolio. The three conditions in Definition 4 (a), (b) and (c) are related as follows:
Proposition 4. Consider the financial market of Definition 1. There is no nontrivial riskless portfolio in if and only if has no arbitrage portfolio and no nontrivial bond replicating portfolio. It follows that no nontrivial riskless portfolio implies no arbitrage portfolio.
Proof. The conclusion follows directly from Definition 4. ☐
Assuming that the financial market has no arbitrage, then no nontrivial riskless portfolio is equivalent to no nontrivial bond replicating portfolio and has the following characterization.
Theorem 2. (Characterization of no Nontrivial Bond Replicating Portfolio) Assuming the financial market in Definition 1 has no arbitrage. Then, the following assertions are equivalent:
- (i)
There is no nontrivial bond replicating portfolio.
- (ii)
For every nontrivial portfolio x with , there exists some such that - (ii*)
For every risky portfolio , there exists some such that - (iii)
The matrixhas rank M, in particular .
Proof. We use a cyclic proof. (i)→ (ii): If (ii) fails, then
for some nontrivial
x. By (i),
x must be an arbitrage, which is a contradiction. (ii)→ (ii*): obvious. (ii*)→ (iii): If (iii) is not true, then
has a nontrivial solution that is a contradiction to (
11). (iii)→ (i): Assume that there exists a portfolio
with
, which replicates the bond. Then,
. This implies that
so that
, which contradicts (iii). ☐
A rather useful corollary of Theorem 2 is that any of the conditions (i)–(iii) of that theorem ensures the covariance matrix of the risky assets to be positive definite.
Corollary 1. (Positive Definite Covariance Matrix)
Assume the financial market in Definition 1 has no nontrivial riskless portfolio. Then, the covariant matrix of the risky assetsis positive definite. Proof. We note that, under the assumption of the corollary, for any nontrivial risky portfolio
,
cannot be a constant. Otherwise,
would be a constant, which contradicts
has no nontrivial riskless portfolio. It follows that, for any nontrivial risky portfolio
,
Thus, is positive definite. ☐
Corollary 1 shows that the standard deviation as a risk measure satisfies the properties (r1), (r1n), (r2) and (r3s) in Assumption 2.
3.2. Efficient Frontier for the Risk-Utility Trade-Off
We note that, to increase the utility, one often has to take on more risk and, as a result, the risk increases. The converse is also true. For example, if one allocates all the capital to the riskless bond, then there will be no risk, but the price to pay is that one has to forgo all the opportunities to get a high payoff on risky assets so as to reduce the expected utility. Thus, the investment decision of selecting an appropriate portfolio becomes one of trading-off between the portfolio’s expected return and risk. To understand such a trade-off, we define, for a set of admissible portfolios
in Definition 2, the set
on the two-dimensional risk-expected utility space for a given risk measure
and utility
u. Given a financial market
and a portfolio
x, we often measure risk by observing
. The following simple proposition is useful in linking such observations to the risk measure in Assumption 2.
Proposition 5. (Induced Risk Measure) (a) Fixing a financial market as in Definition 1. Suppose that is a lower semi-continuous, convex and positive homogeneous function. Moreover, assume that . Then, , is a lower semi-continuous risk measure satisfying properties (r1), (r2) and (r3) in Assumption 2.
The following are two sufficient conditions ensuring that are easy to verify:
- (1)
When ρ is invariant under adding constants, i.e., , for any and . A useful example is when ρ is the standard deviation.
- (2)
When ρ is restricted to a set of admissible portfolios A with unit initial cost. In this case, we can see that
(b) If the financial market has no nontrivial riskless portfolio and ρ is strictly convex, then, for a set A of admissible portfolios with unit initial cost, satisfies (r2s) in Assumption 2.
Similarly, we are interested in when the expected utility of is strictly concave in x. Below, we provide a set of sufficient conditions guaranteeing this. The easy proof is left to the reader.
Proposition 6. (Strict Concavity of Expected Utility) Assume that
- (a)
the financial market has no nontrivial riskless portfolio,
- (b)
the utility function u satisfies condition (u2s) in Assumption 3, and
- (c)
A is a set of admissible portfolios with unit initial cost as in Definition 2.
Then, the expected utility as a function of the portfolio x is upper semi-continuous and strictly concave on A.
When is induced by as in Proposition 5 we also use the notation . Clearly, if then . The following assumption will be needed in concrete applications.
Assumption A4. (Compact Level Sets) Either (a) for each , is compact or (b) for each , is compact.
Proposition 7. Assume that A is a set of admissible portfolios as in Definition 2. We claim: (a) Assume that the risk measure satisfies (r2) in Assumption 2 and the utility function u satisfies (u2) in Assumption 3. Then, set is convex and implies that, for any , and . (b) Assume furthermore that Assumption 4 holds. Then, is closed.
Proof. (a) The property implies that, for any , and follows directly from the definition of .
Suppose that
and
. Then, there exists
such that
Then, convexity of
in
x yields
and (u2) gives
Thus,
so that
is convex.
(b) Suppose that
, for a sequence in
. Then, there exists a sequence
such that
By Assumption 4, a subsequence of
(denoted again by
) converges to, say,
. Taking limits in (
16), by the upper semicontinuity of
u, we arrive at
Thus, and hence is a closed set. ☐
Now, we can represent a portfolio as a point in the two-dimensional risk-expected utility space. Investors prefer portfolios with lower risk if the expected utility is the same or with higher expected utility given the same level of risk.
Definition 5. (Efficient Portfolio and Frontier)
We say that a portfolio is efficient
provided that there does not exist any portfolio such that eitherorWe call the set of images of all efficient portfolios in the two-dimensional risk-expected utility space the efficient frontier
and denote it by . The next theorem characterizes efficient portfolios in the risk-expected utility space.
Theorem 3. (Efficient Frontier)
Efficient portfolios represented in the two-dimensional risk-expected utility space are all located in the (non vertical or horizontal) boundary of the set . Moreover, consider admissible portfolios . If then Proof. If a portfolio
x represented in the risk-expected utility space as
is not on the (non vertical or horizontal) boundary of the
, then, for
small enough, we have either
or
. This means
x can be improved. The inclusion (
18) directly follows from
. ☐
Remark 5. (Empty Efficient Frontier) If for all and the increasing utility function u has no upper bound, then for any risk measure satisfying (r1) and (r1n) in Assumption 2, . By Proposition 7 which implies that . Thus, practically meaningful always correspond to sets of admissible portfolios A such that the initial cost for all is limited. Moreover, if the initial cost has a range and riskless bonds are included in the portfolio, then we will see a vertical line segment on the μ axis and the efficient portfolio corresponds to the upper bound of this vertical line segments. Thus, it suffices to consider sets of portfolios A with unit initial cost.
3.3. Representation of Efficient Frontier
In view of Remark 5, in this section, we will consider a set of admissible portfolios
A with unit initial cost as in Definition 2. By Proposition 7, we can view the set
as an epigraph on the expected utility-risk space or a hypograph on the risk-expected utility space. By Propositions 1 and 2, the set
naturally defines two functions
and
:
and
where we assume Assumption 4 to ensure
is well defined, i.e.,
for all
.
Proposition 8. (Function Related to the Efficient Frontier) Assume that the risk measure satisfies (r2) in Assumption 2 and the utility function u satisfies (u2) in Assumption 3. Furthermore, assume that Assumption 4 holds for a set of admissible portfolios A with unit initial cost. Then, the functions and are increasing lower semi-continuous convex and increasing upper semi-continuous concave, respectively. Moreover, for any , and .
Proof. The increasing property of
and
follows directly from the second representation in (
19) and (
20), respectively.
The properties for the domains of and follow directly from Proposition 7.
The other properties of and follow directly from Propositions 1 and 2 since is closed and convex according to Proposition 7.
Alternatively, we can also directly apply Proposition 3 to the second representation in (
19) and (
20) to derive the convexity and concavity of
and
, respectively. ☐
To describe a representation of the efficient frontier in the next theorem, we will use the exchange operator defined by .
Theorem 4. (Representation of the Efficient Frontier)
Assume that the risk measure satisfies (r2) in Assumption 2 and the utility function u satisfies (u2) in Assumption 3. Furthermore, assume that Assumption 4 holds for a set of admissible portfolios A with unit initial cost. Then, the efficient frontier has the following representationor equivalentlyMore specifically, settingandwe find that I and J are intervals and the representationholds, where and are continuous. Moreover, and are strictly increasing, bijective and inverse to each other, i.e., Proof. First, we show that the right-hand side of (
21) is a subset of the left-hand side. Let
. Since
and
necessarily
. Note that, in particular, (
22) holds. Using
, we get from (
20)
With (
27), we can select a sequence
such that
and
. By Assumption 4, either
or
is compact. Hence, without loss of generality, we may assume that
with
and
by the upper semicontinuity of
. Note that
would contradict (
28). Thus,
, so that
. Now, consider
. If
and
, then
contradicting that
is increasing. On the other hand, if
and
, then
contradicting the increasing property of
. Thus,
.
To conclude (
21), it remains to show that the left-hand side of (
21) is a subset of the right-hand side. Let
. Then, there exists some efficient
with
and
. This means both the supremum in (
27) and the infimum in (
28) are attained at
so that
and
. It follows that
Since, by Proposition 8,
and
are convex and concave functions, respectively, they are continuous in the interior of its domain. When
is not a single point, it is therefore a continuous curve except for the possible finite endpoints. By Proposition 8, if
contains
then
and
. Thus, if
has a finite left endpoint, we can represent it in the form
where
is in the interior of
. Thus, for any
,
so that
is right continuous. Similarly, if
has a finite right endpoint, then it is left continuous at this endpoint. Finally, representation (
22) implies that the projection of
onto the
r and
axises are intervals
I and
J, respectively, giving (
23) and (
24). Moreover, the representations in (
25) follow immediately. Furthermore, since
contains no vertical or horizontal lines (see Theorem 3),
and
are strictly increasing. Thus, both are injective, and surjectivity follows from (
23) and (
24). Finally, (
26) follows from (
22). ☐
3.4. Efficient Portfolios
We now turn to analyze how the corresponding efficient portfolios behave. Ideally, we would want that each point on the efficient trade-off frontier corresponds to exactly one portfolio. For this purpose, we need additional assumptions on risk measures and utility functions.
Theorem 5. (Efficient Portfolio Path) Consider a financial market as defined in Definition 1 and assume that A is a set of admissible portfolios with unit initial cost as in Definition 2. We also assume Assumption 4 holds and
- (c0)
there exists some with and finite.
In addition, suppose that one of the following conditions holds:
- (c1)
The risk measure satisfies conditions (r1) and (r2s) in Assumption 2 and the utility function satisfies conditions (u1) and (u2) in Assumption 3.
- (c2)
The risk measure satisfies conditions (r1) and (r2) in Assumption 2 and the utility function satisfies conditions (u1) and (u2s) in Assumption 3.
- (c3)
The risk measure satisfies conditions (r1), (r1n) and (r3s) in Assumption 2 and the utility function satisfies conditions (u1) and (u2) in Assumption 3.
Then, each point corresponds to a unique efficient portfolio and the mapping is continuous on (onesided continuous at the finite endpoint(s)). Moreover, efficient portfolios have the continuous representation and on intervals I defined in (23) and J defined in (24), respectively. Proof. Note that Assumption 4 and condition (c0) ensures that is nonempty.
We first show the uniqueness of the efficient portfolio. Suppose that portfolios
both correspond to
. We consider only the case when (c1) is satisfied (and the case when (c2) or (c3) is satisfied can be argued in a similar way). Then, by (r1) and (
21), we must have
and
. Note that because
A has unit initial cost,
. Since
A is convex,
. Conditions (r2s) and (u2) imply that
and due to the strict convexity of
by (r1),
, a contradiction. Thus, the efficient portfolio corresponding to
is unique and we denote it by
. The mapping
is well defined.
Next, we show the continuity of the mapping
. If
is a single point, there is nothing to prove. When
is not a single point by Theorem 4, we can represent all the efficient portfolios either as the image of the mapping
on
I or as the image of the mapping
on
J. Suppose that
is discontinuous at
. We first focus on the case when Assumption 4 (a) holds. Then, for a fixed positive number
, there exist sequences
(
if
or
if
) and such that
where
By Assumption 4 (a), we may assume without loss of generality that
converges to some portfolio
with
. Furthermore, by Proposition 8,
is concave, and by Theorem 4 continuous on
J. Taking limits in (
29) and using the upper semicontinuity of
yields
However, the uniqueness of the efficient portfolio (
30) implies that
, which is a contradiction. If Assumption 4 (b) holds, we can use the mapping
on the interval
I to obtain a similar contradiction. ☐
Remark 6. Interval is always bounded from below by 0 because the risk measure is always none negative, other than that, both and can be open, closed, half open and half closed. They can be finite or infinite. Although various situations are possible, we do have a precise characterization of their endpoints in the next proposition.
Proposition 9. Under the conditions of Theorem 5, defineandThen,and Proof. We start with (
31). Let
. It is clear that, for any
,
so that
is a lower bound for
, i.e.,
. For any
, there exist some finite
such that
By Assumption 4,
is compact. Thus,
is attained by some
with
. It follows that
defined in (
35) is nonempty and, therefore, compact by Assumption 4. Thus,
implying
and hence
. However, since
was arbitrary,
can be chosen close to
implying
and in conclusion
.
Note that, since
is always finite, we have
Thus, the proof of (
32) is parallel to that of (
31). Having determined
and
, we have
and
. Hence, representations (
33) and (
34) directly follow from the definitions of
and
, respectively. ☐
Corollary 2. Under the conditions of Theorem 5, we have
- (a)
if and only if , and if and only if .
- (b)
If then and .
- (c)
If then and .
- (d)
- (i)
If and then and .
- (ii)
If and then and .
- (iii)
If and then and .
- (iv)
If and then and .
Proof. Let . Then, for some by Theorem 4. Since is an increasing function, we have . Hence, and . Then, follows since is the identity mapping on I. The converse and the case for max can be proved analogously. This proves (a), (b) and (c). Moreover, (d)(i) directly follows from (b) and (c).
If , we show . In fact, if , then, for any natural number n, we can select such that and . By Assumption 4, we may assume without loss of generality that . Taking limits as , we conclude that and and both have to be equality. Thus, , a contradiction. This shows (d)(ii).
Analogously, one gets that implies , which shows (d)(iii) and (d)(iv). ☐
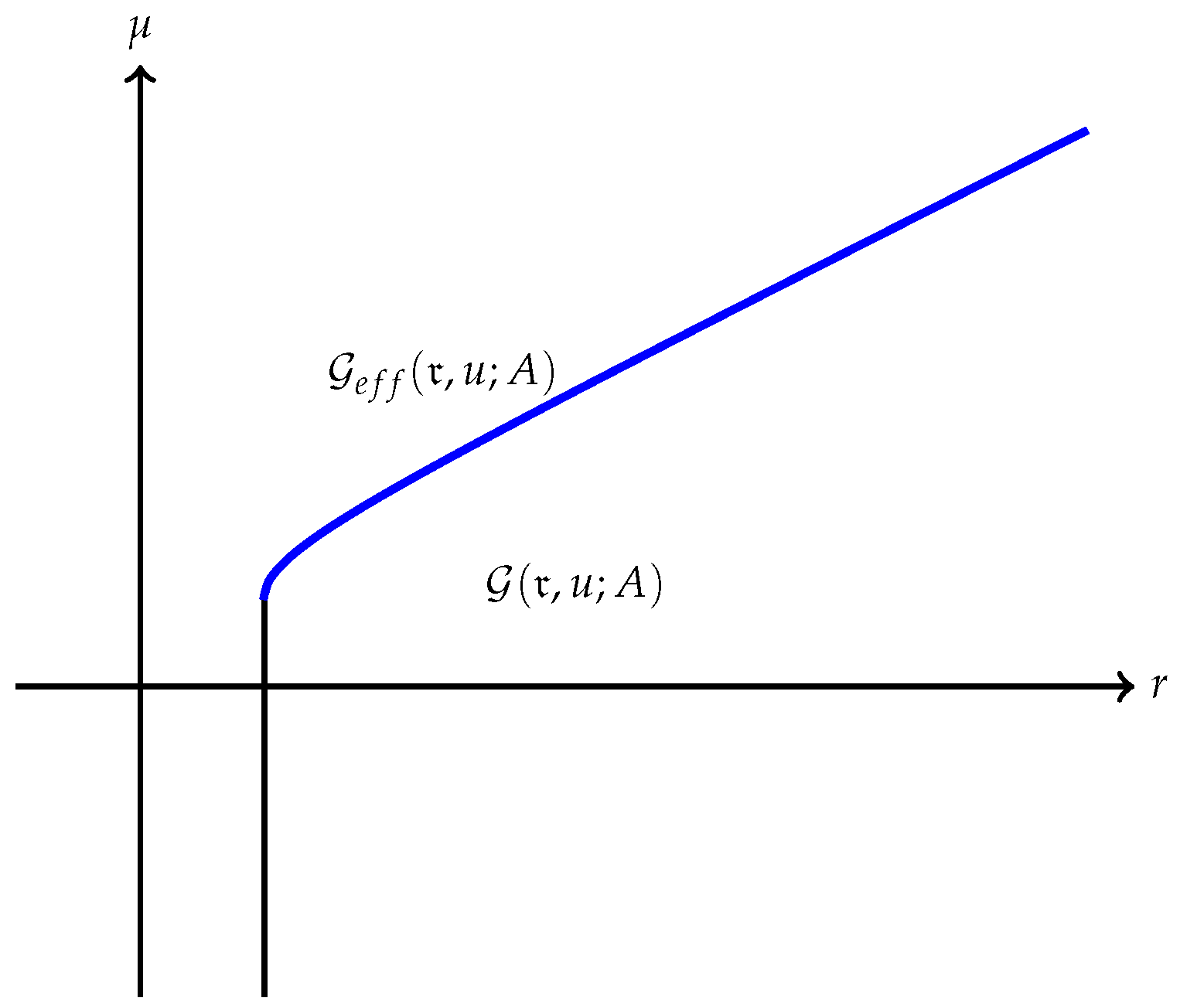
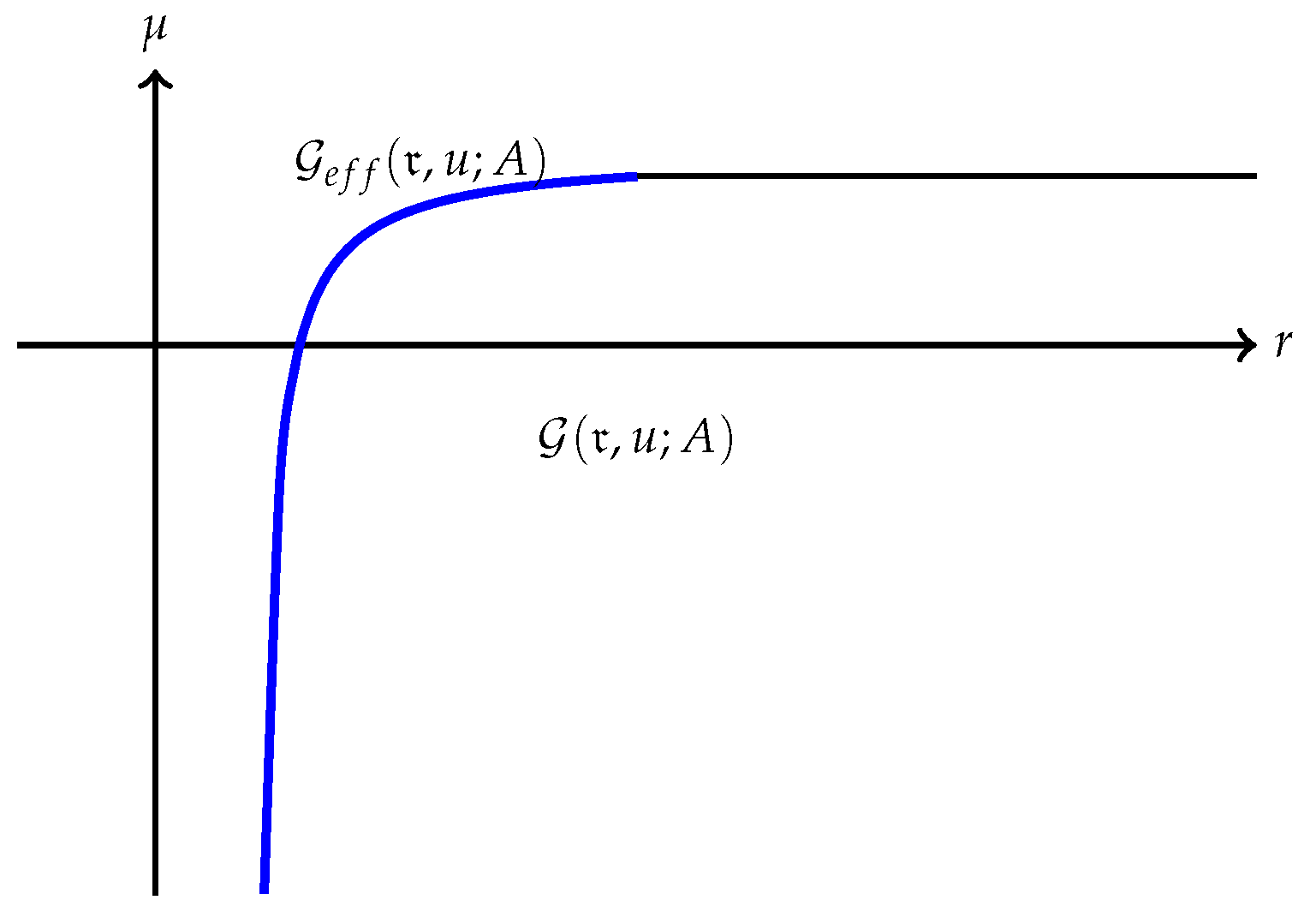
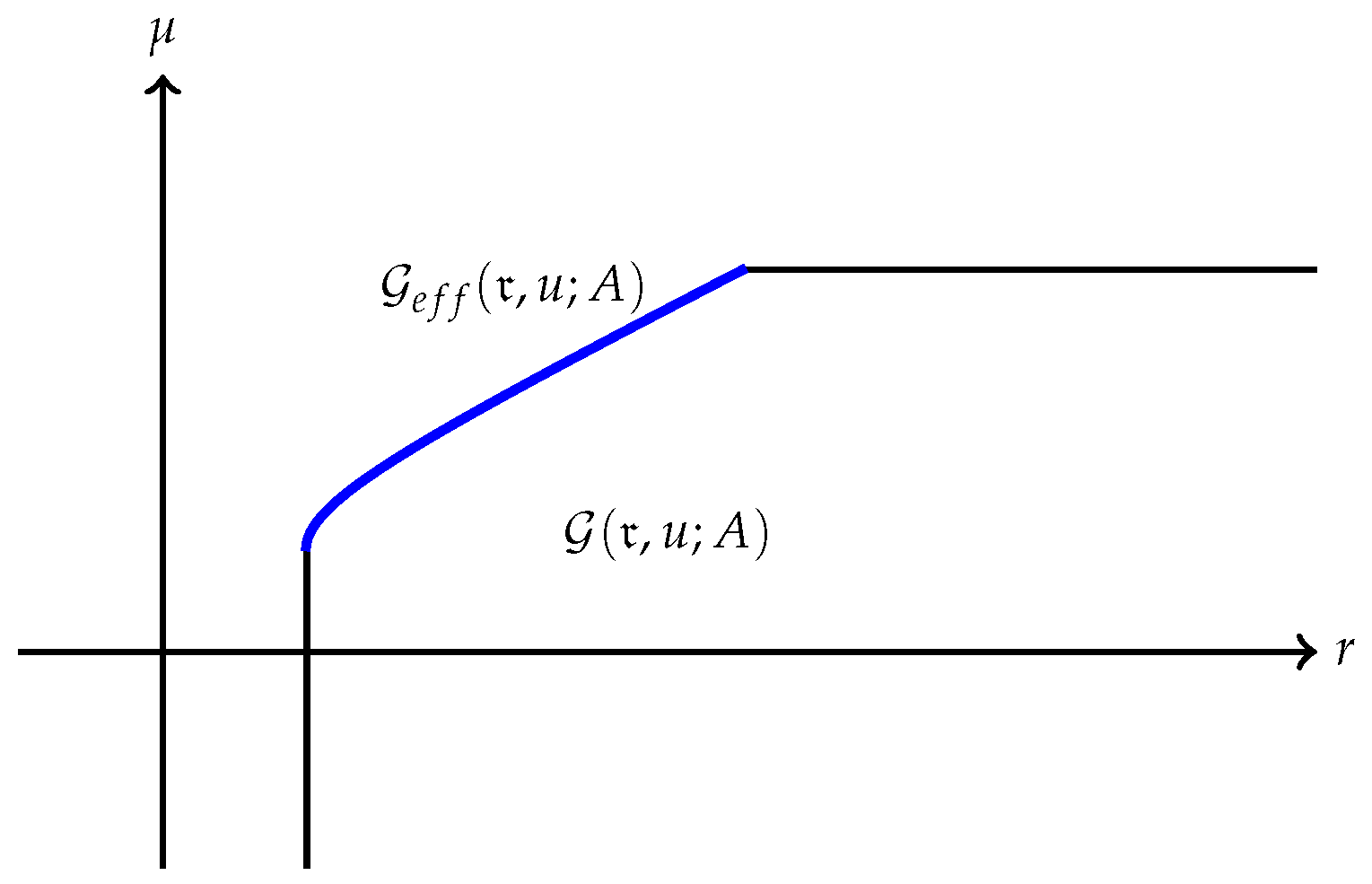
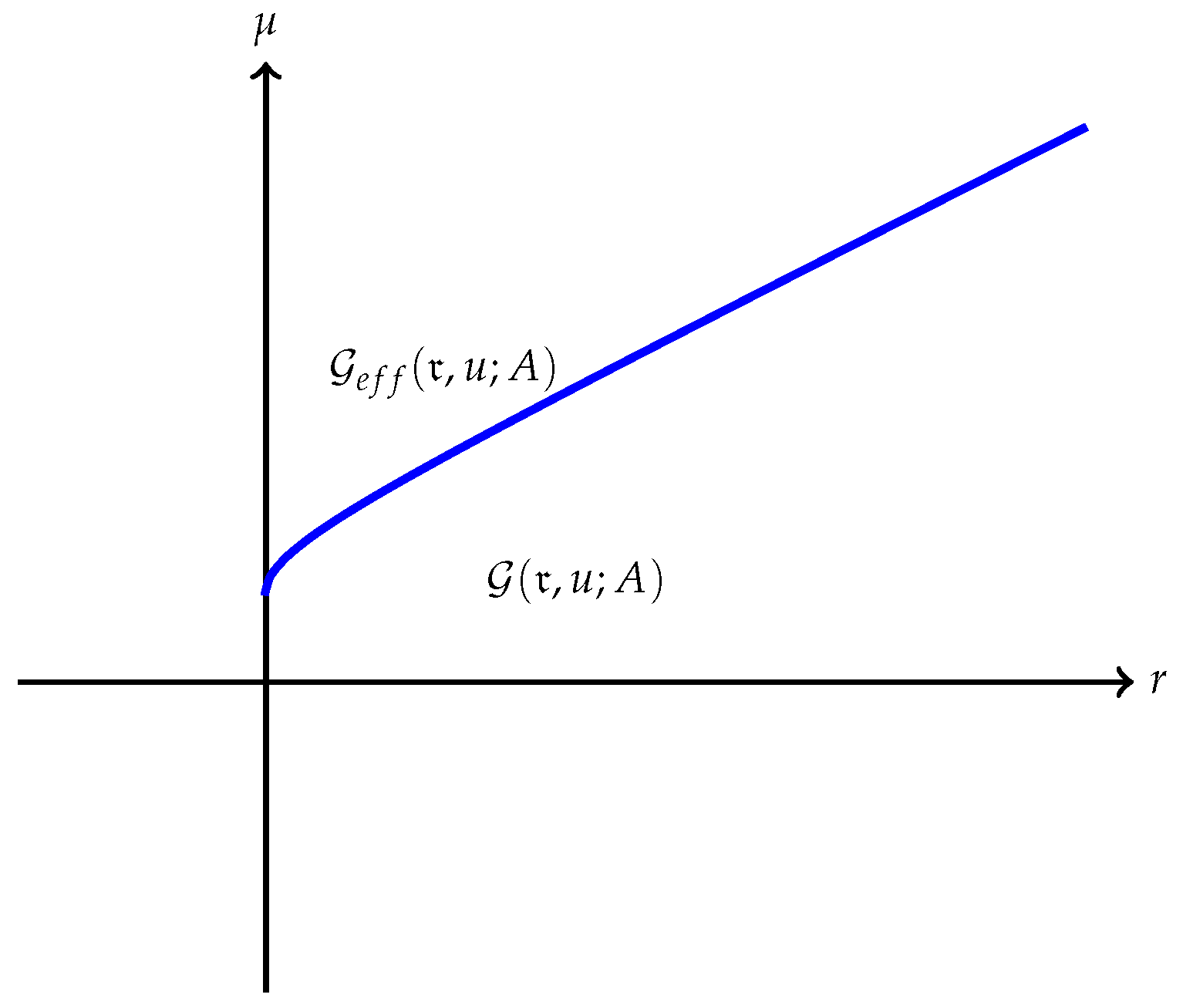
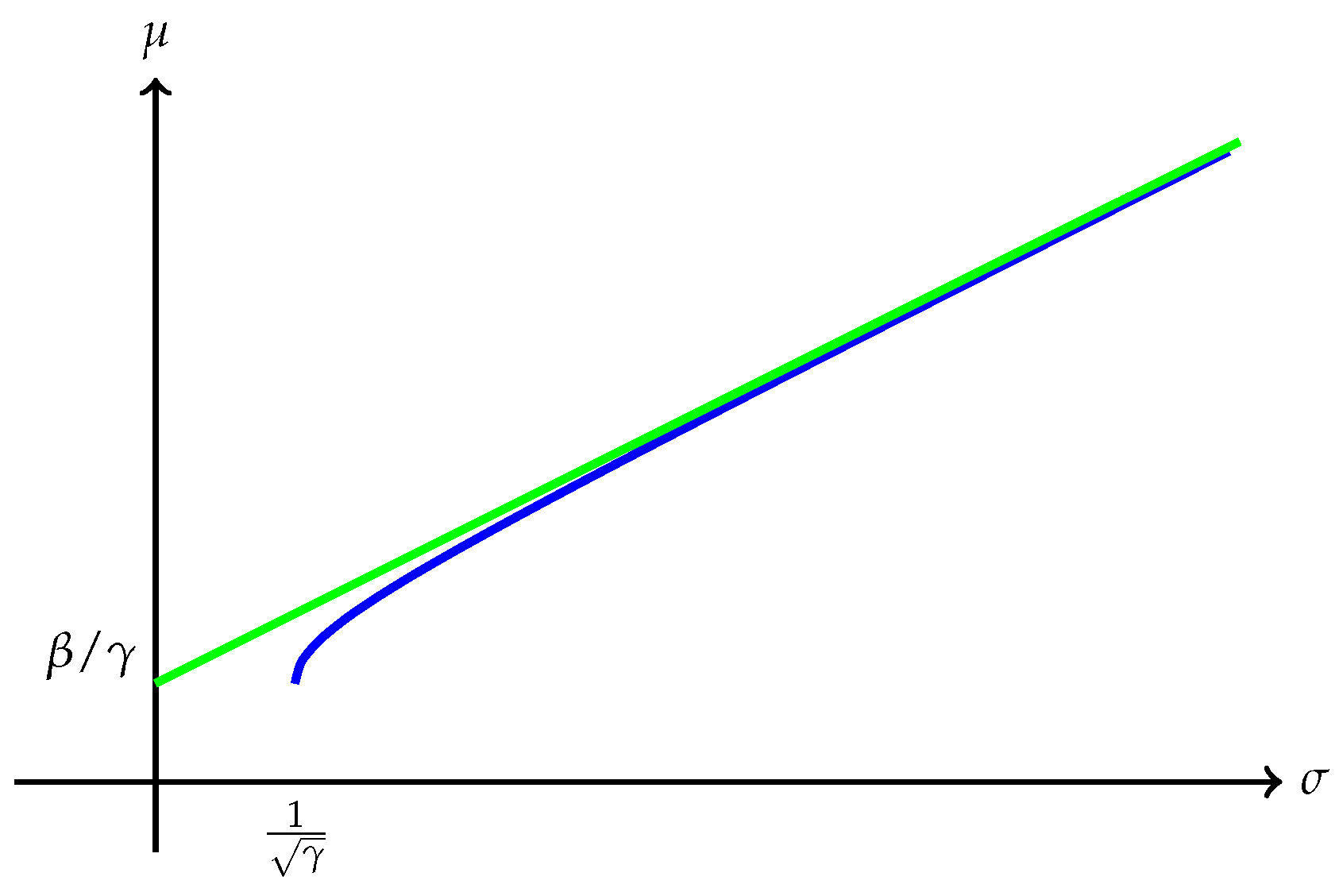
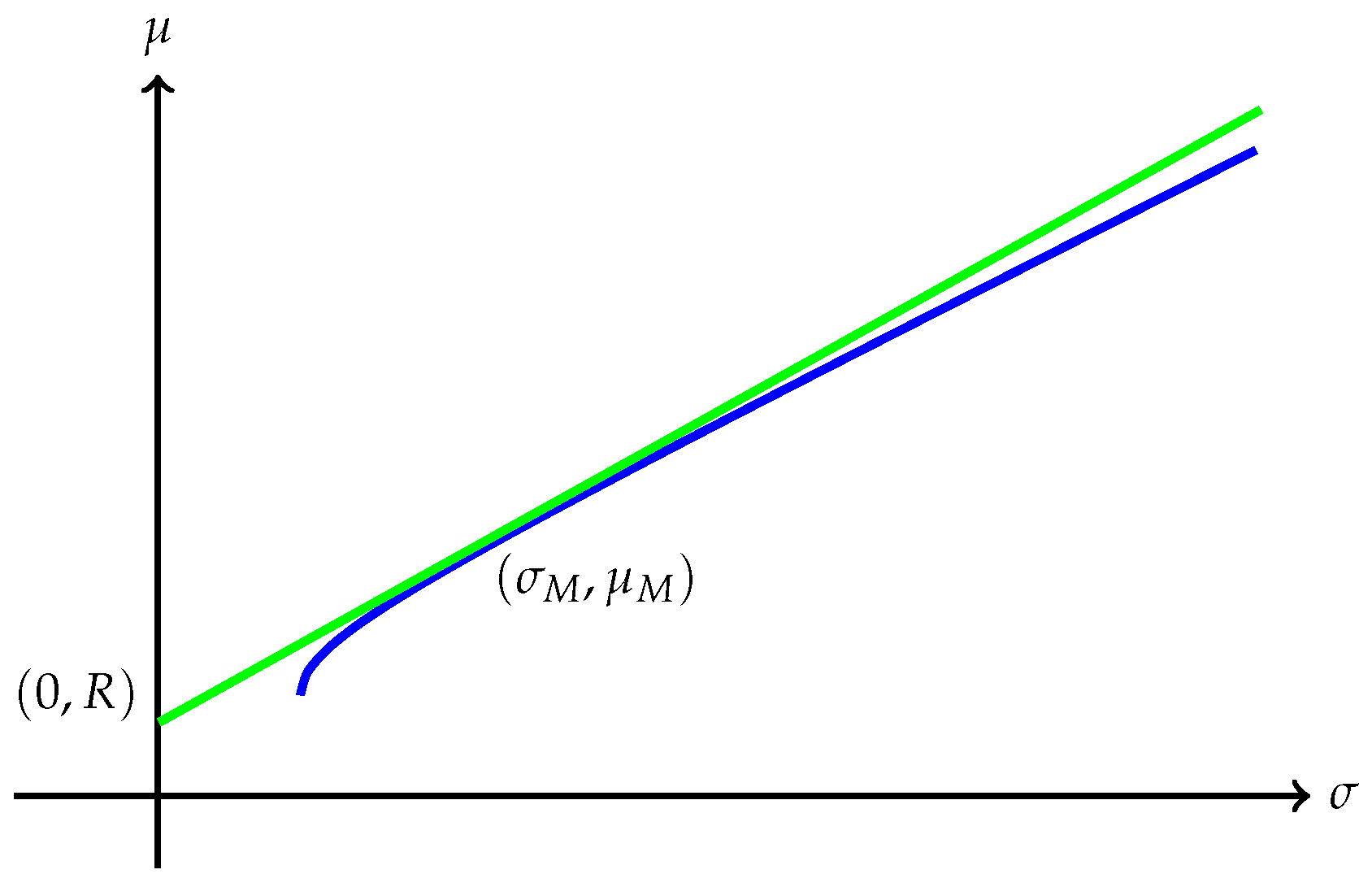
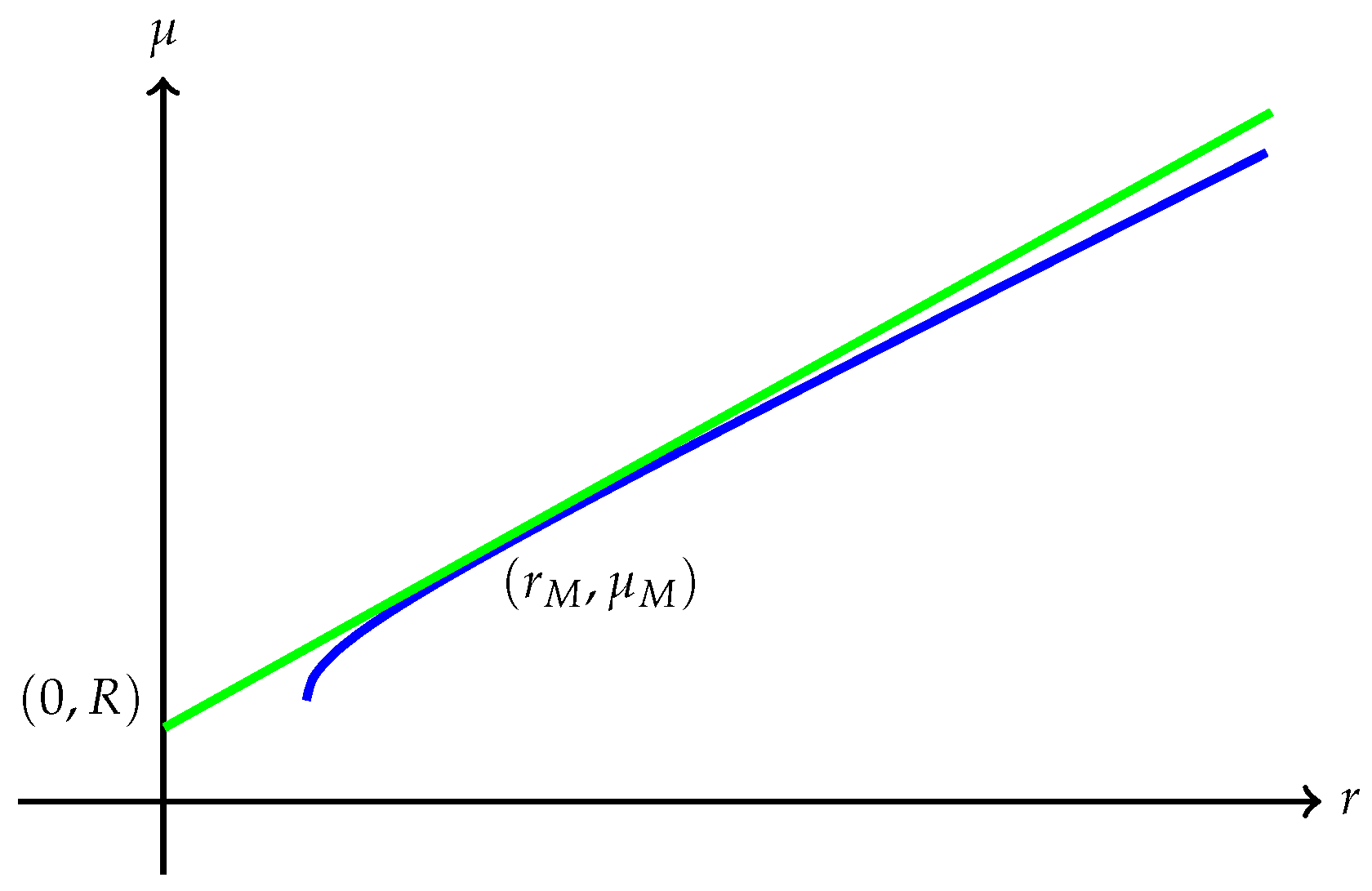
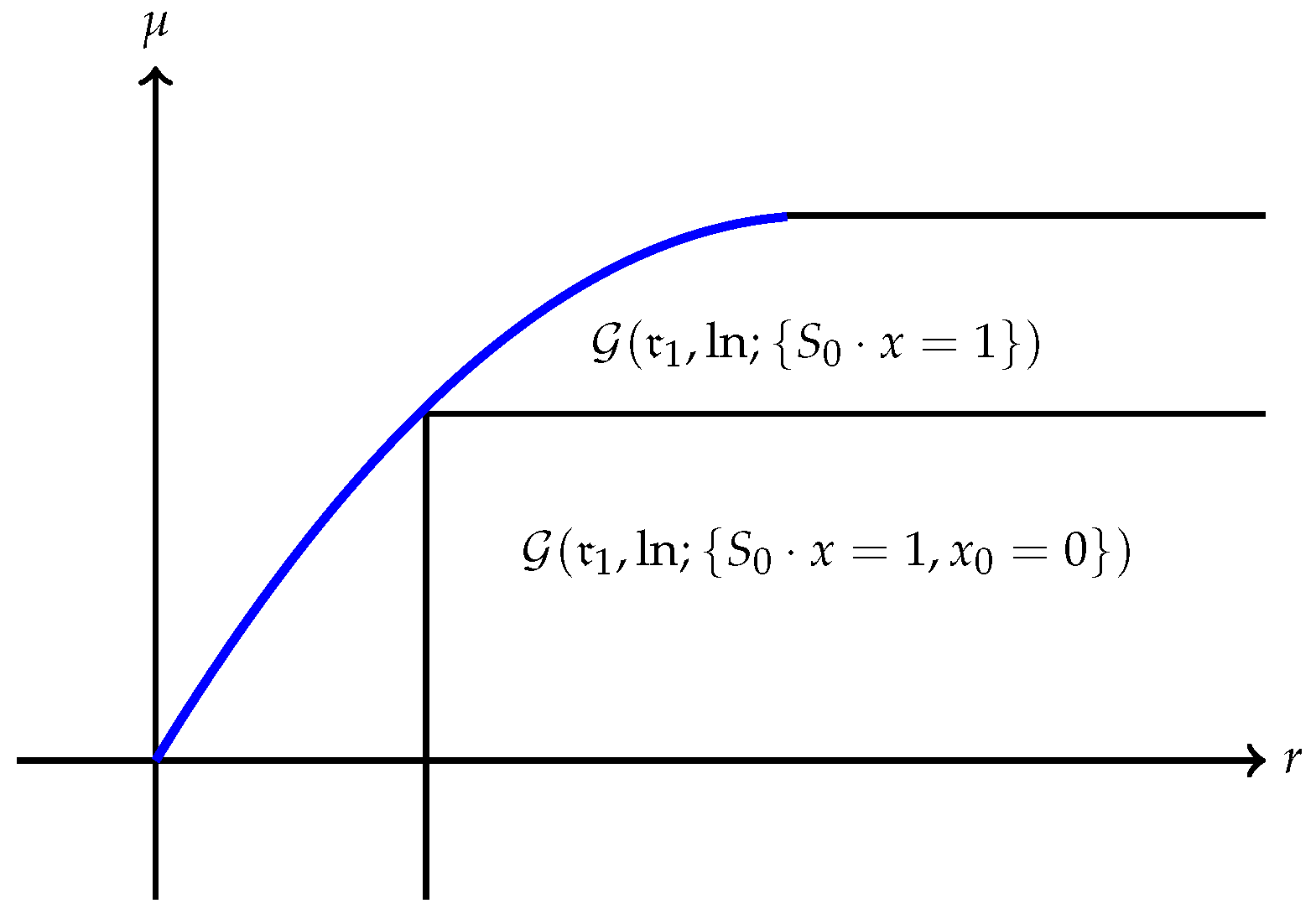
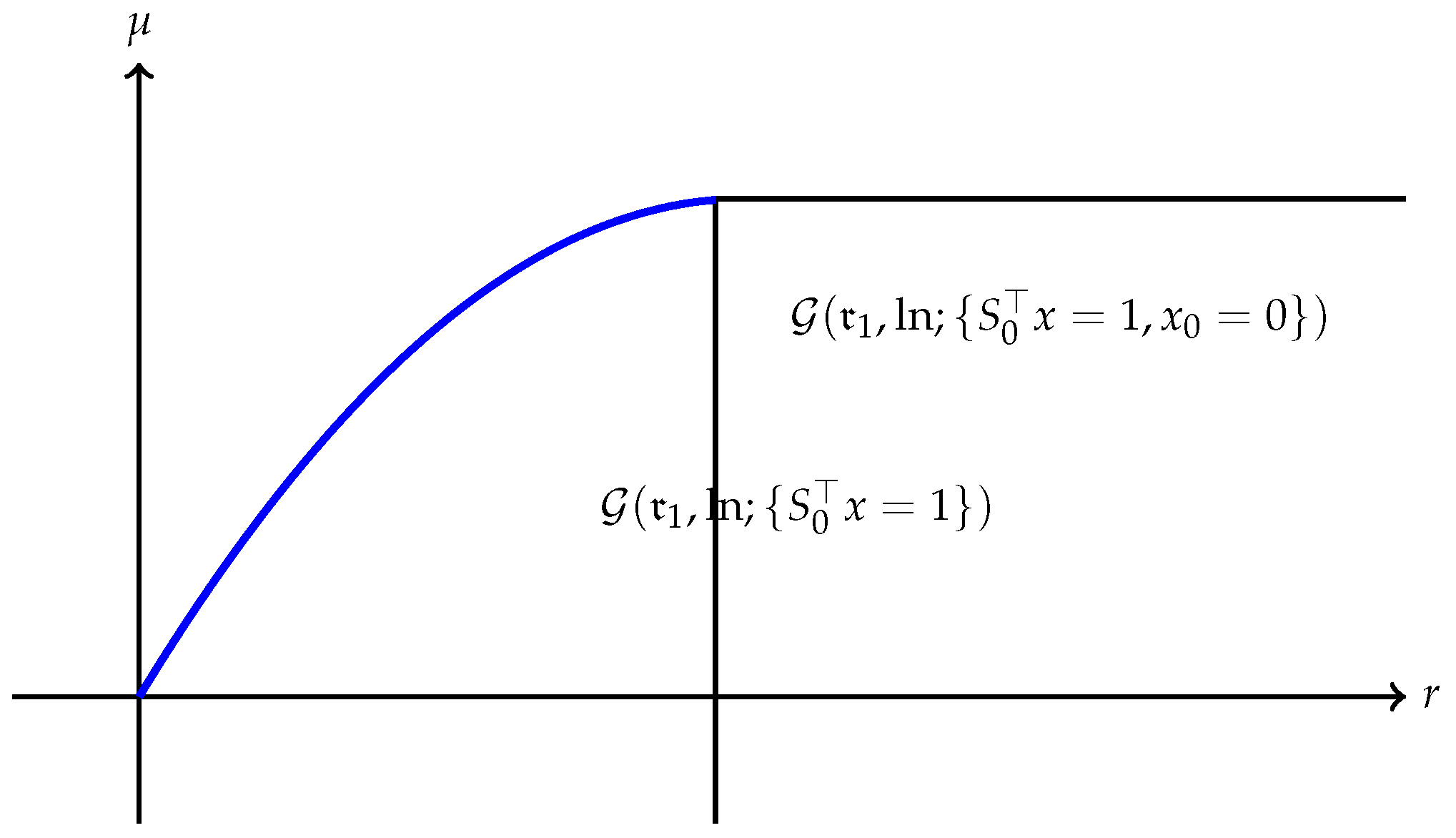
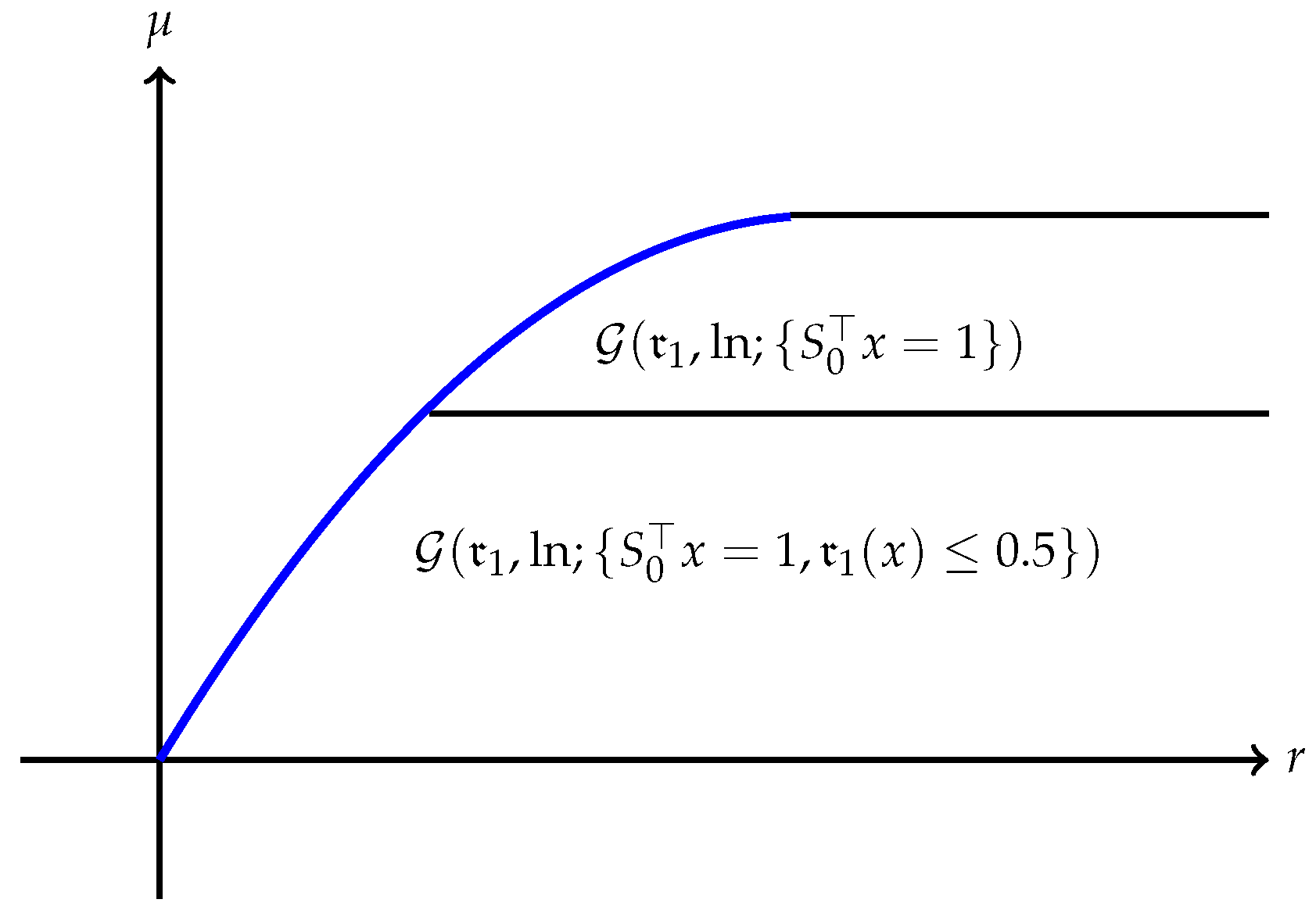
Remark 7. Several interesting cases when has finite endpoints are discussed below:
(a) The quantity is always finite and may be finite as well as illustrated in Figure 1. However, may also be , as Example 1 shows. A typical efficient frontier corresponding to this case is illustrated in Figure 2. (b) Suppose is finite and attained at an efficient portfolio . Under the conditions of Theorem 5, the portfolio is unique and independent of the risk measure. A graphic illustration is given in Figure 3. (c) Trade-off between utility and risk is thus implemented by portfolios that trace out a curve in the so-called leverage space introduced by Vince (2009). Note that the curve depends on the risk measure as well as the utility function u. This provides a method for systematically selecting portfolios in the leverage space to reduce risk exposure. (d) If, in addition, satisfies (r1n) in Assumption 2 and then , and (see Figure 4). (e) Unlike in (b), finite can also happen when the efficient frontier is unbounded (see Example 2).
Example 1. (for
)
Consider a portfolio problem with the log utility on a financial market that contains no bond and two risky assests (i.e., )The financial market (since the riskless asset is not involved in (36), it is irrelevant to the problem) is specified as follows: , is a random vector on the sample space with and a payoff matrix Note that, for instance with , this market has no nontrivial riskless portfolio. We use the risk measurewhich satisfies (r1), (r1n) and (r3s) and, therefore, Assumption 4(b) holds. Clearly, and finite. Notice that on the feasible set , i.e., . It follows that the risk measureattains a minimum at . Observing , we must have and Example 2. (for
and
)
Consider the same risk measure as in the previous example, but use instead the utility function . We analyzewhere the financial market is defined byon the sample space with . Again, on the feasible set , i.e., . The portfolio as a function of impliesAs , we can see that and . Hence, and . Notice that (40) with, e.g., , has an arbitrage portfolio , but the existence of an arbitrage seems to be necessary in constructing such an example. 5. Affine Efficient Frontier for Positive Homogeneous Risk Measure
The affine dependence of the efficient portfolio on the return
observed in the CAPM still holds when the standard deviation is replaced by the more general deviation measure (see
Rockafellar et al. (
2006)). In this section, we derive this affine structure using the general framework discussed in
Section 3 and provide a proof different from that of
Rockafellar et al. (
2006). Moreover, we provide a sufficient condition for the existence of the master fund in the one fund theorem generalizing condition
(see (
70)) for the existence of the market portfolio in the CAPM model. We also construct a counter-example showing that the two fund theorem (Theorem 7) fails in this setting. Let us consider a risk measure
that satisfies (r1), (r1n), (r2) and (r3) in Assumption 2 and the related problem of finding efficient portfolios becomes
Since, for
, there is an obvious solution
corresponding to
, we have
and
. In what follows, we will only consider
. Moreover, we note that for
satisfying the positive homogeneous property (r3) in Assumption 2,
implies that
In fact, for any
,
and (
76) follows. Now we can state and prove the theorem on affine dependence of the efficient portfolio on the return
.
Theorem 10. (Affine Efficient Frontier for Positive Homogeneous Risk Measures)
Assume that the risk measure satisfies assumptions (r1), (r1n), (r2) and (r3) in Assumption 2 with and Assumption 4 (b) holds. Furthermore, assumeThen, there exists an efficient portfolio corresponding to on the efficient frontier for problem (75) such that the efficient frontier for problem (75) in the risk-expected return space is a straight line that passes through the points (0,R) corresponding to a portfolio of pure bond and corresponding to the portfolio , respectively. Moreover, the straight line connecting and in the portfolio space, namely for ,represents a set of efficient portfolios for (75) that corresponds toin the risk-expected return space (see Definition 5 and (19)). Proof. The Lagrangian of this convex programming problem (
75) is
where
and
.
Condition (
78) implies that there exists some
, such that
. Hence, for any
, there exists a portfolio of the form
satisfying
because the matrix in (
82) is invertible. Thus, for any
, Assumption 4 (b) with
and condition (
78) ensure the existence of an optimal solution to problem (
75).
Denoting one of those solutions by
(may not be unique), we have
Fixing
, denote
. Then,
Since
is independent of
, we have
Substituting (
85) into (
84) we have
so that, for all
,
because, at the optimal solution
the constraint is binding. Using (r3), it follows from (
76) and (
86) that
Thus, we can write (
87) as
For
define the homotopy between
and
We can verify that
and
so that
On the other hand, it follows from assumptions (r1) and (r3) that
Thus, for any
x satisfying
and
it follows from (
89) that
For any
, letting
, we have
and hence
. Thus, by inequality (
93), we have
. On the other hand,
is an efficient portfolio implies that
yielding equality
In other words,
is an affine function in
. In addition, we conclude that points
on this efficient frontier correspond to efficient portfolios
as an affine mapping of the parameter
into the portfolio space showing (
79).
In addition, using
we can write (
94) as
That is to say, the efficient frontier of (
75) in the risk-expected return space is given by the parameterized straight line (
80). ☐
Corollary 3. In Theorem 10, if instead of (r3) the stronger condition (r3s) holds, then the portfolio constructed there is unique and, therefore, for each fixed , the efficient portfolio in (79) is unique. Proof. Apply Theorem 5 with condition (c3). ☐
Theorem 10 and Corollary 3 manifest a full generalization of Theorem 8 on the capital market pricing model to positive homogeneous risk measures. Note that the necessary conditions on the financial market in (
67) and (
78) are the same.
Remark 9. (a) Clearly, corresponds to the portfolio with . If , setting and we see that on the efficient frontier corresponds to a purely risky efficient portfolio of (75) Since belongs to the image of the affine mapping in (95), the family of efficient portfolios as described by the affine mapping in (95) contains both the pure bond and the portfolio that consists only of purely risky assets. In fact, we can represent the affine mapping in (95) as a parametrized line passing through and aswhich is a similar representation of the efficient portfolios as (79). The portfolio is called a master fund
in Rockafellar et al. (2006). When , it is the market portfolio
in the CAPM. For a general risk measure satisfying conditions (r1), (r1n), (r2) and (r3) in Assumption 2, the master funds are not necessarily unique. However, all master funds correspond to the same point in the risk-expected return space. (b) We can also consider problem (75) on the set of admissible portfolios of purely risky assets, namely . Then, similar to the relationship between the Markowitz efficient frontier and the capital market line, it follows from Theorem 10 thatas illustrated in Figure 7. (c) If , then the efficient portfolios in (79) are related to μ in a much simpler fashionThere is no master fund as observed in Rockafellar et al. (2006) in this case. In the language of Rockafellar et al. (2006), the portfolio is called a basic fund.
Thus, Theorem 10 recovers the results in Theorem 2 and Theorem 3 in Rockafellar et al. (2006) with a different proof and a weaker condition (condition (78) is weaker than (A2) on page 752 of Rockafellar et al.). However, Corollary 3 is a significant improvement yielding uniqueness in case (r3s) holds. This will help below when we derive a sufficient condition for the existence of a master fund, which is solely depending on the risk measure and the financial market. We see in Remark 9 that the existence of a master fund depends on whether or not . Below, we characterize this condition in terms of and its Fenchel conjugate , defined by .
Theorem 11. Under the conditions of Corollary 3, assuming that is differentiable at , a master fund exists if and only if .
Proof. Combining (
86) and (
88) and using the chain rule, we can see that
It follows that
is equivalent to
The last equality is because implies . ☐
Remark 10. We refer to Borwein and Vanderwerff (2009) for conditions ensuring the differentiability of in Theorem 11. In the CAPM model and . Thus, the master fund exists if and only ifwhich exactly recovers the condition in (70) for the existence of a market portfolio in the one fund theorem (cf. Theorem 9). In general, for a risk measure with (r1), (r1n) and (r3s), if is , then where is the Hessian of f at . Thus, a criterion for the existence of a master fund similar to (70) holds with Σ
replaced by . Another very useful case is . It is not hard to show that the conjugate of is . In fact, it follows from the Cauchy inequality that Thus, On the other hand, for any , defining , we have The maximum of the expression in (106) as a function of t is . It follows thatCombining (105) and (107), we arrive at . This example illustrates that using and its conjugate often helps. In fact, is differentiable everywhere except for the coordinate axises. However, is an indicator function on the closed set (see (Carr and Zhu forthcoming), Proposition 2.4.2)), whose derivative is 0 at any differentiable point and, therefore, is not useful for our purpose. Since the standard deviation satisfies Assumptions (r1), (r1n), (r2) and (r3s), the result above is a generalization of the relationship between the CAPM model and the Markowitz portfolio theory. We note that the standard deviation is not the only risk measure that satisfies these assumptions. For example, some forms of approximation to the expected drawdowns also satisfy these assumptions (cf.
Maier-Paape and Zhu (
2017)).
Theorem 10 and Corollary 3 are a full generalization of Theorem 8 on the CAPM and Theorem 11 is a generalization of the one fund theorem in Theorem 9. On the other hand, in
Rockafellar et al. (
2006), footnote 10, it has been noted that a similar generalization of the two fund theorem (Theorem 7) is not to be expected. We construct a concrete counter-example below.
Example 3. (Counter-example to a Generalized Two Fund Theorem)
Let us consider, for example,with .Choose all , so that is . Choose the payoff such that so that at the optimal solution. Finally, let us construct so that the optimal solution is not affine in μ.
We do so by constructing a convex set G with (interior of G) and then set for (boundary of G) and extend to be positive homogeneous. Then, (r1), (r1n), (r2) and (r3) are satisfied.
Now, let us specify G. Take the convex hull of the set and five other points. One point is and the other four points and D, are the corner points of a square that lies in the plane and has unit side length. To obtain that square, take the standard square with unit side length in , i.e., the square with corner points and rotate this square by 30 degrees counter clockwise in the -plane. Doing some calculation, one gets: Obviously for the optimal solution is with . For with small, we have (they lie on the ray through a point on the convex combination of C and ), and, for with large, we have (they lie on the ray through a point on the set . Therefore, cannot be affine in μ.
6. Growth Optimal and Leverage Space Portfolio
Growth portfolio theory is proposed by
Lintner (
1965) and is also related to the work of
Kelly (
1956). It is equivalent to maximizing the expected log utility:
Remark 11. Problem (109) is equivalent to The following theorem establishes the existence of the growth optimal portfolio as a corollary of our results in
Section 3. This theorem reconfirms previous results in
Hermes and Maier-Paape (
2017) with somewhat different conditions and a shorter proof.
Theorem 12. (Growth Optimal Portfolio)
Assume that the financial market of Definition 1 has no nontrivial riskless portfolio. Then, problem (109) has a unique optimal portfolio, which is often referred to as the growth optimal portfolio
and is denoted . To prove Theorem 12, we need the following lemma.
Lemma 2. Assume that the financial market of Definition 1 has no nontrivial riskless portfolio. Let u be a utility function satisfying (u3) in Assumption 3. Then, for any ,is compact (and possibly empty in some cases). Proof. Since, by Assumption 3,
u is upper semi-continuous, the set in (
111) is closed. Thus, we need only to show it is also bounded. Assume the contrary that there exists a sequence of portfolios
with
and
satisfying
Equation (
112) implies that
. Then, without loss of generality, we may assume
converges to
where
. Condition (u3) and (
113) for arbitrary
imply that, for each natural number
n,
Dividing (
112) and (
114) by
and taking limits as
we derive
and
. Thus, we have
and thus
is a nontrivial riskless portfolio, which is a contradiction. ☐
Proof of Theorem 12. We can verify that the utility function
satisfies conditions (u1), (u2s), (u3) and (u4). In addition,
because it contains
. Thus, Lemma 2 implies that problem (
109) has at least one solution and
is finite. By Proposition 6,
is strictly concave. Thus, problem (
109) has a unique optimal portfolio. ☐
Assuming one repeatedly invests in the identical one period financial market, the growth optimal portfolio has the nice property that it provides the fastest compounded growth of the capital. By Remark 7(b), it is independent of any risk measures. In the special case that all the risky assets are representing a certain gaming outcome,
is the Kelly allocation in
Kelly (
1956). However, the growth portfolio is seldomly used in investment practice for being too risky. The book (
MacLean et al.2009) provides an excellent collection of papers with chronological research on this subject. These observations motivated
Vince (
2009) to introduce his
leverage space portfolio to scale back from the growth optimal portfolio. Recently,
De Prado et al. (
2013);
Vince and Zhu (
2015) further introduce systematical methods to scale back from the growth optimal portfolio by, among other ideas, explicitly accounting for limiting a certain risk measure. The analysis in
Vince and Zhu (
2015) and
De Prado et al. (
2013) can be phrased as solving
where
is a risk measure that satisfies conditions (r1) and (r2). Alternatively, to derive the efficient frontier, we can also consider
Applying Proposition 8, Theorem 5 and Remark 7 to the set of admissible portfolios , we derive:
Theorem 13. (Leverage Space Portfolio and Risk Measure)
We assume that the financial market in Definition 1 has no nontrivial riskless portfolio and that the risk measure satisfies conditions (r1), (r1n) and (r2). Then, the problemhas a bounded efficient frontier that can be parameterized as follows:(a) problem (116) defines as a continuous increasing convex function, where and κ is the optimal growth portfolio. Moreover, problem (116) has a continuous path of unique solutions that maps the interval into a curve in the leverage portfolio space . Finally, , , and . (b) problem (117) defines as a continuous increasing concave function, where κ is the optimal growth portfolio. Moreover, problem (117) has a continuous path of unique solutions that maps the interval into a curve in the leverage portfolio space . Finally, , , and . Proof. Note that Assumption 4 (a) holds due to Lemma 2 and (c2) in Theorem 5 is also satisfied. Then, (a) follows straightforwardly from Theorem 5, where and are finite and attained and (b) follows from Theorem 5 with and . ☐
Remark 12. Theorem 13 relates the leverage portfolio space theory to the framework setup in Section 3. It becomes clear that each risk measure satisfying conditions (r1), (r1n) and (r2) generates a path in the leverage portfolio space connecting the portfolio of a pure riskless bond to the growth optimal portfolio. Theorem 13 also tells us that different risk measures usually correspond to different paths in the portfolio space. Many commonly used risk measures satisfy conditions (r1) and (r2). The curve provides a pathway to reduce risk exposure along the efficient frontier in the risk-expected log utility space. As observed in De Prado et al. (2013); Vince and Zhu (2015), when investments have only a finite time horizon, then there are additional interesting points along the path such as the inflection point and the point that maximizes the return/risk ratio. Both of which provide further landmarks for investors. Similar to the previous sections, we can also consider the related problem of using only portfolios involving risky assets, i.e.,
Theorem 14. (Existence of Solutions)
Suppose thatThen, problem (119) has a solution. Proof. As in the proof of Theorem 13, we can see that Assumption 4 (a) holds due to Lemma 2. Observe that, for
, we get from (
120) that
is finite. Then, we can directly apply Theorem 5 with
. ☐
With the help of Theorem 14, we can conclude that problem
generates an efficient frontier as well (comparable to the Markowitz bullet for
). However, due to the involvement of the log utility function, the relative location of efficient frontiers stemming from (
118) and (
121) may have several different configurations. The following is an example.
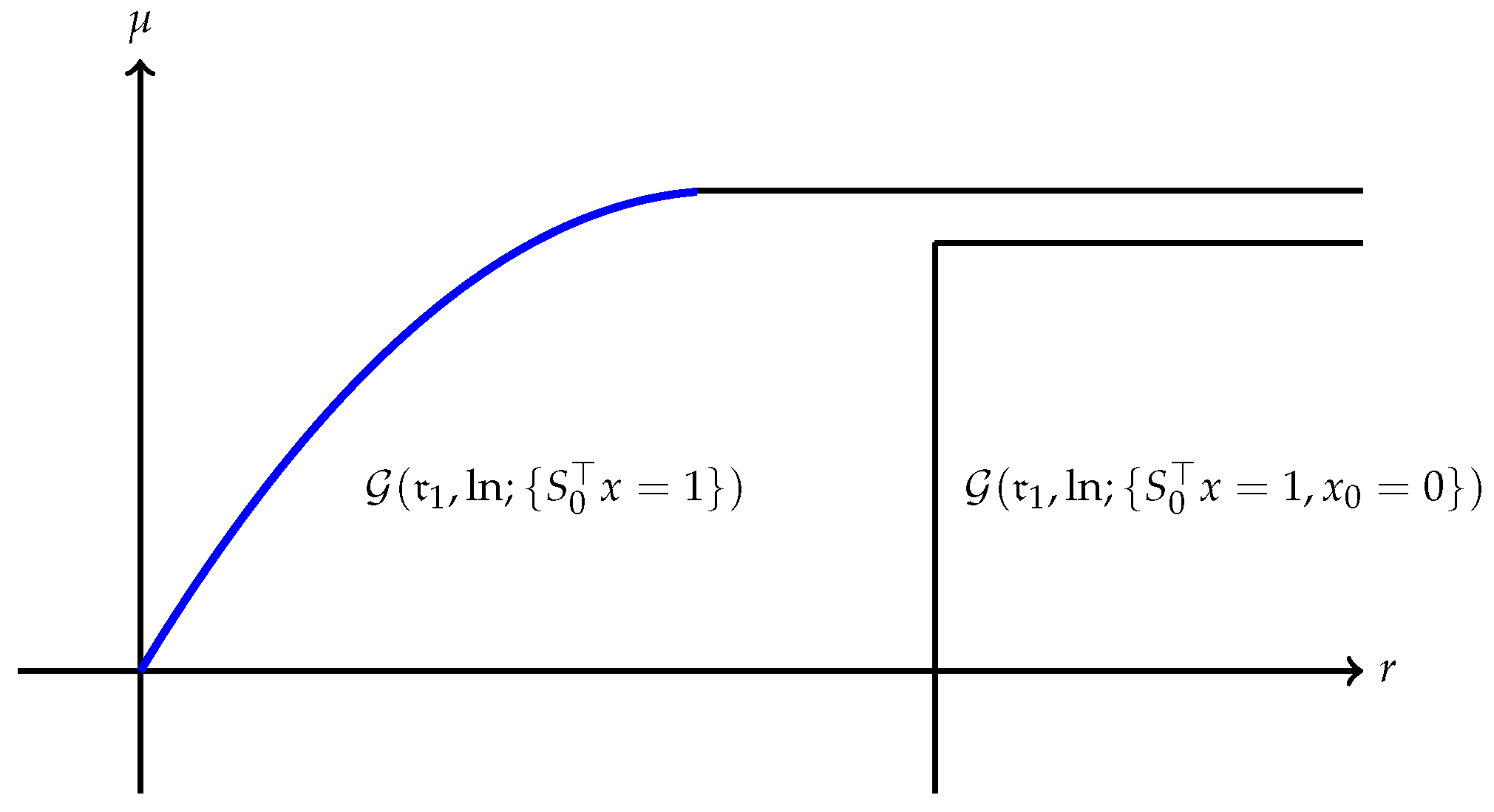
Example 4. Let . Consider a sample space with probability and and a financial market involving a riskless bond with and one risky asset specified by , and with so that . Use the risk measure (which is an approximation of the drawdown cf. Vince and Zhu (2015)). Then, it is easy to calculate that the efficient frontier corresponding to (118) iswhere . On the other hand, the efficient frontier stemming from (121) is a single point where . When , the two efficient frontiers corresponding to (118) and (121) have no common points (see Figure 8). However, when , (see Figure 9). In particular, when , coincides with the point on corresponding to the growth optimal portfolio as illustrated in Figure 10. In fact, a far more common restriction to the set of admissible portfolios are limits of risk. For this example, if, for instance, we restrict the risk by , then we will create a shared efficient frontier from (118) when is a priori restricted (see Figure 11). Remark 13. (Efficiency Index)
Although the growth optimal portfolio is usually not implemented as an investment strategy, the maximum utility corresponding to the growth optimal portfolio κ, empirically estimated using historical performance data, can be used as a measure to compare different investment strategies. This is proposed in Zhu (2007) and called the efficiency index. When the only risky asset is the payoff of a game with two outcomes following a given playing strategy, the efficiency coefficient coincides with Shannon’s information rate (see Kelly (1956); Shannon and Weaver (1949); Zhu (2007)). In this sense, the efficiency index gauges the useful information contained in the investment strategy it measures. 7. Conclusions
Following the pioneering idea of Markowitz to trade-off the expected return and standard deviation of a portfolio, we consider a general framework to efficiently trade-off between a concave expected utility and a convex risk measure for portfolios. Under reasonable assumptions, we show that (i) the efficient frontier in such a trade-off is a convex curve in the expected utility-risk space, (ii) the optimal portfolio corresponding to each level of the expected utility is unique and (iii) the optimal portfolios continuously depend on the level of the expected utility. Moreover, we provide an alternative treatment and enhancement of the results in
Rockafellar et al. (
2006) showing that the one fund theorem (Theorem 9) holds in the trade-off between a deviation measure and the expected return (Theorem 11) and construct a counter-example illustrating that the two fund theorem (Theorem 7) fails in such a general setting. Furthermore, the efficiency curve in the leverage space is supposedly an economic way to scale back risk from the growth optimal portfolio (Theorem 13).
This general framework unifies a group of well known portfolio theories. They are Markowitz portfolio theory, capital asset pricing model, the growth optimal portfolio theory, and the leverage portfolio theory. It also extends these portfolio theories to more general settings.
The new framework also leads to many questions of practical significance worthy of further explorations. For example, quantities related to portfolio theories such as the Sharpe ratio and efficiency index can be used to measure investment performances. What other performance measurements can be derived using the general framework in
Section 3? Portfolio theory can also inform us about pricing mechanisms such as those discussed in the capital asset pricing model and the fundamental theorem of asset pricing (see (
Carr and Zhu forthcoming, Section 2.3). What additional pricing tools can be derived from our general framework?
Clearly, for the purpose of applications, we need to focus on certain special cases. Drawdown related risk measures coupled with the log utility attracts much attention in practice. In Part II of this series
Maier-Paape and Zhu (
2017), several drawdown related risk measures are constructed and analyzed.