Abstract
We introduce a multistep-ahead forecasting methodology that combines empirical mode decomposition (EMD) and support vector regression (SVR). This methodology is based on the idea that the forecasting task is simplified by using as input for SVR the time series decomposed with EMD. The outcomes of this methodology are compared with benchmark models commonly used in the literature. The results demonstrate that the combination of EMD and SVR can outperform benchmark models significantly, predicting the Standard & Poor’s 500 Index from 30 s to 25 min ahead. The high-frequency components better forecast short-term horizons, whereas the low-frequency components better forecast long-term horizons.
1. Introduction
Forecasting financial data is a challenging task. Future prices are difficult to predict because market imperfections are quickly discovered, exploited and corrected by market participants. Nonetheless, forecasting financial time series is a very active research area with applications spanning from trading strategies to risk management (Alexander 2001; Aymanns et al. 2016; Caccioli et al. 2016; Clements et al. 2004; Kim 2003; Varga-Haszonits et al. 2016).
There are a vast number of methodologies used for forecasting purposes (Brooks 2014). Over the last few decades, efforts to improve forecasting techniques have also included the use of empirical mode decomposition (EMD) (Huang et al. 1998). The EMD method decomposes the signal into a finite set of nearly orthogonal oscillating components, called intrinsic mode functions (IMFs). IMFs have characteristic time-scales of oscillations defined by the local maxima and the local minima of the data; they are retrieved by the data itself without imposing any functional form.
There are two major challenges associated with forecasting financial time series: (1) nonstationarity (i.e., the statistical properties of the time series change with time); (2) multi-scaling (i.e., the statistical properties of the time series change with time-horizons) (Di Matteo 2007; Nava et al. 2016a, 2016b). EMD brings two elements that directly address both issues. First, the IMF components are locally stationary, oscillating around zero. Indeed, we can describe the EMD as a highly adaptable and granular detrending procedure where, starting from high frequencies, the local trend of each IMF component is contained within the cycle of the next component. Second, each IMF is associated with a characteristic oscillation period, and, as such, each component is associated with a characteristic time-scale and -horizon. The general idea behind the use of EMD for forecasting purposes is therefore that by dividing a signal into IMF components, the residual component can reduce the complexity of the time series, separating trends and oscillations at different scales, improving in this way the forecasting accuracy at specific time-horizons.
The application of EMD to forecasting has been already explored in the literature. For instance, Yu et al. demonstrated in Yu et al. (2008) that this timescale decomposition is indeed an efficient methodology following the “divide-and-conquer” philosophy. Such a divide-and-conquer philosophy has been used in different areas: crude oil spot prices (Yu et al. 2008), foreign exchange rates (Lin et al. 2012), market stock indices (Cheng and Wei 2014), wind speed (Wang et al. 2014), computer sales (Lu and Shao 2012), and tourism demand (Chen et al. 2012), to mention a few. For instance, a hybrid EMD combined with an artificial neural network (ANN) approach was used by Liu et al. (2012) to forecast one-, two- and three-steps-ahead wind-speed time series. Different forecasting powers from high- to low-frequency and long-term trend components were investigated by Zeng and Qu (2014), who showed the forecasting effectiveness of EMD combined with ANNs for the Baltic Dry Index (BDI). We note that in the literature, often the EMD is applied to the whole dataset before “forecasting” (Chen et al. 2012; Cheng and Wei 2014; Lin et al. 2012; Lu and Shao 2012; Wang et al. 2014; Yu et al. 2008). This implies that the future forecasted data are used to construct the EMD, which therefore contains future information not obtainable in real forecasting scenarios. This could explain the good performance of some of the proposed EMD-based models.
In this paper we combine EMD and support vector regression (SVR) (Christianini and Shawe-Taylor 2000; Kim 2003; Smola and Schölkopf 2004; Suykens et al. 2002; Tay and Cao 2001) techniques. The main purpose of the paper is to demonstrate that EMD can improve forecasting and, in particular, that the high- and low-frequency components are associated with different forecasting powers for short and long time-horizons, respectively. We have chosen SVR as a forecasting tool because it is a general nonlinear regression methodology that has been proved to be effective for the prediction of financial time series, and it is particularly suited to handle multiple inputs. We have tested several ways of using the EMD method combined with both direct and recursive SVR forecasting strategies (Kazem et al. 2013; Lu et al. 2009; Tay and Cao 2001). We have used both univariate and multivariate settings, and we have used both single EMD components and combinations of them. Our main finding is the identification of the best EMD–SVR strategies among various combinations. We report results for the prediction of the S&P 500 from 30 s to 25 min ahead, showing that the EMD–SVR methodology significantly outperforms other forecasting methodologies, including SVR, on the original time series. In this paper, we have divided the dataset into training and testing sets and have applied EMD on the training set only, forecasting the testing set without using information from it.
This paper is organized as follows. Performances of the EMD–SVR methodology for the prediction of the Standard & Poor’s 500 (S&P) indext up to 25 min ahead are reported in Section 2. Discussions of the outcomes are provided in Section 3. The methodology used to combine EMD and SVR, originally proposed in this paper, is outlined in Section 4. Conclusions are drawn in Section 5.
2. Results: Forecasting the S&P 500 Index up to 25 min Ahead
2.1. Data
The combination of EMD and SVR for financial time series forecasting proposed in this paper (see Section 4) has been tested on the S&P 500 index. The dataset consisted of 128 days of intraday data sampled at 30 s intervals. The forecasting was performed independently for each single day using a training sample of 500 prices (4 h and 10 min) and forecasting the following steps ahead (25 min). We note that the trading day for the S&P 500 index is between 08:30 and 15:15, of which we excluded the first 5 min. We therefore forecasted the period 12:45–13:10. The choice of this forecasting interval was an incidental consequence of the procedure. We also tested some later intervals, finding comparable outcomes. We note that the purpose of this paper is not to produce a methodology for trading but to demonstrate that by EMD, one can obtain better forecasting results with respect to benchmark methods. The problem of the size of the training set is common across all methodologies, and, to avoid trading only in the second half of the day, one can adopt several tricks. However, this is beyond the scope of this paper. The EMD construction and the SVM calibration were performed exclusively using the training sample. Forecasting results were computed exclusively for the following testing sample. We note that in the literature, EMD is instead sometimes applied to the whole dataset, including the testing part (see, e.g., Chen et al. 2012; Cheng and Wei 2014; Lin et al. 2012; Lu and Shao 2012; Wang et al. 2014; Yu et al. 2008). The inclusion of (future) testing data in the forecasting methodology is clearly wrong, providing meaningless “forecasts”.
2.2. Intraday Forecasting: Example of a Single Time Series for 7 August 2014
For the sake of clarity, we first exemplify our forecasting methodology and calibration procedure for one randomly chosen day of the S&P 500 index (7 August 2014), keeping in mind that we performed the same analysis on all the remaining time series all for the other days. The day was chosen at random and has no special significance. It appeared to be an “ordinary” trading day. Figure 1 illustrates the behaviors of the price during this particular day.
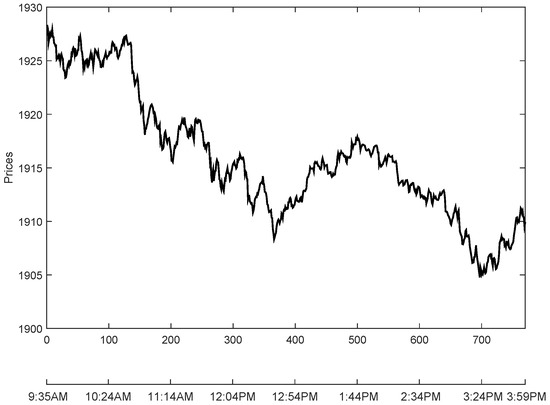
Figure 1.
Values of the S&P 500 index for the trading day, 7 August 2014. The first 5 min of the trading day are not included.
The first step of the forecasting methodology is the application of the EMD to the training data (see Section 4.1, Equation (1)). In this particular case, we obtained IMF components and one residue by using the stopping criteria of Rilling et al. (2003) that takes into consideration the local mean and the local amplitude of the envelope functions. The second step is to create an input vector to predict the h-steps-ahead value of the index from the m previous values , ... , for each of the five () IMF components and the residue (see Equations (2), (3) and (5)–(9)).
We tested three input vectors of different lengths m, as follows:
- lagged values of each IMF and the residue.
- lagged values of each IMF and the residue.
- , where p denotes the number of autoregressive terms and d is the number of differentiations of an autoregressive integrated moving average (ARIMA) model that was fitted to each of the IMFs and to the residue. For the implementation of the ARIMA models, the software package auto.arima function available in R was used (Hyndman and Khandakar 2008) (see Appendix A).
We applied SVR with a Gaussian kernel and performed a grid search to find the optimal parameters, which were the following: regularization parameter C, the Gaussian kernel’s bandwidth and the precision parameter . The grid search was implemented within the following ranges of parameters: , , and (Christianini and Shawe-Taylor 2000; Kim 2003; Smola and Schölkopf 2004; Suykens et al. 2002; Tay and Cao 2001). A sixfold moving validation was used in each iteration of the grid search to avoid overfitting. For this SVR, we used the LIBSVM software system (Available at https://www.csie.ntu.edu.tw/~cjlin/libsvm).
We describe separately the results for the univariate and multivariate EMD–SVR frameworks.
2.2.1. Univariate EMD–SVR Results
The univariate EMD–SVR approach was implemented following the methodology described in Section 4.5.1 (Equations (4)–(8)) using both the recursive and the direct strategies. For the recursive strategy, we forecasted all steps ahead, but we only report here eight values for . For the direct strategy, we trained eight models corresponding to . We computed results for three input vectors of lengths , and , but for this example, we only report the results for the input vector, , which produced the best outcomes. We note that in several of the studied cases, . The autoregressive terms, p, and the number of differentiations, d, estimated with an ARIMA model applied to each IMF are reported in Table 1.

Table 1.
Order of the autoregressive integrated moving average (ARIMA) models fitted to each intrinsic mode function (IMF) and to the residue. The number of lagged values was used to construct the input vectors for the empirical mode decomposition–support vector regression (EMD–SVR) models.
In Figure 2, we compare the forecasted IMFs using the recursive and the direct strategies. Figure 2a illustrates the results of the first IMF. Figure 2b illustrates forecasting results for the second IMF, and so on, until Figure 2f, which shows the forecasted residue. The black line in each plot represents the input IMF, the blue line represents the recursive-strategy forecasting and the red line is the direct-strategy forecasting. We observe that both strategies captured some of the oscillating patterns of the IMFs.
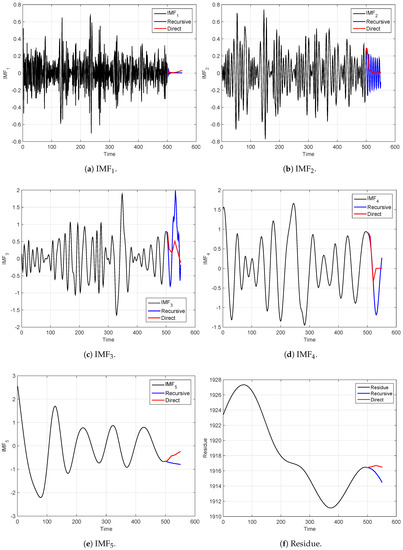
Figure 2.
True (black lines) and forecasted (red and blue lines) intrinsic mode functions (IMFs) and residue extracted from the S&P 500 index for 7 August 2014 shown in Figure 1. The forecasted values were obtained using the univariate empirical mode decomposition–support vector regression (EMD–SVR) model, using both the recursive (blue line) and the direct strategies (red line). We note that the black lines end when forecasting begins. EMD was performed on the training set only.
The forecasted values of the IMFs and the residue have been used to generate a coarse-to-fine reconstruction, which generated six forecasting models. The results of these models are illustrated in Figure 3. The first coarse model only considered the residue, which is denoted as R; see Figure 3a. The second model used the forecasting of the residue and the fifth IMF (); see Figure 3b. We continued this process until we included all the IMFs (; see Figure 3f.
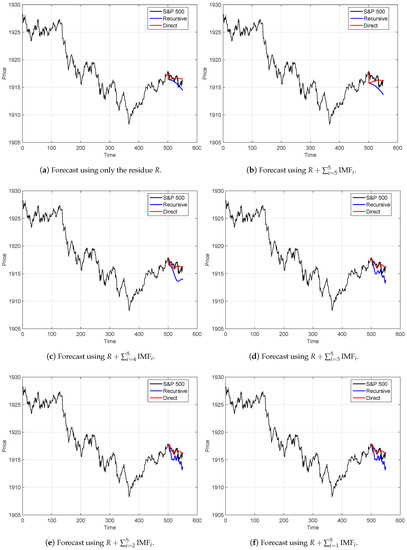
Figure 3.
True and forecasted values for the S&P 500 index for 7 August 2014 shown in Figure 1. Forecasted values were obtained using partial reconstructions of the univariate empirical mode decomposition–support vector regression (EMD–SVR) model (Equations (5)–(8)), both the recursive (blue line) and the direct (red line) strategies. We note that the EMD was performed on the training set only (i.e., using only data before beginning of forecasting).
2.2.2. Multivariate EMD–SVR Results
The multivariate EMD–SVR approach was implemented following the methodology described in Section 4.5.2 using the direct strategy (Equation (9)). We tested the three input vectors with , and , but we only report the results for the input vector , which produced the best results. As before, we used the forecast horizons .
A forecasting example of the multivariate EMD–SVR models for 7 August 2014 is reported in Figure 4. The black line represents the S&P 500 index values, whereas the red line represents the forecasted values from to steps ahead.
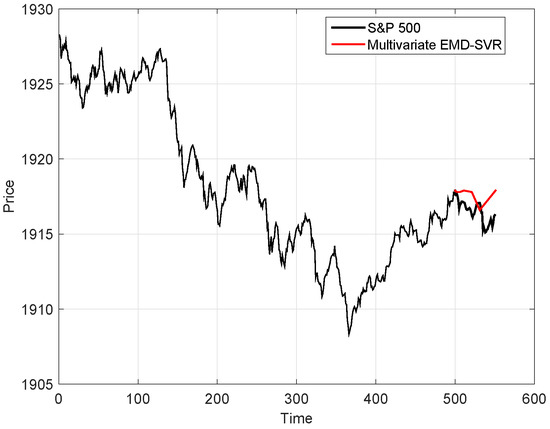
Figure 4.
True (black line) and forecasted (red line) values for the S&P 500 index. Forecasted values were obtained using the multivariate empirical mode decomposition–support vector regression (EMD–SVR) model (Equation (9)). The true S&P 500 index values are the same as in Figure 1 and Figure 3. We note that the EMD was performed on the training set only (i.e., using only data before beginning of forecasting).
2.3. Intraday Forecasting: Analysis of the Complete Dataset
We performed the same intraday forecasting described in the previous two sub-sections for each of the 128 daily time series of the S&P 500 index. In order to fairly compare the forecasting capabilities of the different methodologies, each time series was decomposed into five IMFs and a residue.
To estimate the performance of the proposed models at each forecast horizon , we calculated the mean absolute error (MAE) (see Section 4.7, Equation (10)) over the time series. The proposed EMD–SVR models are compared with other commonly used benchmark models, which were applied to the initial time series (without the EMD). These benchmark models were the following:
- Naive model, which keeps constant the last observed value in the time series.
- ARIMA model.
- SVR model on the original (nondecomposed) time series, with the same setting as for the EMD–SVR models (i.e., Gaussian kernel; three-dimensional grid to look for the optimal parameters: , , and ; and a sixfold moving validation used in each iteration of the grid search for parameter tuning).
Table 2 reports the comparison between the MAEs of the EMD–SVR models and the benchmarks. The table refers to the case using , which returned the best results. For each forecast horizon, the smallest error across the compared models is set in boldface. The cases for vector of lengths and are reported in Table A1 and Table A2 in the Appendix. Across the three tables (Table 2, Table A1 and Table A2), the smallest errors are indicated with a dagger (†).

Table 2.
Mean and standard deviation (std) of mean absolute error (MAE) computed for all the 128 days for all the forecasting models: Naive, ARIMA, direct and recursive SVR on the original data, direct and recursive univariate and multivariate EMD-SVR with input vector lagged values, the same input vector as the ARIMA model. Small MAE indicate better forecasting. The smallest MAE of each forecast horizon is set in boldface. The values marked with a dagger (†) indicate the smallest MAE of each horizon across all the models with different input vector m (see Table A1 and Table A2).
Figure 5 reports the mean MAE versus the forecast horizon for the EMD–SVR models, as well as the benchmarks for . It is a graphical representation of Table 2. Cases for and are reported in Figure A1 and Figure A2 in the Appendix.
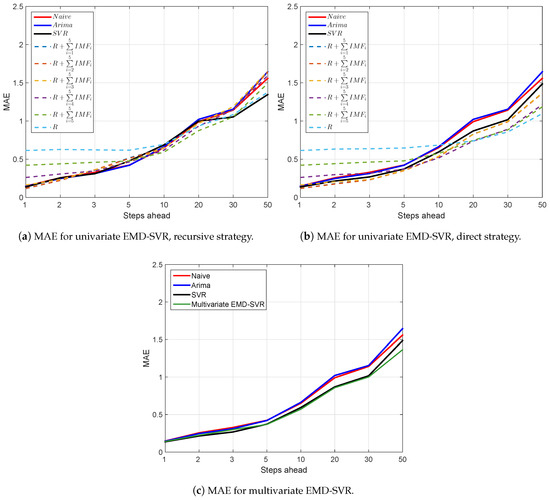
Figure 5.
Mean absolute error (MAE) as a function of the forecast horizon for all forecasting models: naive, ARIMA, SVR on the original data, univariate and multivariate EMD-SVR with input vector lagged values. Smaller MAE indicate better forecasts. Direct strategy univariate EMD-SVR with different number of components (Equations (5)–(8)) outperform all benchmarks for at all steps ahead. Multivariate EMD-SVR also outperforms all benchmarks for .
2.4. Statistical Significance
We applied the Wilcoxon test (see Section 4.8) between all the forecasting modes and the naive model (benchmark) for each forecast horizon. In Table 3, we report the Z-statistic values of the two-tailed Wilcoxon signed-rank test with and . The results for and are reported in Table A3 and Table A4 in the Appendix. We recall that in this test, values of Z larger than zero indicate that the model is performing better than the benchmark, whereas negative values indicate that the benchmark is performing better. In general, the larger the deviation from zero, the more significant the test is. In Table 3, Table A3 and Table A4, we mark the 5% and the 1% significance levels with a (*) and (**), respectively.

Table 3.
Z-statistic for the Wilcoxon signed-rank testing difference between naive model and the other models: autoregressive integrated moving average (ARIMA), direct and recursive support vector regression (SVR) on the original data, and univariate and multivariate empirical mode decomposition–SVR (EMD–SVR) with input vector . Positive values indicate better performances than naive model; negative values indicate worse performance instead. The larger the value, the more significant the overperformance is with respect to naive model. Statistics were computed over all 128 days in the dataset. Best-performing models for each step ahead h are highlighted in boldface. * Statistically significant at the 5% confidence level. ** Statistically significant at the 1% confidence level.
3. Discussion
The analysis of the forecasting errors’ MAE (Table 2) reveals the following:
- Across all forecasting models, the MAE increased with the forecast horizon following the intuition that the distant future is harder to predict.
- The direct strategy achieved more accurate forecasts than the recursive strategy in almost all the tested models.
- The smallest errors were observed for the input vector of length . Similar results were obtained for models with input vector , as was often around 5, whereas the case produced poorer results.
- For short time-horizons (), the best results were obtained by the direct univariate EMD–SVR model that included all IMFs and the residue. For large time-horizons (), the best results were obtained by the direct univariate EMD–SVR model that included the residue only. The intermediate case of favored the inclusion of the last two IMFs.
- The direct EMD–SVR multivariate strategy performed better than the naive and ARIMA benchmarks across all horizons and performed better than the direct and recursive SVR benchmarks for .
The statistical significance results (Wilcoxon test; Table 3) show the following:
- The direct EMD–SVR strategy provides consistently better results than the recursive strategy.
- For short time-horizons (), better results are obtained with models including all the IMFs and the residue. For longer time-horizons (), models with the residue only or models with only few slowly oscillating IMFs become significantly better than the naive model.
- The direct EMD–SVR multivariate strategy provides forecasting results that significantly outperform the naive model for all time-horizons greater than and outperforms the other models from .
Overall, these outcomes indicate that statistically significant forecasting of the S&P 500 index can be obtained across all time-horizons from 30 s to 25 min ahead. For all the time-horizons, the decomposition of the time series into IMF components improved the SVR forecasting power. The results also demonstrate that the residue and the low-frequency IMF components contribute to the forecasting of long time-horizons and that the high-frequency components become relevant for the forecast of short time-horizons. This follows the intuition that the forecasting horizon is best captured by components at the same time-scale.
We observe that the best-performing results with the mean MAE were obtained by using direct univariate EMD–SVR with different aggregations of EMD components (Equations (5)–(8)). Conversely, the best-performing results with Z-statistics were obtained by using the direct multivariate EMD–SVR model (Equation (9)). This apparent contradiction is a consequence of the fact that some models with a small mean MAE had a large standard deviation (std) MAE, making the overall statistical significance poorer.
4. Materials and Methods
4.1. EMD
The EMD consists of subdividing a time series into a number of components , , called IMFs, and a residual .
IMFs are oscillating components of the signal. Although theoretically there is no guarantee of stationarity, they oscillate around zero, and therefore they are at least locally stationary. IMFs are automatically discovered from local maxima and minima of the data without imposing any functional form. They are nearly orthogonal and oscillate with different characteristic times. There are several implementations for EMD in the literature; in this paper, we adopt a variation of the procedure introduced by Flandrin and Gonçalves (2004); Huang et al. (1998). The interested reader can see our previous papers (Nava et al. 2016a, 2017) for further details). Typically in the EMD, the number of IMF components n is automatically discovered by the method, which stops when only a nonoscillating residual is left. In our analysis, we have instead imposed by ending the decomposition before fully achieving a nonoscillating residual. This helped us to compare results across the entire dataset. Conventionally, indices rank components from high to low frequency with being the highest and being the lowest.
4.2. Forecasting Financial Time Series
Given a time series with values , forecasting consists of estimating the (future) values of the time series at h-steps ahead from (present) time t. The challenge is to find the function that best maps some past m values of the time series into the value h-steps ahead, that is, The distance between the forecasted value and the true value quantifies the accuracy of the forecasting. This is a regression problem between the sets of variables and . In financial time series, the main complications arise from the nonstationarity of the underlying process, the nonlinearity of the regression function and its dependence on the time-scale of the forecasting horizon. In the present EMD–SVR approach, nonstationarity and forecasting horizon time-scales are handled with EMD, whereas nonlinearity is handled with SVR.
4.3. Recursive and Direct Strategies for h-Steps-Ahead Forecast
In this paper, we use two common strategies to forecast time series h-steps ahead:
- The recursive strategy constructs a prediction model, which optimizes the one-step-ahead prediction: . Then it uses the same model for the next forecasted value: , with the forecasted value of used instead of the true value, which is unknown. The procedure continues recursively:We note that when h becomes larger than m, all the input values are forecasted, and this is likely to deteriorate the accuracy of the prediction.
- The direct strategy uses a different model for each forecast horizon. The various forecasting models are independently estimated. In this case, the h-step-ahead forecast is expressed as follows:The previous forecasted values are not used as inputs; therefore the errors do not propagate through the steps.
4.4. Support Vector Regression
We estimate the forecasting function by using a SVR approach that is one of the most popular and best-performing nonlinear regression methodologies (Christianini and Shawe-Taylor 2000; Kim 2003; Smola and Schölkopf 2004; Suykens et al. 2002; Tay and Cao 2001). It is based on the same formalism originally developed for support vector machines (SVMs), which are instead classifiers. SVR requires an input training set made of couples of variables , from which a nonlinear relation is inferred in the form of a sum of kernel functions (Christianini and Shawe-Taylor 2000; Schölkopf et al. 2001). In our case, we identify , and .
The regression coefficients are estimated by solving a quadratic optimization. The other parameters of the SVR model (kernel parameters, the regularization constant and insensitive coefficient) are estimated through a grid search (Bennett et al. 2006).
4.5. EMD–SVR Forecasting
In this paper, we have used the EMD components for forecasting by applying both a univariate and a multivariate EMD–SVR scheme. These both use the IMF components from EMD as input for forecasting with SVR. The difference is that the univariate approach attempts to forecast each component and the residue independently, whereas the multivariate approach uses all components and the residue to forecast the future value of the signal.
4.5.1. Univariate EMD–SVR
The univariate EMD–SVR approach can be written as follows:
The forecasted IMFs are then combined to obtain the forecast for the input time series. With this method, we can create a set of forecasting functions by partially adding component by component starting from the residue:
With this method, we can use both the direct and recursive forecasting strategies.
4.5.2. Multivariate EMD–SVR
The multivariate EMD–SVR scheme can be written as follows:
A different value of is used for each and for the residue. Only the direct strategy can be used in this multivariate model because the forecasting is done on the complete signal and not on each IMF. One of the advantages of this method is that a single forecasting model needs to be trained, and therefore it results in a faster algorithm.
4.6. Model Selection and Parameter Estimation
The estimation of the parameters and the validation of the model are a crucial part of any forecasting strategy. Model parameters are estimated by training the regression on a set of “training data”, searching for optimal (penalized) outputs. The performance of the regression is then tested on another set of “testing data”. Model selection criteria such as the Akaike information criterion (AIC) and the Schwarz Bayesian information criterion (BIC) can be used to select the best-performing model (Montgomery et al. 2008).
4.7. Measure of Performance
The performance of the forecasting model is measured by quantifying the mismatch between the forecasted values and the real values (in the testing set). In this paper, we quantify this mismatch by using the MAE, which is a commonly used error measure defined as follows Willmott and Matsuura (2005):
where M is the number of forecasted data points.
4.8. Statistical Significance Test
In order to further evaluate the forecasting performance, we have tested for the null hypothesis of equal forecast accuracy between the proposed EMD–SVR models and the benchmark models. Specifically, we have used the Wilcoxon signed-rank test (Wilcoxon 1945), a nonparametric test that estimates the statistically significant difference between a pair of models. We applied the Wilcoxon test to the rank of the difference of the absolute errors and to evaluate the null hypothesis that the two related error samples had the same distribution. The test returns a Z-score that follows a standard normal distribution for large normal samples. A positive value of Z indicates that the tested model had smaller errors than the naive model. On the contrary, a negative value indicates that the naive model outperformed the tested model. The larger the value of Z, the more significant the difference between the EMD–SVR and the benchmark models.
5. Conclusions
We have introduced a multistep-ahead forecasting methodology for nonlinear and nonstationary time series on the basis of a combination of EMD and SVR. The EMD can fully capture the local fluctuations of the analyzed time series and can be used as a preprocessor to decompose nonstationary data into a finite set of IMFs and a residue. The extracted IMFs are locally stationary (except the residue), they have simpler structures and they are associated to oscillations within a characteristic time-scale range. The underlying idea that we tested successfully in this paper is that IMFs are better suited for forecasting than the original time series. The construction of EMD is algorithmically very simple and computationally undemanding, with complexity scaling linearly with the time series length.
We tested both univariate and multivariate EMD–SVR forecasting schemes. For the univariate scheme, we forecasted each IMF and the residue separately and then constructed the forecasted input time series as the sum of the forecasted components. We defined coarse-to-fine reconstruction models using the cumulative sum of sequential IMFs, that is, adding details to the low-frequency components. The multivariate EMD–SVR scheme instead combined information of all the IMFs and the residue into one input vector used for forecasting the financial time series. We used two multistep-ahead prediction strategies, the recursive and the direct strategies.
We evaluated the performance of our multistep-ahead forecasting models on intraday data from the S&P 500 index. The results suggest that the multivariate EMD–SVR models perform better than benchmark models. The best results were obtained with the direct strategy applied to the univariate EMD–SVR with an input vector of length (p and d obtained from a fitted ARIMA model with, in our case, ).
We observed that the IMFs with high oscillation frequencies contribute to forecasting on short time-horizons but do not improve forecasting on longer horizons. For short-term forecasting, the model using the full reconstruction (all IMFs) performed better. For long-term forecasting, the residue conveyed the most important features for the forecasting of the original data. This was a novel yet expected outcome, because it is intuitive that the main contributors to forecasting on some time-horizons should be those with a similar time-scale. Shorter time-scales introduce essentially only noise and longer time-scales are slow varying trends with small effects.
We conclude that the EMD can improve forecasting performances with the most significant improvements over the benchmark models achieved for longer-term horizons (). The limited improvement for short-term horizons may be due to the boundary effects of the EMD, which produce swings in the extremes of the IMFs and perturb the first few forecasting steps.
This paper aims to demonstrate the feasibility of using EMD for forecasting purposes. Although the proposed EMD–SVR forecasting methodology has achieved good predictive performances, therefore proving the starting hypothesis, there is plenty of scope for further refining of the methodology. For instance, the selection of the input vector and the choice of parameters for the SVR can be improved. Further, EMD can be better adapted for forecasting purposes by better implementing special handling of the right boundary values and by better processing propagation of noise from large fluctuations.
Acknowledgments
The authors wish to thank Bloomberg for providing the data. Noemi Nava would like to acknowledge the financial support from Conacyt, Mexico. Tomaso Aste and Tiziana Di Matteo wish to thank the Systemic Risk Centre at LSE.
Author Contributions
Noemi Nava, Tiziana Di Matteo and Tomaso Aste conceived and designed the experiments; Noemi Nava and Tomaso Aste performed the experiments; Noemi Nava and Tomaso Aste analyzed the data; Noemi Nava, Tiziana Di Matteo and Tomaso Aste wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Autoregressive Integrated Moving Average
The autoregressive integrated moving average (ARIMA) model (Box et al. 1994) is commonly used to forecast nonstationary time series. The assumption to apply an ARIMA model is that after differencing d times the input time series, the obtained values are a stationary time series with zero mean. It is also assumed that future values of this time series are a linear function of p past observations and q past errors .
The ARIMA model is thus expressed as follows:
where ,..., are the parameters of the autoregressive part of the model, ,..., are the parameters of the moving average part and the error is defined by . The order of the model is defined by the values of p and q, which are identified from the autocorrelation function and the partial autocorrelation function (Brockwell and Davis 2002). The model parameters, and , are estimated using the maximum likelihood method.
Appendix B. Results for m = 1 and m = 5
For comparison, we report the results for input vectors of lengths and . Table A1 and Table A2 correspond to and , respectively, and they must be compared with the results reported for in Table 2. Figure A1 and Figure A2 correspond to and , respectively, and they must be compared with the results reported for in Figure 5. Table A3 and Table A4 correspond to and , respectively, and they must be compared with the results reported for in Table 3.

Table A1.
Mean absolute error (MAE): mean and standard deviation (std) for the considered forecasting models with input vector lagged values. The smallest MAE of each forecast horizon is set in boldface.
Table A1.
Mean absolute error (MAE): mean and standard deviation (std) for the considered forecasting models with input vector lagged values. The smallest MAE of each forecast horizon is set in boldface.
| Steps Ahead h | 1 | 2 | 3 | 5 | 10 | 20 | 30 | 50 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| Benchmarks | Naive | 0.147 | (0.186) | 0.256 | (0.322) | 0.328 | (0.418) | 0.423 | (0.514) | 0.651 | (0.801) | 0.991 | (1.053) | 1.143 | (1.294) | 1.559 | (1.803) |
| ARIMA | 0.145 | (0.185) | 0.247 | (0.303) | 0.313 | (0.374) | 0.421 | (0.477) | 0.663 | (0.783) | 1.021 | (1.035) | 1.154 | (1.304) | 1.644 | (1.789) | |
| Direct SVR | 0.204 | (0.200) | 0.313 | (0.395) | 0.378 | (0.473) | 0.529 | (0.610) | 0.832 | (1.040) | 1.270 | (1.380) | 1.540 | (1.587) | 2.185 | (2.336) | |
| Recursive SVR | 0.204 | (0.200) | 0.283 | (0.365) | 0.324 | (0.412) | 0.439 | (0.556) | 0.628 | (0.831) | 0.986 | (1.140) | 1.077 | (1.221) | 1.599 | (1.868) | |
| Direct EMD–SVR | Multivariate | 0.162 | (0.180) | 0.264 | (0.317) | 0.330 | (0.374) | 0.417 | (0.484) | 0.650 | (0.718) | 0.921 | (1.010) | 1.229 | (1.292) | 1.642 | (1.947) |
| 0.196 | (0.205) | 0.308 | (0.356) | 0.378 | (0.425) | 0.491 | (0.504) | 0.748 | (0.805) | 1.180 | (1.259) | 1.498 | (1.361) | 1.903 | (2.103) | ||
| 0.196 | (0.198) | 0.304 | (0.354) | 0.376 | (0.432) | 0.489 | (0.502) | 0.747 | (0.803) | 1.181 | (1.258) | 1.498 | (1.362) | 1.903 | (2.102) | ||
| 0.243 | (0.244) | 0.310 | (0.345) | 0.384 | (0.433) | 0.490 | (0.514) | 0.749 | (0.806) | 1.180 | (1.259) | 1.505 | (1.362) | 1.904 | (2.098) | ||
| 0.380 | (0.430) | 0.436 | (0.452) | 0.478 | (0.483) | 0.543 | (0.532) | 0.799 | (0.867) | 1.198 | (1.265) | 1.488 | (1.349) | 1.919 | (2.093) | ||
| 0.616 | (0.677) | 0.657 | (0.712) | 0.691 | (0.709) | 0.730 | (0.764) | 0.869 | (1.021) | 1.218 | (1.317) | 1.506 | (1.382) | 1.915 | (2.085) | ||
| R | 0.890 | (0.971) | 0.924 | (0.989) | 0.934 | (0.946) | 0.964 | (0.966) | 1.033 | (1.076) | 1.297 | (1.358) | 1.546 | (1.505) | 1.924 | (2.036) | |
| Recursive EMD–SVR | Multivariate | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| 0.196 | (0.205) | 0.278 | (0.331) | 0.333 | (0.432) | 0.416 | (0.474) | 0.633 | (0.774) | 0.939 | (1.036) | 1.143 | (1.307) | 1.545 | (1.775) | ||
| 0.196 | (0.198) | 0.279 | (0.331) | 0.333 | (0.432) | 0.415 | (0.474) | 0.631 | (0.774) | 0.940 | (1.036) | 1.143 | (1.307) | 1.545 | (1.775) | ||
| 0.243 | (0.244) | 0.301 | (0.332) | 0.354 | (0.402) | 0.437 | (0.469) | 0.653 | (0.770) | 0.950 | (1.035) | 1.158 | (1.312) | 1.557 | (1.789) | ||
| 0.380 | (0.430) | 0.431 | (0.444) | 0.458 | (0.471) | 0.514 | (0.508) | 0.710 | (0.775) | 1.010 | (1.074) | 1.209 | (1.309) | 1.621 | (1.800) | ||
| 0.616 | (0.677) | 0.647 | (0.708) | 0.675 | (0.695) | 0.685 | (0.741) | 0.816 | (0.982) | 1.076 | (1.237) | 1.295 | (1.282) | 1.644 | (1.851) | ||
| R | 0.890 | (0.971) | 0.920 | (0.987) | 0.923 | (0.940) | 0.937 | (0.951) | 0.989 | (1.049) | 1.209 | (1.237) | 1.414 | (1.389) | 1.721 | (1.848) | |

Table A2.
Mean absolute error (MAE) and standard deviation (std) for the considered forecasting models: naive, autoregressive integrated moving average (ARIMA), univariate and multivariate empirical mode decomposition–support vector regression (EMD–SVR) with input vector lagged values. The smallest MAE of each forecast horizon is set in boldface.
Table A2.
Mean absolute error (MAE) and standard deviation (std) for the considered forecasting models: naive, autoregressive integrated moving average (ARIMA), univariate and multivariate empirical mode decomposition–support vector regression (EMD–SVR) with input vector lagged values. The smallest MAE of each forecast horizon is set in boldface.
| Steps Ahead h | 1 | 2 | 3 | 5 | 10 | 20 | 30 | 50 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| Benchmarks | Naive | 0.147 | (0.186) | 0.256 | (0.322) | 0.328 | (0.418) | 0.423 | (0.514) | 0.651 | (0.801) | 0.991 | (1.053) | 1.143 | (1.294) | 1.559 | (1.803) |
| ARIMA | 0.145 | (0.185) | 0.247 | (0.303) | 0.313 | (0.374) | 0.421 | (0.477) | 0.663 | (0.783) | 1.021 | (1.035) | 1.154 | (1.304) | 1.644 | (1.789) | |
| Direct SVR | 0.145 | (0.146) | 0.242 | (0.289) | 0.294 | (0.362) | 0.408 | (0.450) | 0.615 | (0.723) | 0.943 | (0.981) | 1.101 | (1.201) | 1.641 | (1.733) | |
| Recursive SVR | 0.145 | (0.146) | 0.257 | (0.357) | 0.393 | (0.566) | 0.577 | (0.841) | 1.080 | (1.922) | 1.228 | (1.939) | 1.338 | (2.054) | 1.627 | (2.366) | |
| Direct EMD–SVR | Multivariate | 0.144 | (0.180) | 0.222 | (0.289) | 0.284 | (0.353) | 0.379 | (0.448) | 0.585 | (0.711) | 0.866 | (0.928) | 1.017 | (1.153) | 1.379 | (1.585) |
| 0.120 | (0.146) | 0.181 | (0.226) | 0.234 | (0.278) | 0.371 | (0.426) | 0.557 | (0.667) | 0.874 | (0.896) | 1.024 | (1.046) | 1.430 | (1.601) | ||
| 0.124 | (0.138) | 0.182 | (0.228) | 0.234 | (0.286) | 0.371 | (0.421) | 0.557 | (0.658) | 0.879 | (0.898) | 1.023 | (1.049) | 1.433 | (1.602) | ||
| 0.173 | (0.184) | 0.217 | (0.240) | 0.247 | (0.283) | 0.373 | (0.387) | 0.556 | (0.637) | 0.886 | (0.910) | 1.029 | (1.053) | 1.441 | (1.611) | ||
| 0.277 | (0.324) | 0.316 | (0.331) | 0.334 | (0.349) | 0.389 | (0.390) | 0.544 | (0.604) | 0.795 | (0.848) | 0.916 | (0.930) | 1.298 | (1.425) | ||
| 0.449 | (0.495) | 0.471 | (0.519) | 0.491 | (0.511) | 0.503 | (0.536) | 0.594 | (0.714) | 0.788 | (0.903) | 0.927 | (0.916) | 1.258 | (1.393) | ||
| R | 0.655 | (0.709) | 0.675 | (0.725) | 0.679 | (0.694) | 0.688 | (0.707) | 0.729 | (0.782) | 0.788 | (0.811) | 0.908 | (0.876) | 1.167 | (1.234) | |
| Recursive EMD–SVR | Multivariate | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — | — |
| 0.120 | (0.1460) | 0.241 | (0.321) | 0.383 | (0.463) | 0.634 | (0.813) | 0.829 | (0.915) | 1.077 | (1.138) | 1.298 | (1.391) | 1.807 | (1.949) | ||
| 0.124 | (0.138) | 0.239 | (0.302) | 0.381 | (0.460) | 0.612 | (0.820) | 0.826 | (0.921) | 1.085 | (1.153) | 1.299 | (1.389) | 1.806 | (1.950) | ||
| 0.173 | (0.184) | 0.245 | (0.299) | 0.370 | (0.442) | 0.535 | (0.703) | 0.823 | (0.909) | 1.082 | (1.143) | 1.341 | (1.410) | 1.807 | (1.939) | ||
| 0.277 | (0.324) | 0.315 | (0.312) | 0.383 | (0.380) | 0.544 | (0.560) | 0.724 | (0.791) | 1.076 | (1.123) | 1.327 | (1.390) | 1.777 | (1.906) | ||
| 0.449 | (0.495) | 0.464 | (0.501) | 0.482 | (0.497) | 0.522 | (0.552) | 0.673 | (0.773) | 0.929 | (1.070) | 1.211 | (1.329) | 1.736 | (1.896) | ||
| R | 0.655 | (0.709) | 0.666 | (0.709) | 0.657 | (0.669) | 0.651 | (0.674) | 0.736 | (0.756) | 0.962 | (1.019) | 1.134 | (1.240) | 1.523 | (1.887) | |
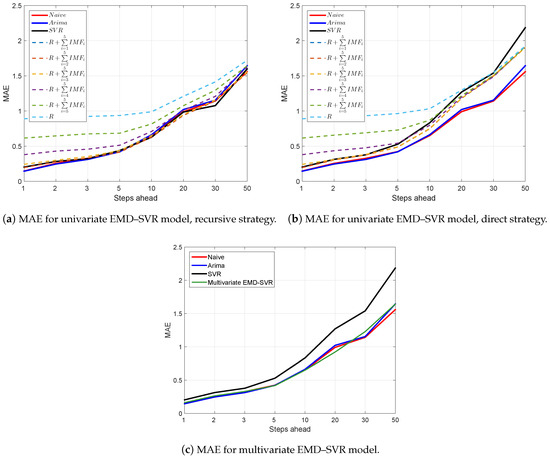
Figure A1.
Mean absolute error (MAE) as a function of the forecast horizon for the considered forecasting models: naive, autoregressive integrated moving average (ARIMA), and univariate and multivariate empirical mode decomposition–support vector regression (EMD–SVR) with input vector lagged values.
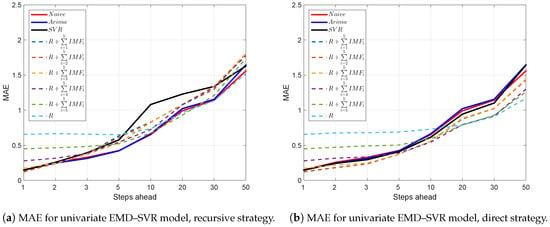
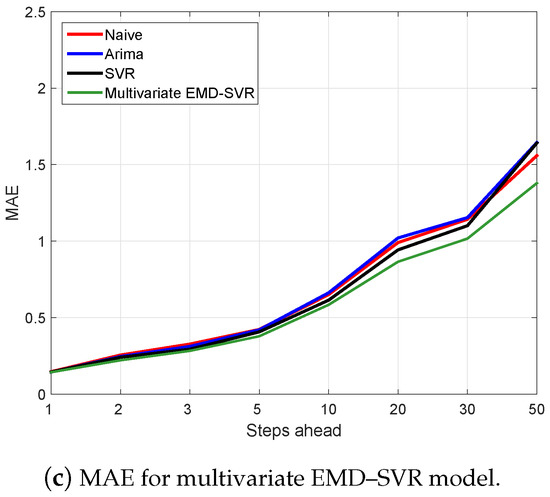
Figure A2.
Mean absolute error (MAE) as a function of the forecast horizon for the considered forecasting models: naive, autoregressive integrated moving average (ARIMA), univariate and multivariate empirical mode decomposition–support vector regression (EMD–SVR) with input vector lagged values.

Table A3.
Z-statistic for the Wilcoxon signed-rank test for the null hypothesis that the naive model is as accurate as the studied models: autoregressive integrated moving average (ARIMA), and univariate and multivariate empirical mode decomposition–support vector regression (EMD–SVR) with input vector . Top: direct strategy; bottom: recursive strategy. * Statistically significant at the 5% confidence level. ** Statistically significant at the 1% confidence level.
Table A3.
Z-statistic for the Wilcoxon signed-rank test for the null hypothesis that the naive model is as accurate as the studied models: autoregressive integrated moving average (ARIMA), and univariate and multivariate empirical mode decomposition–support vector regression (EMD–SVR) with input vector . Top: direct strategy; bottom: recursive strategy. * Statistically significant at the 5% confidence level. ** Statistically significant at the 1% confidence level.
| Model\Steps Ahead h | 1 | 2 | 3 | 5 | 10 | 20 | 30 | 50 | |
|---|---|---|---|---|---|---|---|---|---|
| Benchmarks | ARIMA | −0.22 | 0.16 | 0.89 | 0.30 | −1.45 | −1.59 | −0.49 | −1.47 |
| Direct SVR | −4.72 ** | −3.05 ** | −2.54 * | −3.24 ** | −3.47 ** | −2.75 ** | −3.35 ** | −3.39 ** | |
| Recursive SVR | −4.72 ** | −1.83 | −0.44 | −0.58 | 0.03 | 1.01 | 1.37 | 0.27 | |
| Direct EMD–SVR | Multivariate | −1.83 | −0.80 | −0.39 | 0.94 | 0.22 | 1.37 | −0.18 | 1.41 |
| −4.07 ** | −3.07 ** | −3.11 * | −2.96 ** | −2.72 ** | −2.11 * | −3.70 ** | −2.32 * | ||
| −4.21 ** | −3.12 ** | −2.84 ** | −2.88 ** | −2.73 ** | −2.12 * | −3.71 ** | −2.32 * | ||
| −5.62 ** | −3.18 ** | −2.99 ** | −2.60 ** | −2.69 ** | −2.12 * | −3.74 ** | −2.37 * | ||
| −7.25 ** | −5.73 ** | −4.65 ** | −3.48 ** | −3.37 ** | −2.33 * | −3.51 ** | −2.45 * | ||
| −8.35 ** | −7.51 ** | −6.36 ** | −4.99 ** | −3.84 ** | −2.46 * | −3.20 ** | −2.47 * | ||
| R | −9.06 ** | −8.14 ** | −7.84 ** | −7.00 ** | −5.51 ** | −3.10 ** | −3.66 ** | −2.66 ** | |
| Recursive EMD–SVR | Multivariate | — | — | — | — | — | — | — | — |
| −4.07 ** | −1.96 | −0.41 | −0.21 | 0.63 | 1.95 | 0.90 | 1.55 | ||
| −4.21 ** | −2.08 * | −0.62 | −0.13 | 0.76 | 1.93 | 0.92 | 1.51 | ||
| −5.62 ** | −2.82 ** | −1.76 | −1.11 | −0.09 | 1.44 | 0.43 | 1.34 | ||
| −7.25 ** | −5.55 ** | −4.48 ** | −3.38 ** | −2.17 * | −1.09 | −1.05 | −0.10 | ||
| −8.35 ** | −7.33 ** | −6.28 ** | −4.46 ** | −2.95 ** | −1.18 | −1.90 | 0.11 | ||
| R | −9.06 ** | −8.13 ** | −7.77 ** | −6.78 ** | −5.25 ** | −2.26 * | −2.84 ** | −0.86 |

Table A4.
Z-statistic for the Wilcoxon signed-rank test for the null hypothesis that the naive model is as accurate as the studied models: autoregressive integrated moving average (ARIMA), univariate and multivariate empirical mode decomposition–support vector regression (EMD–SVR) with input vector . Top: direct strategy; bottom: recursive strategy. * Statistically significant at the 5% confidence level. ** Statistically significant at the 1% confidence level.
Table A4.
Z-statistic for the Wilcoxon signed-rank test for the null hypothesis that the naive model is as accurate as the studied models: autoregressive integrated moving average (ARIMA), univariate and multivariate empirical mode decomposition–support vector regression (EMD–SVR) with input vector . Top: direct strategy; bottom: recursive strategy. * Statistically significant at the 5% confidence level. ** Statistically significant at the 1% confidence level.
| Model\Steps Ahead h | 1 | 2 | 3 | 5 | 10 | 20 | 30 | 50 | |
|---|---|---|---|---|---|---|---|---|---|
| Benchmarks | ARIMA | −0.22 | 0.16 | 0.89 | 0.30 | −1.45 | −1.59 | −0.49 | −1.47 |
| Direct SVR | −0.45 | 1.08 | 1.54 | 0.72 | 0.57 | 1.24 | 0.67 | 0.14 | |
| Recursive SVR | −0.45 | 1.53 | 1.15 | 0.87 | 0.36 | 1.79 | 1.59 | 2.29 * | |
| Direct EMD–SVR | Multivariate | 0.20 | 5.58 ** | 4.70 ** | 4.57 ** | 5.67 ** | 8.43 ** | 7.70 ** | 7.66 ** |
| 3.33 ** | 6.71 ** | 6.41 ** | 3.17 ** | 2.79 ** | 2.79 ** | 1.61 | 2.39 ** | ||
| 2.49 * | 5.94 ** | 6.24 ** | 3.21 ** | 2.64 ** | 2.72 ** | 1.70 | 2.37 * | ||
| −1.94 | 1.88 | 3.93 ** | 1.75 | 1.94 | 2.54 * | 1.66 | 2.31 * | ||
| −5.66 ** | −2.31 * | −0.47 | 0.59 | 2.57 * | 4.02 ** | 3.99 ** | 3.55 ** | ||
| −7.45 ** | −5.54 ** | −3.82 ** | −1.76 | 0.61 | 3.56 ** | 3.42 ** | 3.98 ** | ||
| R | −8.59 ** | −7.12 ** | −6.28 ** | −4.12 ** | −2.12 * | 3.37 ** | 3.19 ** | 4.10 ** | |
| Recursive EMD–SVR | Multivariate | — | — | — | — | — | — | — | — |
| 3.33 ** | 1.43 | −0.51 | −2.26 * | −1.31 | −0.15 | −0.95 | −1.24> | ||
| 2.49 * | 1.45 | −0.49 | −1.98 * | −1.23 | −0.08 | −1.02 | −1.19 | ||
| −1.94 | 1.03 | 0.11 | −1.32 | −1.38 | −0.22 | −1.33 | −1.31 | ||
| −5.66 ** | −2.30 * | −1.72 | −2.38 * | −0.73 | 0.07 | −1.18 | −1.28 | ||
| −7.45 ** | −5.59 ** | −3.86 ** | −2.01 * | −0.03 | 2.14 * | 0.34 | −1.00 | ||
| R | −8.59 ** | −7.13 ** | −6.06 ** | −3.86 ** | −2.11 * | 1.55 | 1.04 | 1.22 |
References
- Alexander, Carol. 2001. Market Models: A Guide to Financial Data Analysis. New Yrok: John Wiley & Sons. [Google Scholar]
- Christianini, Nello, and John Shawe-Taylor. 2000. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge: Cambridge University Press. ISBN 0-521-78019-5. [Google Scholar]
- Aymanns, Christoph, Fabio Caccioli, J. Doyne Farmer, and Vincent W.C. Tan. 2016. Taming the Basel leverage cycle. Journal of Financial Stability 27: 263–77. [Google Scholar] [CrossRef]
- Bennett, Kristin P., Jing Hu, Xiaoyun Ji, G. Kunapuli, and Jong-Shi Pang. 2006. Model selection via bilevel optimization. Paper present at the IJCNN ’06 International Joint Conference on Neural Networks, Vancouver, BC, Canada, July 6–21; pp. 1922–29. [Google Scholar]
- Box, George E. P., Gwilym M. Jenkins, and Gregory C. Reinsel. 1994. Time Series Analysis: Forecasting and Control, 3rd ed. Michigan: Prentice Hall. [Google Scholar]
- Brockwell, Peter J., and Richard A. Davis. 2002. Introduction to Time Series and Forecasting, 2nd ed. New York: Springer. [Google Scholar]
- Brooks, Chris. 2014. Introductory Econometrics for Finance. Cambridge: Cambridge University Press. [Google Scholar]
- Caccioli, Fabio, Imer Kondor, Matteo Marsili, and Susnne Still. 2016. Liquidity risk and instabilities in portfolio optimization. International Journal of Theoretical and Applied Finance 19: 1650035. [Google Scholar] [CrossRef]
- Chen, Chun-Fu, Ming-Cheng Lai, and Ching-Chiang Yeh. 2012. Forecasting tourism demand based on empirical mode decomposition and neural network. Knowledge-Based Systems 26: 281–87. [Google Scholar] [CrossRef]
- Cheng, Ching-Hsue, and Liang-Ying Wei. 2014. A novel time-series model based on empirical mode decomposition for forecasting TAIEX. Economic Modelling 36: 136–41. [Google Scholar] [CrossRef]
- Clements, Michael P., Philip Hans Franses, and Norman R. Swanson. 2004. Forecasting economic and financial time-series with non-linear models. International Journal of Forecasting 20: 169–83. [Google Scholar] [CrossRef]
- Di Matteo, Tiziana. 2007. Multi-scaling in finance. Quantitative Finance 7: 21–36. [Google Scholar] [CrossRef]
- Flandrin, Patrick, and Paulo Goncalves. 2004. Empirical mode decompositions as data-driven wavelet-like expansions. International Journal of Wavelets, Multiresolution and Information Processing 2: 477–96. [Google Scholar] [CrossRef]
- Huang, Norden E., Zheng Shen, Steven R. Long, Manli C. Wu, Hsing H. Shih, Quanan Zheng, Nai-Chyuan Yen, Chi Chao Tung, and Henry H. Liu. 1998. The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 454: 903–95. [Google Scholar] [CrossRef]
- Hyndman, Rob J., and Yeasmin Khandakar. 2008. Automatic time series forecasting: The forecast package for R. Journal of Statistical Software 26: 1–22. [Google Scholar]
- Kazem, Ahmad, Ebrahim Sharifi, Farookh Khadeer Hussain, Morteza Saberi, and Omar Khadeer Hussain. 2013. Support vector regression with chaos-based firefly algorithm for stock market price forecasting. Applied Soft Computing 13: 947–58. [Google Scholar] [CrossRef]
- Kim, Kyoung-Jae. 2003. Financial time series forecasting using support vector machines. Neurocomputing 55: 307–19. [Google Scholar] [CrossRef]
- Lin, Chiun-Sin, Sheng-Hsiung Chiu, and Tzu-Yu Lin. 2012. Empirical mode decomposition based least squares support vector regression for foreign exchange rate forecasting. Economic Modelling 29: 2583–90. [Google Scholar] [CrossRef]
- Liu, Hui, Chao Chen, Hong-Qi Tian, and Yan-Fei Li. 2012. A hybrid model for wind speed prediction using empirical mode decomposition and artificial neural networks. Renewable Energy 48: 545–56. [Google Scholar] [CrossRef]
- Lu, Chi-Jie, Tian-Shyug Lee, and Chih-Chou Chiu. 2009. Financial time series forecasting using independent component analysis and support vector regression. Decision Support Systems 47: 115–25. [Google Scholar] [CrossRef]
- Lu, Chi-Jie, and Yuehjen E. Shao. 2012. Forecasting computer products sales by integrating ensemble empirical mode decomposition and extreme learning machine. Mathematical Problems in Engineering 2012: 831201. [Google Scholar] [CrossRef]
- Montgomery, Douglas C., Cheryl L. Jennings, and Murat Kulahci. 2008. Introduction to Time Series Analysis and Forecasting. Wiley Series in Probability and Statistics; New York: Wiley. [Google Scholar]
- Nava, Noemi, Tiziana Di Matteo, and Tomaso Aste. 2016a. Time-dependent scaling patterns in high frequency financial data. The European Physical Journal Special Topics 225: 1997–2016. [Google Scholar] [CrossRef]
- Nava, Noemi, T. Di Matteo, and Tomaso Aste. 2017. Dynamic correlations at different time-scales with empirical mode decomposition. arXiv, arXiv:1708.06586. [Google Scholar]
- Nava, Noemi, T. Di Matteo, and Tomaso Aste. 2016b. Anomalous volatility scaling in high frequency financial data. Physica A: Statistical Mechanics and its Applications 447: 434–45. [Google Scholar] [CrossRef]
- Rilling, Gabriel, Patrick Flandrin, and Paulo Gonçalves. 2003. On empirical mode decomposition and its algorithms. Paper present at the IEEE EURASIP Workshop on Nonlinear Signal and Image Processing NSIP03, Grado, Italy, June; Rocquencourt: Inria, pp. 8–11. [Google Scholar]
- Schölkopf, Bernhard, Ralf Herbrich, and Alex J. Smola. 2001. A generalized representer theorem. In Computational Learning Theory. Berlin and Heidelberg: Springer, pp. 416–26. [Google Scholar]
- Smola, Alex J., and Bernhard Schölkopf. 2004. A tutorial on support vector regression. Statistics and Computing 14: 199–222. [Google Scholar] [CrossRef]
- Suykens, Johan A.K., Jos De Brabanter, Lukas Lukas, and Joos Vandewalle. 2002. Weighted least squares support vector machines: robustness and sparse approximation. Neurocomputing 48: 85–105. [Google Scholar] [CrossRef]
- Tay, F. E., and L. Cao. 2001. Application of support vector machines in financial time series forecasting. Omega 29: 309–17. [Google Scholar] [CrossRef]
- Varga-Haszonits, Istvan, Fabio Caccioli, and Imre Kondor. 2016. Replica approach to mean-variance portfolio optimization. Journal of Statistical Mechanics: Theory and Experiment 2016: 123404. [Google Scholar] [CrossRef]
- Wang, Jujie, Wenyu Zhang, Yaning Li, Jianzhou Wang, and Zhangli Dang. 2014. Forecasting wind speed using empirical mode decomposition and Elman neural network. Applied Soft Computing 23: 452–59. [Google Scholar] [CrossRef]
- Wilcoxon, Frank. 1945. Individual comparisons by ranking methods. Biometrics Bulletin 1: 80–83. [Google Scholar] [CrossRef]
- Willmott, Cort J., and Kenji Matsuura. 2005. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Climate Research 30: 79–82. [Google Scholar] [CrossRef]
- Yu, Lean, Shouyang Wang, and Kin Keung Lai. 2008. Forecasting crude oil price with an EMD-based neural network ensemble learning paradigm. Energy Economics 30: 2623–35. [Google Scholar] [CrossRef]
- Zeng, Qingcheng, and Chenrui Qu. 2014. An approach for Baltic Dry Index analysis based on empirical mode decomposition. Maritime Policy & Management 41: 224–40. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).