Company Value with Ruin Constraint in a Discrete Model
Abstract
:1. Introduction
2. Methods
2.1. A Modified Bellman Equation
2.2. Iteration Method
2.3. Running Allowed Ruin Probabilities
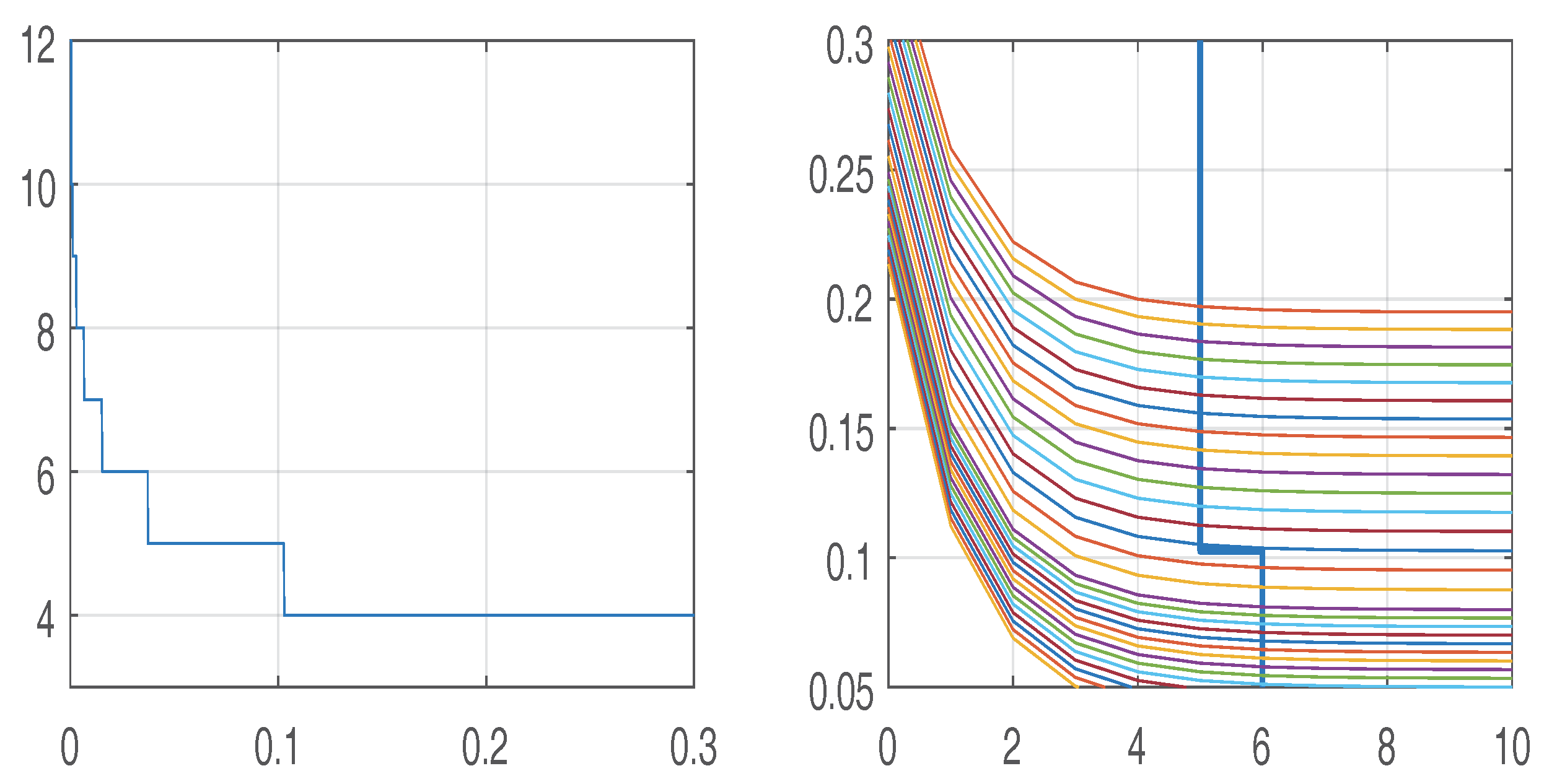
2.4. The Barrier Method
2.5. The Lagrange Multiplier Approach
3. Numerical Example
DeFinettiModel
ds=1;
S0=300; S=0:ds:S0; KS=length(S);
W=zeros(1,KS); V1=W; V2=W; V0=W;
p=0.7; q=1-p;
r=1/1.03;
a1=1.0714285;
a2=0.4;
b2=-.5957446812;
b1=1-b2;
for k=1:KS
W(k)=b1*a1^(k-1)+b2*a2^(k-1);
end
kk=6;
C=1/(W(kk)-W(kk-1));
for k=1:kk
V0(k)=W(k)*C;
end
g=(1-p)/p;
Psi=g.^(1:1:KS);
for i=(kk+1):KS
V0(i)=V0(i-1)+1;
end
Policy improvement with Bellman, with new
formulas for beta1 and beta2 and interpolation
DeFinettiModel;
da=1/100000;
Alpha=da:da:1; KA=length(Alpha);
V1=zeros(KS,KA); V2=V1;
for L=1:400
M=zeros(1,KA);
al0=ceil(Psi(1)/da);
for al=al0:KA
alpha=al*da;
y1=(alpha-q)/p/da;
u1=floor(y1);
z1=(y1-u1);
if u1==0
v1=z1*V1(2,u1+1);
else
v1=V1(2,u1)+z1*(V1(2,u1+1)-V1(2,u1));
end
V2(1,al)=r*p*v1;
end
for s=2:KS-1
for al=1:KA
alpha=al*da;
if Psi(s)>=alpha
V2(s,al)=0;
else
ga=(1-alpha)/(1-Psi(s));
y1=(1-ga+ga*Psi(s+1))/da;
y2=(1-ga+ga*Psi(s-1))/da;
u1=floor(y1);
u2=floor(y2);
z1=(y1-u1);
z2=(y2-u2);
if u1==0
v1=z1*V1(s+1,u1+1);
else
v1=V1(s+1,u1)+z1*(V1(s+1,u1+1)-V1(s+1,u1));
end
if u2==0
v2=z2*V1(s-1,u2+1);
else
v2=V1(s-1,u2)+z2*(V1(s-1,u2+1)-V1(s-1,u2));
end
x=r*p*v1+r*q*v2;
if Psi(s-1)<alpha & x<V2(s-1,al)+1
if M(al)==0
M(al)=s;
end
x=V2(s-1,al)+1;
end
V2(s,al)=max(V1(s,al),x);
end
end
end
V1=V2;
V1(:,KA)=V0;
[L V1(5,round(0.2/da)) V0(5)]’
end
Policy improvement without dynamic equation
clear;
DeFinettiModel;
da=1/100000; Alpha=da:da:1; KA=length(Alpha);
V1=zeros(KS,KA); V2=V1;
V1(:,KA)=V0;
M0=round(0.2/da);
for L=1:150
M=zeros(1,KA);
for s=1:KS
for al=max(round(Psi(s)/da),1):KA-1
Feld=zeros(1,KS);
alpha=al*da;
if M(al)>0 && s>M(al) && Psi(s-1)<al
V1(s,al)=V1(s-1,al)+1;
end
for B=s+1:KS
x1=(Psi(s)-Psi(B))/(1-Psi(B));
x2=1-x1;
y=(alpha-x1)/x2*KA;
aB=floor(y);
z=y-aB;
if aB==0
VF=z*V1(B,aB+1);
end
if aB>0
VF=V1(B,aB)+z*(V1(B,aB+1)-V1(aB));
end
Feld(B-s)=W(s)/W(B)*VF;
end
x=max(Feld);
if s>1
y=V2(s-1,al)+ds;
if (Psi(s-1)<al*da) & (x<y)
V2(s,al)=max(V1(s,al),y);
if M(al)==0
M(al)=s;
end
else
V2(s,al)=max(V1(s,al),x);
end;
end
end
V2(s,KA)=V0(s);
end
V1=V2;
end
Lagrange method
DeFinettiModel;
T0=2000; T=0:T0; KT=length(T);
V=zeros(KS,KT); W=V;
M=zeros(1,KT);
L=2.93;
s0=5; a0=0.2; p=0.7; r=1/1.03;
% computation of value function
V(:,T0)=-L*Psi;
for k=1:T0-1
t=T0-k;
rt=r^(t-1);
V(1,t)=p*V(2,t+1)-q*L;
for i=2:KS-1
V(i,t)=max(p*V(i+1,t+1)+q*V(i-1,t+1),V(i-1,t)+rt);
if p*V(i+1,t+1)+q*V(i-1,t+1)<V(i-1,t)+rt
if M(t+1)==0
M(t+1)=i-1;
end
end
end
end
% computation of corresponding ruin probability
W(:,T0)=Psi;
for k=1:T0-1
t=T0-k;
W(1,t)=p*W(2,t+1)+q;
for i=2:KS-1
W(i,t)=p*W(i+1,t+1)+q*W(i-1,t+1);
if i>M(t+1)
W(i,t)=W(M(t+1),t);
end
end
end
[V(5,1) W(5,1) V(5,1)+L*W(5,1)]’
And finally the MAPLE code for the barrier method:
Barrier.mw
restart; Digits := 25;
p := .7; q := 1-p; r := 1/1.03;
Ps := s->(q/p)^(s+1);
z := solve(r*(p*x^2+q) = x, x);
B0 := solve((1-B)*z[2]+B*z[1] = 0, B);
W := s->(1-B0)*z[1]^s+B0*z[2]^s;
s0 := 4; a0 := .2;
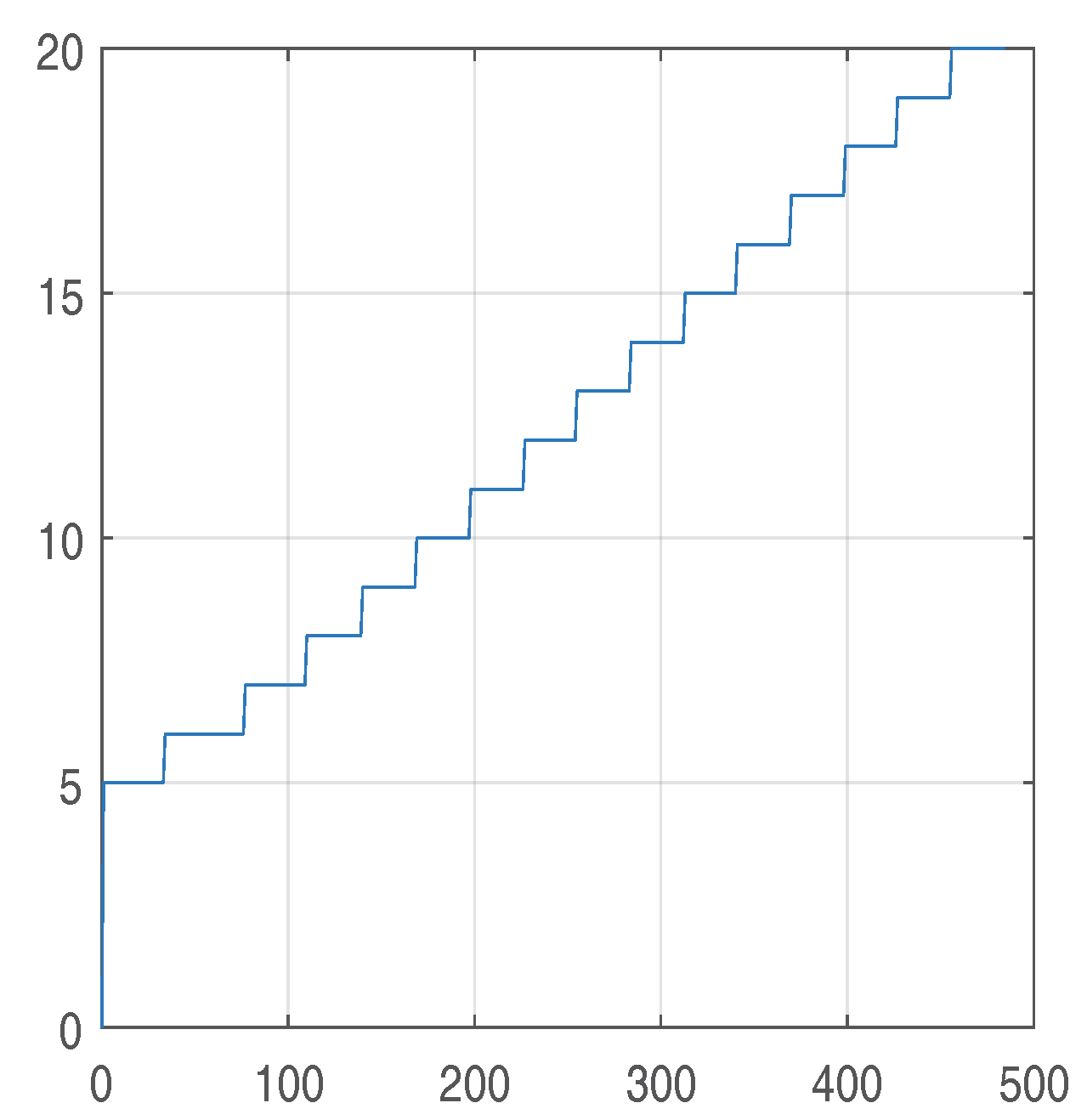
for i from 0 to 6 do B[i] := 4 end do;
for i from 7 to 14 do B[i] := 5 end do;
for i from 15 to 19 do B[i] := 8 end do;
for i from 20 to 30 do B[i] := 12 end do;
for i from 31 to 40 do B[i] := 15 end do;
for i from 41 to 50 do B[i] := 18 end do;
for i from 51 to 101 do B[i] := 24 end do;
g[0] := (1-a0)/(1-Ps(s0));
a[0] := 1-g[0]+g[0]*Ps(B[0]);
for i from 0 to 100 do a[i] := 1-g[i]+g[i]*Ps(B[i]);
g[i+1] := (1-a[i])/(1-Ps(B[i]-1)) end do;
g[100];
A1 := (103/33)*W(s0)/W(B[0]+1); C := 10/11;
U[1] := 1; for i from 2 to 100 do U[i] := U[i-1]*C*W(B[i-1]-1)/W(B[i]+1) end do;
F := evalf(A1*(sum(U[k], k = 1 .. 100)));
Conflicts of Interest
References
- Albrecher, Hansjörg, and Stefan Thonhauser. 2008. Optimal dividend strategies for a risk process under force of interest. Insurance: Mathematics and Economics 43: 134–49. [Google Scholar] [CrossRef]
- Avanzi, Benjamin. 2009. Strategies for dividend distribution: A review. North American Actuarial Journal 13: 217–51. [Google Scholar] [CrossRef]
- Borch, Karl. 1963. Payment of Dividends by Insurance Companies. Econometrics Research Program Research Memorandum 51: 1–17. Available online: www.princeton.edu/~erp/ERParchives/archivepdfs/M51.pdf (accessed on 5 January 2018).
- Choulli, Tahir, Michael Taksar, and Xun Yu Zhou. 2003. A diffusion model for optimal dividend distribution for a company with constraints on risk control. SIAM Journal on Control and Optimization 41: 1946–79. [Google Scholar] [CrossRef]
- De Finetti, Bruno. 1957. Su un’ impostazione alternativa della teoria collettiva del rischio. Transactions of the XVth International Congress of Actuaries 2: 433–43. [Google Scholar]
- Feng, Runhuan, Hans W. Volkmer, Shuaiqi Zhang, and Chao Zhu. 2015. Optimal dividend policies for piecewise-deterministic compound Poisson risk models. Scandinavian Actuarial Journal 5: 423–54. [Google Scholar] [CrossRef]
- Gerber, Hans-Ulrich. 1969. Entscheidungskriterien für den zusammengesetzten Poisson-Prozess. Schweiz Verein Versicherungsmath Mitt 69: 185–228. [Google Scholar] [CrossRef]
- Hipp, Christian. 2003. Optimal dividend payment under a ruin constraint: Discrete time and state space. Blätter der DGVFM 26: 255–64. [Google Scholar] [CrossRef]
- Hipp, Christian. 2016. Dividend payment with ruin constraint. In Risk and Stochastics: Ragnar Norberg at 70. Edited by Pauline Barrieu. Singapore: World Scientific, ISBN 978-1-7863-45. Available online: https://www.researchgate.net/publication/291339576_Dividend_payment_with_ruin_constraint (accessed on 5 January 2018).
- Hipp, Christian. 2017. Working Paper on Dividend Payment under a Ruin Constraint. Available online: https://www.researchgate.net/publication/318983299_Working_paper_on_dividend_payment_under_a_ruin_constraint (accessed on 5 January 2018).
- Loeffen, Ronnie L. 2008. On optimality of the barrier strategy in de Finetti’s dividend problem for spectrally negative Lévy processes. The Annals of Applied Probability 18: 1669–80. [Google Scholar] [CrossRef]
- Schmidli, Hanspeter. 2007. Stochastic Control in Insurance. Heidelberg, Germany: Springer, ISBN 978-1-84800-003-2. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hipp, C. Company Value with Ruin Constraint in a Discrete Model. Risks 2018, 6, 1. https://doi.org/10.3390/risks6010001
Hipp C. Company Value with Ruin Constraint in a Discrete Model. Risks. 2018; 6(1):1. https://doi.org/10.3390/risks6010001
Chicago/Turabian StyleHipp, Christian. 2018. "Company Value with Ruin Constraint in a Discrete Model" Risks 6, no. 1: 1. https://doi.org/10.3390/risks6010001
APA StyleHipp, C. (2018). Company Value with Ruin Constraint in a Discrete Model. Risks, 6(1), 1. https://doi.org/10.3390/risks6010001



