1. Introduction
Due to the new risk based solvency regulations (such as the Swiss Solvency Test
FINMA (
2007) and Solvency II
European Comission (
2009)), insurance companies must perform two core calculations. The first one involves computing and setting aside the risk capital to ensure the company’s solvency and financial stability, and the second one is related to the
capital allocation exercise. This exercise is a process of splitting the (economic or regulatory) capital amongst its various constituents, which could be different lines of business (LoBs), types of exposures, territories or even individual products in a portfolio of insurance policies. One of the reasons for performing such an exercise is to utilize the results for a risk-reward management tool to analyse profitability. The amount of capital (or risk) allocated to each LoB, for example, may assist the central management’s decision to further invest in or discontinue a business line.
In contrast to the quantitative risk assessment, where there is an unanimous view shared by regulators world-wide that it should be performed through the use of
risk measures, such as the Value at Risk (VaR) or Expected Shortfall (ES), there is no consensus on how to perform capital allocation to sub-units. In this work we follow the Euler allocation principle (see, e.g.,
Tasche (
1999) and (
McNeil et al. 2010, sct. 6.3)), which is briefly revised in the next section. For other allocation principles we refer the reader to
Dhaene et al. (
2012).
Under the Euler principle the allocation for each one of the portfolio’s constituents can be calculated through an expectation conditional on a rare event. Even though, in general, these expectations are not available in closed form, some exceptions exist, such as the multivariate Gaussian model, first discussed in this context in
Panjer (
2001) and extended to the case of multivariate elliptical distributions in
Landsman and Valdez (
2003) and
Dhaene et al. (
2008); the multivariate gamma model of
Furman and Landsman (
2005); the combination of the Farlie-Gumbel-Morgenstern (FGM) copula and (mixtures of) exponential marginals from
Bargès et al. (
2009) or (mixtures of) Erlang marginals
Cossette et al. (
2013); and the multivariate Pareto-II from
Asimit et al. (
2013).
In this work we develop algorithms to calculate the marginal allocations for a generic model, which, invariably, leads to numerical approximations. Although simple Monte Carlo schemes (such as rejection sampling or importance sampling) are flexible enough to be used for a generic model, they can be shown to be computationally highly inefficient, as the majority of the samples do not satisfy the necessary conditioning event (which is a rare event). We build upon ideas developed in
Targino et al. (
2015) and propose an algorithm based on methods from Bayesian Statistics, namely a combination of Markov Chain Monte Carlo (for parameter estimation) and (pseudo-marginal) Sequential Monte Carlo (SMC) for the capital allocation.
As a side result of the allocation algorithm, we are able to efficiently compute both the company’s overall Value at Risk (VaR) and also its Expected Shortfall (ES), (partially) addressing one of the main concerns of
Embrechts et al. (
2014): For High Confidence Levels, e.g.,
and beyond, the “
statistical quantity” VaR Can only Be Estimated with Considerable Statistical, as well as Model Uncertainty. Even though the issue of model uncertainty is not resolved, our algorithm can, at least, help to reduce the “statistical uncertainty”, measured by a variance reduction factor taking as basis a standard Monte Carlo simulation with comparable computational cost.
The proposed allocation procedure is described for a fictitious general insurance company with 9 LoBs (see
Table 1 and
Section 8). Further, within each LoB we also allocate the capital to the one-year reserve risk (due to claims from previous years) and the one-year premium risk.
In order to study the premium risk we follow the framework prescribed by the Swiss Solvency Test (SST) in (
FINMA 2007, sct. 4.4). In this technical document, given company-specific quantities, the distribution of the premium risk is deterministically defined and no parameter uncertainty is involved. For the reserve risk, we use a fully Bayesian version of the gamma-gamma chain ladder model, analysed in
Peters et al. (
2017). As this model is described via a set of unknown parameters, two different approaches to capital allocation are proposed: a
marginalized one, where the unknown parameters are marginalized prior to the allocation process and a
conditional one, which is performed conditional on the unknown parameters and the parameter is integrated out numerically ex-poste.
The remainder of this paper is organized as follows.
Section 2 formally describes marginal risk contributions (allocations) under the marginalized and conditional models.
Section 3 reviews concepts of SMC algorithms and how they can be used to compute the quantities described in
Section 2. We set the notation used for claims reserving in
Section 4, before formally defining the models for the reserve risk (
Section 5) and the premium risk (
Section 6); these are merged together through a copula in
Section 7.
Section 8 and
Section 9 provide details of the synthetic data used, the inferential procedure for the unknown parameters and the implementation of the SMC algorithms. Results and conclusions are presented, respectively, in
Section 10 and
Section 11.
2. Risk Allocation for the Swiss Solvency Test
In this section we follow the Euler allocation principle (see, e.g.,
Tasche (
1999) and (
McNeil et al. 2010, sct. 6.3)) and discuss how the risk capital that is held by an insurance company can be split into different risk triggers. As stochastic models for these risks involve a set of unknown parameters, we present an allocation procedure for a marginalized model (which arises when the parameter uncertainty is resolved beforehand) and a conditional model (which is still dependent on unknown parameters).
Although we postpone the construction of the specific claims payments model to
Section 5 we now assume its behaviour is given by a Bayesian model depending on a generic parameter vector
, for which a prior distribution is assigned. Probabilistic statements, such as the calculation of the risks allocated to each trigger, have to be made based on the available data, described by the filtration
and formally defined in
Section 4. This requirement implies that the uncertainty on the parameter values needs to be integrated out, in a process that must typically be performed numerically.
Therefore, to calculate the risk allocations we approximate the stochastic behaviour of functions of future observations, with the functions defined in
Section 4. For the moment, let us denote by
a multivariate function of
, the future data, and
the vector of model parameters. On the one hand, in the
conditional model, we approximate the distribution of the components of the vector
. On the other hand, in the
marginalized model, the approximation is performed after the parameter uncertainty has been integrated out (i.e., marginalized). In this later framework, we approximate the distribution of the components of
, where the random vector
is defined as
, with expectation taken with respect to
. Note that, given
,
is a random variable, as it depends on future information, i.e.,
. Both in the conditional and in the marginalized models we use moment matching and log-normal distributions for the approximations and couple the distributions via a Gaussian copula.
Suppressing the dependence on the available information, , these two models (marginalized and conditional) are defined through their probability density functions (p.d.f.’s), and , respectively, which are both assumed to be combinations of log-normal distributions and a gaussian copula. For the conditional model, as we work in a Bayesian framework, the unknown parameter vector has a (posterior) distribution with p.d.f. . This is, then, combined with the likelihood to construct , the density used for inference under the conditional model.
For the methodology discussed in this work, the important features of these two models are that is known in closed form, whilst is not.
Remark 1. As the “original” model for claims payments is a Bayesian model, we use the Bayesian nomenclature for both the marginalized and the conditional model. For the former, the Bayesian structure of prior and likelihood is hidden in Equation (1), as the parameter has already been marginalized (with respect to its posterior distribution). For the later, we explicitly make use of the posterior distribution of in Equation (2). Another strategy, followed in Wüthrich (2015), is to use an “empirical Bayes” approach, fixing the value of the unknown parameter vector , for example at its maximum likelihood estimator (MLE). Under the marginalized model we define
as the company’s overall risk. The SST requires the total capital to be calculated as the
ES of
S, given by
In turn, the Euler allocation principle states that the contribution of each component
to the total capital in Equation (
3) is given by
The allocations for the conditional model follows the same structure, with
and
S replaced, respectively, by
and
in Equation (
4) and reads as
with
. For the models discussed below the density of
is not known in closed form, adding one more layer of complexity to the proposed method.
Remark 2. Observe that the log-normal approximations are done at different stages in the marginalized and the conditional models. Therefore, we expect that the results will differ.
Although computing
and
is a
static problem, for the sake of transforming the Monte Carlo estimation into an efficient computational framework, we embed the calculation of these quantities into a sequential procedure, where at each step we solve a simpler problem, through a relaxation of the rare-event conditioning constraint to a sequence of less extreme rare-events. In the next section we discuss the methodological Monte Carlo approach used to perform this task. The reader familiar with the concepts of Sequential Monte Carlo methods may skip
Section 3.1.
4. Swiss Solvency Test and Claims Development
For the rest of this work we assume all random variables are defined in the filtered probability space . We denote cumulative payments for accident year until development year (with ) on the LoB by . Moreover, in the ℓ-th LoB incremental payments for claims with accident year i and development year j are denoted by . Remark that these payments are made in accounting year .
The information (regarding claims payments) available at time
for the
ℓ-th LoB is assumed to be given by
and, similarly, the total information (regarding claims payments) available at time
t is denoted as
Remark 6. By a slight abuse of notation we also use and for the sigma-field generated by the corresponding sets. Note that for all , as we assume that contains not only information about claims payments, but also about premium and administrative costs.
The general aim now is to predict the future cumulative payments
for
at time
t, given the information
, in particular, the so-called ultimate claim
. For more information we refer to
Wüthrich (
2015).
4.1. Conditional Predictive Model
As noted previously, we generically denote parameters in the Bayesian model for the ℓ LoB by . For the ease of exposition, whenever a quantity is defined conditional on it is going to be denoted with a bar on top of it.
At time
, LoB
ℓ and accident year
predictors for the ultimate claim
and the corresponding claims reserves are defined, respectively, as
Under modern solvency regulations, such as Solvency II
European Comission (
2009) and the Swiss Solvency Test
FINMA (
2007) an important variable to be analysed is the claims development result (CDR). For accident year
, accounting year
and LoB
ℓ, the CDR is defined as
and an application of the tower property of the expectation shows that (subject to integrability)
Thus, the prediction process in Equation (
21) is a martingale in
t and we aim to study the volatility of these martingale innovations.
Equation (
23) justifies the prediction of the CDR by zero and the uncertainty of this prediction can be assessed by the conditional mean squared error of prediction (msep):
Moreover, we denote the aggregated (over all accident years) CDR and the reserves, conditional on the knowledge of the parameter
, respectively, by
Using this notation we also define the total prediction uncertainty incurred when predicting
by zero as
Remark 7. It should be remarked that, in general, as the parameter vector is unknown none of the quantities presented in this section can be directly calculated unless an explicit estimate for the parameter is used.
4.2. Marginalized Predictive Model
Even though cumulative claims models are defined conditional on unobserved parameter values, any quantity that has to be calculated based on these models should only depend on observable variables. Under the Bayesian paradigm, unknown quantities are modelled using a prior probability distribution reflecting prior beliefs about these parameters.
Analogously to
Section 4.1 we define the marginalized (Bayesian) ultimate claim predictor and its reserves, respectively, as
We also define the marginalized CDR and notice, again using the tower property, that its mean is equal to zero
Furthermore, summing over all accident years
i we follow Equation (
26) and denote by
and
the aggregated version of the marginalized reserves and CDR, where the uncertainty in the later is measured via
4.3. Solvency Capital Requirement (SCR)
In this section we discuss how two important concepts in actuarial risk management, namely the technical result (TR) and the solvency capital requirement (SCR), can be defined for both the conditional and the marginalized models.
In this context the TR is calculated netting all income and expenses arising from the LoBs, while the SCR denotes the minimum capital required by the regulatory authorities in order to cover the company’s business risks. More precisely, the SCR for accounting year quantifies the risk of having a substantially distressed result at time , evaluated in light of the available information at time t.
As an important shorthand notation, we introduce three sets of random variables, representing the total claim amounts of the current year (CY) claims and of prior year (PY) claims, the later for both the conditional and marginalized models. These random variables are defined, respectively, as
In the standard SST model, CY claims do not depend on any unknown parameters and are split into small claims for the LoBs and into large events for the perils . Small claims are also called attritional claims and large claims can be individual large claims or catastrophic events, like earthquakes. In this context the company can choose thresholds such that claims larger than these amounts are classified as large claims in its respective LoBs.
To further simplify the notation we also group all the random variables related to the conditional and the marginalized models in two random vectors, defined as follows
Next we give more details on how the TR and the SCR are calculated in the generic structure of the conditional and the marginalized models.
4.3.1. SCR for the Conditional Model
At time
the technical result (TR) of the
ℓ-th LoB in accounting year
based on the conditional model is defined as the following
–measurable random variable:
where
and
are, respectively, the earned premium and the administrative costs of accounting year
. For simplicity, we assume that these two quantities are known at time
t, i.e., the premium and administrative costs of accounting year
are assumed to be previsible and, hence,
-measurable. Moreover, it should be noticed that in this context
not only includes the claims payment information defined in Equation (
20). The general sigma-field
should be seen as a sigma-field generated by the inclusion in
of the information about
and
, for
.
Given the technical result for all the LoBs, the company’s overall TR based on the conditional model, and aggregated cost and premium are denoted, respectively, by
In order to cover the company’s risks over an horizon of one year, the Swiss Solvency Test is concerned with the 99% ES (in light of all the data up to time
t):
where
denotes the solvency capital requirement.
It is important to notice that even though the ES operator is being applied to a “conditional random variable”, namely
, the operator is
not being taken conditional on the knowledge of
, otherwise this quantity would not be computable (as discussed in Remark 7). Instead, the SCR is calculated based on the marginalized version of the conditional model, where the parameter uncertainty is integrated out. More precisely, the expected shortfall is based on the following (usually intractable) distribution
In order to compute the SCR based on the conditional model we first discuss the measurablity of the terms in the conditional TR, which can be rewritten as
From the above equation we see the first two terms are, by assumption,
measurable and so are all the terms of the form
(payments already completed by time
t), while the last summation is
measurable and, therefore, a random variable at time
t. Due to the dependence on the unknown parameter
the conditional ultimate claim predictor
is usually
not measurable. However, under the special models introduced in
Section 5 we have that
depends only on the claims data up to time
t and not on the unknown parameter vector, making it
measurable. In this case one has
where, by assumption,
is
-measurable.
4.3.2. SCR for the Marginalized Model
As the parameter uncertainty is dealt with in a previous step, the calculation of the SCR for the marginalized model is simpler than its conditional counterpart.
Similarly to the conditional case, we define the TR for the marginalized model as
and its aggregated version as
Furthermore, the SCR for the marginalized model is given by
where in this case the expected shortfall is calculated with respect to the density
.
Remark 8. For the models discussed in Section 5, as does not depend on the parameter vector and we also have that . Remark 9. As we assume the cost of claims processing and assessment and premium are known at time t they do not differ from the conditional to the marginalized model.
5. Modelling of Individual LoBs PY Claims
For the modelling of the PY claims reserving risk we need to model
or
as given in Equation (
29). The uncertainty in these random variables will be assessed by the conditional and marginalized mean square error of prediction (msep), introduced in Equations (25) and (28). In order to calculate the msep we must first expand our analysis to the study of the claims reserving uncertainty. To do so, in this section we present a fully Bayesian version of the gamma-gamma chain-ladder (CL) model, which has been studied in
Peters et al. (
2017).
Since in this section we present the model for individual LoBs, for notational simplicity we omit the upper index from all random variables and parameters.
Model Assumptions 1. [Gamma-gamma Bayesian chain ladder model] We make the following assumptions:
- (a)
Conditionally, given and , cumulative claims are independent (in accident year i) Markov processes (in development year j) withfor all and . - (b)
The parameter vectors and are independent.
- (c)
For given hyper-parameters the components of are independent such thatfor , where the limit infers that they are eventually distributed from an improper uninfomative prior. - (d)
The components of are independent and -distributed, having support in for given constants for all .
- (e)
, and are independent and , for all .
In Model Assumptions 1 (c) the (improper) prior distribution for
should be seen as a non-informative limit when
of the (proper) prior assumption
The limit in (c) does not lead to a proper probabilistic model for the prior distribution, however, based on “reasonable” observations
the posterior model can be shown to be well defined (see Equation (
38)), a result that has been proved using the dominated convergence theorem in
Peters et al. (
2017).
From Model Assumptions 1 (a), conditional on a specific value of the parameter vectors
and
, we have that
which provides a stochastic formulation of the classical CL model of
Mack (
1993).
Even though the prior is assumed improper and does not integrate to one, the conditional posterior for
is proper and, in addition, also gamma distributed (see
Appendix A and (
Merz and Wüthrich 2015, Lemma 3.2)). More precisely, we have that
with the following parameters
Therefore, given
this model belongs to the family of Bayesian models with conjugate priors that allows for closed form (conditional) posteriors – for details see
Wüthrich (
2015).
The marginal posterior distribution of the elements of the vector
is given by
with
and
defined in Equation (
37). We note that as long as Model Assumptions 1 (d) and the conditions in Lemma A1 are satisfied, then one can ensure the posterior distribution of
is proper.
Therefore, under Model Assumptions 1 inference for all the unknown parameters can be performed. It should be noticed, though, that differently from the (conditional) posteriors for
Equation (
36), the posterior for
Equation (
38) is not recognized as a known distribution. Thus, whenever expectations with respect to the distribution of
need to be calculated one needs to make use of numerical procedures, such as numerical integration or Markov Chain Monte Carlo (MCMC) methods.
5.1. MSEP Results Conditional on
Following Model Assumptions 1 we now discuss how to explicitly calculate the quantities introduced in
Section 4. We start with the equivalent of the classic CL factor. From the model structure in Equation (
35) we define the posterior Bayesian CL factors, given
, as
which, using the gamma distribution from Equation (
36), takes the form
i.e.,
is identical to the classic CL factor estimate.
Following Equation (
21) we define the conditional ultimate claim predictor
which can be shown (see (
Wüthrich 2015, Theorem 9.5)) to be equal to
where this is exactly the classic chain ladder predictor of
Mack (
1993). For this reason we may take Model Assumptions 1 as a distributional model for the classical CL method. Additionally, the conditional reserves defined in Equation (
21) and Equation (
26) are also the same as the classic CL ones, that is,
The importance of Equation (
40) relies on the fact that it does not depend on the parameter vector
. In other words, the ultimate claim predictor based on the Bayesian model from Model Assumptions 1 conditional on
– which is, in general, a random variable – is a real number (independent of
). This justifies the argument used on the calculation of Equation (
32).
Remark 10. Using the notation from the previous sections the parameter vector plays the role of as the only unknown, since, due to conjugacy properties, can be marginalized analytically.
For the Bayesian model from Model Assumptions 1 the msep conditional on
has been derived in (
Wüthrich 2015, Theorem 9.16) as follows, for
where
Moreover, the conditional msep has been shown to be finite if, and only if,
. We also refer to Remark 12, below.
The aggregated conditional msep for
is also derived in (
Wüthrich 2015, Theorem 9.16), and given by
Remark 11. The assumption that is made in order to guarantee the conditional msep is finite and we enforce this assumption to hold for all the examples presented in this work. See also Remark 12, below.
5.2. Marginalized MSEP Results
The results in the previous section are based on derivations presented in
Merz and Wüthrich (
2015) and
Wüthrich (
2015) where the parameter vector
is assumed to be known. In this section we study the impact of the uncertainty in
over the mean and variance of
in light of Model Assumptions 1, which can be seen as a fully Bayesian version of the models previously mentioned.
In order to have well defined posterior distributions for , through this section we follow Lemma A1 and assume that, for all development years and , we have or at least one accident year is such that . For all the numerical results presented this assumption is satisfied.
Lemma 1. The ultimate claim estimator under the marginalized model is equal to the classic chain ladder predictor, i.e., .
Proof. Due to the posterior independence of the elements of
(also used in Equations (
39) and (
40)) and the fact that
does not depend on
we have
Proposition 1. The msep in the marginalized model is equal to the posterior expectation of the msep in the conditional model, i.e., Proof. From the law of total variance we have that
and the last equality follows from Lemma 1 and the fact that
is independent of
. ☐
Remark 12. Following the conditions required for finiteness of the conditional msep, in the unconditional case, one can see that whenever . Furthermore, we note that this condition can be controlled during the model specification, i.e., the range of the is chosen such that all posteriors are well-defined.
5.3. Statistical Model of PY Risk in the SST
Note that the distributional models derived in
Section 5.1 and
Section 5.2 are rather complex. To maintain some degree of tractability, the overall PY uncertainty distribution is usually approximated by a log-normal distribution via a moment matching procedure.
5.3.1. Conditional PY Model
As discussed in
Section 4.3, when modelling the risk of PY claims we work with the random variables
, defined in Equation (
29). Due to their relationship with the conditional CDR, see Equations (
22) and (
23) and the results discussed in
Section 5.1, we can use the derived properties of these random variables to construct the model being used for
.
The conditional mean (see Equations (
22), (
23) and (
41)) and variance (see Equations (25) and (44)) of the random variable
are as follows
Given mean and variance, we make the following approximation, also proposed in the Swiss Solvency Test (see (
FINMA 2007, sct. 4.4.10)).
Model Assumptions 2 (Conditional log-normal approximation)
. We assume thatwith and . Although the distribution of
under Model Assumptions 1 can not be described analytically it is simple to simulate from it. To test the approximation of Model Assumptions 2 we simulate its distribution under the gamma-gamma Bayesian CL model (with fixed
) and compare it against the log-normal approximation proposed. For the hyper-parameters presented in
Table 2 (and calculated in
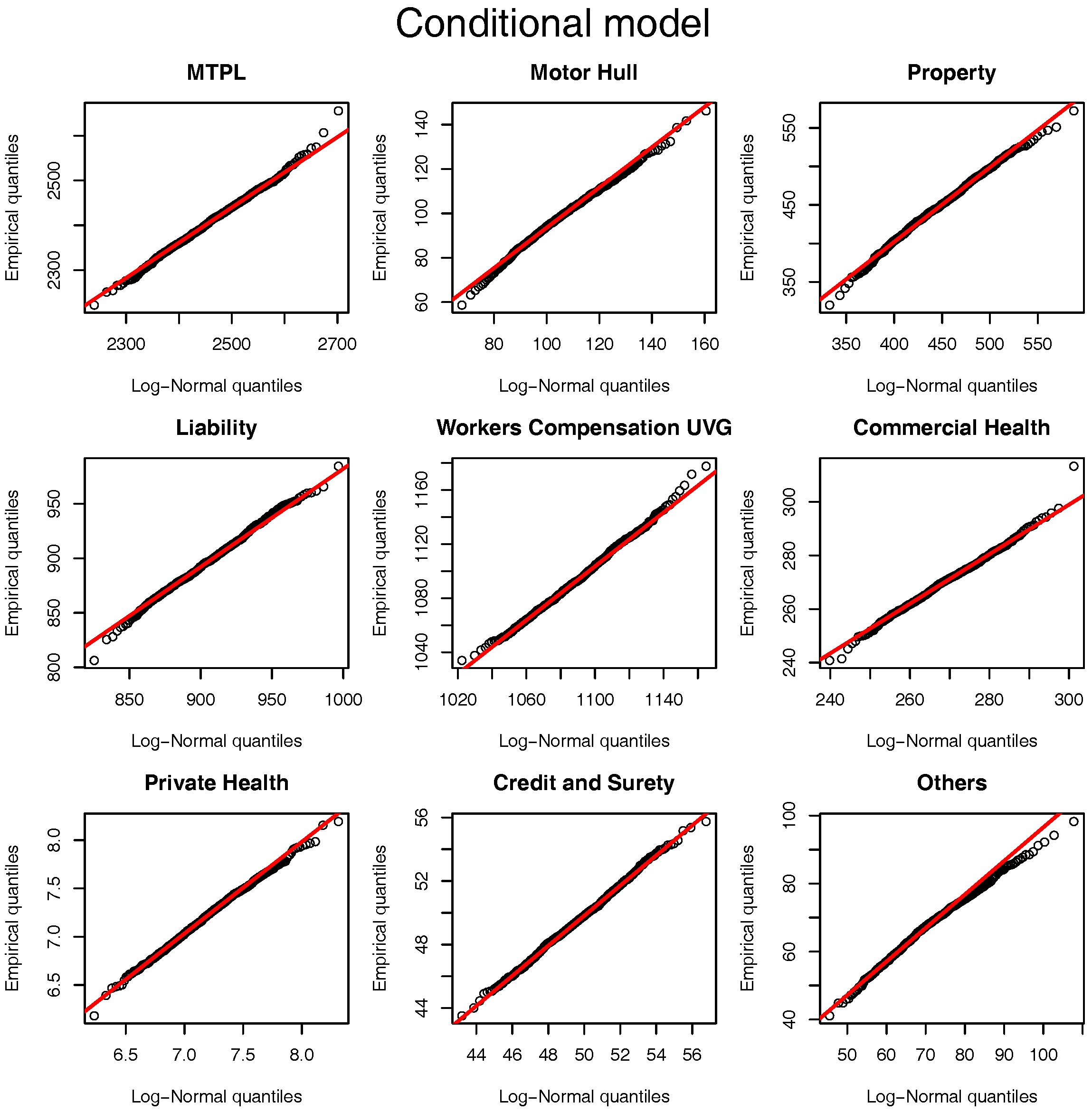
Section 8) the quantile-quantile plot of the approximation is presented in
Figure 1. For all the LoBs we see that the log-normal distribution is a sensible approximation to the original model assumptions. Note that although the parameters used for the comparison are based on the marginalized model Figure 5 and Figure 6 show that they are “representative” values for the distributions of
and
.
5.3.2. Marginalized PY Model
As an alternative to the conditional Model Assumptions 2 we use the moments of
calculated in Lemma 1 and Proposition 1 and then approximate its distribution. Note that due to the intractability of the distribution of
the variance term defined in Equation (
45) can only be calculated numerically, for example, via MCMC.
Model Assumptions 3 (Marginalized log-normal approximation)
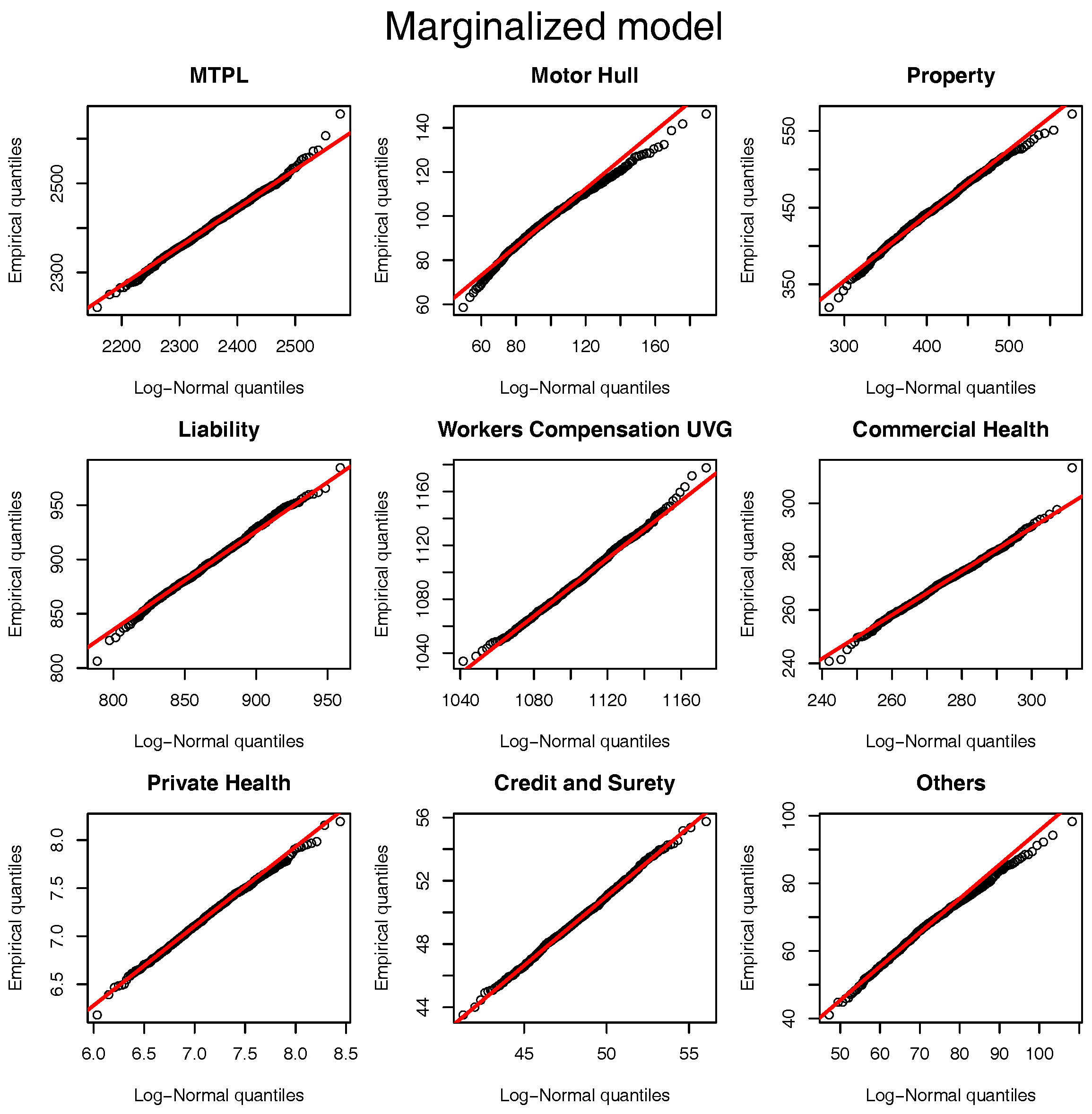
. We assume thatwith and . The same comparison based on the quantile-quantile plot of
Figure 1 can be performed for the marginalized model and the results are presented in
Figure 2. Once again, the log-normal model presents a viable alternative to the originally postulated gamma-gamma Bayesian CL model, even though for Motor Hull, Property and Others the right tail of the log-normal distribution is slightly heavier.
7. Joint Distribution of PY and CY Claims
Although the SST does not assume any parametric form for the joint distribution of
or
(defined in Equations (
30) and (
31), respectively) it is required that a pre-specified
correlation matrix is used (see
FINMA (
2016)). In this section we discuss how to use the conditional and marginalized models to define a joint distribution satisfying this correlation assumption.
It is important to notice, though, that the SST correlation matrix may not be attainable for some joint distributions, as discussed in
Appendix B in the case of log-normal marginals (in
Devroye and Letac (
2015) the authors discuss a similar problem). Let us denote by
the set of all
, symmetric, positive semi-definite matrices with diagonal terms equal to 1; and by
the correlation matrix of a random vector
, with elements
. The question asked in
Devroye and Letac (
2015) is: given
, does there exist a copula
C such that
? The answer is
yes, if
and the authors postulate that for
there exists
such that there is no copula
C such that
.
It should be noted that, since in the SST the CY large claims are assumed to be independent from all the other risks, the correlation matrix of is essentially a correlation matrix between and the same is true also for the conditional model.
Regardless of assuming a conditional or a marginalized model, SST’s correlation matrix
should be such that, for
(recall that
L are the number of LoBs and
P the number of perils),
Remark 14. In the conditional model we need to “integrate out” the parameter uncertainty, otherwise the (conditional) correlation would be dependent on an unknown parameter and could not be matched with the numbers provided by the SST.
7.1. Conditional Joint Model
Under Model Assumptions 2, 4, 5 and 6 our interest lies on modelling the joint behaviour of the vector . Under Model Assumptions 1 it can be shown that the required conditional independence between and given is equivalent to the conditional independence between and given and .
Moreover, since all the marginal conditional distributions of the prior year claims and small current year claims are assumed to be log-normal, following Equations (
30) and (
31), the notation can be further simplified to
with
, and
defined in Model Assumptions 2 and 4. For example, for
,
, defined in Model Assumptions 4.
We are now ready to define the joint conditional model to be used.
Model Assumptions 7 (Conditional joint model)
. Based on Model Assumptions 2 and 4 we link the marginals of the conditional model through a Gaussian copula with correlation matrix , with elements . More formally, given and the joint distribution of is given bywhere denotes the conditional distribution of defined in Equation (52) and is the Gaussian copula with correlation matrix denoted by . Remark 15. In this section the parameter matrix should be understood as a deterministic variable, differently from and . For this reason we do not include it on the right hand side of the conditioning bar. Instead, whenever needs to be explicitly written, we include it on the left hand side of the bar, separated by the function (or functional, for expectations) arguments by a semicolon.
In order to match SST’s correlation matrix
, under Model Assumptions 1 and 4, the following equation needs to be solved with respect to
:
To compute the right hand side of the equation above we first notice that
where, from Equation (
46) and the discussion in
Section 6.1,
and from Equation (A3),
Appendix B,
Therefore, to satisfy Equation (
53)
needs to be chosen such that the following implicit relationship (which can be solved through any univariate root search algorithm) holds:
7.2. Marginalized Joint Model
Similarly to
Section 7.1, in this section we will fully characterize the joint distribution of
under Model Assumptions 3, 4, 5 and 6.
From these assumptions we define the following notation:
Model Assumptions 8 (Marginalized joint model)
. Based on Model Assumptions 3 and 4 we link the marginal distributions of the marginalized model through a Gaussian copula with correlation matrix , with elements . More formally, given the joint distribution of is given bywhere denotes the conditional distribution of defined in (Equation 54) and is the Gaussian copula with correlation matrix . In order to match SST’s correlation matrix, in the joint marginalized model the Gaussian copula correlation
is chosen such that (see Equation (A4),
Appendix B) it satisfies
10. Results
In this section we present the results of the SMC procedure when used to calculate the expected shortfall allocations from Equations (
4) and (
5) of the solvency capital requirement.
Before proceeding to the results calculated via the SMC algorithm, in order to understand the simulated data presented in
Figure 4, in
Table 2 we present some results based on a “brute force” Monte Carlo (rejection-sampling) simulation, which is taken as the base line for comparisons with the SMC algorithm. The table is divided in three blocks of rows, with PY claims, CY small (CY,s) claims and CY large (CY,l) claims.
First of all, it should be noticed that the reserves presented on the first block of
Table 2 are the ones implied by the data, which we then assume to be the true ones (ignoring, from now on, the initial synthetic data from
Table 1). That is, based on initial parameters we have generated synthetic claims development triangles, which naturally deviate slightly from their expected values. The parameters
and
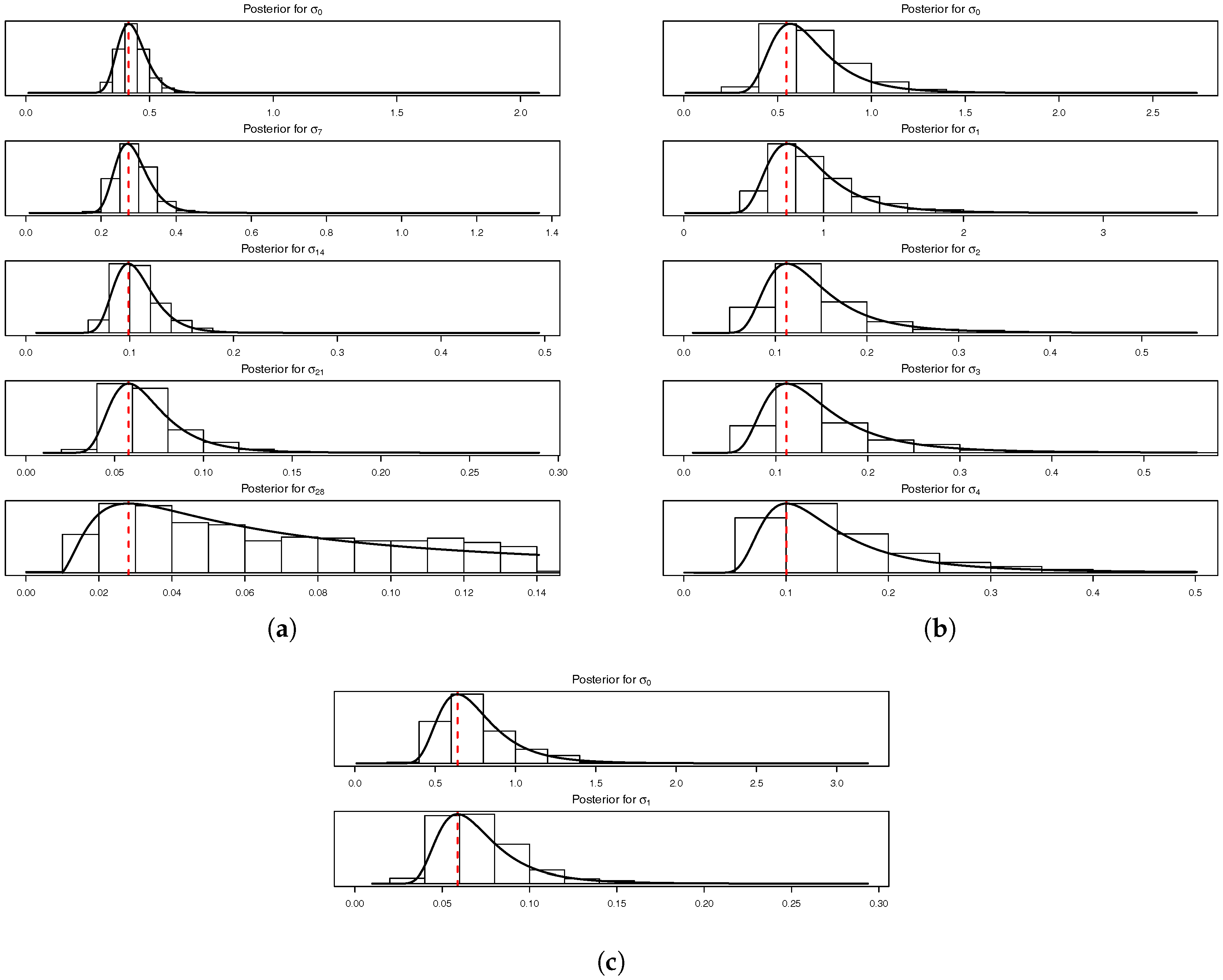
for PY claims are related to the marginalized model (for the parameters of the conditional model see
Figure 5 and
Figure 6). It is also important to note that only the PY parameters are different between the conditional and marginalized models.
For each LoB the standalone expected shortfall (ES) is calculated analytically and its value is, then, combined with the LoB’s expectation to calculate the solvency capital requirement (SCR). These values are added up, both within risk type (i.e., PY, CY,s and CY,l) and globally, in order to calculate the overall standalone capital. For the marginalized and conditional models the columns “ES” and “SCR” denote, respectively, the expected shortfall and capital allocations to each LoB. These values are compared to their standalone counterparts to generate the diversification benefit, which is around 45% for PY and CY,s claims (regardless of the model used) and ranges between 30% and 70% within the PY and CY,s groups. Due to the independence assumptions the largest diversification benefit comes from the CY,l claims, where the capital is reduced by around 95%.
The data presented in
Table 2 is calculated as follows. For the marginalized model (and conditional model in brackets),
(
) independent samples of the model are generated in order to calculate the overall
. Conditional on this value, for each LoB we then generate
(
) samples above the VaR and use the average of these samples as the true ES allocation (presented in
Table 2). In order to asses the variance of the estimators, we divide these samples into
groups of
(
for the conditional model) simulations. More formally, we approximate the ES allocations
, defined in Equation (
4), by
where
stands for the estimate (using
particles) from the
k-th run (out of
), which is defined according to
Similarly to the analysis performed in
Peters et al. (
2017) the impact of the prior density can be assessed by comparing the sum of the SCR allocations with the SCR from the “empirical Bayes model”, i.e., the model where the prior for
is set as a Dirac mass on
, see Equation (
55). In this case we have that the total capital is equal to SCR = 505.48 and the fully Bayesian model with prior defined with
(see
Section 8.3) requires
more capital (both in the marginalized and conditional cases).
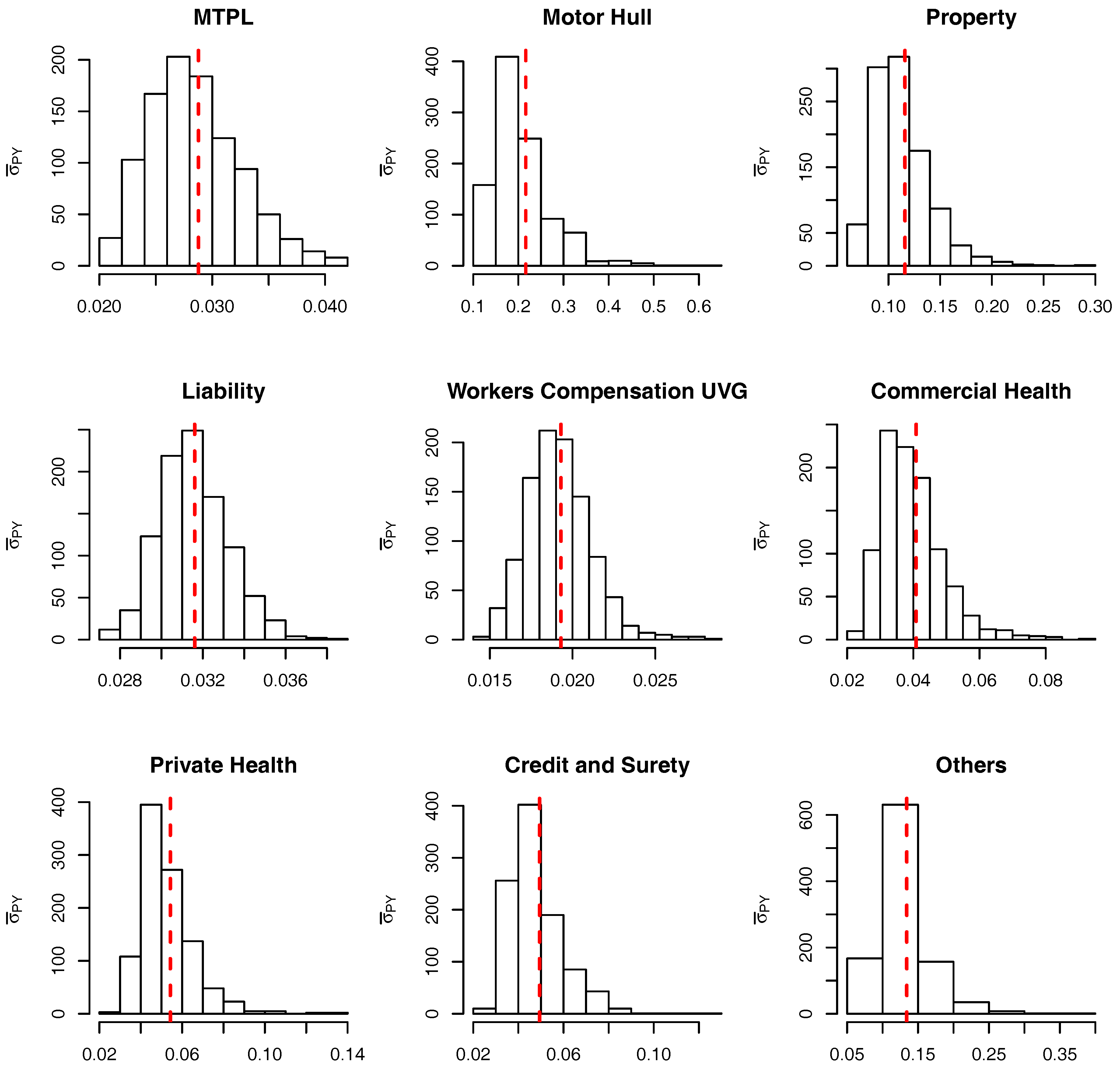
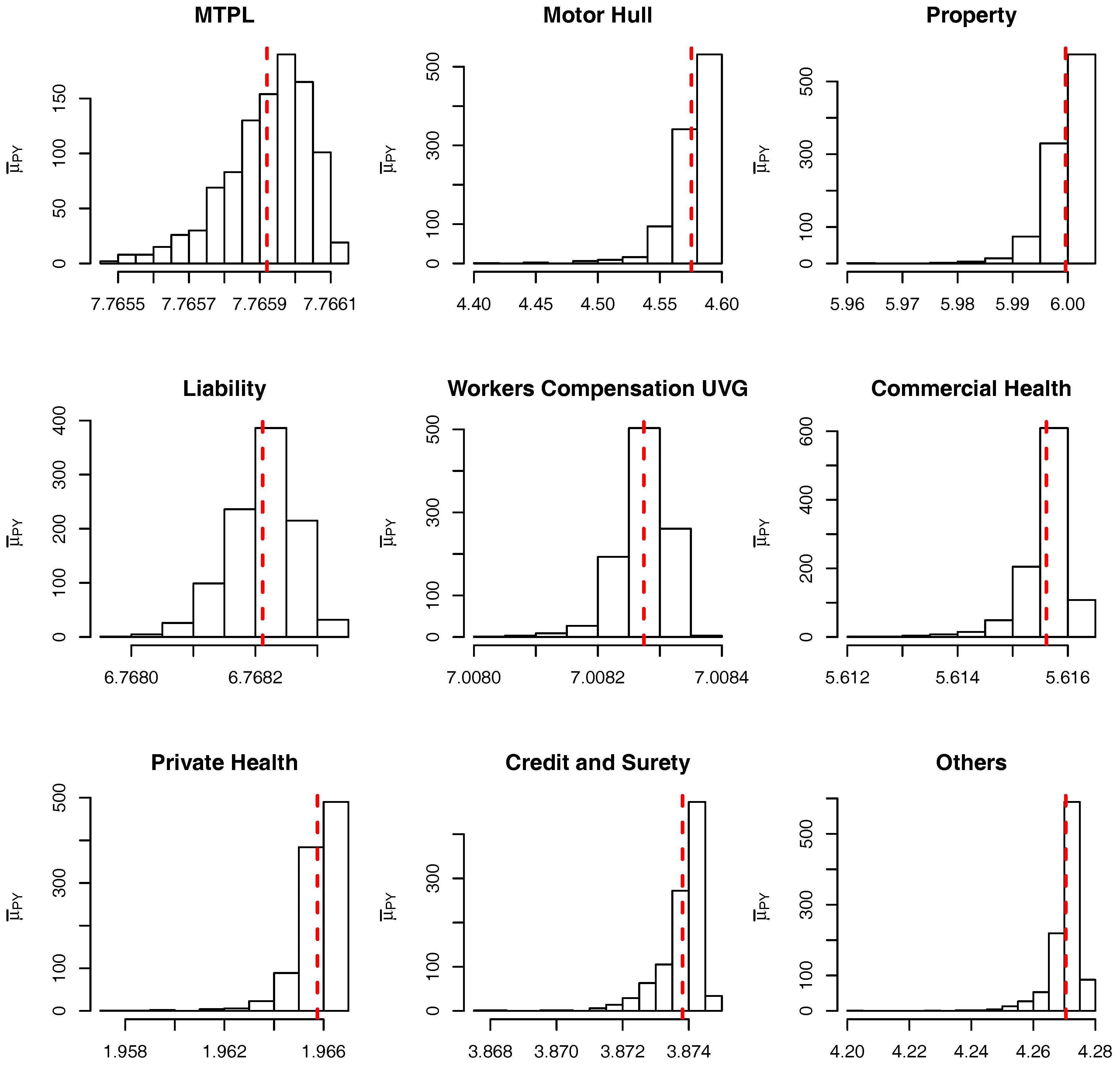
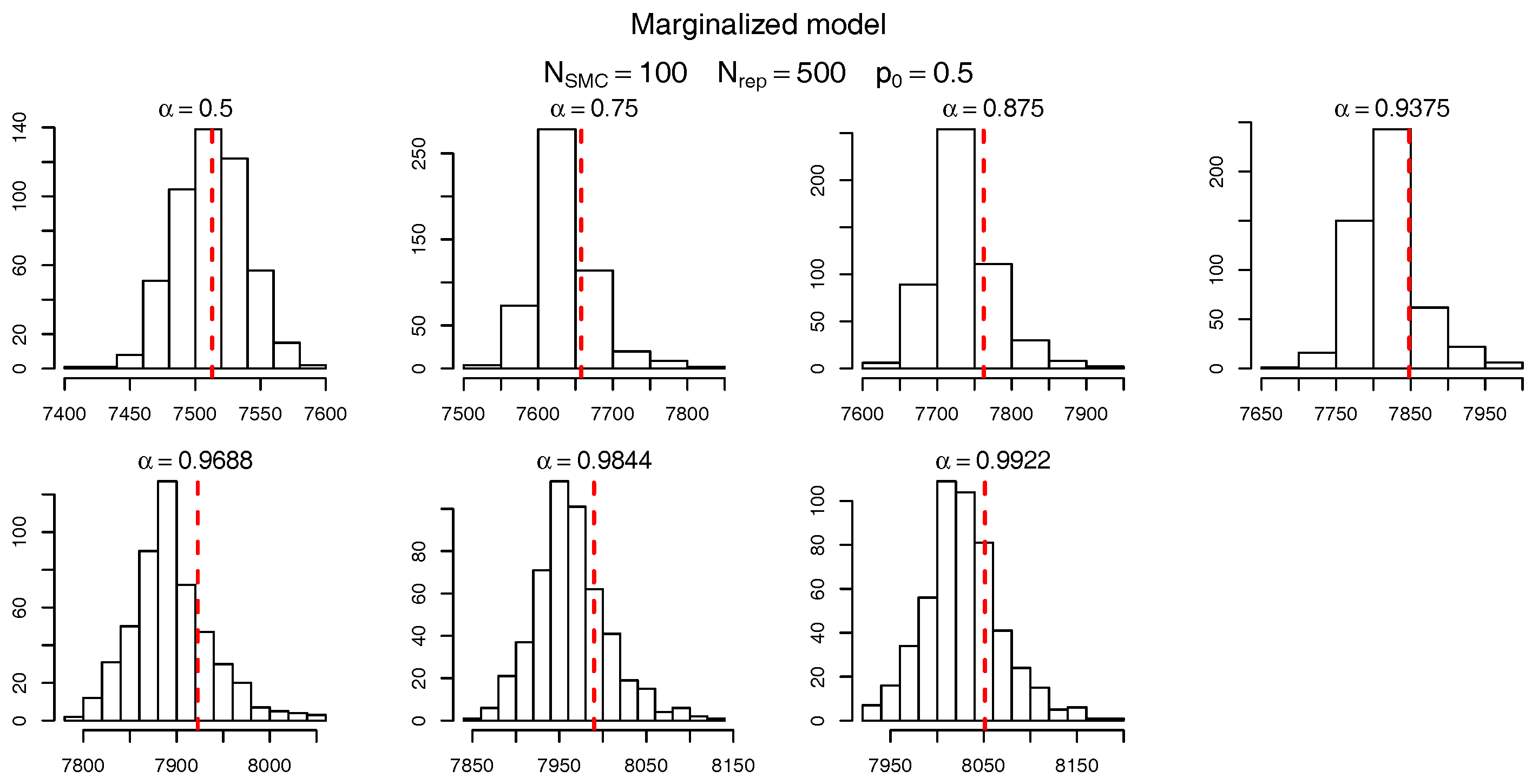
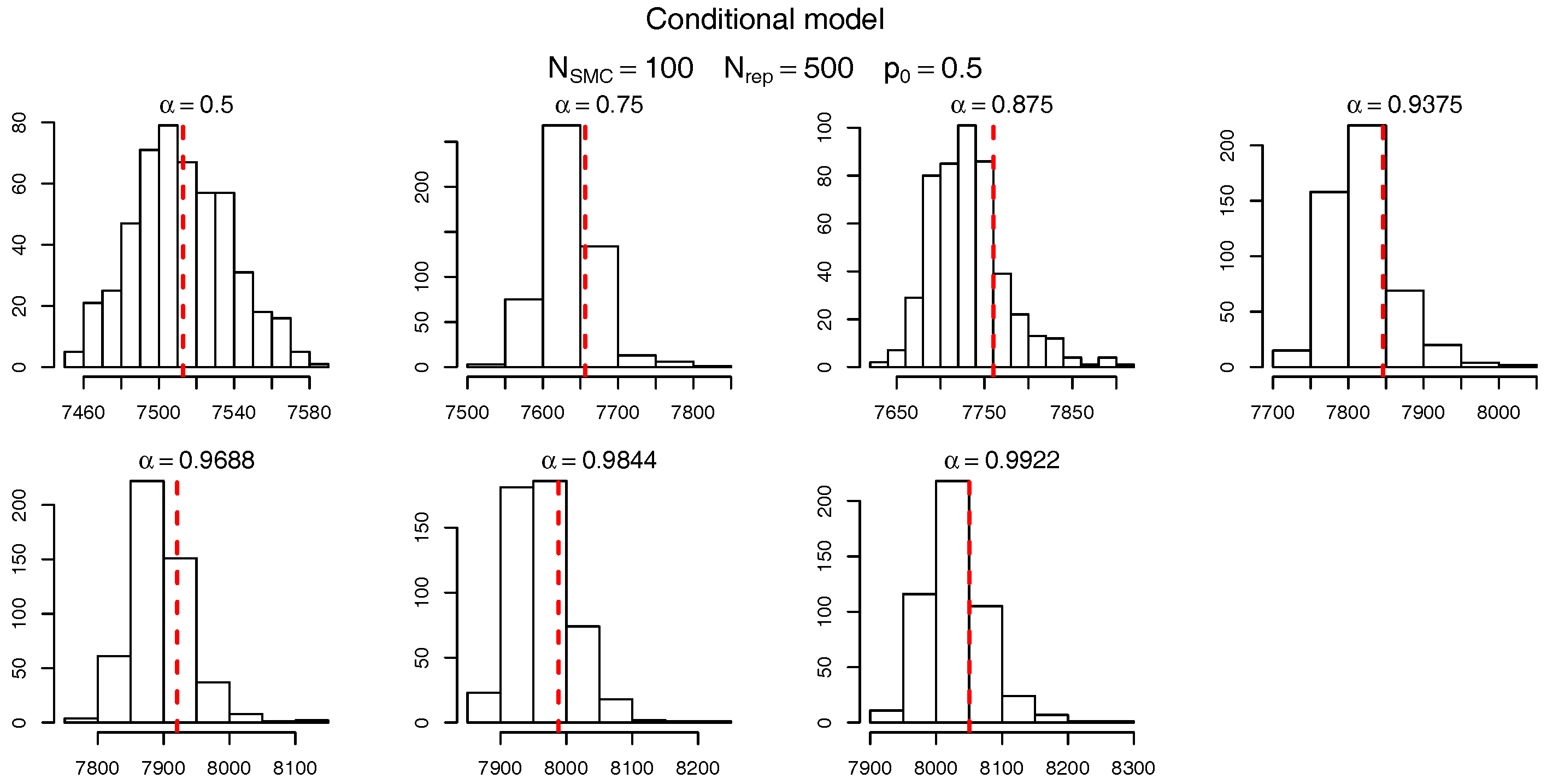
To check the accuracy of the SMC procedure we first analyse the estimate of the level sets (intermediate VaRs). For
,
Figure 7 and
Figure 8 show, respectively, the histogram of the levels
(as per
Table 10) for the marginalized and conditional models. The red dashed bars represent the true value of the quantiles (based on the “brute force” MC simulations), which is very close to the mode of the empirical distribution of the SMC estimates. It should be noticed, though, that the SMC estimates seem to be negatively biased and the bias appears to become more pronounced for extreme quantiles. Apart from this negligible bias we assume the levels are being sensibly estimated and proceed, as in
Targino et al. (
2015), to calculate the relative bias and the variance reduction of the SMC method when compared to a MC procedure.
For each of the LoBs the plots on the
Figure 9 and
Figure 10 show the relative bias, defined as
where
is computed analogously to the MC estimate but, instead, using the SMC method, with
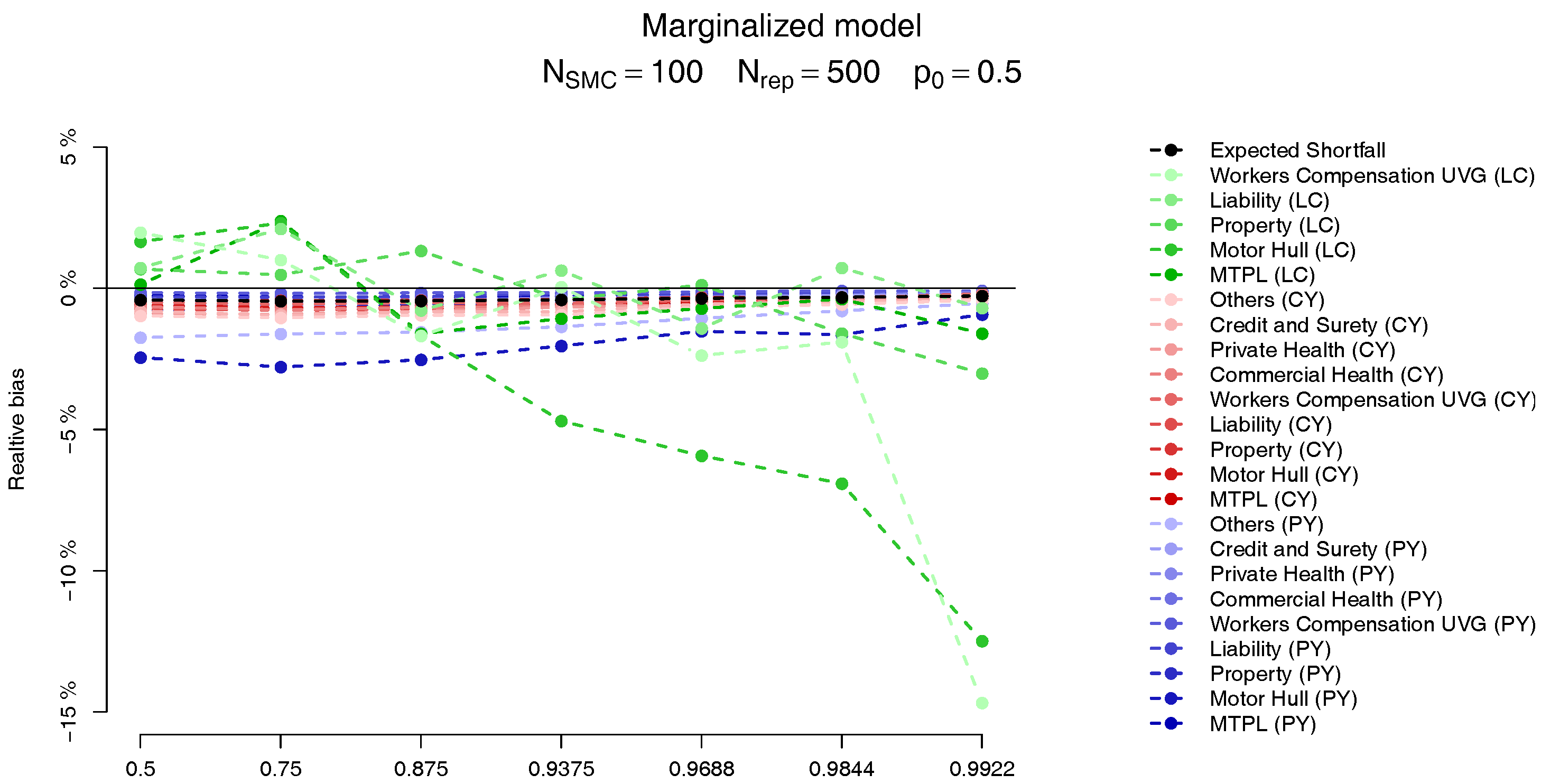
. The behaviour of the two models is very similar, and we observe that the bias in the PY and CY,s allocations are negligible (less than 5%) while for some of the large CY risks a higher bias (of more than 10%) may be observed. Apart from the difficulty of performing the estimation based on Pareto distributions we stress the fact that although these errors may look large, as we can see from
Table 2, their impact in the overall capital are almost imperceptible, due to the small capital charge due to these risks.
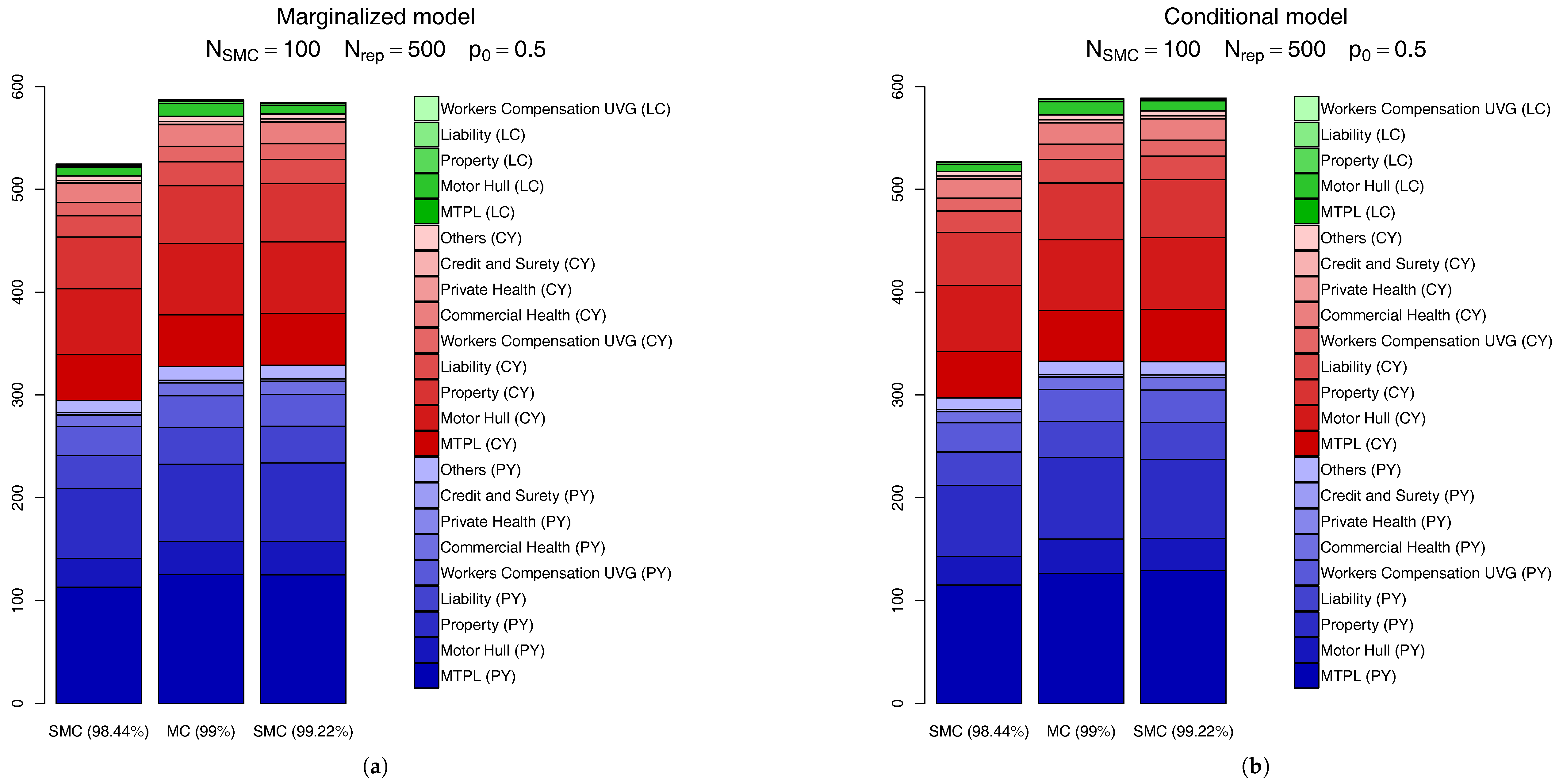
Another way to compare the SMC calculations is through the actual capital charges, as seen in
Figure 11. In this figure we compare the
SCR calculated via the MC scheme discussed above with the SMC results for the quantile level right before
(which, for
is
) and the one right after it (
). From this figure we see the SMC calculation based on the
quantile is very precise, for both the marginalized and conditional models. Visually, the only perceivable difference comes from the CY,l claims, which accounts (in total) for less than
of the overall capital.
To calculate the improvement generated by the SMC algorithm compared to the MC procedure we need to analyse the variance of the estimates generated by both methods, under similar computational budgets.
We start by noticing that the expected number of samples in the Monte Carlo scheme in order to have
samples satisfying the
condition is equal to
, which can be prohibitive if
is very close to 1. Then, similarly to Equation (
59) we define the empirical variance of the MC and the SMC algorithms which are, then, compared as follows
The variance reduction statistics defined in Equation (
60) takes into account how many samples one needs to use in order to generate
samples via rejection sampling or
using the SMC algorithm. The later also takes into account the fact that
T levels are being used and in each one
samples need to be generated. For the conditional model we further multiply the denominator by the number of samples used to estimate the unknown density, which in our examples is set to
.
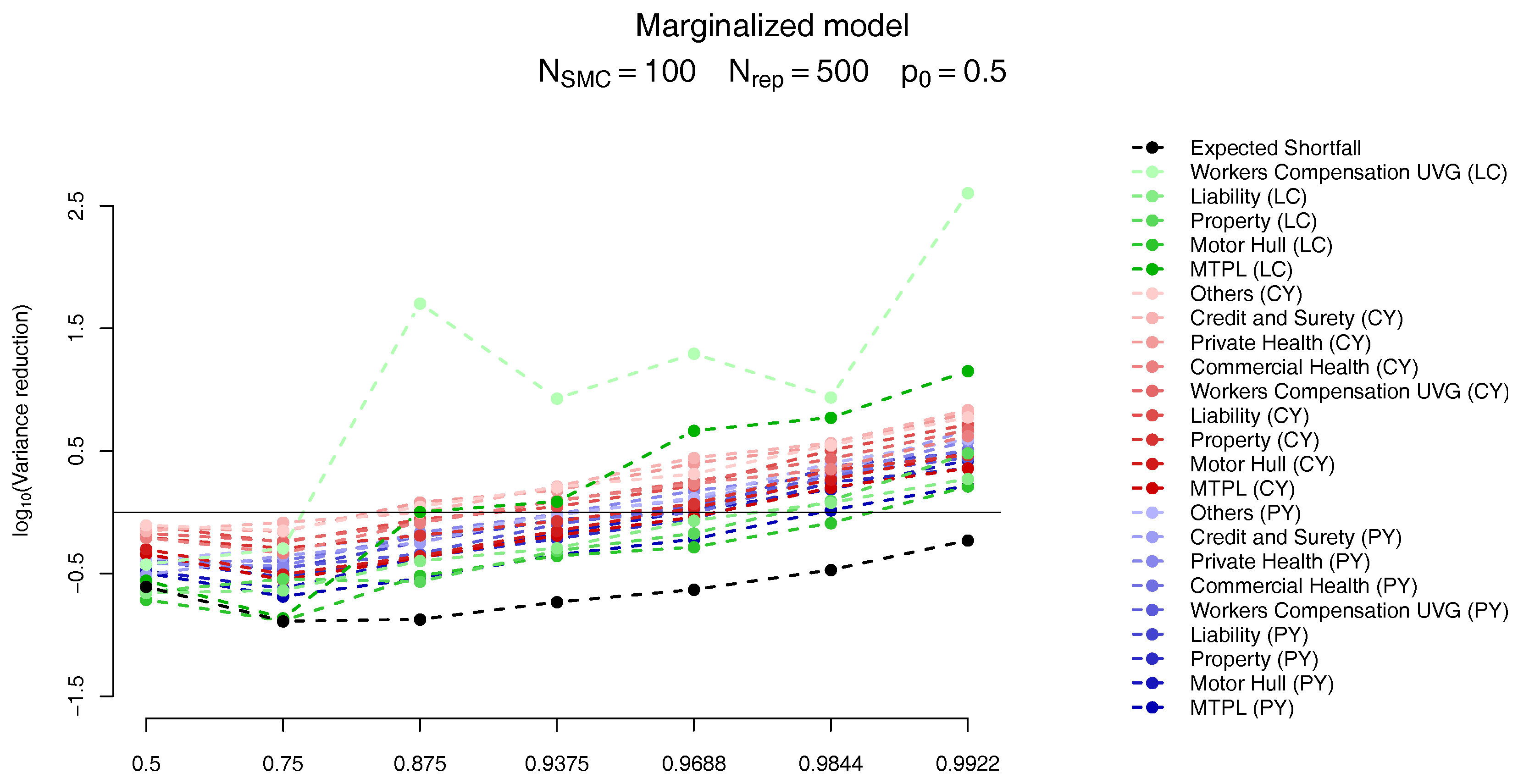
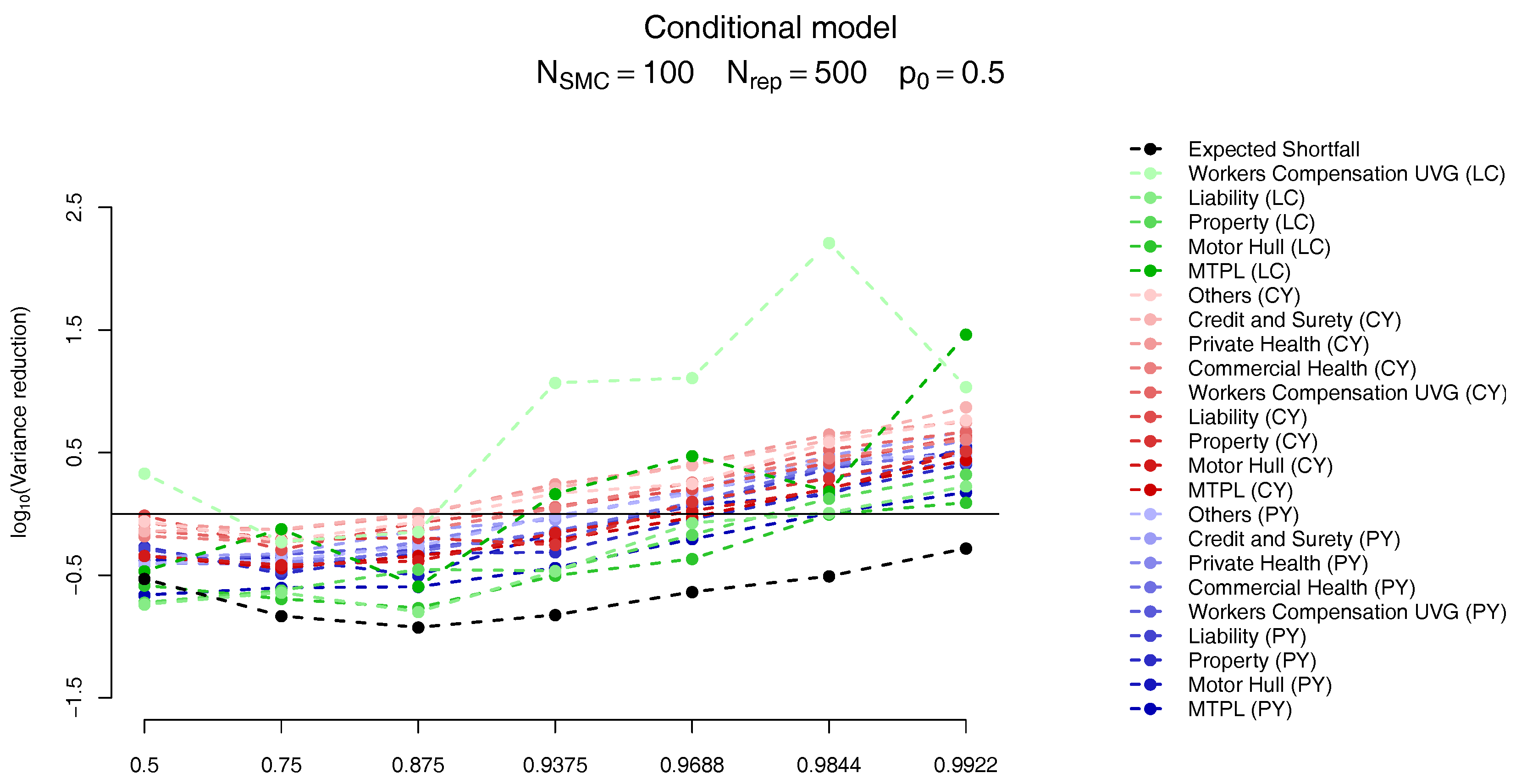
The results follow on
Figure 12 and
Figure 13. As in
Targino et al. (
2015) we observe that the variance of the SMC estimates become smaller (compared to the MC results) for larger quantiles. In particular, for the quantiles of interest the variance of the marginal ES allocation estimates are around
times smaller than its MC counterparts, while the overall ES estimate is slightly less variable for the MC scheme.
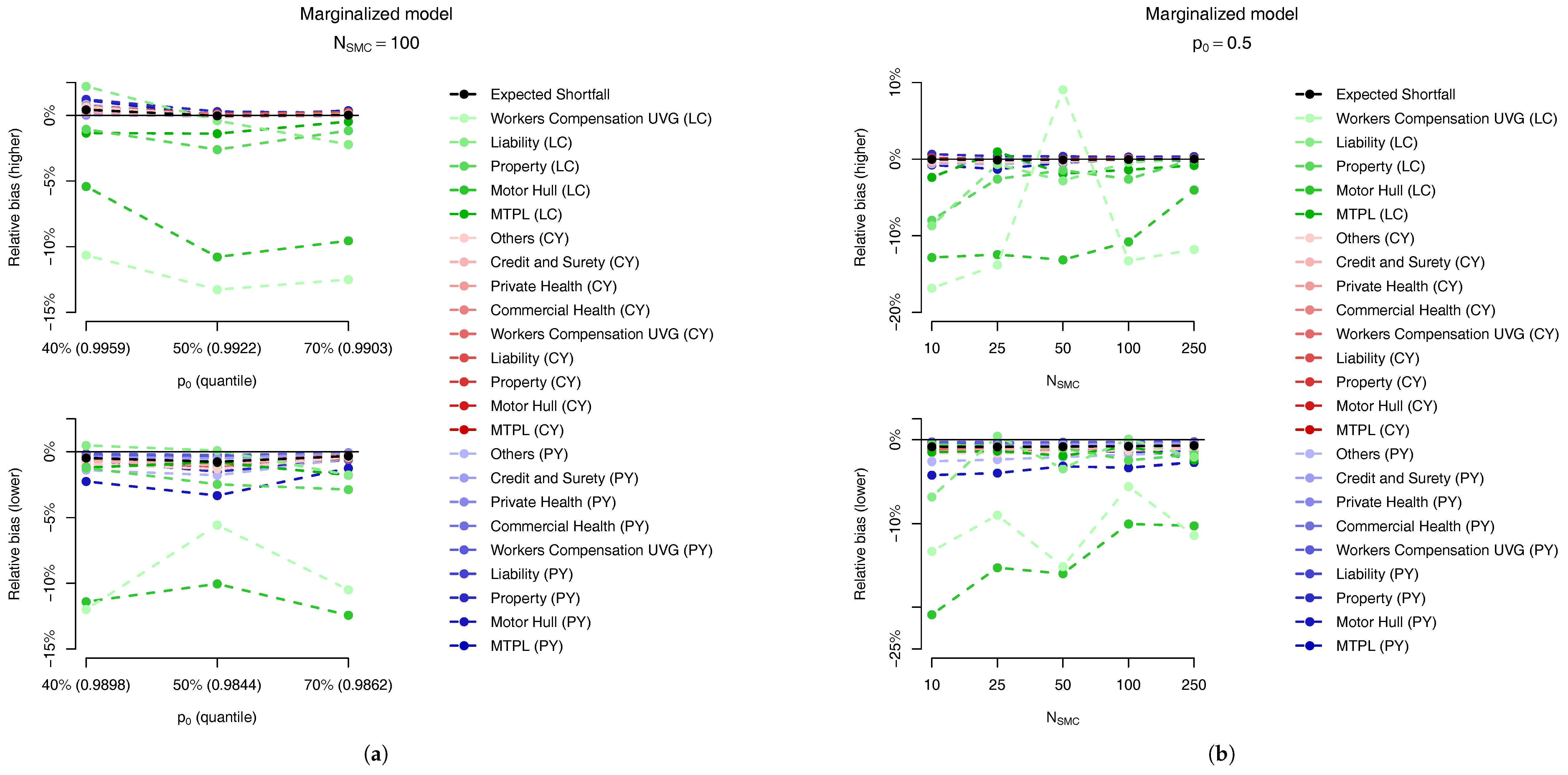
For the marginalized model we also present two plots in
Figure 14, related, respectively, to the sensitivity to (a) the parameter
and (b) the number of samples,
. In
Figure 14a, for the same number of samples,
we analyse the bias relative to the
ES allocations of the first quantile larger than
(top plot) and the previous one (bottom plot) for
. The quantiles used in these different setups are presented in
Table 10. Although the results may look slightly different, the main message is the same: the “higher” quantile is effectively unbiased for PY and CY,s risks but presents a negative bias of around
for some of the CY,l risks.
Regarding the sensitivity to the number of particles in the SMC algorithm, as expected, the absolute bias decreases when the number of samples increases, as seen in
Figure 14b. Although the SMC algorithm is generically guaranteed to be unbiased when
the trade-off between bias and the variance reduction in the allocation problem may lead us to accept a small bias in order to have a smaller variance.
11. Conclusions
In this paper we provide a complete and self-contained view of the capital allocation process for general insurance companies. As prescribed by the Swiss Solvency Test we break down the company’s overall Solvency Capital Requirement (SCR) into the one-year reserve risk, due to claims from previous years (PY) and the one-year premium risk due to claims’ payments in the current year (CY). The later is further split into the risk of normal/small claims (CY,s) and large claims (CY,l). For the premium risk in each line of business we assume a log-normal distribution for CY,s risks with mean and variance as per the SST, which also describe a distribution for CY,l risks, in this case Pareto. For the reserve risk, as in
Peters et al. (
2017), we postulate a Bayesian gamma-gamma model which, for allocation purposes, is approximated by log-normal distributions leading to what we name the conditional (when the log-normal approximation is performed conditional on the unknown parameters) and the marginalized (when the log-normal approximation is performed after the parameter uncertainty has been integrated out) models.
As seen in
Figure 1 and
Figure 2, when assuming a Bayesian gamma-gamma model these two approximations do not deviate considerably from the actual model assumptions. Regarding the allocations,
Figure 11 shows the results for both models are, once again, very close to each other (and to the “true” allocations, calculated via a large Monte Carlo exercise). Therefore, the decision on which approximation to use should not interfere with the allocation or reserving results, and is left to the reader.
The allocation process is performed using state-of-the-art (pseudo-marginal) Sequential Monte Carlo (SMC) algorithms, which are presented in a self-contained and accessible format. Although the algorithms described form an extremely flexible class, we provide an off-the-shelf version, where minimal or no tuning is needed. The algorithms are also shown to be computationally efficient in a series of numerical experiments.
One of the advantages of our proposed methodology is that it is able to compute in one single loop (1) the value at risk (VaR) and (2) the Expected Shortfall (ES), both at the company level and (3) the capital allocations for the risk drivers. This procedure should be compared with routinely applied methodologies, where one simulation is performed to compute the VaR, which is used in a different simulation to compute the allocations, in a process that accumulate different errors.
Moreover, even ignoring the computational cost of calculating a precise estimate for the required VaR in a “brute force” Monte Carlo scheme, the proposed SMC algorithm is numerically shown to provide estimates that are less volatile than comparable “brute force” implementations.