Interest Rates Term Structure under Ambiguity
Abstract
:1. Introduction
“The practical difference between the two categories, risk and uncertainty, is that in the former the distribution of the outcome in a group of instances is known (either through calculation a priori or from statistics of past experience), while in the case of uncertainty this is not true, the reason being in general that it is impossible to form a group of instances, because the situation dealt with is in a high degree unique”.
2. From a Multi-Factor Exponential-Affine Model to the HJM Model with Ambiguity
Zero Coupon Bond Price Dynamics and HJM Model
- absence of correlation among Brownian motions;
- dependence or presence of some correlation among Brownian motions.We prove the following proposition.
3. A Three-Factor Exponential Affine Model: The Economic Framework
- the known-unknown, which reflects the dispersion among investors’ opinions about validity of Ricardian equivalence. This refers to a policy intervention uncertainty because it reflects the attempt of government to systematically change the consumption growth;
- the unknown-unknown, which represents uncertainty about the future effectiveness of a government’s interventions on future consumption. This uncertainty is harder to measure, and can be numerically translated into a multiplier uncertainty which is directly proportional to the growth of economy and the inflation.
- In a non-Ricardian world, if the government acts in a “benevolent” way (i.e., introducing policies which maximize economic agents utility), consumption’s instantaneous rate of growth will increase based on the following factor:
- If the government instead acts in a “malevolent” way (i.e., minimizing economic agents’ utility—in this way, the government does not act for their sake), the sign of the intervention will be opposite to the one we saw as optimal solution (see Equation (9) ).
3.1. A Three-Factor Exponential Affine Model: HJM Model under Ambiguity
3.1.1. Absence of Correlation among the Sources of Risk
3.1.2. Dependence among the Sources of Risk
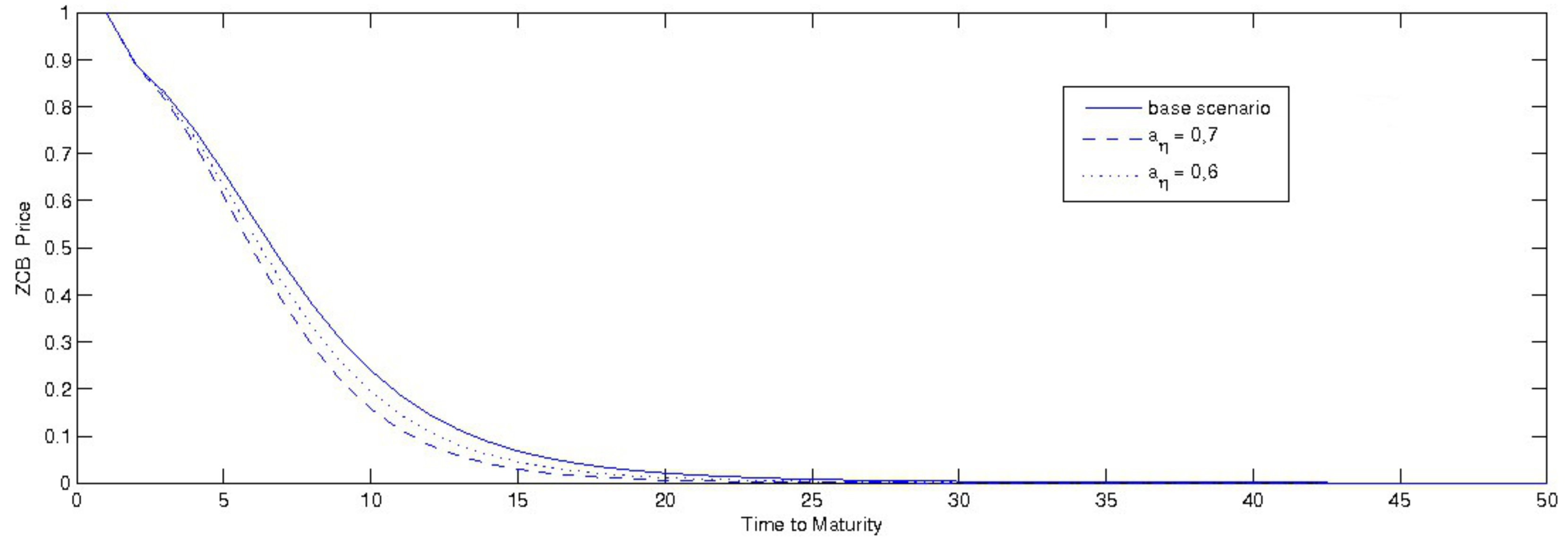
3.2. Sensitivity Analysis
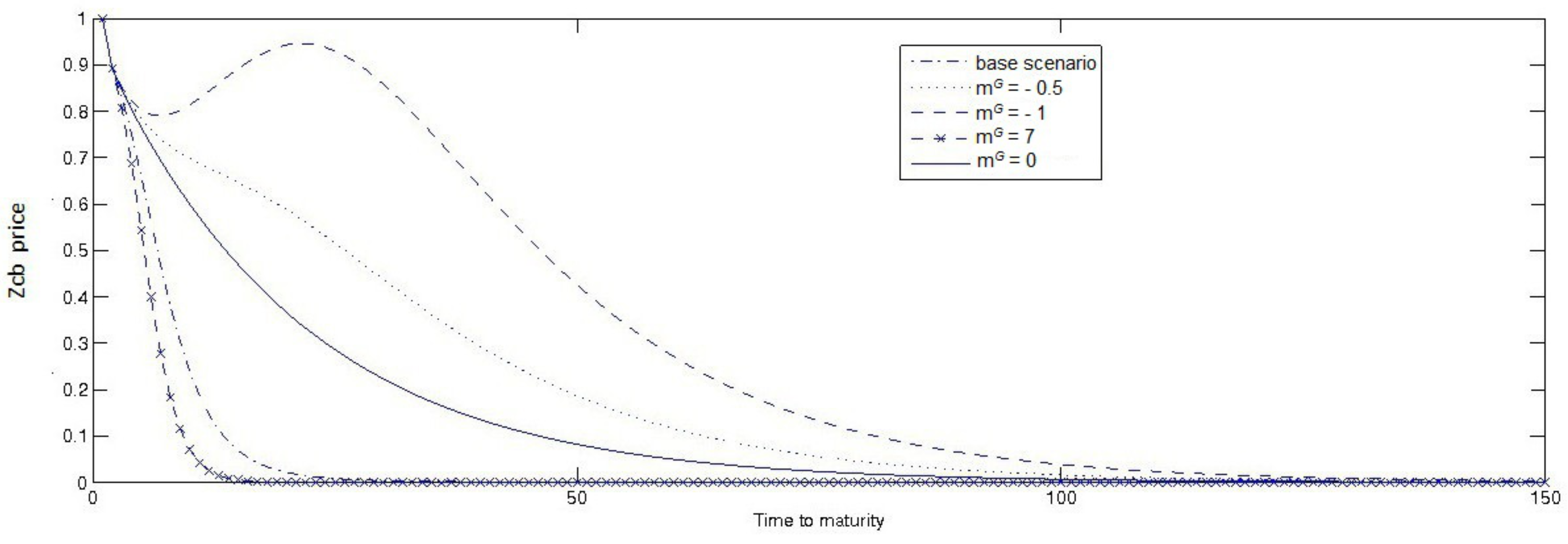
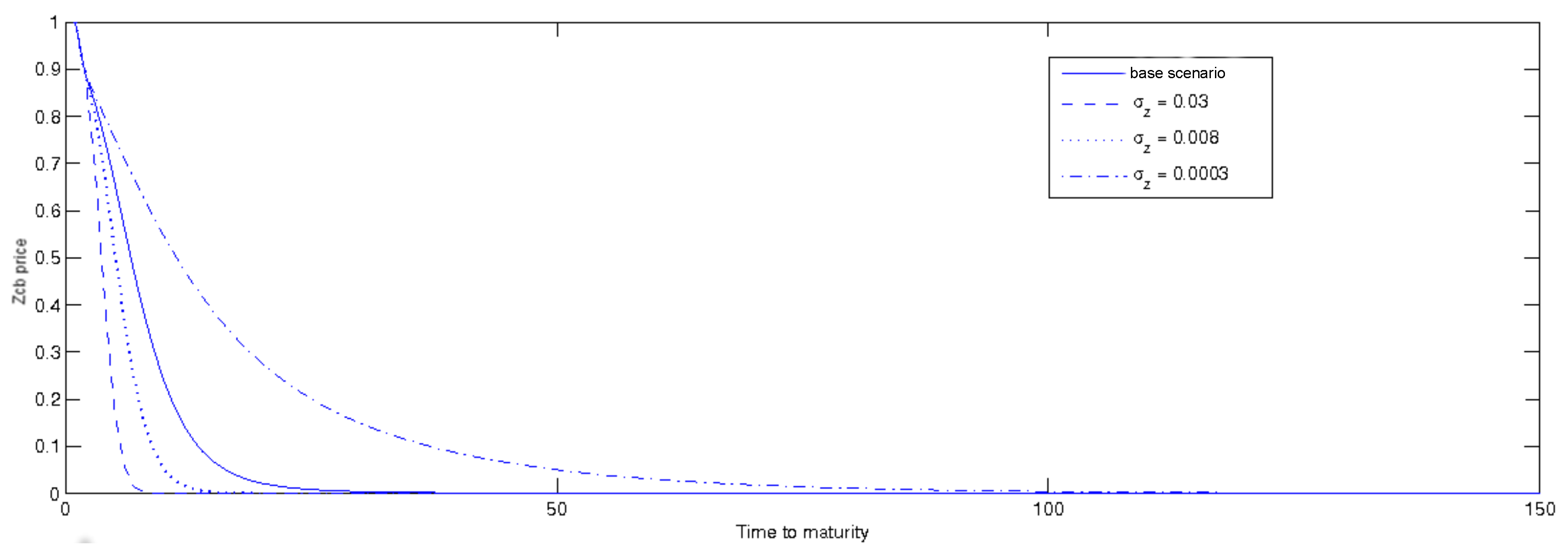
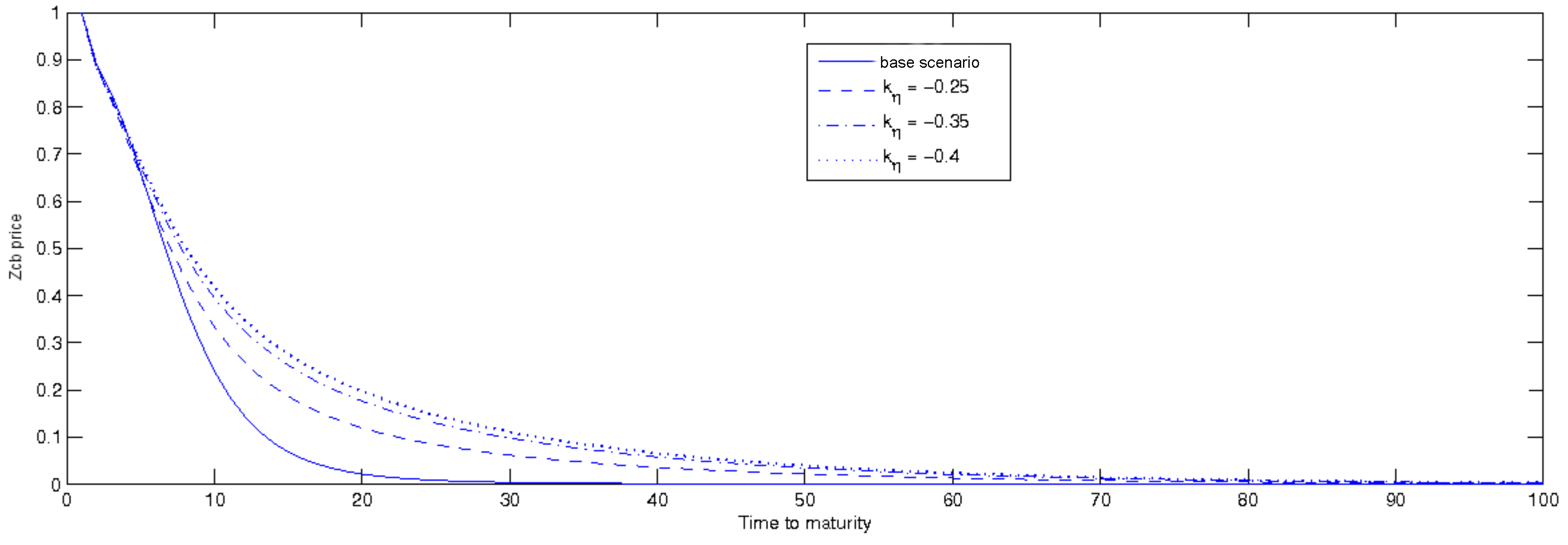
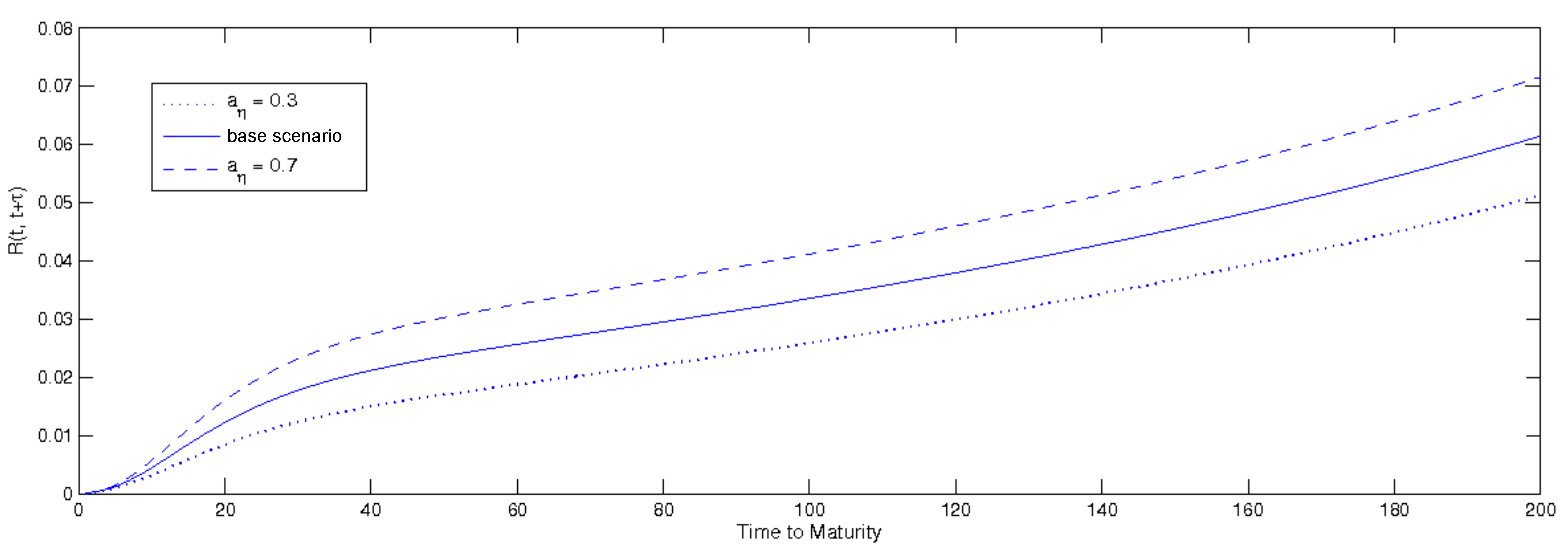
3.2.1. Zcb Real Price: A Sensitivity Analysis
- correlation coefficients are all equal to zero (case of independence of Brownian motions);
- both kinds of perceived ambiguity ( and ) are equal to an average value (i.e., 0.5);
- the volatility parameters have been calibrated on low but realistic values: , , ;
- the coefficients , and have been calibrated on −0.1, −0.15, −0.05.
- : the government action maximizes economic agents utility, and thus is “benevolent”;
- : the government does not act to influence economic agents’ utility, behaving as described in the Ricardian equivalence. This is the case of no ambiguity;
- : government interventions minimize economic agents’ utility. In other words, government actions are “malevolent”; i.e., harmful for the economic agents in the economy.
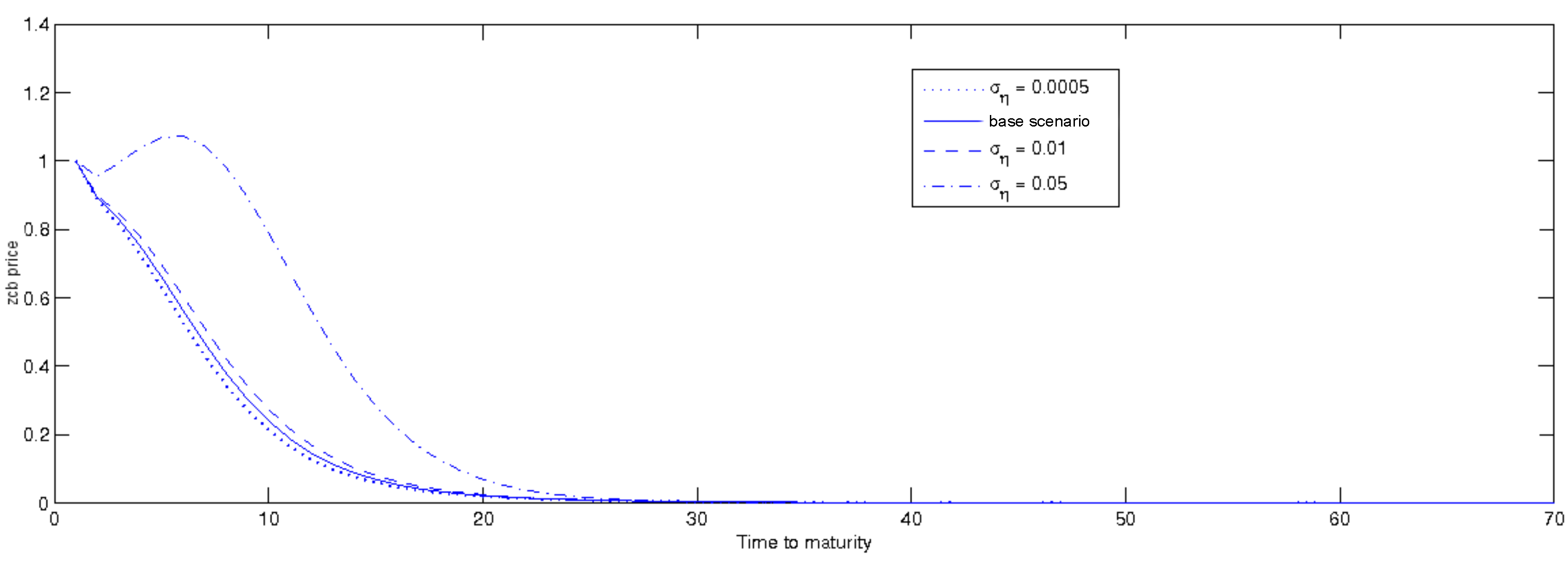
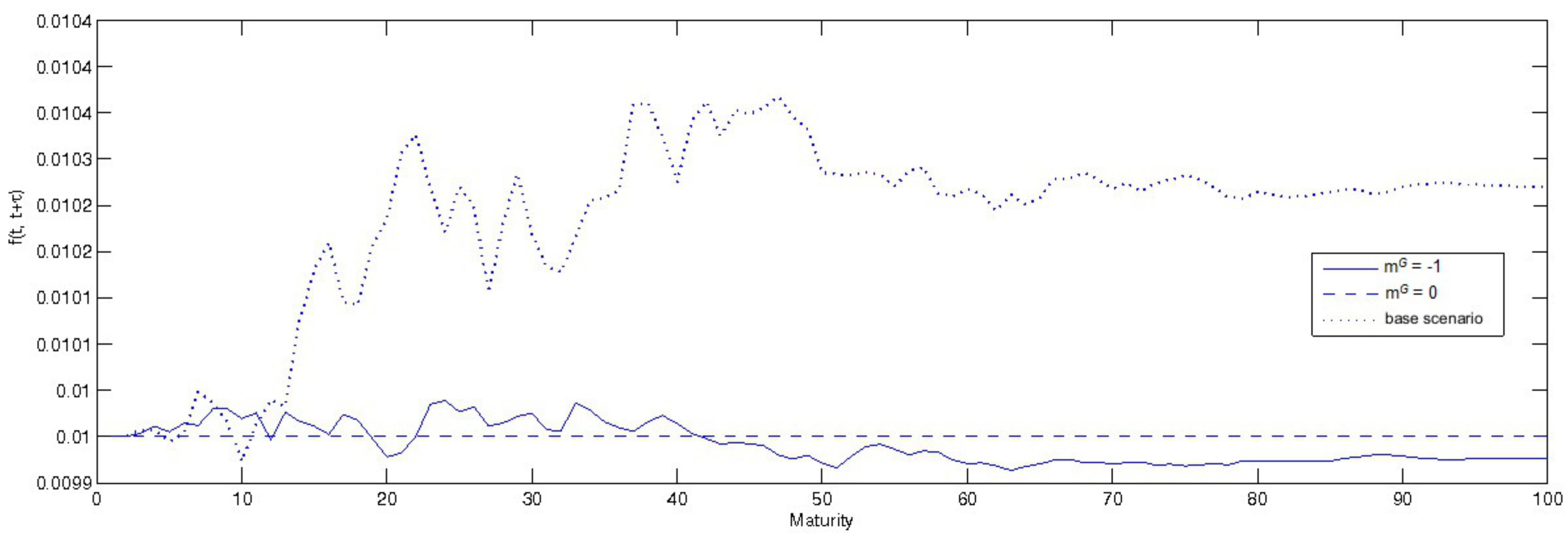
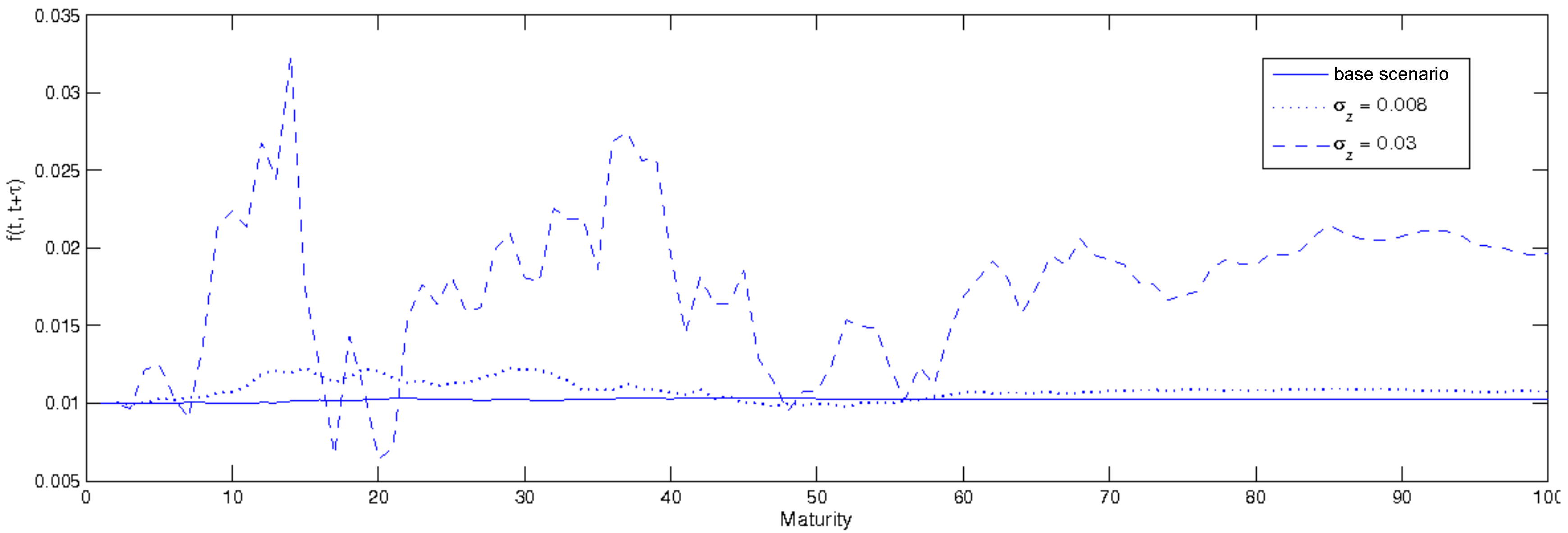
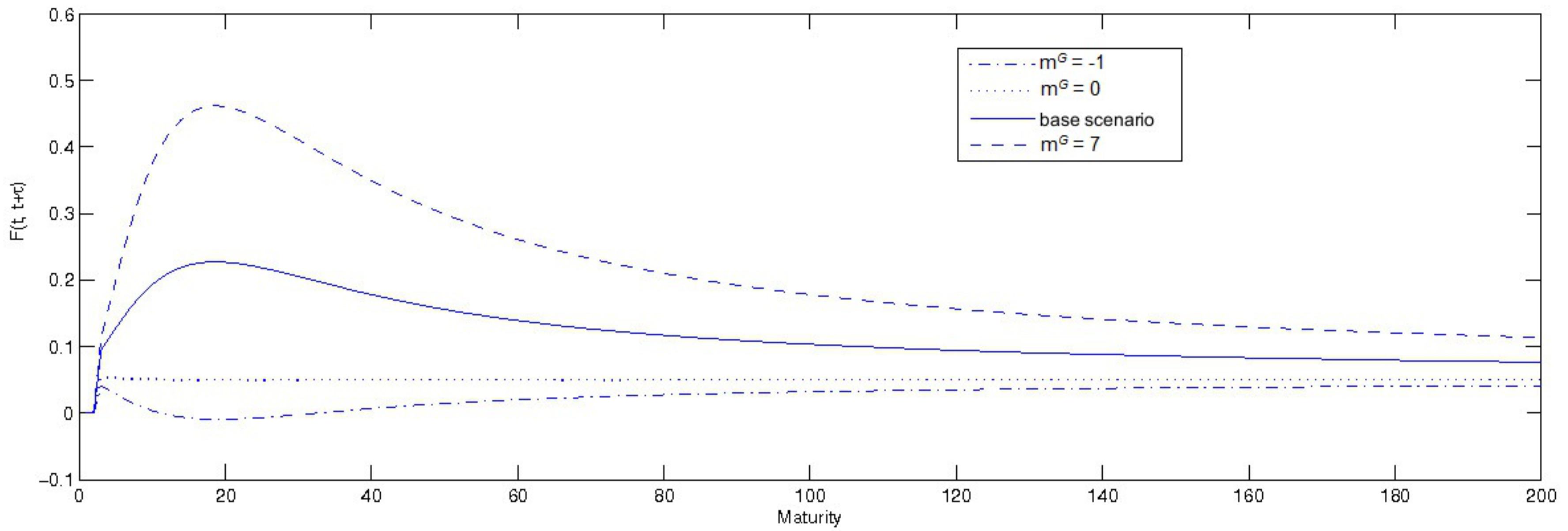
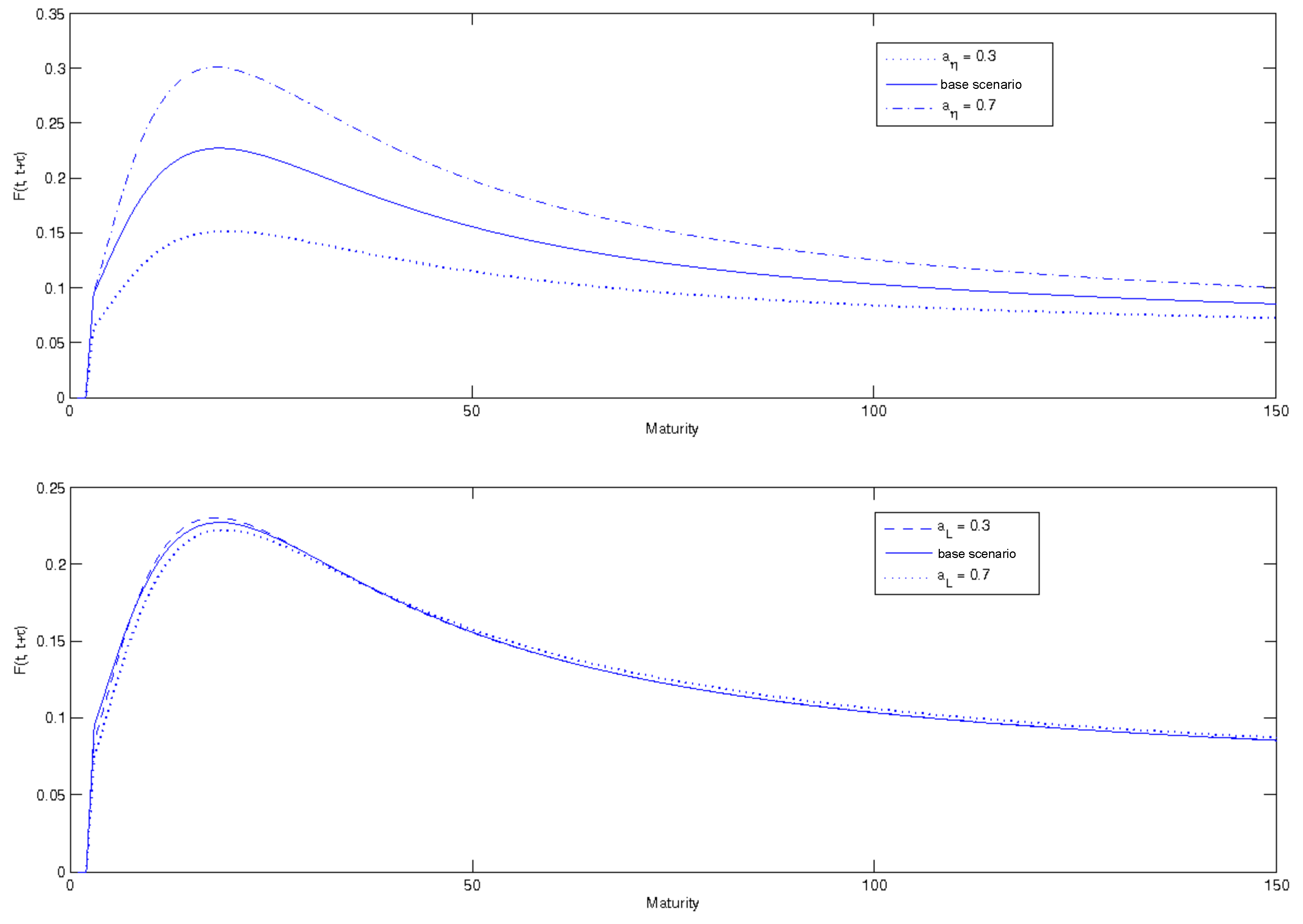
3.2.2. Forward Instantaneous Rate: A Sensitivity Analysis
- = 10;
- zero correlation between Brownian motions;
- both kinds of perceived ambiguity ( and ) are equal to 0.5 and 0.6, respectively;
- volatilities set to ;
- the coefficients , and have been set equal to −0.015, −0.03, −0.035.
- correlation coefficients are all equal to zero;
- the uncertainties perceived by the economic individuals ( and ) are equal to an average value (0.5);
- the volatility parameters have been calibrated on low but realistic values: , , ;
- the coefficients and have been calibrated on −0.15, −0.1, −0.05.
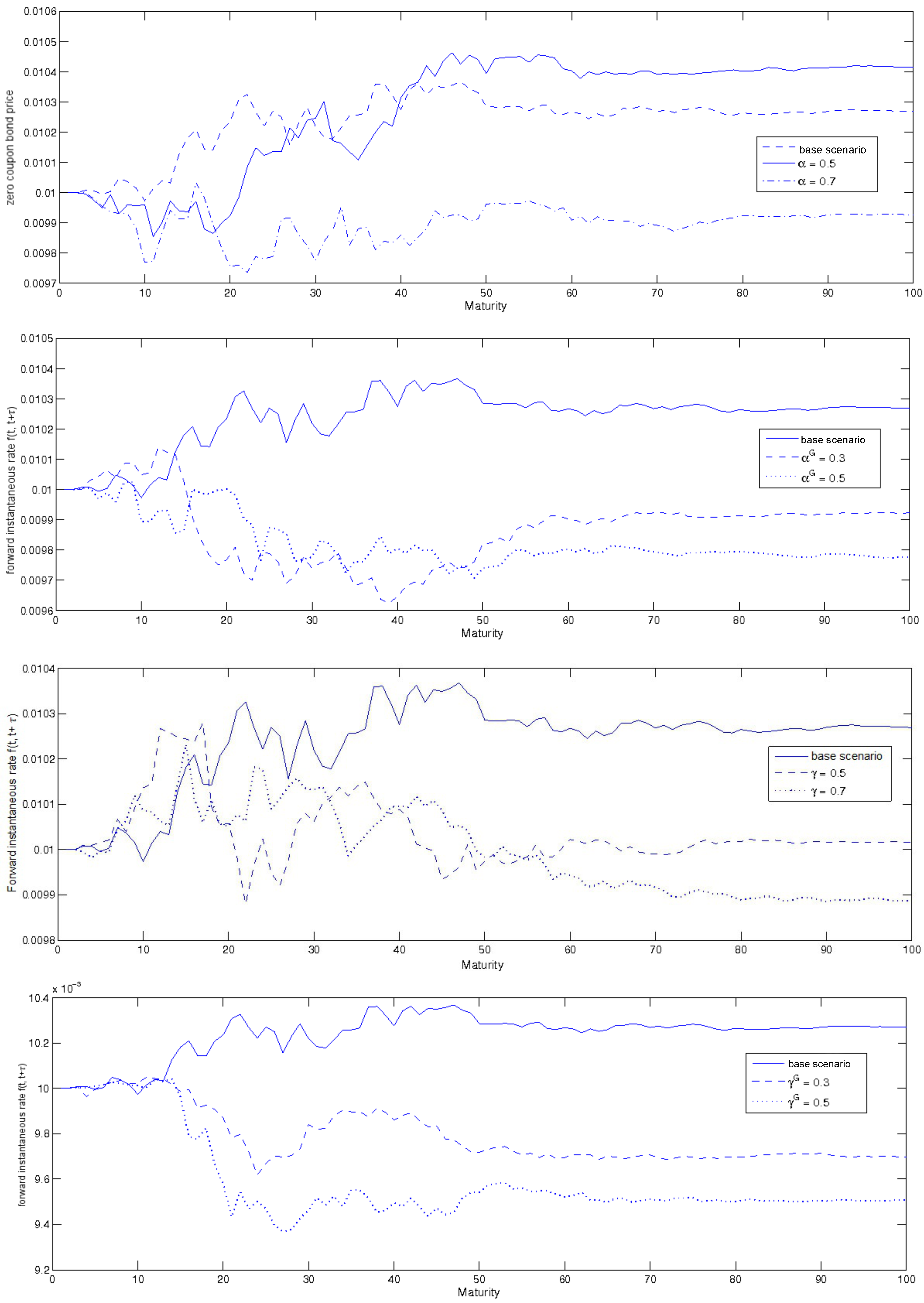
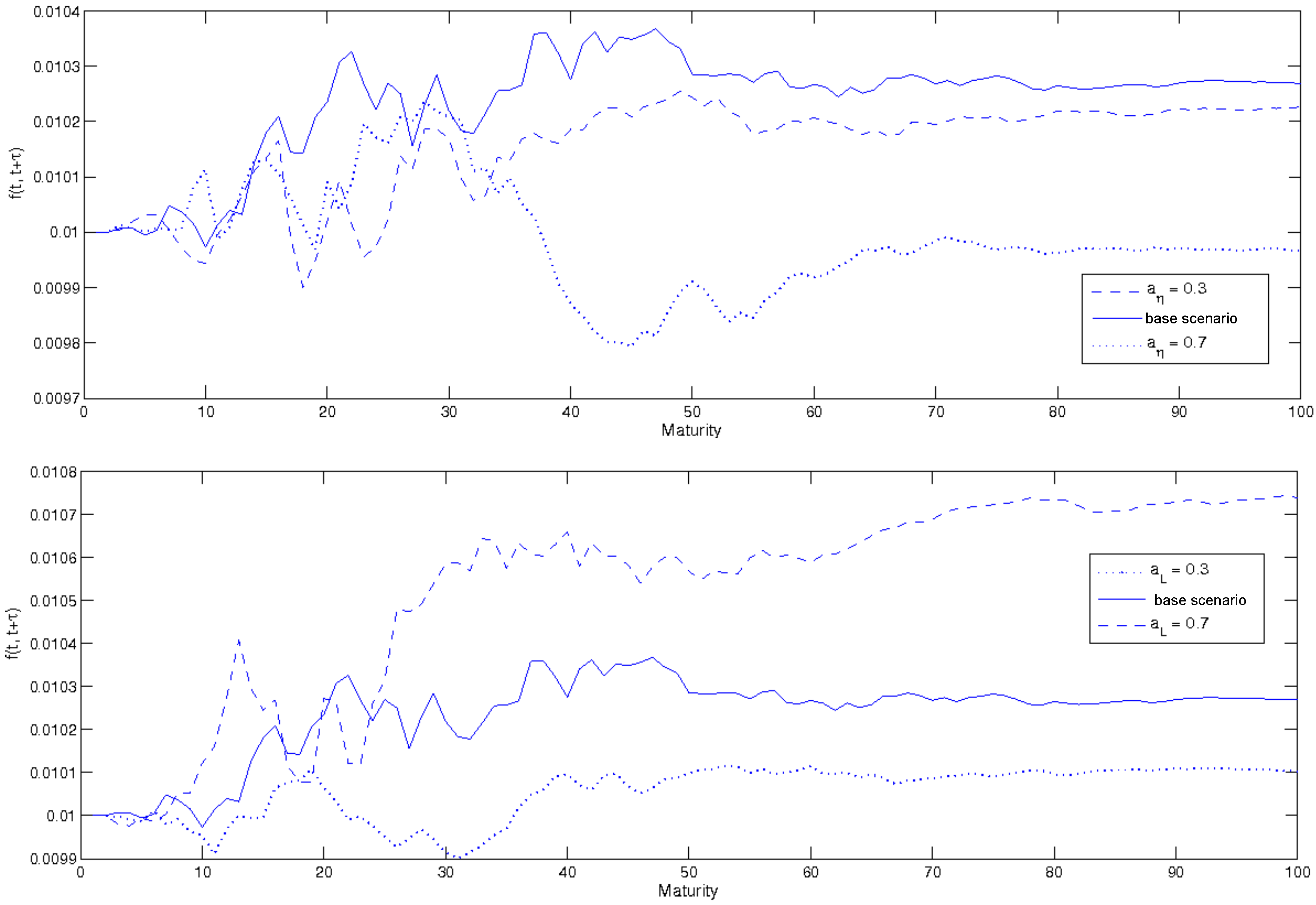
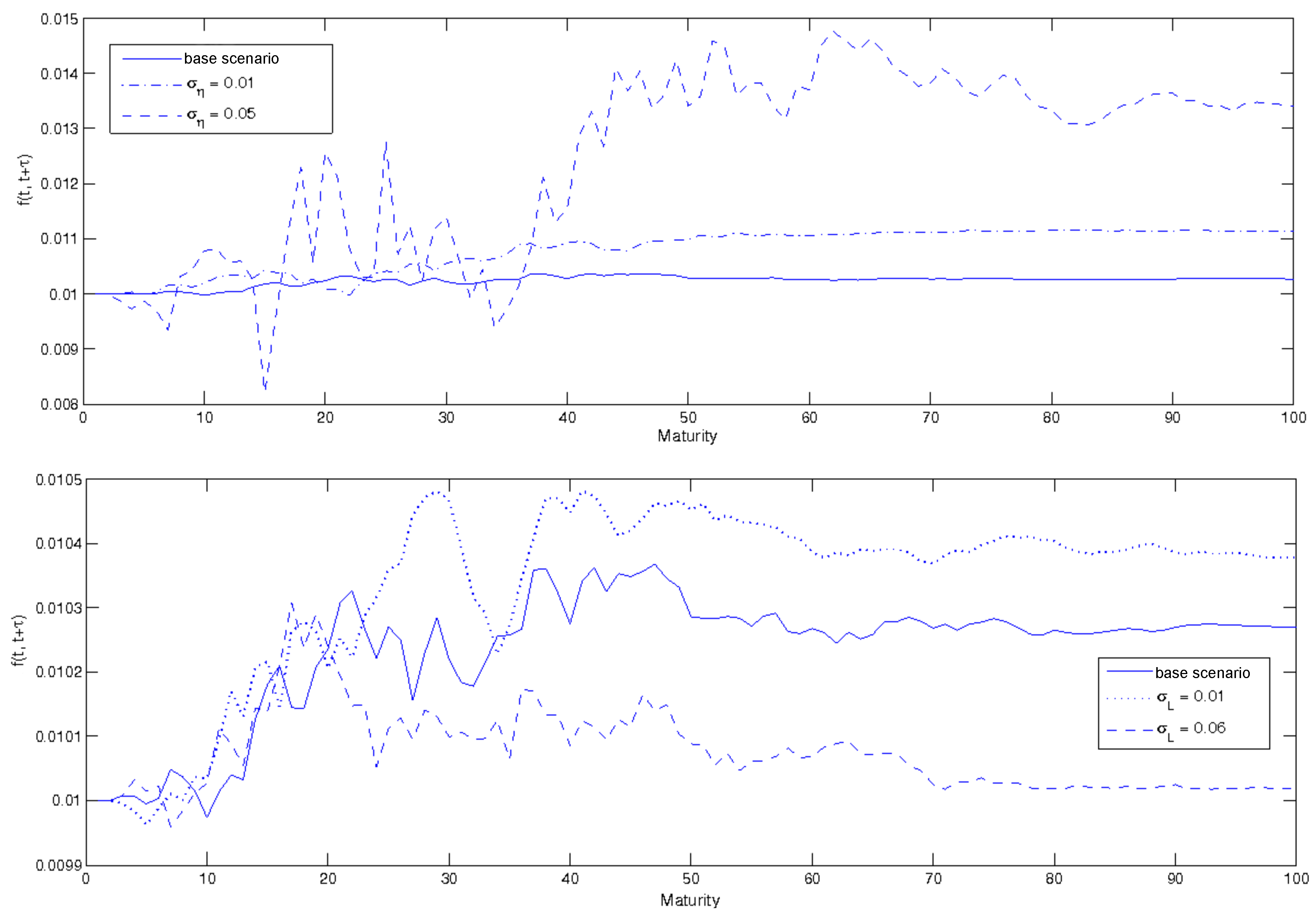
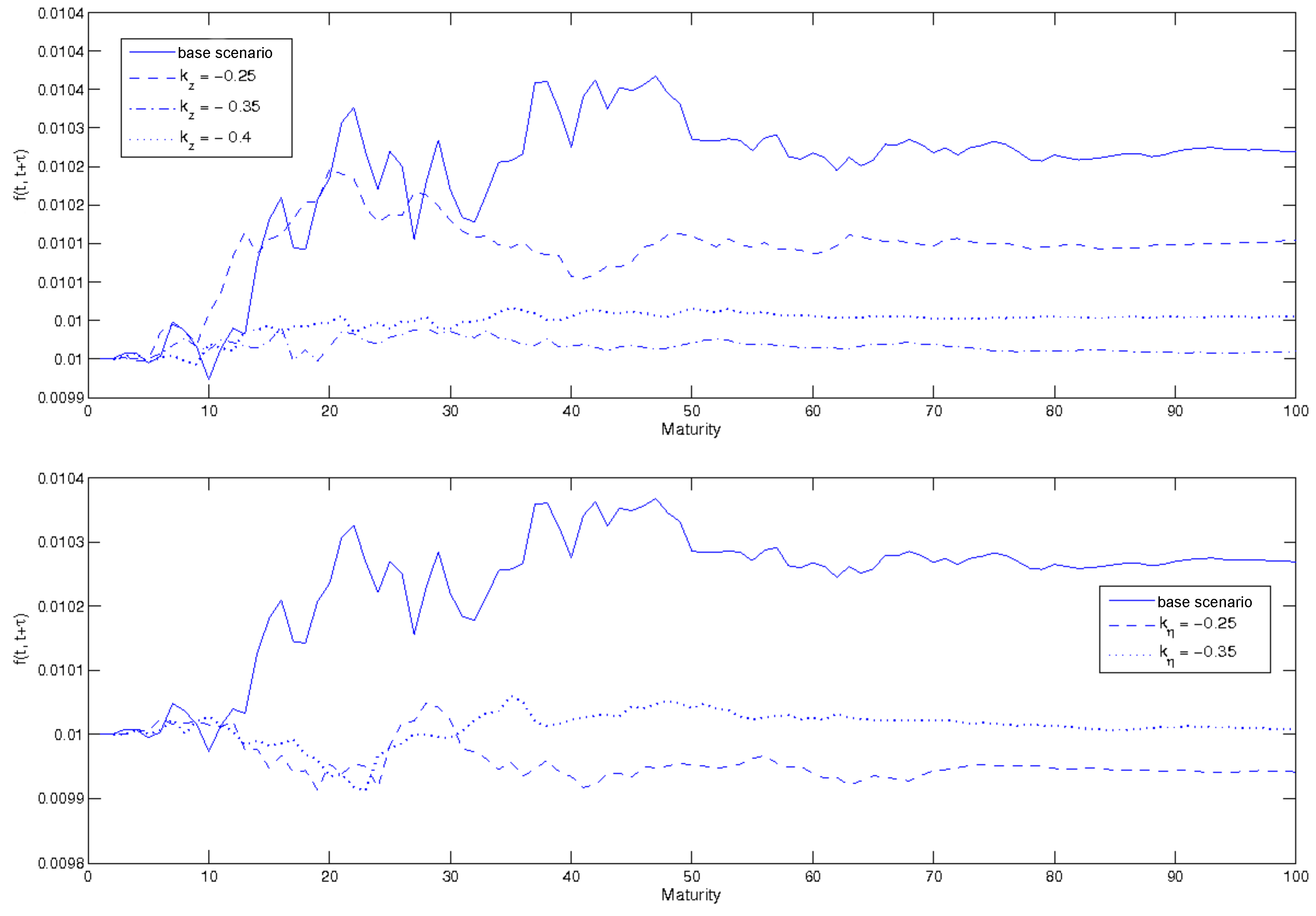
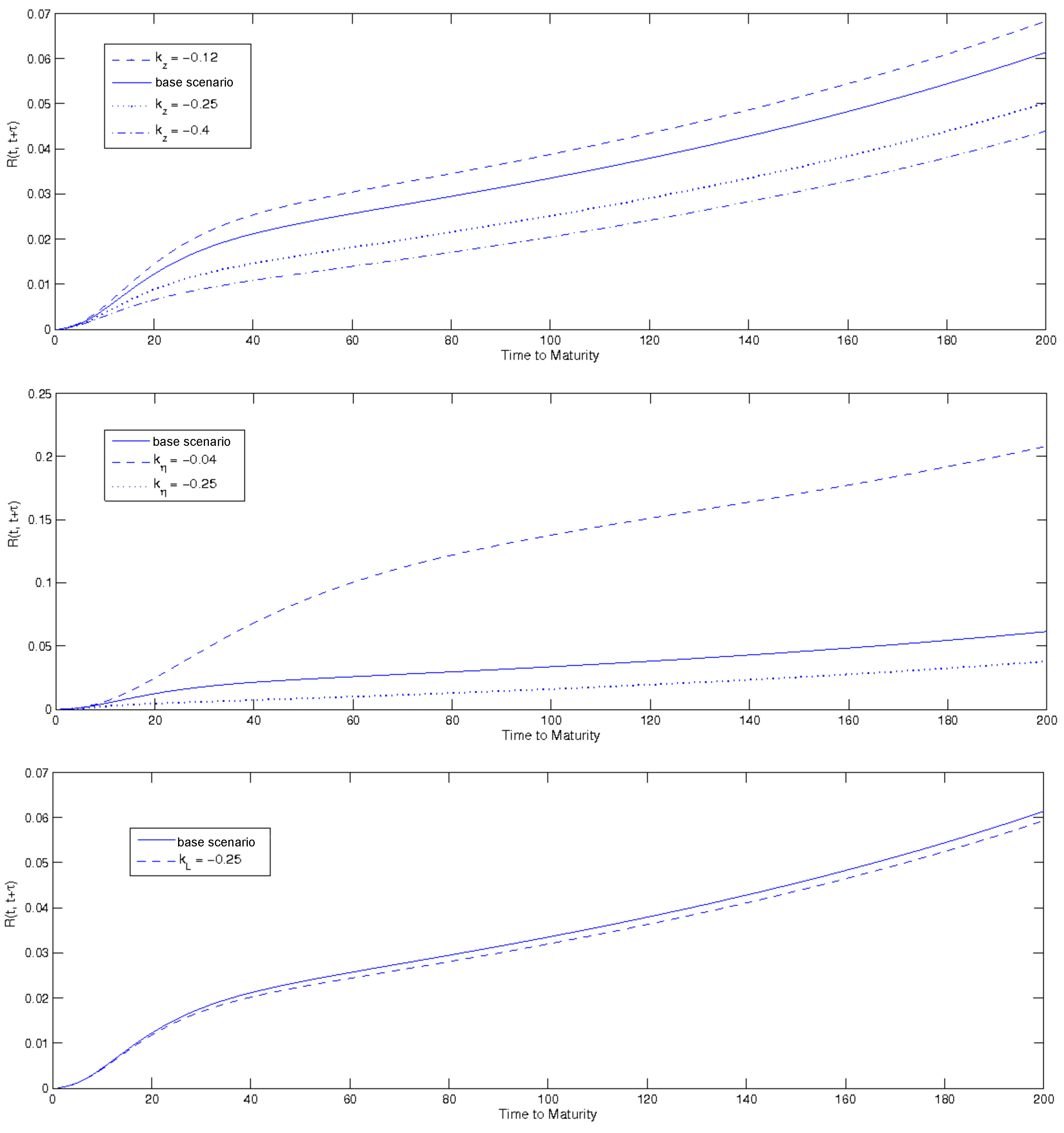
3.2.3. Spot and Forward Yields: A Sensitivity Analysis
- correlation coefficients are all equal to zero;
- the number of policies available for government’s use () is set to 3, which is linked to “normal” ambiguity scenario, as we saw earlier in this section;
- the uncertainties perceived by the economic individuals ( and ) are equal to an average value (0.5);
- the volatility parameters have been calibrated on low but realistic values: , , ;
- the coefficients , and have been calibrated at −0.15, −0.1, −0.05.
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Cox, John C., Jonathan E. Ingersoll Jr., and Stephen A. Ross. 1985. A Theory of the Term Structure of Interest Rates. Econometrica 53: 385–408. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Rui Kan. A yield-factor model of interest rates. Mathematical Finance 6: 379–406. [CrossRef]
- El Karoui, Nicole, and Vincente Lacoste. 1992. Multifactor Models of the Term Structure of Interest Rates. In AFFl Conference Proceedings. Paris: University of Paris. [Google Scholar]
- Ellsberg, Daniel. 1961. Risk, ambiguity and the Savage Axioms. The Quarterly Journal of Economics 75: 643–69. [Google Scholar] [CrossRef]
- Fox, Craig R., and Amos Tversky. 1995. Ambiguity aversion and comparative ignorance. The Quarterly Journal of Economics 110: 585–603. [Google Scholar] [CrossRef]
- Gagliardini, Patrick, Paolo Porchia, and Fabio Trojani. 2009. Ambiguity aversion and the term structure of interest rates. Review of Financial Studies 22: 4157–88. [Google Scholar] [CrossRef]
- Ghirardato, Paolo, Fabio Maccheroni, and Massimo Marinacci. 2004. Differentiating ambiguity and ambiguity attitude. Journal of Economic Theory 118: 133–73. [Google Scholar] [CrossRef]
- Gilboa, Itzhak, and David Schmeidler. 1989. Maxmin Expected Utility with non unique prior. Journal of Mathematical Economics 18: 141–53. [Google Scholar] [CrossRef]
- Hansen, Lars Peter, and Thomas J. Sargent. 2008. Robustness. Princeton: Princeton University Press. [Google Scholar]
- Heath, David, Robert Jarrow, and Andrew Morton. 1992. Bond Pricing and the Term Structure of Interest Rates: A New Methodology for Contingent Claims Valuation. Econometrica 60: 77–105. [Google Scholar] [CrossRef]
- Ho, Thomas SY, and Sang-Bin Lee. 1986. Term Structure Movements and Pricing Interest Rate Contingent Claims. Journal of Finance 41: 1011–29. [Google Scholar] [CrossRef]
- Ilut, Cosmin L., and Martin Schneider. 2014. Ambiguous business cycles. The American Economic Review 104: 2368–99. [Google Scholar] [CrossRef]
- Kast, Robert, André Lapied, and David Roubaud. 2014. Modelling under ambiguity with dinamically consistent Choquet random walks and Choquet-Brownian motions. Econ Modell 38: 495–503. [Google Scholar] [CrossRef]
- Knight, Frank H. 1921. Risk, Uncertainty, and Profit. Boston: Houghton Mifflin. [Google Scholar]
- Musiela, Mark. 1994. Nominal Annual Rates and Lognormal Volatility Structure. Working paper, The University of New South Wales, Sydney, Australia. [Google Scholar]
- Savage, Leonard J. 1954. The Foundations of Statistics. New York: Wiley. [Google Scholar]
- Schmeidler, David. 1989. Subjective probability and expected utility without additivity. Econometrica 57: 517–87. [Google Scholar] [CrossRef]
- Ulrich, Maxim. 2008. Inflation Ambiguity and the Term Structure of Arbitrage Free US Government Bonds. New York: Columbia University. [Google Scholar]
- Ulrich, Maxim. 2011. How Does the Bond Market Perceive Government Interventions? WFA 2011, NBER Asset Pricing. New York: Columbia Business School. [Google Scholar]
- Vasicek, Oldrich. 1997. An Equilibrium Characterization of the Term Structure. Journal of Financial Economics 5: 177–88. [Google Scholar] [CrossRef]
| 1 | |
| 2 | A capacity is a function which on a set (S, ) is monotonous and normalized. Moreover, a capacity becomes a probability measure if it is finitely additive. On the other side, the Choquet integral was set up to work with capacities. |
| 3 | We restrict the model to the affine structure of the factors which are affine on a single factor (i.e., the instantaneous interest rate). In this way, we work in line with Duffie and Kan (1996) and El Karoui and Lacoste (1992), where the dynamic of the factors—which are interest rates for several maturities—is chosen in order to ensure the absence of arbitrage assumption. The famous Vasicek (1997), Cox et al. (1985) models for the factors are both coherent with this assumption because they lead to an affine structure of the factors on the instantaneous interest rate. |
| 4 | In the case of an n-dimensional Brownian motion with independent component, the completeness condition is ; in the dependent case, we must include the covariances in the computation of the sources of risk. |
| 5 | In line with the previous modeling, the ambiguous version of a one-dimensional exponential-affine model will be a two-factor model in order to include the ambiguity as an exogenous factor. On the other hand, if the single factor is modeled in terms of a Choquet–Brownian, as suggested in Kast et al. (2014), we would be able to endogenously introduce the ambiguity, preserving the original dimension of the factors’ set. |
| 6 | If Ricardian equivalence is true, this component is zero. |
| 7 | This set is defined in order to have a relative entropy between a non-zero multiplier policy and a zero-multiplier policy which is bounded from above by a positive but small number; i.e., , variable in time. Hence, the complexity of is variable in time as well as the agent’s uncertainty. |
| 8 | A max-max agent aims to invest into a robust portfolio; i.e., paying off well if government was indeed implementing first-best policies not corresponding to the benchmark (zero-multiplier policy). |
| 9 | For this reason, we can see the dynamic of as an approximation of a squared root process. |
| 10 | For this reason we can see the dynamic of as an approximation of a squared root process. |
| 11 | We use (i.e., the sample mean of quarterly GDP growth) to demean the median forecast. |
| 12 | The case of post-election in France was not examined due to a lack of data. |
| 13 | The analysis led on the parameter has been omitted due to the absence of relevant results. |
| 14 | represents the stochastic part inside economic cycle, meaning with this the technological progress achieved in the economy, while represents the known-unknown ambiguity. |
| 15 | |
| 16 | has been omitted because of the lack of sensitivity in the analysis. |








| Pre-Brexit | 1.86648 | 0.2 |
| Post-Brexit | 2.35766 | 0.2 |
| Pre-referendum Italy | 4.427 | 0.1 |
| Post-referendum Italy | 2.7673 | 0.2 |
| Pre-election France | 6.23052 | 0.1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romagnoli, S.; Santoro, S. Interest Rates Term Structure under Ambiguity. Risks 2017, 5, 50. https://doi.org/10.3390/risks5030050
Romagnoli S, Santoro S. Interest Rates Term Structure under Ambiguity. Risks. 2017; 5(3):50. https://doi.org/10.3390/risks5030050
Chicago/Turabian StyleRomagnoli, Silvia, and Simona Santoro. 2017. "Interest Rates Term Structure under Ambiguity" Risks 5, no. 3: 50. https://doi.org/10.3390/risks5030050
APA StyleRomagnoli, S., & Santoro, S. (2017). Interest Rates Term Structure under Ambiguity. Risks, 5(3), 50. https://doi.org/10.3390/risks5030050





