Assessment of Policy Changes to Means-Tested Age Pension Using the Expected Utility Model: Implication for Decisions in Retirement
Abstract
:1. Introduction
2. Model
2.1. Utility Functions
- Consumption preferences: It is assumed that utility comes from consumption exceeding the consumption floor, weighted with a time-dependent “health” status proxy6. The utility function for consumption is defined as:where is the risk aversion and is the consumption floor parameters. The scaling factor normalises the utility a couple receives in relation to a single household. The utility parameters , and are subject to family state ; hence, they will have different values for couple and single households. Furthermore, is the utility parameter for the “health” status proxy, which controls the declining consumption between current time t and time of retirement .
- Bequest preferences: Utility is also received from luxury bequest, where the utility function for bequest is then defined as:Here, is the liquid assets available for bequest; H is the value of the home and the risk aversion parameters for single households7. The parameter is the degree of altruism, which controls the preference of bequest over consumption, and is the threshold for luxury bequest up to where the retiree leaves no bequest8.Note that the inclusion of housing in the bequest function simply adjusts the threshold for luxury bequest, as the allocation to housing is a one-off decision and remains constant after retirement. Because of this, if the retiree is a homeowner, then the marginal utility of bequest will be lower for a given liquid wealth; hence, additional consumption is preferred. The optimal consumption with respect to liquid wealth will have the same shape, although be slightly higher with higher house values. This justifies the simplification in Andreasson et al. (2017), where housing has been dropped from the bequest, as it is conceptually the same and avoids an extra state variables, while the impact on optimal control is marginal.
- Housing preferences: The utility from owning a home comes in the form of preferences over renting, but is approximated by the home value. The housing utility is defined as:where is the risk aversion parameter for housing (allowed to be different from risk aversion for consumption and bequest), is the same scaling factor as in Equation (7), is the market value of the family home at time of purchase and is the preference of housing defined as a proportion of the market value.
2.2. Policies and Scenarios
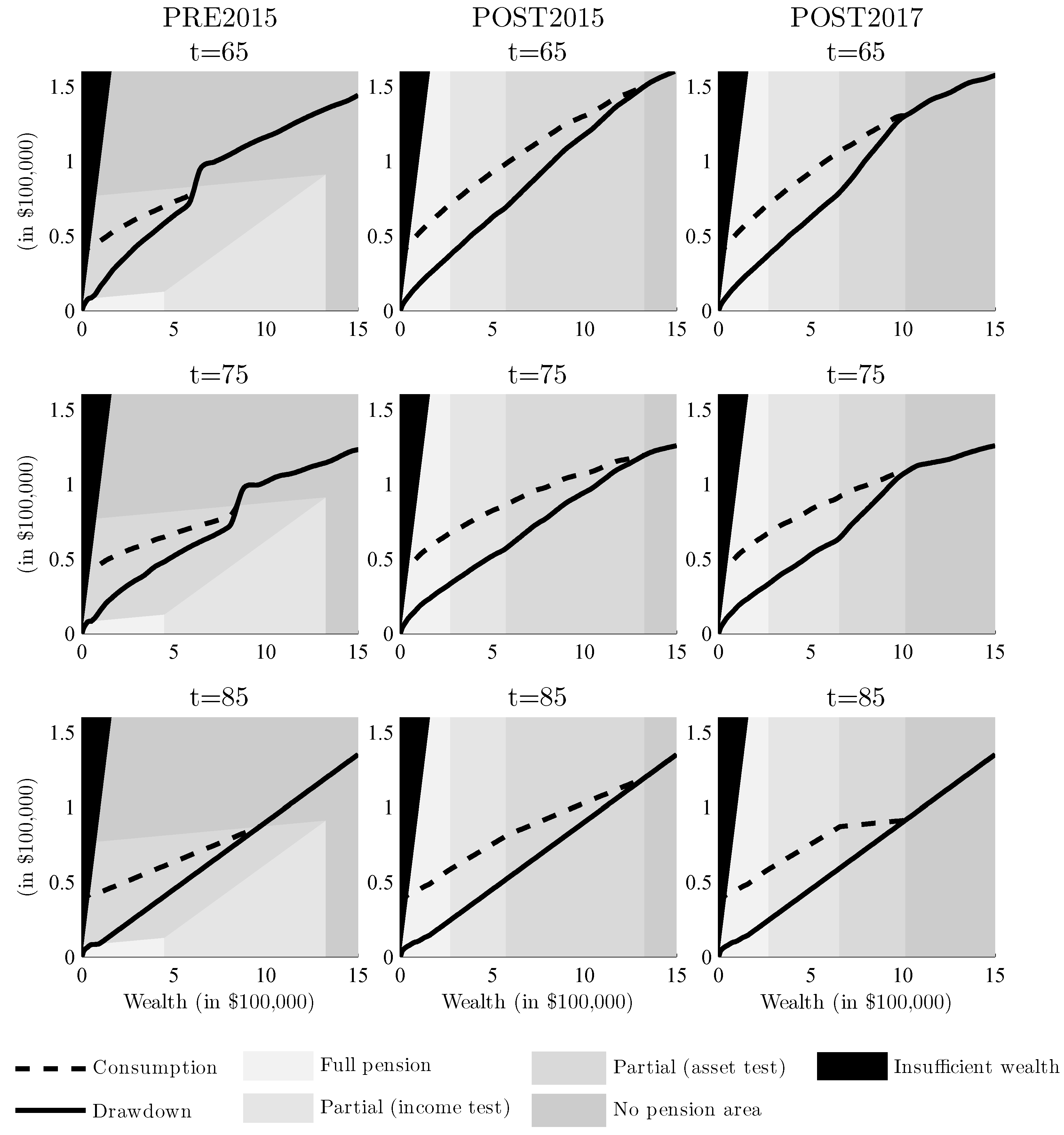
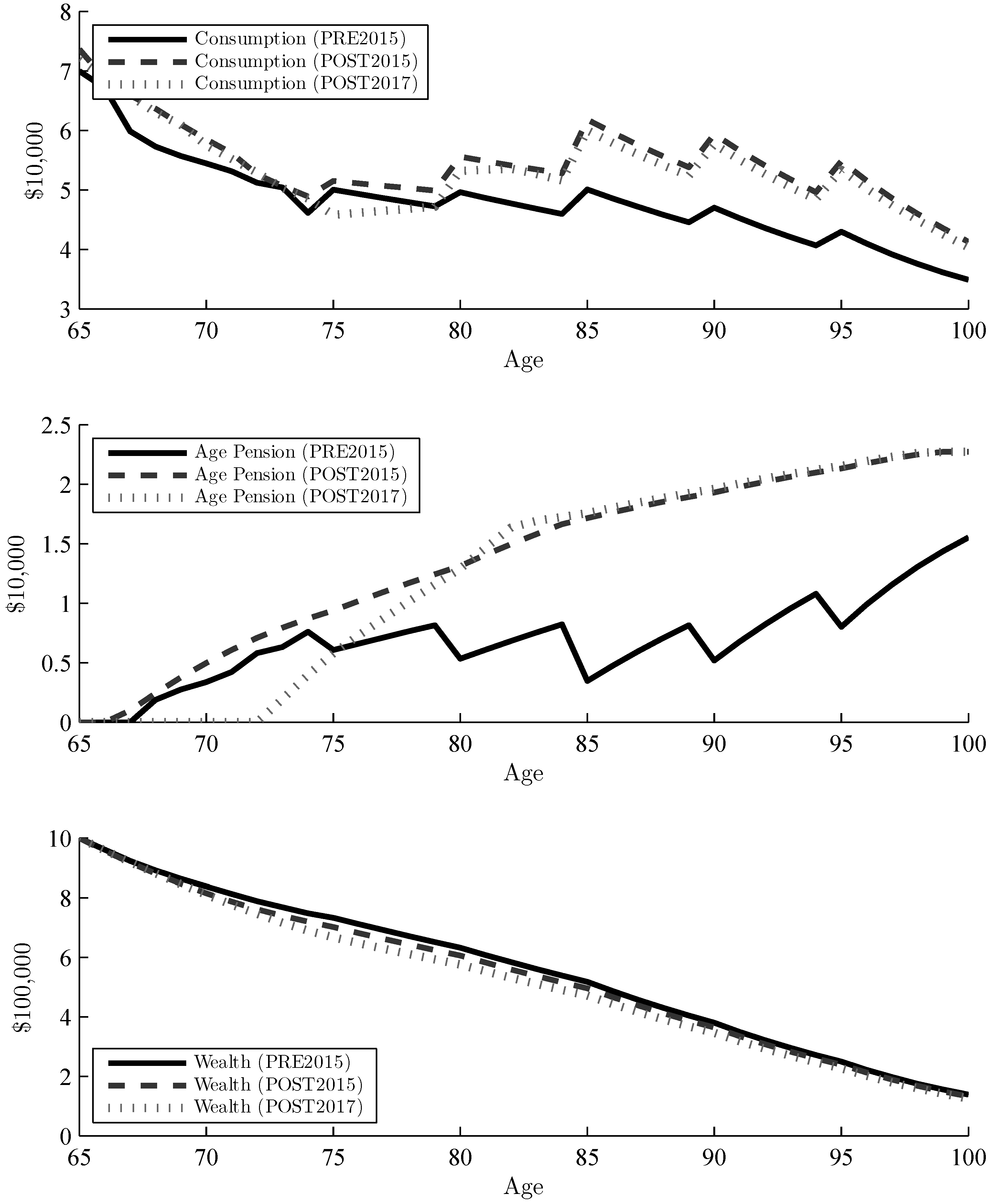
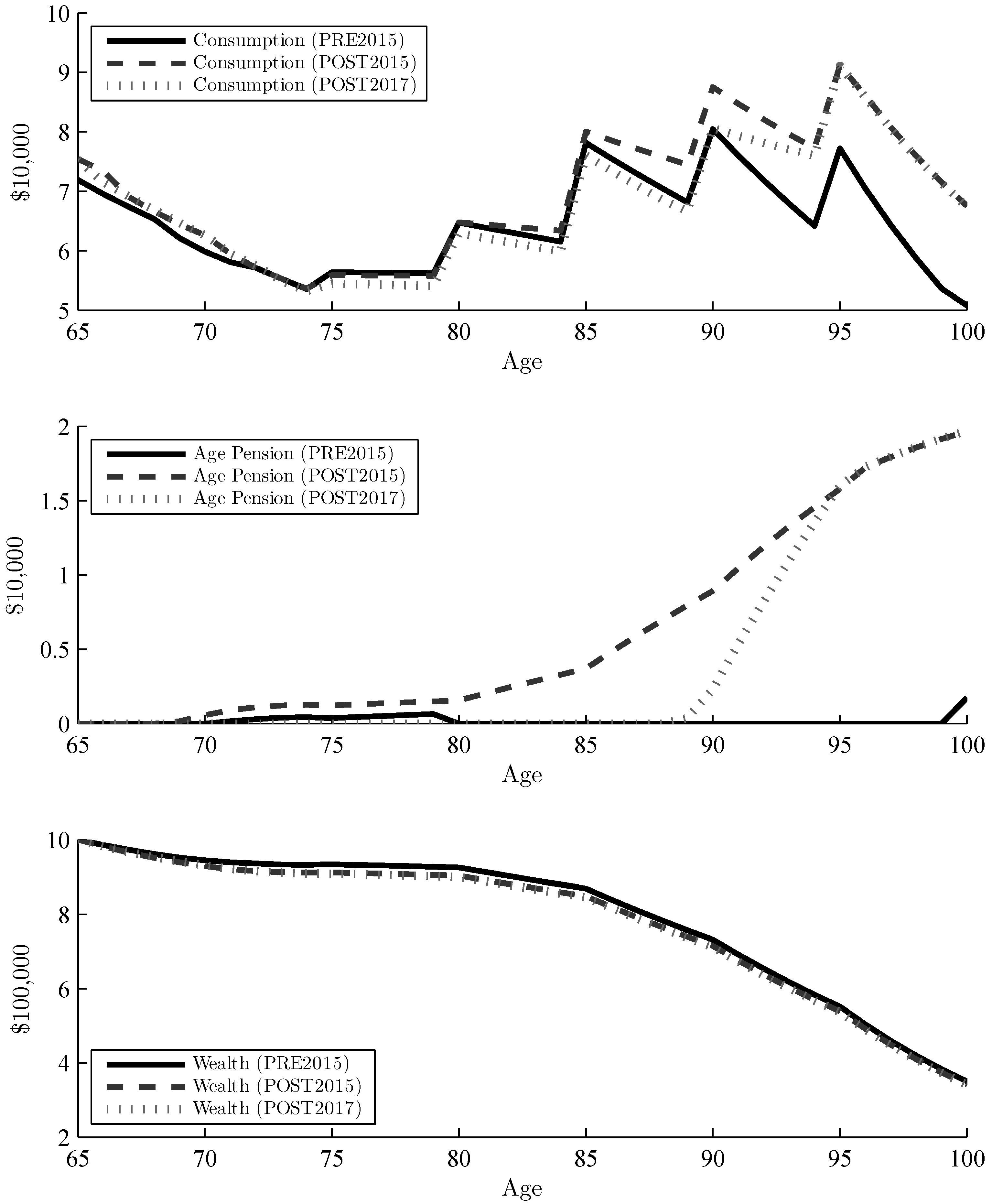
- Policy 1, Pre-January 2015 (PRE2015): The first policy reflects the means-test and policy rules prior to 1 January 2015, which is what the majority of Australian retirees are being tested under. Any drawdown from the Allocated Pension account is counted towards the income-test, where minimum withdrawal rates impose a lower bound on optimal consumption (withdrawals from liquid wealth must be larger or equal to these rates).
- Policy 2, Post-January 2015 (POST2015): This policy focuses on the changes for the income-test of Allocated Pension accounts. The income-test now uses deemed income rather than drawdown; thus, the liquid wealth is used in both the asset and income-test. The retiree can therefore withdraw more liquid wealth without missing out on Age Pension payments.
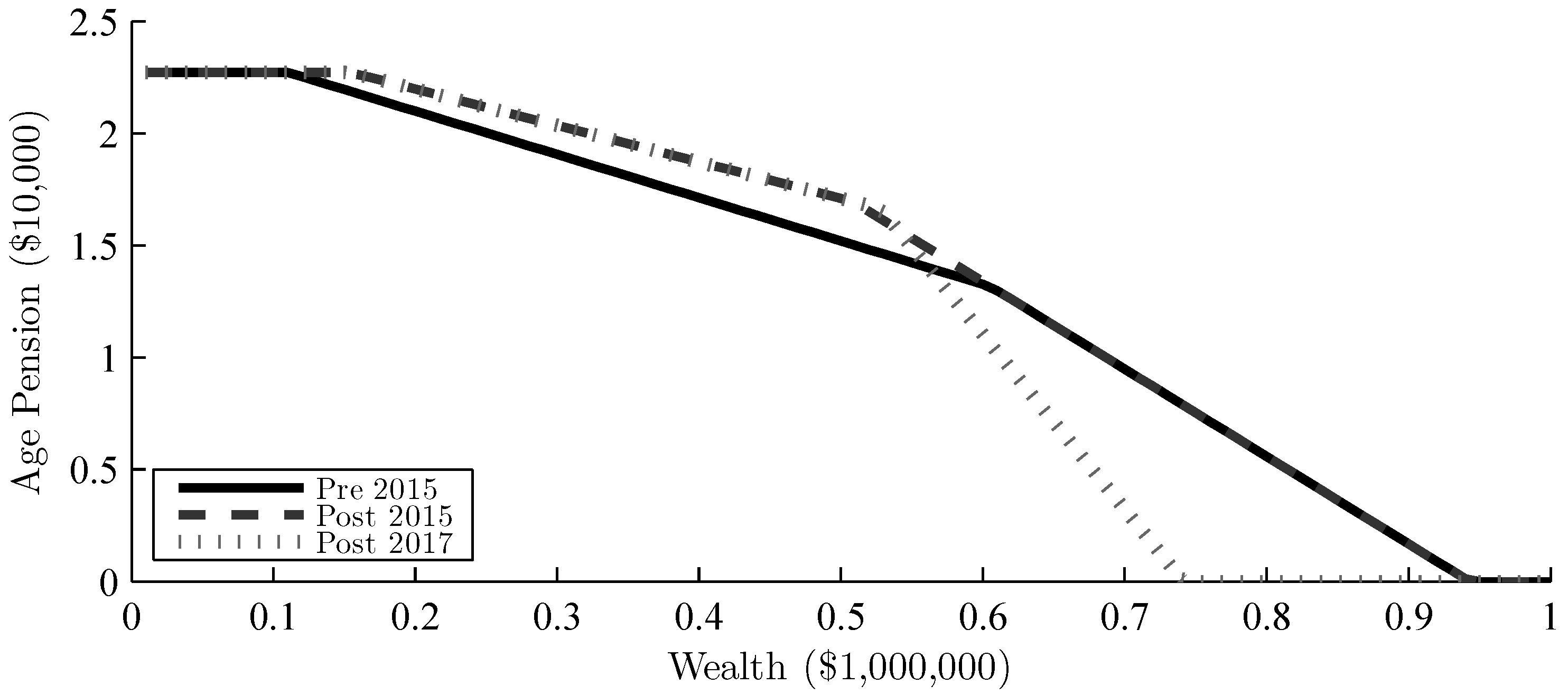
- Policy 3, asset-test changes January 2017 (POST2017): On 1 January 2017, the thresholds of the asset-test were ‘rebalanced’, hence changed significantly. The thresholds for the asset-test increased, and the taper rate doubled. This effectively means that retirees will now receive full Age Pension for a higher level of wealth, but once the asset-test binds, the partial Age Pension will decrease twice as fast, causing them to receive no Age Pension at a lower level of wealth than before. No adjustments were made to the full Age Pension or income-test threshold.
2.3. Age Pension
2.3.1. Deemed Income
2.3.2. Age Pension Function
2.4. Parameters
- -
- A retiree is eligible for Age Pension at age and lives no longer than .
- -
- The lower threshold for housing is set to $30,000. That is, a retiree with wealth below this level cannot be a homeowner, hence 30,000.
- -
- A unisex survival probability is used to avoid separating the sexes, as it would add an extra state variable. The survival probabilities for a couple are assumed to be mutually exclusive, based on the oldest partner in the couple. The actual mortality probabilities are taken from Life Tables published by Australian Bureau of Statistics (2014).
- -
- The subjective discount rate is set in relation to the real interest rate so that .
2.5. Numerical Implementation
3. Results
3.1. Optimal Consumption
3.2. Optimal Risky Asset Allocation
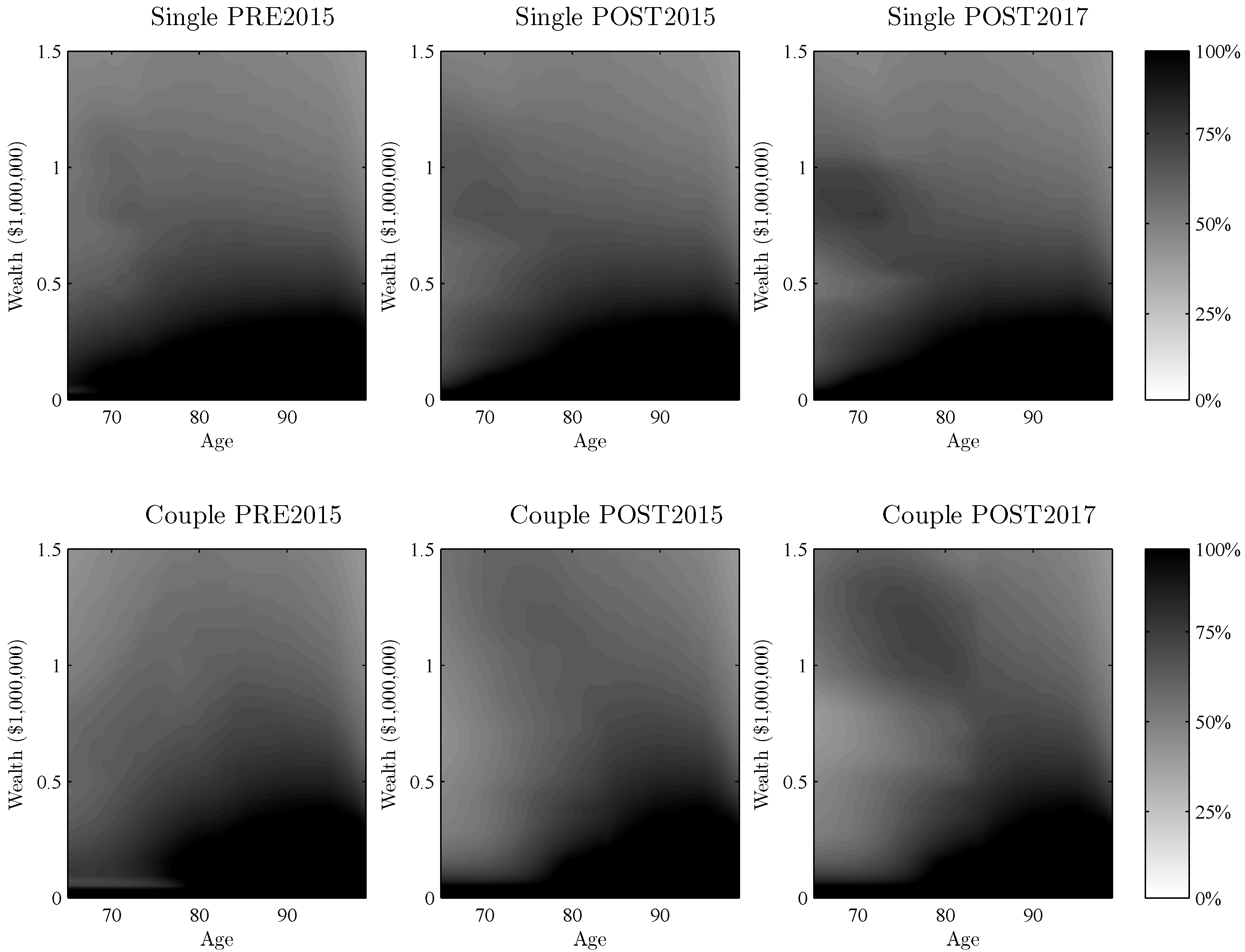
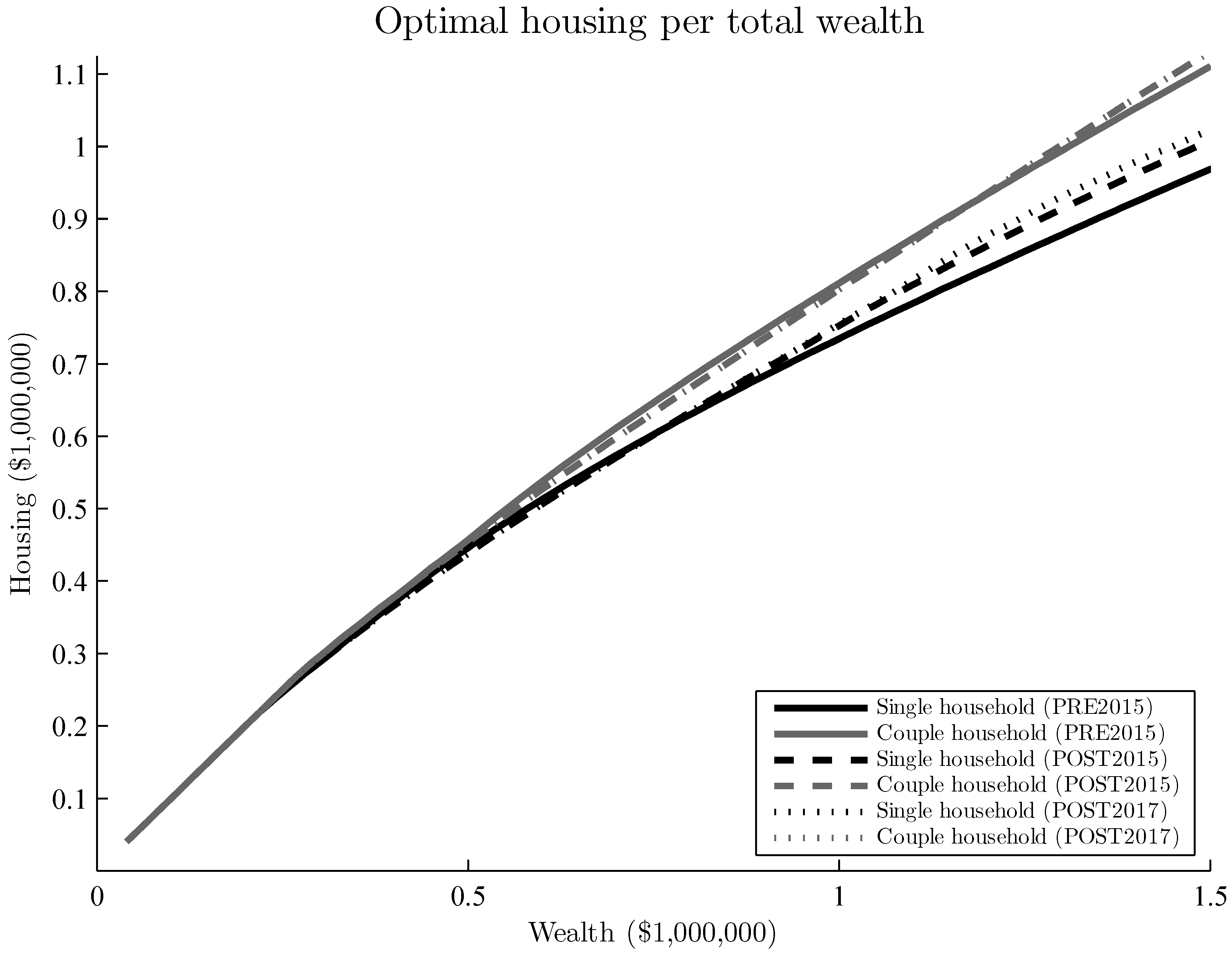
3.3. Optimal Housing Allocation
3.4. Limitations
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Andreasson, Johan G., Pavel V. Shevchenko, and Alex Novikov. 2017. Optimal Consumption, Investment and Housing with Means-tested Public Pension in Retirement. Insurance Mathematics and Economics 75: 32–47. [Google Scholar] [CrossRef]
- Australian Bureau of Statistics. 2011. Household Expenditure Survey and Survey of Income and Housing Curf Data. Available online: http://www.abs.gov.au/ausstats/abs@.nsf/mf/6503.0 (accessed on 6 June 2014).
- Australian Bureau of Statistics. 2014. 3302.0.55.001 - Life Tables, States, Territories and Australia, 2012–2014. Available online: http://www.abs.gov.au/ausstats/abs@.nsf/mf/3302.0.55.001 (accessed on 4 November 2014).
- Australian Government Department of Veterans’ Affairs. 2017. Rebalanced Assets Test to Apply from 2017. Available online: http://www.dva.gov.au/rebalanced-assets-test-apply-2017/ (accessed on 19 January 2017).
- Australian Taxation Office. 2016. Minimum Annual Payments for Super Income Streams. Available online: https://www.ato.gov.au/rates/key-superannuation-rates-and-thresholds/ (accessed on 27 October 2016).
- Bateman, Hazel, Susan Thorp, and Geoffrey Kingston. 2007. Financial engineering for Australian annuitants. In Retirement Provision in Scary Markets, 1st ed. Edited by Hazel Bateman. Northampton: Edward Elgar Publishing, pp. 123–44. [Google Scholar]
- Blake, David, Douglas Wright, and Yumeng Zhang. 2014. Age-dependent investing: Optimal funding and investment strategies in defined contribution pension plans when members are rational life cycle financial planners. Journal of Economic Dynamics and Control 38: 105–24. [Google Scholar] [CrossRef]
- Boender, G. C., P. C. van Aalst, and F. Heemskerk. 1997. Modelling & Management of Assets & Liabilities of Pension Plans in the Netherlands. Rotterdam: Erasmus University Rotterdam. [Google Scholar]
- Cocco, João, and Francisco Gomes. 2012. Longevity risk, retirement savings, and financial innovation. Journal of Financial Economics 103: 507–29. [Google Scholar] [CrossRef]
- Cocco, João, Francisco Gomes, and Pascal Maenhout. 2005. Consumption and portfolio choice over the life cycle. Review of Financial Studies 18: 491–533. [Google Scholar] [CrossRef]
- Department of Social Services. 2017. Guides to Social Policy Law. Available online: http://guides.dss.gov.au/guide-social-security-law (accessed on 4 January 2017).
- Ding, Jie. 2014. Essays on Post-Retirement Financial Planning and Pension Policy Modelling in Australia. Ph.D. Dissertation, Macquarie University, Sydney, Australia. [Google Scholar]
- Ding, Jie, Geoffrey Kingston, and Sachi Purcal. 2014. Dynamic asset allocation when bequests are luxury goods. Journal of Economic Dynamics and Control 38: 65–71. [Google Scholar] [CrossRef]
- Dupačová, Jitka, and Jan Polívka. 2009. Asset-liability management for Czech pension funds using stochastic programming. Annals of Operations Research 165: 5–28. [Google Scholar] [CrossRef]
- Fisher, Lance. 1930. The Theory of Interest: As Determined by Impatience to Spend Income and Opportunity to Invest it, (1 ed.). New York: The Macmillan Company. [Google Scholar]
- Henry, Ken. 2009. Australia’s Future Tax System—Report to the Treasurer (Overview). Technical Report December, Commonwealth of Australia. Available online: http://taxreview.treasury.gov.au/content/downloads/ (accessed on 20 April 2017).
- Hilli, Petri, Matti Koivu, Teemu Pennanen, and Antero Ranne. 2007. A stochastic programming model for asset liability management of a Finnish pension company. Annals of Operations Research 152: 115–39. [Google Scholar] [CrossRef]
- Hulley, Hardy, Rebecca Mckibbin, Andreas Pedersen, and Susan Thorp. 2013. Means-Tested Public Pensions, Portfolio Choice and Decumulation in Retirement. Economic Record 89: 31–51. [Google Scholar] [CrossRef]
- Iskhakov, Fedor, Susan Thorp, and Hazel Bateman. 2015. Optimal Annuity Purchases for Australian Retirees. Economic Record 91: 139–54. [Google Scholar] [CrossRef]
- Kahaner, David, Cleve Moler, Stephen Nash, and George Forsythe. 1988. Numerical Methods and Software. Upper Saddle River: Prentice Hall. [Google Scholar]
- Kahneman, Daniel, and Amos Tversky. 1979. Prospect Theory: An Analysis of Decision under Risk. Econometrica 47: 263–92. [Google Scholar] [CrossRef]
- Kopa, Miloš, Vittorio Moriggia, and Sebastino Vitali. 2016. Individual optimal pension allocation under stochastic dominance constraints. Annals of Operations Research 14: 1–37. [Google Scholar] [CrossRef]
- KPMG. 2010. KPMG Econtech CGE Analysis of the Current Australian Tax System. Technical Report March. Available online: https://www.cpaaustralia.com.au (accessed on 17 September 2016).
- Levy, Haim. 2006. Investment Decision Making under Uncertainty, 2nd ed. Dordrecht: Springer. [Google Scholar]
- Lockwood, Lee. 2014. Incidental Bequests: Bequest Motives and the Choice to Self-Insure Late-Life Risks. NBER Working Paper No. 20745. [Google Scholar] [CrossRef]
- Merton, Robert. 1969. Lifetime Portfolio Selection Under Uncertainty: The Continuous Time Case. Review of Economics and Statistics 51: 247–57. [Google Scholar] [CrossRef]
- Merton, Robert. 1971. Optimum consumption and portfolio rules in a continuous-time model. Journal of Economic Theory 3: 373–413. [Google Scholar] [CrossRef]
- Modigliani, Franco, and Richard Brumberg. 1954. Utility Analysis and the Consumption Function: An Interpretation of Cross-Section Data. In Post Keynesian Economics. Edited by Kenneth K. Kurihara. London: George Allen & Unwin, pp. 388–436. [Google Scholar]
- Plan For Life. 2016. Report on the Australian Reitrement Income Market. Technical Report, Plan For Life. Available online: http://www.pflresearch.com.au (accessed on 3 April 2016).
- Rice Warner. 2015. Quo Vadis? Superannuation needs effective policy...not politics. Submission to Tax White Paper Task Force. Available online: http://ricewarner.com/wp-content/uploads/2015/07/Tax-White-Paper.pdf (accessed on 20 April 2017).
- Samuelson, Paul. 1969. Lifetime portfolio selection by dynamic stochastic programming. The Review of Economics and Statistics 51: 239–46. [Google Scholar] [CrossRef]
- Shevchenko, Pavel V. 2016. Analysis of Withdrawals From Self-Managed Super Funds Using Australian Taxation Office Data; CSIRO Technical Report EP164438; Canberra: CSIRO Australia.
- Spicer, Alexandra, Olena Stavrunova, and Susan Thorp. 2016. How Portfolios Evolve after Retirement: Evidence from Australia. Economic Record 92: 241–67. [Google Scholar] [CrossRef]
- The Commonwealth of Australia. 2015. Budget 2015 Overview. Technical Report. Available online: http://www.budget.gov.au (accessed on 1 October 2014).
- Vitali, Sebastino, Vittorio Moriggia, and Miloš Kopa. 2017. Optimal pension fund composition for an Italian private pension plan sponsor. Computational Management Science 14: 135–60. [Google Scholar] [CrossRef]
- Yaari, Menahem. 1964. On the consumer’s lifetime allocation process. International Economic Review 5: 304–17. [Google Scholar] [CrossRef]
- Yaari, Menahem. 1965. Uncertain Lifetime, Life Insurance, and the Theory of the Consumer. The Review of Economic Studies 32: 1–137. [Google Scholar] [CrossRef]
| 1 | Certain account types for retirement savings have a minimum withdrawal rate once the owner is retired. |
| 2 | The pension system in Australia is called ‘superannuation’. |
| 3 | The recommendations to introduce deeming was made in Henry (2009), where the fiscal sustainability is evaluated with the general equilibrium model ‘KPMG Econtech MM900’ (KPMG 2010). The model shows the estimation over a 10-year window; hence, we do not know the short-term or year-to-year estimates. In addition to this, the model includes additional suggested tax- and budget-related changes; hence, the effect of introducing deeming rates cannot be isolated. |
| 4 | As of 4 May 2017, the current three-month rate offered by Commonwealth Bank is 2.05% (https://www.commbank.com.au/personal/accounts/term-deposits/rates-fees.html, accessed on June 8, 2017). |
| 5 | By defining the model in real terms (adjusted for inflation), time-dependent variables do not have to include inflation, which otherwise would be an additional stochastic variable. |
| 6 | Note that the purpose is not to model health among the retirees, but rather to explain decreasing consumption with age. |
| 7 | The risk aversion is considered to be the same as consumption risk aversion for singles since a couple is expected to become a single household before bequeathing assets. |
| 8 | Because the marginal utility is constant for the bequest utility with zero wealth, in a model with perfect certainty and CRRA utility, the optimal solution will suggest consumption up to level a before it is optimal to save wealth for bequest (Lockwood 2014). |
| 9 | As of 1 July 2017, this increased to 65.5 years for people born after 1 July 1952, but for our dataset, the entitlement age was 65. Already retired Australians might have had earlier entitlement ages. |
| 10 | The current rates are at a historical low. In 2008, the deeming rates were as high as 4%/6%, but in March 2013, they were set to 2.5%/4% due to decreasing interest rates, then in November 2013 to 2%/3.5% and to the current levels of 1.75%/3.25% in March 2015. Note that despite the model being defined in real terms, it can be shown with simple algebra that the deeming rates shall not be adjusted to ‘real’ deeming rates. |
| 11 | It should be noted that the findings are for the account-based pension only, as other products that do not enforce the minimum withdrawal rates could incur additional savings for the government under the new rules. |
| 12 | A 401(k) is a defined-contribution retirement savings plan sponsored by the employer. |
| PRE2015 | POST2015 | POST2017 | |
|---|---|---|---|
| Full Age Pension singles () | $22,721 | $22,721 | $22,721 |
| Full Age Pension couples () | $34,252 | $34,252 | $34,252 |
| Income-Test | Drawdown | Deemed | Deemed |
| Threshold singles () | $4264 | $4264 | $4264 |
| Threshold couples () | $7592 | $7592 | $7592 |
| Rate of reduction () | $0.5 | $0.5 | $0.5 |
| Deeming threshold singles () | - | $49,200 | $49,200 |
| Deeming threshold couples () | - | $81,600 | $81,600 |
| Deeming rate below () | - | 1.75% | 1.75% |
| Deeming rate above () | - | 3.25% | 3.25% |
| Asset-Test | |||
| Threshold homeowners singles () | $209,000 | $209,000 | $250,000 |
| Threshold homeowners couples () | $296,500 | $296,500 | $375,000 |
| Threshold non-homeowners singles () | $360,500 | $360,500 | $450,000 |
| Threshold non-homeowners couples () | $448,000 | $448,000 | $575,000 |
| Rate of reduction () | $0.039 | $0.039 | $0.078 |
| a | ||||||||
|---|---|---|---|---|---|---|---|---|
| Single household | 0.96 | $27,200 | $13,284 | 1.18 | 0.044 | 1.0 | ||
| Couples household | 0.96 | $27,200 | $20,607 | 1.18 | 0.044 | 1.3 |
| Age | ≤64 | 65–74 | 75–79 | 80–84 | 85–89 | 90–94 | ≤95 |
| Min. drawdown | 4% | 5% | 6% | 7% | 9% | 11% | 14% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andréasson, J.G.; Shevchenko, P.V. Assessment of Policy Changes to Means-Tested Age Pension Using the Expected Utility Model: Implication for Decisions in Retirement. Risks 2017, 5, 47. https://doi.org/10.3390/risks5030047
Andréasson JG, Shevchenko PV. Assessment of Policy Changes to Means-Tested Age Pension Using the Expected Utility Model: Implication for Decisions in Retirement. Risks. 2017; 5(3):47. https://doi.org/10.3390/risks5030047
Chicago/Turabian StyleAndréasson, Johan G., and Pavel V. Shevchenko. 2017. "Assessment of Policy Changes to Means-Tested Age Pension Using the Expected Utility Model: Implication for Decisions in Retirement" Risks 5, no. 3: 47. https://doi.org/10.3390/risks5030047
APA StyleAndréasson, J. G., & Shevchenko, P. V. (2017). Assessment of Policy Changes to Means-Tested Age Pension Using the Expected Utility Model: Implication for Decisions in Retirement. Risks, 5(3), 47. https://doi.org/10.3390/risks5030047







