Abstract
Building a social security system to ensure Singapore residents have peace of mind in funding for retirement has been at the top of Singapore government’s policy agenda over the last decade. Implementation of the Lifelong Income For the Elderly (LIFE) scheme in 2009 clearly shows that the government spares no effort in improving its pension scheme to boost its residents’ income after retirement. Despite the recent modifications to the LIFE scheme, Singapore residents must still choose between two plans: the Standard and Basic plans. To enhance the flexibility of the LIFE scheme with further streamlining of its fund management, we propose some plan modifications such that scheme members do not face a dichotomy of plan choices. Instead, they select two age parameters: the Payout Age and the Life-annuity Age. This paper discusses the actuarial analysis for determining members’ payouts and bequests based on the proposed age parameters. We analyze the net cash receipts and Internal Rate of Return (IRR) for various plan-parameter configurations. This information helps members make their plan choices. To address cost-of-living increases we propose to extend the plan to accommodate an annual step-up of monthly payouts. By deferring the Payout Age from 65 to 68, members can enjoy an annual increase of about 2% of the payouts for the same first-year monthly benefits.
1. Introduction
Building a social security system to ensure Singapore residents have peace of mind in funding for retirement has been at the top of the Singapore government’s policy agenda over the last decade. Implementation of the Minimum Sum Scheme in 1987, the Central Provident Fund (CPF) Lifelong Income For the Elderly (LIFE) scheme in 2009, the simplified LIFE scheme in 2013 and the recently proposed changes to the LIFE scheme in 2016 clearly show that the government spares no effort in improving its pension scheme to boost its residents’ income after retirement.1
Although many developed countries have valuable experience in establishing and implementing public pension schemes, it is evident that the Singapore government desires to build a system based on its own principles of governance and unique social structure, rather than simply adopting an existing system. Several characteristics of the current LIFE scheme distinguish it from other public pension systems. First, it is a defined-contribution scheme in which individuals get their benefits based on what they have contributed. Second, the scheme is compulsory and comprehensive, casting a wide safety net and mitigating the self-selection problem. Third, members in the scheme receive life-annuity payouts, which reduces longevity risk. Fourth, the scheme is managed by the government, with low operating costs and no credit risk. Fifth, there is a guarantee of return for the cash contributions in the form of bequests to the beneficiaries.
The many changes made since the first implementation of the LIFE scheme should be viewed as a commitment on the part of the government to make the system responsive to the needs and perceptions of Singapore residents. For instance, the revamp of the LIFE scheme in 2013 resulted in reducing the number of plan choices from four to two; namely, the Standard and Basic Plans. Although both plans provide life-annuity payouts, they differ in the amounts of monthly payouts and bequests to the beneficiaries when the CPF member passes away.
As more Singapore residents enter retirement, their experiences and needs become better known. This led the government to form the CPF Advisory Panel in 2014 to review the overall social security system2. In Part I of their report issued in 2015, the Panel laid down three guiding considerations—adequacy, flexibility and simplicity—based on which of several recommendations were made. In adopting these recommendations, the government has made several changes to the LIFE scheme and implemented them beginning in 2016. First, the starting age of the annuity payouts can be selected by the CPF members, ranging from age 65 up to 70. Second, members are given the option to increase their contributions if desired, so that they receive higher payouts and bequests. Third, members can withdraw lump sums from their CPF accounts after reaching the Payout Eligibility Age. Fourth, members can top up their spouses’ CPF accounts to enable them to enjoy the benefits of the LIFE scheme.
Despite the abovementioned flexibility provided by the enhanced LIFE scheme, members must still choose between only two plans: Standard and Basic. These two plans differ from each other in that the Standard Plan pays higher monthly payouts but lower bequests compared to the Basic Plan3. In this paper we propose to modify the LIFE scheme, while maintaining the key features of the two plans. Our proposed scheme allows members to choose monthly payouts between the two existing plans to suit their personal preference. We call our modified scheme the Unified Plan.
Under the Unified Plan, CPF members do not face a dichotomy of plan choices. Instead, they select two age parameters: the Payout Age and the Life-annuity Age. The Payout Age is the age at which the member starts to receive monthly payouts from the Retirement Account, and the Life-annuity Age is the age at which the member starts to receive monthly payouts from a life-annuity fund. Similar to a universal life insurance policy, the Unified Plan considers each installment payable from the Retirement Account as a contribution to a notional account rather than the premium for an insurance product.4 With this new feature, the adjustments of payouts and bequests under the Unified Plan are streamlined.
In sum, we propose modifications of the CPF LIFE scheme to enhance its flexibility. Our proposal of a single notional fund facilitates the risk management of the fund sponsor and administrator. Our study also contributes to the actuarial analysis of similar nation-wide pension systems.5
The remainder of this paper is organized as follows. Section 2 presents the major features of the proposed Unified Plan. Section 3 analyzes the cash flows under different parameter configurations of the Unified Plan and discusses the choice of the configurations. Section 4 examines a possible step-up payout extension of the plan, and Section 5 provides a case study under the Unified Plan with different options. Finally, Section 6 summarizes the findings and discusses possible extensions of the CPF LIFE scheme.
2. The Proposed Unified Plan
Under the proposed Unified Plan, CPF members select two age parameters: the Payout Age (PA) and the Life-annuity Age (LA). According to their choice of age parameters, members receive different amounts of payouts and bequests, thus enhancing the flexibility of the dichotomized LIFE scheme. To fund the monthly payouts and possible bequests, two funding sources are established: the Retirement Account (RA) and the Lifelong Income Fund (LIF). In the current LIFE scheme, the two installments transferred from the RA to the LIF are considered as separate premiums to two different funds. As a result, each of these funds is used to fund part of the monthly payouts and part of the bequest. However, under the Unified Plan, only the annuity fund LIF is considered as a notional account directly funding the life-annuity payouts and possible bequests.6 The amount in the notional account works as a basis for the plan administrator to determine the payouts and bequests. Our proposal simplifies the life-annuity funding arrangement without losing any flexibility. In this section, we outline the major features of the Unified Plan.
The framework of the Unified Plan is presented in Figure 1. Following the LIFE scheme, an RA is created for each member at age 55, provided the member’s CPF accounts have sufficient funds. The first installment is then transferred from the RA to the LIF. Upon reaching the Payout Eligibility Age of 65, the member has five years to decide when the monthly payouts will start. At the time the PA is selected, the member also selects the LA. In other words, the possible values of the PA range from 65 to 70, whereas the LA is higher than or equal to the PA.7
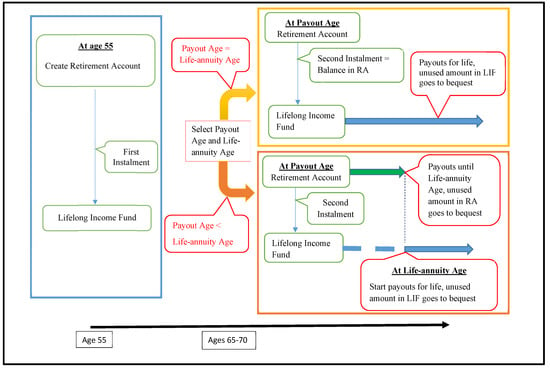
Figure 1.
The proposed unified plan. RA: Retirement Account; LIF: Lifelong Income Fund.
If a member specifies that the LA should be the same as the PA, the balance in his RA is completely transferred to the LIF as the second installment. After the transfer, the RA is closed and the member receives monthly annuity payouts from the LIF for life. Upon the member’s death, if the total amount of monthly payouts is less than the sum of the two installments to the LIF, the difference is payable to the member’s beneficiaries as bequests. Otherwise, no bequest is payable. Under this parameter configuration (i.e., PA = LA), the plan works as an ordinary life annuity, with the premium refund feature as the bequest. This plan configuration is similar to the current default Standard Plan, and is illustrated in the upper right-hand panel of Figure 1. Therefore, we suggest using the configuration (70, 70) as the default option of the Unified Plan.
In contrast, if the member chooses an LA that is higher than the PA, the amount of the second installment is determined actuarially. This amount is then transferred from the RA to the LIF at the PA, and the remaining balance in the RA acts as the source of an annuity certain to fund payouts for the period from the PA to the LA. If he dies before reaching the LA, any outstanding balance in his RA, together with the two installments to the LIF, are paid to his beneficiaries as bequests. If he survives and reaches the LA, the RA is closed and the monthly payouts are payable for life from the LIF. Upon the death of the member after the LA, if the total amount of the monthly payouts from the LIF is less than the sum of the two installments to the LIF, the difference is paid to the member’s beneficiaries as a bequest. Otherwise, no bequest is payable.8 This age-parameter configuration is illustrated in the lower right-hand panel of Figure 1. Note that this choice is similar to the current Basic Plan. Given that the current Basic Plan has fixed 90 as the starting age for the life-annuity payments, we propose to set the upper limit of the LA at 90, while allowing members to select lower values, such as 80 or 85, for higher payouts and lower bequests.
Given the same amount of contributions to the scheme, different configurations of PA and LA in the Unified Plan result in different monthly payout and bequest amounts, providing additional flexibility to meet the members’ needs. Furthermore, under the Unified Plan, only one LIF operates for each member, unlike the current LIFE scheme, which has two annuity income funds. Thus, when interest rate and mortality experience deviate from the actuarial assumptions, or when there is any lump sum withdrawal from the scheme, it is straightforward to evaluate their effect on the LIF balance and the necessary adjustments to the monthly payouts. This results in much desired simplicity for fund management while also enhancing the flexibility of the plan options.
When the PA is equal to the LA, the computation of the monthly payouts is straightforward for a given amount of total contributions to the LIF. In this case, the LIF acts as a universal life annuity with the premium refund feature. When the PA is less than the LA, however, the monthly payouts come from two funding sources in two different phases. To ensure that CPF members receive level payouts (‘stable’ payouts as required by the Advisory Panel) for life, the required amounts of the installments to the LIF must be computed according to sound actuarial principles. The installments and monthly payouts can be determined using the actuarial framework proposed in [3], based on the actuarial equivalence principle. In this paper we adopt the methodology therein to evaluate the Unified Plan, with the details of the analysis summarized in Appendix A. We determine the appropriate amount to be transferred to the RA at age 55, as well as the level monthly payouts starting from the Payout Age. Further analysis is summarized in Appendix B, which determines the benefits and costs provided by the LIF at different stages of the plan under different plan parameter configurations.
3. Illustrative Plan Outcomes
In this section we present some results on comparing different plan parameter choices. To facilitate easy comparison we use age and fund contribution figures based on CPF illustrations. We first present the results for the monthly payouts, some of which can be compared against the CPF illustrations. Plan parameter choices are then evaluated based on net cash flows and internal rate of return. Finally, we further analyze the plans as compositions of different insurance products at different stages of the payouts. These results provide additional insights into the LIFE scheme and show the relative importance of the payouts and bequests in different plan parameter configurations.
3.1. Plan Assumptions
We now consider the assumptions of the investment return and mortality in the actuarial models. As the CPF Board is currently crediting 4% interest for the RA savings, we assume the investment return rate to be fixed at 4% per annum. For the mortality assumption, we first note that life tables for the CPF members are not available. If the Singapore Complete Life Tables are used for the CPF members, the mortality rate is likely to be overstated, as the survival rates of the CPF members are expected to be higher than those of the general population. To construct the survival distributions of the CPF members, we propose using the U.S. RP-2014 annuitant mortality tables as a proxy.9 With possible mortality improvement, we also modify the RP-2014 mortality tables by incorporating the MP-2014 mortality improvement factors.10 As the sensitivity study of applying RP-2014 and MP-2014 to our model does not show any significant differences in the analysis of the Unified Plan, MP-2014 is used to construct the life table for the cohort age 55 in 2014 as the mortality assumption. Furthermore, we adopt the constant force-of-mortality assumption within each year of age.11
3.2. Monthly Payouts
To evaluate the financial effects on the annuity payouts under different configurations of the Unified Plan and varied contribution amounts, we construct a Unified Plan Estimator to calculate the cash flows. To illustrate the plan outcomes based on the Estimator, we consider some retirement savings cases. Following the recent CPF LIFE scheme descriptions, we consider the following Retirement Account savings at age 55: Basic Retirement Sum (BRS) of 80 5000, Full Retirement Sum (FRS) of 161 000 and Enhanced Retirement Sum (ERS) of 241 500.12 BRS, FRS and ERS are the amounts of retirement sums CPF uses as illustrations of monthly payouts. In particular, ERS is the maximum amount a CPF member is currently allowed to transfer to the Retirement Account.13 We also consider cases in which the member makes new money contributions to the RA at age 65, such that the FRS and ERS can be reached. Table 1 provides the monthly payouts for a male CPF member under different savings contribution amounts and age-parameter configurations, with the PA equaling 65 to 70 and the LA equaling the PA, 80 and 90.

Table 1.
Payouts of the Unified Plan for a male Central Provident Fund (CPF) member.
Table 1 shows the following results. First, for every one-year deferment in the PA, the monthly payouts increase by about 6–7% for any LA choices.14 If a member defers his PA to 70, he gets about 35% more in his monthly payouts than what he receives if he opts to start the payout at age 65. Second, for a selected PA, if a member chooses an LA of 80, he receives about 3–4% less each month than if he chooses an LA that is the same as the PA. The drop in the monthly payouts increases to about 10% if he chooses an LA of 90. In return, he is covered by a longer term insurance and leaves more bequests to his beneficiaries. Third, while the total contributions to the RA for Cases C, E and F are the same, the monthly payouts for Case C and F are about 14% (28%) more than those for Case E. Due to the higher contributions at an earlier age for Cases C and F, compared to Case E, the former earns more interest over a longer period, resulting in higher monthly payouts. Likewise, payouts for Case B are about 20% more than those for Case D, although the total contributions to the RA for the two cases are the same.
3.3. Net Cash Receipts Analysis
To assess the Unified Plan’s cash flows, we define the members’ Net Cash Receipts (NCRs) as the sum of the aggregate monthly payouts and bequests minus the total contributions to the RA. As the Unified Plan provides returns of the unused contributions, the NCRs are always positive. To evaluate the effect that the age-parameter configuration choice has on the net cash receipts, we plot the latter at different age-at-death values under a variety of parameter configurations and contributions in Figure 2. To facilitate exposition, we denote a plan choice by the duplet (PA, LA). Figure 2 reveal the following results. First, the net cash receipts in configuration (70, 70) dominate those in configuration (65, 65). Likewise, (70, 90) dominates (65, 90). These results are perhaps not surprising, as deferring monthly payouts enables the funds to earn more interest, giving rise to higher aggregate payments over time. Second, (70, 70) dominates (70, 90) and (65, 65) dominates (65, 90) in terms of the net cash receipts if the member lives to an age of approximately 90 or beyond. As configurations with PA equaling LA provide higher payouts and lower bequests than those with a PA of less than the LA, the net cash receipts for plans of the former configuration are lower (higher) than those of the latter if the member dies earlier (later).
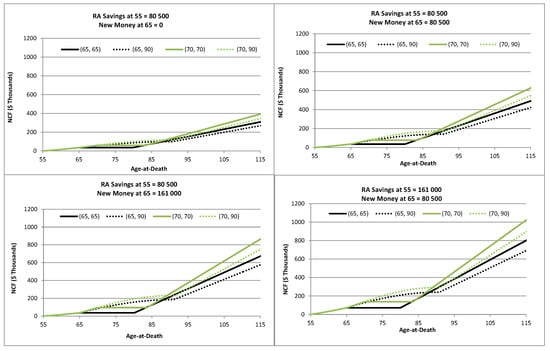
Figure 2.
Net Cash Receipts (NCR) under various parameter configurations and plan choice (PA, LA).
3.4. Internal Rate of Return Analysis
Although NCR is easy to calculate, it does not consider the time value of money. An alternative measure of the plan outcome is the Internal Rate of Return (IRR), evaluated over different age-at-death. Figure 3 presents the IRR of four selected plan configurations under different fund contributions, and shows the following results. First, the IRR of configuration (70, 70) is significantly higher than that of (65, 65) if the member dies earlier (approximately age 82 or before). Otherwise, the IRR values of the two plans are very close. This result is in line with the results from Figure 2, and shows the advantage of deferring the monthly payouts. Second, the IRR of configuration (65, 80) is higher than that of (65, 65) if the member dies earlier (approximately age 83 or before). Otherwise, the IRR of configuration (65, 65) is slightly higher. When the member dies earlier, the higher bequest for the plan (65, 80) compensates for its lower monthly payouts and leads to a higher IRR when compared to configuration (65, 65). Third, the configuration (70, 90) has a stable IRR of slightly less than 4% until age-at-death of around 90. Beyond this point, the IRR rises, although it is lower than the IRR values of the other three plans. Overall, this plan configuration is the best choice under a maximin IRR criterion of selecting the plan parameters.
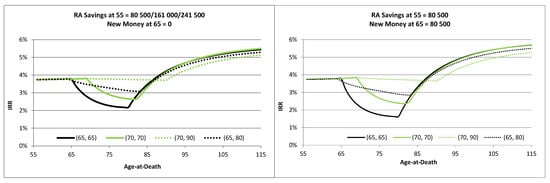
Figure 3.
Internal Rate of Returns (IRR) under various parameter configurations and plan choices (PA, LA).
3.5. Analysis of the Lifelong Income Fund
As the plan administrator, the CPF Board shares the profit and loss of the LIFE scheme, due to the uncertainty in mortality and investment returns, with its members through the credited rate of interest rate declared periodically. The LIF, which is made up of the contributions from the RA and credited interest, is subject to monthly payout deductions and life insurance coverage costs. Thus, from an actuarial perspective, the LIF is like the notional account of a universal life product, as the underlying assets are not segregated from the CPF’s general account. In this section, we analyze the balance of the LIF as the premiums of life annuity and life insurance coverage at members’ different life stages. We consider the actuarial evaluation of each component over these stages. The mathematical details are summarized in Appendix B. This analysis clarifies the relative importance of the insurance components in different plan parameter choices.16
We first consider the case when the LA is set to be equal to the PA. In this case, the LIFE scheme can be divided into two stages. Stage 1 is from age 55 to the PA, and Stage 2 is from the PA onward. The first installment made at age 55 (the beginning of Stage 1) and can be considered as the sum of two premiums: one for purchasing a pure endowment policy that matures at the PA and the other for purchasing a term insurance policy (for the bequest). When the member survives to the PA, the balance of the LIF is equal to the survival benefit of the pure endowment insurance. Any new contribution from the RA to the LIF plus the survival benefit is then used to purchase a life annuity and a decreasing term insurance policy in Stage 2.17
To illustrate the breakdown of these components, we consider a case of a male member with 80 500 savings in his RA at age 55 and a new contribution of 161 000 to the RA at age 65. Among the parameter configurations of PA equal to LA, we consider three different configurations (PA = LA = 65, 67 and 70) and analyze the LIF in these two stages. The results are summarized in Panel A of Table 2. At age 55, the amount in the RA to be transferred to the LIF is 5190.18 If PA = LA = 65, the balance of the LIF at age 55 is 4891 for the premium of the pure endowment insurance and 299 for the premium of the term insurance, which represent 94% and 6%, respectively, of the first installment. If the member survives to the PA, the survival benefit of the pure endowment insurance is 7792 and the second installment from the RA to the LIF is 272 477. The sum of the survival benefit and the second installment is divided into the premium of a life annuity of 257 910 and the premium of a decreasing term insurance of 22 359, with the term being 15 years and 2 months. This implies that it takes 15 years and 2 months to repay back the total amount of the two installments to the LIF as monthly payouts. Thus, the relative weights of the premiums of the life-annuity and term insurance are, respectively, 92% and 8%. The results for the other two configurations are similar, and it can be seen that the term insurance components increase with the PA, but are at most 10% in all three cases.

Table 2.
An illustrative example of the premium components of the LIF.
For the case where the PA is less than the LA, three stages of policy separation can be considered. Stage 1, from age 55 to the PA, is the same as Stage 1 of the case with PA = LA. Stage 2 now refers to the period from PA to LA, in which the member receives an annuity certain from the RA. Stage 3, which is from the LA onward, consists of a life annuity and a decreasing term insurance.
Again, we consider the case of a male member with 80 500 savings in his RA at age 55 and a new contribution of 161 000 to the RA at age 65. The results of three different configurations in which the PA is less than the LA are summarized in Panel B of Table 2. It can be seen that in Stage 1 (age 55 to PA) the results are the same as those in Panel A (with PA = LA). Similar to Stage 1, Stage 2 also consists of a pure endowment and a term insurance. However, the premium component of the term insurance policy in Stage 2 is much higher than that in Stage 1, reaching 30% for the case of PA = 70 and LA = 90, as the cost of the term insurance is higher due to higher mortality rates in this stage. Finally, in Stage 3, the weight of the decreasing term insurance component drops to below 5% as the death benefit reduces rapidly. The duration of the decreasing term insurance is larger for lower LA or/and higher PA, as the amount of the second installment is higher under these two situations. As the amount of LIF is used to fund the future benefits in terms of payouts and bequests, the single LIF of the Unified Plan for each member provides a simple and direct mechanism to adjust the payouts and bequests according to the balance of the LIF.
4. Plan Extension with Step-up Payouts
Currently, the LIFE scheme makes level monthly payouts throughout the life of a CPF member. As inflation risk is a major risk for retirement funding, it may be useful to consider extending the Unified Plan to allow for a step-up of monthly payouts. Assuming a constant step-up rate for monthly payouts, it is straightforward to modify the method in Appendix A to evaluate the payouts based on the principle of actuarial equivalence. To illustrate this extension, we consider Cases C and E in Table 1, with level payouts and a payout step-up of 2% per annum.19 In Table 3, we summarize the results of the payouts in the first year, with different PA and LA parameters. It can be seen that with a step-up, there is a drop in the first year payout of about 20% if PA = 65, with the same LA. This drop is reduced to about 18% if PA = 70, with the same LA. Regardless of the contribution amounts, with a step-up of 2% in the monthly payouts, the maximum starting payout is about 57% more than the minimum starting payout over the possible PA and LA choices. As this figure is higher than the corresponding value of about 50% when there is no step-up, the plan extension provides an even wider range of payout amounts for the members to choose from. By deferring the Payout Age for three years, members can enjoy an annual increase of about 2% of the payouts versus the first-year monthly benefits for all the considered cases.

Table 3.
Payouts of the Unified Plan with a step-up feature for a male CPF member.
5. An Illustrative Case Study
We now consider an illustrative case discussed in the CPF booklet for a CPF male member whose Ordinary Account, Special Account and Medisave Account balances are 100 000, 200 000 and 43 500, respectively.20 The member is currently aged 55 and is considering several options in planning for his retirement. He has to decide whether he should withdraw savings from his CPF accounts, the amount to withdraw, the amount to transfer to the RA and whether he should pledge his property to make additional transfers to the RA. Furthermore, he needs to decide whether he should work beyond age 65 and defer receiving his retirement income.
Suppose the member considers the following options: (a) transfer 80 500 to the RA now and then 161 000 at age 65 or (b) transfer 241 500 to the RA now.21 If he also has a plan to work until age 67, he can decide to start receiving payouts at that age. Our calculations show that his monthly payouts will range from 1527 to 1 708 for option (a) (see Case E in Table 3) and 1 965 to 2 188 for option (b) (see Case C in Table 3), depending on his choice of LA. If he chooses a payout step-up plan with a 2% increase per year, he will receive initial monthly payouts of 1 216 to 1 381 for option (a) (see Case E in Table 3) and 1 565 to 1 770 for option (b) (see Case C in Table 3).
We now assume the member finally chooses option (a) and picks a PA and LA of 67 and 90, respectively, with no payout step-up. Table 4 presents the summary of the projected cash flows and premium components funded by the LIF, with some hypothetical death age scenarios. We note that the member will receive a projected level monthly payout of 1527. His first and second projected installment to the LIF are 5190 and 16 582, respectively, whereas his projected RA balance at age 67 is 277 508. Table 4 provides his projected aggregate payouts and bequests at different death ages. The breakdown of his premium components shows that the term insurance constitutes 7% of the total amount of the LIF in Stage 1, and this component increases to 28% of the LIF in Stage 2 and then drops to 1% for the decreasing term insurance with a duration of 1 year and 2 months in Stage 3.

Table 4.
Illustrative outcomes of a plan choice.
6. Summary
We propose a modified version of the Singapore CPF LIFE Scheme, called the Unified Plan, which requires CPF members to select two age parameters: the Payout Age and the Life-annuity Age. Depending on the plan-parameter choice, retirees receive different amounts of monthly payouts and bequests to suit their preferences. Our proposal streamlines the funding sources for the payouts to the member’s own RA and a pooled LIF. It is not only flexible in incorporating the recent changes in the LIFE scheme, but also simplifies the financial arrangements of the member’s future benefits. The latter is important in modifying the payouts in response to changes in the actual mortality experience and investment returns. We adopt the actuarial framework in [3] to determine the payouts under different plan parameter configurations. Relating the key features of the Unified Plan to insurance products and explaining how the annuity fund can be managed, our analysis may be of use to other nation-wide defined-contribution pension systems. A Unified Plan Estimator is constructed to project the cash flows under a given set of input parameters. The Net Cash Receipts analysis and the internal rate of return analysis provide a useful guide for the CPF members to choose the parameter configurations to meet their needs.
Our models can be used to study possible future enhancements of the scheme. In particular, operating with a single notional fund account facilitates easier fund and risk management. It also opens up the possibility of transferring the fund return risk to the retirees.
Acknowledgments
Tse acknowledges funding support from the Singapore Ministry of Education Academic Research Fund Tier 3 Official Grant Number MOE2013-T3-1-017. Any opinions, findings, conclusions and recommendations expressed in this paper are those of the authors and do not necessarily reflect the views of the Singapore Ministry of Education. We thank the two reviewers for their insightful comments on our paper and Mr Mingyang Chen for excellent research assistance.
Author Contributions
The three authors have equally contributed to the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this paper:
| BRS | Basic Retirement Sum |
| CPF | Central Provident Fund |
| FRS | Full Retirement Sum |
| IRR | Internal Rate of Return |
| LA | Life-annuity Age |
| LIF | Lifelong Income Fund |
| LIFE | Lifelong Income for the Elderly |
| PA | Payout Age |
| RA | Retirement Account |
Glossary of Insurance Terms
The following insurance terms are used in this paper:
| Decreasing term insurance | A life insurance product for which the amount of death benefit is decreasing during the term |
| of coverage. | |
| Life-annuity | An income annuity that makes regular payments subject to the survival of the insured. |
| Notional account | For a universal life insurance product, the notional account is made up of the premium and |
| credited interest, and is subject to regular deductions due to the costs of insurance and expenses. | |
| Premium | The amount of payment that the insured needs to pay for the insurance policy. |
| Pure endowment | A life insurance product that pays a fixed amount of survival benefit when the insured survives |
| to a certain date, and nothing otherwise. | |
| Term insurance | A life insurance product that pays a fixed amount of death benefit when the insured dies |
| within a specified period of time. | |
| Universal life insurance | A particular form of insurance product with the features of flexible premium, notional account, |
| flexible face value and unbundled components. It is similar to a savings account combined | |
| with a term insurance. | |
| Variable insurance product | An insurance product for which the policy benefit is determined by the outstanding balance of |
| an investment fund. The insured bears the investment risk of the fund for possible higher | |
| investment return. |
Appendix A. Determination of Annuity Payouts and Bequests
We first define the following notations:22
| c = Payout Age |
| d = Life-annuity Age |
| e = Number of years payouts funded by RA, i.e., |
| i = Annual effective interest rate |
| v = Discount factor = 1/(1+i) |
| = Bequest payable at age g |
| = First installment from RA to LIF at age 55 |
| = Second installment from RA to LIF at Payout Age |
| = Monthly curtate future lifetime random variable at age g |
| = Monthly payout estimate at age 55 |
| P = Monthly payout |
| = Balance of RA at age g |
| = Aggregate amount of payouts from LIF up to age g |
We adopt the actuarial framework in [3] to determine the monthly payouts of the Unified Plan based on the actuarial equivalence principle. The key input variables are the return of the Life Income Fund and the mortality rates. The fund return rate is specified by the government as the plan sponsor. While various mortality tables are used in [3], we adopt the U.S. MP2014 table in this paper. For sensitivity of the results with respect to mortality assumption, see [3].
Under the Unified Plan, the cash outflows consist of the monthly payouts P starting at the Payout Age c until death at age g, with possible bequest payable upon death. If c is less than the Life-annuity Age d, the payouts are funded by the RA from age c to age d and then by the LIF from age d until death. The minimum value of c is the Payout Eligibility Age (currently set to be 65), and it cannot exceed 70. In contrast, the value of d may be from c to 90. If , the annuity payouts are entirely funded by the LIF for life and the configuration is similar to the Standard Plan.
As per the plan design, if a member dies at age g before reaching age c, the bequest consists of the balance of his RA and his first installment to the LIF, i.e., , for . If a member lives to start receiving monthly payouts and chooses , a second installment , which is the balance in his RA, is transferred to the LIF. Thus, his RA is depleted and the monthly payouts are funded by the LIF. If he dies after age c, the bequest is the difference between the sum of two installments and the aggregate amount of payouts from the LIF , i.e., for .
If his choice is , to the LIF is only part of the RA balance, as the rest is used to fund the annuity-certain up to age d. If he dies between ages c and d, the bequest to his beneficiaries is the sum of two installments plus the balance of RA, i.e., for ; otherwise, the bequest is the difference between the summation of two installments and the aggregate amount of payouts from the LIF. In summary, we can write the bequest as
for and
for .
We now determine the amount to be transferred from the RA to the LIF at age 55, and the initial estimate of the monthly payout . As the age-parameter configuration is determined at age , our strategy is to determine the value of so that no transfer from the LIF to the RA is required should other age parameters be chosen later. To this effect, we adopt the minimum value of c and the maximum value of d for the determination of , i.e., and .23 Under this configuration, the present value of the future loss of the LIF at age 55, denoted by , is given by
where for .
Let be the term (in years) of the monthly decreasing term insurance benefit covered by after age 90. Invoking the equivalence principle that the actuarial present value of cash inflows equals the actuarial present value of cash outflows, , and can be obtained simultaneously by solving a system of equations and inequalities, so that
subject to and the annuity-certain constraint .24
At age 65, if the member really chooses the age-parameter configuration of and , and no new money is contributed to the RA, the monthly payout is . In other cases, we have to re-calculate the monthly payouts.
If the member chooses the configurations of , the RA is closed after is transferred from the RA to the LIF. The payouts are then funded by the LIF for life. Under the configuration of , the monthly payouts are funded from two sources. From ages c to d, the payouts are paid from the RA as an annuity-certain and from age d onward they are paid from the LIF as a life-annuity. However, the payouts have to be level throughout the two periods so that members receive a stable monthly income. To meet this condition, and P have to be determined jointly according to actuarial principles.
Note that can be regarded as the cost of purchasing two insurance products at age 55: a -year term insurance with death benefit and a -year pure endowment insurance policy with survival benefit , where can be determined by solving the following equation
Thus, if the CPF member survives to age c, the balance in the LIF is actuarially equivalent to the survival benefit of a pure endowment insurance policy.
Let be the present value of the future loss of the LIF at age c and be the term of the monthly decreasing term insurance covered by LIF at age d. The variable is then given by:
where and for . Based on the equivalence principle, P, , and can be evaluated by solving
subject to and
where is the balance in the RA at age c, inclusive of any new money amount.
Finally, we note that if , is the RA balance and P can be calculated directly after solving for . If , however, and P have to be determined jointly by iteration.
Appendix B. Determination of LIF Components
As discussed in Section 2, the annuity fund LIF is a notional account directly funding the life-annuity payouts and possible bequests, resulting in simplicity in analyzing the benefits and costs provided by the LIF at different stages of the plan under different plan parameter configurations.
The Unified Plan can be divided into three stages. Stage 1 is from ages 55 to c, Stage 2 is from ages c to d and Stage 3 is from age d to death. If , Stages 2 and 3 are collapsed into a single stage. As discussed in Appendix A, transferred from the RA to the LIF at age 55 is the cost to cover a term insurance and a pure endowment insurance with maturity at age c. If the member lives to age c, the LIF balance is equivalent to the survival benefit of a pure endowment insurance. Otherwise, the bequest payable is the sum of the death benefit from the LIF and the balance in the RA at the time of death.
If in Stage 2, the amount at age c is used to cover the costs of two insurance products: an e-year term insurance with death benefit and an e-year pure endowment insurance with survival benefit . Hence,
from which we can solve for . If the member lives to age d, the LIF balance is equivalent to the survival benefit of the pure endowment insurance. Otherwise, the amount of bequest payable is the sum of from the LIF and the balance in the RA at the time of death. From age d onward (Stage 3), the reserve at age d is used to fund two insurance products: a life-annuity with monthly payments P and a decreasing -year term insurance with bequest for and zero for .
However, if the amount is used to fund the life-annuity and decreasing term insurance. In summary, we have the following result:
References
- “Melbourne Mercer Global Pension Index.” 2016. Available online: http://www.globalpensionindex.com/ (accessed on 3 December 2016).
- Chi-Kwong Law. “Public Annuity Scheme.” In Appendix 6 of Retirement Protection Forging Ahead; Hong Kong: Hong Kong SAR Government, 2015. Available online: http://www.rp.gov.hk/en/consultation_documents.php (accessed on 31 March 2017). [Google Scholar]
- Koon-Shing Kwong, Yiu-Kuen Tse, and Wai-Sum Chan. Singapore’s LIFE Program: Actuarial Framework, Longevity Risk and Impact of Annuity Fund Return. Working Paper; 2016. [Google Scholar]
- Society of Actuaries (SOA). “RP-2014 Mortality Tables Report.” Available online: https://www.soa.org/Research/Experience-Study/pension/research-2014-rp.aspx (accessed on 3 December 2016).
- Society of Actuaries (SOA). “Mortality Improvement Scale MP-2014 Report.” Available online: https://www.soa.org/Research/Experience-Study/pension/research-2014-mp.aspx (accessed on 3 December 2016).
- Singapore Central Provident Fund (CPF) Board. “CPF: Your Assurance in Retirement. ” Available online: https://www.cpf.gov.sg/Assets/members/Documents/CPF_Retirement_Booklet.pdf (accessed on 3 December 2016).
- Newton Bowers, Hans Gerber, James Hickman, Donald Jones, and Cecil Nesbitt. Actuarial Mathematics. Schaumburg: Society of Actuaries, 1997. [Google Scholar]
- 1According to the Melbourne Mercer Global Pension Index 2016 [1], Singapore’s retirement income system is ranked the highest among all of the Asian countries considered.
- 2The CPF Advisory Panel was formed by the Ministry of Manpower to study possible changes of the LIFE scheme. Part I of the Panel’s recommendations have been implemented from January 2016. The government has accepted Part II of the Panel’s recommendations: escalating payouts to address increases in the cost of living and providing a new simple and low-fee investment option.
- 3The CPF Board provides the CPF LIFE Payout Estimator on its official website. Members enter their personal information such as age, gender and Retirement Account balance to obtain estimates of their payouts and bequests under the two plans. However, the Estimator does not allow members to input the projected contributions at age 65. The Standard Plan is the default if a member does not make a personal choice out of the two plans.
- 4A glossary of insurance terms is provided at the end of the paper.
- 5An example of a similar nation-wide pension system is the proposal initiated by the Hong Kong government. On 18 January 2017, the Chief Executive of Hong Kong SAR government announced in his 2017 Policy Address that “The Government will study the feasibility of a public annuity scheme and explore whether we can have life-annuity plans run by the public sector, so as to help elderly persons turn their one-off assets into a stable monthly retirement income to reduce uncertainty……” (see http://www.policyaddress.gov.hk/2017/eng/p197.html). Prior to that, Law [2] proposed a public annuity scheme similar to Singapore CPF LIFE scheme.
- 6We note that the notional account of the Unified Plan can be easily modified as an investment fund, rendering it similar to variable products in the insurance market for which an investment option may be offered to the policy holder.
- 7Adopting Part I of the CPF Advisory Panel recommendations, the government has allowed CPF members to make the choice for both the Payout Age and the Plan (Standard or Basic) any time after the Payout Eligibility Age of 65 but before 70.
- 8Instead of calculating the bequest as the refund of two premium contributions from two annuity funds, as in the current scheme, the Unified Plan simplifies the determination of the amount of bequest as the unused amount in the LIF.
- 9See RP-2014 Mortality Tables Report [4] for a description of the mortality table construction methodology.
- 10See Mortality Improvement Scale MP-2014 Report [5] for a description of the mortality improvement estimation methodology.
- 11These assumptions are also considered in [3], which discusses other model assumptions and evaluates the sensitivity of the results with respect to the assumptions.
- 12All monetary amounts in this paper are in Singapore dollars. For simplicity, however, the dollar signs are suppressed. It should be noted that CPF may revise the BRS, FRS and ERS amounts in future.
- 13See CPF: Your Assurance in Retirement [6] for details of these examples.
- 14Note that this result is in line with the CPF LIFE scheme description.
- 15A reviewer raises the concern of incurring adverse selection costs due to the additional options offered to the CPF members in the Unified Plan. As discussed in Section 2, the Unified Plan has a self-adjustment mechanism for the payouts. Any additional cost (due to mortality and return experience) is eventually transferred to the CPF members based on the actuarial equivalence principle. As a result, CPF members bear all the risks and there is no financial impact on the government as the plan provider. This mechanism is made easier by operating with one LIF rather than two.
- 16The balance of the LIF represents the cash value for a surrendering policyholder. As a result, this analysis is important in assessing the financial outcomes of the Unified Plan, should the option of plan switch or early termination be granted to the member.
- 17As the bequest is equal to the difference between the total amount of monthly payouts and the sum of the two installments to the LIF, the amount of possible bequest is decreasing as time goes on.
- 18See Appendix A for the computation of the cash flows.
- 19This step-up payout arrangement is similar to one of the recent recommendations of the CPF Advisory Panel.
- 20Refer to CPF: Your Assurance in Retirement (Singapore CPF board [6]).
- 21He is allowed to transfer the maximum amount of 241 500; namely, the Enhanced Retirement Sum, to the RA at age 55.
- 22Commonly used actuarial notations are not defined in this paper. Readers may refer to [7] for the details.
- 23With this conservative age-parameter assumption, is the minimum amount of installment transferred from the RA to the LIF under any possible age-parameter configurations chosen at age c. As a result, no matter what age-parameter configuration is finally chosen, there is no need to transfer funds back from the LIF to the RA.
- 24Note that is the projected balance in the RA at age 65 based on the balance of the RA after the first installment transferred to the LIF at age 55.
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).