2. The Model
We consider a continuous-time financial market with regime switching. The regime of the economy is represented by an observable, continuous-time and stationary Markov chain with finite state space . Here, is the terminal time, and is the number of regimes in the economy. We assume that the Markov chain ϵ has a strongly irreducible generator , where for every .
In the financial market, there exist one riskless asset (e.g., a bond) and
K risky assets (e.g., stocks). The price processes of the riskless asset and the risky assets are represented by
and
,
, respectively, which satisfy the Markov-modulated stochastic differential equations:
Here,
,
, is a standard one-dimensional Brownian motion defined on a complete probability space
, and
is independent of
for every
. For every
, the coefficients
1 ,
,
are constants for every
. Furthermore, we denote the
matrix
and assume
is positive definite and invertible for every
. We introduce the following vector notations:
,
,
(in
K dimensions) and
, where prime
denotes the transpose operation of a matrix or a vector. Since
exists,
also exists for every
.
We consider an insurer who chooses the proportions of her/his wealth to invest in all available assets in the financial market. We denote an investment policy by a K-dimensional process , where is the proportion of wealth invested in the m-th risky asset at time t. Hence, the proportion invested in the riskless asset at time t is . Here, we assume for each , which means that we allow short-selling in the market.
We assume that the insurer sells insurance policies at a unit premium
at time
t, where
for every
. Here,
is the premium at time
t per dollar of insurance liabilities. We allow the premium
to depend on the regime of the economy
ϵ because of some empirical arguments (see, for example, [
28] and [
29]). For those insurance products for which the premium is independent of the regime of the economy, we simply write
for every
. In the meantime, the insurer is subject to the risk (liabilities) from the written insurance policies. Generalizing [
9] by allowing regime switching, we assume that the unit risk (dollar amount per liability) is modeled by a jump-diffusion process:
where
is a standard one-dimensional Brownian motion and
N is a Poisson process with constant intensity
. For every
, the coefficients
,
and
are positive constants. Therefore, in our setting, the insurer’s unit profit (loss if being negative) over the time period
is
Our risk model is applicable not only to traditional insurance, but also to non-traditional insurance in which the risk is strongly affected by the regime of the economy (like CDS).
As proposed by [
21] (Chapter 6), the risk process
R is negatively correlated with the capital gains in the financial market. We assume such negative correlation is captured by:
where
for every
.
We denote
and
, where
is a row vector. Then, we obtain:
where
is a standard Brownian motion defined on
, which is independent of
.
In the insurance market, we assume insurers can control their total liabilities at time
t, denoted by
. Then, the dynamics of the insurer’s total profit is given by:
Following [
24], we assume that the Brownian motions
,
and
, the Poisson process
N and the Markov chain
ϵ are mutually independent. We take the
augmented filtration generated by
and
ϵ as our filtration
.
Remark 1. The above model (
1)
for the risk process can be understood as a limiting process of the classical Cramér–Lundberg model; see, e.g., [9,17,27]. Remark 2. We assume the coefficients satisfy and for every . Such an assumption is reasonable and is also in accordance with the financial markets in real life. This is due to the well-accepted conclusion that extra uncertainty must be compensated by extra return.
At time
t, the insurer selects her/his investment policy
and her/his liability ratio
, defined as the ratio of total liabilities over wealth. We define the control
. For every control
u, we denote
as the insurer’s wealth (surplus) at time
t, and thus,
, where
represents the total liabilities at time
t. The insurer’s total wealth
can be decomposed into two parts: wealth from investing in the financial market
and wealth from the businesses in the insurance market
, i.e.,
. We derive the dynamics of
, (see, e.g., [
5]):
The process of
is governed by:
From the decomposition of
in Equation (
2), we obtain the dynamics of
:
with
.
We denote by
the set of all admissible controls under the initial conditions
and
, where
,
and
. We say that
if
u is a predictable process and satisfies for every
:
and
According to Equations (
14) and (
22) below, we remark that the last condition above says that the insurer selects her/his liability ratio
κ so that bankruptcy does not occur at jumps. Note that for any admissible control
u, there exists a unique strong solution to Equation (
3); see, e.g., Equations (
14) and (
22).
We define the criterion functional
J by:
where the utility function
U is strictly increasing and concave and satisfies the linear growth condition:
The notation
means taking conditional expectation given
and
under the probability measure
.
We then formulate the optimal investment and liability ratio problem as follows.
Problem 1. Select an admissible control that attains the value function V, defined by:The control is called an optimal control or an optimal policy. The work in [
22] studied the special case in which there is only one risky asset (stock) in the financial market, and neither the financial market nor the risk process is affected by the regime of the economy. In other words, our model generalizes the model of [
22] by allowing more than one risky asset (stock) in the financial market (we allow
) and by allowing the regime of the economy to affect both the financial market and the risk process (we allow
). The work in [
22] applied the martingale method, while we apply the dynamic programming method.
4. Construction of Explicit Solutions
In this section, we obtain explicit solutions to Problem 1 in a regime switching model. There are two standard tools to solve stochastic control problems: (1) the dynamic programming method (HJB); and (2) the martingale method. The market is generally incomplete in a regime switching model, such as the one considered in this paper, which adds extra difficulty when applying the martingale method. Hence, we apply the dynamic programming method (HJB) to solve Problem 1. Our strategy is to conjecture that the value function is strictly increasing and strictly concave. Such a conjecture will give a candidate for the value function and a candidate for the optimal control. Next, we will apply Verification Theorem 1 to prove that the candidate for the value function is indeed the value function, and the candidate for the optimal control is indeed an optimal control.
To obtain a candidate for the optimal control, we separate the optimization problem in the HJB Equation (
4) into two optimization problems:
for the investment portfolio
and:
for the liability ratio
κ.
Under the conjecture that
is strictly increasing and strictly concave, we obtain the candidate for the optimal investment strategy,
, as:
while the candidate for the optimal liability ratio,
, is solved through the following equation:
We will impose the technical condition:
That is, we are assuming that the premium
is large enough. We will see below that this inequality guarantees that Equation (
8) has a unique solution.
We consider two utility functions:
;
, where and .
We note that logarithmic utility is a limit case of power utility when .
4.1.
In this case, we conjecture that the solution to the HJB Equation (
4) is given by:
where
will be determined below.
We obtain
and
. Hence, the candidate policy is given by:
and:
where:
Lemma 1. If the technical condition (
9)
holds, then there exists a unique solution to Equation (
11).
Proof. Define the function
. Then, we obtain:
Furthermore,
, so
is strictly convex. Therefore, there exists a unique solution
to Equation (
11). ☐
By substituting candidate strategies
and
, given by Equations (
10) and (
11), into the HJB Equation (
4), we obtain the following system of linear differential equations:
where
is defined by:
In addition,
g also satisfies the boundary condition:
Notice that the linear ODE system (
13) has a unique solution
, and the candidate for the optimal control, given by Equations (
10) and (
11), is square integrable. Next, we show that the corresponding wealth process
with the candidate control
is almost surely positive.
Let us denote:
We define
as the
i-th jump time of the wealth process
, where
. Then, by solving the SDE (
3) with
, we obtain:
Between any two adjacent jump times
and
, the wealth process
is in exponential form, implying that
stays positive in
. In addition, due to
,
is positive at any jump
,
. Thus, the positiveness of
follows.
Therefore, the candidate
, from Equations (
10) and (
11), is indeed an optimal control, and
is the value function to Problem 1.
Theorem 2. Consider the logarithmic utility given by . Let be the unique solution in to the equation:and:Then, is optimal control to Problem 1. The corresponding optimal wealth is provided by Equation (
14)
with given by the two equations above. The value function V is given by , where is the solution to Equation (
13).
We observe that Equation (
15) is simply a quadratic function, so it is easy to calculate
. After calculating
, we can obtain
from Equation (
16). This equation can be decomposed in two summands. The first term:
is a generalization of the Merton-proportion that takes into account the regime switching. The value function
V can be decomposed into two summands, as well. The first term
depends only on
x, while the second term
depends only on time
t and regime
i.
4.2. and
In this case, the utility function is of the hyperbolic absolute risk aversion (HARA) type, and the relative risk aversion coefficient is .
The solution to the HJB (
4) is given by:
where
for every
will be determined below.
From Equations (
7) and (
8), we obtain that the candidate for the optimal liability ratio
is a solution to the equation:
and the candidate for the optimal portfolio
is:
Define
and
by:
Then, Equation (
17) becomes:
Lemma 2. If the technical condition (
9)
holds, then there exists a unique solution in to Equation (
20).
Proof. Let
. To show there exists a unique solution in
to Equation (
20), we only need to prove that the following equation has a unique solution in
:
Consider the function
. At the two end points, we have:
where the above inequality comes from Equation (
9).
Furthermore, we have , and is continuous in , which together give the desired result. ☐
By plugging the candidate for the optimal control into the HJB (
4), we obtain:
where
is defined by:
The boundary condition for
is given by:
We remark that the linear ODE system above has a unique solution. Furthermore, to verify our conjecture that is strictly increasing and strictly concave, we need to show that is strictly positive for every , which is given by Lemma 3.
Lemma 3. The function solving Equation (
21)
is strictly positive. Proof. Using Ito’s formula for the Markov-modulated process, we obtain:
where
is a square integrable martingale with
.
Taking conditional expectation and using Equation (
21), we get:
which is equivalent to (recall the boundary condition
)
We find the unique solution given by:
Hence, the positiveness of
follows. ☐
From the construction of
and Lemma 3,
is the candidate for the value function to Problem 1. It can shown in a similar way as in
Section 4.1 that the wealth process
associated with the candidate control
satisfies:
Then, by Lemma 2,
is admissible, where
and
are given by Equations (
18) and (
17). Hence Theorem 3 follows accordingly.
Theorem 3. Consider the power utility given by , where and . Then, is optimal control to Problem 1, where is the unique solution in to the equation:and: The corresponding optimal wealth is given by Equation (
22)
with solved from the above two equations. The value function V is given by , where is the solution to Equation (
21).
We observe that Equation (
23) is more complicated than the quadratic function (
15) of the logarithmic utility case. After calculating
, we can calculate
from Equation (
24). This equation can be decomposed in two summands. The first term
is a generalization of the Merton-proportion that takes into account the regime switching. The value function
V can be decomposed into two products. The first term
depends only on
x, while the second term
depends only on time
t and regime
i.
5. Economic Analysis
In this section, we study the impact of the insurer’s risk attitude, the negative correlation ρ and the regime of the economy on the optimal policy. To this purpose, we assume there are two regimes in the economy. Regime 1 represents a bull market, in which the economy is booming. Regime 2 represents a bear market, meaning the economy is in recession. We take , i.e., there is only one risky asset in the financial market. We denote the return and volatility of this risky asset by and , respectively. For comparative analysis, we consider HARA utility functions, namely, , where ( is associated with the case of logarithmic utility function ). Insurers are high risk-averse when , moderate risk-averse when and low risk-averse when .
We assume
and
,
(Remark 2). The works in [
30] and [
31] find that capital returns are higher in a bull market; hence, we assume
and
. The work in [
32] shows that the stock volatility is greater when the economy is in recession, which implies
. Furthermore, we assume
, as supported by [
31]. Motivated by non-traditional insurance policies like CDS, we assume that the risk process (claims) is negatively correlated with the stock returns and interest rate; see, e.g., [
33] and [
34]. This conclusion leads to the assumption that
,
,
and
. When the economy is in recession, the insurance companies charge a higher premium; hence,
. In
Table 1, we set the basic parameter values that we are going to use in our analysis.
Remark 3. Notice that the coefficients in the standard model (see Table 1) satisfy the technical condition (
9).
Denote the loading factor of the insurer by χ. We apply the expected value principle to calculate the premium rate by:In Table 1, the premium rate is calculated at .
5.1. Analysis of the Impact of the Risk Aversion Parameter α on the Optimal Policy
We first discuss the impact of the insurer’s risk aversion on the optimal policy. In this subsection, we study the impact of the risk aversion parameter
α on the optimal investment
and the optimal liability ratio
. To concentrate on the influence of
α, we set:
and consider
and
in this analysis.
For moderate risk-averse insurers (i.e.,
), we calculate the optimal policy, given by Equations (
15) and (
16), from Theorem 2 and list the results in
Table 2.
For both high risk-averse (
) and low risk-averse (
) insurers, we obtain the corresponding optimal policy, given by Equations (
23) and (
24), through Theorem 3. We plot the optimal policy
as a function of
α under three different values of the correlation coefficient
ρ. The case
is graphed in
Figure 1 while the case
is presented in
Figure 2. By Equation (
18), the optimal investment
will explode as
α approaches one, so we choose the interval of
α to be
instead of
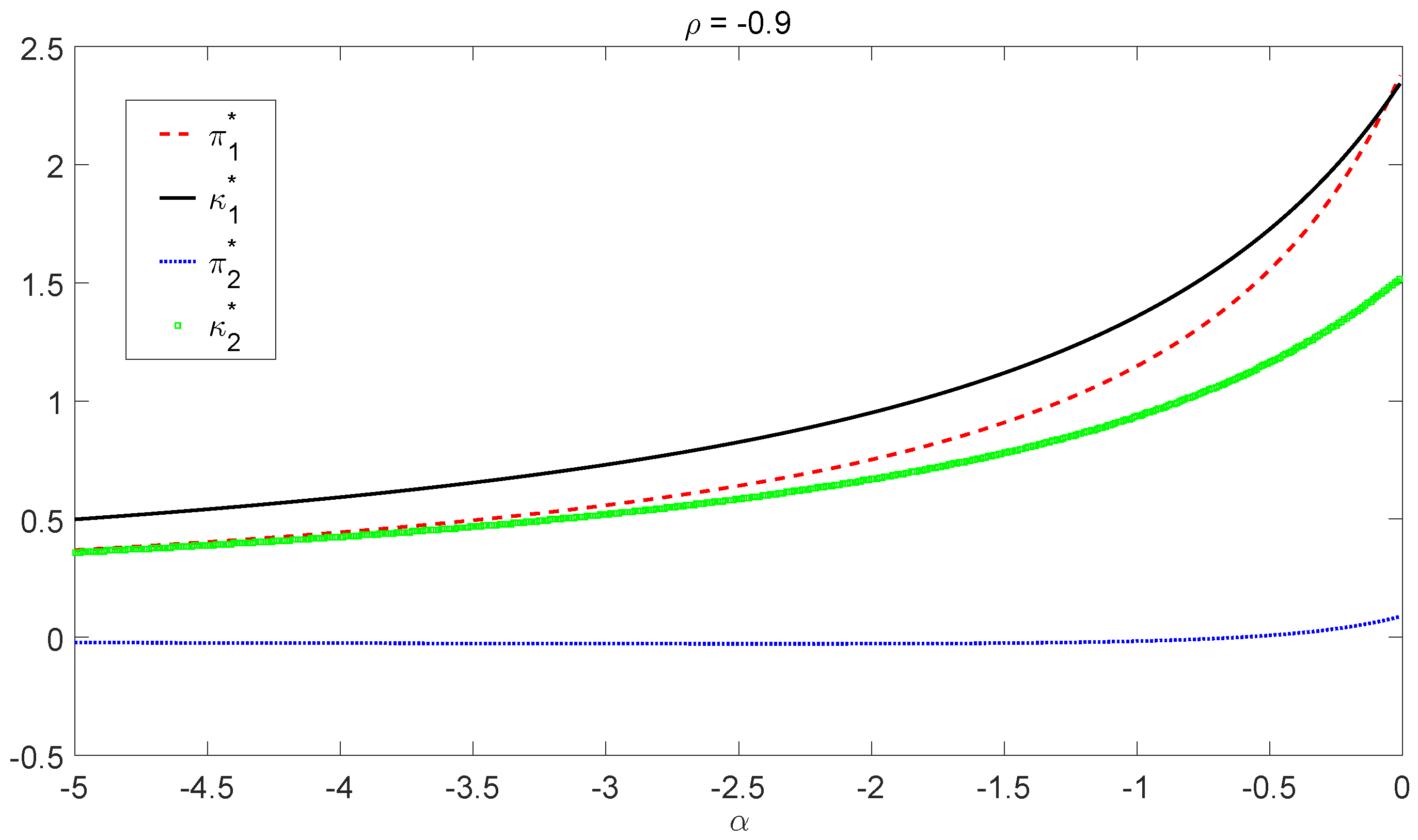
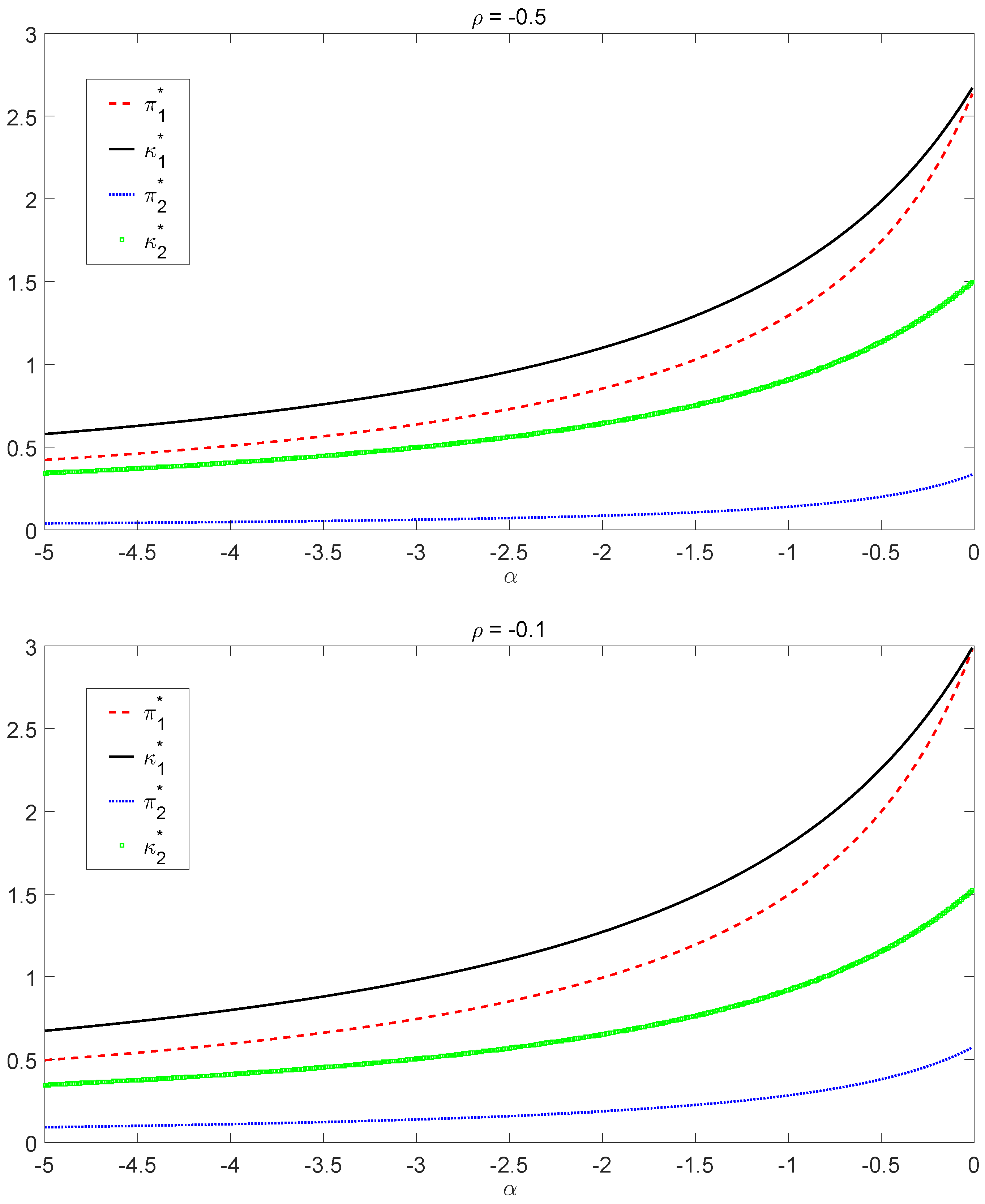
for low risk-averse insurers.
From the graphs in
Figure 1 and
Figure 2, we observe that the optimal investment
and the optimal liability ratio
are increasing with respect to
α in both bull and bear regimes for all chosen
ρ. Hence, less risk-averse insurers (that is, insurers with large
α) invest proportionally more in the risky asset and choose a higher liability ratio.
Figure 1 shows that after
α drops below some threshold (e.g., around
in the bear regime when
), the optimal policy is not sensitive to the change of
α, indicating that there exists a “saturation” level for the risk aversion. For high risk-averse insurers (
α small enough), risk aversion does not affect the optimal liability ratio
, nor the optimal investment
that much in both regimes. On the other hand, when
α gets close to one, there is a dramatic effect of the risk aversion on the optimal investment
. In this scenario, the optimal investment
will clearly explode due to the factor
going to infinity. We also notice that borrowing (
) is necessary to reach the optimal policies in some cases. Furthermore, the optimal policies obtained in
Figure 1 and
Figure 2 converge to the one in
Table 2 as
from both sides.
5.2. Analysis on the Impact of the Correlation Coefficient ρ on the Optimal Policy
As pointed out in [
21] (Chapter 6), a major mistake that contributed significantly to AIG’s sudden collapse was the negligence of the negative correlation between the risk and the capital returns (equivalently, AIG assumed
instead of
). Thus, in this subsection, we focus on the impact of the correlation coefficient on the optimal policy.
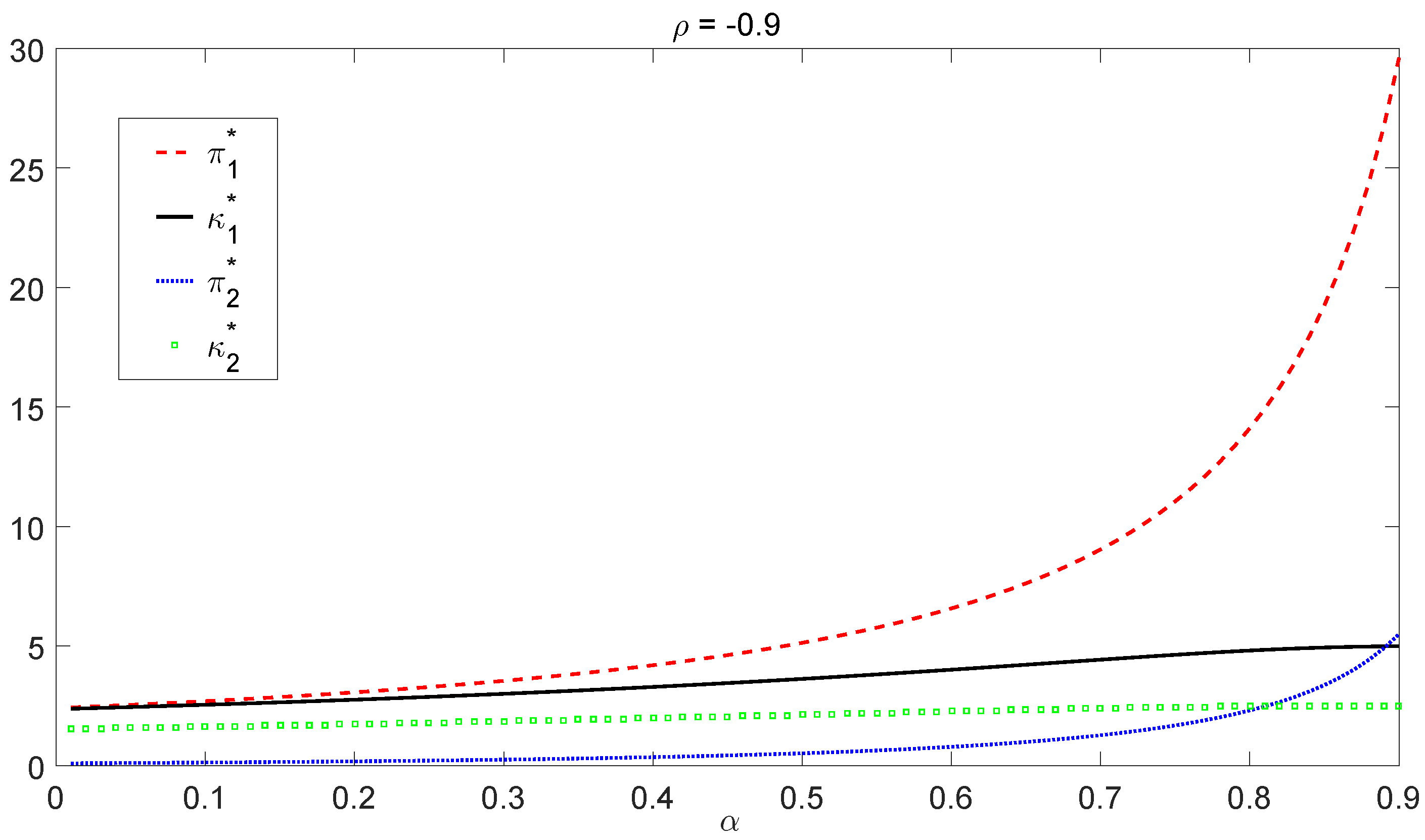
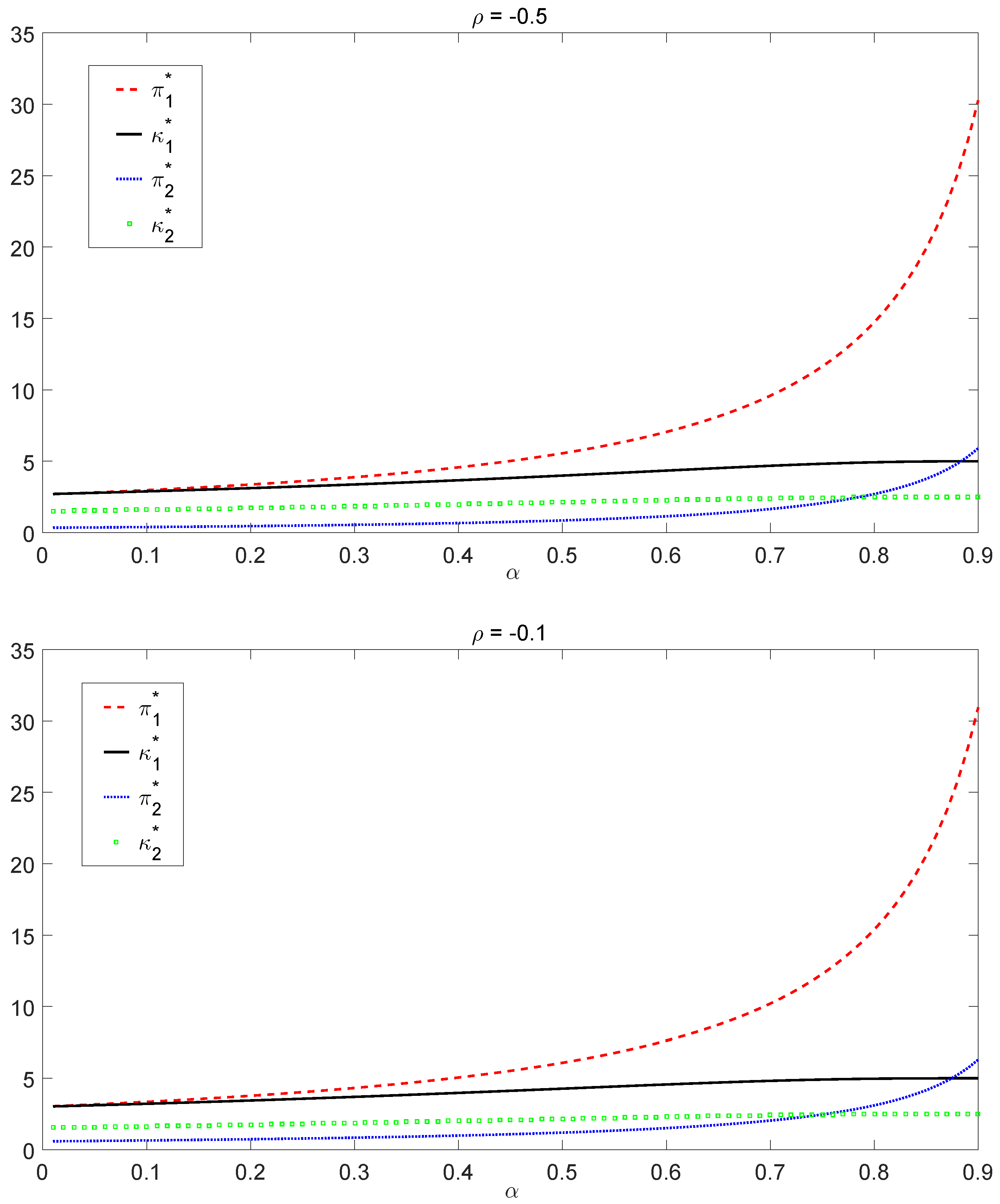
We consider
and
, representing high risk-averse, moderate risk-averse and low risk-averse insurers, respectively. We first study a simplified case in which the correlation coefficient is the same in both bull and bear regimes, namely
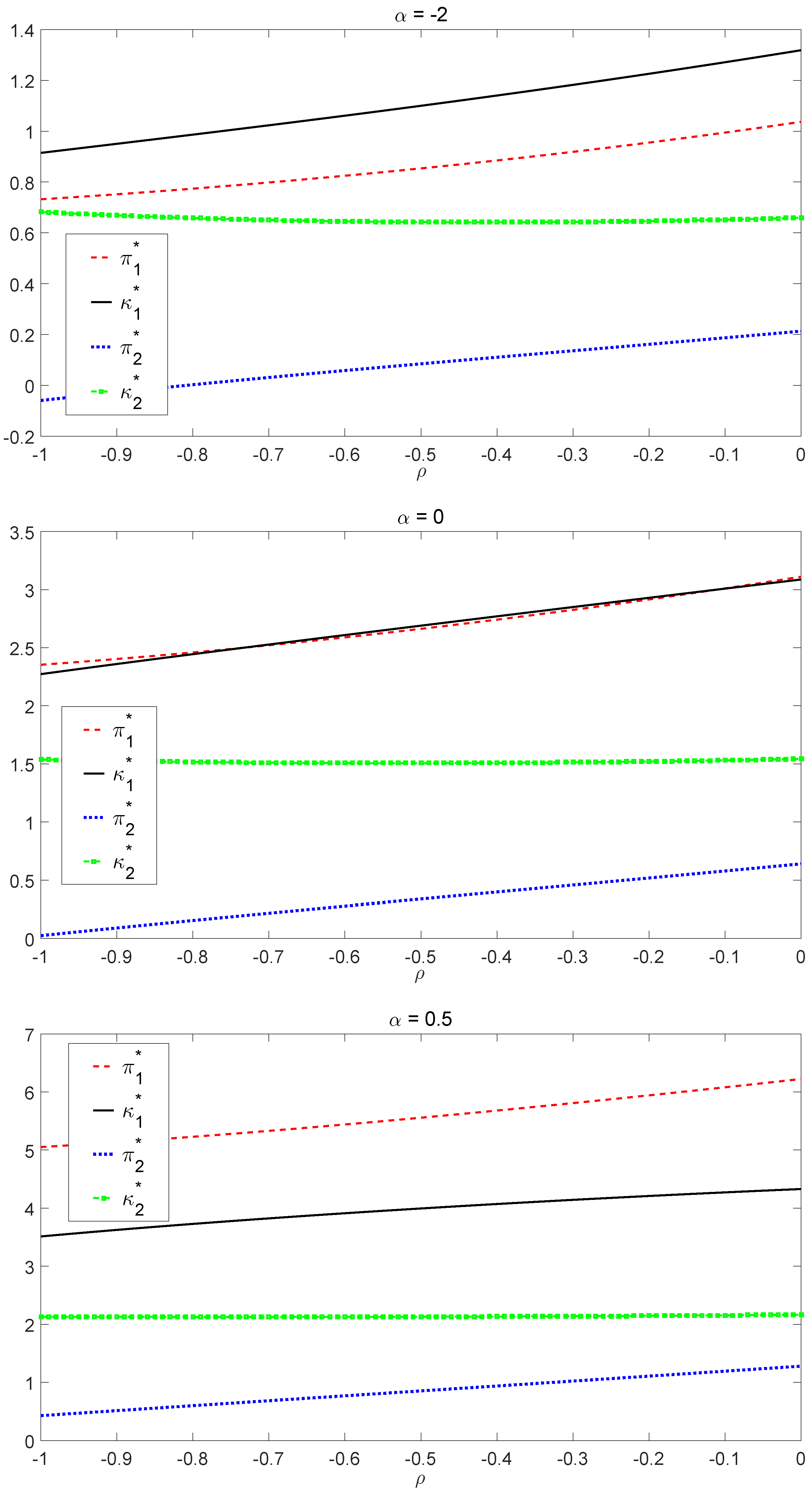
. Based on the results in
Figure 3, we find that the optimal investment strategy
is an increasing function of
ρ in both regimes and in all cases of
α. In addition, since
does not fluctuate significantly with respect to the change of
ρ, the increasing magnitude of
in
ρ is close to linear growth, which is consistent with Equations (
10) and (
18). However, the impact of
ρ on the optimal liability ratio
is more complicated. In the bull market,
increases as the negative correlation strength reduces (that is,
increases as
decreases). In the bear market,
is somehow immune to
ρ, especially in the case of
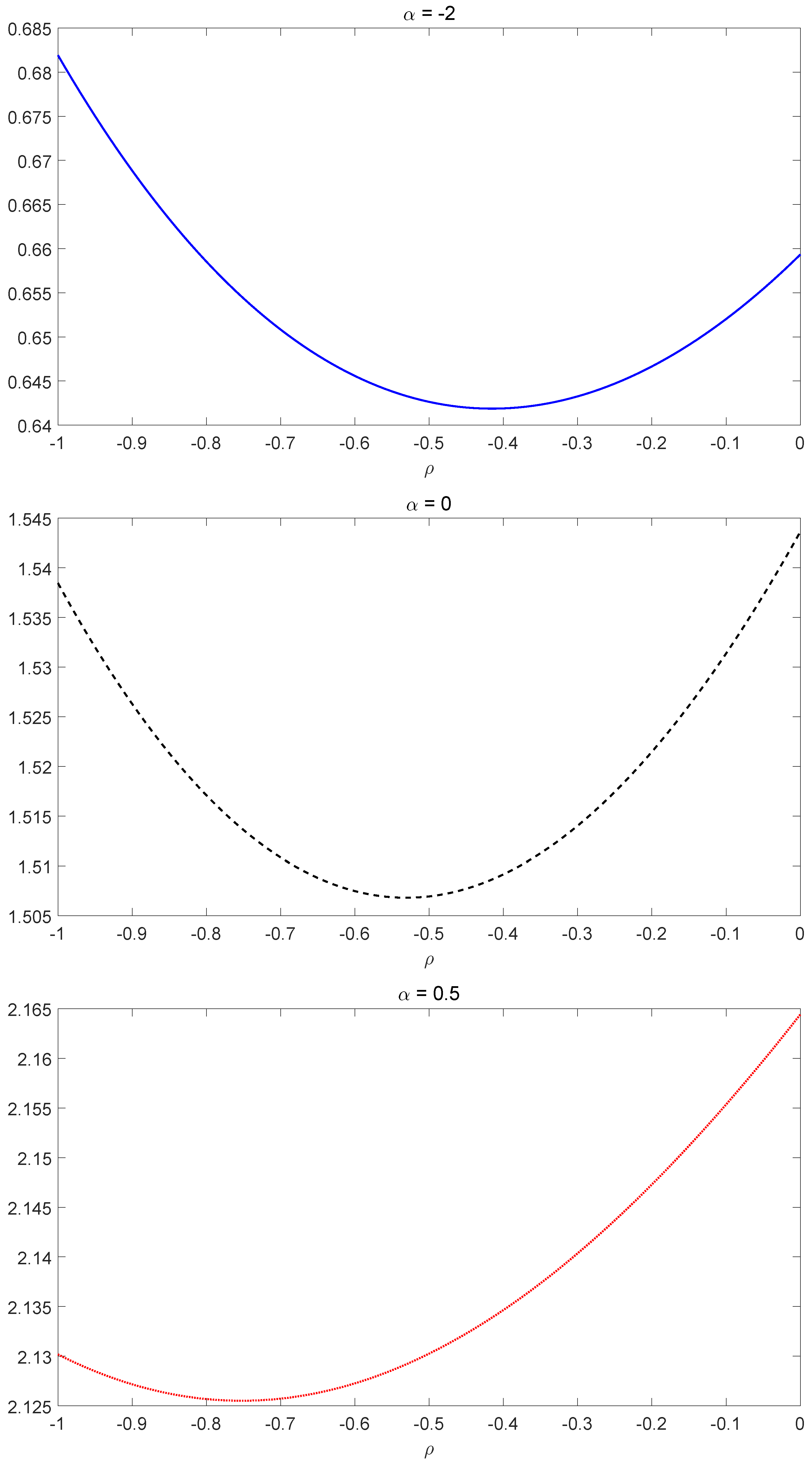
. To further investigate the relationship between
(
) and
ρ in the bear market, we draw the graph of
against
ρ separately in
Figure 4. We conclude that in the bear market, the optimal liability ratio
is a convex function of
ρ, where
. This conclusion is consistent with the findings in [
22] for the case of only one regime.
Next, we proceed to deal with the more realistic case where
(equivalently,
), in which the negative correlation between the liabilities and the capital returns is stronger in the bear market. For the basic parameter values (with parameter values given by
Table 1), we calculate the optimal policy under the following four cases for
and
:
The results are presented in
Table 3, which are consistent with the findings when
above.
2 Namely, we still observe that the optimal investment in both regimes (
and
) and the optimal liability ratio in the bull regime (
) are increasing with respect to
,
, while the optimal liability ratio in the bear regime (
) is a convex function of
,
. We also notice that in some cases,
is negative, which means the optimal investment involves short-selling the risky asset.
It is surprising to observe that in the case
,
is not only a convex function, but also increases as the economy goes from Case 4–Case 1. To understand this situation, we consider only two regimes and rewrite Equation (
18) in the form:
where:
We recall that we are assuming
, as supported by [
31]. Thus, when the economy is good, both
and
take large positive values. That is not surprising and agrees with the above equation. When the economy is bad,
approaches zero, especially when the investor is very risk averse. In addition,
approaches
. In a case of severe recession,
would take even negative values. To compensate for that, the above equation says that
should take large positive values.
5.3. Analysis of the Impact of the Regimes on the Optimal Policy
The numerical results obtained in
Section 5.1 and
Section 5.2 allow us to reach some conclusions on the impact of the market regimes on the optimal policy.
In all of the above studies, the optimal policy depends on the market regime. Furthermore, we always have:
This result shows that all insurers, regardless of risk aversion, should invest a greater proportion in the risky asset and choose a higher liability ratio when the economy is in the bull regime.
6. Conclusions
The 2007–2009 financial crisis brought new challenges on risk management to all market participants. For instance, AIG did not follow proper risk management strategies and, as a consequence, almost went bankrupt in 2008. There were two major contributors to AIG’s sudden collapse. First, AIG did not pay full attention to the business cycles (regime switching) in the U.S. housing market, which directly caused a significant underestimation of the risk of CDS policies. Second, AIG ignored the negative correlation between its liabilities and the capital gains in the financial market.
Taking the lessons from the AIG case, we set up a regime switching model from an insurer’s perspective. In the model, we assume that not only the financial market, but also the insurer’s risk process depend on the regime of the economy. An insurer makes investment decisions in a financial market, which consists of a riskless asset and K risky assets, and faces an external risk that is negatively correlated with the capital returns of the risky assets. The insurer wants to maximize her/his expected utility of terminal wealth by selecting simultaneously the optimal investment proportions in the risky assets and the optimal liability ratio. We obtain explicitly optimal investment and liability ratio policies when the insurer’s utility is given by the logarithmic and power utility functions.
Through an economic analysis, we find that the optimal policy depends strongly on both the business cycles (market regimes) and the negative correlation between the liabilities and the capital returns. To be more specific, all insurers should invest a greater proportion in the risky assets and select a higher liability ratio when the market is in a bull regime. The optimal investment proportions in the risky assets are increasing with respect to ρ (correlation coefficient) in both bull and bear regimes. The relationship between the optimal liability ratio and ρ is more complicated: there is an increasing relationship in the bull regime and a convex relationship in the bear regime. Furthermore, we find that the optimal investment proportions and the optimal liability ratios are increasing functions of α (risk aversion parameter) in both market regimes. That means a less risk-averse insurer will invest a greater proportion in the risky assets and select a higher liability ratio, no matter what regime the market is in.