The Effects of Largest Claim and Excess of Loss Reinsurance on a Company’s Ruin Time and Valuation
Abstract
:1. Introduction
2. Reinsurance Models
3. Methods
3.1. Compound Poisson Process Methodology
3.2. Tail Regimes
- (i)
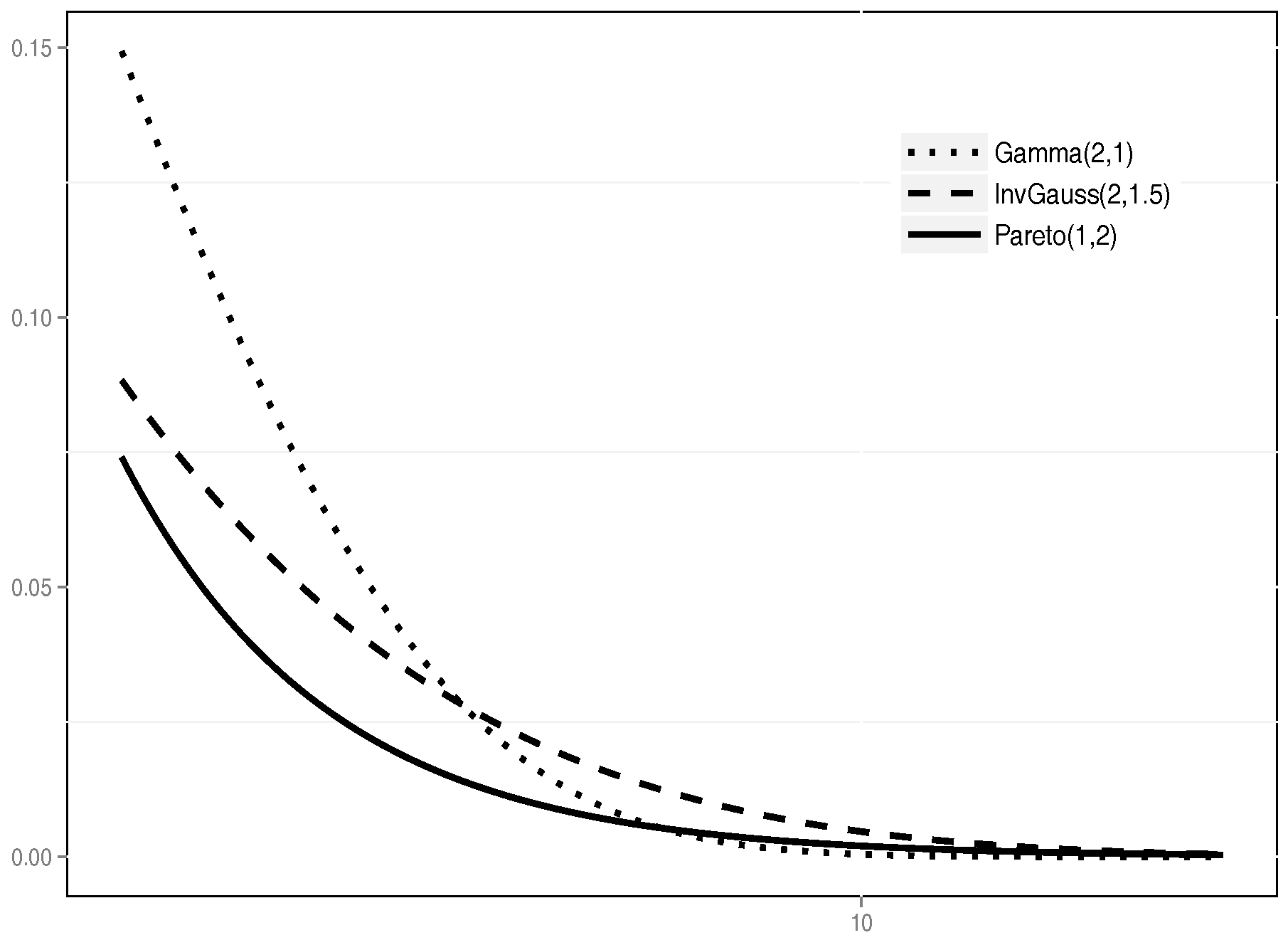
- Cramér case: There exists a finite positive constant such that the claim distribution F satisfieswhere is the moment generating function (mgf) of F, assumed finite for . These are relatively “light-tailed” (exponentially small) distributions. As a typical example in our simulations we choose F to be a Gamma distribution with density
- (ii)
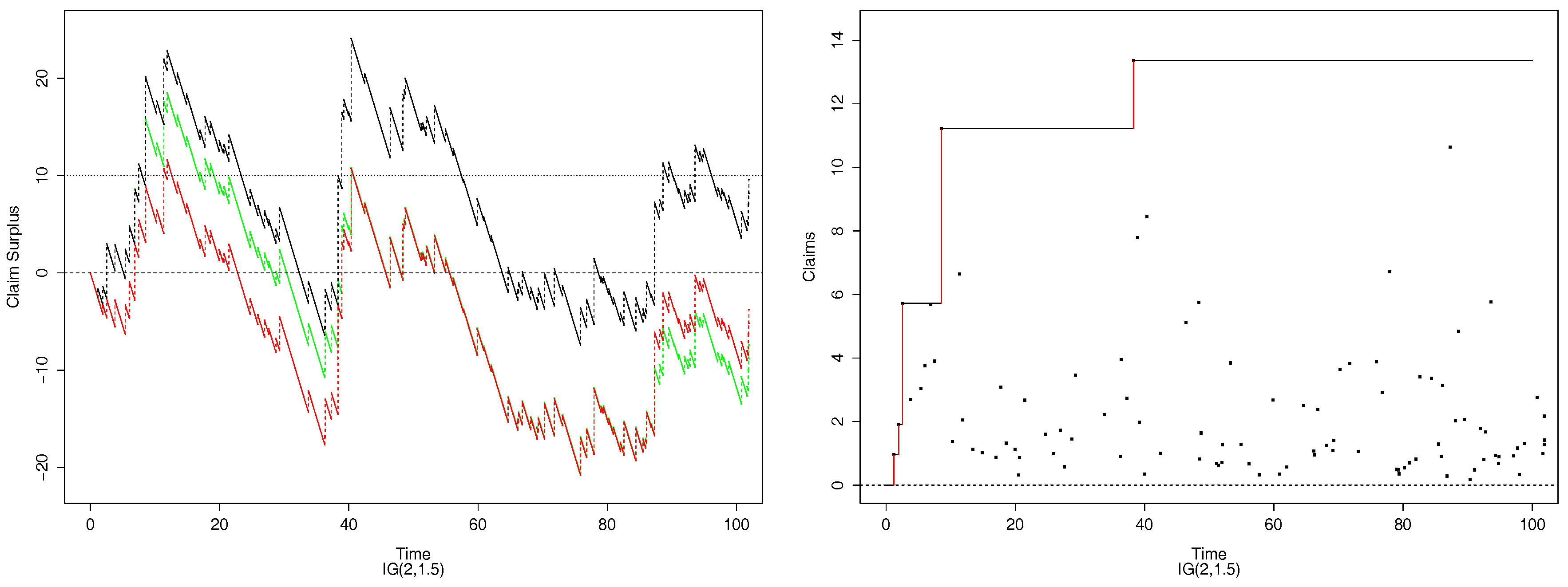
- Convolution equivalent case: The claims distribution function F is said to be convolution equivalent with index , if its tail , , satisfieswhere is the convolution, . The distribution function F has the propertiesThese distributions have “medium-heavy” tails in the sense that a convolution equivalent distribution of index α has a finite exponential moment of order α, but any larger order moment is infinite. Typical examples are distributions with tails of the formfor some , , . One important example of a class of distributions which are convolution equivalent is the Inverse Gaussian family with densities parametrised as in Chapter 2.2 of [11]:Here is the mean parameter and is called the scale parameter. We denote such a distribution as . In our simulations we choose and .
- (iii)
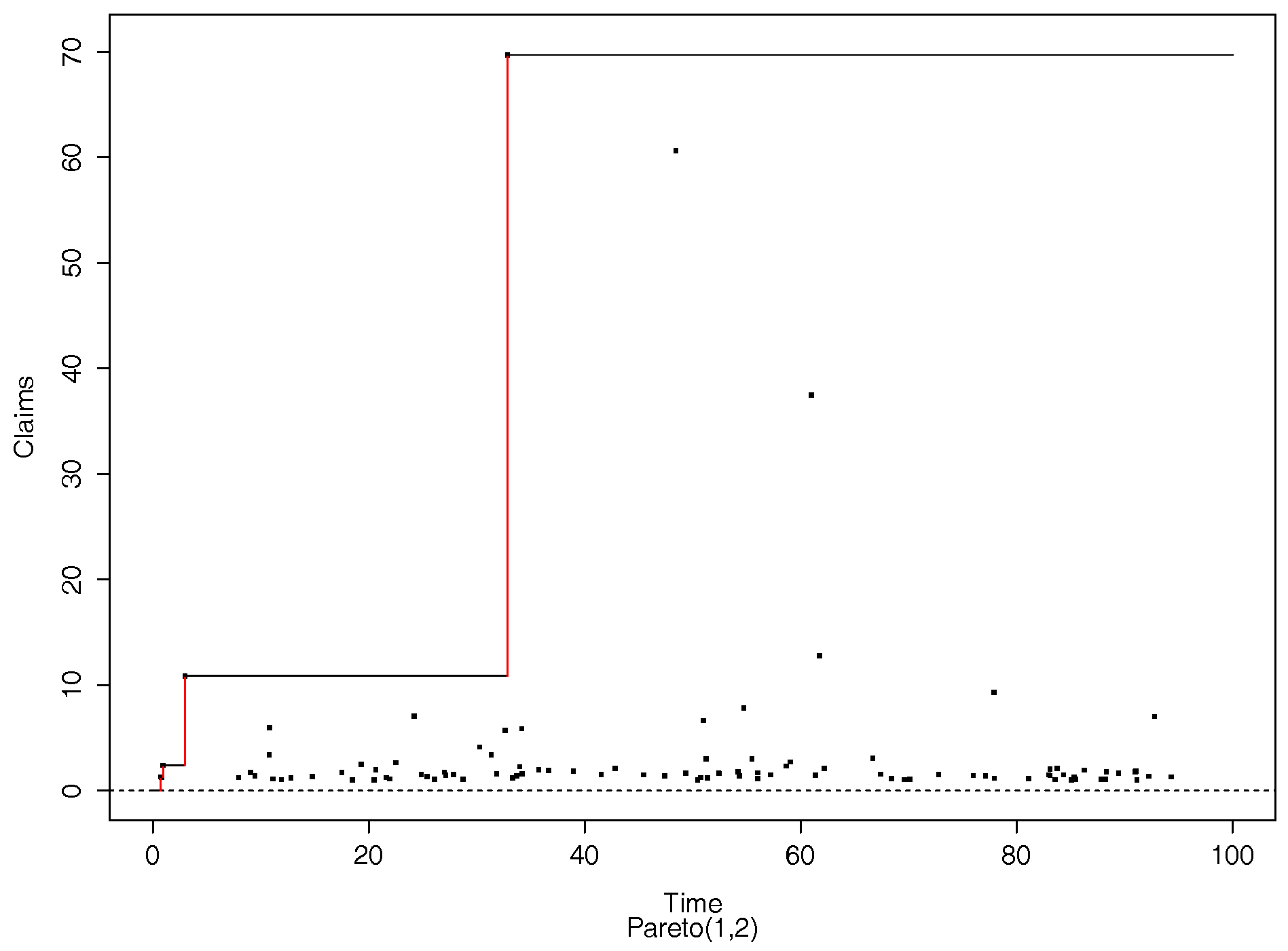
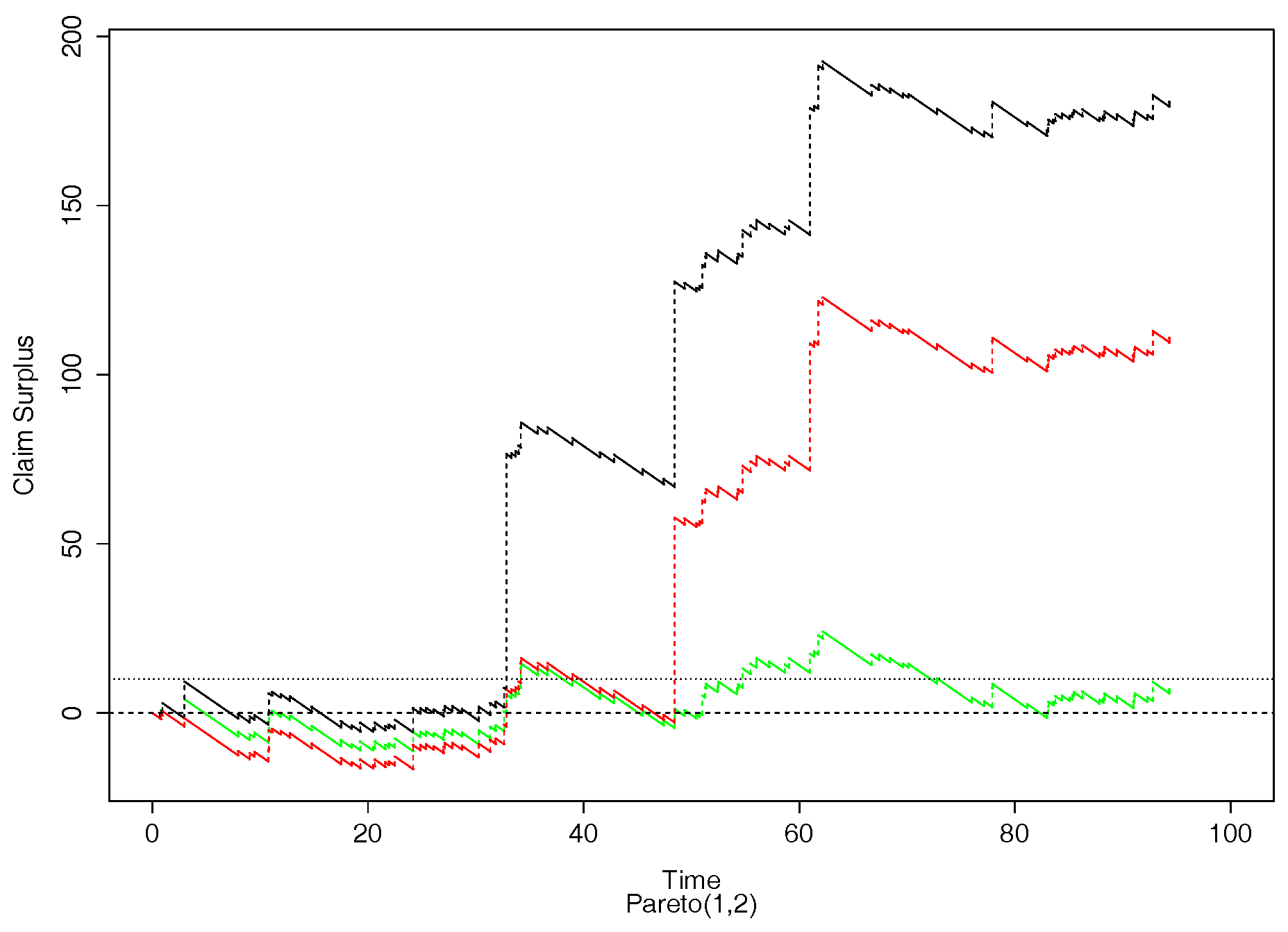
- Subexponential case: When (8) is satisfied with , F is said to have a subexponential tail. Typical examples are the Pareto distributions. In our simulations we used a Pareto distribution with (power law) tail of the formThese distributions have very heavy tails, giving rise to occasional extremely large jumps.
3.3. Simulation Methodology
- (a)
- Neither nor transits above u in . Suppose there are such paths among the N.
- (b)
- transits above u in but does not. Suppose there are such paths among the N.
- (c)
- transits above u in and hence does also. There are such paths among the N.
4. Results
4.1. Largest Claim Reinsurance
4.2. Excess of Loss Reinsurance
4.3. Comparisons Across Distributions
5. Cost of Reinsurance
5.1. Reinsurance Premium and Dividend Adjustment
5.2. Choice of Parameters
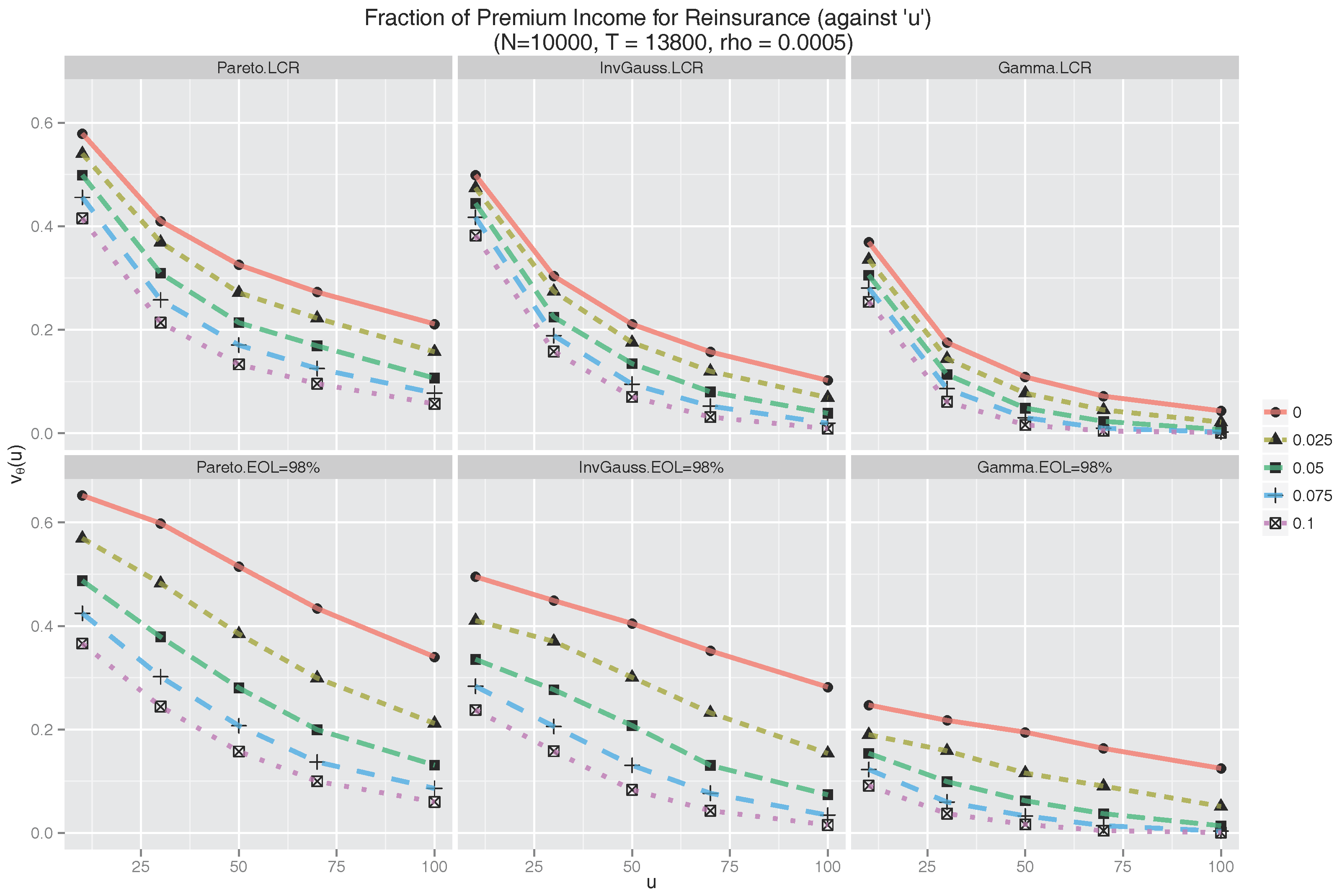
5.3. Proportion of Dividend Paid for Reinsurance
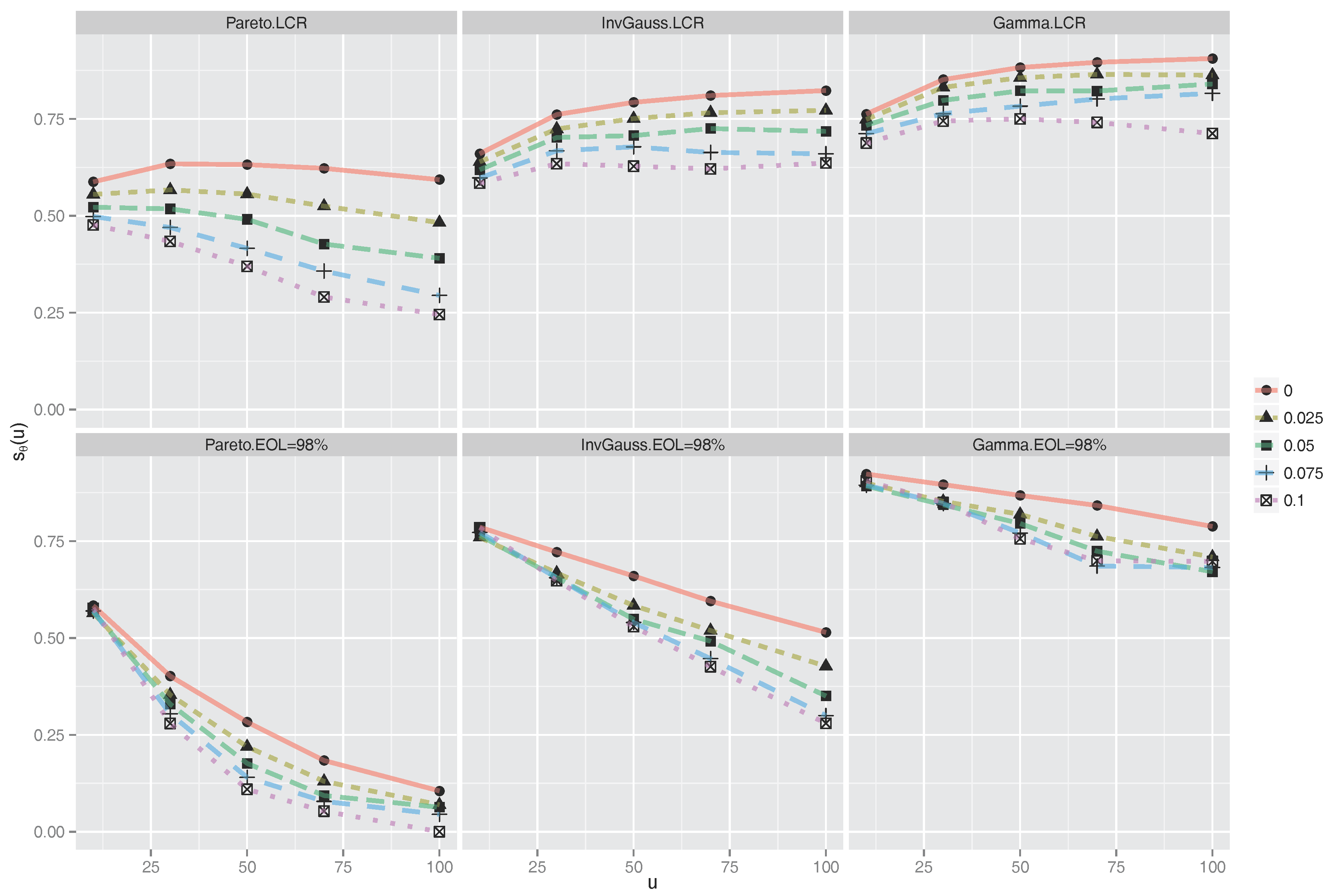
5.4. Standard Deviation of Dividend Income
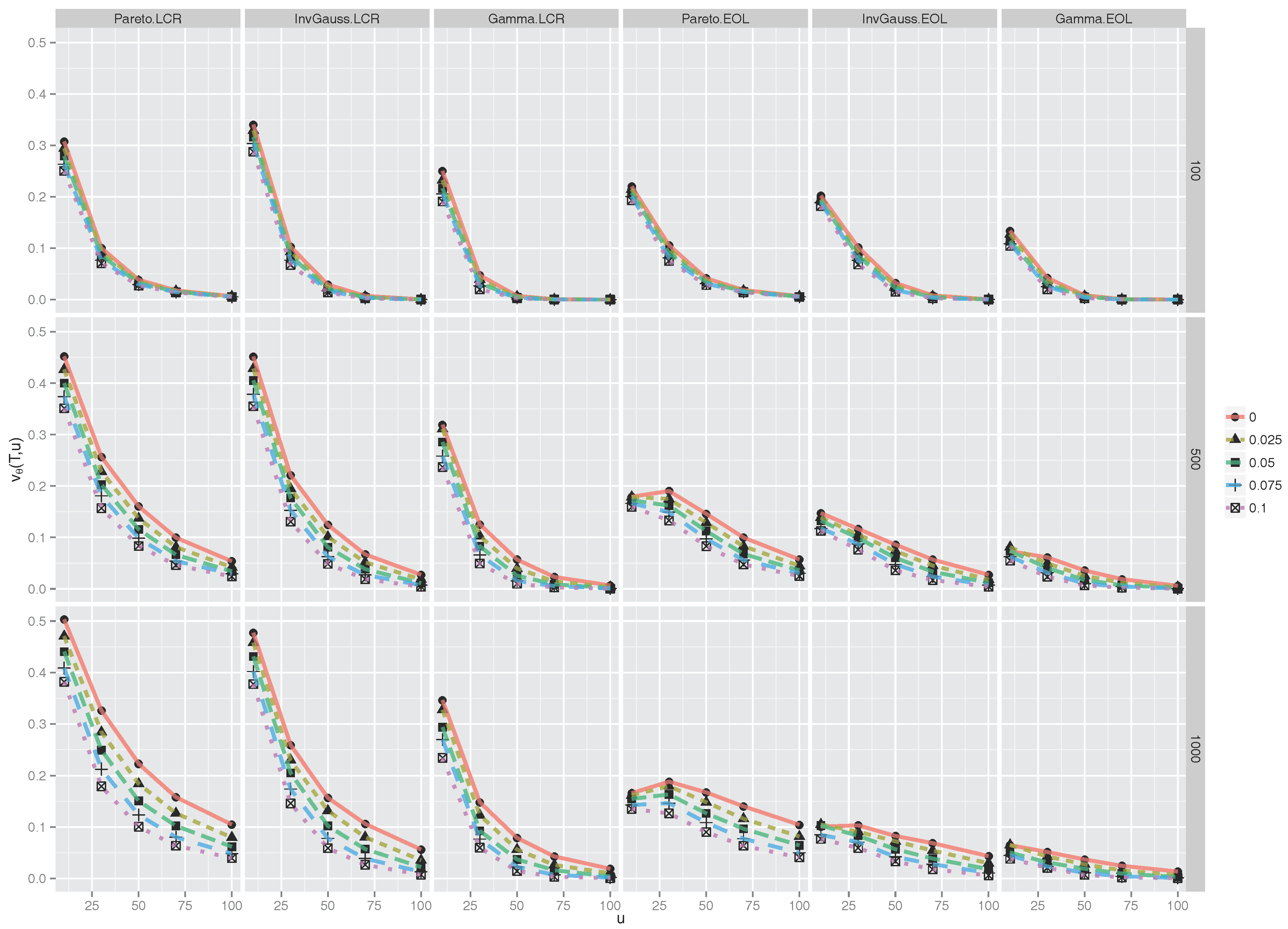
5.5. Dividend Adjustment and Reinsurance Premium, Finite Horizon
6. Related Literature and Discussion
6.1. Beveridge, Dickson and Wu Simulations
6.2. Trimming More Values
6.3. The “Light-Medium-Heavy” Classification
6.4. Lévy Insurance Risk Models
7. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Laplace Transforms
References
- K. Böcker. “and Klüppelberg, C. Multivariate models for operational risk.” Quant. Finance 10 (2010): 855–869. [Google Scholar] [CrossRef]
- P. Embrechts, C. Klüppelberg, and T. Mikosch. Modelling Extremal Events for Insurance and Finance. Applications of Mathematics (New York); Berlin, Germany: Springer, 1997. [Google Scholar]
- P. Embrechts, and G. Samorodnitsky. “Ruin problem and how fast stochastic processes mix.” Ann. Appl. Probab. 13 (2003): 1–36. [Google Scholar]
- N. Doherty, and K. Smetters. “Moral hazard in reinsurance markets.” J. Risk Insur. 72 (2005): 375–391. [Google Scholar] [CrossRef]
- Z. Yan. “Testing for moral hazard in reinsurance markets.” Manag. Finance 39 (2013): 696–713. [Google Scholar] [CrossRef]
- S. Asmussen. Ruin Probabilities. Advanced Series on Statistical Science Applied Probability; Hackensack, NJ, USA: World Scientific Publishing Co., Inc., 2000, Volume 2. [Google Scholar]
- R.A. Doney, C. Klüppelberg, and R.A. Maller. “Passage time and fluctuation calculations for subexponential Lévy processes.” Bernoulli 22 (2016): 1491–1519. [Google Scholar] [CrossRef]
- C. Klüppelberg, A. Kyprianou, and R.A. Maller. “Ruin probabilities and overshoots for general Lévy insurance risk processes.” Ann. Appl. Probab. 14 (2004): 1766–1801. [Google Scholar] [CrossRef]
- P.S. Griffin, R.A. Maller, and D. Roberts. “Finite time ruin probabilities for tempered stable insurance risk processes.” Insur. Math. Econom. 53 (2013): 478–489. [Google Scholar] [CrossRef]
- P.S. Griffin, R.A. Maller, and K. van Schaik. “Asymptotic distributions of the overshoot and undershoots for the Lévy insurance risk process in the Cramér and convolution equivalent cases.” Insur. Math. Econom. 51 (2012): 382–392. [Google Scholar] [CrossRef]
- R.J. Chhikara, and J.L. Folks. The Inverse Gaussian Distribution: Theory, Methodology, and Applications. New York, NY, USA: Marcel Dekker, 1989. [Google Scholar]
- S. Asmussen, and K. Binswanger. “Simulation of ruin probabilities for subexponential claims.” Astin Bull. 27 (1997): 297–318. [Google Scholar] [CrossRef]
- H.U. Gerber. An Introduction to Mathematical Risk Theory. Monograph No. 8; Philadelphia, PA, USA: University of Pennsylvania, 1979, p. 478. [Google Scholar]
- H.U. Gerber, and S. Loisel. Why Ruin Theory Should Be of Interest for Insurance Practitioners and Risk Managers Nowadays. Bruxelles, Belgium: Actuarial and Financial Mathematics, 2012. [Google Scholar]
- G. Benktander. “Largest claims reinsurance (LCR). A quick method to calculate LCR-risk rates from excess of loss risk rates.” Astin Bull. 10 (1978): 54–58. [Google Scholar] [CrossRef]
- R.M. Berglund. “A note on the net premium for a generalized largest claims reinsurance cover.” Astin Bull. 28 (1998): 153–162. [Google Scholar] [CrossRef]
- E. Kremer. “Rating of largest claims and ECOMOR reinsurance treaties for large portfolios.” Astin Bull. 13 (1982): 47–56. [Google Scholar] [CrossRef]
- E. Kremer. “Distribution-free upper bounds on the premiums of the LCR and ECOMOR treaties.” Insur. Math. Econom. 2 (1983): 209–213. [Google Scholar] [CrossRef]
- E. Kremer. “The asymptotic efficiency of largest claims reinsurance treaties.” Astin Bull. 20 (1990): 11–22. [Google Scholar] [CrossRef]
- E. Kremer. “Largest claims reinsurance premiums under possible claims dependence.” Astin Bull. 28 (1998): 257–267. [Google Scholar] [CrossRef]
- J. Grandell. Aspects of Risk Theory. Springer Series in Statistics; New York, NY, USA: Springer, 1991. [Google Scholar]
- N. Wikstad. “Exemplification of ruin probabilities.” Astin Bull. 6 (1971): 147–152. [Google Scholar] [CrossRef]
- A.J. Bradshaw, M. Bride, A.B. English, D.J. Hindley, and G.P.M. Maher. Reinsurance and Retentions—A London Market Actuaries’ Group Paper. Arlington, VA, USA: Casualty Actuarial Society, 1991, Volume I. [Google Scholar]
- C.J. Beveridge, D.C.M. Dickson, and X. Wu. “Optimal dividends under reinsurance.” Bulletin de l’Association Suisse des Actuaires 2 (2008): 149–166. [Google Scholar]
- B. De Finetti. “Su un’impostazion alternativa dell teoria collecttiva del rischio.” Trans. Internat. Congr. Actuar. 2 (1957): 433–443. [Google Scholar]
- D.C.M. Dickson, and H.R. Waters. “Some optimal dividends problems.” Astin Bull. 34 (2004): 49–74. [Google Scholar] [CrossRef]
- H.U. Gerber, and E.S.W. Shiu. “Optimal dividends: Analysis with Brownian motion.” N. Am. Actuar. J. 8 (2004): 1–20. [Google Scholar] [CrossRef]
- S.A. Ladoucette, and J.L. Teugels. “Reinsurance of large claims.” J. Comput. Appl. Math. 186 (2006): 163–190. [Google Scholar] [CrossRef]
- A. Thépaut. “Une nouvelle forme de réassurance: Le traité d’excédent du coût moyen relatif (ECOMOR).” Bull. Trim. Inst. Actu. Fr. 49 (1950): 273–343. [Google Scholar]
- J.L. Teugels. Reinsurance Actuarial Aspects. EURANDOM Report 2003-006; Eindhoven, The Netherlands: Technical University of Eindhoven, 2003. [Google Scholar]
- B. Buchmann, Y. Fan, and R.A. Maller. “Distributional representations and dominance of a Lévy process over its maximal jump processes.” Bernoulli 22 (2016): 2325–2371. [Google Scholar] [CrossRef]
- B. Buchmann, Y. Fan, and R.A. Maller. “Functional Laws for Trimmed Lévy Processes.” Available online: https://arxiv.org/abs/1609.07206 (accessed on 21 November 2016).
- V. Brazauskas, and A. Kleefeld. “Modeling Severity and Measuring Tail Risk of Norwegian Fire Claims.” N. Am. Actuar. J. 20 (2016): 1–16. [Google Scholar] [CrossRef]
- P.S. Griffin. “Convolution equivalent Lévy processes and first passage times.” Ann. Appl. Probab. 23 (2013): 1506–1543. [Google Scholar] [CrossRef]
- P.S. Griffin, and R.A. Maller. “Path decomposition of ruinous behaviour for a general Lévy insurance risk process.” Ann. Appl. Probab. 22 (2012): 1411–1449. [Google Scholar] [CrossRef]
- J. Garrido, and M. Morales. “On The expected discounted penalty function for Lévy risk processes.” N. Am. Actuar. J. 10 (2006): 196–216. [Google Scholar] [CrossRef]
- A. Kyprianou. Introductory Lectures on Fluctuations of Lévy Processes with Applications. Berlin, Germany: Springer, 2006. [Google Scholar]
- D.C.M. Dickson, and G.E. Willmot. “The density of the time to ruin in the classical Poisson risk model.” Astin Bull. 35 (2005): 45–60. [Google Scholar] [CrossRef]
- M. Elghribi, and E. Haouala. “Laplace transform of the time of ruin for a perturbed risk process driven by a subordinator.” IAENG Int. J. Appl. Math. 39 (2009): 221–230. [Google Scholar]
- F.D.P. Lima, J.M.A. Garcia, and A.D. Egídio dos Reis. “Fourier/Laplace transforms and ruin probabilities.” Astin Bull. 32 (2002): 91–105. [Google Scholar] [CrossRef]
- E.A. Percheskii, and B.A. Rogozin. “On the joint distribution of random variables associated with fluctuations of a process with independent increments.” Theory Probab. Appl. 14 (1969): 410–423. [Google Scholar] [CrossRef]
- 1.The LCR procedure can be made prospective by implementing it as a forward looking dynamic procedure in real time, from the cedant’s point of view. Designate as time zero the time at which the reinsurance is taken out. At this time, the cedant company’s assets amount to , say. The first claim arriving after time 0 is referred to the reinsurer and not debited to the cedant. Subsequent claims smaller than the initial claim are paid by the cedant until a claim larger than the first (the previous largest) arrives. The difference between these two claims is referred to the reinsurer and not debited to the cedant. The process continues in this way so that at time t, the accumulated amount referred to the reinsurer equals the largest claim up till that time. This procedure has the same effect as referring the largest claim up till time t retrospectively to the reinsurer.
- 2.Indeed, from a theoretical perspective, very little appears to be known about the effects of trimming on an insurance risk process and the subsequent ruin quantities. A series of approximate premium calculations for LCR treaties has been made in the literature; see, for example, [15,16], and [17,18,19,20], and their references.
- 3.The work of [23] suggests that one common principle in choosing L is to keep it at “a level at which claims become very infrequent”.
- 4.There are other possibilities here, for example requiring , instead of and . We chose our formulation since it most clearly mirrors the infinite horizon problem. The interested reader may investigate other versions of the optimization problem.
- 6.But our particular choice of and makes the Inverse Gaussian heavier-tailed than the Gamma(2,1).

| u | T | % Changes | ||||
|---|---|---|---|---|---|---|
| 10 | 100 | 0.43 | 0.14 | 19.06 | 37.03 | 93.34 |
| 500 | 0.53 | 0.20 | 38.14 | 85.45 | 124.02 | |
| 1000 | 0.55 | 0.21 | 44.75 | 104.35 | 133.19 | |
| ∞ | - | - | - | - | ||
| 30 | 100 | 0.14 | 0.02 | 35.78 | 58.97 | 64.84 |
| 500 | 0.26 | 0.06 | 90.65 | 164.25 | 81.19 | |
| 1000 | 0.28 | 0.06 | 113.18 | 214.20 | 89.25 | |
| ∞ | - | - | - | - | ||
| 50 | 100 | 0.06 | 0.00 | 44.64 | 66.40 | 55.74 |
| 500 | 0.14 | 0.02 | 129.20 | 215.24 | 66.59 | |
| 1000 | 0.17 | 0.03 | 172.73 | 303.81 | 75.89 | |
| ∞ | - | - | - | - | ||
| 70 | 100 | 0.03 | 0.00 | 45.66 | 73.67 | 61.37 |
| 500 | 0.09 | 0.01 | 157.07 | 263.60 | 67.82 | |
| 1000 | 0.11 | 0.01 | 221.55 | 380.55 | 71.77 | |
| ∞ | - | - | - | - | ||
| 100 | 100 | 0.01 | 0.00 | 37.32 | 75.64 | 102.71 |
| 500 | 0.05 | 0.00 | 180.25 | 300.30 | 66.60 | |
| 1000 | 0.06 | 0.00 | 258.22 | 450.58 | 74.50 | |
| ∞ | - | - | - | - |
| u | T | % Changes | ||||
|---|---|---|---|---|---|---|
| 10 | 100 | 0.43 | 0.25 | 22.22 | 34.91 | 57.11 |
| 500 | 0.49 | 0.32 | 44.35 | 70.81 | 61.18 | |
| 1000 | 0.50 | 0.32 | 47.79 | 77.57 | 63.39 | |
| 30 | 100 | 0.08 | 0.04 | 47.95 | 59.49 | 24.08 |
| 500 | 0.14 | 0.08 | 115.46 | 145.61 | 26.11 | |
| 1000 | 0.15 | 0.09 | 135.16 | 170.45 | 26.11 | |
| 50 | 100 | 0.01 | 0.00 | 62.13 | 72.35 | 16.45 |
| 500 | 0.04 | 0.02 | 177.90 | 208.29 | 17.08 | |
| 1000 | 0.04 | 0.02 | 214.04 | 254.08 | 18.71 | |
| 70 | 100 | 0.00 | 0.00 | 68.07 | 79.12 | 16.24 |
| 500 | 0.01 | 0.01 | 233.81 | 264.30 | 13.04 | |
| 1000 | 0.01 | 0.01 | 292.09 | 327.81 | 12.23 | |
| 100 | 100 | 0.00 | 0.00 | - | - | - |
| 500 | 0.00 | 0.00 | 315.52 | 347.89 | 10.26 | |
| 1000 | 0.00 | 0.00 | 393.28 | 438.94 | 11.61 |
| u | T | % Changes | ||||
|---|---|---|---|---|---|---|
| 10 | 100 | 0.51 | 0.24 | 18.63 | 35.88 | 92.61 |
| 500 | 0.59 | 0.33 | 40.69 | 83.27 | 104.67 | |
| 1000 | 0.60 | 0.34 | 47.97 | 100.35 | 109.18 | |
| 30 | 100 | 0.16 | 0.05 | 38.97 | 56.63 | 45.33 |
| 500 | 0.27 | 0.13 | 101.28 | 153.44 | 51.51 | |
| 1000 | 0.28 | 0.14 | 122.80 | 189.76 | 54.53 | |
| 50 | 100 | 0.04 | 0.01 | 52.30 | 68.41 | 30.81 |
| 500 | 0.12 | 0.05 | 150.57 | 205.16 | 36.25 | |
| 1000 | 0.13 | 0.06 | 197.59 | 272.25 | 37.79 | |
| 70 | 100 | 0.01 | 0.00 | 61.72 | 78.22 | 26.73 |
| 500 | 0.05 | 0.02 | 197.71 | 253.26 | 28.10 | |
| 1000 | 0.06 | 0.03 | 261.72 | 339.91 | 29.88 | |
| 100 | 100 | 0.00 | 0.00 | 54.87 | 64.62 | 17.77 |
| 500 | 0.01 | 0.00 | 250.91 | 303.45 | 20.94 | |
| 1000 | 0.02 | 0.01 | 368.16 | 455.16 | 23.63 |
| u | T | % Changes | No Effect | ||||
|---|---|---|---|---|---|---|---|
| 10 | 100 | 0.43 | 0.20 | 15.88 | 21.36 | 34.55 | 0.08 |
| 500 | 0.53 | 0.39 | 31.50 | 36.55 | 16.03 | 0.30 | |
| 1000 | 0.55 | 0.44 | 38.93 | 43.54 | 11.84 | 0.38 | |
| 30 | 100 | 0.14 | 0.01 | 33.48 | 49.71 | 48.47 | 0.00 |
| 500 | 0.26 | 0.08 | 71.37 | 92.83 | 30.08 | 0.03 | |
| 1000 | 0.28 | 0.12 | 87.85 | 106.86 | 21.63 | 0.07 | |
| 50 | 100 | 0.06 | 0.00 | 45.22 | 67.26 | 48.76 | 0.00 |
| 500 | 0.14 | 0.02 | 107.64 | 145.85 | 35.50 | 0.00 | |
| 1000 | 0.17 | 0.03 | 134.88 | 172.85 | 28.15 | 0.01 | |
| 70 | 100 | 0.03 | 0.00 | 70.52 | 79.83 | 13.20 | 0.00 |
| 500 | 0.09 | 0.00 | 144.90 | 195.31 | 34.79 | 0.00 | |
| 1000 | 0.11 | 0.01 | 182.04 | 243.62 | 33.82 | 0.00 | |
| 100 | 100 | 0.01 | 0.00 | - | - | - | 0.00 |
| 500 | 0.05 | 0.00 | 181.23 | 281.15 | 55.13 | 0.00 | |
| 1000 | 0.06 | 0.00 | 235.18 | 318.21 | 35.31 | 0.00 |
| u | T | % Changes | No Effect | ||||
|---|---|---|---|---|---|---|---|
| 10 | 100 | 0.43 | 0.32 | 20.02 | 24.34 | 21.55 | 0.13 |
| 500 | 0.49 | 0.45 | 40.67 | 44.52 | 9.45 | 0.32 | |
| 1000 | 0.50 | 0.47 | 45.80 | 48.49 | 5.85 | 0.38 | |
| 30 | 100 | 0.08 | 0.03 | 44.45 | 53.24 | 19.77 | 0.00 |
| 500 | 0.14 | 0.11 | 106.87 | 116.82 | 9.31 | 0.04 | |
| 1000 | 0.15 | 0.13 | 127.08 | 135.13 | 6.33 | 0.07 | |
| 50 | 100 | 0.01 | 0.00 | 57.85 | 68.12 | 17.74 | 0.00 |
| 500 | 0.04 | 0.03 | 165.39 | 181.42 | 9.69 | 0.01 | |
| 1000 | 0.04 | 0.03 | 200.86 | 214.19 | 6.64 | 0.01 | |
| 70 | 100 | 0.00 | 0.00 | 66.66 | 80.33 | 20.52 | 0.00 |
| 500 | 0.01 | 0.01 | 219.09 | 239.44 | 9.29 | 0.00 | |
| 1000 | 0.01 | 0.01 | 279.28 | 294.17 | 5.33 | 0.00 | |
| 100 | 100 | 0.00 | 0.00 | - | - | - | 0.00 |
| 500 | 0.00 | 0.00 | 306.48 | 334.20 | 9.04 | 0.00 | |
| 1000 | 0.00 | 0.00 | 385.12 | 410.96 | 6.71 | 0.00 |
| u | T | % Changes | No Effect | ||||
|---|---|---|---|---|---|---|---|
| 10 | 100 | 0.51 | 0.33 | 15.99 | 21.11 | 32.05 | 0.15 |
| 500 | 0.59 | 0.52 | 35.92 | 41.51 | 15.55 | 0.39 | |
| 1000 | 0.60 | 0.56 | 44.17 | 48.64 | 10.10 | 0.47 | |
| 30 | 100 | 0.16 | 0.04 | 35.16 | 47.97 | 36.44 | 0.00 |
| 500 | 0.27 | 0.18 | 89.10 | 106.78 | 19.85 | 0.07 | |
| 1000 | 0.28 | 0.22 | 109.79 | 124.45 | 13.35 | 0.12 | |
| 50 | 100 | 0.04 | 0.00 | 46.48 | 63.63 | 36.89 | 0.00 |
| 500 | 0.12 | 0.06 | 133.06 | 159.35 | 19.76 | 0.01 | |
| 1000 | 0.13 | 0.09 | 175.11 | 199.22 | 13.77 | 0.03 | |
| 70 | 100 | 0.01 | 0.00 | 55.19 | 71.45 | 29.44 | 0.00 |
| 500 | 0.05 | 0.02 | 177.18 | 211.36 | 19.29 | 0.00 | |
| 1000 | 0.06 | 0.03 | 233.06 | 267.53 | 14.79 | 0.01 | |
| 100 | 100 | 0.00 | 0.00 | - | - | - | 0.00 |
| 500 | 0.01 | 0.00 | 227.50 | 272.16 | 19.63 | 0.00 | |
| 1000 | 0.02 | 0.00 | 333.10 | 384.93 | 15.56 | 0.00 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Griffin, P.S.; Maller, R.; Szimayer, A.; Wang, T. The Effects of Largest Claim and Excess of Loss Reinsurance on a Company’s Ruin Time and Valuation. Risks 2017, 5, 3. https://doi.org/10.3390/risks5010003
Fan Y, Griffin PS, Maller R, Szimayer A, Wang T. The Effects of Largest Claim and Excess of Loss Reinsurance on a Company’s Ruin Time and Valuation. Risks. 2017; 5(1):3. https://doi.org/10.3390/risks5010003
Chicago/Turabian StyleFan, Yuguang, Philip S. Griffin, Ross Maller, Alexander Szimayer, and Tiandong Wang. 2017. "The Effects of Largest Claim and Excess of Loss Reinsurance on a Company’s Ruin Time and Valuation" Risks 5, no. 1: 3. https://doi.org/10.3390/risks5010003
APA StyleFan, Y., Griffin, P. S., Maller, R., Szimayer, A., & Wang, T. (2017). The Effects of Largest Claim and Excess of Loss Reinsurance on a Company’s Ruin Time and Valuation. Risks, 5(1), 3. https://doi.org/10.3390/risks5010003







