The Wasserstein Metric and Robustness in Risk Management

Abstract

In the aftermath of the financial crisis, it was realized that the mathematical models used for the valuation of financial instruments and the quantification of risk inherent in portfolios consisting of these financial instruments exhibit a substantial model risk. Consequently, regulators and other stakeholders have started to require that the internal models used by financial institutions are robust. We present an approach to consistently incorporate the robustness requirements into the quantitative risk management process of a financial institution, with a special focus on insurance. We advocate the Wasserstein metric as the canonical metric for approximations in robust risk management and present supporting arguments. Representing risk measures as statistical functionals, we relate risk measures with the concept of robustness and hence continuity with respect to the Wasserstein metric. This allows us to use results from robust statistics concerning continuity and differentiability of functionals. Finally, we illustrate our approach via practical applications.

1. Introduction

In the aftermath of the financial crisis, it was realized that the mathematical models for financial markets carry a substantial amount of model risk. Ref. [1], with a discussion from a banking point of view, and [2], who provide an overview with a focus on systemic risk, investigate various aspects of model risk, while [3,4] give some early examples. Accounting for model risk is particularly important for the forecast of risk inherent to portfolios consisting of financial instruments as this forecast is used to calculate economic and regulatory capital within financial institutions. Hence, it is no surprise that if a financial institution opts (e.g., under Solvency II or Basel III) for an application of an internal model, its stakeholders, such as regulators and rating agencies, require that such internal models are reliable. For that reason, the EU directive for Solvency II imposes explicitly that internal models have to meet statistical quality, calibration, and validation standards and have to pass the use test (see Articles 120, 121, 122 and 124, respectively, of the Solvency II directive [5]). By means of these quantitative and qualitative requirements, it is intended to achieve a high level of comfort with respect to the reliability of internal models. Furthermore, regulators require explicitly the robustness of a model as an overarching modelling principle (see [6]). This is especially important because both internal and external model users, who include the results of the models in their decision-making process, are often non-experts in stochastic models. In this respect, robustness of models is a necessary condition to introduce a sustainable risk culture.

Motivated by the above, we pose the problem of a consistent robust modeling approach by considering an axiomatic setting for monetary risk measures that ensures robustness on the one hand and emphasizes the approximative nature of internal models on the other hand by making the need for formulating a suitable distance explicit. Thus, we focus on the statistical robustness of the risk measurement procedure and in doing so complement recent approaches to evaluate model risk as in [7] or to use statistical concepts to evaluate the performance of risk measures as suggested in e.g., [8] or [9].

Within our approach, we consider risk functionals, which treat risk measures on the level of distributions, and allow so to exploit established statistical theory. Risk functionals are typically not continuous with respect to the weak topology as this topology ignores the tails of the distribution. Ref. [10] pointed out this fact and suggested to use a stronger topology. We will thus use robustness in the sense of continuity with respect to an appropriate metric, namely the Wasserstein metric, which was introduced in a general setting in [11] and in the financial context in [12] (p. 79), as the uniform metric between inverse distribution functions. Our approach is in line with [13,14], who provide extensions and introduce an index of qualitative robustness, and the approaches suggested by [15], who prefer robust methods for estimating parameters (Value-at-Risk, expectations, etc.) of forecast distributions. Our framework allows for utilisation of several results that have been established recently in [16].

In addition, we provide various real-life examples to support and to emphasise the applicability of our results. We thus extend and clarify results in [17], who provide real-life examples that highlight the need for robust models for both valuation and calculation of risk in order to control model risk. In addition, in an insurance context [18] recently, applied robust methods to the estimation of loss triangles.

2. A Suitable Distance for Risk Management

We consider monetary risk measures that are related to capital requirements. These risk measures, ρ, are typically introduced for (random) financial positions X defined on an appropriate probability space $(\mathsf{\Omega },\mathcal{F},\mathbb{P}),$ by

$$\rho :L^{\infty }(\mathsf{\Omega },\mathcal{F},\mathbb{P})\to \mathbb{R},$$

(1)

where $L^{\infty }$ denotes the space of real valued bounded functions.

We refer the reader for definitions and the various variants of monetary risk measures to [19,20]. Important for us is the contribution by [21], who introduced natural risk statistics. This concept bridges the gap between risk measures and statistics by defining natural risk statistics on a sample space in contrast to the definition of risk measures on a probability space (1).

In situations when we are dealing with possibly unbounded financial positions X, the space $L^{\infty }$ is not suitable. Following the observation of [22] that Orlicz spaces or Orlicz hearts (see Proposition 2 below) are appropriate in this case, [16] show that for $p\in [0,\infty ),$ $L^p$ is an Orlicz heart and thus can serve as a space of financial positions. In fact, based on [23], Theorem 2.10 of [16] shows that law-invariant convex risk measures on $L^{\infty }$ has a unique extension to $L^1$ (convex, monotone, and lower semicontinuous with respect to the $L^1$-norm), which inherits continuity properties.

In order to discuss the robustness (estimation) of risk measures, we need the following concept:

Definition 1. 

Statistical functional. Let $\mathbb{F}$ denote the set of all cumulative distribution functions on $\mathbb{R}$ and $\overline{\mathbb{F}}\subset \mathbb{F}$ an appropriate subset. We consider maps

$$T:\overline{\mathbb{F}}\subseteq \mathbb{F}⟶\mathbb{R}.$$

(2)

Now, let $X_1,\dots ,X_n$ be a sample from a population with distribution function $F\in \overline{\mathbb{F}}$ and empirical distribution $F_n$. If a statistic $T_n=T_n(X_1,\dots ,X_n)$ can be written as a functional T of $F_n$, say $T_n=T\left(F_n\right)$, then we will call T a statistical functional.

This is particularly important as we assess the risk $\rho \left(X\right)$ of a financial position X with distribution function F. Typically, we will use a Monte Carlo simulation or a sequence of historical data. For law-invariant ρ, a natural estimate of $\rho \left(X\right)$ is $T_{\rho }\left(F_n\right)$, where $F_n$ is the empirical distribution function and

$$T_{\rho }\left(F\right)=\rho \left(X\right),\mathrm{for}X\mathrm{with\; distribution\; function}F.$$

(3)

Now, robustness of the risk measure ρ can be related to continuity of $T_{\rho }$. Here, robustness refers to a certain insensitivity of ρ to variations in the approximating distribution for F. For this, the concept of continuity is crucial.

Note that any statistical functional $T\left(F\right)$ can be approximated with $T\left(F_n\right)$, provided that $F_n$ is in a neighborhood of F and the functional T is sufficiently well behaved. This leads us to consider F as a “point” in $\mathbb{F}$ and to investigate continuity, differentiability and other regularity properties for functionals defined on (subsets of) $\mathbb{F}$.

In order to define these concepts properly, we need to introduce:

Definition 2. 

Simple probability metric. Let $\overline{\mathbb{F}}\subset \mathbb{F}$ be a convex class of distribution functions on $\mathbb{R}$ containing all degenerate distributions. A mapping

$$d:\overline{\mathbb{F}}\times \overline{\mathbb{F}}\to [0,\infty )$$

is called a simple probability metric (or distance) if

1. 

$F\left(x\right)=G\left(x\right)forallx\in \mathbb{R}iffd(F,G)=0$,

2. 

$d(F,G)=d(G,F)forallF,G\in \overline{\mathbb{F}}$,

3. 

$d(F,G)\le d(F,H)+d(G,H)forallF,G,H\in \overline{\mathbb{F}}$.

Unfortunately, there are plenty of possible metrics to choose. In order to select a specific metric as a preferable one from a practitioner’s point of view, two questions have to be answered:

• Does the chosen metric fit well in the context of application, i.e., has the chosen metric a natural interpretation? Is it perhaps the canonical metric for a particular field of application?
• Is the metric not too strong? This means—do we have a sufficiently rich set of continuous objects?

The following example lists very common risk measures that should fit into the risk measurement framework from a practitioner’s point of view.

Example 1. 

Examples of statistical functionals and risk measures: The central piece of many (internal) risk management models is risk measures such a Value-at-Risk (VaR) and Tail-VaR (TVaR). We give representations of these important risk measures as statistical functionals. Let $F_n$ be the empirical distribution function related to a given data set. In addition, recall that, for a cumulative distribution function F, the (upper) quantile of order $\alpha \in (0,1)$ is defined as $F^{-1}\left(\alpha \right)=inf\{x\in \mathbb{R}:F\left(x\right)>\alpha \}$.

• Value-at-Risk. For a fixed $0<\alpha <1$ (usually $\alpha \le 0.05$), we define the Value-at-Risk at level α (VaR${}_{\alpha }$) as

  $$Va{R}_{\alpha }=-F^{-1}\left(\alpha \right).$$

  (4)

  The statistical functional for estimating Value-at-Risk is then

  $$T\left(F_n\right)=-F_n^{-1}\left(\alpha \right)=-{\int }_0^1{F}_n^{-1}\left(\tau \right)d{\delta }_{\alpha }\left(\tau \right),$$

  where ${\delta }_{\alpha }$ puts mass one to $\alpha \in (0,1)$.
• Tail-VaR (TVaR).1 The statistical functional for estimating TVaR is

  $$\begin{array}{cc}\hfill T\left(F_n\right)& =-{(1-\alpha )}^{-1}{\int }_{\alpha }^1{F}_n^{-1}\left(x\right)dx.\hfill \end{array}$$

  (5)

If we substitute F for $F_n$ in the examples above, we obtain the associated risk measures. In particular, any law-invariant2 risk measure can be written as a statistical functional (see [19] for further discussion). For the VaR, this yields $T\left(F\right)=-F^{-1}\left(\alpha \right)$. From (4) and (5), we conclude the important role of the empirical distribution for determining risk measures. Hence, a metric for risk management should be based on the whole cumulative distribution function.

We now turn to the question of robustness of risk measures in more detail. Given that we want to use the empirical distribution in praxis, we need to specify how to quantify the effect of a small deviation from the true distribution on the risk measure. We need the following definition:

Definition 3. 

Continuity of statistical functionals. Let $\overline{\mathbb{F}}\subset \mathbb{F}$ be a convex class of distribution functions on $\mathbb{R}$ containing all degenerate distributions. A functional T defined on $\overline{\mathbb{F}}$ is continuous at $F\in \overline{\mathbb{F}}$ if

$$T\left(G\right)-T\left(F\right)=o\left(1\right)as d(G,F)=o\left(1\right),F,G\in \overline{\mathbb{F}},$$

where $d(G,F)$ denotes a distance of two distribution G and F.

In the axiomatic approach of [24], the continuity of a risk measure is not required. Consequently, the class of coherent risk measures includes discontinuous risk measures such as the TVaR. Given the approximative character of stochastic models, we think that continuity, and, hence, robustness, are, from a practitioner’s point of view, even more important than subadditivity.

Example 2. 

TVaR is not continuous w.r.t. the weak topology: Consider the sequence

$$G_n=\frac{n-1}{n}U[0,1]+\frac{1}{n}{\mathbf{1}}_{n^2},$$

where $U[0,1]$ denotes the uniform distribution on $[0,1]$ and ${\mathbf{1}}_{n^2}$ puts its mass one to $n^2$, $n\in \mathbb{N}$. Obviously, $G_n$ converges weakly to $U[0,1]$:

$$G_n\stackrel{w}{⟶}U[0,1].$$

However, the associated TVaRs do not. For all α, we have:

$$TVa{R}_{\alpha }\left(G_n\right)={\int }_{-Va{R}_{\alpha }}^{\infty }xd{G}_n>n,$$

whereas

$$TVa{R}_{\alpha }\left(U[0,1]\right)={\int }_{-Va{R}_{\alpha }}^{1}xdx\le 1$$

is finite.

The above example clearly highlights the fact that risk measures, which put emphasis on the tail of a distribution cannot be expected to be continuous with respect to topologies that ignore the tails of distributions. In contrast, it can be shown that the VaR at level α is continuous w.r.t the weak topology (see Theorem 3.7 in [25]) at $F\in \mathbb{F}$ if $F^{-1}$ is continuous at α. Given that VaR and TVaR are the risk measures that are of overwhelming importance in practice, we suggest using a metric that implies the continuity of the associated functionals.

We will now discuss properties of a metric that are particularly useful for the risk management process. In terms of practical applications, it is important to strike a balance between properties in the centre of a distribution and its tail behaviour. Thus, as outlined in Example 1, the following requirements are natural in order that the statistical functionals allow for estimating all of the risk measures given in Example 1 consistently:

$$\begin{array}{c}\hfill F_n\stackrel{w}{⟶}F\mathrm{and}{\int }_{\mathbb{R}}{x}^{p}d{F}_n\left(x\right)⟶{\int }_{\mathbb{R}}{x}^{p}dF\left(x\right)\end{array}$$

(6)

for some $p\ge 0$ and $F_n\in \overline{\mathbb{F}}\subset \mathbb{F}$. Note that the linear functional ${\int }_{\mathbb{R}}{x}^{p}dF\left(x\right)$ is now continous in F w.r.t. a given metric. For applications in risk management, the cases $p=1$ and $p=2$ are of particular importance. Thus, we are looking for a metric that combines these two properties.

We will show that with the Wasserstein metric (especially, the case $p=2$), both types of risk measures are considered: one-tail measures (such as VaR) and two-tail measures (such as volatility). Hence, this approach comprises both concepts.

We will only need the Wasserstein metric for two distributions $F,G$ on the real line.

Definition 4. 

Wasserstein Metric. Let $X\sim F,Y\sim G$ random variables with their corresponding distribution functions. The Wasserstein distance, $W_p(X,Y)=W_p(F,G)$ for two distributions is given by:

$$\begin{array}{c}\hfill W_p(X,Y)=W_p(F,G)={\int }_0^1{|F^{-1}\left(u\right)-G^{-1}\left(u\right)|}^{p}du,p\ge 1.\end{array}$$

(7)

For a general definition of the Wasserstein metric in Banach spaces, the reader will find appropriate definitions in [11]. Refs. [26,27] show the equivalence of the above definition with the general case. An example for the use of the Wasserstein metric in the context of investments is [28].

Proposition 1. 

Properties of Wasserstein Metric. The Wasserstein metric has the following properties:

1. 

For $X,Y$ random variables we have the following scaling properties of $W_p$:

$$\begin{array}{cc}\hfill W_p(aX,aY)& =|a|W_p(X,Y),foranyscalea.\hfill \end{array}$$

(8)

The scaling property (8) is important for risk management because it allows the change of numéraire, e.g., change of home currency.

2. 

For $F_1,F_2,G_1,G_2$ in ${\mathsf{\Gamma }}_2$ and $ϵ\in (0,1)$

$$\begin{array}{c}\hfill W_2(ϵF_1+(1-ϵ)F_2,ϵG_1+(1-ϵ)G_2)\le ϵW_2(F_1,G_1)+(1-ϵ)W_2(F_2,G_2).\end{array}$$

(9)

If $ϵ=0.5$ and $G_1=F_1$, then we have the regularity property:

$$\begin{array}{c}\hfill W_2(F_1+F_2,F_1+G_2)\le W_2(F_2,G_2).\end{array}$$

(10)

3. 

Let $U_j,V_i,i,j=1,\dots ,m$ be independent and assume that the laws are in ${\mathsf{\Gamma }}_2$. Then,

$$\begin{array}{c}\hfill W_2(\sum _{i=1}^m{U}_j,\sum _{j=1}^m{V}_j)\le \sum _{j=1}^m{W}_2(U_j,V_j).\end{array}$$

(11)

This property is key to proving the consistency for bootstrapping mean statistics (see [11]).

4. 

The Wasserstein metric is a one-ideal metric (see the Appendix A for a definition of one- ideal).

Example 3. 

Wasserstein and $L^p$ distance: For $F,G$ distribution functions, the $L^p$-distance, ${\mathsf{\Theta }}_p(F,G)$ is defines as:

$$\begin{array}{c}\hfill {\mathsf{\Theta }}_p(F,G)={\left({\int }_{-\infty }^{\infty }{|F\left(u\right)-G\left(u\right)|}^{p}du\right)}^{1/p},p\ge 1.\end{array}$$

(12)

We compare this distance with the Wasserstein metric for a standard normal distribution Φ, which we perturbate such that there is a difference in the right tail. Thus, let

$$G\left(x\right)=(1-\epsilon )\mathsf{\Phi }\left(x\right)+\epsilon Exp(x;\lambda ),$$

where $Exp(x;\lambda )$ is an exponential distribution.

Table 1. Wasserstein and $L^p$ distance, $\epsilon =0.1,\lambda =0.5$.

p	1	2	3	4
$W_p$	0.054	0.067	0.075	0.085
${\mathsf{\Theta }}_p$	0.054	0.039	0.038	0.038

shows that the Wasserstein distance increases in p while the $L^p$ distance decreases. Thus, the weighting of differences in the tail increase for the Wasserstein metric in p, while it decreases for $L^p$.

The convexity properties are closely related to the independence axiom of the Von–Neumann–Morgenstern approach to utility theory. Therefore, the Wasserstein metric fits smoothly into this framework. As the results of the risk measuring exercise need to have an impact on decisions within the company (the use test in Solvency II) and as utility theory is widely used in this context, this is a very desirable property.

Recently, [16] have investigated the robustness properties of convex risk measures, in particular regarding the Wasserstein metric.

Proposition 2. 

[16] (Theorems 2.5 & 2.7). Let $X_1,X_2,\dots \in L^p(\mathsf{\Omega },\mathcal{F},\mathbb{P})$ be a stationary and ergodic sequence of random variables with the same law as $X\in H^p,p\in [1,\infty )$3 with

$$\begin{array}{c}\hfill H^p(\mathsf{\Omega },\mathcal{F},\mathbb{P})=\left\{X\in L^0{:E[|cX|}^p/p\left)\right]<\infty \forall c>0\right\}.\end{array}$$

Then, for a law-invariant convex risk measure ρ with corresponding statistical functional $T_{\rho }$, the estimator

$$\begin{array}{c}\hfill {\widehat{\rho }}_n=T_{\rho }\left(\frac{1}{n}\sum _{i=1}^n{\delta }_{X_i}\right)\end{array}$$

is consistent, that is, ${\widehat{\rho }}_n\to \rho \left(X\right)$ as $n\to \infty$ $\mathbb{P}-$ a.s., and continuous with respect to the p-Wasserstein metric4.

The proposition implies, for instance, the continuity of the TVaR w.r.t. the Wasserstein metric.

Many statistical functionals are so-called L - functionals (see [21] for a discussion of the role of L-statistics in terms of natural risk measures). We can relate them to the Wasserstein-metric with the following:

Theorem 1. 

Continuity of L-statistical functional w.r.t the Wasserstein metric. Let T be an L-statistical functional of the form

$$\begin{array}{c}\hfill T\left(G\right)={\int }_0^1{F}^{-1}\left(t\right)J\left(t\right)dt={\int }_{-\infty }^{\infty }xdK\left(G\left(x\right)\right),G\in \mathbb{F}\end{array}$$

(13)

for ${\int }_0^1{F}^{-1}\left(t\right)J\left(t\right)dt<\infty$, $K\left(t\right)={\int }_0^{t}J\left(u\right)dt$, and J a weights generating function bounded on [0,1]. Then, T is continuous w.r.t to Wasserstein metric $W_p,p\in [1,\infty )$.

Proof. 

The claim follows as a special case from [16], Proposition 2.22. We provide an independent proof in the Appendix B. □

Theorem 1 implies the continuity of mean, trimmed mean, and TVaR w.r.t. the Wasserstein metric. □

As we discussed above, we extended the classical concept of qualitative robustness, which is based on the weak topology, by using a more suitable topology, and therefore we made it useful for tail sensitive functionals such as most risk measures. Ref. [16] propose the alternative notion of ψ-robustness. Here, $\psi :{\mathbb{P}}_{+}\to [0,\infty ]$ is a left-continuous, nondecreasing convex (Young) function, which we call weight function in the following. We denote by ${\mathcal{M}}_1$ the set of all probability measures5 on $\mathbb{R}$ and by ${\mathcal{M}}_1^{\psi }\subset {\mathcal{M}}_1$ the set of all probability measures μ on $\mathbb{R}$ with ${\int }_{\mathbb{R}}\psi d\mu <\infty$. Additionally, we have to impose a product structure on the underlying probability space, setting $\mathsf{\Omega }={\mathbb{R}}^N$, $X_i\left(\omega \right)=\omega \left(i\right)$ for $\omega \in \mathsf{\Omega },i\in \mathbb{N}$, $\mathcal{F}=\sigma \{X_1,X_2,\dots \}$, and, for $\mu \in {\mathcal{M}}_1$, ${\mathbb{P}}_{\mu }={\mu }^{\otimes N}$.

Definition 5. 

Qualitative robustness and ψ-robustness. Let $\mathcal{N}\subset {\mathcal{M}}_1$, and let $d_A$ and $d_B$ be metrics on $\mathcal{N}$ and ${\mathcal{M}}_1$, respectively. The functional $T_{\rho }$ is called (qualitatively) $\mathcal{N}$-robust with respect to $d_A$ and $d_B$, if for all $\mu \in {\mathcal{M}}_1$ and $ϵ>0$, there exist $\delta >0$ and $n_0\in \mathbb{N}$ such that

$$\begin{array}{c}\hfill \nu \in \mathcal{N},d_A(\mu ,\nu )\le \delta \Rightarrow d_B({\mathbb{P}}_{\mu }\circ {\widehat{\rho }}_n^{-1},{\mathbb{P}}_{\nu }\circ {\widehat{\rho }}_n^{-1})ϵforn\ge n_0.\end{array}$$

Let ψ be a weight function. A risk functional ${\mathcal{R}}_{\rho }$ is called ψ-robust on $\mathcal{M}\subset {\mathcal{M}}_1$ if ${\mathcal{R}}_{\rho }$ is robust with respect to $d_A$ and $d_B$ on all subsets $\mathcal{N}\subset \mathcal{M}$, which are uniformly integrating, that is

$$\begin{array}{c}\hfill \underset{M\to \infty }{lim}\underset{\nu \in \mathcal{N}}{sup}{\int }_{\psi \ge M}\psi dv=0.\end{array}$$

The key inside (already pointed out in [10]) is that, when insisting on distances that generate the usual weak topology of measures, one can have distributions that are rather close in the weak topology but will have completely different tail behaviour. Thus, the notion of robustness should allow an insensitivity with respect to tail behaviour. As [16] point out, the Prohorov distance

$$d_{\mathrm{Proh}}(\mu ,\nu ):=inf\left\{ϵ>0:\mu \left(A\right)\le \nu \left(A^{ϵ}\right)+ϵ\mathrm{for\; all}A\in \mathcal{B}\left(\mathbb{R}\right)\right\}$$

(14)

and the Prohorov $\psi -$metric

$$d_{\psi }(\mu ,\nu ):=d_{\mathrm{Proh}}(\mu ,\nu )+\left|\int \psi d\mu -\int \psi d\nu \right|,\mu ,\nu \in {\mathcal{M}}_1$$

(15)

are appropriate choices. Ref. [16] (Theorem. 2.14 rso Theorem 2.25) characterize robust risk measures rsp. show that it is sufficient to study law-invariant convex risk measures on $\mathcal{M}\left(L^{\infty }\right)$.

A special case for ${\psi }_p={|x|}^p/p$, the function that is also implicitly used in Proposition 2, allows for stating the result for the p- Wasserstein metric.

Proposition 3. 

Every law-invariant convex risk measure $\rho :L^p\to \mathbb{R}$, $p\in [1,\infty )$ is ${\psi }_p$-robust with respect to the p-Wasserstein metric.

In particular, the proposition shows that the TVaR is ${\psi }_p$-robust for any $p\ge 1$. The value at risk is qualitatively robust even in the classical sense, that is, with $d_A$ and $d_B$ equal to the Prohorov metric and $\mathcal{N}={\mathcal{M}}_1$ (see ([14], Example 4.3 )).

Example 4. 

Wasserstein metric for p=1: for heavy tailed distributions as they appear in finance, the mean absolute deviation is preferable, due to its robustness properties. Hence,

$$\begin{array}{c}\hfill \int |x-F^{-1}\left(0.5\right)|dF,\end{array}$$

where $F^{-1}\left(0.5\right)$ denotes the median, is a suitable substitute for $E\left(X^2\right)$, and thus for volatility-sensitive risk measures, in (6) which is much more in line with our overall robustness approach. In requiring

$$\begin{array}{c}\hfill F_n\stackrel{w}{⟶}Fand\int |x-F_n^{-1}\left(0.5\right)|d{F}_n⟶\int |x-F^{-1}\left(0.5\right)|dF.\end{array}$$

(16)

We are in the $L^1$ setting of the Wasserstein framework. Note that for the $L^1$ case, we have:

$$\begin{array}{c}\hfill d_{L^1}(F_n,F)={\int }_{-\infty }^{\infty }|F_n-F|dx={\int }_0^1|F_n^{-1}-F^{-1}|dx=d_{{\ell }_1}(F_n,F).\end{array}$$

(17)

This may be used with advantage, when we consider Fréchet differentiable functions. Following [29], we consider the following norms:

$$\begin{array}{cc}\hfill ||F-{G||}_{\infty +p}& =||F-{G||}_{\infty }+||F-{G||}_p\hfill \\ & =\underset{x}{sup}|F\left(x\right)-G\left(x\right)|+{\left(\int {|F-G|}^{p}dx\right)}^{1/p}.\hfill \end{array}$$

(18)

For $p=1$, this means that if a statistical functional is strongly differentiable w.r.t supremum norm, then it is automatically differentiable with respect to the sum of the Wasserstein and supremum norm.

This norm implies, for statistical functionals which satisfy a Fréchet differentiability condition, that jackknifing and bootstraps yield consistent estimators.

3. Application of the Wasserstein Metric in Risk Management

This section is devoted to exemplifying the importance of the Wasserstein Metric by analyzing application from real-life risk management.

Example 5. 

Consistency of summary statistics and estimated capital requirement: nearly any statistical analysis starts with the computation of a table of summary statistics comprising means such as the expectation, standard deviation, skewness and kurtosis, and quantiles such as the interquantile range and other characteristics.

Of course, the minimum requirements for interpreting these statistics would be that the statistics are consistent estimators for the associated parameter. Obviously, for means and quantile types of statistics, a convergence with respect to the Wasserstein distance would imply consistency. Hence, also for statistical analysis, the Wasserstein metric is quite natural for bridging the gap between descriptive statistics and inferential type approaches. This is very much in line with the approach advocated by [30].

To see the importance of consistency in regulation, we consider an important risk measure under Solvency II: the Solvency Capital Required, denoted by $SCR$. Note that $SCR$ is defined by a difference6 of a quantile and an expectation, which we can write as a difference of statistical functionals i.e.,

$$\begin{array}{}\text{(19)}\hfill & \hfill SCR& :=& E\left(X\right)+{VaR}_{\alpha }\left(X\right)\hfill \text{(20)}\hfill & & =& {\int }_0^1{F}_n^{-1}\left(x\right)dx-{\int }_0^1{F}_n^{-1}\left(\tau \right)d{\delta }_{\alpha }\left(\tau \right)\hfill \text{(21)}\hfill & & =& T_1\left(F_n\right)-T_2\left(F_n\right)=S\left(F_n\right).\hfill \end{array}$$

In the light of (19), the Wasserstein Metric for $p=1$ is sufficient to ensure the continuity of the functional S at F:

$$S\left(F_n\right)\to S\left(F\right),$$

(22)

if

$$W_1(F_n,F)\to 0.$$

(23)

Example 6. 

Robustness and materiality: the implementation of internal models calls for a concept of materiality that allows for working with various proxies. In light of Example 2, the sequence of distributions $\left(G_n\right)$ seems to provide a good approximation for the uniform distribution U, due to the fact that

$$d(G_n,U)\le \frac{1}{n^2},$$

(24)

w.r.t. the weak topology; roughly speaking: the error is arbitrarily small, hence immaterial. However, neither the TVaR nor the expectation is a continuous functional at U with respect to the weak convergence. If the SCR is based on (19)—or if we substitute $Va{R}_{\alpha }$ by $TVa{R}_{\alpha }$, as it is proposed under Basel III—the SCR is difficult to be used as a yardstick to gauge the materiality of proxies, if the considered risk functional is not continuous or respectively robust. However, the choice of the Wasserstein metric for $p=1$ allows for judging the materiality of the error. Note that from a mathematical point of view, materiality is closely related to robustness and continuity.

Example 7. 

Test statistic consistently chosen to the natural distance: in light of the previous examples, it is natural to use the Wasserstein Metric for $p=1$ in the context of risk management. In the process of the application of an internal model, a number of statistical analyses are necessary, especially in the validation process (see Article 124 of the Solvency Directive [5]).

Due to simplicity in practical risk management applications, tools in software packages available are often applied for statistical tests. A point in case is the application of the Kolmogoroff–Smirnow test statistic, which is based on the Kolmogoroff–Smirnow distance as defined in (25):

$$d_K(F_n,F)=\underset{x\in \mathbb{R}}{sup}|F_n\left(x\right)-F\left(x\right)|.$$

(25)

However, from a principal point of view, it might be questioned whether this is a suitable test statistic for a given problem at hand.

Again, we advocate the application of the Wasserstein distance ($p\ge 1$) as a test statistic. The distribution function of this test may be determined by the application of the bootstrap. For a sample of size $n=10000$,

Table 2. Wasserstein metric, multiplied by 100.

	Normal	Gamma	GEV
$E_1$	5.14	4.08	14.36
$E_2$	4.74	1.55	1.18
$E_3$	5.17	1.78	1.27
$E_4$	4.95	1.59	1.60
$E_5$	6.41	5.45	9.22
$E_6$	9.90	5.92	1.15
$E_7$	7.55	4.53	1.39

contains the distances

$$W_1(F_n\left(x\right),F_{\widehat{\theta }})$$

(26)

between the empirical distribution function, $F_n\left(x\right)$, and some estimated parametric models $F_{\widehat{\theta }}$, namely the Normal, Gamma and Generalized Extreme Value distribution.

Real life examples have shown that results based on the application of the Kolmogoroff–Smirnow test yield very different results comparable to those based on the Wasserstein Metric. Due to the lengthy exposition, however, we omitted these examples in this exposition.

Instead, we consider in the following situation only the output of a Monte-Carlo simulation from an internal model in terms of the Wasserstein metric. Though Monte-Carlo simulations have a number of advantages, it is often very cumbersome to figure out relationships. For that reason, we approximate the output by some parametric densities. Table 2 shows for various companies (denoted by $E_i$) the Wasserstein distance between the empirical distribution function and fitted parametric models as outlined above. From this table, we may conclude which parametric model might be chosen per company.

This table may be understood in analogy to those cases where the well-known Kolmogoroff distance is applied and used as a test statistic. From Table 2, we might conclude that the Normal distribution as a simple fitting does not perform badly from an overall perspective. Of course, the Gamma distribution seems to be preferable; however, it has more parameters than the Normal distribution. The performance of the Generalized Extreme Value (GEV) distribution is very volatile; it performs well in some cases, very badly in others. Of course, it would be possible to support these judgements by some formal tests by bootstrapping the Wasserstein distance. However, given the case that the simulation is based on 10,000 scenarios, the result is quite clear.

Example 8. 

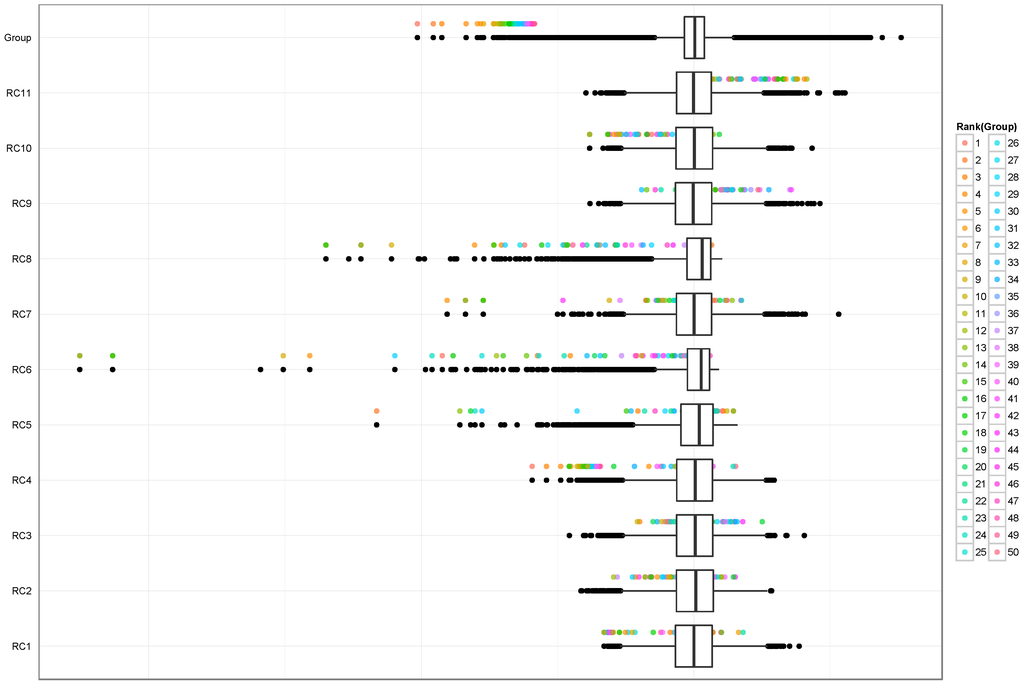
Is the focus of risk management just on the tails? Typically, risk management is focused very much on the tails of distributions, where very adverse events are modeled. The risk measures $Va{R}_{\alpha }$, $TVaR$ and all the progress made in the application of Extreme Value Theory over the last decade confirms this attitude. We think this is completely right; however, the following real-life example highlights that tails alone do not tell the whole story.

This example is taken from the aggregation of risks. Aggregation in itself is of highest importance due to the measurement of the amount of diversification induced by the considered method of aggregation.

The aggregation considered in Figure 1 is based on a so-called factor approach. In this framework, n scenarios of a common set of risk factors related to a number of risk categories are simulated. The result is a $n\times d$ matrix. For each column, the portfolio is evaluated and yields n potential changes of the considered portfolio.

The first box plot of Figure 1 is related to an insurance company, whereas the other eleven ones belong to risk categories such as market risk, natural catastrophes and others. With coloured points, the fifty most adverse scenarios or events are depicted. It is important to note that, for the risk categories, these fifty scenarios are related to realizations that are not necessarily located in the tail. It is interesting to see that these fifty scenarios are spread across the whole body of the distributions involved. In order to build an adequate risk model, it is of crucial importance to ensure that the whole distribution function is correctly specified and not only their tails. The Wasserstein distance fits very well to these needs because it averages the quantiles of a distribution as given in (4).

Example 9. 

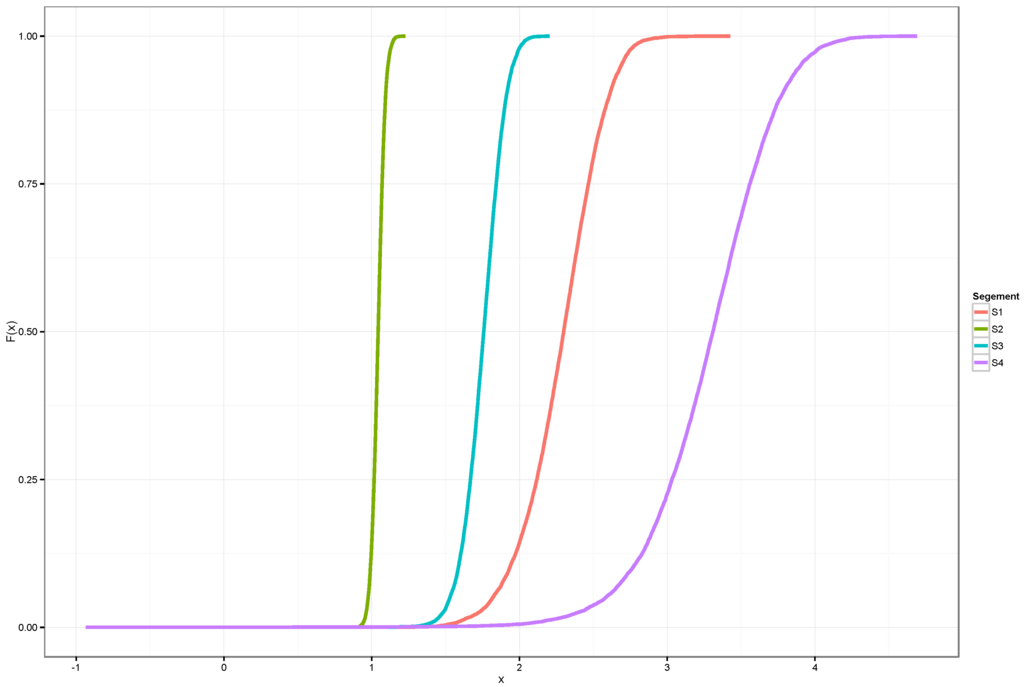
Ranking opportunities: in financial applications, one is often requested to choose one investment out of several ones. This might be achieved by the means a stochastic ordering of the random variables associated with the investment possibilities.

An important approach for ordering is stochastic dominance. Let X and Y be random variables with distribution functions $F_X$ and $F_Y$. Then, X is said to be stochastically dominated by Y, denoted by $X{\le }_{st}Y$, if

$$F_X\left(t\right)\ge F_Y\left(t\right),$$

(27)

for all $t\in \mathbb{R}$. In many practical circumstances, especially in capital allocation, the random variables involved are stochastically ordered by ${\le }_{st}$.

Figure 2 contains such a real-life situation, where the random variables represent divisions of an insurance group. In this situation, the Wasserstein Metric can be easily calculated, if stochastic dominance, $X{\le }_{st}Y,$ can be assumed, then:

$$W_1(X,Y)=|E\left(X\right)-E\left(Y\right)|.$$

(28)

Again, in this situation, the Wasserstein Metric is easily interpreted and calculated.

4. Conclusions

In this paper, we provide a consistent framework for a robust, quantitative risk management process. We argue that various approximations take place in this process and that we can take this into account by using a suitable metric throughout. The Wasserstein metric has convenient properties for applications in risk management, especially its focus on the tails of the distributions. It also features in recent work on the robustness of statistical functionals such as [14,16]. This strengthens our case for the Wasserstein metric as the canonical distance for risk management. The robustness results allow us—together with the concept of natural risk statistics—to recognize the approximative nature of the risk management process in the risk estimation step. We combine these results into the risk management space, adding an ordering to facilitate decision making based on the risk measurements. Several examples show how the process can be applied in practice and provide evidence for the use of the Wasserstein metric in a number of applications within a financial institution.