An Optimal Turkish Private Pension Plan with a Guarantee Feature

Abstract

The Turkish Private Pension System is an investment system which aims to generate income for future consumption. This is a volunteer system, and the contributions are held in individual portfolios. Therefore, management of the funds is an important issue for both the participants and the insurance company. In this study, we propose an optimal private pension plan with a guarantee feature that is based on Constant Proportion Portfolio Insurance (CPPI). We derive a closed form formula for the optimal strategy with the help of dynamic programming. Moreover, our model is evaluated with numerical examples, and we compare its performance by implementing a sensitivity analysis.

1. Introduction

The Turkish social security system has played a crucial role in daily social life for decades. The system basically guarantees the living standards of individuals after retirement, their health insurances and also protects the families in case of the death of insured individuals. However, sustainability of the system has not proven to be an easy task for governments. For instance, recently, a drawback has arisen in the system due to early retirement ages and the longevity problem. In order to overcome these problems, governments have taken some precautions and implemented some reforms, but, unfortunately, none of them were able to succeed. As a final precaution, a law numbered 5510 was accepted by the government on 30 April 2008. Depending on the relevant law, the retirement age has been gradually increased, and the income replacement rate has been reduced. Therefore, this has caused a discrepancy between current retirees and future retirees. In other words, in Turkey, the level of welfare of future retirees will not be as high as today’s retirees. This leads future retirees to look for additional funds in order to keep their living standards high by having additional refunds after retirement. The Turkish private pension plan is such an alternative. The system was initially proposed by the drafting of a law called the “Private Pension Savings and Investment System” on 16 May 2000. After the approval of the law on 28 March 2001, the private pension system came into operation on 27 October 2003. Today, almost all insurance companies have an additional section for private retirement.

The Turkish private pension plans’ structure is completely different than the Turkish social security system. In private pension plans, the retirement age is 56, and before retirement, participants have to be registered in the system at least for 10 years. The savings of participants are protected under the individual investment accounts, and, in addition, the participants have some rights to their accounts, which can be listed as follows [1]:

• The participant has the right to choose his/her amount of contribution; however, this amount can not be below the minimum amount of contribution which is determined by the retirement company;
• The participant can select one of the three pension funds that are specified by the law:

  • Money market funds including Liquid Government Funds, Liquid Private Sector Funds, Liquid Mixed Funds, other funds, etc;
  • Government/Private Sector/International debt instruments funds/precious metals/Index Funds;
  • Stocks/Other Funds: Stock funds, international stock funds, foreign country funds, sector funds, flexible funds, mixed funds, etc;
• The participant has the right to change the allocation of his/her own retirement fund among specified funds at most six times in a year;
• The participant has the right to change the pension plan at most four times in a year;
• The participant has the right to change the amount of contribution and has the right to suspend paying contribution. During the period of suspension, his/her account is protected, and, at any convenient time, he/she might continue contribution payments;
• The participant has the right to transfer his/her savings to another company if he/she is already in the system at least for two years;
• The participant has the right to quit the system.

On the other hand, some additional charges might be collected by the company. Once a participant is enrolled in the system, a registration fee is collected. Then, the company has the right to collect a fund management charge of at most 2% of the contributions. The company also has some rights to collect fund investment and performance charges that mostly depend on the selected pension fund.

It can be seen that the Turkish private pension system is somehow flexible, but, at the same time, there are some limitations on the pension fund management. The funds are pre-defined and fund allocations are done according to participant’s personal choices, hence the optimal allocation is currently not considered. Furthermore, the guarantee, which is an essential feature of a pension product, is not considered on a preferential basis. If we have a closer look at both the actuarial and financial economic literature for the last 15–20 years, we encounter many papers about the pension fund management. For example, Haberman and Sung [2] try to minimize the ‘solvency’ and ‘contribution rate’ risks in order to stabilize the pension fund, and Cairns et al. try to optimize the terminal utility gained from the pension fund with a stochastic interest rate [3]. Some other examples of the studies that deal with the optimal asset allocations for pension funds can be found in [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. On the other hand, there are limited numbers of studies that consider a target or a guaranteed wealth concept. Gerrard et al. aim to minimize the quadratic loss function for a specified target value of wealth [21]. Then, in 2006, Gerrard et al. consider an optimal allocation problem. They propose an optimal investment and consumption rate that minimizes the total expected loss from the target value [22]. Di-Giacinto et al. consider a similar loss minimization problem. They minimize the quadratic loss gained from the performance variable, which is defined as the optimal portfolio over the target benchmark portfolio [23]. Di-Giacinto et al. solve a portfolio selection problem with a minimum guarantee for a defined contribution pension fund [24]. Moreover, Gerrard et al. [19] study the problem of maximizing the expected utility of the difference between the terminal wealth and the fixed guarantee. In the relevant study, they assume a Black–Scholes market and consider a pension fund in which the premiums and withdrawals are constant.

The main aim of the present study is to propose an optimally allocated Turkish private pension plan with a guarantee feature to deal with the limitations of the Turkish private pension system. We focus on a problem that aims to generate a guarantee with the help of the constant proportion portfolio insurance (CPPI) strategy. In order to obtain an optimal strategy, dynamic programming provides a convenient framework.

The study proposes an optimal Turkish private pension plan with a guarantee feature. This can be effective to develop some new products in the sector. Additionally, the plan is an extended version of the study of Gerrard et al. [19], in which a linear function of wealth is modeled by a geometric Brownian motion, and the optimal multiplier is obtained accordingly (see also [25,26]).

The paper is organized as follows. In Section 2, we present the market setting. Then, we state the problem and derive a solution. The quality of the proposed pension plan is compared numerically with industry models. The results of the numerical study and a sensitivity analysis of our model are given in Section 3. We close with conclusions and outlooks.

2. Model Setting and Maximizing Utility

The Constant Proportion Portfolio Insurance is a popular strategy with a guarantee feature not only in practice but also in theory. It was firstly introduced by Black and Jones [27] and then followed by the early studies of Perold [28] and Black and Perold [29]. CPPI focuses on the decision of the risky investment, and that is what makes CPPI advantageous against the classical portfolio strategy.

In CPPI, two parameters are specified in advance, namely a constant multiplier, m and the guarantee (minimum acceptable level of the portfolio), called the floor. Then, the CPPI strategy is defined as follows:

$$m{C}_t=m\left(V_t-F_t\right),t\in \left[0,T\right],$$

(1)

where $V_t$ is the value (wealth) of the pension fund at time t, $F_t$ is the discounted value of the guarantee (floor), and $C_t$ is the Cushion process, which is defined as the difference between the value of the fund and guarantee at time t.

The CPPI was firstly implemented for modeling an individual Turkish private pension fund by Alp and Cekic in 2013 [30]. Referring to them, we assume that trading holds continuously and, in addition, we consider a Black–Scholes financial market, consisting of a riskless money market account, $B_t$ and a risky fund (could be one of the two risky private pension funds), $S_t$. In this setting, the market is driven by the processes as follows:

$$\begin{array}{ccc}\hfill d{B}_t& =& r{B}_{t}dt,B_0=b_0,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill d{S}_t& =& S_t\left(\mu dt+\sigma d{W}_t\right),S_0=s_0,\hfill \end{array}$$

(3)

where r denotes the risk free interest rate, W is a one dimensional Brownian motion, μ, and σ are the constant drift and volatility parameters, respectively.

We assume that the participant wants the value of his/her pension fund to be at least $F_T$ at the end of T years of payment, which is known as maturity. In order to reduce the complexity of the setting, the mortality before the age $x+T$ is omitted. In addition, we also assume that the contribution over the payment period is fixed and denoted by p, and, after all the charges are deducted from the contribution, the remaining part is invested in a CPPI type portfolio. Then, the wealth process of the participant’s pension fund can be written as follows [30]:

$$d{V}_t=(1-c_1)pdt+m{C}_t\frac{d{S}_t}{S_t}+\left(V_t-m{C}_t\right)\frac{d{B}_t}{B_t}-c_2{V}_{t}dt,$$

(4)

where p the instantaneous contribution at time t, $c_1$ is the instantaneous fund management charges collected by the company, and similarly, $c_2$ is the instantaneous fund investment charges that is deducted from the total value of the fund.

In the present study, we assume that the participant’s main problem here is to estimate the value of the multiplier, m, of the CPPI portfolio. For this purpose, we will introduce a pension fund allocation problem where the multiplier is selected optimally. We consider the portfolio problem in which the aim is to maximize the participant’s utility obtained from the cushion at maturity T referring to [19,25,26].

$$\begin{array}{cc}\hfill \underset{m\in \mathrm{\Theta }(v,t)}{max}& E\left[\frac{{\left(V_T-F_T\right)}^{1-\gamma }}{1-\gamma }\right],\hfill \\ \hfill \mathrm{subject}\mathrm{to}& d{V}_t=(1-c_1)pdt+(r-c_2)V_{t}dt\hfill \\ & +m\left(V_t-F_t\right)\left((\mu -r)dt+\sigma d{W}_t\right),t\in \left[0,T\right],\hfill \end{array}$$

(5)

where $\mathrm{\Theta }\left(v,t\right)$ denotes the set of all admissible portfolio strategies at time $t\in [0,T]$ when value of pension fund at time t is $V_t=v$. In the present study, we assume that initial value of the participant’s pension fund is his/her first contribution, i.e., $V_0=p$.

In order to make the notation simpler, we consider that ${\tilde{V}}_t=e^{-\left(r-c_2\right)t}{V}_t$ and ${\tilde{F}}_t=e^{-\left(r-c_2\right)t}{F}_t$. Then, the portfolio Problem (5) is equivalent to the following problem

$$\begin{array}{cc}\hfill \underset{m\in \mathrm{\Theta }(\tilde{v},t)}{max}& e^{\frac{\left(r-c_2\right)T}{1-\gamma }}E\left[\frac{{\left({\tilde{V}}_T-{\tilde{F}}_T\right)}^{1-\gamma }}{1-\gamma }\right],\hfill \\ \hfill \mathrm{subject}\mathrm{to}& d{\tilde{V}}_t=(1-c_1)p{e}^{-\left(r-c_2\right)t}dt\hfill \\ & +m({\tilde{V}}_t-{\tilde{F}}_t)\left((\mu -r)dt+\sigma d{W}_t\right),\hfill \end{array}$$

(6)

where ${\tilde{V}}_t=\tilde{v}$.

We denote the value function of the Problem (6) as $\varphi (\tilde{v},t)$. Then, it can be written as follows:

$$\varphi \left(\tilde{v},t\right)=\underset{m\in \mathrm{\Theta }(\tilde{v},t)}{sup}{E}^{t,\tilde{v}}\left[e^{\frac{\left(r-c_2\right)T}{1-\gamma }}\frac{{(\tilde{v}-{\tilde{F}}_T)}^{1-\gamma }}{1-\gamma }\right],$$

(7)

where $\mathrm{\Theta }\left(\tilde{v},t\right)$ denotes the set of all admissible portfolio strategies starting at time t with a wealth of $\tilde{v}$. Moreover, $E^{t,\tilde{v}}$ denotes the conditional expectation when the wealth process satisfies ${\tilde{V}}_t=v$ at time t.

The Hamilton-Jacobi-Bellmann(HJB) equation of the problem is then obtained as follows:

$$\begin{array}{ccc}\hfill 0& =& \frac{\partial \varphi }{\partial t}+\underset{m}{max}[{\varphi }_{\tilde{v}}\left(m(\tilde{v}-\tilde{f})\left(\mu -r\right)+e^{-\left(r-c_2\right)t}\left(1-c_1\right)p\right)\hfill \\ \hfill & & +\frac{1}{2}{\varphi }_{\tilde{v}\tilde{v}}{m}^2{(\tilde{v}-\tilde{f})}^2{\sigma }^2],\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill \varphi \left(\tilde{v},T\right)& =& e^{\frac{\left(r-c_2\right)T}{1-\gamma }}\frac{{(\tilde{v}-{\tilde{F}}_T)}^{1-\gamma }}{1-\gamma },\hfill \end{array}$$

(9)

where $\varphi \left(\tilde{v},T\right)$ is the final condition.

The first order optimality conditions imply that a candidate for the optimal leverage is given

$$m^{*}=-\frac{\mu -r}{{\sigma }^2}\frac{1}{\tilde{v}-\tilde{f}}\frac{{\varphi }_{\tilde{v}}}{{\varphi }_{\tilde{v}\tilde{v}}}.$$

(10)

Plugging (10) into the HJB-equation given in Equation (8), we obtain a non-linear partial differential equation (PDE)

$$0=\frac{\partial \varphi }{\partial t}+{\varphi }_{\tilde{v}}{e}^{-\left(r-c_2\right)t}\left(1-c_1\right)p-\frac{1}{2}\frac{{\left(\mu -r\right)}^2}{{\sigma }^2}\frac{{\left({\varphi }_{\tilde{v}}\right)}^2}{{\varphi }_{\tilde{v}\tilde{v}}},$$

(11)

for which the terminal condition is given by Equation (9). The Equation (11) can be expressed in a linear form by applying the Legendre transform as given in [31] and [32].

For the Legendre transform, we firstly introduce a dual variable $z>0$ to $\tilde{v}$ via the following equation:

$$\widehat{\varphi }(z,t):=\underset{\tilde{v}}{sup}\left\{\varphi (\tilde{v},t)-z\tilde{v}|\tilde{x}>0,t\in (0,T)\right\}.$$

(12)

We define the function $g(t,z)$ for the value of $\tilde{v}$ at the optimum,

$$g(z,t):=\underset{\tilde{v}}{inf}\{\tilde{v}|\varphi (t,\tilde{v})\ge \widehat{\varphi }(t,z)+z\tilde{v},t\in (0,T)\}.$$

(13)

Then, by plugging Equation (13) into Equation (12), we obtain

$$\widehat{\varphi }(z,t)=\varphi (g,t)-zg.$$

(14)

From Equation (14), we obtain the relation between g and φ as follows:

$$g=-{\widehat{\varphi }}_z.$$

(15)

Furthermore, under the assumption of φ being strictly concave and smooth in $\tilde{v}$, we have

$${\varphi }_{\tilde{v}}\left(g(z,t),t\right)=z\mathrm{or}\mathrm{equivalently}g={\varphi }_{\tilde{v}}^{-1}.$$

(16)

If we differentiate the function φ with respect to $\tilde{v}$ and t, we obtain

$${\varphi }_{t,\tilde{v}}=-\frac{g_t}{g_z}{\varphi }_{\tilde{v}\tilde{v}}=\frac{1}{g_z}{\varphi }_{\tilde{v}\tilde{v}\tilde{v}}=-\frac{g_{zz}}{g_z^3}.$$

(17)

Now, if we differentiate Equation (11) with respect to $\tilde{v}$ and substitute the partial derivatives with those we obtained above, and then we transform the non-linear PDE in Equation (11) to a linear form as follows:

$$\begin{array}{ccc}\hfill 0& =& g_t+\frac{{\left(\mu -r\right)}^2}{{\sigma }^2}z{g}_z+\frac{{\left(\mu -r\right)}^2}{2{\sigma }^2}{z}^2{g}_{zz}-e^{-\left(r-c\right)t}\left(1-\nu \right)p,\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill g(z,T)& =& e^{-\left(r-c\right)T}{F}_T+z^{-1/\gamma }{e}^{\frac{\left(r-c\right)T}{\gamma \left(1-\gamma \right)}}.\hfill \end{array}$$

(19)

The solution of the transformed problem is given in Proposition 1.

Proposition 1. 

The explicit analytical (closed-form) solution to the HJB-Equation (18), with a final Condition (19) is given by

$$\begin{array}{ccc}\hfill g(t,z)& =& {\tilde{F}}_T+z^{-1/\gamma }{e}^{\frac{\left(r-c_2\right)T}{\gamma \left(1-\gamma \right)}}{e}^{\frac{1-\gamma }{{\gamma }^2}\left(\frac{{\left(\mu -r\right)}^2}{2{\sigma }^2}\right)\left(T-t\right)}\hfill \\ & +& \frac{\left(1-c_1\right)p}{r-c_2}\left(e^{-\left(r-c_2\right)T}-e^{-\left(r-c_2\right)t}\right).\hfill \end{array}$$

(20)

Finally, the optimal multiplier at time t is therefore given in the following corollary.

Corollary 2. 

The optimal multiplier m for the Problem (5) is given as

$$m^{*}=\frac{1}{\gamma }\frac{\mu -r}{{\sigma }^2}\frac{1}{V_t-F_t}\left[\left(V_t-e^{-\left(r-c_2\right)\left(T-t\right)}{F}_T\right)+\phi \left(t\right)\right],$$

(21)

where

$$\phi \left(t\right)=\frac{\left(1-c_1\right)p}{r-c_2}\left(1-e^{-\left(r-c_2\right)\left(T-t\right)}\right).$$

Here, we obtain the optimal strategy that is not in the classical form of CPPI given in Equation (1). The amount invested in the risky stock is positive whenever the inequality $V_t>K_t=e^{-\left(r-c\right)\left(T-t\right)}{F}_T-\phi \left(t\right)$ is preserved. Otherwise, the strategy becomes a shortselling one. In addition, the optimal strategy exactly consists of two terms. The first term can be converted to the the classical form of CPPI (look Remark 1 and Remark 2) and the second term, $\phi \left(t\right)$, is a correction term that compensates the effects of charges.

Remark 1. 

Special Case of the Model as a classical CPPI Strategy

If we assume that $p=c_1=c_2=0$ (i.e., no contribution, no charges) and $F_t$ satisfies the equality $F_t=e^{-r(T-t)}{F}_T$, where $F_T$ is a constant guarantee, then the optimal m turns to

$$m^{*}=\frac{1}{\gamma }\frac{\mu -r}{{\sigma }^2}.$$

This optimal multiplier coincides with the optimal multiplier in the classical CPPI stated in [25] and [26], in which the portfolio is a self-financing one.

Remark 2. 

Special Case of the Model as a classical CPDO Strategy

The Constant Proportion Debt Obligations (CPDO) is a form of the portfolio based strategies. CPDO strategy offers a rate of return over the London Interbank Offered Rate (LIBOR), and, for this purpose, it follows a strategy which is called leverage. The leverage is the inverse of the CPPI multiplier (i.e., shortselling strategy).

As a special case after some assumptions and reorganizations of the parameters, the standard form of the optimal leverage stated in [31], and [33] can be obtained. The stated strategies are not self-financing and liabilities (similar to the guarantee in CPPI) can be achieved only by shortselling.

3. Application

In this section, we compare the pension fund of our optimal strategy with the strategies used in industry by considering some real-life applications. Additionally, we illustrate the sensitivity of some characteristic features corresponding to our hedging strategy of the private pension plan via some numerical examples. Finally, we analyze how the optimal strategy depends on the value of the volatility of the risky fund, σ, and the risk-aversion parameter γ.

In Turkey, the monthly minimum contribution offered by the companies is, on average, 100 Turkish Liras (TL). Moreover, the average amount of charges that are collected by the companies can be listed as follows:

• Fund management charge—$2\%$ of the monthly contribution ($0.0645\%$ on a daily basis);
• Total fund investment charges—annually $2.25\%$ of the fund’s total fund value ($0.00617\%$ on a daily basis).

In order to make the private pension system more attractive, the government has given a promotion that is exactly equal to $25\%$ of the monthly contribution. However, this government promotion is invested in a separate fund which is under the control of the government. Therefore, our analysis does not consider this promotion as a part of the contribution.

In the application, we use a daily time scale, and we assume that the monthly contribution is the minimum (i.e., 100 TL). For this reason, we consider the corresponding daily amounts of contribution and charges such that $p=3.225$, $\nu =0.000645$ and $c=0.0000617$, respectively. We also choose values for the interest rate, r, and the maturity, T such that they represent the market well:

$$r=0.0002916,T=10.$$

Suppose that a participant wants to earn a minimum interest to his/her contributions, we denote it with $r_{min}$. Then, at any time $t\in [0,T]$, the value of the guarantee can be written as follows:

$$F_t=\frac{p}{r_{min}}(e^{r_{min}t}-1).$$

3.1. Comparison of Optimal Strategy with the Strategies Used in Industry

In this part, we implement a simulation study with 10,000 simulations, and we compare our optimal strategy with the strategies used in the private pension fund industry by considering the parameters described above. The most widely used industry strategies are as follows:

• Domestic government bond based pension fund (GBF): on average include $80\%$ of the government bonds, $15\%$ of other riskless instruments and $5\%$ of risky stocks (totally $95\%$ of riskless assets);
• Stock based pension fund (SBF): on average include $80\%$ of stocks and $20\%$ of other riskless instruments.

Here, we consider two different scenarios for risky funds (i.e., according to return distributions of the private pension funds.). These are described as less and more risky regarding the parameters in which $\mu =0.0004049$ and $\sigma =0.015,0.025$, respectively. In the analysis, we follow a performance measurement methodology similar to the methodology (PM) stated in [34]. PM aims to compare the strategies with different risk profiles. In PM, the risk equivalent benchmark strategy of the corresponding strategy is searched for, and then the internal returns of these two strategies are compared [19,35]. For this purpose, we follow the procedure as follows:

• The values of pension funds at maturity, $V_T$ for the GBF and SBF strategies are simulated;
• $V_T$ values under optimal strategy are simulated for various $r_{min}/\mathrm{year}\in [-1,0.45]$, and the volatilities are calculated;
• Then, the risk equivalent benchmark optimal strategy of the corresponding strategy is determined;
• The internal returns $(r^{int})$ of the strategies for mean, $E\left(V_T\right)$ and median value of the pension fund at maturity are calculated;
• Finally, the comparison is done.

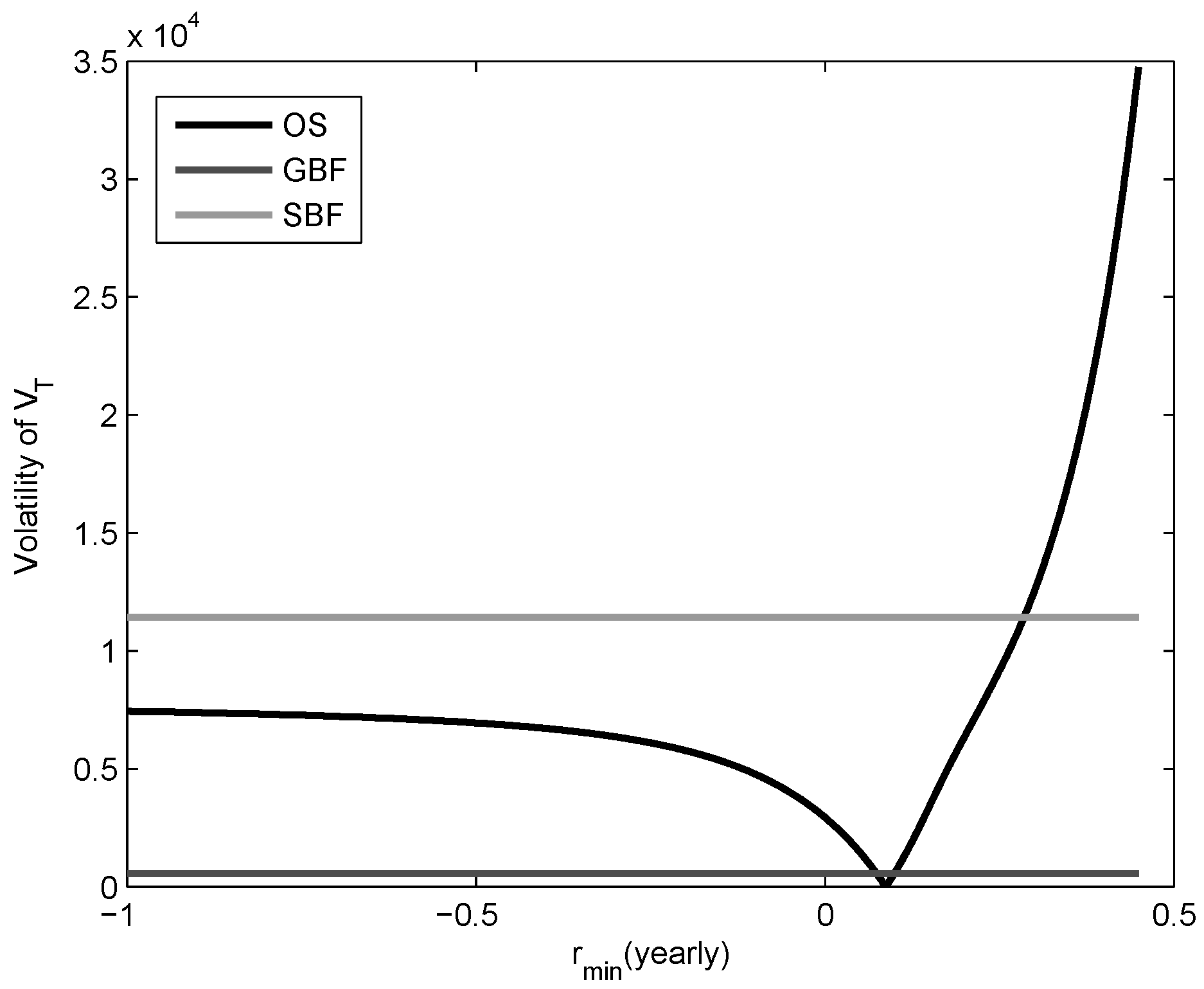
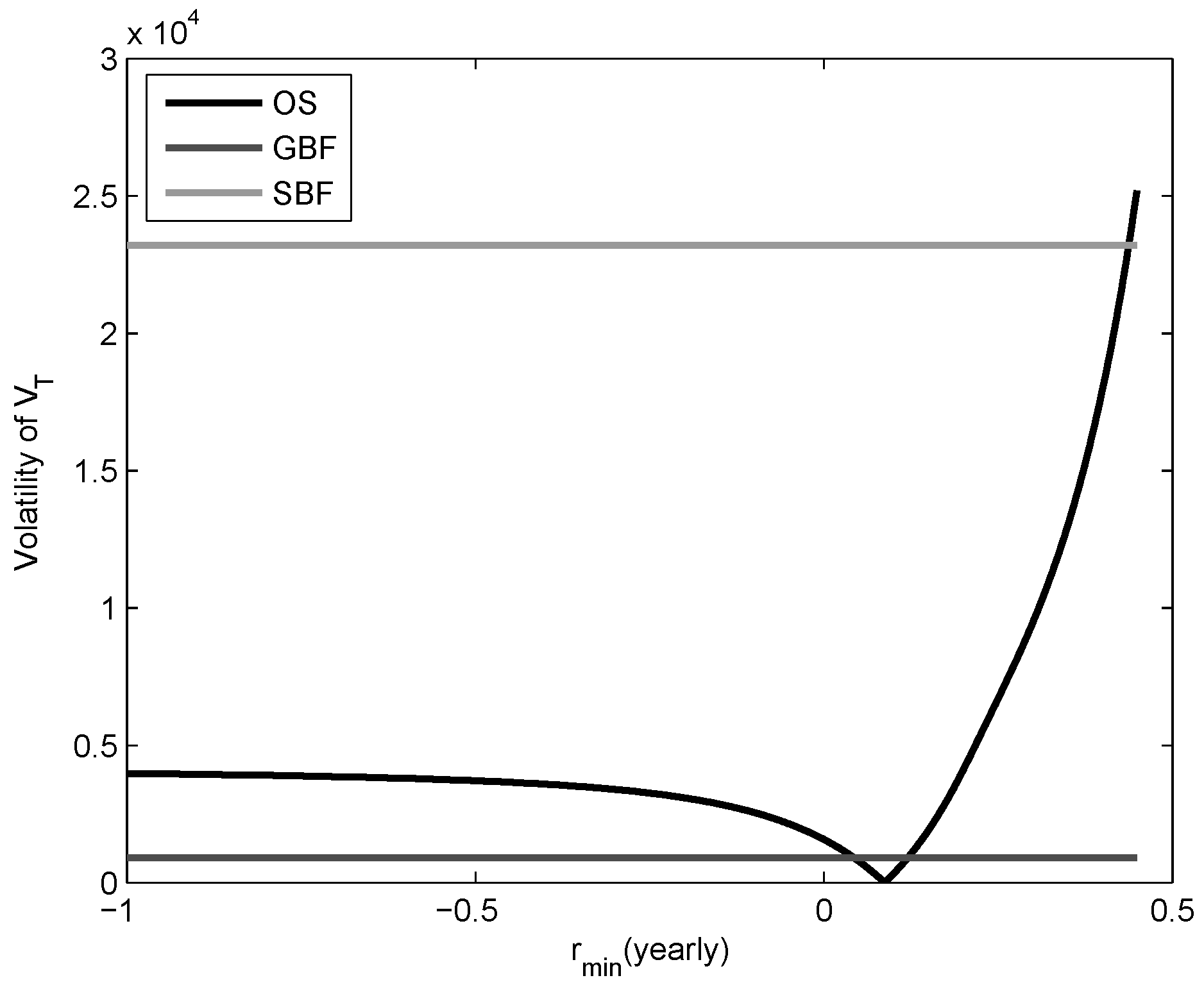
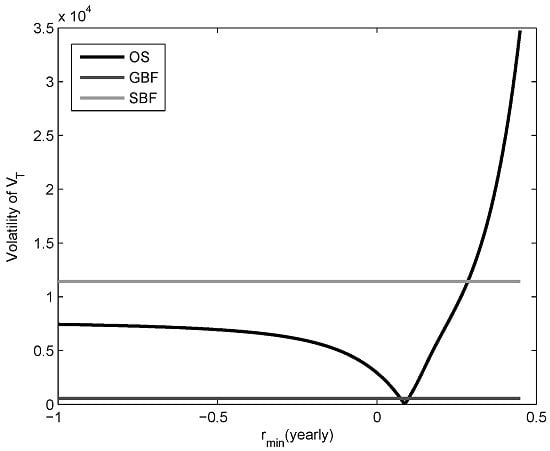
Based on the 10,000 independent simulations, Figure 1 and Figure 2 show the evolution of the volatility of the pension fund at maturity (i.e., ${\sigma }_{V_T}$) under the optimal strategy and the minimum rate of guarantee, $r_{min}$ when $\sigma =0.015$ and $\sigma =0.025$, respectively. We can see that the volatility decreases until $r_{min}$ reaches the value $r_{min}=0.087/$ year, and then begins to increase again. However, if we decrease the desired minimum level of guarantee, then the increase in volatility begins to fall down and stabilizes. This is an interesting result because even though the minimum volatilities of the optimal pension fund is very low for both cases (i.e., ${\sigma }_{V_T}^{min}=2.1022$ and ${\sigma }_{V_T}^{min}=1.1486$), the desired guarantees $F_T$ are reached. In addition, under the optimal strategy assumption, some volatilities are attainable for two different values of $r_{min}$, but, indeed, these two optimal funds have different mean values at maturity. This shows that the mean value of the pension fund has an inverse relation with the minimum rate of guarantee. Therefore, our optimal strategy becomes either an efficient or an inefficient pension fund depending on the guarantee level. Namely, optimal strategy is inefficient for higher values of the minimum rate of guarantee and vice versa. On behalf of these, we can see that the equivalent optimal strategy for SBF is inefficient, and an efficient risk equivalent optimal strategy for SBF is not attainable.

Table 1. Internal return of Domestic Government Based Fund(GBF), Stock Based Fund(SBF) and Equivalent Optimal Strategy(OS) based on mean and median final value of the pension funds at maturity (fixed $r_{min}$ and $\sigma =0.015$).

			Mean		Median
Portfolio	${\mathit{\sigma }}_{{\mathit{V}}_{\mathit{T}}}$	${\mathit{r}}_{\mathit{min}}$ (Corresponding ${\mathit{F}}_{\mathit{T}}$ )	${\mathit{r}}_{\mathit{int}}$	${\mathit{r}}_{\mathit{int}}^{\mathit{OS}}$	${\mathit{r}}_{\mathit{int}}$	${\mathit{r}}_{\mathit{int}}^{\mathit{OS}}$
GBF	550	2.0327$\times {10}^{-4}$ and 2.7027$\times {10}^{-4}$ (17,452 and 20,068)	0.0888	0.0888 and 0.0851	0.0887	0.0880 and 0.0859
SBF	11423	3.0227$\times {10}^{-4}$ (21,489)	0.1166	0.0831	0.0944	0.0848

and

Table 2. Internal return of Domestic Government Based Fund(GBF), Stock Based Fund(SBF) and Equivalent Optimal Strategy (OS) based on mean and median value of the pension funds at maturity (fixed $r_{min}$ and $\sigma =0.025$).

			Mean		Median
Portfolio	${\mathit{\sigma }}_{{\mathit{V}}_{\mathit{T}}}$	${\mathit{r}}_{\mathit{min}}$ (Corresponding ${\mathit{F}}_{\mathit{T}}$ )	${\mathit{r}}_{\mathit{int}}$	${\mathit{r}}_{\mathit{int}}^{\mathit{OS}}$	${\mathit{r}}_{\mathit{int}}$	${\mathit{r}}_{\mathit{int}}^{\mathit{OS}}$
GBF	915	1.1727$\times {10}^{-4}$ and 3.3027$\times {10}^{-4}$ (14,692 and 22,834)	0.0888	0.0890 and 0.0850	0.0885	0.0882 and 0.0858
SBF	23197	1.1970$\times {10}^{-4}$ (21,0231)	0.1168	0.1926	0.0556	0.1807

show internal returns of GBF and SBF and their risk equivalent optimal strategies when $\sigma =0.015$ and $\sigma =0.025$, respectively. For $\sigma =0.015$, the efficient equivalent optimal strategy and the corresponding GBF perform nearly the same for both mean and median values of pension funds at maturity. However, the equivalent optimal strategy outperforms the SBF. On the other hand, when $\sigma =0.025$, the performances of the GBF and its equivalent optimal strategy are nearly the same, but the equivalent optimal strategy of SBF performs better. The internal return of the SBF is very small when the median value of pension fund is considered. This shows that when volatility of the risky fund increases, then the distribution of SBF’s return becomes more skewed, and this may cause participants to earn lower than risk free rates.

3.2. Sensitivity of Some Characteristic Features

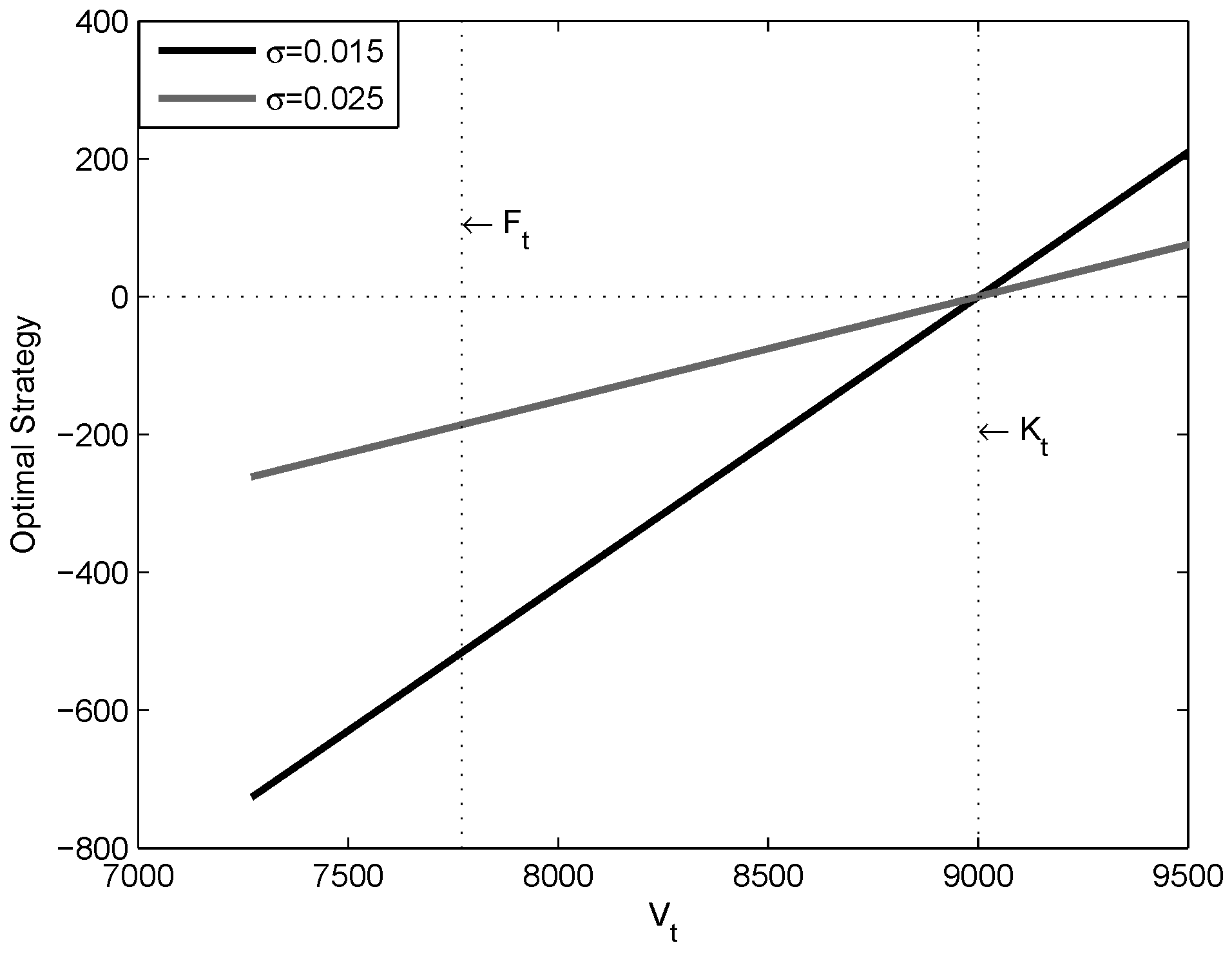
In this part of the paper, we firstly implement a sensitivity analysis to the optimal strategy with respect to the volatility of the pension fund. To achieve this goal, we consider two different risky funds described previously (i.e., $\mu =0.0004049$ and $\sigma =0.015,0.025$).

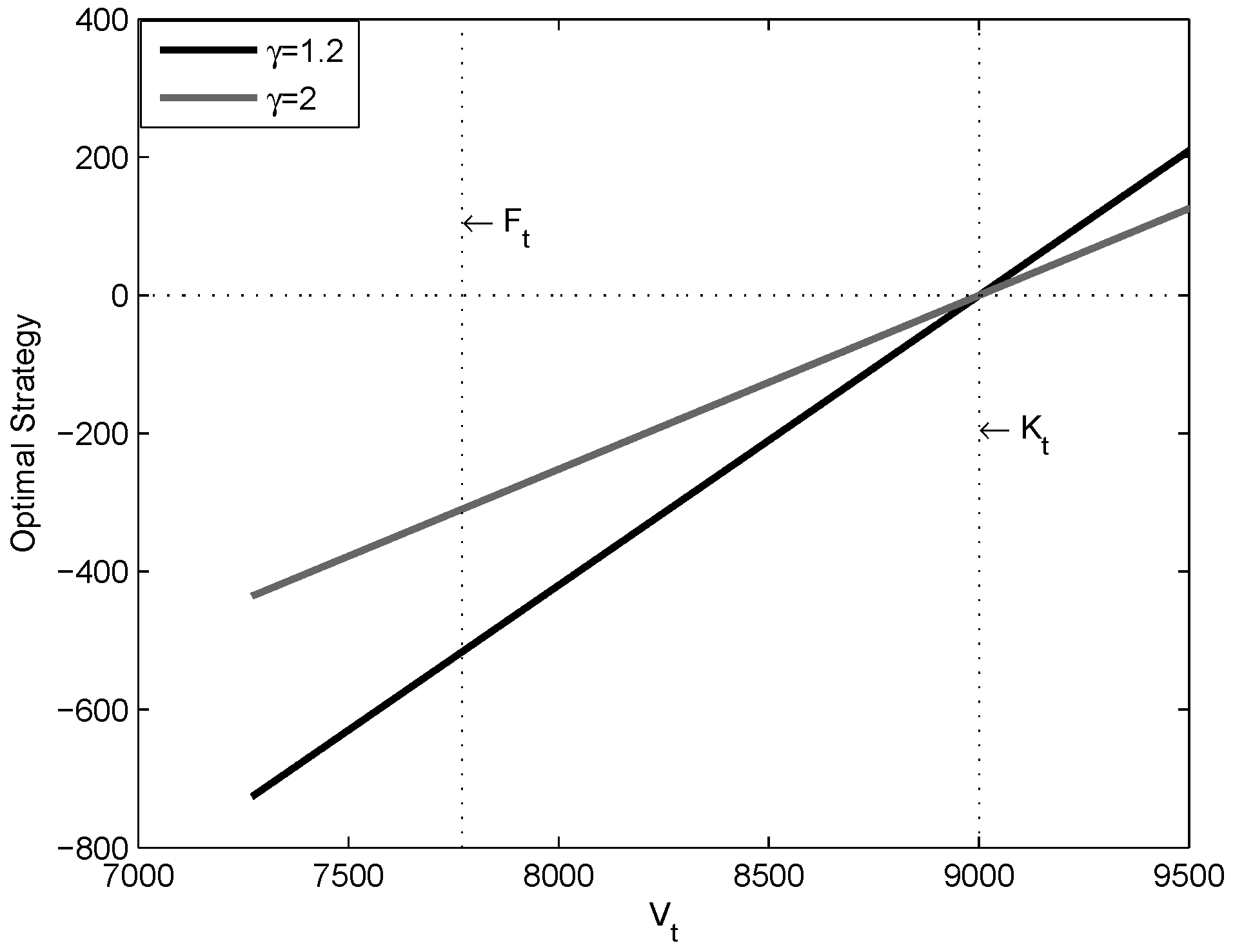
Figure 3 shows how the optimal multiplier evolves by the change of the values of the pension fund for less and more volatility levels. Figure 3 matches with our expectations. The optimal multiplier takes positive values when the value of pension fund decreases. On the contrary, the optimal multiplier takes negative values for the higher values of pension funds. If we consider the optimal strategy, then it can be seen in Figure 4 that the optimal strategy always remains negative for values of $V_t$ that are smaller than the $K_t$ ($F_T\approx 21,001.4860251$).

Interestingly, for very low (the gap between the guarantee and fund is the maximum) and very high values of pension funds (the guarantee has already been satisfied), optimal multiplier approaches 0, although the optimal strategy does not approach 0. The risky investment is closed only when $V_t=K_t$. Accordingly, once the volatility attains higher values, the optimal strategy follows a more preserving path.

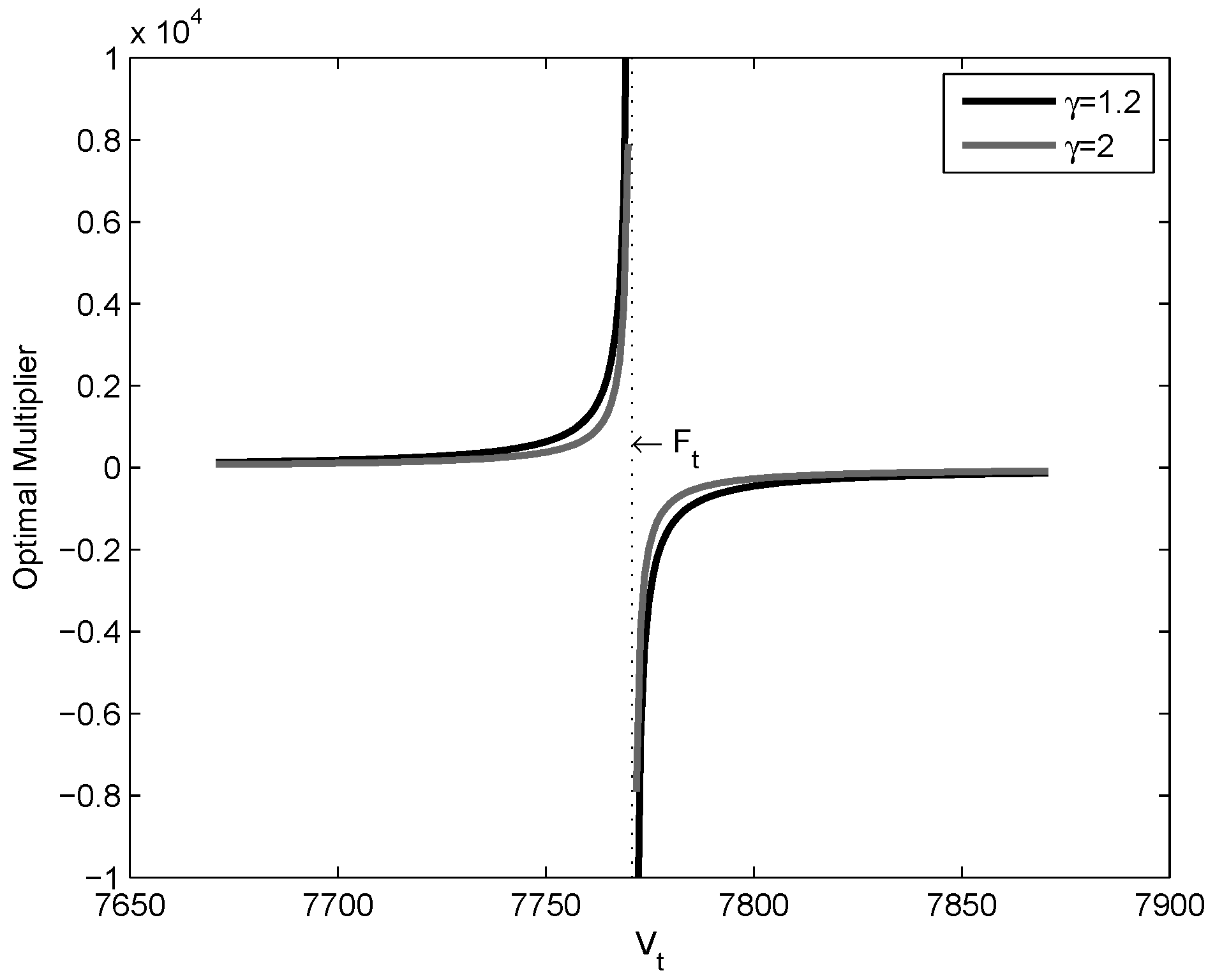
As a second sensitivity analysis, we consider the optimal multiplier versus the risk aversion parameter γ. We take two different values of $\gamma =1.2$ and $\gamma =2$. Figure 5 and Figure 6 show how the optimal multiplier and optimal strategy evolve for different levels of risk aversion, respectively. Higher values of γ correspond to higher risk aversion for participants. From Figure 5 and Figure 6, it can be seen that if a participant is more risk averse, then the optimal strategy becomes more protective.

4. Conclusions

In this paper, we considered an alternative Turkish private pension fund with a guarantee feature. We proposed an asset allocation problem that minimizes the utility gained from the shortfall between the value of the pension fund and the guarantee at maturity. The main motivation of this paper is to use CPPI strategy in the investment instead of the constant proportion strategy. We obtained a completely explicit analytical solution of the optimal strategy in a Black–Scholes market setting by using a dynamic programming approach. The optimal strategy is not a CPPI type used in the industry (which is constant). The proposed optimal multiplier is time-dependent and has an additional part which compensates for charges.

In the analysis, we used stochastic simulations to compare the optimal strategy with the strategies used in the industry. We applied a performance measurement strategy that is based on the risk equivalent benchmark strategies. The results show that the optimal strategy has an efficient and inefficient boundary. When the minimum rate of guarantee decreases, the internal return of our proposed strategy grows and the fund volatility stabilizes. In addition, the proposed strategy performs better when the market contains more risk. Especially, for more risky markets, if a participant holds a stock based fund, then it would not be possible to earn a riskless rate.

We also examined the sensitivity of our proposed strategy with respect to the volatility and the risk aversion level. The optimal multiplier of the proposed strategy seems to show different characteristics on different sides of the present value of the guarantee, $F_t$. On the other hand, the optimal strategy is increasing in accordance with the value of the pension fund and attains some positive values only after some high level of the pension fund is reached.

As a conclusion, we can say that, in the paper, a set of simplifying assumptions for the dynamics of the market are made. Therefore, the results could be considered limited. The proposed model can be extended by a stochastic interest rate, mortality before maturity, etc. However, one has to check whether these extensions have closed form solutions. Future work will examine these extensions.