Multi-Objective Stochastic Optimization Programs for a Non-Life Insurance Company under Solvency Constraints

Abstract

In the paper, we introduce a multi-objective scenario-based optimization approach for chance-constrained portfolio selection problems. More specifically, a modified version of the normal constraint method is implemented with a global solver in order to generate a dotted approximation of the Pareto frontier for bi- and tri-objective programming problems. Numerical experiments are carried out on a set of portfolios to be optimized for an EU-based non-life insurance company. Both performance indicators and risk measures are managed as objectives. Results show that this procedure is effective and readily applicable to achieve suitable risk-reward tradeoff analysis.

1. Introduction

One of the most important aims in the insurance industry is to manage risk and capital properly. The first attempt in connecting solvency requirements to risk measures relies on the investment of a minimum capital required into a single security, often considered as a risk-free asset. However, this choice has been proven to be non-optimal, whereas the investment in multiple traded assets results in being the correct alternative (see, for instance, [1] for an example and [2] for a theoretical introduction). In this process, the choices of the solvency margin and of the optimal portfolio are treated separately. Only in recent years, actuarial research has begun to focus on optimization problems involving both solvency capital and portfolio weights as decision variables. The first example of this interest is represented by [3], where the maximization of the expected return on risk-adjusted capital is subject to a conditional value-at-risk constraint. Similarly, in [4], the capital requirement is minimized on the basis of both a ruin probability constraint and a return-on-capital constraint. A dynamic improvement of this approach is provided in [5], where the portfolio optimization is analyzed under three different solvency regimes.

This new strand of research may be placed in the more general field of portfolio selection problems where an investor utility function is maximized in order to identify the optimal portfolio (see [6] for a treatment of contemporary applications of the standard portfolio selection framework, while [7] for an introduction to asset and liability management). All of these papers model the portfolio selection procedure as a single-objective optimization process in which both the constraints due to policyholders and stakeholders are taken into account in order to optimize allocations. At the same time, the classical reward-to-risk analysis carried out on the first two moments of the loss-profit distribution or on quantile-based risk measures may result in being insufficient to provide a complete characterization of the optimal portfolio, because of being unable to capture all of the aspects of stakeholders’ utility function and the liability distribution of the insurer (see [8] for an introduction to reward-to-risk analysis in portfolio optimization). Therefore, a multiple objective approach may be advisable in order to capture all of these complexities [9]. In the literature, there are several ways to implement procedures from multiple criteria optimization into portfolio selection in order to better serve the needs of both institutional investors and shareholders [10]. The main goal is to represent the Pareto front and, more specifically, to guarantee a satisfactory balance between convergence to optimal solutions and diversity among points on the efficient frontier. There are several algorithms that may be implemented to this end, and a preliminary review needs to be done. A classification useful for our purposes has been provided by [11], according to which we can distinguish between classical methods, which use direct or gradient-based procedures following some mathematical or geometrical principles, and non-classical methods, which are inspired by biological or physical principles. To the first category belongs, for instance, the ϵ-constraint method that reformulates a multi-objective problem into a single-objective one by converting all, but one of the objectives to constraints with the corresponding right-hand sides set to target values at the discretion of the user. An interesting application is provided by [12], who proposes a mean-risk model with a portfolio expected value, variance and conditional value-at-risk (CVAR) as optimization criteria. The motivation for extending the standard Markowitz mean-variance analysis by including two risk measures is that there may be an improvement in the solution when a mean-variance-efficient portfolio has an excessively large CVAR or a mean-CVAR-efficient portfolio has an excessively large variance. A promising variant on the subject is represented by the approach developed in [13], where the risk aversion, prudence, temperance and other higher-order risk characteristics of investors are handled in the multidimensional single-period portfolio optimization. A shortage function is defined in this case that looks for possible increases in odd moments and decreases in even moments. The method ensures sufficient conditions for global optimality. In [14], the authors compare polynomial goal programming with the shortage function method in constructing mean-variance-skewness portfolios.

Besides the ϵ-constraint method, the weighted sum method is probably the best known technique to solve multi-criteria optimization problems. As the name suggests, the original multi-objective problem is transformed into a single-objective problem, where the function to optimize is an aggregation of the criteria, with weights provided at the discretion of the user. This procedure has been used in [15], where the authors propose a four-objective portfolio selection problem where an entropy measure is added to the mean, variance and skewness in order to include explicitly the diversification into portfolio optimization. A complete introduction to this classical type of methods and conditions guaranteeing Pareto optimality can be found in [16] and in [17], respectively.

Among the non-classical methods, the multi-objective evolutionary algorithms (MOEAs) seem to be the most important, since they represent a promising tool for complex real-world optimization problems. In general, they attempt to find multiple Pareto optimal solutions in a single run by considering a set of potential candidate solutions that form the so-called initial population. A selection operator based on Pareto domination and a reproduction operator are used iteratively to evolve the population towards the Pareto optimal front. A procedure that has been extensively analyzed in the evolutionary computing literature is the non-dominated sorting genetic algorithm-II (NSGA-II [18]). It builds a population of competing individuals and sorts them with a non-dominated sorting procedure, which results in all of the chromosomes being assigned a rank. The selection that follows uses the crowded tournament strategy. Crossover and mutation are then applied to create a new pool of offspring, which are combined with parents, before partitioning the enlarged pool into fronts. Elitism is then conducted by adding a crowding distance to each member to generate the next population. This ensures diversity in the population and helps the algorithm to explore the fitness landscape. The chromosomes in the first front of the final population constitute the set of solutions. A recent application in the financial area is given by [19], who proposes a method to generate technical trading systems for stock timing by selecting the most informative signals by means of a variant of the NSGA-II with variable string length coding. A novel multi-objective optimization algorithm, called DEMPO, has been developed by [20] to solve mean-variance, mean-expected shortfall and mean-value-at-risk portfolio optimization problems with real-world constraints. The algorithm integrates the differential evolution principle with the paradigms of the NSGA-II. The work in [21] proposes a variant of the multi-objective particle swarm optimization algorithm based on non-dominated sorting and compares its performance to those of the four other MOEAs. They solved a set of mean-variance problems with budget, floor, ceiling and cardinality constraints. This approach is capable of identifying good Pareto optimal solutions, maintaining adequate diversity.

An example of a procedure that combines classical and evolutionary methods is described in [22]. The authors integrate an NBI-style Tchebycheff approach in the decomposition phase of a standard MOEA/D [23]. A portfolio management problem represented by a mean-variance optimization with cardinality constraints and transaction costs is considered to test the effectiveness of the algorithm. Experiments on real data show very promising results.

In the actuarial context, the study conducted in [24] represents a first attempt to analyze and compare the capabilities of genetic programming and the particle swarm algorithm to find optimal solutions with respect to inspection algorithms for reinsurance problems (see also [25] for a precise definition). They concluded that the evolutionary algorithms are excellent options to find good solutions in short computation times. A multi-objective framework for EU-based non-life insurance companies is developed in [26] in order to find the best asset allocation that maximizes simultaneously expected utility and technical efficiency. In this manner, it is possible to consider both shareholders’, as well as customers’ objectives. The optimization is performed by integrating a simulation model into a multi-objective particle swarm optimization algorithm.

For a detailed exposition of other methods and algorithms in the MOEA literature, the interested read may consult [27,28], while for a complete survey on portfolio management and economics applications, he/she may refer to [29,30].

According to these findings, we aim at introducing a flexible and efficient multi-objective simulation-based optimization framework to better represent the tradeoff between portfolio performance and risks associated with both assets and liabilities for a non-life insurance company under the Solvency II Directive. More precisely, we propose to use a Pareto frontier-generating algorithm in the category of classical methods, called the normal constraint optimization method (NC) [31], to transform multi-objective portfolio problems into single-objective ones by means of a sequential reduction of the feasible space by hyperplanes passing through particular points on the plane spanned by individual function minimizers, the so-called utopia hyperplane. Thus, multi-objective strategies for portfolio selection may be handled as standard stochastic programs with continuous variables. We employ the sample path method, also called the sample average approximation method or the stochastic counterpart method, in order to solve this type of optimization problem. The procedure consists of replacing the original stochastic problem with its sampling approximation and of applying the deterministic optimization techniques to solve the modified problem (see, for example, [32,33] for a detailed treatment of the subject). In our context, we propose to estimate the objectives by combining the semiparametric approach recently proposed by [4] with the GARCH-extreme value theory (EVT)-Copula model in order to reduce the number of simulated scenario and to capture the dependence tail structure of asset return distributions more satisfactorily than traditional multivariate GARCH models and Copula-based models (the interested reader may refer to [34] for an introduction to the subject and to [35,36] for other applications in portfolio optimization).

From a theoretical point of view, to the best of our knowledge, this is the first attempt to develop a general multi-objective scheme that hybridizes the normal constraint method with a global single-objective optimizer in order to solve multi-objective stochastic optimization problems with chance constraints. From an empirical point of view, we furthermore provide a detailed comparison of several standard insurance and financial reward-to-risk portfolio performance measures and analyze how these criteria impact the portfolio selection process. To this end, three portfolio optimization strategies are developed. The first focuses exclusively on the shareholders’ objectives of obtaining maximum profits with minimum capital invested. The second extends the standard reward-to-risk analysis by considering as objectives the expected return on risk-adjusted capital and two risk measures. The last strategy point out the interactions among three performance indicators that usually characterize an insurance company, i.e., expected return on capital, expected return on risk-adjusted capital and the Sharpe ratio.

The paper is organized as follows. Section 2 provides an introduction to risk measures, performance indicators and regulatory constraints that characterize an EU-based non-life insurance company. Moreover, three stochastic programming problems that integrate at different levels both financial and insurance criteria are also described. The multi-objective optimization procedure is explained in Section 3. Whereas Section 4 describes the estimation methods for assets, liabilities and portfolio objectives, in Section 5, we perform an empirical analysis of the multi-objective portfolio selection problems and discuss the results. Finally in Section 6, some remarks and ideas are reported for further improvements.

2. Portfolio Optimization Framework

2.1. Preliminaries

We consider a non-life insurance company interested in assessing the risk exposure where both assets and liabilities are included. The insurer operates on a single line of business over a one-month investment period. The liability is expressed by the random variable Y and represents the total sum of contingent claims payable at the end of the period. In order to cover future liabilities, the insurance company receives the premiums paid by the policyholders at the beginning of the period. We assume the premium volume to be proportional to the expected liability, i.e., $p=(1+\eta )E\left(Y\right)$, where η is the relative security loading factor. Let c denote the amount of capital that, free from constraints due to policyholders, is generally provided by the insurance company’s shareholders, and it can be invested in the same manner as the premium volume in financial markets. Note that the main purpose of c is to ensure the availability of a regulatory capital required of the insurer by the Solvency II Directive. Investment decisions on the total amount $p+c$ are assumed to be made at the beginning of the month.

Suppose that a portfolio consisting of n assets is available for investments, with $R_{\tau }={\left(R_{1,\tau },\dots ,R_{n,\tau }\right)}^T$ representing the expected value of the assets’ gross returns over the investment period τ1. Let $x={\left(x_1,\dots ,x_n\right)}^T$ be the vector of portfolio weights, whose components satisfy the standard budget constraint:

$$\sum _{i=1}^n{x}_i=1$$

and a set of box constraints of the type:

$$a_j\le x_j\le b_j,j=1,\dots ,n$$

where $a_j,b_j\in \mathbb{R}$ are respectively the lower bound and the upper bound of the j-th portfolio decision variable. Box constraints are usually considered in portfolio selection problems for both denoising the asset returns covariance matrix [37], as well as for defining the investment profile of the portfolio [38]. In this paper, they will be used to better describe the strategic investment plan of the insurance company.

In summary, the net loss at the end of the period is defined as the excess of liabilities over assets, i.e.,

$$L_{\tau }(c,x)\stackrel{▵}{=}Y-(p+c)R_{\tau }^{T}x$$

(1)

and it depends on both shareholders’ invested capital and portfolio weights, while the set of admissible portfolios is:

$${\mathcal{X}}_0\stackrel{▵}{=}\left\{(c,x)\in \mathbb{R}\times {\mathbb{R}}^n:c\ge 0,\sum _{i=1}^n{x}_i=1,a_i\le x_i\le b_i,i=1,\dots ,n\right\}.$$

(2)

Our optimization framework jointly solves for c and x and minimizes the risk of mismatch between assets and liabilities depending on how the solvency requirement is defined.

2.2. Risk Measures and Performance Indicators for an Insurance Company

A general definition of a risk measure may be stated as follows [39].

Definition 1. Let $\left(\Omega ,\mathcal{A},\mathbb{P}\right)$ be a probability space, ${\mathcal{M}}_{\mathcal{B}}\left(\Omega ,{\mathbb{R}}^k\right)$ be the space of ${\mathbb{R}}^k$-valued random variables and $\mathcal{M}\left(\Omega ,\mathbb{R}\right)\subseteq {\mathcal{M}}_{\mathcal{B}}\left(\Omega ,\mathbb{R}\right)$ be a suitable vector subspace; a risk measure is then a map from $\mathcal{M}\left(\Omega ,\mathbb{R}\right)$ to $\mathbb{R}$.

Among the plethora of possible sources of uncertainty that may impact the performance of a portfolio, we mainly focus on insurance and market risks.

Since the insurance risk is usually identified with the tail behavior of the loss distribution, we will adopt the value-at-risk and the conditional value-at-risk as possible risk measures. The value-at-risk represents the α-quantile of the loss distribution and is given by:

$$Va{R}^{\alpha }\left(c,x\right)\stackrel{▵}{=}inf\left\{l\in \mathbb{R}:\text{Prob}\left(L_{\tau }(c,x)\le l\right)\ge \alpha \right\}.$$

(3)

It provides the minimal portfolio loss that occurs in $100(1-\alpha )\%$ of the worst scenarios.

The conditional (or average) value-at-risk is instead defined as the average of losses in the $100(1-\alpha )\%$ worst scenarios [8]. When the loss distribution is continuous, as it is in our case, it is equivalent to the definitions of tail value-at-risk and expected shortfall. Accordingly, there are several ways to compute this quantity; however, the most convenient formulation in this context is the one proposed, for instance, in [40], where conditional value-at-risk is defined as the solution of a convex optimization problem. Another relevant feature of this risk measure, which will be fundamental in defining selection criteria for our portfolio strategies, is that it can be minimized over the set of decision variables. These results are based on [41,42] and are summarized below.

Proposition 1. Let $L_{\tau }(c,x)$ be the net loss defined in Equation (1), with the vector of decision variables $(c,x)\in {\mathcal{X}}_0$, and $\alpha \in (0,1)$ denote the confidence level. Consider the function:

$$F^{\alpha }(c,x,s)=s+\frac{1}{1-\alpha }E\left({\left[L_{\tau }\left(c,x\right)-s\right]}^{+}\right)$$

where ${\left[L_{\tau }\left(c,x\right)-s\right]}^{+}=max\left\{L_{\tau }\left(c,x\right)-s,0\right\}$.

The following results hold:

(a)

$F^{\alpha }$ is finite and continuous as a function of s;

(b)

the conditional value-at-risk can be evaluated as:

$$CVa{R}^{\alpha }\left(c,x\right)=\underset{s\in \mathbb{R}}{inf}{F}^{\alpha }(c,x,s);$$

(4)

(c)

the set of solutions to the stochastic program defined in Equation (4) is the non-empty, closed and bounded interval:

$$S^{\alpha }(c,x)=\left[Va{R}^{\alpha }\left(c,x\right),{\overline{VaR}}^{\alpha }\left(c,x\right)\right]$$

where ${\displaystyle {\overline{VaR}}^{\alpha }\left(c,x\right)=sup\left\{l\in \mathbb{R}:Prob\left(L_{\tau }\left(c,x\right)\le l\right)\le \alpha \right\}}$;

(d)

minimizing $CVa{R}^{\alpha }$ with respect to $(c,x)\in {\mathcal{X}}_0$ is equivalent to minimizing $F^{\alpha }$ with respect to $(c,x,s)\in {\mathcal{X}}_0\times \mathbb{R}$, i.e.,

$$\underset{(c,x)\in {\mathcal{X}}_0}{min}CVa{R}^{\alpha }\left(c,x\right)=\underset{(c,x,s)\in {\mathcal{X}}_0\times \mathbb{R}}{min}{F}^{\alpha }(c,x,s)$$

(moreover, a triple $(c^{*},x^{*},s^{*})$ minimizes the right-hand side if and only if $(c^{*},x^{*})$ minimizes the left-hand side and $s^{*}\in S^{\alpha }(c^{*},x^{*})$);

(e)

$CVa{R}^{\alpha }$ is convex with respect to $(c,x)$, and $F^{\alpha }$ is convex with respect to $(c,x,s)$.

As a consequence, the conditional value-at-risk may be expressed in terms of the value-at-risk as follows:

$$CVa{R}^{\alpha }\left(c,x\right)=Va{R}^{\alpha }\left(c,x\right)+\frac{1}{1-\alpha }E\left({\left[L_{\tau }\left(c,x\right)-Va{R}^{\alpha }\left(c,x\right)\right]}^{+}\right).$$

(5)

When $L_{\tau }\left(c,x\right)$ has a positive density in a neighborhood of $Va{R}^{\alpha }\left(c,x\right)$, as it is customary to assume in financial applications, Equation (4) has a unique solution, i.e., $Va{R}^{\alpha }\left(c,x\right)={\overline{VaR}}^{\alpha }\left(c,x\right)$. Thus, if one knows $Va{R}^{\alpha }\left(c,x\right)$, he can apply Equation (5) to directly estimate the conditional value-at-risk instead of solving the stochastic program in Equation (4). Alternatively, by solving (4), one can deduce the value for $Va{R}^{\alpha }\left(c,x\right)$.

The portfolio volatility will be defined as the standard deviation of the net profit distribution. Assuming the aggregate liability Y to be nonnegative and independent of the gross returns of portfolio constituents $R_{\tau }$, this quantity may be evaluated as follows:

$$\sigma \left(c,x\right)=\sqrt{\text{var}\left(Y\right)+{(p+c)}^2{x}^T\Sigma x}$$

(6)

where $\text{var}\left(Y\right)$ is the variance of the liabilities and Σ represents the covariance matrix of asset gross returns.

In the strategic asset allocation process, it is fundamental to identify a set of objectives that a portfolio has to achieve at the best, according to certain assumptions for the future dynamics of assets and liabilities. The ex ante choice of the optimal portfolio is then related to the efficient frontier generated by a reward-risk analysis that concerns the tradeoff comparisons among the key performance indicators associated with the predetermined portfolio objectives [8]. Accordingly, we consider the following performance measures. On the one hand, in order to point out the risk-adjusted reward of the portfolio, two reward-to-risk measures are implemented. The former is the expected gross return on the invested capital and is given by:

$$ROC\left(c,x\right)\stackrel{▵}{=}\frac{E\left(-L_{\tau }\left(c,x\right)\right)}{c}$$

(7)

where c represents shareholders’ invested capital. The latter is the ratio of the expected gross return to the risk-adjusted capital:

$$RORAC\left(c,x\right)\stackrel{▵}{=}{\left.\frac{E\left(-L_{\tau }\left(\widehat{c},x\right)\right)}{\widehat{c}}\right|}_{\widehat{c}=CVa{R}^{\alpha }(c,x)}$$

(8)

Finally, a reward-to-variability indicator, similar to the Sharpe ratio, is defined as:

$$SR\left(c,x\right)\stackrel{▵}{=}{\left.\frac{E\left(-L_{\tau }\left(\widehat{c},x\right)\right)}{\sigma (\widehat{c},x)}\right|}_{\widehat{c}=CVa{R}^{\alpha }(c,x)}$$

(9)

Note that in the second and third ratio, the conditional value-at-risk is invested instead of general capital c.

2.3. Multi-Objective Portfolio Optimization Problems with Solvency Constraint

Since the Solvency II Directive requires a minimum capital to be held by EU-based insurance companies in order to guarantee a target level for the ruin probability over a specified period of time, we add to the set of linear constraints represented by Equation (2) the following chance constraint:

$$\text{Prob}\left(L_{\tau }(c,x)>0\right)\le 1-\alpha$$

(10)

where α represents the prespecified solvency level. A major difficulty in dealing with this type of constraint is that its evaluation may involve multidimensional integrals. Alternatively, we can express the solvency constraint in terms of expected value as:

$$E\left[\mathbb{1}\left(L_{\tau }(c,x)>0\right)\right]\le 1-\alpha$$

(11)

with $\mathbb{1}(·)$ denoting the indicator function, or, in terms of the value-at-risk (see [43]), as:

$$Va{R}^{\alpha }(c,x)\le 0.$$

(12)

However, these equivalent formulations may be non-convex, since, in general, $Va{R}^{\alpha }$ is non-convex with respect to $(c,x)$. In order to overcome this drawback, we follow the semi-parametric approach used, for instance, in [5] and assume claim amounts to be modeled with a lognormal distribution. This condition is sufficient in most practical cases to guarantee the convexity of the solvency constraint (a more detailed treatment will be provided in the section where we describe the estimation methods).

Therefore, the set of efficient portfolios for an EU-based insurance company may be represented by:

$$\mathcal{X}\stackrel{▵}{=}\left\{(c,x)\in \mathbb{R}\times {\mathbb{R}}^n:c\ge 0,\sum _{i=1}^n{x}_i=1,a_i\le x_i\le b_i,i=1,\dots ,n,Va{R}^{\alpha }\left(c,x\right)\le 0\right\}$$

(13)

and results in being convex and compact.

Due to the fact that different subjects act in the identification of an optimal insurance portfolio, we model this decision process from a multi-objective point of view. In this manner, it is possible to extend the standard risk-reward analysis from the study of tradeoff curves to the study of multi-dimensional tradeoff surfaces [44]. Three portfolio selection problems are introduced in order to integrate at different levels both financial and insurance criteria.

The first portfolio is bi-objective in nature and takes into account the shareholders’ expectations of obtaining a satisfactory rate of return on the provided capital. The objectives may be stated as follows:

$$\left\{\begin{array}{c}maxROC\left(c,x\right)\hfill \\ minc\hfill \end{array}\right.\text{subject}\text{to}(c,x)\in \mathcal{X}.$$

(14)

In this case, a stockholder tries to maximize profits and minimize the invested capital. The problem is equivalent to the one in [5], but a multi-objective approach is here adopted instead of an ϵ-constraint scheme. In the Experimental Section, we will investigate the benefits of this choice.

The second portfolio selection model represents the case of an insurance company that could be characterized as using the $RORAC$ concept and two risk measures (conditional value-at-risk at the confidence level α and portfolio volatility). On the basis of Proposition (1), the resulting tri-objective optimization problem may be formulated as follows:

$$\left\{\begin{array}{c}maxRORAC\left(c,x\right)\hfill \\ minCVa{R}^{\alpha }\left(c,x\right)\hfill \\ min\sigma \left(c,x\right)\hfill \end{array}\right.\text{subject}\text{to}(c,x,s)\in {\mathcal{X}}^s$$

(15)

where the feasible set has been modified as:

$${\mathcal{X}}^s\stackrel{▵}{=}\left\{(c,x,s)\in \mathbb{R}\times {\mathbb{R}}^n\times \mathbb{R}:c\ge 0,\sum _{i=1}^n{x}_i=1,a_i\le x_i\le b_i,i=1,\dots ,n,s\le 0\right\}$$

(16)

once the relation between value-at-risk and conditional value-at-risk is exploited (see Equations (4) and (5)).

The third selection strategy identifies as optimal those portfolios that simultaneously maximize the performance indicator Equations (7–9) and can be written as:

$$\left\{\begin{array}{c}maxROC\left(c,x\right)\hfill \\ maxRORAC\left(c,x\right)\hfill \\ maxSR\left(c,x\right)\hfill \end{array}\right.\text{subject}\text{to}(c,x,s)\in {\mathcal{X}}^s.$$

(17)

According to this version of the portfolio selection problem, a sensitivity analysis may be conducted, linking company-level interests, represented by $RORAC$, with both stockholders and actuarial goals, characterized by $ROC$ and $SR$, respectively.

3. The Normalized Normal Constraint Method

In this section, we briefly present essential concepts and methods from the nonlinear multi-objective optimization literature that will be exploited to solve the insurance portfolio optimization problems previously introduced. The treatment relative to the technical preliminaries is based on the survey paper [16] and the references therein. The general description of the optimization scheme we will adopt follows the seminal papers [31,45].

3.1. Basic Concepts and Definitions

Multi-objective optimization, or vector optimization, is the process according to which a decision-maker optimizes multiple objective functions, usually conflicting in nature, at the same time [46].

A multi-objective problem (MOP) can be stated in the following form:

$$minf\left(x\right)={\left(f_1\left(x\right),\dots ,f_m\left(x\right)\right)}^T,m\ge 2$$

(18)

subject to r equality constraints:

$$g_i\left(x\right)=0,i=1,\dots ,r$$

(19)

and s inequality constraints:

$$h_j\left(x\right)\le 0,j=1,\dots ,s$$

(20)

where $x={(x_1,\dots ,x_n)}^T\in {\mathbb{R}}^n$ represents the decision, or design, vector.

A relevant subclass of inequality constraints is represented by the box constraints discussed earlier.

The feasible design space is defined as the set:

$$\mathcal{X}=\left\{x\in {\mathbb{R}}^n|g_i\left(x\right)=0,i=1,\dots ,r\text{and}{h}_j\left(x\right)\le 0,j=1,\dots ,s\right\}.$$

(21)

Feasibility means that no constraints are violated.

The objective, or criterion, space is defined as the set:

$$\mathcal{Y}=\left\{f\left(x\right)\in {\mathbb{R}}^m|x\in \mathcal{X}\right\}.$$

(22)

In practice, for the empirical analysis we will conduct on insurance portfolios, we will only consider linear equality and inequality constraints and quasiconvex objective functions [8].

For Problem (18–20), there is not in general one global solution that simultaneously satisfies all the objectives best. It is thus necessary to provide a definition for an optimal point able to take into account the tradeoffs among the objectives. The predominant concept in this sense is the Pareto optimality, which is defined as follows:

Definition 2. A point $x^{*}\in \mathcal{X}$ is Pareto optimal to Problem (18–20) if and only if there does not exist another point $x\in \mathcal{X}$ such that:

$$\forall i\in \left\{1,\dots ,m\right\}{f}_i\left(x\right)\le f_i\left(x^{*}\right)\text{and}\exists j\in \left\{1,\dots ,m\right\}:f_i\left(x\right)<f_i\left(x^{*}\right).$$

(23)

The image of $x^{*}$ in $\mathcal{Y}$, i.e., $f\left(x^{*}\right)={\left(f_1\left(x^{*}\right),\dots ,f_m\left(x^{*}\right)\right)}^T$, is called a Pareto optimal (objective) vector.

The set of all Pareto points forms the so-called Pareto set (PS), while the set represented by all of the Pareto optimal objective vectors is called the Pareto, or efficient, frontier (PF). Saying that PS represents optimal solutions to (18–20) means that any improvement in one objective of an optimal point must lead to a deterioration in at least one other objective. According to this feature, PF results in being a subset of the boundary of the objective set [17].

Associated with every MOP are the following important reference points, which constitute the building blocks of the optimization procedure that we analyze.

Definition 3. An anchor point $f^{i*}$ is a specific point in the objective space $\mathcal{Y}$ that corresponds to the minimum value of an i-th objective function $f_i$, $i=1,\dots ,m$, subject to Constraints (19) and (20), and is expressed as:

$$f^{i*}\stackrel{▵}{=}{\left(f_1(x^{i*}),\dots ,f_m(x^{i*})\right)}^T.$$

(24)

where ${\displaystyle x^{i*}=\underset{x\in \mathcal{X}}{argmin}{f}_i\left(x\right)}$2.

Definition 4. An hyperplane that comprises all of the anchor points is said to be the utopia hyperplane.

Clearly, for bi-objective optimization problems, this hyperplane is called the utopia line, while for tri-objective optimization problems, it is called the utopia plane.

Definition 5. The point in the objective space $\mathcal{Y}$ that corresponds to all objectives simultaneously being at their best possible values is said to be utopia, or ideal:

$$f^U\stackrel{▵}{=}{\left(f_1(x^{1*}),\dots ,f_m(x^{m*})\right)}^T.$$

(25)

Observe that the utopia point does not lie on the utopia hyperplane.

Definition 6. An anti-anchor point $f^{i\circ }$ is a specific point in the objective space $\mathcal{Y}$ that corresponds to the maximum value of an i-th objective function $f_i$, $i=1,\dots ,m$, subject to Constraints (19) and (20), and is expressed as:

$$f^{i\circ }\stackrel{▵}{=}{\left(f_1(x^{i\circ }),\dots ,f_m(x^{i\circ })\right)}^T.$$

(26)

where ${\displaystyle x^{i\circ }=\underset{x\in \mathcal{X}}{argmax}{f}_i(x)}$.

Definition 7. The point in the objective space $\mathcal{Y}$ that corresponds to all objectives simultaneously being at their worst possible values is said to be nadir:

$$f^N\stackrel{▵}{=}{\left(f_1(x^{1\circ }),\dots ,f_m(x^{m\circ })\right)}^T.$$

(27)

All of the just given definitions are illustrated in the left chart in Figure 1.

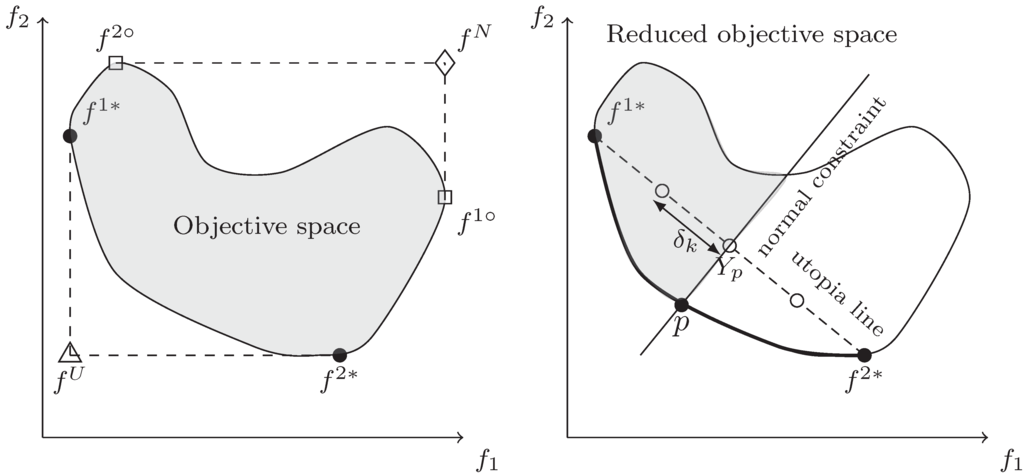
Figure 1. Graphical representation of the reference points (on the left) and of the normal constraint (NC) method (on the right) for a bi-objective sample optimization problem.

Figure 1. Graphical representation of the reference points (on the left) and of the normal constraint (NC) method (on the right) for a bi-objective sample optimization problem.

3.2. A New Variant of the Normal Constraint Algorithm

The normal constraint (NC) method is a PF generator able to produce full coverage of the PF throughout an even distribution of points on the utopia hyperplane and is effective for MOPs with an arbitrary number of objective functions [45].

Under this optimization scheme, the dotted representation of the PF is obtained by transforming the original MOP into a series of single-objective optimization problems, each with a different set of additional linear constraints. This sequential reduction is intended to generate a set of uniformly-distributed solutions on the boundary of the objective space $\mathcal{Y}$ from a set of uniformly-distributed points on the utopia hyperplane. In order to mitigate possible disparate objective scaling issues, we consider in the experiments the so-called normalized version of the NC method, which will be outlined in what follows.

Step 1 

Generation of reference points:

Use (24) to identify the m anchor points $f^{1*},\dots ,f^{m*}$ and calculate the utopia point according to (25).

Step 2 

Objective normalization:

To avoid scaling deficiencies, objective functions are transformed according to the following normalization equation:

$${\overline{f}}_i(x)=\frac{f_i(x)-f_i^U(x)}{f_i^N(x)-f_i^U(x)},i=1,\dots ,m$$

with $x\in \mathcal{X}$.

Note that ${\overline{f}}_i(x)$ has values between zero and one, for all $x\in \mathcal{X}$. The optimization will now take place in the normalized objective space.

Step 3 

Utopia line vector:

Let ${\overline{N}}_k$ indicate the difference between the k-th normalized anchor point and the normalized anchor point corresponding to dimension m:

$${\overline{N}}_k\stackrel{▵}{=}{\overline{f}}^{k*}-{\overline{f}}^{m*},k=1,\dots ,m-1.$$

In this way, $m-1$ utopia line vectors are defined, all of which point to ${\overline{f}}^{m*}$.

Step 4 

Normalized utopia line increments:

Based on the prescribed number of utopia line points $m_k$, $k=1,\dots ,m-1$, that the user fixes along each normalized utopia line direction ${\overline{N}}_k$, a normalized increment ${\delta }_k$ is given using the equation:

$${\delta }_k=\frac{\parallel {\overline{N}}_k\parallel }{m_k-1},k=1,\dots ,m-1$$

where $\parallel ·\parallel$ is the Euclidean norm.

Step 5 

Hyperplane point generation:

Evaluate a set of evenly-distributed points on the normalized utopia hyperplane as:

$$Y_{pj}=\sum _{k=1}^m{\alpha }_{kj}{\overline{f}}^{k*}j=1,\dots ,J$$

where $J={\prod }_{i=1}^{m-1}{m}_k$ and parameters ${\alpha }_{kj}$ are such that ${\alpha }_{kj}\in [0,1]$ and ${\displaystyle \sum _{k=1}^m{\alpha }_{kj}=1}$.

Step 6 

Pareto point generation:

Using the set of points $Y_{pj}$, $j=1,\dots ,J$, on the normalized utopia hyperplane, generate a corresponding set of Pareto optimal points on the PF by solving the following series of single-objective problems:

$$\underset{x\in \mathcal{X}}{min}{\overline{f}}_m(x)$$

(28)

subject to:

$${\overline{N}}_j{\left(\overline{f}(x)-Y_{pj}\right)}^T\le 0$$

(29)

where $\overline{f}(x)$ is the generic point in the normalized objective space.

The plane Constraints (29) enforce the optimization to operate on the portion of the objective space in which the vectors pointing to $Y_{pj}$ are in opposition to the normalized utopia hyperplane. When Constraints (29) reduces to being equal to zero, it represents the equation of a hyperplane orthogonal to the normalized utopia hyperplane.

Step 7 

Pareto design metric values:

Evaluate the non-normalized metrics by using the equation:

$$f_i(x)={\overline{f}}_i(x)\left[f_i^N(x)-f_i^U(x)\right]+f_i^U(x),i=1,\dots ,m.$$

The right chart in Figure 1 provides a graphical representation of the normalized NC method for a bi-objective sample problem where the Pareto point p is obtained by solving Problem (28–29) using the utopia line point $Y_p$.

Unfortunately, the basic NC method is unable to cover the entire PF for MOPs with $m>2$. In [45], the authors describe a procedure to overcome this pitfall. Their idea is to extend the region bounded by the anchor points in order to also include all regions resulting in the orthogonal projection of the anti-anchor points on the identified utopia hyperplane. For a detailed presentation of the method, we refer to [45].

The tri-objective portfolio Problems (15) and (17) will be tackled by considering this extended version of the NC procedure, even if other more efficient solutions are possible (see, for instance, [47,48,49]), because these improvements necessitate much more modifications to the original optimization scheme.

A second drawback of the NC procedure pertains to the possibility of failing to produce global Pareto solutions if a gradient-based approach is used to solve Problem (28–29). A Pareto filter is usually introduced after Step 6 to delete local and non-Pareto optimal points. A different solution is represented by the hybridization of the NC method with a global optimization. An example is [50], in which the normalized NC algorithm is combined with a genetic algorithm (GA).

Following this strand of research, we propose to incorporate another heuristic in order to guarantee global Pareto optimality for the solutions, the so-called OQNLPalgorithm [51]. This optimizer is easier to implement compared to GAs and necessitates less effortin the preliminary parameters setup phase to perform best (see, for instance, [52] for a deep analysis of GAs parameter tuning). OQNLP is a multi-start algorithm, designed to find global optima of smooth constrained nonlinear programs by combining the ability of heuristic search methods to identify good local solutions with the strength of gradient-based nonlinear programming (NLP) solvers in dealing with nonlinear equality constraints, as well as in producing highly accurate approximations to local optima. It operates as follows: first, the scatter search algorithm generates a set of starting points according to some predefined filter criteria (merit/distance), and successively, a gradient-based NLP solver identifies optimal solutions. Further details on the algorithm may be found in [51].

4. Estimation Methods

This section is devoted to the description of the procedures we adopt to simulate assets and liabilities and to approximate the objectives for our portfolio selection strategies.

4.1. Liability Distribution and Asset Return Scenario Generation

As previously stated, we assume that insurer liability follows a lognormal distribution:

$$Y\sim LGN({\mu }_Y,{\sigma }_Y)$$

(30)

where the parameters ${\mu }_Y$ and ${\sigma }_Y$ may be calculated with a maximum likelihood estimator on the monthly claims amounts.

An AR(1)-GJR-GARCH(1,1) model fits to each gross return series ($i=1,\dots ,n$) according to the following equations:

$$\begin{array}{cc}& ln{r}_{i,t}=c_i+{\theta }_{i}ln{r}_{i,t-1}+{ϵ}_{i,t}\hfill \end{array}$$

(31)

$$\begin{array}{cc}& {\sigma }_{i,t}^2={\kappa }_i+{\alpha }_i{\sigma }_{i,t-1}^2+\left({\varphi }_i+{\psi }_i{I}_{i,t-1}\right){ϵ}_{i,t-1}^2\hfill \end{array}$$

(32)

$$\begin{array}{cc}& {ϵ}_{i,t}={\sigma }_{i,t}{z}_{i,t}\hfill \end{array}$$

(33)

with $I_{i,t-1}$ equal to one if ${ϵ}_{i,t-1}<0$ and zero otherwise, and $z_{i,t}$ are the standardized random variables upon which the extreme value theory (EVT) estimation of the sample cumulative distribution function (CDF) tails is based.

The $AR(1)$ in Equation (31) could capture autocorrelation, while the GJR-GARCH(1,1) in Equations (32) and (33) could identify volatility clustering, allowing one to represent both leverage effects, as well as asymmetric responses of volatility to return shocks. Moreover, in this paper, we assume that the standardized residuals $z_{i,t}$ follow a Student t distribution in order to allow for the fat tails often associated with asset returns.

For each return series, we model the marginal distribution of the standardized innovations by subdividing the sample into three parts and by employing the generalized Pareto (GP) distribution estimation for the corresponding upper and lower tails and the Gaussian kernel estimate for the center of the distribution. The GP distribution function is thus defined as follows:

$$F(z_{i,t})=\left\{\begin{array}{cc}\frac{N_l}{N}{\left(1+\frac{{\xi }_l(l-z_{i,t})}{{\beta }_l}\right)}^{MM-1/{\xi }_l},\hfill & z_{i,t}<l\hfill \\ 1-\frac{N_u}{N}{\left(1+\frac{{\xi }_u(z_{i,t}-u)}{{\beta }_u}\right)}^{MM-1/{\xi }_u},\hfill & z_{i,t}>u\hfill \end{array}\right.$$

for $i=1,\dots ,n$, where ${\xi }_l$ and ${\xi }_u$ are the shape parameters for the lower and upper tail, respectively, ${\beta }_l$ and ${\beta }_u$ the corresponding scale parameters and l and u the thresholds. In the empirical analysis, we identify l with the 10th percentile of the sample, while u is the 90th percentile, in order to guarantee an optimal tradeoff between precision and low variance (see [53] for more details).

The marginal distributions are collected together by means of a t-Copula for properly capturing the tail dependence structure among innovations. The maximum likelihood estimation procedure provides Copula parameters, i.e., the degrees of freedom and the correlation matrix.

Asset return scenarios are thus generated by first simulating the corresponding jointly-dependent standardized innovations.

4.2. Quantile-Based Risk Measures and Objective Estimation

Based on the returns generated by the GARCH-EVT-Copula model, we can replace theoretical quantiles and loss distribution moments with their scenario-based counterparts.

The quantile-based risk measures are estimated, following the semi-parametric approach of [4], by using a Monte Carlo-type estimator for the expected value of the survival function of the liability distribution. Let m be the number of simulated scenarios, and denote the vector of gross returns for the k-th scenario with $R_{\tau }(k)$. Assuming the standard regularity conditions that ensure the uniform convergence in the probability of Monte Carlo estimators to be satisfied [54], the chance constraint given in Equation (10) may be written as:

$$\begin{array}{cc}\hfill \text{Prob}\left\{L_{\tau }>0\right\}& \approx \frac{1}{m}\sum _{k=1}^m\text{Prob}\left\{Y>(p+c)R_{\tau }{(k)}^{T}x\right\}\hfill \\ & =\frac{1}{m}\sum _{k=1}^m\Phi \left(\frac{-ln\left[(p+c)R_{\tau }{(k)}^{T}x\right]+{\mu }_Y}{{\sigma }_Y}\right)\le 1-\alpha \hfill \end{array}$$

(34)

where $\Phi (·)$ denotes the Gaussian cumulative distribution function. Convexity is guaranteed if:

$$\frac{-ln\left[(p+c{R}_{\tau }{(k)}^{T}x\right]+{\mu }_Y}{{\sigma }_Y}\le 0k=1,\dots ,m⟺\underset{1\le k\le m}{min}(p+c)R_{\tau }{(k)}^{T}x\ge exp({\mu }_Y)$$

i.e., the value of the assets investment in the worst case scenario is greater than the median of the liability distribution. The expectation in Equation (4) is approximated according to [5] by exploiting the log normality of Y and the Black–Scholes call price formula; the result is:

$$\begin{array}{c}E\left[{\left(L_{\tau }-s\right)}^{+}\right]=\frac{1}{m}\sum _{k=1}^m\{exp\left({\mu }_Y+\frac{{\sigma }_Y^2}{2}\right)\Phi \left(\frac{-ln\left[(p+c)R_{\tau }{(k)}^{T}x+s\right]+{\mu }_Y+{\sigma }_Y^2}{{\sigma }_Y}\right)\hfill \end{array}$$

$$\begin{array}{r}-(p+c)R_{\tau }{(k)}^{T}x\Phi \left(\frac{-ln\left[(p+c)R_{\tau }{(k)}^{T}x+s\right]+{\mu }_Y}{{\sigma }_Y}\right)\}\end{array}$$

(35)

Putting this expression into Equation (4), we obtain a Monte Carlo estimate for the conditional value-at-risk, whose convexity is a direct consequence of the convexity property of the European call price with respect to the strike price (for more details, we point the interested reader to [5]).

By virtue of the liability log normality, the expected net profit can be written as:

$$E\left(-L_{\tau }\right)=-exp\left({\mu }_Y+\frac{{\sigma }_Y^2}{2}\right)+\frac{1}{m}\sum _{k=1}^m\left[(p+c)R_{\tau }{(k)}^{T}x\right]$$

(36)

and the portfolio volatility becomes:

$$\sigma =\sqrt{\left[exp\left({\sigma }_Y^2\right)-1\right]exp\left(2{\mu }_Y+{\sigma }_Y^2\right)+{(p+c)}^2{x}^T\widehat{\Sigma }x}$$

(37)

where $\widehat{\Sigma }$ represents the sample covariance matrix of asset returns.

Therefore, the objectives in Portfolios (14), (15) and (17) can be expressed in terms of these quantities.

5. Empirical Results and Discussion

In this section, we analyze the effectiveness of the selection Strategies (14), (15) and (17) for a portfolio of an EU-based non-life insurance company. The strategic investment plan is represented by a set of box constraints limiting the exposure to each asset in the portfolio. More precisely, we impose a minimum percentage of the available capital $p+c$ to be invested in each asset equal to $1\%$ and a maximum allowed investment equal to $30\%$, i.e., $0.01\le x_i\le 0.30$, $i=1,\dots ,n$. The investment horizon is fixed to one month, and the confidence level to estimate $Va{R}^{\alpha }$ and $CVa{R}^{\alpha }$ is $\alpha =99.5\%$

5.1. Data Description and Model Estimation

The liability is represented by the data published in [5] where monthly property insurance claim amounts are considered for the period from 3 January 2005–29 July 2011 for a total of 79 observations. Asanga et al. have modeled these claims with a lognormal distribution.

The investment universe is constituted by the following six assets: the EMUTracker Government Bond Index with 1–3 year maturities (TEMGVG1), the Markit iBoxx Euro Corporate Bond Index with 1–3 year maturities (IBCRP13), the Markit iBoxx Benchmark Collateralized Index (IBCOLAL), which includes covered and other securitized bonds at all maturities, the Markit iBoxx Euro High Yield Fixed Rate Bonds Index (IBEHYFR), the MSCI EMU Index (MSEMUIL) and the MSCI BRIC Index (MSBRICL). Note that the first four assets represent benchmark bond indices, while the last two are equity indices. In particular, MSEMUIL covers approximately $85\%$ of the free float-adjusted market capitalization of the European Economic and Monetary Union, while MSBRICL provides a broad measure of the performance of emerging market equities inside the Brazil, Russia, India and China markets. Assets data have been recorded on a daily basis, covering the same time frame of liabilities, for a total of 1714 observations. Table 1 reports the descriptive statistics for each asset log-return series.

In terms of the first moment, it emerges that TEMGVG1, IBCRP13, IBCOLAL and MSEMUIL present the same value ($0.01\%$), whereas MSBRICL stands out from the others with a value of $0.05\%$. The inspection of the standard deviation reveals that, as expected, equity indices are the most volatile, with values around $1.40\%$; conversely, TEMGVG1 and IBCRP13 have lower values ($0.07\%$ and $0.08\%$, respectively). All of the assets have a negative skewness and a kurtosis larger than three, indicating non-normal distributions for the log-returns series. In particular, the IBEHYFR bond index displays the most negative skewness (−1.5211) and the highest kurtosis (28.3298).

Table 1. Descriptive statistics for the daily asset log-returns from 3 January 2005–9 July 2011 for a total of 1714 observations: EMUTracker Government Bond Index with 1–3 year maturities (TEMGVG1); Markit iBoxx Euro Corporate Bond Index with 1–3 year maturities (IBCRP13); Markit iBoxx Benchmark Collateralized Index (IBCOLAL); Markit iBoxx Euro High Yield Fixed Rate Bonds Index (IBEHYFR); MSCI EMU Index (MSEMUIL); MSCI BRIC Index (MSBRICL).

	TEMGVG1	IBCRP13	IBCOLAL	IBEHYFR	MSEMUIL	MSBRICL
	descriptive statistics
Min	−0.0044	−0.0047	−0.0073	−0.0354	−0.0818	−0.1015
Max	0.0041	0.0034	0.0072	0.0347	0.0993	0.1223
Mean	0.0001	0.0001	0.0001	0.0002	0.0001	0.0005
SD	0.0007	0.0008	0.0017	0.0035	0.0137	0.0156
Skewness	−0.0050	−0.6480	−0.0914	−1.5211	−0.0106	−0.1709
Kurtosis	8.3629	6.8593	3.8708	28.3298	10.5776	12.8170

Table 1. Descriptive statistics for the daily asset log-returns from 3 January 2005–9 July 2011 for a total of 1714 observations: EMUTracker Government Bond Index with 1–3 year maturities (TEMGVG1); Markit iBoxx Euro Corporate Bond Index with 1–3 year maturities (IBCRP13); Markit iBoxx Benchmark Collateralized Index (IBCOLAL); Markit iBoxx Euro High Yield Fixed Rate Bonds Index (IBEHYFR); MSCI EMU Index (MSEMUIL); MSCI BRIC Index (MSBRICL).

	TEMGVG1	IBCRP13	IBCOLAL	IBEHYFR	MSEMUIL	MSBRICL
	descriptive statistics
Min	−0.0044	−0.0047	−0.0073	−0.0354	−0.0818	−0.1015
Max	0.0041	0.0034	0.0072	0.0347	0.0993	0.1223
Mean	0.0001	0.0001	0.0001	0.0002	0.0001	0.0005
SD	0.0007	0.0008	0.0017	0.0035	0.0137	0.0156
Skewness	−0.0050	−0.6480	−0.0914	−1.5211	−0.0106	−0.1709
Kurtosis	8.3629	6.8593	3.8708	28.3298	10.5776	12.8170

Table 2. Statistical tests for normality, autocorrelation and conditional heteroskedasticity relative to the daily asset log-returns from 3 January 2005–29 July 2011 for a total of 1714 observations. The p-values corresponding to the test statistics are reported in parentheses. ARCH(2) is Engle’s LM test for the ARCH effect in the residuals up to the second order.

	TEMGVG1	IBCRP13	IBCOLAL	IBEHYFR	MSEMUIL	MSBRICL
	normality
Jarque–Bera	2054.01 **	1183.66 **	56.54 **	46,481.79 **	4100.75 **	6891.07 **
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
Lilliefors	0.07 **	0.08 **	0.02 *	0.17 **	0.09 **	0.10 **
	(0.001)	(0.001)	(0.022)	(0.001)	(0.001)	(0.001)
Shapiro–Wilk	0.93 **	0.95 **	0.99 **	0.73 **	0.91 **	0.88 **
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	autocorrelation
Ljung-Box	56.25 **	166.22 **	20.05	1546.96 **	42.68 **	107.62 **
	(0.000)	(0.000)	(0.455)	(0.000)	(0.002)	(0.000)
	conditional heteroskedasticity
ARCH(2)	39.75 **	190.53 **	51.90 **	331.18 **	160.05 **	430.06 **
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)

Note: ** and * denote rejection of the null hypothesis at the 1% and 5% significance levels, respectively.

Table 2. Statistical tests for normality, autocorrelation and conditional heteroskedasticity relative to the daily asset log-returns from 3 January 2005–29 July 2011 for a total of 1714 observations. The p-values corresponding to the test statistics are reported in parentheses. ARCH(2) is Engle’s LM test for the ARCH effect in the residuals up to the second order.

	TEMGVG1	IBCRP13	IBCOLAL	IBEHYFR	MSEMUIL	MSBRICL
	normality
Jarque–Bera	2054.01 **	1183.66 **	56.54 **	46,481.79 **	4100.75 **	6891.07 **
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
Lilliefors	0.07 **	0.08 **	0.02 *	0.17 **	0.09 **	0.10 **
	(0.001)	(0.001)	(0.022)	(0.001)	(0.001)	(0.001)
Shapiro–Wilk	0.93 **	0.95 **	0.99 **	0.73 **	0.91 **	0.88 **
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)
	autocorrelation
Ljung-Box	56.25 **	166.22 **	20.05	1546.96 **	42.68 **	107.62 **
	(0.000)	(0.000)	(0.455)	(0.000)	(0.002)	(0.000)
	conditional heteroskedasticity
ARCH(2)	39.75 **	190.53 **	51.90 **	331.18 **	160.05 **	430.06 **
	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)	(0.000)

Note: ** and * denote rejection of the null hypothesis at the 1% and 5% significance levels, respectively.

In order to properly identify the characteristics of the log-return distributions, we conduct the following set of tests: the Jarque–Bera, the Lilliefors and Shapiro–Wilk tests are used to infer the assumption of normality; the Ljung–Box test to verify the presence of autocorrelation; and Engle’s LMtest to check the ARCH effect in the residuals. The corresponding statistics and p-values are reported in Table 2. The results, on the one hand, confirm that the log-returns are non-normally distributed and, on the other hand, suggest the presence of serial correlation in all indices, except for IBCOLAL and conditional heteroskedasticity in the residuals up to the second order in all of the series, implying that the current returns are affected by spillover effects due to the returns of previous periods.

As described in Section 4, the generation of scenarios for asset returns is a complex process with several passages. In the following, we describe the results step by step. Firstly, an AR(1)-GJR-GARCH(1,1) model is estimated for each log-return series. The corresponding parameters and t-ratios are presented in Table 3. The AR(1) parameter θ results in being significant in all series, except for MSEMUIL. The ARCH parameter α is significant for all series, while the GARCH parameter ϕ is significant for all series, except MSEMUIL, for which the GARCH effect is absent. The parameter ψ, representing asymmetric leverage effects for volatility clustering, is significant only for the IBEHYFR, MSEMUIL and MSBRICL indices. Furthermore, the degrees of freedom $DoF$ for the Student t-distribution of residuals is significant in all series, suggesting that this distributional assumption fits reasonably well in our context.

Table 3. Parameter estimates of the AR(1)-GJR-GARCH(1,1) model for each log-return series for the period from 3 January 2005–29 July 2011. The t-ratios are given in parentheses.

	TEMGVG1	IBCRP13	IBCOLAL	IBEHYFR	MSEMUIL	MSBRICL
	AR(1) model
c	8.58E-05 **	1.23E-04 **	1.16E-04 **	2.00E-04 **	5.57E-04 **	8.88E-04 **
	(6.280)	(7.480)	(2.979)	(6.808)	(2.614)	(3.702)
θ	0.1176 **	0.1402 **	0.0648 *	0.4350 **	−0.0139	0.1824 **
	(4.486)	(5.153)	(2.508)	(20.591)	(−0.516)	(7.259)
	GJR-GARCH(1,1) model
κ	2E-07 ${}^{+}$	2E-07 ${}^{+}$	2E-07 ${}^{+}$	2E-07	2.2784E-06 **	5.2582E-06 **
	(1.660)	(1.670)	(1.656)	(1.242)	(2.865)	(3.671)
α	0.4544 **	0.4564 **	0.8466 **	0.6913 **	0.8837 **	0.8464 *
	(8.190)	(10.075)	(55.928)	(30.266)	(55.716)	(44.279)
ϕ	0.4800 **	0.3647 **	0.0912 **	0.2436 **	–	0.0480 **
	(4.395)	(4.444)	(4.061)	(5.559)		(2.472)
ψ	−0.2037	−0.0633	−0.0186	0.1302 *	0.2010 **	0.1526 **
	(−1.610)	(−0.689)	(−0.658)	(2.353)	(7.107)	(4.703)
	t distribution
$DoF$	3.2411 **	4.2279 **	24.2761 **	3.5620 **	9.8494 **	6.8035**
	(11.943)	(8.383)	(6.06E+06)	(14.036)	(4.413)	(5.533)

Note: **, * and ${}^{+}$ denote coefficient significance at the 1%, 5% and 10% levels, respectively.

Table 3. Parameter estimates of the AR(1)-GJR-GARCH(1,1) model for each log-return series for the period from 3 January 2005–29 July 2011. The t-ratios are given in parentheses.

	TEMGVG1	IBCRP13	IBCOLAL	IBEHYFR	MSEMUIL	MSBRICL
	AR(1) model
c	8.58E-05 **	1.23E-04 **	1.16E-04 **	2.00E-04 **	5.57E-04 **	8.88E-04 **
	(6.280)	(7.480)	(2.979)	(6.808)	(2.614)	(3.702)
θ	0.1176 **	0.1402 **	0.0648 *	0.4350 **	−0.0139	0.1824 **
	(4.486)	(5.153)	(2.508)	(20.591)	(−0.516)	(7.259)
	GJR-GARCH(1,1) model
κ	2E-07 ${}^{+}$	2E-07 ${}^{+}$	2E-07 ${}^{+}$	2E-07	2.2784E-06 **	5.2582E-06 **
	(1.660)	(1.670)	(1.656)	(1.242)	(2.865)	(3.671)
α	0.4544 **	0.4564 **	0.8466 **	0.6913 **	0.8837 **	0.8464 *
	(8.190)	(10.075)	(55.928)	(30.266)	(55.716)	(44.279)
ϕ	0.4800 **	0.3647 **	0.0912 **	0.2436 **	–	0.0480 **
	(4.395)	(4.444)	(4.061)	(5.559)		(2.472)
ψ	−0.2037	−0.0633	−0.0186	0.1302 *	0.2010 **	0.1526 **
	(−1.610)	(−0.689)	(−0.658)	(2.353)	(7.107)	(4.703)
	t distribution
$DoF$	3.2411 **	4.2279 **	24.2761 **	3.5620 **	9.8494 **	6.8035**
	(11.943)	(8.383)	(6.06E+06)	(14.036)	(4.413)	(5.533)

Note: **, * and ${}^{+}$ denote coefficient significance at the 1%, 5% and 10% levels, respectively.

Successively, a generalized Pareto distribution is calibrated to the upper and to the lower tail of the standardized residuals for each series. As thresholds, we consider the 10th and 90th percentiles, respectively. Table 4 reports the parameter estimates of these distributions. The remaining part of the data is modeled according to a Gaussian kernel.

Table 4. Generalized Pareto distribution parameter estimates for the standardized residuals from the AR(1)-GJR-GARCH(1,1) model for each log-return series for the period from 3 January 2005–29 July 2011.

	TEMGVG1	IBCRP13	IBCOLAL	IBEHYFR	MSEMUIL	MSBRICL
l	−0.9577	−1.0920	−1.2775	−1.1539	−1.3427	−1.2551
${\xi }_l$	0.2713	0.0753	−0.1543	0.3202	−0.0585	−0.1005
${\beta }_l$	0.4083	0.6323	0.6093	0.6305	0.6699	0.7073
u	1.0050	1.1145	1.2844	1.1038	1.2142	1.1771
${\xi }_u$	0.0981	0.0281	−0.0866	0.0996	−0.1323	−0.0287
${\beta }_u$	0.5041	0.5177	0.5176	0.6019	0.4834	0.5830

Table 4. Generalized Pareto distribution parameter estimates for the standardized residuals from the AR(1)-GJR-GARCH(1,1) model for each log-return series for the period from 3 January 2005–29 July 2011.

	TEMGVG1	IBCRP13	IBCOLAL	IBEHYFR	MSEMUIL	MSBRICL
l	−0.9577	−1.0920	−1.2775	−1.1539	−1.3427	−1.2551
${\xi }_l$	0.2713	0.0753	−0.1543	0.3202	−0.0585	−0.1005
${\beta }_l$	0.4083	0.6323	0.6093	0.6305	0.6699	0.7073
u	1.0050	1.1145	1.2844	1.1038	1.2142	1.1771
${\xi }_u$	0.0981	0.0281	−0.0866	0.0996	−0.1323	−0.0287
${\beta }_u$	0.5041	0.5177	0.5176	0.6019	0.4834	0.5830

After transforming the standardized residuals into uniform variates using the semi-parametric empirical cumulative distribution functions just derived, the next step is to use the maximum likelihood estimation method in order to fit the multivariate Student t-Copula to these data. The dependence matrix and the corresponding t-ratios are provided in Table 5. It can be noted that 13 out of 15 parameters are significant at the $1\%$ level. Moreover, the degrees of freedom for the multivariate Student t-Copula ν are relatively low (13.156), indicating the existence of tail dependence for all pairs of assets.

Table 5. Parameter estimates of the multivariate Student t-Copula involving the standardized residuals from the AR(1)-GJR-GARCH(1,1) model associated with each log-return series for the period from 3 January 2005–29 July 2011. The t-ratios are given in parentheses.

ν = 9.4947 **	IBCRP13	IBCOLAL	IBEHYFR	MSEMUIL	MSBRICL
(13.156)
TEMGVG1	0.8145 **	0.7828 **	−0.0272	−0.3179 **	−0.1812 **
	(114.414)	(95.986)	(−1.075)	(−14.081)	(−7.368)
IBCRP13		0.8067 **	0.1426 **	−0.2498 **	−0.1168 **
		(109.054)	(5.721)	(−10.603)	(−4.609)
IBCOLAL			−0.0003	−0.3339 **	−0.1674 **
			(−0.012)	(−14.986)	(−6.783)
IBEHYFR				0.2905 **	0.3029 **
				(12.617)	(13.209)
MSEMUIL					0.5929 **
					(39.938)

Note: ** denotes the coefficient significance at the 1% level.

Table 5. Parameter estimates of the multivariate Student t-Copula involving the standardized residuals from the AR(1)-GJR-GARCH(1,1) model associated with each log-return series for the period from 3 January 2005–29 July 2011. The t-ratios are given in parentheses.

ν = 9.4947 **	IBCRP13	IBCOLAL	IBEHYFR	MSEMUIL	MSBRICL
(13.156)
TEMGVG1	0.8145 **	0.7828 **	−0.0272	−0.3179 **	−0.1812 **
	(114.414)	(95.986)	(−1.075)	(−14.081)	(−7.368)
IBCRP13		0.8067 **	0.1426 **	−0.2498 **	−0.1168 **
		(109.054)	(5.721)	(−10.603)	(−4.609)
IBCOLAL			−0.0003	−0.3339 **	−0.1674 **
			(−0.012)	(−14.986)	(−6.783)
IBEHYFR				0.2905 **	0.3029 **
				(12.617)	(13.209)
MSEMUIL					0.5929 **
					(39.938)

Note: ** denotes the coefficient significance at the 1% level.

Finally, we simulate jointly-dependent asset log-returns by first simulating the corresponding dependent standardized residuals using the fitted multivariate Student t-Copula. We follow the suggestion of [4] about sample size and consider 20,000 scenarios. The daily log-returns are now converted into gross returns in accordance to our framework.

5.2. Pareto Frontiers and Portfolio Analysis

We preliminary evaluate the effectiveness of the proposed multi-objective optimization procedure in the case of two criteria by solving Problem (14). The quality of the dotted representation of the efficient frontier obtained by using the proposed version of the NNCmethod with 20 solutions is compared to that provided by the approximation with 20 optimal portfolios detected by the ϵ-constraint method in terms of both performance metrics and qualitative charts. The last set of solutions has been obtained by minimizing the invested capital c for different targets of the expected return on capital $ROC$. The chosen values for $ROC$ correspond to 20 equally-spaced points on the interval with the minimum and the maximum admissible value for $ROC$ as end-points. We analyze the optimality of these solution sets according to the following two criteria.

(i)

Deb’s diversity metric Δ [18] measures the spread of solutions in the given optimal set S. It is defined as:

$$\Delta (S)=\sum _{i=1}^{\left|S\right|-1}\frac{|d_i-\overline{d}|}{\left|S\right|-1}$$

where $\left|S\right|$ is the cardinality of S, $d_i$ represents the Euclidean distance between two consecutive solutions $i-1$ and i and $\overline{d}$ is the average of these distances. A low value of Δ indicates a better diversity of the non-dominated solution set.

(ii)

Hypervolume $HV$ [55] is defined as the volume in the objective space that is dominated by the optimal solution set S. It measures both the convergence to the true Pareto front and the diversity information. In fact, the larger is the value of $HV$, the closer are the solutions of S to the true Pareto front. At the same time, a higher $HV$ could indicate that the solutions of S are scattered more evenly in the objective space.

The results are reported in Table 6. It emerges that the proposed NNC method obtains a value for the Δ metric equal to half of that measured for the ϵ-constraint method and an $HV$ value that is slightly higher. These findings validate the superior ability of the proposed method to produce non-dominated optimal solution sets with respect to the classical method from a quantitative point of view.

Table 6. Performance metric results of the proposed version of the NNCmethod and of the ϵ-constraint method for Problem (14).

	Proposed NNC	ϵ-Constraint
Δ	0.0570	0.0987
$HV$	8.2265E-04	8.1539E-04

Table 6. Performance metric results of the proposed version of the NNCmethod and of the ϵ-constraint method for Problem (14).

	Proposed NNC	ϵ-Constraint
Δ	0.0570	0.0987
$HV$	8.2265E-04	8.1539E-04

It is also useful, for practical purposes, to conduct a qualitative analysis based on the direct comparison of the two dotted approximations of the true Pareto front. Figure 2 displays on the chart at the left the dotted representation of the efficient frontier obtained by using the proposed version of the NNC method with 20 solutions, whereas the chart on the right provides the solution set detected by the ϵ-constraint method. The comparison of the plots highlights the ability of the proposed version of the NNC method to identify Pareto optimal solutions along the entire Pareto front with respect to the ϵ-constraint method. In fact, while the former detects four solutions for optimal capital values between 3251.5 and 3252.5, the latter is unable to find any optimal portfolios in that rage, crucially limiting the set of optimal risk-return alternatives to the decision-maker. Thus, we will adopt the proposed version of the NNC method as the procedure for generating the Pareto front in the remaining experiments.

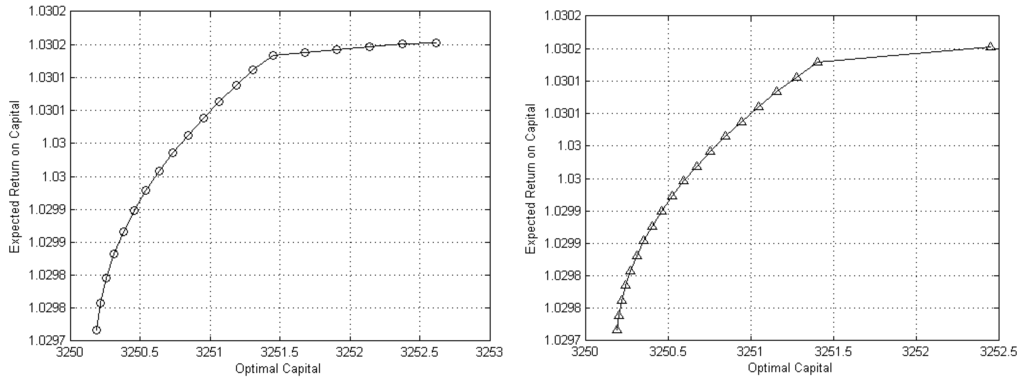
Figure 2. Graphical representations of the efficient frontier for the problem given by (14) drawn by the NNC method (on the left) and by the ϵ-constraint method (on the right).

Figure 2. Graphical representations of the efficient frontier for the problem given by (14) drawn by the NNC method (on the left) and by the ϵ-constraint method (on the right).

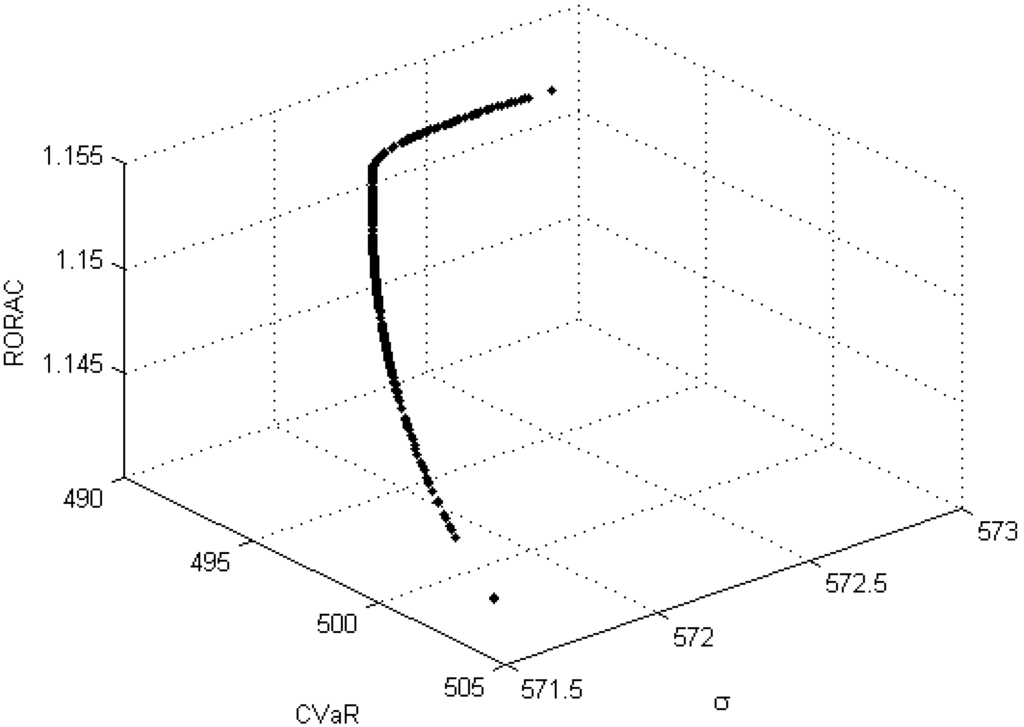
Figure 3. Graphical representations of the efficient frontier for the problem given by (15) drawn by the proposed version of the NNC method.

Figure 3. Graphical representations of the efficient frontier for the problem given by (15) drawn by the proposed version of the NNC method.

The optimal asset allocation in the presence of two risk measures is represented by Problem (15). On the basis of the dotted approximation in Figure 3 made by 453 optimal points, it can be noted that the set of solutions is a curve in the tri-criteria space σ-$CVaR$-$RORAC$. In order to analyze the interactions among the objectives, it is useful to consider the projections of this curve onto the σ-$CVaR$, σ-$RORAC$ and $CVaR$-$RORAC$ planes. The results are displayed in Figure 4, where the colored scatter plots represent the solutions in the corresponding plane with the color providing the intensity of the third objective. A color bar below each chart is added to describe the range of the third objective. The following qualitative considerations may be derived. The first chart sheds light on the link between risk-adjusted capital and portfolio volatility: until $\sigma \le 572.14$, $CVaR$ decreases as volatility increases, conversely, when $\sigma >572.14$, $CVaR$ increases as volatility increases. The second chart reveals that $RORAC$ is a non-decreasing and concave function of σ. Furthermore, by integrating the information of the first chart, we can conclude that for $\sigma \le 572.14$, a decision-maker may increase the performance measure $RORAC$ by simultaneously increasing σ and reducing $CVaR$. However, if he aims to obtain $RORAC$ values greater than 1.154, he has to handle more risk in terms of both σ, as well as $CVaR$. If an investor mainly focuses on the tradeoff between $CVaR$ and $RORAC$, he may operate his decisions in accordance to the third chart in Figure 3, where the efficient frontier in the plane $CVaR$-$RORAC$ is displayed. If the analysis is extended to include the considerations relative to the volatility, he may conclude that the $CVaR$-$RORAC$ solutions correspond to those portfolios for which the $CVaR$ increases when σ increases.

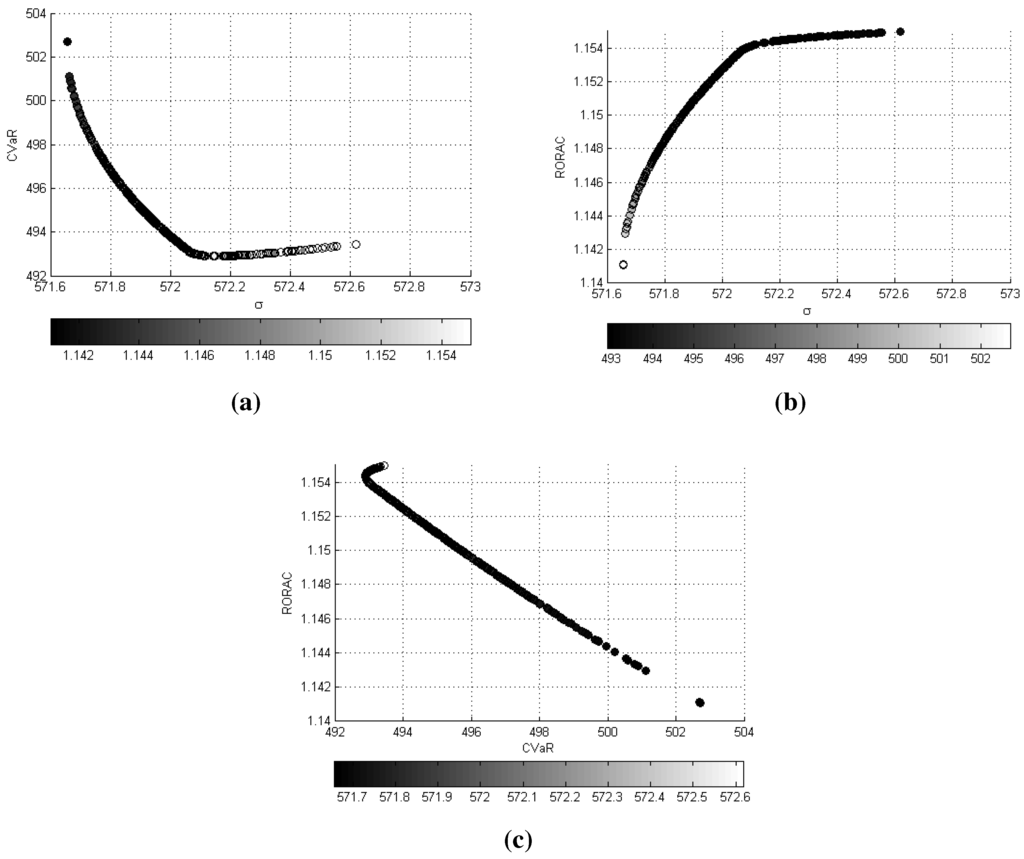
Figure 4. The projection of the efficient frontier for the problem given by (15) onto the $\sigma -CVaR$ plane is reported in (a), the projection onto the $\sigma -RORAC$ is displayed in (b) and (c) provides the projection onto the $CVaR-RORAC$ plane.

Figure 4. The projection of the efficient frontier for the problem given by (15) onto the $\sigma -CVaR$ plane is reported in (a), the projection onto the $\sigma -RORAC$ is displayed in (b) and (c) provides the projection onto the $CVaR-RORAC$ plane.

The third portfolio selection strategy, given in Problem (17), optimizes at the same time three performance measures. A dotted approximation of the Pareto front with 275 optimal portfolios is provided in Figure 5 from which we can argue that this set is a surface in the $ROC$-$SR$-$RORAC$ space. The qualitative tradeoff analysis is conducted by considering the bi-dimensional projections of the Pareto front displayed in Figure 6, as well as by evaluating the correlation matrix of objectives reported in Table 7. More precisely, the first chart on the left displays the region in the $SR$-$ROC$ plane where the efficient portfolios lay; however, it does not assist in the tradeoff analysis; at the same time, from Table 7, it emerges that the correlation between $SR$ and $ROC$ is $77.41\%$, indicating that $ROC$ shows the same upward movements of $SR$. Conversely, the $RORAC$ decreases as $SR$ increases, as suggested by the inspection of the chart on the right and confirmed by the sign of the correlation ($-63.07\%$). Analogous considerations affect the relation between $ROC$ and $RORAC$, which presents the behavior displayed in the chart below of Figure 6 with a negative correlation ($-43.22\%$). Furthermore, it may be interesting for risk management purposes to conduct a tradeoff analysis of the implicit risks and capital involved. In Figure 7 are displayed the charts of $CVaR$ vs. invested capital and of $CVaR$ vs. portfolio volatility, while in Table 8 are reported the corresponding correlations. By comparing the results, on the one hand, the pronounced negative relation between $CVaR$ and shareholders’ invested capital stands out, with a correlation equal to $-76.26\%$, which is a direct consequence of the definitions of $L_{\tau }$ and $CVaR$ given in Equations (1) and (4), respectively, and, on the other hand, the positive dependence between $CVaR$ and σ, with a correlation equal to $81.48\%$, which supports the findings relative to the $SR$-$RORAC$ tradeoff analysis.

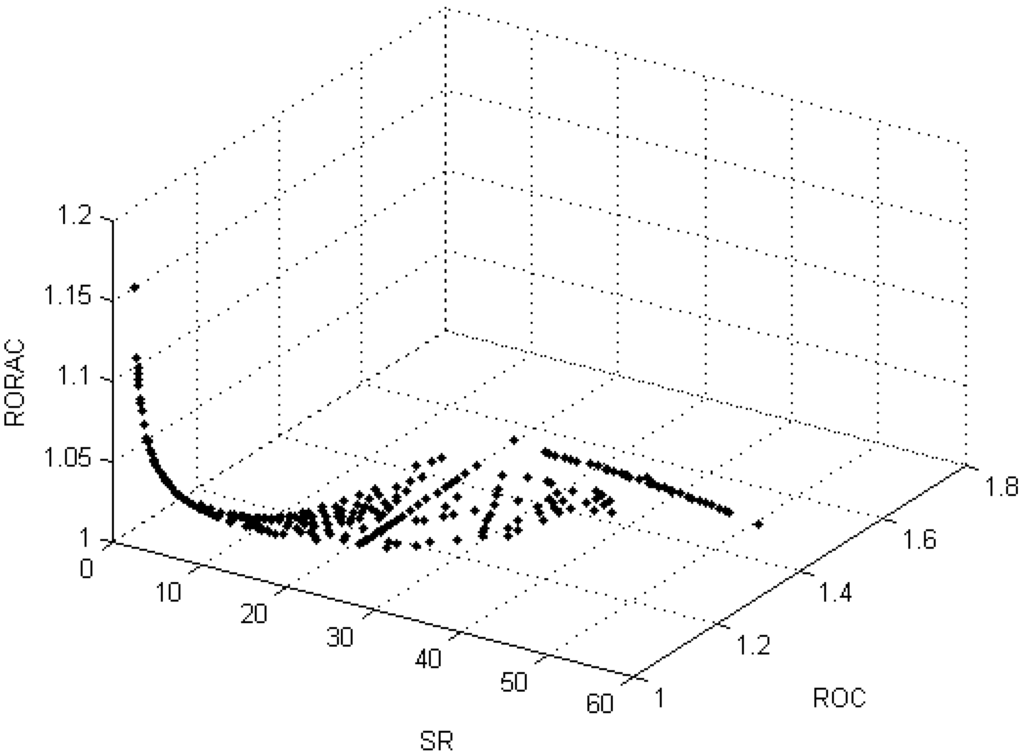
Figure 5. Graphical representations of the efficient frontier for the problem given by (17) drawn by the proposed version of the NNC method.

Figure 5. Graphical representations of the efficient frontier for the problem given by (17) drawn by the proposed version of the NNC method.

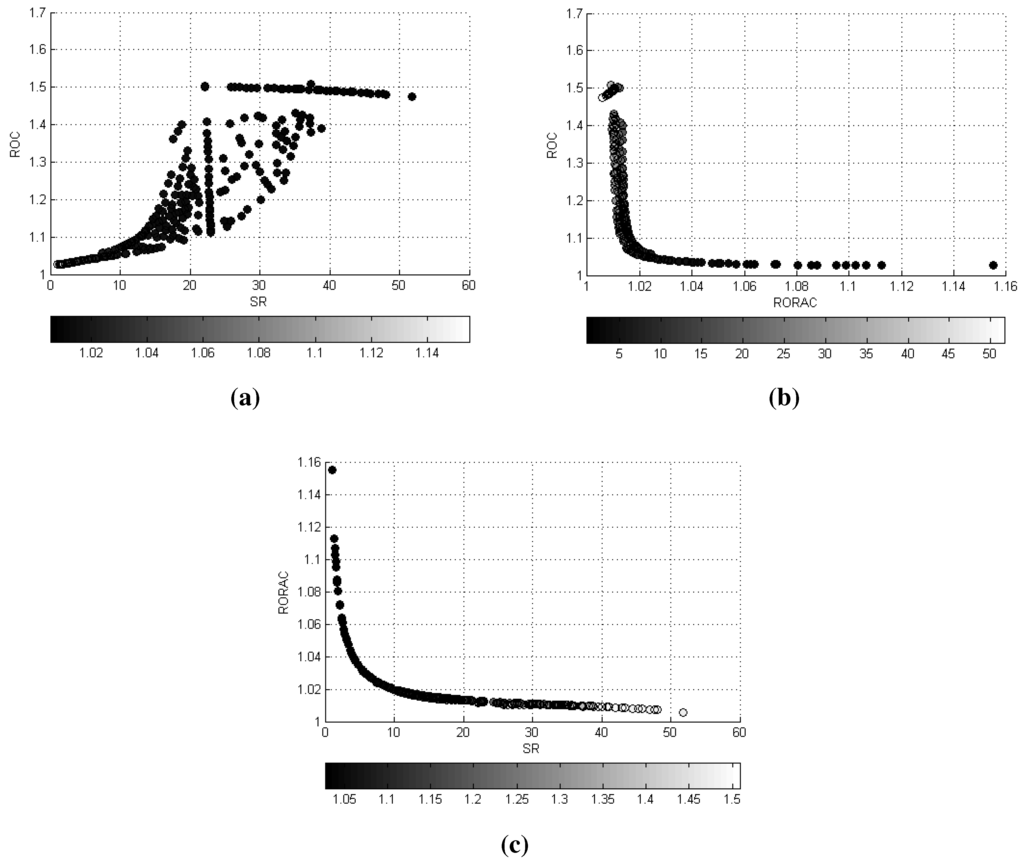
Figure 6. The projection of the efficient frontier for the problem given by (17) onto the $SR-ROC$ plane is reported in (a), the projection onto the $SR-RORAC$ is displayed in (b) and (c) provides the projection onto the $RORAC-ROC$ plane.

Figure 6. The projection of the efficient frontier for the problem given by (17) onto the $SR-ROC$ plane is reported in (a), the projection onto the $SR-RORAC$ is displayed in (b) and (c) provides the projection onto the $RORAC-ROC$ plane.

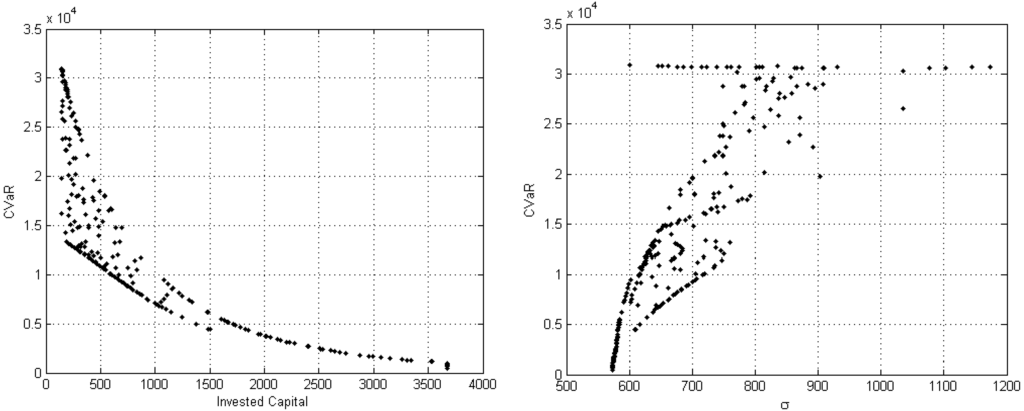
Figure 7. Scatter plot displaying displaying the link between $CVaR$ and invested capital (on the left) and between $CVaR$ and portfolio volatility (on the right) for the 275 portfolios detected on the Pareto front for the problem given by (17).

Figure 7. Scatter plot displaying displaying the link between $CVaR$ and invested capital (on the left) and between $CVaR$ and portfolio volatility (on the right) for the 275 portfolios detected on the Pareto front for the problem given by (17).

Table 7. Correlation matrix for objectives of the problem given by (17).

	ROC	RORAC
$SR$	0.7741	−0.6307
$ROC$		−0.4322

Table 7. Correlation matrix for objectives of the problem given by (17).

	ROC	RORAC
$SR$	0.7741	−0.6307
$ROC$		−0.4322

Table 8. Correlation of the conditional value-at-risk with shareholders’ invested capital and with portfolio volatility, respectively.

	Invested Capital	σ
$CVaR$	−0.7626	0.8148

Table 8. Correlation of the conditional value-at-risk with shareholders’ invested capital and with portfolio volatility, respectively.

	Invested Capital	σ
$CVaR$	−0.7626	0.8148

6. Summary and Conclusions

In this paper, we propose an alternative approach to tackle multi-objective portfolio optimization problems with chance constraints. The procedure involves semi-parametric techniques to generate scenarios and implements an alternative version of the normalized normal constraint method in order to provide an even dotted approximation of the Pareto front. High accuracy in solutions is achieved by integrating a global optimizer.

We apply this optimization framework in the portfolio selection process of an EU-based non-life insurance company that, on the one hand, aims at jointly solving for shareholders’ capital and investment weights and, on the other hand, seeks to minimize the risk of mismatch between assets and liabilities under the Solvency II Directive.

Three instances of the problem are experimentally investigated. In the first case, the shareholders’ expectations of obtaining a satisfactory rate of return on the provided capital are represented through a bi-objective optimization program. The comparison of the results with those obtained by the ϵ-constraint method confirms the superior ability of the proposed method to guarantee high quality approximations of the complete risk-reward profile.

The second portfolio strategy extends the analysis by including two risk measures in the optimization process; the insurance company is now characterized by the $RORAC$ concept with the conditional value-at risk and the portfolio volatility. The Pareto front results in being a curve in the σ-$CVaR$-$RORAC$ space. The objective tradeoff analysis is conducted by exploiting the bi-dimensional projections of this curve on the σ-$CVaR$, σ-$RORAC$ and $CVaR$-$RORAC$ planes. From the empirical study, the fundamental contribution of the knowledge of the link between risks in order to guide the decision-maker in the selection identification of an optimal portfolio emerges.

The third experiment takes into account the performance measures $ROC$, $RORAC$ and Sharpe ratio $SR$. The solutions set results in being a surface in the $ROC$-$RORAC$-$SR$ space. The tradeoff analysis in this case is based on the bi-dimensional projections and on the correlation matrix of the objectives. Considerations of the behavior of $CVaR$ in relation to the optimal invested capital and to the portfolio volatility are also derived.

The combination of mathematical programming methods and multiple criteria techniques has been proven to be very successful in portfolio optimization problems, also providing a useful tool to represent the relations among different risk measures, as well as performance indicators. In future work, we plan to proceed in analyzing other types of criteria and investments, possibly including more than three objectives.