1. Introduction and Rationale
In this paper, we focus on the solutions (w.r.t.
u and
c) of the nonlinear equation
where
is a sufficiently small number and
is the probability of ruin within finite time
in the standard diffusion risk model,
i.e., when the annual risk reserve at time
is defined as
Here
is the initial risk reserve and
is the premium rate. By
,
, we denote a standard Brownian motion. The aggregate claims payout process
,
, is a diffusion with continuous time, starting at zero. Its drift coefficient is
and diffusion coefficient is
. The variance is
.
Bearing in mind the well known result for diffusion with linear drift (see, e.g., Equation 1.1.4 in Part II, Chapter 2 of [
1]), we have in this model
Here
and
are the standard normal c.d.f. and p.d.f. respectively.
The solution of Equation (
1) with respect to
u is called the
α-level initial capital, or ruin capital. We denote it by
. The solution with respect to
c is called the
α-level premium rate. We denote it by
. Since (see Equation (
3))
for any
, and since
monotone decreases, as
(
) increases, the solution
exists for all
, but only small
α are of interest. This solution is bounded from above by
and monotone decreases to zero, as
c increases.
It is easy to see that for any
and for any
The inverse functions for both
and
obviously exist
1. From Equation (
4) and Equation (
5), we have
for any
and
for any
. So, enough is to focus on the ruin capital
.
The idea to look at the dependence of the initial capital u on the premium rate c, or vice versa, holding the probability of ruin at a prescribed level α, i.e., to use this probability merely as a binder, agrees with insurance regulation. In a nutshell, each insurance year the premium may be set within sensible limits, while the corresponding initial capital must be so large that the probability of ruin remains at a prescribed level.
Developing a sensible control over the years
2, insurance managers are interested not in the probability of ruin as itself, but in a good balance between the control leverages, such as the initial capital and premium rate, which makes the solvency controllable. Typically, the expressions for the probability of ruin within finite time like Equation (
3) are either absent or intractable, and the decision makers perform their calculations numerically
3.
Even when an explicit formula like Equation (
3) exists, to find
in an explicit form, using elementary functions, is a tremendous endeavor. This can not be done even in our diffusion model Equation (
2). However, in order to develop a sensible control, we need to scrutinize the behavior of
for all possible values of
. To this end, we propose in this paper informative and elementary upper and lower bounds. These bounds are compound and give valuable information about
in the both cases of profitable (
) and unprofitable (
) risk reserve process. The fundamental observation underlying the proof in the former case is the convexity (concavity downward) of
, as a function of
c.
In [
5], we have considered the similar problem in the classical Lundberg model. The classical Lundberg model yields the second exceptional case where the analytical expression for the probability of ruin within finite time is known. Unlike in [
5], the bounds in this paper are given for each
t rather than asymptotically, as
.
The rest of the paper is arranged as follows.
In
Section 2, we formulate some background results obtained previously.
In
Section 3, we formulate the main results. The fundamental remark about convexity of
as a function of
c, as
, is proved by showing that
is positive. To find this second derivative, we apply the implicit function theorem. The other technical tool are the inequalities for the Mill’s ratio proved in [
6].
In
Section 4, we formulate some auxiliary results.
3. The Main Results
In this section, our goal is to improve the upper bounds in Theorem 3, as , and in Corollary 2, as . This improvement makes these rather rough upper bounds much more accurate and informative.
Our plan regarding Theorem 3 is as follows. First, for
, we prove the convexity (concavity downward) of
, as a function of
c. Then we enhance Theorem 3, as illustrated in
Figure 2 and
Figure 3. We draw the tangent line to hyperbola
which is an upper bound for the ruin capital for
. Since
is a convex function of
, this tangent line is the required upper bound on
to the left of the point of tangency.
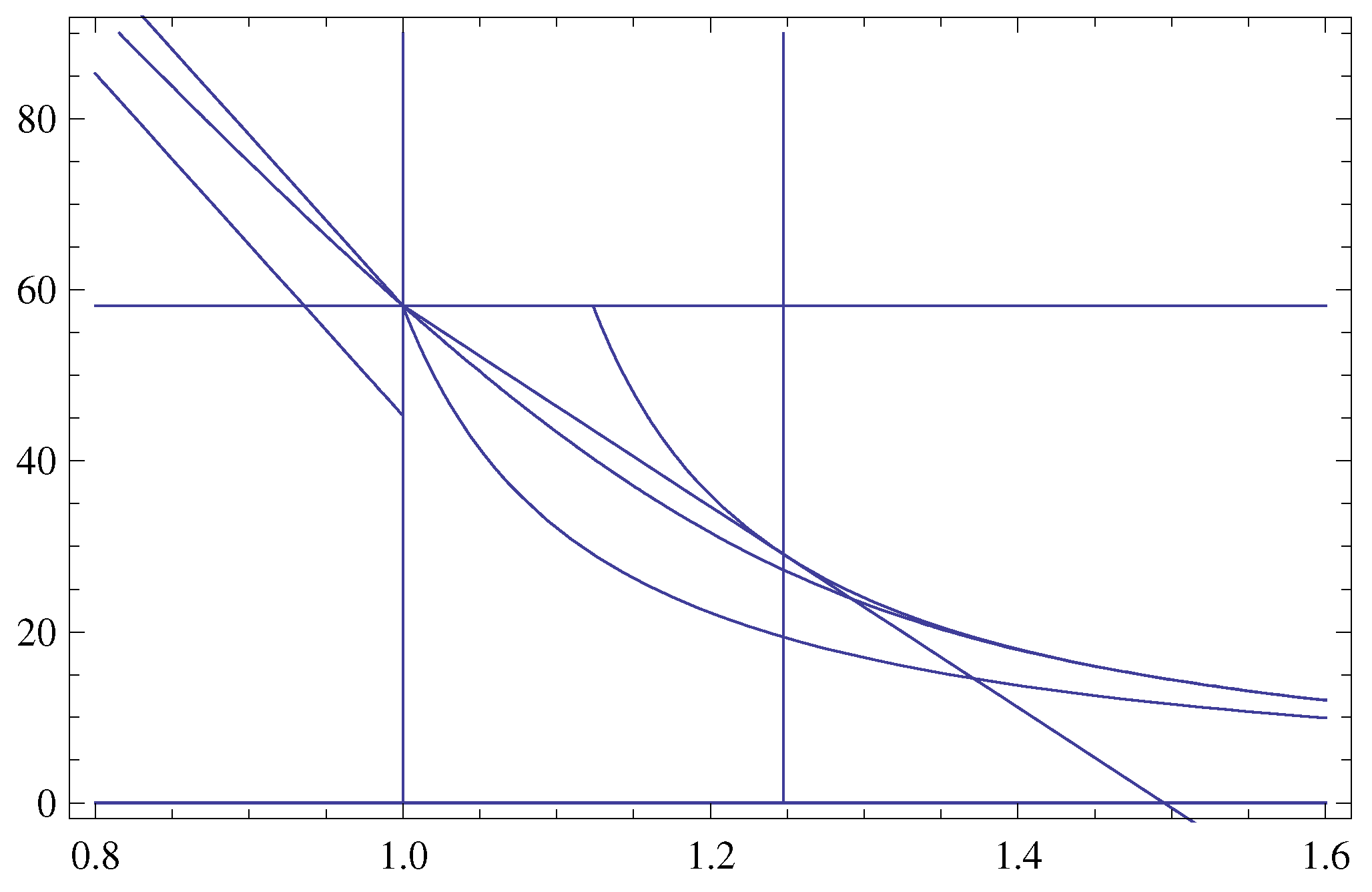
Figure 2.
Graphs shown in
Figure 1, with the graph of sloping straight line
starting from the point with abscissa
ϑ and ordinate
, and tangent to the hyperbola
at (right vertical line)
.
Figure 2.
Graphs shown in
Figure 1, with the graph of sloping straight line
starting from the point with abscissa
ϑ and ordinate
, and tangent to the hyperbola
at (right vertical line)
.
We formulate the following Theorem 4 which yields the improved upper bounds for
, as
. It is illustrated in
Figure 3. The proof of Theorem 4 is illustrated in
Figure 2 and will be presented at the end of this section.
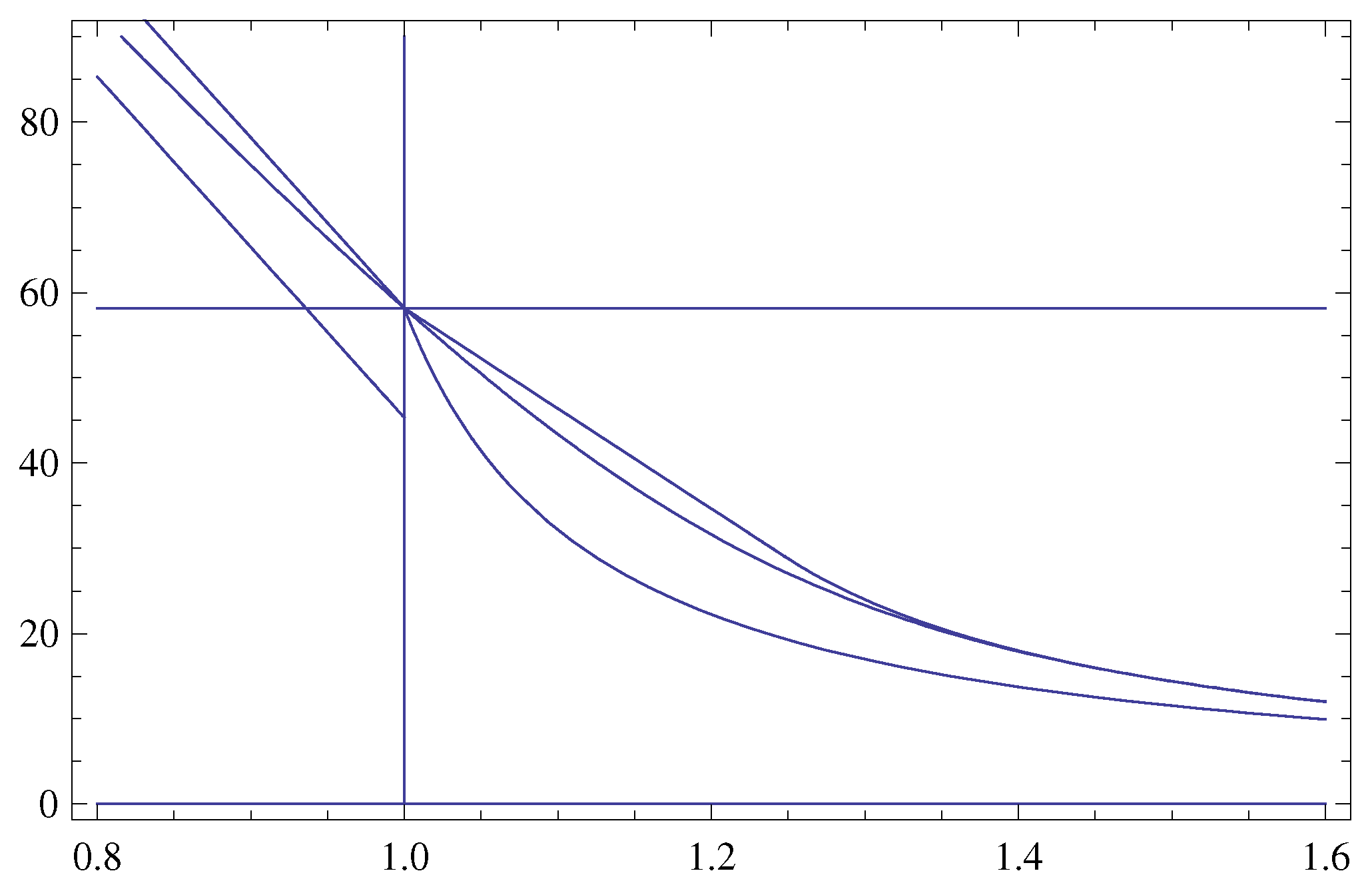
Figure 3.
The function of the variable (X-axis), as , , , and the bounds of Theorem 3 improved in Theorem 4.
Figure 3.
The function of the variable (X-axis), as , , , and the bounds of Theorem 3 improved in Theorem 4.
Theorem 4 In the diffusion model Equation (2), for we have The following result yields the improved upper bounds for , as .
Corollary 3 In the diffusion model Equation (2), for we have The following result is fundamental.
Theorem 5 For , the function of the variable c is convex.
Proof of Theorem 5 It suffices to show that . Bearing in mind Equation (1), apply Theorem 6. We haveand7 Bearing in mind Equation (3), introduce8We haveandFurthermore9, for Direct algebraic manipulations yieldwhereand (see Section 4.2)is Mill’s ratio. Note thatwhereand Prove that for . Bearing in mind that and for any finite w (see inequalities Equation (14)), it follows fromtrue for , and fromWe finally have for all and and the proof is complete. Proof of Theorem 4 Bearing in mind the convexity10 of established in Theorem 5, apply Theorem 6 with , , . We have the straight linetangent to the hyperbolaThis hyperbola is (see Theorem 3) the upper bound for , as . Abscissa and ordinate of the point of tangency are and . Taking the tangent line as the bound for and the hyperbola as the bound for , we complete the proof.
Proof of Corollary 3 It follows straightforwardly from Theorem 4 and from the fact that for any .