Cooperative Game Theory of Hierarchies: One Approach to Solving the Low-Risk Puzzle?

Abstract

In this article, we extend the application of cooperative game theory to the so-called low-risk puzzle. Specifically, we apply concepts that consider hierarchies on the assets in the allocation of portfolio risk. These hierarchies have not previously been considered in portfolio risk allocation using cooperative game theory. We demonstrate our idea through a simulation study. Our results show that considering hierarchies can contribute to solving the low-risk puzzle. Our findings may advance further developments in portfolio theory.

1. Introduction

This article builds on previous studies of the so-called low-risk puzzle (also called the low-risk anomaly) by incorporating concepts from cooperative game theory. These studies have used concepts such as the Shapley value to allocate portfolio risk to individual assets. The Shapley value is probably the best-known value-like solution concept in cooperative game theory (Roth 1988). An advantage is that it takes into account all contributions that an asset makes to the risks of all other asset groups. When applying the Shapley value, no other structures in the set of assets are taken into account. In reality, however, there are many structures or relationships between assets. One such structure is represented by hierarchies between assets. An example of a hierarchical structure between assets is the relationship between a firm’s equity and its debt capital (Modigliani and Miller 1958). Another example is the interdependence between different asset classes such as stocks, bonds and commodities over time (Bekaert and Harvey 1995). These interdependencies could be structured hierarchically. In this case, the portfolio optimization problem consists of finding the optimal diversification across a set of potentially interdependent assets in order to maximize return and minimize the risk (Muzy et al. 2010). In addition, the hierarchical risk parity is an advanced investment portfolio optimization framework developed by Lopez de Prado (2016). In this approach, assets are grouped into clusters based on their correlations, forming a hierarchical tree structure. Our paper applies the values of cooperative game theories that take into account these hierarchies among assets when allocating portfolio risk across assets.

In addition to the conventional approach of assessing an asset’s risk on an isolated basis—as evidenced by metrics such as asset variance—capital market theory offers several techniques for the distribution of portfolio risk across distinct assets. These include the activity-based method (Hamlen et al. 1977), the Beta method (Homburg and Scherpereel 2008), the machine learning-based dynamic capital asset pricing model (Wang and Chen 2023) and the incremental approach (Jorion 1985). Furthermore, a large body of scientific literature has emerged that applies the methods of cooperative game theory, particularly the Shapley value (Shapley 1953), the nucleolus (Schmeidler 1969) and the $\tau$ value—also known as the cost gap method (Tijs and Driessen 1986)—to this problem (Auer and Hiller 2019, 2021; Balog et al. 2017; Colini-Baldeschi et al. 2018; Mussard and Terraza 2008; Ortmann 2016, 2018; Shalit 2020, 2023; Simonian 2019; Terraza and Mussard 2007).

Nevertheless, even in the absence of a cooperative game-theoretic approach, empirical evidence from capital market theory indicates that the measurement of risk for an asset has remained a significant challenge. Contemporary theory suggests that assets with higher returns inevitably carry a corresponding level of risk (Lintner 1965; Markowitz 1952; Mossin 1966; Rubinstein 2002; Sharpe 1964). Empirically, an opposing phenomenon has been observed, which is referred to as the ‘low-risk puzzle’. Moreover, the existence of this phenomenon remains consistent across different classical risk measures (Auer and Schuhmacher 2021; Baker et al. 2011; Blitz et al. 2014; Dutt and Humphery-Jenner 2013; Frazzini and Pedersen 2014). The empirical evidence indicates that assets with low risk (volatility) consistently generate higher returns, a phenomenon that remains consistent across global large-cap assets, as well as the U.S., European and Japanese markets. Moreover, the low-risk puzzle cannot be attributed to other factors, such as the book-to-market ratio or free float market value. This puzzle demonstrates resilience when evaluated across different periods of volatility measurement (Blitz and van Vliet 2007). The analysis by Schneider et al. (2020) indicates that the low-risk puzzle in the capital asset pricing model and in traditional factor models exist when investors require compensation for coskewness risk. A recent literature review is provided by Traut (2023). One potential explanation for this empirical phenomenon is the inherent challenge of allocating portfolio risk to individual assets (Baker et al. 2011). Auer and Hiller (2019; 2021) show, in simulation studies, that using the Shapley value instead of classical risk measures has the potential to solve the low-risk puzzle.

In addition to considering all marginal contributions, cooperative game theory provides a framework for the incorporation of a hierarchy between assets. In Gilles et al. (1992), van den Brink and Gilles (1996) and van den Brink (1997), values for games with a hierarchical structure (H values) were introduced. In H values, single-dominance relationships, i.e., the influence of a predecessor on direct successors, are equally strong. These values assume that a player has to obtain permission from all their superiors to generate a certain amount of worth. Without all superior players, a player could not be productive. In other words, the superiors of a player have veto power against the player. However, it is a plausible assumption that the relationships between players may have different strengths. Using this idea to improve the modeling of hierarchies, Casajus et al. (2009) introduced a weighted hierarchy value based on the Shapley value—the ${\mathrm{wH}}^{\mathrm{Sh}}$ value. This approach uses a weighted directed graph to model hierarchies. Two elements form the basis of the ${\mathrm{wH}}^{\mathrm{Sh}}$ value. First, all players cooperate symmetrically to produce the output. In this step, the output is distributed to the players according to the Shapley value (Shapley 1953). In a second step, the weighted hierarchy redistributes a certain fraction of these payoffs. The weighted hierarchy has only allocational effects.1 In Hiller (2014), the ${\mathrm{wH}}^{\mathrm{Sh}}$ value has been generalized to games with a graph/network. One value for these games is the Myerson value, My (Myerson 1977). Hence, the ${\mathrm{wH}}^{\mathrm{My}}$ value is one generalized wH value. In addition to games with hierarchical structures with directed graphs, there are analogous structures in cooperative game theory. These include undirected graphs/networks (Borm et al. 1992; Gómez et al. 2003; Herings et al. 2008; Myerson 1977; Navarro 2020), which were analyzed in Hiller (2023) and Hiller (2025) with regard to their contribution to solving the low-risk puzzle. In these games, the players are connected by a graph, but there is no superior–subordinate relationship between them. The undirected networks could be interpreted as communication channels. In addition, undirected graphs could model similarities between assets, e.g., branches, company size or the regional origin of an asset. Suppose that there are three assets: an American car manufacturer, an American technology company and a European technology company. The first and last assets have nothing in common, while the second asset is somewhere in between the other two and can ‘dock’ with both (Alvarez-Mozos et al. 2013). In van den Brink (2012), the distinction between hierarchies and undirected graphs/networks is explained in more detail and, in addition, with respect to economic applications. van den Brink et al. (2017) establish the formal connection between undirected graphs/networks and hierarchies. In games with level structures (Kalai and Samet 1987), players are divided into different levels, but there is no concrete assignment of a player from a lower level to a player in a higher level. The German stock market, for example, offers the DAX, MDAX and SDAX, which are different levels in terms of the market capitalization of companies.

As mentioned, games with a hierarchical structure are the starting point for our article. By simulation, we seek to analyze whether the technical inclusion of hierarchies on the set of assets can increase the number of corrections of the rankings between the assets—hence solving the low-risk puzzle. Concretely, we apply the H value, the ${\mathrm{wH}}^{\mathrm{Sh}}$ value and the ${\mathrm{wH}}^{\mathrm{My}}$ value. For our analysis, we conduct a simulation study based on the ideas of Auer and Hiller (2019, 2021). We consider an investor who is interested in combining individual assets into a portfolio and assess the riskiness of each asset based on payoffs according to the weights of assets. Our setup is designed such that the low-risk puzzle lies in the variances of the individual assets. We then generate the covariance matrix of the assets repeatedly at random. We consider three schemes for the asset shares in a portfolio. Based on these data, we calculate the asset risks and the percentage of cases in which they lead to asset rankings that differ from the individual asset variances. We also calculate Shapley risk distributions as a benchmark and determine whether there are more corrections when hierarchical relationships between assets are taken into account.

This paper is organized as follows. In Section 2, we explain the basic notions of cooperative game theory. In the next section, our simulation study and our results are the subject. Finally, Section 4 summarizes the paper and outlines directions for future research.

2. Cooperative Game Theory

2.1. Games $\left(N,v\right)$

A transferable utility (TU) game in cooperative game theory is denoted by $\left(N,v\right)$, where $N=\{1,2,\cdots ,n\}$ is the non-empty and finite set of players. The number of players in N is n or $\left|N\right|.$ The coalitional function v assigns every subset $K\subseteq N$ a certain worth $v\left(K\right)$-the risk of a portfolio of K-i.e., $v\in \{f:2^N\to \mathbb{R},\left|f(\varnothing )=0\right.\},$ where $2^N$ denotes the power set of N.

A value is an operator $\varphi$ that assigns (unique) payoff vectors to all games $\left(N,v\right)$, i.e., uniquely determines a payoff for every player in every TU game. One value is the Shapley value. In order to calculate the players’ payoffs, rank orders $\rho$ on N are used. They are written as $({\rho }_1,\cdots ,{\rho }_n)$, where ${\rho }_1$ is the first player in the order, ${\rho }_2$ the second player, etc. The set of these orders is $RO\left(N\right)$; $n!$ rank orders exist. The set of players before i in rank order $\rho$ and player i is $K_i\left(\rho \right).$ For $i,$ we have (Shapley 1953)

$${\mathrm{Sh}}_i\left(N,v\right)={\displaystyle \frac{1}{n!}}\sum _{\rho \in RO\left(N\right)}v\left(K_i\left(\rho \right)\right)-v\left(K_i\left(\rho \right)\setminus \left\{i\right\}\right).$$

(1)

2.2. Games $\left(N,v,S\right)$

As in Gilles et al. (1992), van den Brink and Gilles (1996), van den Brink (1997), Casajus et al. (2009) and van den Brink and Dietz (2014), for example, a permission structure is a mapping $S:N\to 2^N.$ To each player, we assign the players who are direct successors of $i.$S can be interpreted as a directed graph (Bollobás 2002). $S\left(i\right)$ denotes the direct successors of $i$ with $i\notin S\left(i\right).$ The players in $S^{-1}\left(i\right)=\left\{j\in N:i\in S\left(j\right)\right\}$ are the direct predecessors of i; $S^{-1}\left(K\right)={\bigcup }_{i\in K}{S}^{-1}\left(i\right).$

For the hierarchy between assets, we assume a tree structure. Within this structure, a path T in N from i to j is a sequence $T\left(i,j\right)=〈r_0,r_1,\cdots ,r_{k-1},r_k〉$ with $i=r_0$, $j=r_k$ and $r_{l+1}\in S\left(r_l\right)$∀$l=0,\cdots ,k-1$. A path can be interpreted as a chain of commands or chain of reporting between i and j, whereby i is a predecessor of j. The set of successors of i is $\widehat{S}\left(i\right):=\left\{j\in N\setminus \left\{i\right\}:\mathrm{there}\mathrm{is}\mathrm{a}\mathrm{path}\mathrm{from}i\mathrm{to}j\right\}$. Analogously, we denote the set of i’s predecessors by ${\widehat{S}}^{-1}\left(i\right):=\left\{j\in N\setminus \left\{i\right\}:\mathrm{there}\mathrm{is}\mathrm{a}\mathrm{path}\mathrm{from}j\mathrm{to}i\right\}$. A tree structure formally satisfies two conditions:

• there is one player $i_0\in N$, such that $S^{-1}\left(i_0\right)=\varnothing$ and $\widehat{S}\left(i_0\right)=N\setminus \left\{i_0\right\}$, and
• for every player $i\in N\setminus \left\{i_0\right\}$, we have $\left|S^{-1}\left(i\right)\right|=1$.

A hierarchical game is a tuple $\left(N,v,S\right).$ For these games, a value is an operator $\psi .$ Gilles et al. (1992), van den Brink and Gilles (1996) and van den Brink (1996) introduced two values $\psi$—the conjunctive approach value and the disjunctive approach value. Both values coincide if the hierarchy has a tree structure. To calculate a player’s payoff, for each coalition $K\subseteq N$, the feasible set ${\left.K\right|}_S$ has to be determined: ${\left.K\right|}_S=\left\{\left.i\in K\right|{\widehat{S}}^{-1}\left(i\right)\subseteq K\right\}.$ The restricted coalitional function ${\left.v\right|}_S$ is given by

$${\left.v\right|}_S\left(K\right):=v\left({\left.K\right|}_S\right).$$

(2)

Based on this function, the conjunctive approach value and the disjunctive approach value calculate player’s i payoff by

$$H_i\left(N,v,S\right)=S{h}_i\left(N,{\left.v\right|}_S\right).$$

(3)

2.3. Games $\left(N,v,S,\omega \right)$

One disadvantage of the concepts for games $\left(N,v,S\right)$ is that the hierarchical relationship is fixed. Besides the hierarchy S, weighted relationships between the players can be considered. The vector $w:N\to \mathbb{R}$ assigns every player i a weight ${\omega }_i,$$0\le {\omega }_i\le 1$ with ${\omega }_{i_0}=0.$ If a vector maps all players with the same weight $\omega$, except $i_0,$ i.e., ${\omega }_i={\omega }_j=\omega$ for all $i,j\in N\setminus \left\{i_0\right\},$ we denote the vector by $\overline{\omega }$. A weighted hierarchical game is a tuple $\left(N,v,S,\omega \right).$ A value for these games is an operator $\phi .$ The ${\mathrm{wH}}^{\mathrm{Sh}}$ value is one value for $\left(N,v,S,\omega \right)$. All players $j,$ with $j\in {\widehat{S}}^{-1}\left(g\right),$ respectively, and all players in the path $T\left(i_0,g\right)$, receive a fraction of g’s Shapley payoff. For $i\in N$, the fraction of $g’$s payoff is (Casajus et al. 2009)

$$f_i\left(S,\omega ,g\right)=\left\{\begin{array}{cc}\left[1-{\omega }_i\right]{\displaystyle \prod _{\begin{array}{c}l\in \widehat{S}\left(i\right),\\ l\in T\left(i_0,g\right)\end{array}}}{\omega }_l,\hfill & i\in T\left(i_0,g\right),\hfill \\ 0,\hfill & \mathrm{else}.\hfill \end{array}\right.$$

(4)

From this, we have, for the ${\mathrm{wH}}^{\mathrm{Sh}}$ payoff of player $i\in N$,

$${\mathrm{wH}}_i^{\mathrm{Sh}}\left(N,v,S,\omega \right)=\sum _{j=1}^n{f}_i\left(S,\omega ,j\right)·S{h}_j\left(N,v\right).$$

(5)

To honor players who coordinate other players, the wH value based on the Myerson value (Myerson 1977) has been axiomatized (Hiller 2014). Some further preliminaries are necessary to introduce this value. First, a graph L on the set of players is considered. The set of possible pairwise links between players is $L^N=\left\{\left\{i,j\right\}:i,j\in N,i\ne j\right\},$ whereat $\left\{i,j\right\}$ and $\left\{j,i\right\},$ respectively (or $ij$ and $ji$), is the direct link between players i and j. A cooperation structure CO on N is a graph $\left(N,L\right)$ with $L\subseteq L^N.$ A CO game is characterized by $(N,v,L)$. From hierarchy $S,$ we construct $L_S$: $L_S=\left\{ij:i\in S\left(j\right)\right\}$∀$i,j\in N$; thus, the CO game $(N,v,L_S)$ results. The graph $L_{S.}$ partitions N into components $C_1,\cdots ,C_k.$ This partition is called $N\setminus L_S.$ Each player is in one component; $C_i\cap C_j=\varnothing ,$$i\ne j,$$N=\bigcup C_j.$$N\setminus L_S\left(i\right)$ denotes the component of i. Two players i and j with $N\setminus L_S\left(i\right)=N\setminus L_S\left(j\right)$ are connected. The restricted coalitional function ${\left.v\right|}_{L_S}$ is given by

$${\left.v\right|}_{L_S}\left(K\right):=\sum _{C\in K\setminus L_S}v\left(C\right)\forall K\subseteq N.$$

(6)

The worth of a coalition K is the sum of the worth of its components. In the case $\left|K\backslash L_S\right|=1$, we have $v\left(K\right)={\left.v\right|}_{L_S}\left(K\right).$ A CO value is an operator $\psi$ that assigns (unique) payoff vectors to all CO games. One CO value is the Myerson value (Myerson 1977). According to this value, player $i’$s payoff is2

$$M{y}_i\left(N,v,L_S\right)=S{h}_i\left(N,{\left.v\right|}_{L_S}\right).$$

(7)

With these preliminaries, ${\mathrm{wH}}_i^{\mathrm{My}}$ is (Hiller 2014, 2021)

$${\mathrm{wH}}_i^{\mathrm{My}}\left(N,v,S,\omega \right)=\sum _{j=1}^n{f}_i\left(S,\omega ,j\right)·{\mathrm{My}}_j\left(N,v,L_S\right).$$

(8)

For a literature review regarding values in games with hierarchies, see van den Brink (2017).

3. Simulation

3.1. General Setting

In our application, we determine the coalition function v by

$$v\left(K\right)=\sum _{i\in K}{w}_i^2·{\sigma }_i^2+2·\sum _{i\in K}\sum _{j\in K,j>i}{w}_i·w_j·{\sigma }_i·{\sigma }_j·{\sigma }_{ij}$$

(9)

whereby $w_i$ are asset weights; ${\sum }_{i\in N}{w}_i=1,$${\sigma }_{ij}$ are correlations between two assets i and j; and ${\sigma }_i$ are standard deviations.

Since our study is similar to those by Auer and Hiller (2019, 2021), we adopt some of their simulation settings. We analyze a three-asset scenario, $N=\left\{1,2,3\right\}.$ We assume mean returns ${\mu }_1>{\mu }_2>{\mu }_3$ and variances ${\sigma }_1^2<{\sigma }_2^2<{\sigma }_3^2.$ Therefore, the low-risk puzzle emerges, given that the asset with the lowest risk/variance (asset 1) achieves the highest return. Further, we have a $3\times 3$ covariance matrix $\mathbb{V}$ of asset returns. For asset shares $w_i$, we have ${\sum }_{i\in N}{w}_i=1.$ In this study, we analyze three asset allocation schemes within a portfolio. In the first weighting scheme, the investor is assumed to be a minimum-variance investor with respect to $v\left(N\right)$. Thus, the asset weights are determined in such a way that $v\left(N\right)$ is minimized. The second weighting scheme has random shares assuming a uniform distribution of asset shares between 0 and $1.$ The third scheme is a naive one with $w_i={\displaystyle \frac{1}{3}}\forall i\in N.$

Furthermore, we implement an additional technical configuration of the simulation proposed by Auer and Hiller (2019). The covariance matrix $\mathbb{V}$ and the asset shares in the second weight scheme are simulated 100,000 times; the standard deviations of assets range from 0 to 10 and asset correlations range from $-1$ to $1.$3

We consider the hierarchies shown in Figure 1. In each of the hierarchies A to C, one asset is at the top of the hierarchy and the other two assets are direct successors of this asset. In hierarchies D to I, the asset at the top of the hierarchy is directly followed by only one asset. The third asset is the direct successor to this asset. In addition, we assume four weight vectors $\overline{\omega }$ with respect to the ${\mathrm{wH}}^{\mathrm{Sh}}$ value and the ${\mathrm{wH}}^{\mathrm{My}}$ value-$\overline{\omega }=0.25,$ $\overline{\omega }=0.50,$ $\overline{\omega }=0.75$-and random weights assuming a uniform distribution of $\overline{\omega }$ between 0 and $1.$ This broad approach, with all possible hierarchical structures on the set of three assets and a variety of weight vectors, allows for a detailed analysis of how hierarchies affect the correction of the low-risk puzzle.

3.2. Analytical Framework

Our results reflect the proportions of cases in which

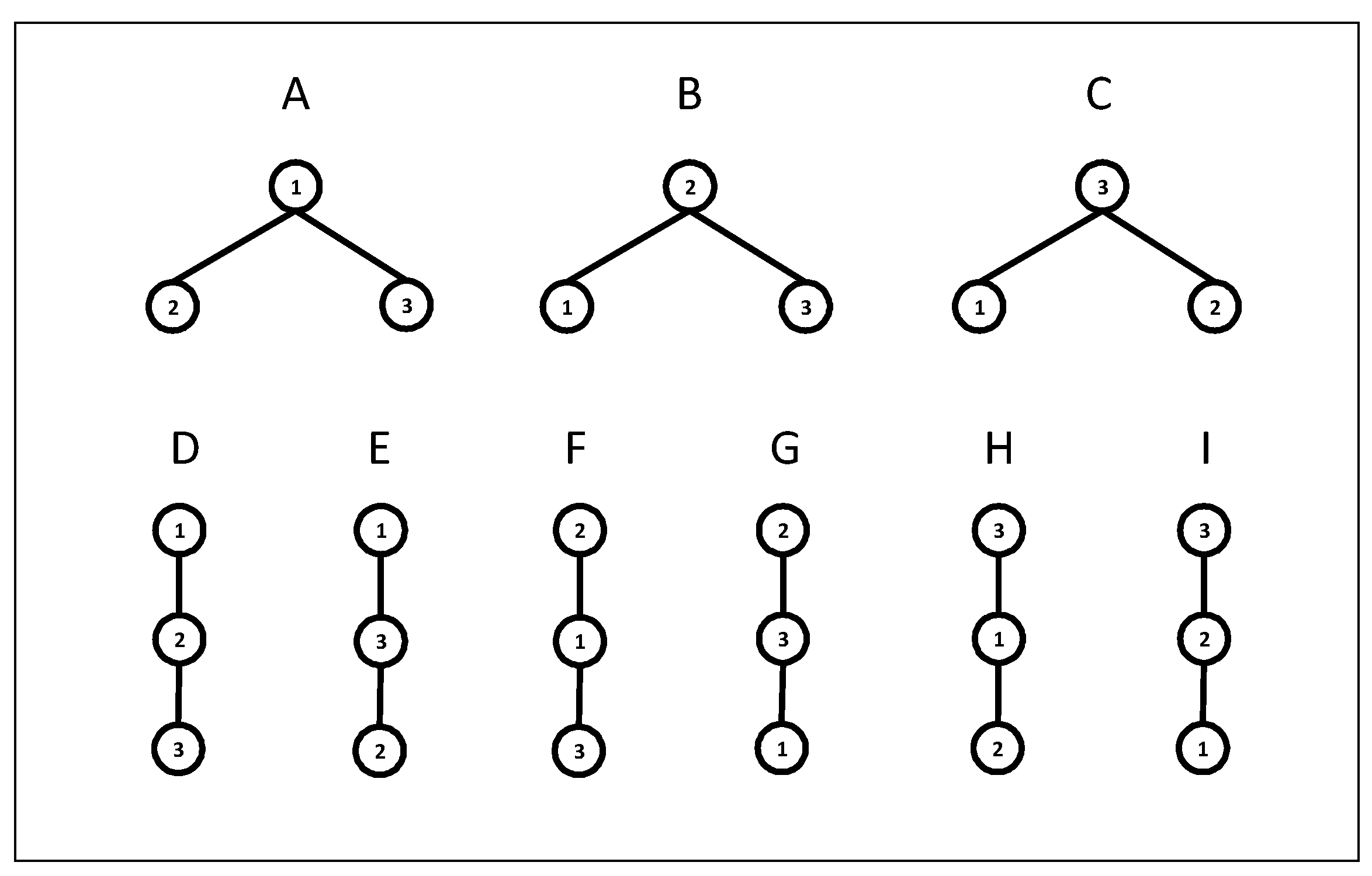
• a rank correction between assets 1 and 2;
• any partial correction (two assets change ranks); or
• full correction

occurs. In addition, we compute the so-called risk–return relationship. We apply the least-squares method to a linear equation linking the mean return vector (with arbitrary values of [3 2 1] for the assets) to the risk allocation vector (computed by the weighted values). Very similarly, Auer and Hiller (2021) use this method to analyze the best remedy for the low-risk anomaly on the basis of cooperative game theory values. If the slope of the regression line is positive, the low-risk puzzle is solved for the average. In our analysis, the results of the Shapley value are used as benchmarks (

Table 1. Results for the Shapley value.

Correction	Directional	Full	Proportion Pos.
1 and 2	Correction	Correction	Risk–Return Rel.
0.0961	0.1414	0.0024	0.0134

). We analyze in detail our results for asset weights that minimize $v\left(N\right).$

3.3. Results for the H Value

The first results analyzed are those for the H value (

Table 2. Results for the H value, minimum-variance asset share.

Hierarchy	Correction	Directional	Full	Proportion Pos.
	1 and 2	Correction	Correction	Risk–Return Rel.
A	1.0000 *	1.0000 *	0.4077 *	1.0000 *
B	0	1.0000 *	0	0.1945 *
C	0.2436 *	0.2436 *	0	0
D	1.0000 *	1.0000 *	0.1684 *	1.0000 *
E	1.0000 *	1.0000 *	0.7416 *	1.0000 *
F	0	1.0000 *	0	0
G	0	1.0000 *	0	0.8370 *
H	0	0	0	0
I	1.0000 *	1.0000 *	0	0

* Results above the results of the Shapley value.

). With *, we mark results that are above the results of the Shapley value. Hierarchies $A,$ C, D, E and I correct better between assets 1 and 2 with respect to Shapley. In hierarchies $A,$ D and E, asset 1 is on top in the hierarchy and asset 2 is on a lower level. In hierarchies C and $I,$ both assets are not at the top position, and, for both assets, the chances of making marginal contributions are greatly reduced. If any directional correction is considered, all hierarchies except H perform better compared to Shapley. With respect to full corrections, only hierarchies $A,$ D and E outperform Shapley. Regarding the proportion of positive risk–return relations, $A,$ B, $D,$ E and G provide better results than Shapley. Considering all four dimensions, hierarchies A, D and E improve the results in terms of solving the low-risk puzzle in all dimensions compared to Shapley.

3.4. Results for the ${\mathit{wH}}^{\mathit{Sh}}$ Value

The next step is to look at the results for the ${\mathrm{wH}}^{\mathrm{Sh}}$ value (

Table 3. Results for the wH Shapley value, minimum-variance asset share.

Hierarchy	Weight	Correction	Directional	Full	Proportion Pos.
	Vector	1 and 2	Correction	Correction	Risk–Return Rel.
A	0.25	0.1254 *	0.1688 *	0.0043 *	0.0222 *
	0.50	0.1859 *	0.2247 *	0.0089 *	0.0518 *
	0.75	0.3052 *	0.3350 *	0.0180 *	0.1420 *
	rand.	0.2349 *	0.2708 *	0.0119 *	0.1096 *
B	0.25	0.0815	0.1596 *	0.0028 *	0.0134
	0.50	0.0737	0.2167 *	0.0024	0.0134
	0.75	0.0828	0.3468 *	0.0015	0.0134
	rand.	0.0912	0.2835 *	0.0021	0.0134
C	0.25	0.0961	0.1312	0.0015	0.0100
	0.50	0.0961	0.1287	0.0014	0.0087
	0.75	0.0961	0.1427 *	0.0024	0.0155 *
	rand.	0.0961	0.1457 *	0.0028 *	0.0218 *
D	0.25	0.0451	0.1563 *	0.0045 *	0.0184 *
	0.50	0.0482	0.2483 *	0.0134 *	0.0346 *
	0.75	0.1044 *	0.3921 *	0.0519 *	0.0983 *
	rand.	0.1061	0.2948 *	0.0447 *	0.0866 *
E	0.25	0.1888 *	0.2138 *	0.0028 *	0.0209 *
	0.50	0.2779 *	0.2922 *	0.0034 *	0.0482 *
	0.75	0.3974 *	0.4048 *	0.0045 *	0.1420 *
	rand.	0.3050 *	0.3225 *	0.0034 *	0.1102 *
F	0.25	0.3473 *	0.3931 *	0.0030 *	0.0161 *
	0.50	0.5008 *	0.5755 *	0.0026 *	0.0209 *
	0.75	0.5679 *	0.7288 *	0.0019	0.0299 *
	rand.	0.4294 *	0.5597 *	0.0022	0.0242 *
G	0.25	0.0614	0.3379 *	0.0018	0.0115
	0.50	0.0446	0.5427 *	0.0011	0.0098
	0.75	0.0409	0.7223 *	0.0006	0.0089
	rand	0.0616	0.5322 *	0.0012	0.0101
H	0.25	0.0706	0.1463 *	0.0018	0.0101
	0.50	0.0586	0.1559 *	0.0015	0.0089
	0.75	0.0515	0.1630 *	0.0012	0.0159 *
	rand.	0.0626	0.1608 *	0.0015	0.0218 *
I	0.25	0.1788 *	0.1910 *	0.0029 *	0.0110
	0.50	0.2674 *	0.2733 *	0.0030 *	0.0095
	0.75	0.3718 *	0.3777 *	0.0048 *	0.0117
	rand.	0.2786 *	0.2926 *	0.0082 *	0.0189 *
	sum	17	34	20	21

* Results above the results of the Shapley value.

). In terms of corrections between asset 1 and asset 2, hierarchies $A,$ $E,F$ and I outperform the Shapley value with all weight schemes. For hierarchies $A,$ $B,$ $D,$ $E,$ $F,$ $G,$ H and I and all weights $\overline{\omega }$, more directional corrections occur with respect to Shapley. Considering full corrections, hierarchies $A,$ $D,$ E and I outperform Shapley. In the case of positive risk–return relationships, $A,$ $D,$ E and F yield higher proportions for all weight schemes. When all four dimensions are considered, hierarchies A and E perform better then Shapley. With respect to the weights $\overline{\omega },$ for hierarchies $A,$ D and E, a positive influence can be seen across all four dimensions. For the other hierarchies, a clear statement cannot be made. In no hierarchy do the weights $\overline{\omega }$ have an exclusively negative influence.

Table 4. Influence of $\overline{\omega }$, wH Shapley value, minimum-variance asset share.

Hierarchy	Correction	Directional	Full	Proportion Pos.
	1 and 2	Correction	Correction	Risk–Return Rel.
A	↑	↑	↑	↑
B	∪	↑	↓	~
C	~	∪	∪	∪
D	↑	↑	↑	↑
E	↑	↑	↑	↑
F	↑	↑	↓	↑
G	↓	↑	↓	↓
H	↓	↑	↓	∪
I	↑	↑	↑	∪

↑ increasing $\overline{\omega }$, increasing corrections/proportions; ↓ increasing $\overline{\omega }$, decreasing corrections/proportions; ~ no influence of $\overline{\omega }$; ∪ minimum corrections/proportions at $\overline{\omega }=0.5$.

compiles our results with respect to weights $\overline{\omega }.$

3.5. Results for the ${\mathit{wH}}^{\mathit{My}}$ Value

Finally, we analyze our results for the ${\mathrm{wH}}^{\mathrm{My}}$ value (

Table 5. Results for the wH Myerson value, minimum-variance asset share.

Hierarchy	Weight	Correction	Directional	Full	Proportion Pos.
	Vector	1 and 2	Correction	Correction	Risk–Return Rel.
A	0.25	0	0.0478	0	0
	0.50	0.0011	0.0488	0.0001	0.0004
	0.75	0.0450	0.0885	0.0043 *	0.0291 *
	rand.	0	0.0478	0	0
B	0.25	0.8807 *	0.8807 *	0	0.0134
	0.50	0.8434 *	0.8448 *	0.0001	0.0134
	0.75	0.7164 *	0.7703 *	0.0005	0.0134
	rand.	0.8841 *	0.8841 *	0	0.0134
C	0.25	0.0961	0.5794 *	0.0384 *	0.2053 *
	0.50	0.0961	0.5421 *	0.0318 *	0.1688 *
	0.75	0.0961	0.4522 *	0.0217 *	0.1304 *
	rand.	0.0961	0.5833 *	0.0392 *	0.2113 *
D	0.25	0.6883 *	0.6883 *	0	0.0121
	0.50	0.3198 *	0.3198 *	0	0.0206 *
	0.75	0.2092 *	0.2092 *	0	0.0705 *
	rand.	0.7434 *	0.7434 *	0	0.0120
E	0.25	0.1631 *	0.6306 *	0.0443 *	0.1845 *
	0.50	0.2301 *	0.6464 *	0.0611 *	0.1735 *
	0.75	0.3406 *	0.6639 *	0.1055 *	0.2237 *
	rand.	0.1491 *	0.6245 *	0.0428 *	0.1916 *
F	0.25	0.0012	0.0271	0	0
	0.50	0.0126	0.0501	0	0
	0.75	0.2662 *	0.3699 *	0	0
	rand.	0.0006	0.0280	0	0
G	0.25	0.0769	0.6529 *	0.0394 *	0.2392 *
	0.50	0.0686	0.7315 *	0.0367 *	0.2611 *
	0.75	0.0661	0.8148 *	0.0304 *	0.2957 *
	rand	0.0796	0.6372 *	0.0399 *	0.2358 *
H	0.25	0	0.1491 *	0	0
	0.50	0	0.2171 *	0	0
	0.75	0	0.2433 *	0	0.0002
	rand.	0	0.1285	0	0
I	0.25	0.9260 *	0.9260 *	0	0.0166 *
	0.50	0.9605 *	0.9605 *	0	0.0190 *
	0.75	0.9887 *	0.9887 *	0.0002	0.0263 *
	rand.	0.9181 *	0.9181 *	0	0.0161 *
	sum	17	28	13	19

* Results above the results of the Shapley value.

). Again, we start with corrections between asset 1 and asset 2. For hierarchies $B,$ D, E and I and all weights $\overline{\omega }$, more corrections occur compared to Shapley. Considering any directional correction, $B,$ C, D, E, G and I and all weight schemes $\overline{\omega }$ outperform the results for Shapley. If we consider full corrections, the hierarchies $C,$ E and G obtain a higher number of corrections with respect to Shapley. Regarding all four dimensions, only hierarchy E performs better than Shapley. With respect to $\overline{\omega },$ in hierarchies A, $F,$ H and I, there is no negative influence for all four dimensions. For hierarchy C, we obtain no positive influence. In

Table 6. Influence of $\overline{\omega }$, wH Myerson value, minimum-variance asset share.

Hierarchy	Correction	Directional	Full	Proportion Pos.
	1 and 2	Correction	Correction	Risk–Return Rel.
A	↑	↑	↑	↑
B	↓	↓	↑	~
C	~	↓	↓	↓
D	↓	↓	~	↑
E	↑	↑	↑	∪
F	↑	↑	~	~
G	↓	↑	↓	↑
H	~	↑	~	↑
I	↑	↑	↑	↑

↑ increasing $\overline{\omega }$, increasing corrections/proportions; ↓ increasing $\overline{\omega }$, decreasing corrections/proportions; ~ no influence of $\overline{\omega }$; ∪ minimum corrections/proportions at $\overline{\omega }=0.5$.

, the results with respect to weights $\overline{\omega }$ are presented.

3.6. Comparison of the Results

When comparing the values, we start by comparing ${\mathrm{wH}}^{\mathrm{Sh}}$ and ${\mathrm{wH}}^{\mathrm{My}}$. Overall, the $w{H}^{\mathrm{My}}$ value leads to fewer improvements when directional corrections, full corrections and the proportion of positive risk–return relationships are considered. Only in a few cases, such as hierarchy G and when full corrections and the proportion of positive risk–return relationships are taken into account, does the ${\mathrm{wH}}^{\mathrm{My}}$ value produce better results than the wH$Sh$ value.

If we compare the H value with the two wH values, it is noticeable that the H concept leads to more extreme results/proportions of corrections. Overall, the H value can lead to improvements in all four dimensions with three hierarchies. This is a result that does not exist at such a high level for the wH concepts. Thus, if the real-world hierarchical relationship between assets is very clear, the H concept can solve the entire low-risk puzzle. However, because of their weighting, the two wH concepts offer the possibility of mapping the dominance relationships between the assets in a more granular way, which may also better reflect the realities of the asset market. In

Table 7. Number of results above the results of the Shapley value for three hierarchy categories, H value, minimum-variance asset share.

Hierarchy	Correction	Directional	Full	Proportion Pos.
Category	1 and 2	Correction	Correction	Risk–Return Rel.
$\left\{2\right\}\in \widehat{S}\left(1\right)$	3	3	3	3
$\left\{2\right\}\notin \widehat{S}\left(1\right)$ and $\left\{1\right\}\notin \widehat{S}\left(2\right)$	1	4	0	2
$\left\{1\right\}\in \widehat{S}\left(2\right)$	1	1	0	0

,

Table 8. Number of results above the results of the Shapley value for three hierarchy categories, wH Shapley value, minimum-variance asset share.

Hierarchy	Correction	Directional	Full	Proportion Pos.
Category	1 and 2	Correction	Correction	Risk–Return Rel.
$\left\{2\right\}\in \widehat{S}\left(1\right)$	9	16	12	14
$\left\{2\right\}\notin \widehat{S}\left(1\right)$ and $\left\{1\right\}\notin \widehat{S}\left(2\right)$	0	2	1	2
$\left\{1\right\}\in \widehat{S}\left(2\right)$	8	16	7	5

and

Table 9. Number of results above the results of the Shapley value for three hierarchy categories, wH Myerson value, minimum-variance asset share.

Hierarchy	Correction	Directional	Full	Proportion Pos.
Category	1 and 2	Correction	Correction	Risk–Return Rel.
$\left\{2\right\}\in \widehat{S}\left(1\right)$	8	11	5	7
$\left\{2\right\}\notin \widehat{S}\left(1\right)$ and $\left\{1\right\}\notin \widehat{S}\left(2\right)$	0	4	4	4
$\left\{1\right\}\in \widehat{S}\left(2\right)$	9	13	4	8

, we show the number of corrections/number of proportions with positive risk–return relationships above the results of the Shapley value for three hierarchy categories. The first category consists of hierarchies $A,$ $D,$ E and $H.$ In these hierarchies, asset 1 is a direct/indirect predecessor of asset 2. The second category contains hierarchy $C.$ In this hierarchy, neither asset 1 is a predecessor of asset 2 nor vice versa. Finally, the last category consists of hierarchies where asset 2 is a direct/indirect predecessor of asset 1.

Our results for the random asset shares and the naive weight scheme can be found in Appendix A. They do not differ from the results for asset weights that minimize $v\left(N\right)$.

4. Research Outlook

In our paper, the application of cooperative game theory to the problem of allocating portfolio risk to assets in portfolios has been extended. The results obtained show that the consideration of hierarchies may contribute to solving the low-risk puzzle.

We leave open the question of which hierarchical structure and which value for hierarchical games best solves the low-risk puzzle. The low-risk puzzle is an empirical problem. Therefore, empirical studies are the only means by which it is possible to determine the extent to which the presented approach could solve the low-risk puzzle. In addition to empirical analyses of which hierarchical values and which hierarchical structures make the greatest contribution to solving the low-risk puzzle, empirical studies could, for example, determine the optimal calibration/translation of the hierarchical strength of the relationship between assets in the ${\mathrm{wH}}^{\mathrm{Sh}}$ approach and the ${\mathrm{wH}}^{\mathrm{My}}$ approach. The ability to consider hierarchies between assets is just one building block that can help in solving the low-risk puzzle through cooperative game theory. In cooperative game theory alone, there are many other ways to model structures on the set of assets, such as coalition structures (Aumann and Dreze 1974; Casajus 2009; Owen 1977), asset weights (Béal et al. 2018; Haeringer 2006; Kalai and Samet 1987) and weighted level structures (Besner 2019, 2022). At best, some implications for the theoretical development of capital market models can be drawn from studies applying cooperative game theory, especially hierarchical games (Simonian 2019).

With respect to the methods of cooperative game theory, there are many approaches to modeling hierarchical structures. With regard to hierarchies, it is possible to dispense with the assumption of a tree structure. In this case, the conjunctive approach value and the disjunctive approach value generate different payoffs. Furthermore, as mentioned in the Introduction, undirected graphs/networks and level structures are similar approaches. van den Brink (2010) provides an approach where the Banzhaf concept (Banzhaf 1965) is the basis for the H value. The generalization of permission values using antimatroids is described by Algaba et al. (2003). Other concepts for the determination of player payoffs in hierarchical games have been introduced by del Pozo et al. (2011), Khmelnitskaya et al. (2016), Alvarez-Mozos et al. (2017), Algaba et al. (2018) and Algaba and van den Brink (2019). In addition, games with trees (Bilbao et al. 2006; Béal et al. 2010, 2022; Hamiache 1999, 2004; Herings et al. 2008; Kang et al. 2022; Navarro 2020) and digraphs (Borm and van Den Brink 2002) are structures that are similar to hierarchies.