Rating the Impact of Risks in Banking on Performance: Utilizing the Adaptive Neural Network-Based Fuzzy Inference System (ANFIS)
Abstract
:1. Introduction
2. Literature Review
2.1. Credit Risk and Performance
2.2. Liquidity Risk and Performance
2.3. Capital Adequacy and Performance
3. The Research Methodology and Analysis
3.1. Data Collection
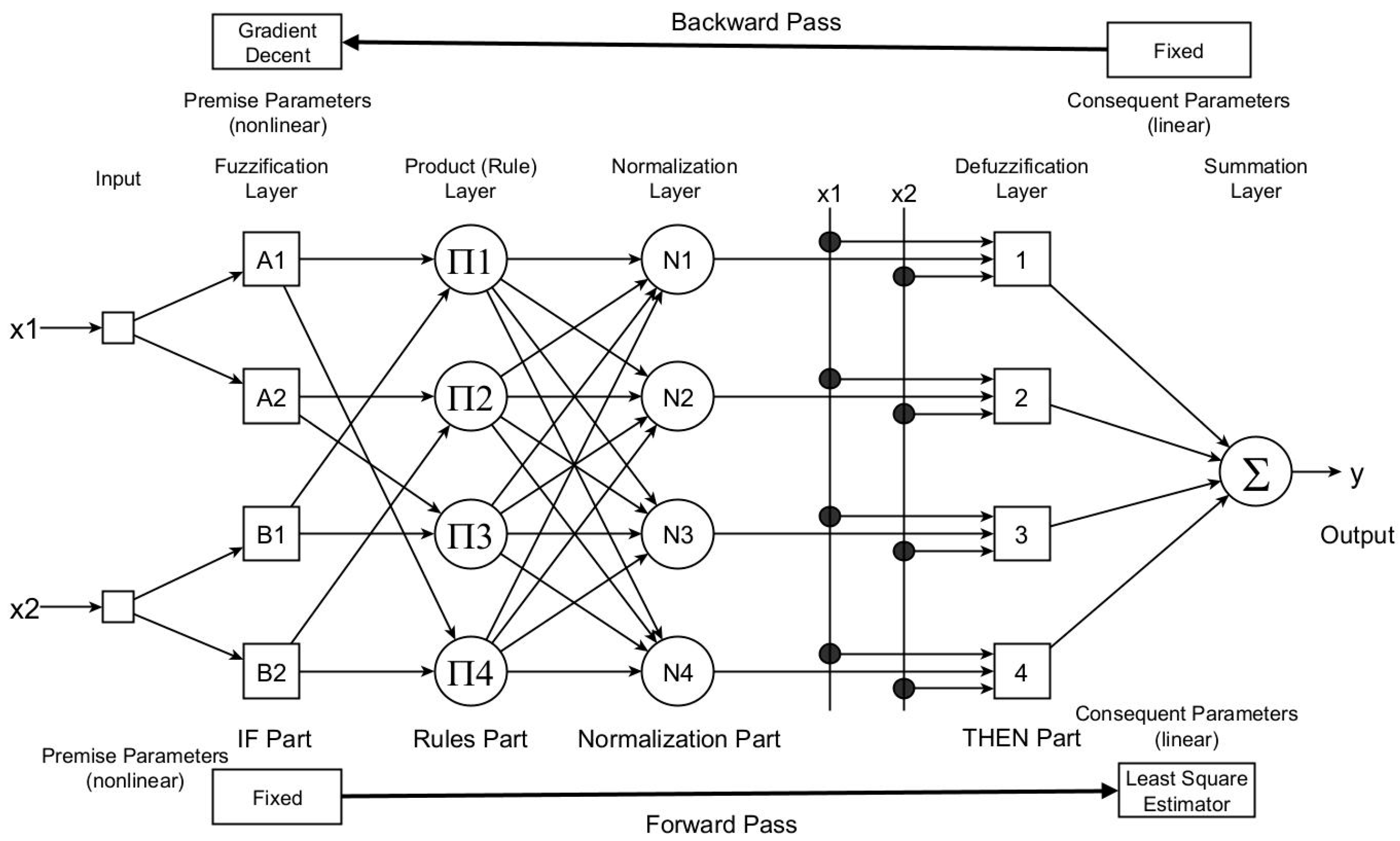
3.2. Fuzzy Inference System Based on Adaptive Neural Networks
3.3. ANFIS Architecture
3.4. ANFIS Learning
3.5. Building the Fuzzy Model
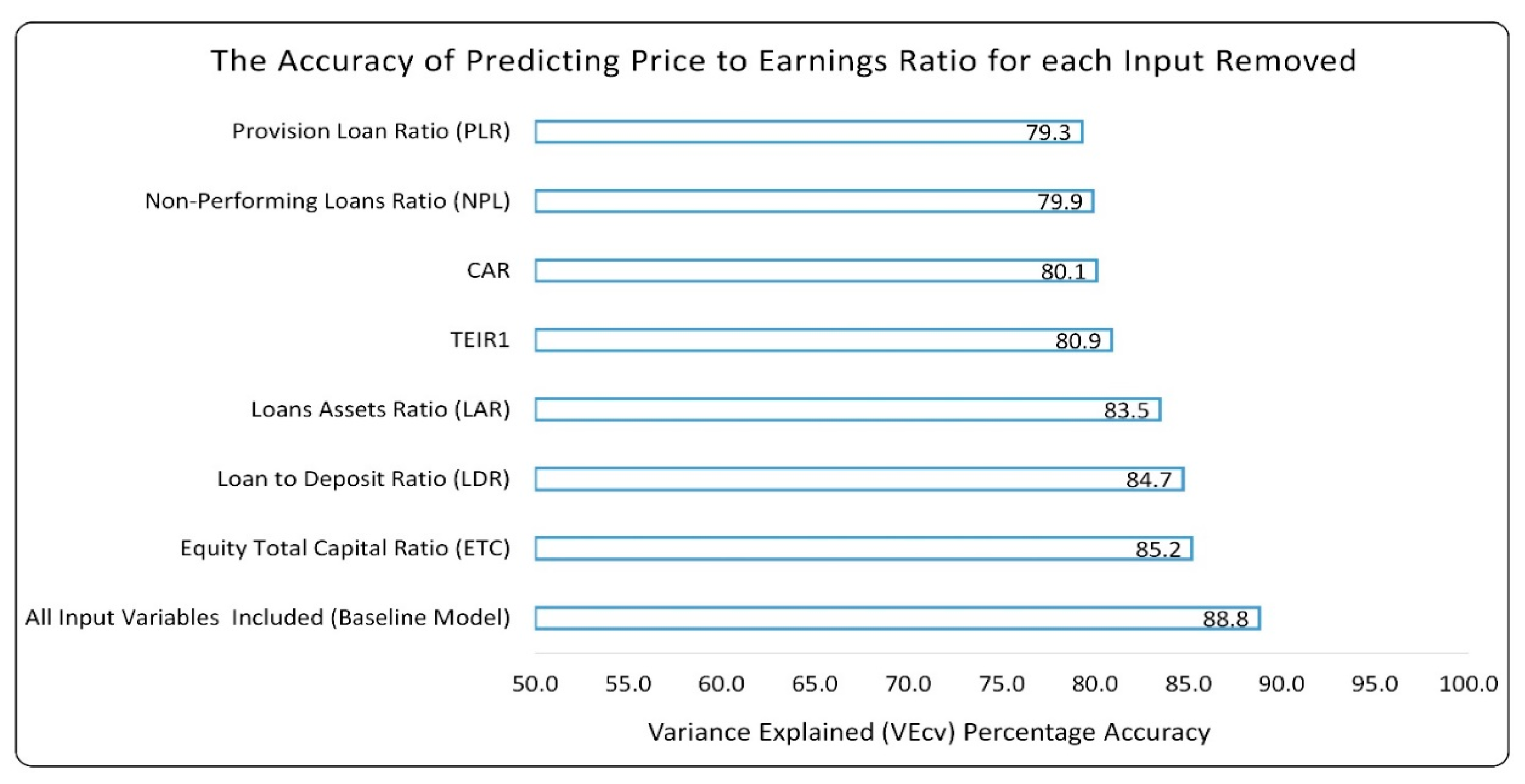
3.6. Predictive and Explanatory Performance of the Model
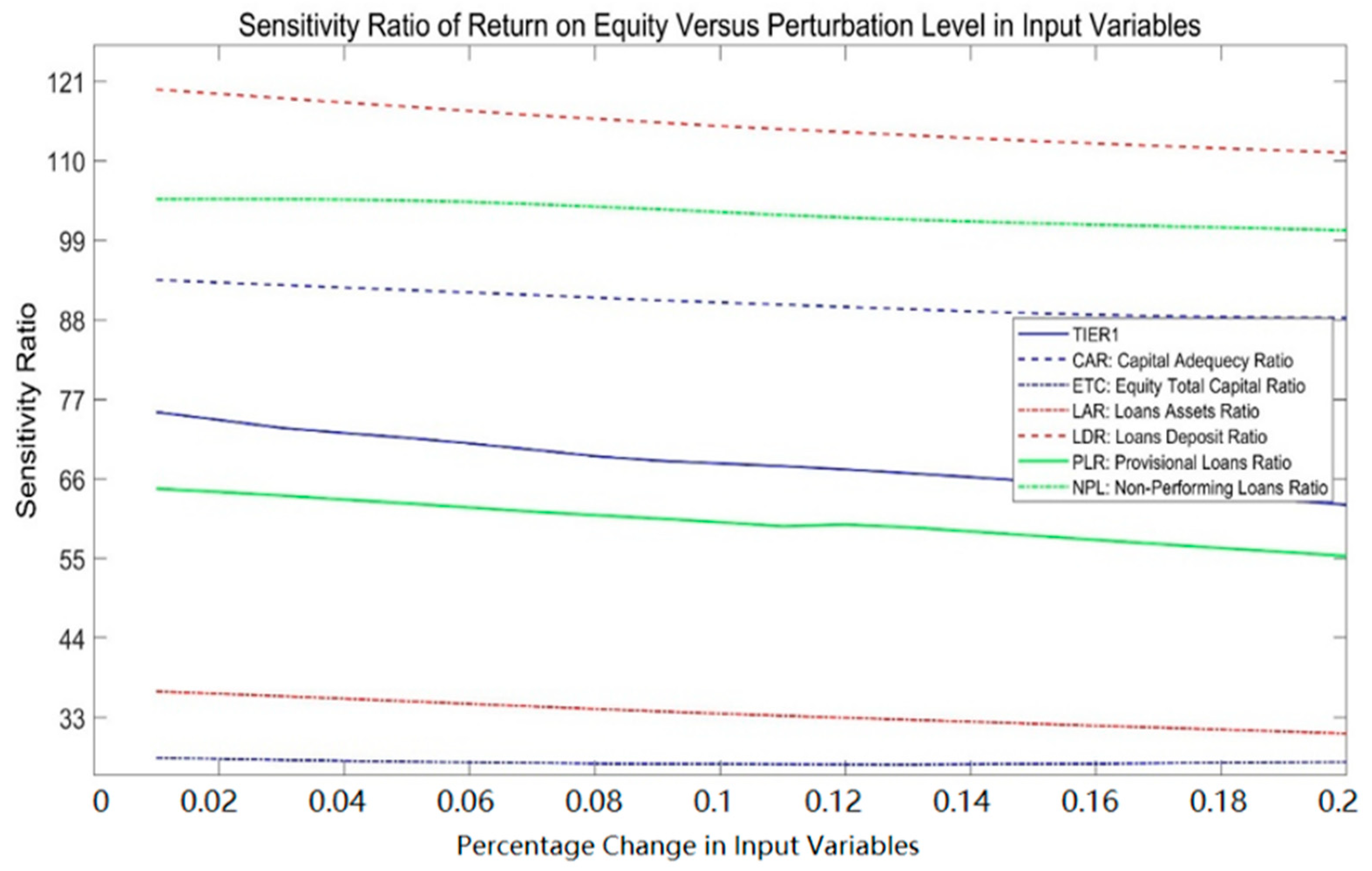
3.7. Significance of the Input Variables in Prediction
3.8. Model’s Explanatory Performance
4. Discussion
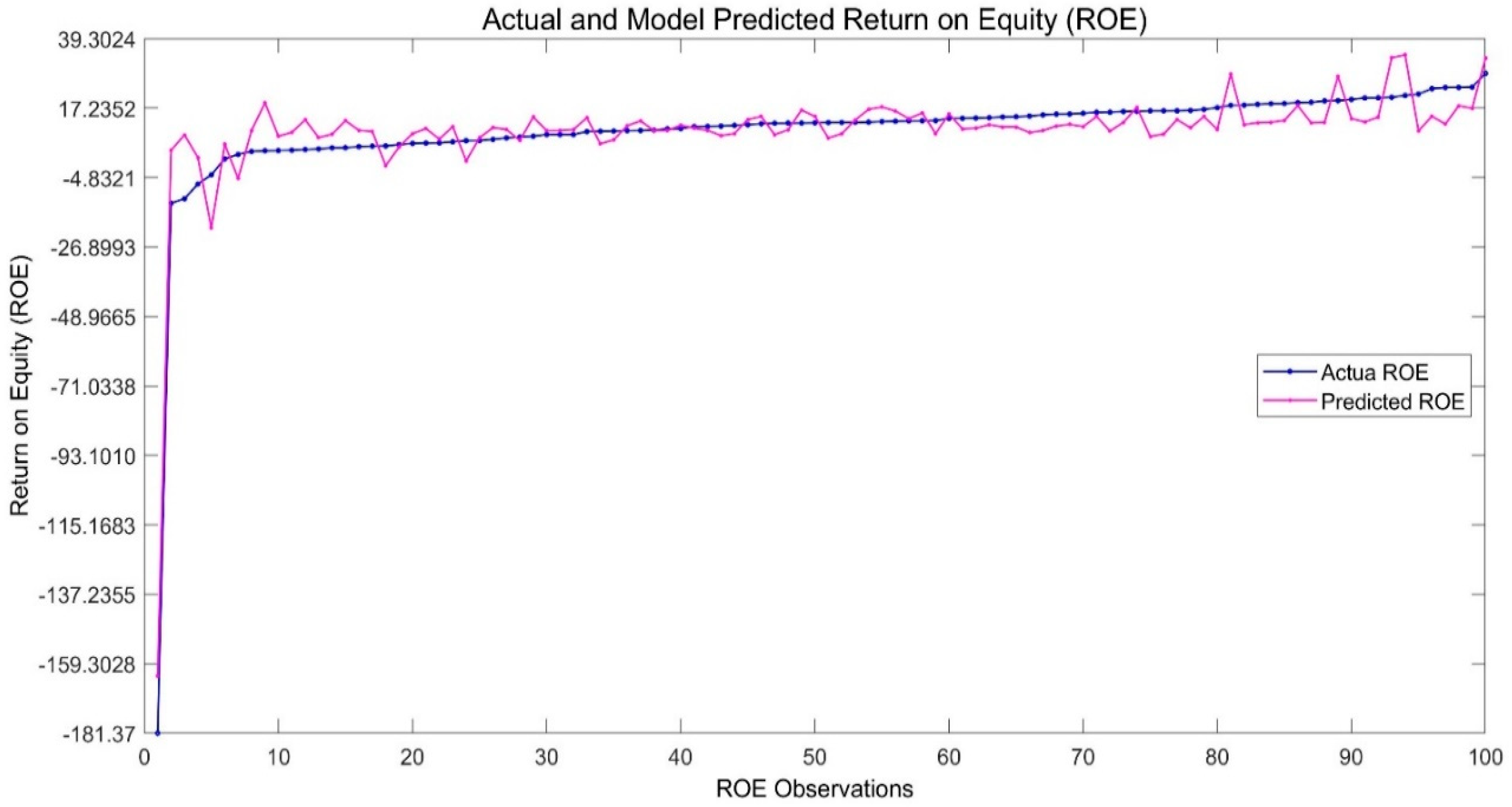
4.1. Return on Equity (ROE)
4.1.1. Relative Significance of ROE Predictors
4.1.2. Explaining Variations in ROE
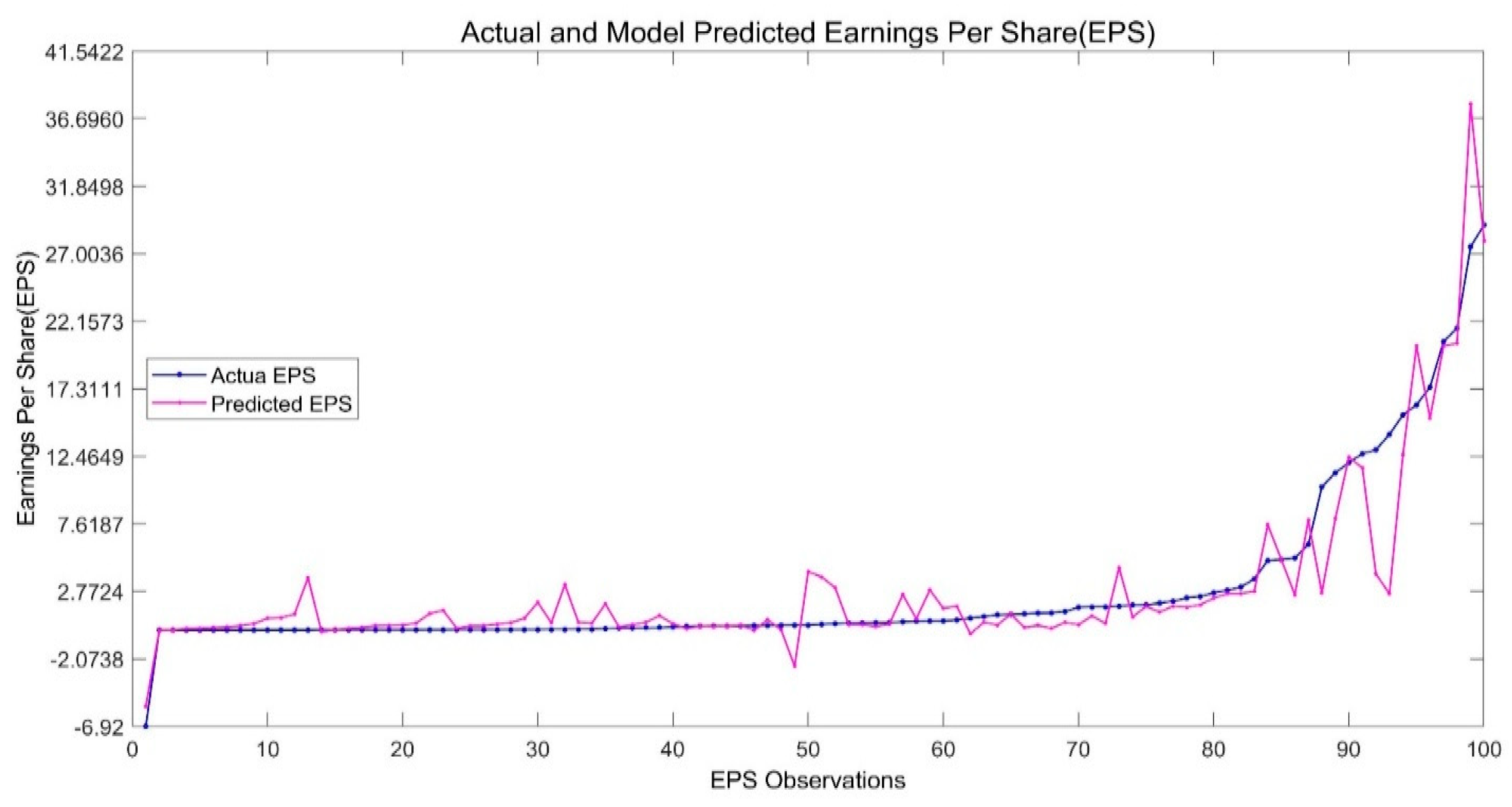
4.2. Earnings per Share (EPS)
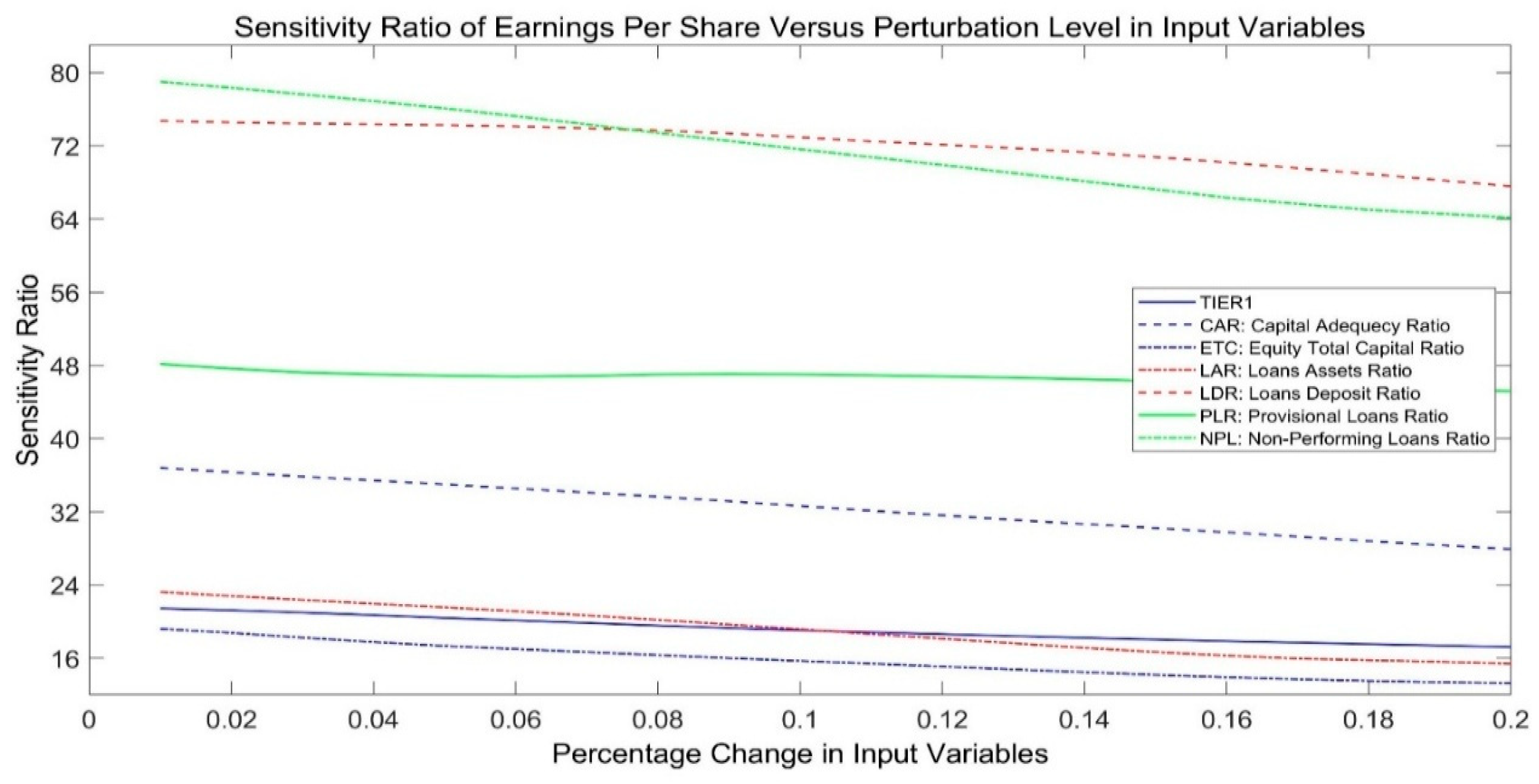
4.2.1. Relative Significance of EPS Predictors
4.2.2. Explaining Variations in EPS
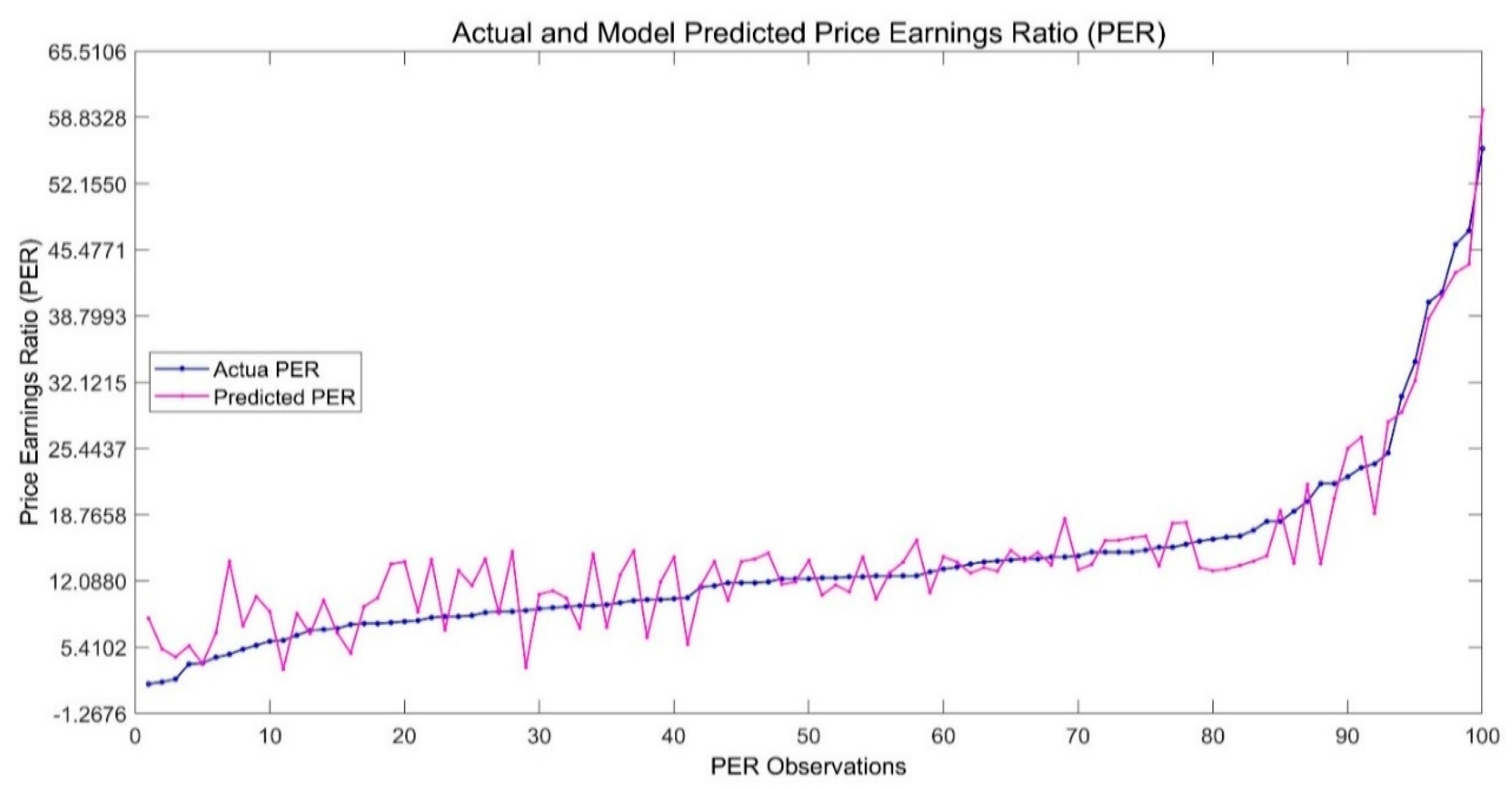
4.3. Price-Earnings Ratio (PER)
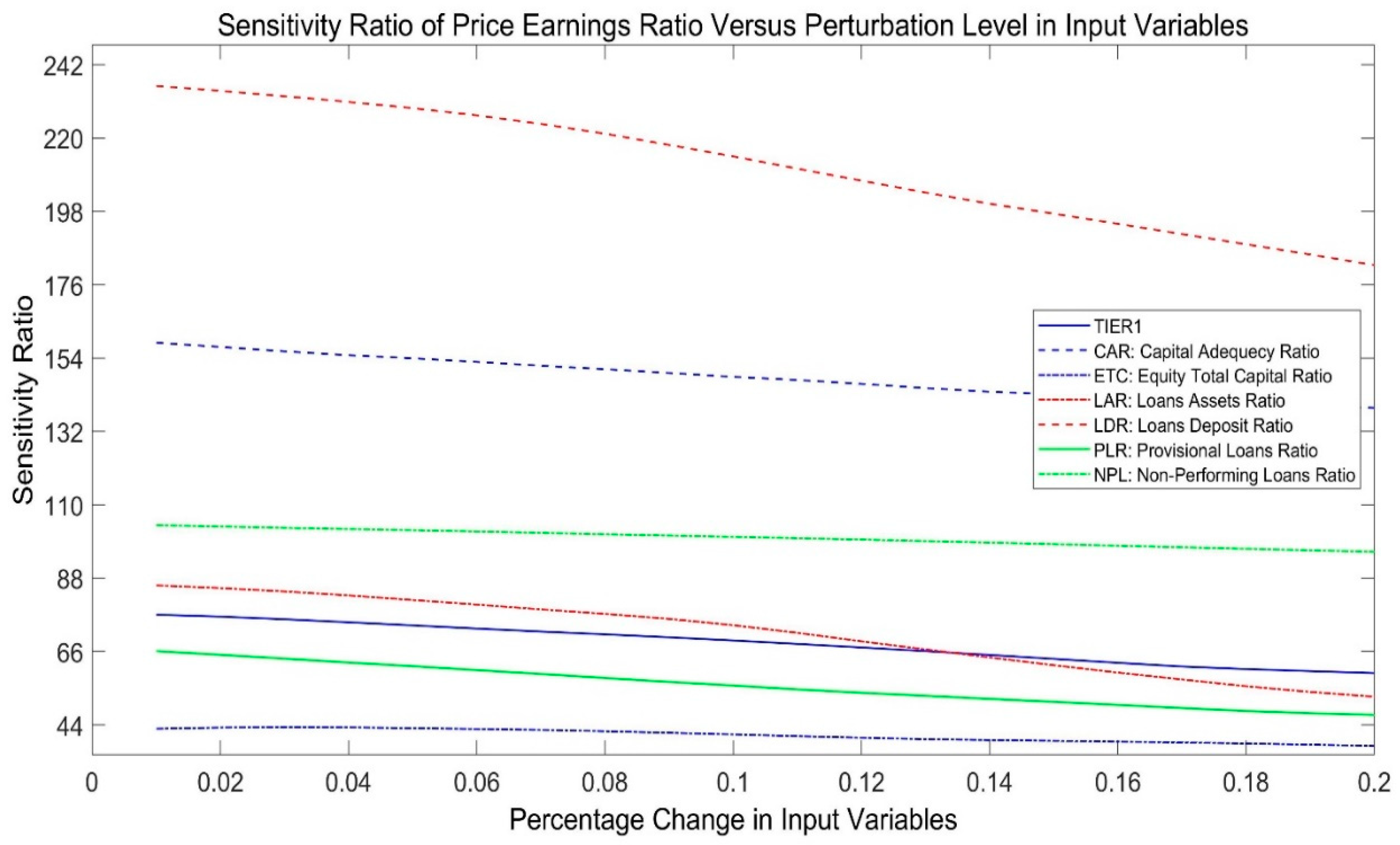
4.3.1. Relative Significance of PER Predictors
4.3.2. Explaining Variations in PER
5. Conclusions
6. Implications
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abiola, Idowu, and Awoyemi Samuel Olausi. 2014. The impact of credit risk management on the commercial banks performance in Nigeria. International Journal of Management and Sustainability 3: 295–306. [Google Scholar] [CrossRef]
- AbouElaz, Mona A., Bilal Naji Alhasnawi, Bishoy E. Sedhom, and Vladimír Bureš. 2025. ANFIS-optimized control for resilient and efficient supply chain performance in smart manufacturing. Results in Engineering 25: 104262. [Google Scholar] [CrossRef]
- Abraham, Ajith. 2005. Adaptation of Fuzzy Inference System Using Neural Learning. 2005. In Fuzzy Systems Engineering: Theory and Practice. Edited by Nadia Nedjah and Luiza de Macedo Mourelle. Studies in Fuzziness and Soft Computing. Berlin: Springer, vol. 181, pp. 53–83. [Google Scholar] [CrossRef]
- Abu Huson, Yazan, Laura Sierra-García, and María Antonia Garcia-Benau. 2023. A bibliometric review of information technology, artificial intelligence, and blockchain on auditing. Total Quality Management & Business Excellence 35: 91–113. [Google Scholar] [CrossRef]
- Alam, S. M. Shamsul, Mohammad Abdul Matin Chowdhury, and Dzuljastri Bin Abdul Razak. 2021. Research evolution in banking performance: A bibliometric analysis. Future Business Journal 7: 66. [Google Scholar] [CrossRef]
- Al-Khouri, Ritab. 2011. Assessing the risk and performance of the GCC banking sector. International Research Journal of Finance and Economics 65: 72–78. [Google Scholar]
- Alonso-Robisco, Andrés, and José Manuel Carbó. 2022. Can machine learning models save capital for banks? Evidence from a Spanish credit portfolio. International Review of Financial Analysis 84: 102372. [Google Scholar]
- Al-Sharkas, Adel A., and Tamara A. Al-Sharkas. 2022. The impact on bank profitability: Testing for capital adequacy ratio, cost-income ratio and non-performing loans in emerging markets [Special issue]. Journal of Governance & Regulation 11: 231–43. [Google Scholar] [CrossRef]
- Alshatti, Ali Sulieman. 2015. The effect of credit risk management on financial performance of the Jordanian commercial banks. Investment Management and Financial Innovations 12: 338–45. [Google Scholar]
- Areghan, Sibor, Omankhanlen Alexander, Chima Menyelim Mathias, Komolafe Titilope Deborah, and Okereke Karachi Yvonne. 2021. The Impact of Credit Risk Management, Macroeconomic Variables on Bank Performance in Nigeria. Journal of Legal Ethical and Regulatory Issues 24: 1–10. [Google Scholar] [CrossRef]
- Azadeh, A., M. S. Asadzadeh, H. G. Mirseraji, and M. Saberi. 2015. An emotional learning neuro-fuzzy inference approach for optimum training and forecasting of gas consumption estimation models with cognitive data. Technological Forecasting and Social Change 91: 47–63. [Google Scholar] [CrossRef]
- Bai, Runbo, Hailei Jia, and Pingzhou Cao. 2011. Factor Sensitivity Analysis with Neural Network Simulation based on Perturbation System. Journal of Computational 6: 1402–7. [Google Scholar] [CrossRef]
- Bandyopadhyay, Arindam, and Mayuri Saxena. 2021. Linkage Between Credit Risk and Liquidity Risk in Indian Banks: A Comparison of the Pre & Post Basel 3 Conditions? NIBM Working Paper Series, WPS05/November. Available online: https://www.nibmindia.org/static/working_paper/NIBM_WP05_ABMS.pdf (accessed on 27 April 2025).
- Banerjee, Ameet Kumar, Molla Ramizur Rahman, Arun Kumar Misra, and Ahmet Sensoy. 2025. Risk sharing framework and systemic tolerance in Indian banks: Double layer network approach. Research in International Business and Finance 73: 102636. [Google Scholar] [CrossRef]
- Wanjiru, Beatrice Nyokabi, Ambrose O. Jagongo, and Fredrick W. S. Ndede. 2024. Effect of capital adequacy on financial performance of commercial banks in Kenya. The Strategic Journal of Business & Change Management 11: 327–49. [Google Scholar] [CrossRef]
- Bhattarai, Yuga Raj. 2016. Effect of credit risk on the performance of Nepalese commercial banks. NRB Economic Review 28: 41–64. [Google Scholar] [CrossRef]
- Bolívar, Fernando, Miguel A. Duran, and Ana Lozano-Vivas. 2023. Business model contributions to bank profit performance: A machine learning approach. Research in International Business and Finance 64: 101870. [Google Scholar] [CrossRef]
- Boyacioglu, Melek Acar, and Derya Avci. 2010. An adaptive network-based fuzzy inference system (ANFIS) for the prediction of stock market return: The case of the Istanbul stock exchange. Expert Systems with Applications 37: 7908–12. [Google Scholar] [CrossRef]
- Cao, Maosen, Nizar F. Alkayem, Lixia Pan, and Drahomír Novák. 2016. Advanced Methods in Neural Networks-Based Sensitivity Analysis with their Applications in Civil Engineering. In Artificial Neural Networks—Models and Applications. London: IntechOpen, pp. 335–53. [Google Scholar] [CrossRef]
- Castillo, Oscar, Juan R. Castro, and Patricia Melin. 2023. Forecasting the COVID-19 with interval Type-3 fuzzy logic and the fractal dimension. International Journal of Fuzzy Systems 25: 182–97. [Google Scholar] [CrossRef]
- Chang, Victor, Sharuga Sivakulasingam, Hai Wang, Siu Tung Wong, Meghana Ashok Ganatra, and Jiabin Luo. 2024. Credit Risk Prediction Using Machine Learning and Deep Learning: A Study on Credit Card Customers. Risks 12: 174. [Google Scholar] [CrossRef]
- Chen, Tao. 2022. Prediction Calculation of Stock Composite Index Closing Price Based on Grey Correlation Analysis Method. In International Conference on Frontier Computing. Singapore: Springer Nature Singapore, pp. 177–83. [Google Scholar]
- Cheng, Antony Y., and Daniel S. Yeung. 1999. Sensitivity analysis of neocognitron. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews) 29: 238–49. [Google Scholar] [CrossRef]
- Chiu, Stephen L. 1996. Selecting input variables for fuzzy models. Journal of Intelligent & Fuzzy Systems 4: 243–56. [Google Scholar]
- Chou, Te-Kuang, and Agung Dharmawan Buchdadi. 2016. Bank Performance and Its Underlying Factors: A Study of Rural Banks in Indonesia. Accounting and Finance Research 5: 55–63. [Google Scholar] [CrossRef]
- Colesnic, Olga, Konstantinos Kounetas, and Polemis Michael. 2020. Estimating risk efficiency in Middle East banks before and after the crisis: A metafrontier framework. Global Finance Journal 46: 100484. [Google Scholar] [CrossRef]
- Dimopoulos, Yannis, Paul Bourret, and Sovan Lek. 1995. Use of some sensitivity criteria for choosing networks with good generalization ability. Neural Processing Letters 2: 1–4. [Google Scholar] [CrossRef]
- Dubois, Didier, Henri Prade, and Ronald R. Yager, eds. 1997. Fuzzy Information Engineering: A Guided Tour of Applications. Hoboken: John Wiley & Sons, Inc. [Google Scholar]
- Ekinci, Ramazan, and Gulden Poyraz. 2019. The effect of credit risk on financial performance of deposit banks in Turkey. Procedia Computer Science 158: 979–87. [Google Scholar] [CrossRef]
- Eltweri, Ahmed, Nedal Sawan, Krayyem Al-Hajaya, and Zineb Badri. 2024. The Influence of Liquidity Risk on Financial Performance: A Study of the UK’s Largest Commercial Banks. Journal of Risk and Financial Management 17: 580. [Google Scholar] [CrossRef]
- Erasmus, Afriyie. 2022. The impact of custom-made internal risk control systems on bank performance in Ghana. In Forum Scientiae Oeconomia. Dąbrowa Górnicza: Wydawnictwo Naukowe Akademii WSB, vol. 10, pp. 151–74. [Google Scholar]
- Febiyanni, Febiyanni, and Hermanto Hermanto. 2023. The influence of capital risk, liquidity risk, and credit risk, on profitability with macroprudential intermediation ratio as a moderating variable. Enrichment Journal of Management 13: 1984–92. Available online: https://digilib.esaunggul.ac.id/the-influence-of-capital-risk-liquidity-risk-and-credit-risk-on-profitability-with-macroprudential-intermediation-ratio-as-a-moderating-variable-31131.html (accessed on 5 August 2023).
- Gedeon, Tamás D. 1997. Data mining of inputs: Analysing magnitude and functional measures. International Journal of Neural Systems 8: 209–18. [Google Scholar] [CrossRef]
- Geisser, Seymour. 1975. The predictive sample reuse method with applications. Journal of the American Statistical Association 70: 320–28. [Google Scholar] [CrossRef]
- Geisser, Seymour. 1993. Predictive Inference: An Introduction. London: Chapman and Hall. [Google Scholar]
- Goddard, John, Phil Molyneux, and John O. S. Wilson. 2004. Dynamics of Growth and Profitability in Banking. Journal of Money, Credit and Banking 36: 1069–1090. [Google Scholar] [CrossRef]
- Grau-Vera, David, and Gonzalo Rubio. 2024. Risk-adjusted performance of new economy indices and thematic sectors. Research in International Business and Finance 71: 102438. [Google Scholar] [CrossRef]
- Hamam, Abdelwahab, and Nicolas D. Georganas. 2008. A comparison of Mamdani and Sugeno fuzzy inference systems for evaluating the quality of experience of Hapto-Audio-Visual applications. Paper presented at 2008 IEEE International Workshop on Haptic Audio-Visual Environments and Games, Ottawa, ON, Canada, October 18–19; Piscataway: IEEE, pp. 87–92. [Google Scholar]
- Hamza, Syed Muhammad. 2017. Impact of Credit Risk Management on Banks Performance: A Case Study in Pakistan Banks. European Journal of Business and Management 9: 57–64. [Google Scholar]
- Han, Jiawei, Micheline Kamber, and Jian Pei. 2012. Data Mining Concepts and Techniques. Waltham: Morgan Kaufmann. [Google Scholar]
- Hersugondo, Hersugondo, Nabila Anjani, and Imang Dapit Pamungkas. 2021. The Role of Non-Performing Asset, Capital, Adequacy and Insolvency Risk on Bank Performance: A Case Study in Indonesia. The Journal of Asian Finance, Economics and Business 8: 319–29. [Google Scholar]
- Himeur, Yassine, Mariam Elnour, Fodil Fadli, Nader Meskin, Ioan Petri, Yacine Rezgui, Faycal Bensaali, and Abbes Amira. 2023. AI-big data analytics for building automation and management systems: A survey, actual challenges and future perspectives. Artificial Intelligence Review 56: 4929–5021. [Google Scholar] [CrossRef]
- Huang, An, Youlong Yang, and Yuanyuan Liu. 2024. A Binary Risk Linguistic Fuzzy Behavioral TOPSIS Model for Multi-attribute Large-Scale Group Decision-Making Based on Risk Preference Classification and Adaptive Weight Updating. International Journal of Fuzzy Systems 26: 1852–78. [Google Scholar] [CrossRef]
- Huang, Xiaoxia. 2012. A risk index model for portfolio selection with returns subject to experts’ estimations. Fuzzy Optimization and Decision Making 11: 451–63. [Google Scholar] [CrossRef]
- Hussain, Kashif, Mohd Salleh, and Mohd Najib. 2015. Analysis of techniques for anfis rule-base minimization and accuracy maximization. ARPN Journal of Engineering and Applied Sciences 10: 9739–46. [Google Scholar]
- Jang, Jyh-Shing R. 1991. Fuzzy modeling using generalized neural networks and Kalman filter algorithm. Paper presented at Ninth National Conference on Artificial Intelligence, Anaheim CA, USA, July 14–19, vol. 2, pp. 762–67. [Google Scholar]
- Jang, Jyh-Shing R. 1993. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Transactions on Systems Man and Cybernetics 23: 665–85. [Google Scholar] [CrossRef]
- Jang, Jyh-Shing Roger, Chuen-Tsai Sun, and Eiji Mizutani. 1997. Neuro-fuzzy and soft computing-a computational approach to learning and machine intelligence [Book Review]. IEEE Transactions on Automatic Control 42: 1482–84. [Google Scholar] [CrossRef]
- Jovic, Srdjan, Jasmina Smigic Miladinovic, Radmila Micic, Sanja Markovic, and Goran Rakic. 2019. Analysing of exchange rate and gross domestic product (GDP) by adaptive neuro fuzzy inference system (ANFIS). Physica A: Statistical Mechanics and its Applications 513: 333–38. [Google Scholar] [CrossRef]
- Kacem, Oumeima, and Sana El Harbi. 2022. Do risk governance and effective board affect bank performance? Evidence from large banks worldwide. Risk Management 24: 461–83. [Google Scholar] [CrossRef]
- Kaur, Raminder Preet, and Amanjot Singh Klair. 2012. Investigation of Grid partitioning and Subtractive Clustering based Neuro-Fuzzy Systems for Evaluation of Fault-Proneness in Open source software system. Paper presented at International Conference on Computer Graphics, Simulation and Modeling, Pattaya, Thailand, July 28–29; pp. 143–45. [Google Scholar]
- Kim, Jong-Min, Ning Wang, Yumin Liu, and Kayoung Park. 2020. Residual control chart for binary response with multicollinearity covariates by neural network model. Symmetry 12: 381. [Google Scholar] [CrossRef]
- Kodithuwakku, Sujeeva. 2015. Impact of Credit Risk Management on the Performance of Commercial Banks in Sri Lanka. International Journal of Scientific Research and Innovative Technology 2: 1–6. [Google Scholar]
- Kohavi, Ron, and George H. John. 1997. Wrappers for feature selection. Artificial Intelligence 97: 273–324. [Google Scholar] [CrossRef]
- Kristóf, Tamás, and Miklós Virág. 2022. EU-27 bank failure prediction with C5. 0 decision trees and deep learning neural networks. Research in International Business and Finance 61: 101644. [Google Scholar] [CrossRef]
- Kwashie, Angela Akpemada, Samuel Tawiah Baidoo, and Enock Kojo Ayesu. 2022. Investigating the impact of credit risk on financial performance of commercial banks in Ghana. Cogent Economics & Finance 10: 2109281. [Google Scholar]
- Lamy, D. 1996. Modeling and sensitivity analysis of neural networks. Mathematics and Computers in Simulation 40: 535–48. [Google Scholar] [CrossRef]
- Li, Jin. 2016. Assessing spatial predictive models in the environmental sciences: Accuracy measures, data variation and variance explained. Environmental Modelling & Software 80: 1–8. [Google Scholar]
- Li, Jin. 2017. Assessing the accuracy of predictive models for numerical data: Not r nor r2, why not? Then what? PLoS ONE 12: e0183250. [Google Scholar] [CrossRef]
- Li, Minghui, Kaiyue Li, Yeni Huang, and Zhongyu Cao. 2025. Commercial bank NSFR adjustment and risk: Evidence from China. Research in International Business and Finance 73: 102559. [Google Scholar] [CrossRef]
- Liu, Jinpei, Zijie Qiang, Peng Wu, and Pengcheng Du. 2022. Multiple stage optimization driven group decision-making method with interval linguistic fuzzy preference relations based on ordinal consistency and DEA cross-efficiency. Fuzzy Optimization and Decision Making 22: 309–36. [Google Scholar] [CrossRef]
- Luthfi, Emha Taufiq, and Ferry Wahyu Wibowo. 2017. Loan Payment Prediction Using Adaptive Neuro Fuzzy Inference System. International Journal of Simulation: Systems Science & Technology 18: 9.1–9.6. [Google Scholar]
- Mamdani, Ebrahim H. 1974. Applications of fuzzy algorithms for a simple dynamic plant. Proceedings of the Institution of Electrical Engineers 121: 1585–88. [Google Scholar] [CrossRef]
- Mamdani, Ebrahim H., and Sedrak Assilian. 1975. An experiment in linguistic synthesis with a fuzzy logic controller. International Journal of Man-Machine Studies 7: 1–13. [Google Scholar] [CrossRef]
- MathWorks. 2023a. “Fuzzy Logic Toolbox, User’s Guide” R2020a. Available online: https://www.mathworks.com/products/fuzzy-logic.html?s_tid=srchtitle_fuzzy%20logice_1 (accessed on 8 March 2023).
- MathWorks. 2023b. Available online: https://www.mathworks.com/help/fuzzy/genfis.html (accessed on 8 March 2023).
- MathWorks. 2023c. Available online: https://www.mathworks.com/help/fuzzy/anfis.html?s_tid=srchtitle (accessed on 8 March 2023).
- Meliza, Norraidah Abu Hasan, and Saputri Hermilasari. 2024. The influence of banking liquidity risk on profitability: The moderating role of capital adequacy ratio. Banks and Bank Systems 19: 140–51. [Google Scholar] [CrossRef]
- Mirashk, Hamed, Amir Albadvi, Mehrdad Kargari, and Mohammad Ali Rastegar. 2024. News Sentiment and Liquidity Risk Forecasting: Insights from Iranian Banks. Risks 12: 171. [Google Scholar] [CrossRef]
- Mitra, Sushmita, and Yoichi Hayashi. 2000. Neuro-fuzzy rule generation: Survey in soft computing framework. IEEE Transactions on Neural Networks 11: 748–68. [Google Scholar] [CrossRef]
- Mohamed, Elfadil A., Ibrahim Elsiddig Ahmed, Riyadh Mehdi, and Hanan Hussain. 2021. Impact of corporate performance on stock price predictions in the UAE markets: Neuro-fuzzy model. Intelligent Systems in Accounting, Finance and Management 28: 52–71. [Google Scholar] [CrossRef]
- Nallakaruppan, M. K., Himakshi Chaturvedi, Veena Grover, Balamurugan Balusamy, Praveen Jaraut, Jitendra Bahadur, V. P. Meena, and Ibrahim A. Hameed. 2024. Credit Risk Assessment and Financial Decision Support Using Explainable Artificial Intelligence. Risks 12: 164. [Google Scholar] [CrossRef]
- Negnevitsky, Michael. 2017. Artificial Intelligence: A Guide to Intelligent Systems. Harlow: Addison Wesley. [Google Scholar]
- Neshat, Mehdi, Ali Adeli, Ghodrat Sepidnam, and Mehdi Sargolzaei. 2012. Prediction of concrete mix design using adaptive neural fuzzy inference systems and fuzzy inference systems. International Journal of Advanced Manufacturing Technology 63: 373–90. [Google Scholar] [CrossRef]
- Nguyen, Minh Hong, Binh Nguyen Thanh, Huy Pham, and Thi Thu Tra Pham. 2025. The determinants of funding liquidity risk in decentralized lending. Global Finance Journal 64: 101055. [Google Scholar] [CrossRef]
- Ontiveros, Emanuel, Patricia Melin, and Oscar Castillo. 2024. Towards an Efficient Approach for Mamdani Interval Type-3 Fuzzy Inference Systems. International Journal of Fuzzy Systems 26: 2172–90. [Google Scholar] [CrossRef]
- Pham, N. Thach, Robert Powell, and Deepa Bannigidadmath. 2024. Tail risk network analysis of Asian banks. Global Finance Journal 62: 101017. [Google Scholar] [CrossRef]
- Poudel, Ravi Prakash Sharma. 2012. The Impact of Credit Risk Management on Financial Performance of Commercial Banks in Napal. International Journal of Arts and Commerce 1: 9–15. [Google Scholar]
- Pratiwi, Esha, and Erni Masdupi. 2021. Effect of Credit Risk, Market Risk and Liquidity Risk on Return on Assets of Conventional Commercial Banks Registered in The Financial Services Authority During the COVID-19 Pandemic. Financial Management Studies 4: 29–46. [Google Scholar]
- Qiu, Yue, Shaoguang Qu, Zhentao Shi, and Tian Xie. 2025. Predicting cryptocurrency volatility: The power of model clustering. Economic Modelling 144: 106986. [Google Scholar] [CrossRef]
- Rajab, Sharifa, and Vinod Sharma. 2018. A review on the applications of neuro-fuzzy systems in business. Artificial Intelligence Review 49: 481–510. [Google Scholar] [CrossRef]
- Rastogi, Shailesh, Arpita Sharma, Geetanjali Pinto, and Venkata Mrudula Bhimavarapu. 2022. A literature review of risk, regulation, and profitability of banks using a scientometric study. Future Business Journal 8: 28. [Google Scholar] [CrossRef]
- Saâdaoui, Foued, and Monjia Khalfi. 2024. Revisiting Islamic banking efficiency using multivariate adaptive regression splines. Annals of Operations Research 334: 287–315. [Google Scholar] [CrossRef]
- Shmueli, G. 2010. To Explain or to Predict? Statistical Science 25: 289–310. [Google Scholar] [CrossRef]
- Siddique, Asima, Muhammad Asif Khan, and Zeeshan Khan. 2022. The effect of credit risk management and bank-specific factors on the financial performance of the South Asian commercial banks. Asian Journal Accounting Research 7: 182–94. [Google Scholar] [CrossRef]
- Siddique, Asima, Omar Masood, Kiran Javaria, and Dinh Tran Ngoc Huy. 2020. A comparative study of the performance of commercial banks in ASIAN developing and developed countries. Insights into Regional Development 2: 580–91. [Google Scholar] [CrossRef]
- Stone, Mervyn. 1974. Cross-validatory choice and assessment of statistical predictions (with discussion). Journal of the Royal Statistical Society: Series B (Methodological) 39: 111–47. [Google Scholar] [CrossRef]
- Subhedar, Mansi, and Gajanan Birajdar. 2012. Comparison of Mamdani and Sugeno inference systems for dynamic spectrum allocation in cognitive radio networks. Wireless Personal Communications 1: 805–19. [Google Scholar] [CrossRef]
- TAB Insights. 2022. Report. Available online: https://tabinsights.com/ab500/largest-banks-mea (accessed on 5 August 2023).
- Takagi, Tomohiro, and Michio Sugeno. 1985. Fuzzy identification of systems and its applications to modeling and control. IEEE Transactions on Systems, Man, and Cybernetics 15: 116–32. [Google Scholar] [CrossRef]
- Talpur, Noureen, Said Jadid Abdulkadir, Hitham Alhussian, Mohd Hilmi Hasan, Norshakirah Aziz, and Alwi Bamhdi. 2023. Deep Neuro-Fuzzy System application trends, challenges, and future perspectives: A systematic survey. Artificial Intelligence Review 56: 865–913. [Google Scholar] [CrossRef]
- Vella, Vince, and Wing Lon Ng. 2014. Enhancing risk-adjusted performance of stock market intraday trading with neuro-fuzzy systems. Neurocomputing 141: 170–87. [Google Scholar] [CrossRef]
- Veryzhenko, Iryna. 2021. Who gains and who loses on stock markets? Risk preferences and timing matter. Intelligent Systems in Accounting, Finance & Management 28: 143–55. [Google Scholar] [CrossRef]
- Walker, Thomas, Yixin Xu, Dieter Gramlich, and Yunfei Zhao. 2023. The impact of natural disasters on the performance and solvency of US banks. International Journal of Managerial Finance 19: 136–54. [Google Scholar] [CrossRef]
- Wan, Yuqing, and Yain-Whar Si. 2017. Adaptive neuro fuzzy inference system for chart pattern matching in financial time series. Applied Soft Computing 57: 1–18. [Google Scholar] [CrossRef]
- Wang, Joseph. 2000. Analytical Electrochemistry, 2nd ed. Hoboken: Wiley-VCH. [Google Scholar]
- Xiong, Zhi-Bin, and Rong-Jun Li. 2005. Credit risk evaluation with fuzzy neural networks on listed corporations of China. Paper presented at the 2005 IEEE International Workshop on VLSI Design and Video Technology, Suzhou, China, May 28–30; Piscataway: IEEE, pp. 397–402. [Google Scholar]
- Yazdani-Chamzini, Abdolreza, Mohammad Majid Fouladgar, Edmundas Kazimieras Zavadskas, and S. Hamzeh Haji Moini. 2013. Selecting the optimal renewable energy using a fuzzy multiple criteria decision making model. Journal of Business Economics and Management 14: 957–78. [Google Scholar] [CrossRef]
- Yeom, Chan-Uk, and Keun-Chang Kwak. 2018. Performance comparison of ANFIS models by input space partitioning methods. Symmetry 10: 700. [Google Scholar] [CrossRef]
- Zeng, Xiaoqin, and Daniel S. Yeung. 2003. A quantified sensitivity measure for multilayer perceptron to input perturbation. Neural Computation 15: 183–212. [Google Scholar] [CrossRef]
- Zhao, Yaoteng, Supat Chupradit, Marria Hassan, Sadaf Soudagar, Alaa Mohamd Shoukry, and Jameel Khader. 2022. The role of technical efficiency, market competition and risk in the banking performance in G20 countries. Business Process Management Journal 27: 2144–60. [Google Scholar] [CrossRef]
- Zou, Yijun, and Fan Li. 2014. The Impact of Credit Risk Management on Profitability of Commercial Banks: A Study of Europe. London: Macmillan. [Google Scholar]




| Dependent Variable | Sub-Variable | Measure |
|---|---|---|
| Financial Performance | Return on Equity (ROE) | Net Income/Ordinary Equity |
| Earnings per Share (EPS) | Net Income/Number of Shares | |
| Price-Earnings Ratio (PER) | Share Price/EPS | |
| Independent Variables | Sub-Variable | Measure |
| Capital Adequacy Risk (CAR) | CAR | (Tier 1 + Tier 2)/TA |
| TIER 1 | Core Capital/Risky Weighted Assets | |
| ETC | Equity Tier 1/Total Capital | |
| Liquidity Risk (LR) | Loan to Deposit Ratio (LDR) | Loan/Total Deposits |
| Loans Assets Ratio (LAR) | Loans/Total Assets | |
| Credit Risk (CR) | Provision Loan Ratio (PLR) | Provision |
| Non-Performing Loans Ratio (NPL) | NPL/Loans |
| Independent Variables | Sub-Variable | Average Sensitivity per Risk Component | Average Sensitivity per Risk Type |
|---|---|---|---|
| Capital Adequacy Risk (CAR) | CAR | 90.5 | 61.8 |
| TIER 1 | 68.3 | ||
| ETC | 26.8 | ||
| Liquidity Risk (LR) | Loan to Deposit Ratio (LDR) | 115.0 | 74.3 |
| Loans Assets Ratio (LAR) | 33.6 | ||
| Credit Risk (CR) | Provision Loan Ratio (PLR) | 60.1 | 81.4 |
| Non-Performing Loans (NPL) | 102.8 |
| Independent Variables | Sub-Variable | Average Sensitivity per Risk Component | Average Sensitivity per Risk Type |
|---|---|---|---|
| Capital Adequacy Risk (CAR) | CAR | 32.4 | 22.4 |
| TIER 1 | 19.1 | ||
| ETC | 15.7 | ||
| Liquidity Risk (LR) | Loan to Deposit Ratio (LDR) | 72.2 | 45.6 |
| Loans Assets Ratio (LAR) | 19.0 | ||
| Credit Risk (CR) | Provision Loan Ratio (PLR) | 46.7 | 59.0 |
| Non-Performing Loans (NPL) | 71.3 |
| Independent Variables | Sub-Variable | Average Sensitivity per Risk Component | Average Sensitivity per Risk Type |
|---|---|---|---|
| Capital Adequacy Risk (CAR) | CAR | 148.2 | 85.8 |
| TIER 1 | 68.4 | ||
| ETC | 40.8 | ||
| Liquidity Risk (LR) | Loan to Deposit (LDR) | 211.3 | 141.1 |
| Loans Assets Ratio (LAR) | 70.9 | ||
| Credit Risk (CR) | Provision Loan Ratio (PLR) | 55.8 | 77.9 |
| Non-Performing Loans (NPL) | 100.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehdi, R.; Ahmed, I.E.; Mohamed, E.A. Rating the Impact of Risks in Banking on Performance: Utilizing the Adaptive Neural Network-Based Fuzzy Inference System (ANFIS). Risks 2025, 13, 85. https://doi.org/10.3390/risks13050085
Mehdi R, Ahmed IE, Mohamed EA. Rating the Impact of Risks in Banking on Performance: Utilizing the Adaptive Neural Network-Based Fuzzy Inference System (ANFIS). Risks. 2025; 13(5):85. https://doi.org/10.3390/risks13050085
Chicago/Turabian StyleMehdi, Riyadh, Ibrahim Elsiddig Ahmed, and Elfadil A. Mohamed. 2025. "Rating the Impact of Risks in Banking on Performance: Utilizing the Adaptive Neural Network-Based Fuzzy Inference System (ANFIS)" Risks 13, no. 5: 85. https://doi.org/10.3390/risks13050085
APA StyleMehdi, R., Ahmed, I. E., & Mohamed, E. A. (2025). Rating the Impact of Risks in Banking on Performance: Utilizing the Adaptive Neural Network-Based Fuzzy Inference System (ANFIS). Risks, 13(5), 85. https://doi.org/10.3390/risks13050085






