Abstract
Maximum likelihood estimation (MLE) in infinite mixture distributions often lacks closed-form solutions, requiring numerical methods such as the Newton–Raphson algorithm. Selecting appropriate initial values is a critical challenge in these procedures. This study introduces a bootstrap-based approach to determine initial parameter values for MLE, employing both nonparametric and parametric bootstrap methods to generate the mixing distribution. Monte Carlo simulations across multiple cases demonstrate that the bootstrap-based approaches, especially the nonparametric bootstrap, provide reliable and efficient initialization and yield consistent maximum likelihood estimates even when raw moments are undefined. The practical applicability of the method is illustrated using three empirical datasets: third-party liability claims in Indonesia, automobile insurance claim frequency in Australia, and total car accident costs in Spain. The results indicate stable convergence, accurate parameter estimation, and improved reliability for actuarial applications, including premium calculation and risk assessment. The proposed approach offers a robust and versatile tool both for research and in practice in complex or nonstandard mixture distributions.
1. Introduction
An infinite mixture distribution is an extension of the finite mixture model in which the number of components is not predetermined and may, in principle, be countably infinite. Rather than a finite sum of distributions, the mixture is represented as an infinite sum or an integral over a parameter space (Klugman et al. 2019). In actuarial science, infinite mixture distributions are applied in credibility theory and bonus–malus systems to model both claim frequency and claim severity (Herzog 2010; Lemaire 1995). Compared to standard distributions, they offer the advantage of accommodating complex data structures and high heterogeneity. Such data are often multimodal, skewed, or heavy-tailed in the case of continuous variables (Ghosal and van der Vaart 2001), with variances exceeding those predicted by standard distributional models, particularly the Poisson distribution (Canale and Prünster 2017; Wade and Ghahramani 2018).
Numerous studies have introduced distributions that fall within the class of infinite mixtures, both for discrete and continuous cases, with applications to insurance data. For discrete distributions, examples include the Poisson–Lindley (Sankaran 1970), Poisson–lognormal (Bulmer 1974), Poisson–gamma, Poisson–inverse Gaussian, Poisson–generalized inverse Gaussian, Poisson–beta, and Poisson–uniform distributions (G. Willmot 1986; G. E. Willmot 1987), as well as several variants such as the negative binomial–Lindley (Zamani and Ismail 2010), Poisson–weighted Lindley (Abd El-Monsef and Sohsah 2014), Poisson–Sujatha (Shanker 2016b), Poisson–Amarendra (Shanker 2016a), Poisson–Aradhana (Shanker 2017), and the new Poisson mixed weighted Lindley distribution (Atikankul et al. 2020). For continuous cases, examples include the inverse exponential–gamma (Anantasopon et al. 2015), lognormal–gamma (Moumeesri et al. 2020), exponential–gamma (McNulty 2021), Rayleigh–Rayleigh (Jaroengeratikun et al. 2022), and several mixtures of the Kies distribution (Zaevski and Kyurkchiev 2024).
Maximum likelihood estimation (MLE) of the parameters of infinite mixture distributions typically requires numerical methods such as Newton–Raphson, since closed-form solutions are generally unavailable. A key challenge of Newton–Raphson is the determination of suitable initial values. Several studies have not explicitly addressed this issue (Anantasopon et al. 2015; McNulty 2021; Moumeesri et al. 2020; G. Willmot 1986), despite its critical importance for ensuring convergence. In some cases, alternative estimation methods, such as the method of moments, have been employed to provide initial values (Abd El-Monsef and Sohsah 2014; Jaroengeratikun et al. 2022; Sankaran 1970; Shanker 2016a, 2016b, 2017). However, the method of moments does not always yield analytical solutions (Atikankul et al. 2020; Zamani and Ismail 2010; Zaevski and Kyurkchiev 2024). Therefore, an alternative and more generally applicable approach is needed to reliably determine initial parameter values for the MLE of infinite mixture distributions.
A central challenge in applying infinite mixture distributions lies in selecting appropriate initial values for MLE, as poor initialization can lead to instability or non-convergence. To address this, we propose a bootstrap-based strategy for generating reliable starting values, employing both parametric and nonparametric approaches. In this framework, bootstrap samples are used to construct the mixing distribution, and the resulting parameter estimates serve as initial values for MLE of infinite mixture distributions. The effectiveness of the proposed method is evaluated through Monte Carlo simulations and demonstrated with three real data applications: Indonesian automobile insurance claims, Australian automobile claim frequency data, and Spanish automobile claim severity data. The objective of this study is to enhance the stability and accuracy of MLE for infinite mixture distributions, thereby providing methodological contributions and practical insights for actuarial applications.
2. Infinite Mixture Distributions
In statistics, new probability distributions can be constructed in various ways, one of the most important being mixing. Mixing refers to the process of forming a new distribution by combining two or more component distributions, typically using weights. The resulting distribution is referred to as a mixture distribution. An infinite mixture distribution is a special case in which the number of component distributions is countably infinite. Formally, it can be expressed as
where the integral is taken over the support of , denotes the probability density function (pdf) or probability mass function (pmf) of the random variable conditional on , and is the pdf of the random variable , referred to as the mixing distribution (Klugman et al. 2019). The corresponding distribution function is given by
In general, the -th moment of the infinite mixture distribution can be expressed as
which follows directly from the law of iterated expectations. In particular, the variance of can be decomposed as
In this section, we discuss three distributions that belong to the class of infinite mixture distributions, namely, the Poisson–Lindley distribution (Sankaran 1970), the inverse exponential–gamma distribution (Anantasopon et al. 2015), and the lognormal–gamma distribution (Moumeesri et al. 2020).
2.1. Poisson–Lindley Distribution
The Poisson–Lindley distribution is a discrete probability distribution that arises as a mixed Poisson distribution, in which the Poisson parameter follows a Lindley distribution. Let be a random variable that follows a Poisson distribution with parameter , and assume that itself follows a Lindley distribution with parameter . Then, the marginal distribution of is referred to as the Poisson–Lindley distribution, with the pmf given by (Sankaran 1970)
where is the shape parameter of the Lindley distribution. This distribution provides an alternative to the classical Poisson distribution, particularly for modeling over-dispersed count data, as it typically exhibits variance greater than the mean.
The Poisson–Lindley distribution has been applied to model automobile insurance claim frequency data for the calculation of Bayesian premiums (Moumeesri et al. 2020). Let , , , be a random sample from the Poisson–Lindley distribution, and let , , , denote the corresponding observed values. The parameter of the Poisson–Lindley distribution, , can be estimated using the method of moments (Sankaran 1970):
where . The maximum likelihood estimator of the Poisson–Lindley distribution parameter is obtained as the solution to the following equation (Sankaran 1970):
Since the parameter estimate cannot be obtained in closed form, a numerical method such as the Newton–Raphson algorithm can be used to solve the above equation. The method of moments estimate can serve as the initial value for the Newton–Raphson procedure.
2.2. Inverse Exponential–Gamma Distribution
Let be a random variable following an inverse exponential distribution with parameter , where the parameter itself follows a gamma distribution with parameters and . The marginal distribution of is then referred to as the inverse exponential–gamma distribution, with the pdf given by (Anantasopon et al. 2015)
The inverse exponential–gamma distribution has been applied to model motor insurance claims (Anantasopon et al. 2015). This distribution does not possess -th raw moments for positive integers (Klugman et al. 2019). The parameters and of the inverse exponential–gamma distribution can be estimated using the maximum likelihood method, which involves solving the following two equations (Anantasopon et al. 2015):
Because closed-form solutions for the parameter estimates are unavailable, the two equations must be solved using numerical methods, such as the Newton–Raphson method. However, Anantasopon et al. (2015) did not provide any proposal for selecting initial values when estimating the parameters of the inverse exponential–gamma distribution via the Newton–Raphson method.
2.3. Lognormal–Gamma Distribution
Let be a random variable following a lognormal distribution with parameters and . Suppose the lognormal parameter follows a gamma distribution with parameters and . Then, the marginal distribution of is called the lognormal–gamma distribution, with the pdf (Moumeesri et al. 2020)
In Moumeesri et al. (2020), the lognormal–gamma distribution was used to model automobile insurance claim severity data for the calculation of Bayesian premiums. The log-Cauchy distribution is a special case of the lognormal–gamma distribution when with the pdf
The log-Cauchy distribution does not have well-defined moments; therefore, the method of moments cannot be used to estimate its parameters. The parameters of the log-Cauchy distribution, and , can be estimated using the maximum likelihood method by solving the following two equations:
Since closed-form expressions for the parameters do not exist, numerical methods, such as the Newton–Raphson method, can be used to solve the two equations above.
3. Bootstrap-Based Initialization
The rationale for using the bootstrap approach as an initialization method for the MLE of infinite mixture distributions is as follows. The infinite mixture distribution discussed in Section 2 results from a combination of two components: the likelihood distribution () and the mixing distribution (). The likelihood distribution can be estimated directly from the data, yielding a single estimate of the parameter . However, obtaining the mixing distribution requires multiple estimates of . The bootstrap approach provides a way to generate these estimates by resampling the original data, producing bootstrap replications of . The estimated mixing distribution is then obtained from these bootstrap estimates. Consequently, the proposed initial values for the MLE of the infinite mixture distribution consist of the estimated parameters of the mixing distribution and the estimated parameters of the likelihood distribution, excluding .
Based on the description above, the stages of the bootstrap approach can be used to initialize the MLE for infinite mixture distributions. Two bootstrap approaches, namely, a nonparametric and a parametric bootstrap, are employed in this method. Suppose we have a dataset of size , denoted by . The steps for determining the initial parameter values for the MLE of the infinite mixture distribution using the nonparametric bootstrap approach are as follows:
- Randomly draw a new sample of size with replacement from the original data to create a bootstrap sample, denoted as .
- Calculate the estimated value of the parameter, , which, according to the theory of infinite mixture distributions (Section 2), follows the pdf or pmf for the bootstrap sample. Denote this estimate as .
- Repeat steps 1–2 times to obtain , , , .
- Calculate the estimated values of the parameters of the mixing distribution based on the data , , , . These estimates are then used as the initial parameter values for the MLE of the infinite mixture distribution.
The steps for determining the initial parameter values for the MLE of the infinite mixture distribution using the parametric bootstrap approach are as follows:
- Calculate the estimated value of the parameter using the MLE method, which, according to the theory, follows the pdf or pmf for the original data. Denote this estimate as .
- Randomly draw a new sample of size from the distribution to create a bootstrap sample, denoted as .
- Calculate the estimated value of the parameter for the bootstrap sample. According to the theory of infinite mixture distributions (Section 2), it follows the pdf or pmf . Denote this estimate as .
- Repeat steps 2–3 times to obtain , , , .
- Calculate the estimated values of the parameters of the mixing distribution based on the data , , , . These estimates are then used as the initial parameter values for the MLE of the infinite mixture distribution.
4. Simulation Study
In this section, a simulation study is conducted to evaluate the performance of bootstrap-based initialization in determining the initial parameter values for the MLE of the infinite mixture distribution. The performance of the two bootstrap approaches proposed in Section 3, together with the method of moments, will be evaluated. The three distributions discussed in Section 2 are used to assess the proposed method. Several cases from these distributions are considered in the simulation study, as presented in Table 1. Specifically, there are 9 cases of the Poisson–Lindley distribution, 18 cases of the inverse exponential gamma distribution, and 18 cases of the lognormal–gamma distribution.

Table 1.
Cases in the simulation study.
The results of the simulation study for all cases in Table 1 are summarized in Table 2, Table 3 and Table 4, based on simulation runs with bootstrap replications. Two approaches for initializing the MLE of the infinite mixture distributions are evaluated: the method of moments (MM) and bootstrap-based methods, including the nonparametric (NP) and parametric (P) bootstrap. Their performance is assessed in terms of the average number of iterations and the root mean square error (RMSE), which reflects both the variance and bias of the parameter estimates.

Table 2.
Simulation study results for the Poisson–Lindley distribution.

Table 3.
Simulation study results for the inverse exponential–gamma distribution.

Table 4.
Simulation study results for the lognormal–gamma distribution.
Table 2 presents the simulation results for the Poisson–Lindley distribution. The average number of iterations is below five and is similar across all methods (MM, NP, and P) and cases. This indicates that both the method of moments and bootstrap-based methods perform equally well in initializing the MLE for the Poisson–Lindley distribution. Furthermore, all RMSE values are identical across methods and cases, suggesting that the method of moments and bootstrap-based methods yield the same MLE results for this distribution.
These findings indicate that the optimization algorithm converges rapidly because the starting values provided by all methods are already sufficiently close to the true maximum likelihood estimates. The consistently low number of iterations reflects not only the computational efficiency but also the numerical stability of the estimation procedure for the Poisson–Lindley distribution. Moreover, the equality of RMSE values across methods suggests that the likelihood surface for this distribution is relatively regular and not highly sensitive to the choice of initial values. This explains why both the method of moments and bootstrap-based approaches lead to nearly identical estimates.
Table 3 presents the simulation results for the inverse exponential–gamma distribution. Only bootstrap-based methods were evaluated in this study. The average number of iterations is below 30 for both bootstrap-based approaches (NP and P) across all cases. The nonparametric bootstrap (NP) requires fewer iterations than the parametric bootstrap (P), with differences ranging from 2 to 12 iterations. This indicates that the nonparametric bootstrap performs better than the parametric bootstrap in determining the initial parameter values for the MLE of the infinite mixture distributions. Furthermore, all RMSE values are identical across both approaches and all cases, suggesting that the bootstrap-based methods yield the same MLE for the inverse exponential–gamma distribution.
This finding implies that the nonparametric bootstrap not only ensures accuracy comparable to the parametric bootstrap but also achieves faster convergence, as reflected in the smaller number of iterations required. The reduced computational burden makes the nonparametric approach more efficient and stable, particularly in the context of complex distributions such as the inverse exponential–gamma. Although the RMSE values are identical, the practical advantage of the nonparametric bootstrap lies in its efficiency, which strengthens its methodological relevance for large-scale or repeated estimations.
Table 4 presents the simulation results for the lognormal–gamma distribution. Only bootstrap-based methods were evaluated. The average number of iterations is below 25 and is similar across both bootstrap-based approaches (NP and P) and all cases. This indicates that both approaches perform equally well in initializing the MLE for the lognormal–gamma distribution. Furthermore, all RMSE values are identical across both approaches and all cases, suggesting that the bootstrap-based methods yield the same MLE results for this distribution.
This result indicates that both bootstrap-based approaches provide stable and efficient starting values for the lognormal–gamma distribution, as reflected in the relatively low and comparable number of iterations. The identical RMSE values confirm that the two methods produce estimates of equal accuracy. Hence, in this case, the practical implication is that either bootstrap approach can be reliably applied without significant differences in efficiency or accuracy.
It should also be noted that, in a small number of simulation runs, the numerical optimization procedure failed to converge. This phenomenon arises because the proposed approach relies on randomly generated data, which in rare cases may produce unfavorable starting values or likelihood shapes that slow down the convergence process. However, these instances were infrequent and did not materially affect the overall simulation results. In practice, such convergence issues can be mitigated by increasing the maximum number of iterations, using alternative starting values, or repeating the estimation process. Therefore, despite these occasional occurrences, the proposed methods can still be regarded as numerically stable and reliable for the estimation of infinite mixture distributions.
The likelihood functions of infinite mixture distributions are often multimodal, which makes global optimization challenging. In this study, the log-likelihood was maximized using the Newton–Raphson algorithm with multiple initialization strategies (method of moments, nonparametric bootstrap, and parametric bootstrap). The consistency of the results across these starting values and the rapid convergence observed indicate that the obtained solutions are stable and practically close to the global optimum, even though a theoretical guarantee of global convergence cannot be provided.
5. Applications
5.1. Automobile Insurance Claims Data in Indonesia
In many countries, including Indonesia, automobile insurance is one of the largest branches of non-life insurance and represents a significant portion of household expenditure. In Indonesia, the basic structure of automobile insurance consists of Comprehensive coverage and Total Loss Only coverage, with additional options for extensions. Comprehensive coverage provides protection against both partial and total losses, including minor damages, major accidents, and theft. Total Loss Only coverage applies only when the vehicle is stolen or suffers damage exceeding 75% of its insured value. Third-Party Liability is offered as an extension of automobile insurance, covering bodily injury or property damage to third parties caused by the insured vehicle. Automobile insurance premiums are calculated based on claim frequency and claim severity, as well as risk factors such as the driver’s age, gender, driving experience, and vehicle characteristics. Accurate premium calculation requires modeling both claim frequency and claim severity.
We apply the proposed method to two automobile insurance claim datasets from Indonesia, covering policyholders with comprehensive coverage and expanded third-party liability in the 2019 underwriting year. The first dataset contains the claim frequency for third-party liability, as shown in columns 1 and 2 of Table 5. Among 56,488 policies, 226 claims were reported. Of these, 224 policyholders filed one claim, and one policyholder filed two claims. The sample mean and variance for the claim frequency data are 0.00400 and 0.00402, respectively. The second dataset contains the claim severity for third-party liability and consists of 226 observations. The sample mean and standard deviation for the claim severity data are IDR 5,760,172 and IDR 7,162,913, respectively. Figure 1 shows a histogram of the claim severity data.

Table 5.
Chi-square calculation for claim frequency data in Indonesia.
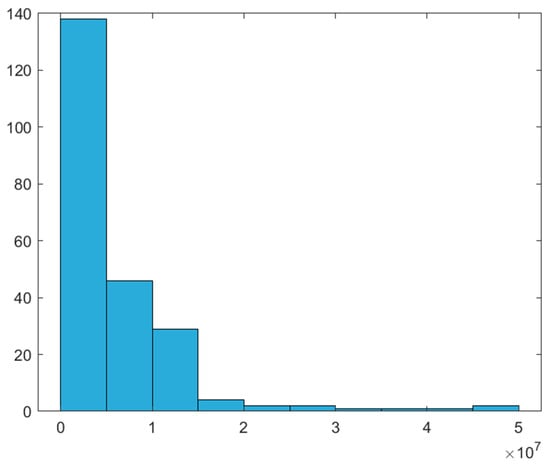
Figure 1.
Histogram of the claim severity data.
The Poisson–Lindley distribution is used to model third-party liability claim frequency data. The inverse exponential–gamma and lognormal–gamma distributions are used to model third-party liability claim severity data. The parameters of these distributions are estimated using MLE via the Newton–Raphson method, with initial values determined using the bootstrap-based approach proposed in this paper.
The bootstrap procedures described in Section 3 are applied to the third-party liability claim frequency data to obtain initial parameter estimates using both nonparametric and parametric bootstrap methods. The estimates were 250.7964 and 250.5977, respectively. These initial values were used to estimate the MLE of the Poisson–Lindley distribution via the Newton–Raphson method. Both approaches yielded the same result: 250.9390 at iteration 3. Table 5 presents the observed claim frequencies, estimated probabilities under the Poisson–Lindley distribution, and the expected frequencies. These values are used to calculate the chi-square test statistic to assess the goodness of fit of the Poisson–Lindley distribution. The results indicate that the Poisson–Lindley distribution adequately models the third-party liability claim frequency data.
Table 6 presents the results of applying the method proposed in Section 3 to third-party liability claim severity data, along with the Kolmogorov–Smirnov (K–S) test results for the inverse exponential–gamma (IEG) and lognormal–gamma (LG) distributions. The initial MLE parameter estimates for the IEG distribution are and for the nonparametric bootstrap, and and for the parametric bootstrap. The MLE values for both approaches are and . These estimates were obtained at iteration 30 for the nonparametric bootstrap and iteration 54 for the parametric bootstrap. The results for the LG distribution are shown in the last column of Table 6.

Table 6.
Calculation results for claim severity data in Indonesia.
The K–S test statistic values for the IEG and LG distributions are 0.0951 and 0.0973, respectively. The critical value of the K–S test at the 1% significance level is 0.1011 (Sheskin 2000). Thus, both the IEG and LG distributions are suitable for modeling third-party liability claim severity data. Figure 2 shows the empirical distribution function (EDF) and the cumulative distribution function curves for the IEG and LG distributions. The cumulative distribution function curve of the IEG distribution is closer to the EDF, indicating that the IEG distribution provides a better fit to the data than the LG distribution. This conclusion is supported by the lower K–S test statistic and higher log-likelihood value for the IEG distribution.
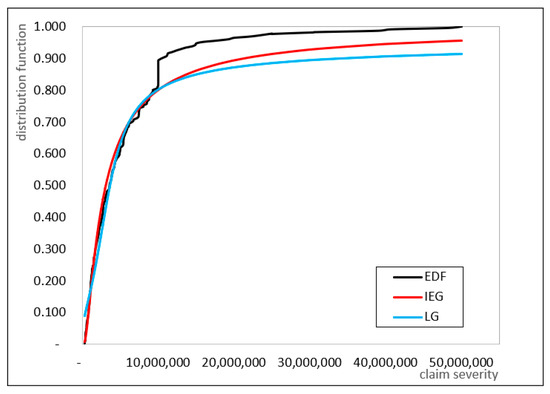
Figure 2.
Cumulative distribution function of claim severity in Indonesia.
Figure 2 shows that the considered distributions do not adequately capture the data, highlighting the need for alternative distributions. The non-smooth shape of the EDF is likely due to the limited sample size (226 observations) and data heterogeneity arising from multiple subpopulations. In Indonesia, where automobile insurance is regulated by the Financial Services Authority, policyholders are classified into three regions. The 56,488 policyholders summarized in Table 5 correspond to these regional classifications. One potential class of alternative distributions for modeling the above data is the finite mixture distributions.
The results of modeling of claim frequency and claim severity data can be applied in practice to calculate the pure premium for automobile insurance with third-party liability coverage. Theoretically, the pure premium is calculated as the product of the expected claim frequency and expected claim severity, i.e.,
Based on the modeling of claim frequency, the expected claim frequency for third-party liability coverage is estimated as the mean of the Poisson–Lindley distribution, 0.0040008. The expected claim severity cannot be determined directly, as the IEG distribution theoretically has no finite mean. For practical purposes, a limited expected value is employed, as recommended in the literature (Daykin et al. 1993; Klugman et al. 2019). The formula for the limited expected value of the IEG distribution is given by
Here, denotes the policy limit, which in this case is IDR 50 million. Using the claim severity model and Equation (16), the estimated limited expected value is IDR 7,848,116. Hence, the pure premium for automobile insurance with third-party liability coverage is calculated as 0.0040008 7,848,116 = IDR 31,399. Applying appropriate loading factors allows insurance companies to determine the final premium payable by policyholders.
5.2. Frequency of Automobile Insurance Claims in Australia
This subsection uses data on one-year automobile insurance policies in Australia for 2004–2005 to illustrate the proposed method (de Jong and Heller 2008). These data have been employed in several studies to validate proposed methodologies (Moumeesri and Pongsart 2022; Ye et al. 2022). Out of 67,856 policies, 4624 (6.8%) recorded at least one claim. Specifically, 4333 policyholders made one claim, 271 made two claims, 18 made three claims, and 2 made four claims. The claim frequency data are presented in columns 1 and 2 of Table 7. The sample mean and variance of the claim frequency data are 0.0728 and 0.0774, respectively.

Table 7.
Chi-square calculation for claim frequency data in Australia.
The Poisson–Lindley distribution was used to model the claim frequency data. Its parameter was estimated using the maximum likelihood method, implemented through the Newton–Raphson algorithm, with initial values obtained from both nonparametric and parametric bootstrap approaches. The resulting initial estimates were 14.6272 and 14.6308, respectively. These values were then employed to obtain the MLE of the Poisson–Lindley distribution using the Newton–Raphson method. Both approaches produced the same result, converging to 250.9390 after three iterations. Based on the values presented in Table 7, the chi-square test statistic is 2.00533 with a p-value of 0.5614, indicating that the Poisson–Lindley distribution provides an adequate fit for modeling the claim frequency data.
Based on the claim frequency modeling, the estimated expected claim frequency is given by the mean of the Poisson–Lindley distribution, 0.0728. This indicates that the expected number of future claims is 728 per 10,000 policyholders. Such information, together with the results of claim severity modeling, can help avoid setting premiums that are too high—potentially driving policyholders to competitors—or too low, which may lead to financial losses for the company. It is also valuable for calculating claim reserves.
5.3. The Total Cost of Car Accidents in Spain
Data on 489 individual car accidents in Spain in 2011 (Guillen et al. 2020) were used to illustrate the proposed method. The data constitute a random sample provided by an insurer. For each accident, information is available on the total cost (in thousands of euros), driver characteristics, and telematics-based driving patterns. In this subsection, the total cost is modeled using the IEG and LG distributions. The sample mean and standard deviation of the total cost are 2870 and 6988, respectively. Figure 3 presents a histogram of the total cost.
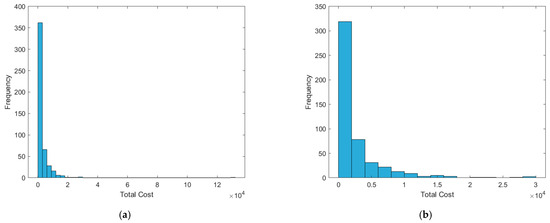
Figure 3.
Histogram of the total cost: (a) all observations; (b) total cost truncated at 30,000.
Table 8 presents the results of applying the method proposed in Section 3 to the total cost, along with the K–S test results for the IEG and LG distributions. The initial MLE values for the IEG distribution were , (nonparametric bootstrap) and , (parametric bootstrap). Both methods converged to and at iteration 22 for the nonparametric bootstrap and iteration 52 for the parametric bootstrap. The results for the LG distribution are reported in the last column of Table 8.

Table 8.
Calculation results for the total cost.
The K–S statistic for the IEG model (0.0361) is lower than that of the LG model (0.0926) and below the 1% critical value of 0.0687 (Sheskin 2000), indicating a superior fit for the total cost. As illustrated in Figure 4, the cumulative distribution function of the IEG model closely follows the empirical distribution, further supported by its smaller K–S value and higher log-likelihood.
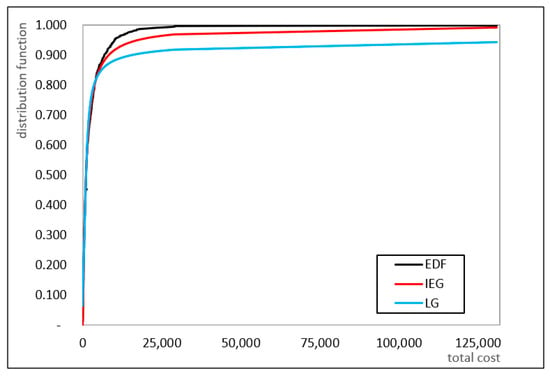
Figure 4.
Cumulative distribution function of the total cost.
The results of the total cost modeling can be directly used to calculate the pure premium, as the total cost represents an aggregate loss. Under the collective risk model in actuarial science (Klugman et al. 2019), the expected aggregate loss—corresponding here to the total cost—is given by
which corresponds to the pure premium formula given in Equation (15). Since the mean of the IEG distribution does not exist, the expected value of the total cost is computed using the limited expected value formula in Equation (16). Let . By applying the formula in Equation (16), the estimated limited expected value of the IEG distribution is 4.614, which represents the estimated pure premium.
6. Discussion and Conclusions
In this paper we proposed a bootstrap-based method to determine initial values for numerical procedures used to obtain maximum likelihood estimators (MLEs) in infinite mixture distributions. Two bootstrap strategies were considered and described in detail: the nonparametric bootstrap and the parametric bootstrap. The procedures outline how to generate candidate starting values from bootstrap samples and how to select stable initial values for iterative optimization routines.
The proposed approach is particularly useful in situations where conventional initial-value selection methods fail or are unavailable—for example, when raw moments of the distribution are undefined or when closed-form solutions for parameters via the method of moments do not exist. In such cases, standard moment-based initial guesses cannot be used, and carefully chosen bootstrap-derived starting values provide a practical alternative to initialize numerical algorithms like Newton–Raphson or other optimization methods.
The simulation study was designed primarily to evaluate the effectiveness of the bootstrap-based initialization procedure rather than to re-assess the intrinsic properties of the estimation method itself. The results show that both bootstrap approaches produce reliable and efficient starting values for the MLE; the nonparametric bootstrap performed particularly well across the scenarios considered. When moments exist, the method of moments and both bootstrap approaches yielded identical MLEs in our simulations, which supports the robustness of the bootstrap initialization. These results indicate that although global convergence cannot always be formally guaranteed, the procedure consistently converged to solutions that were indistinguishable from the global optimum across all tested scenarios. In situations with undefined moments, the bootstrap methods provided a feasible and robust way to obtain starting values that enabled successful estimation. We did observe occasional convergence failures caused by the stochastic variability inherent in bootstrap resampling; however, these failures were rare and did not materially affect the overall findings. Practically, there is an explicit trade-off between computational burden and the stability/accuracy of inference: larger numbers of bootstrap replications tend to improve stability but increase computation time.
Although the simulation scenarios covered several cases of infinite mixture distributions, the range of distributions and model complexities examined here remains limited. Extending the methodology to more complex models—for instance, higher-dimensional mixtures, mixtures with covariate-dependent components, or models with additional latent structure—was beyond the scope of this study. These represent promising directions for future research, including comprehensive sensitivity analyses (e.g., varying the number of bootstrap replications and resampling schemes), comparisons with alternative initialization strategies, and empirical validation across a broader set of heavy-tailed or nonstandard distributions.
The practical value of the proposed method was illustrated through three empirical applications: third-party liability claims in Indonesia, claim frequency data in Australia, and total car accident costs in Spain. In each dataset the bootstrap-based initialization facilitated stable and efficient estimation of distribution parameters. For example, in the Indonesian automobile insurance dataset the method enabled accurate estimation of claim frequency and severity components, which are central to calculating pure premiums and informing policy design. The Spanish total cost example demonstrated applicability in aggregate loss modeling for actuarial tasks, while the Australian frequency data highlighted improved numerical stability in fitting count-type mixture models.
Beyond immediate computational benefits, the bootstrap-based initialization has broader implications both for research and in practice. For researchers, it provides a flexible tool to explore infinite mixture and other heavy-tailed models that are otherwise difficult to fit with conventional initial values. For practitioners—such as actuaries and risk managers—the method can improve the reliability of premium calculations, reserve estimates, and other risk management decisions when standard moment-based initialization is not possible. From an implementation perspective, users should balance the number of bootstrap replications and computational resources, and consider reporting sensitivity checks to demonstrate the robustness of estimates.
In conclusion, the bootstrap-based initialization method offers a robust and practical solution for numerical estimation of MLEs in infinite mixture distributions. It enhances convergence stability and computational reliability when conventional initial value choices are infeasible. Future work could extend the approach to high-dimensional and more complex mixture models, investigate integration with Bayesian estimation frameworks, and assess impacts in large-scale actuarial applications to further gauge practical benefits in premium setting and reserve estimation.
Funding
This work was supported by the Institute for Research and Community Service (LPPM), Universitas Islam Bandung, Indonesia, through grant number 002/B.04/LPPM/I/2025.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to confidentiality restrictions.
Acknowledgments
I thank the three anonymous reviewers for their valuable feedback and suggestions, which have significantly improved the quality of this manuscript.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MLE | maximum likelihood estimation |
| probability density function | |
| pmf | probability mass function |
| MM | method of moments |
| NP | nonparametric bootstrap |
| P | parametric bootstrap |
| RMSE | root mean square error |
| IDR | Indonesian Rupiah |
| IEG | inverse exponential–gamma |
| LG | lognormal–gamma |
| K–S | Kolmogorov–Smirnov |
| EDF | empirical distribution function |
References
- Abd El-Monsef, Mohamed Mohamed Ezzat, and Nora Mohamed Sohsah. 2014. Poisson–Weighted Lindley Distribution. Jökull Journal 64: 192–202. [Google Scholar]
- Anantasopon, Sasithorn, Pairote Sattayatham, and Tosaporn Talangtam. 2015. The Modeling of Motor Insurance Claims with Infinite Mixture Distribution. International Journal of Applied Mathematics and Statistics 53: 40–49. [Google Scholar]
- Atikankul, Yupapin, Ampai Thongteeraparp, and Winai Bodhisuwan. 2020. The new poisson mixed weighted lindley distribution with applications to insurance claims data. Songklanakarin Journal of Science and Technology 42: 152–62. [Google Scholar] [CrossRef]
- Bulmer, Michael George. 1974. On Fitting the Poisson Lognormal Distribution to Species-Abundance Data. Biometrics 30: 101–10. [Google Scholar] [CrossRef]
- Canale, Antonio, and Igor Prünster. 2017. Robustifying Bayesian Nonparametric Mixtures for Count Data. Biometrics 73: 174–84. [Google Scholar] [CrossRef] [PubMed]
- Daykin, Christoper David, Tapio Pentikainen, and Martti Pesonen. 1993. Practical Risk Theory for Actuaries. London: Chapman and Hall/CRC. [Google Scholar] [CrossRef]
- de Jong, Piet, and Gillian Z. Heller. 2008. Generalized Linear Models for Insurance Data. Cambridge: Cambridge University Press. [Google Scholar] [CrossRef]
- Ghosal, Subhashis, and Aad Willem van der Vaart. 2001. Entropies and rates of convergence for maximum likelihood and Bayes estimation for mixtures of normal densities. The Annals of Statistics 29: 1233–63. [Google Scholar] [CrossRef]
- Guillen, Montserrat, Catalina Bolance, and Ricardo Cao. 2020. Motor insurance claim severity. In Mendeley Data, V1. Amsterdam: Elsevier. [Google Scholar] [CrossRef]
- Herzog, Thomas Nelson. 2010. Introduction to Credibility Theory, 4th ed. Winsted: ACTEX Publications. [Google Scholar]
- Jaroengeratikun, Uraiwan, Sukanda Dankunprasert, and Tosaporn Talangtam. 2022. Infinite Mixture of Rayleigh-Rayleigh Distribution and Its Application to Motor Insurance Claims. Pakistan Journal of Statistics 38: 517–27. [Google Scholar]
- Klugman, Stuart Arthur, Harry Herman Panjer, and Gordon Edward Willmot. 2019. Loss Models: From Data to Decisions, 5th ed. Hoboken: John Wiley and Sons, Inc. [Google Scholar]
- Lemaire, Jean. 1995. Bonus-Malus Systems in Automobile Insurance. London: Kluwer Academic Publishers. [Google Scholar]
- McNulty, Greg. 2021. The Pareto-Gamma Mixture. Casualty Actuarial Society E-Forum. Available online: https://www.casact.org/sites/default/files/2023-03/McNulty_The_Pareto_Gamma_Mixture_EForum-Spring2021.pdf (accessed on 14 August 2025).
- Moumeesri, Adisak, and Tippatai Pongsart. 2022. Bonus-Malus Premiums Based on Claim Frequency and the Size of Claims. Risks 10: 181. [Google Scholar] [CrossRef]
- Moumeesri, Adisak, Watcharin Klongdee, and Tippatai Pongsart. 2020. Bayesian Bonus-Malus Premium with Poisson-Lindley Distributed Claim Frequency and Lognormal-Gamma Distributed Claim Severity in Automobile Insurance. WSEAS Transactions on Mathematics 19: 443–51. [Google Scholar] [CrossRef]
- Sankaran, Munuswamy. 1970. The Discrete Poisson-Lindley Distribution. Biometrics 26: 145–49. [Google Scholar] [CrossRef]
- Shanker, Rama. 2016a. The Discrete Poisson-Amarendra Distribution. International Journal of Statistical Distributions and Applications 2: 14–21. [Google Scholar] [CrossRef][Green Version]
- Shanker, Rama. 2016b. The Discrete Poisson-Sujatha Distribution. International Journal of Probability and Statistics 5: 1–9. Available online: http://article.sapub.org/10.5923.j.ijps.20160501.01.html#Sec1 (accessed on 14 August 2025).[Green Version]
- Shanker, Rama. 2017. The Discrete Poisson-Aradhana Distribution. Turkiye Klinikleri Journal of Biostatistics 9: 12–22. [Google Scholar] [CrossRef]
- Sheskin, David Judah. 2000. Handbook of Parametric and Nonparametric Statistical Procedures, 2nd ed. New York: Chapman & Hall/CRC. [Google Scholar]
- Wade, Sara, and Zoubin Ghahramani. 2018. Bayesian Cluster Analysis: Point Estimation and Credible Balls (with Discussion). Bayesian Analysis 13: 559–626. [Google Scholar] [CrossRef]
- Willmot, Gordon. 1986. Mixed Compound Poisson Distributions. ASTIN Bulletin 16: S59–S79. [Google Scholar] [CrossRef]
- Willmot, Gordon Edward. 1987. The Poisson-Inverse Gaussian distribution as an alternative to the negative binomial. Scandinavian Actuarial Journal 3–4: 113–27. [Google Scholar] [CrossRef]
- Ye, Chenglong, Lin Zhang, Mingxuan Han, Yanjia Yu, Bingxin Zhao, and Yuhong Yang. 2022. Combining Predictions of Auto Insurance Claims. Econometrics 10: 19. [Google Scholar] [CrossRef]
- Zaevski, Tsvetelin Stefanov, and Nikolay Kyurkchiev. 2024. On some mixtures of the Kies distribution. Hacettepe Journal of Mathematics and Statistics 53: 1453–83. [Google Scholar] [CrossRef]
- Zamani, Hossein, and Noriszura Ismail. 2010. Negative Binomial-Lindley Distribution and Its Application. Journal of Mathematics and Statistics 6: 4–9. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).