Which Sectoral CDS Can More Effectively Hedge Conventional and Islamic Dow Jones Indices? Evidence from the COVID-19 Outbreak and Bubble Crypto Currency Periods

Abstract

In this study, we aim to provide a comprehensive analysis of the risk management potential of sectoral Credit Default Swaps (CDSs) within financial portfolios. Our objectives are threefold: (i) to investigate the safe haven properties of sectoral CDSs; (ii) to assess their hedging effectiveness and evaluate the diversification benefits of incorporating sectoral CDSs into both conventional and Islamic stock market portfolios; and (iii) to compare these findings with those obtained from alternative assets such as the VSTOXX, gold, and Bitcoin indices. To achieve this, we estimate time-varying hedge ratios using a range of multivariate GARCH (MGARCH) models and subsequently compute hedging effectiveness metrics. Conditional correlations derived from the Asymmetric Dynamic Conditional Correlation (ADCC) model are employed in linear regression analyses to assess safe haven characteristics. This methodology is applied across different subperiods to capture the impact of the crypto currency bubble and the COVID-19 pandemic on hedging performance.

1. Introduction

During pandemics, investors around the world find themselves in search of new alternative investment assets that can provide better portfolio diversification and reduce downside risks. That being said, adding alternative investment instruments, acting as safe havens, into their portfolios and identifying the most effective hedging instruments is a challenge and a non-trivial task, especially with the emergence of more and more frequent periods of financial turmoil such as the bubble crypto currencies in 2017 and the COVID-19 pandemic.

In such a context, a growing number of studies have investigated the potential of the inclusion of alternative assets in the investment portfolio, such as gold (Baur and Lucey 2010; Beckmann et al. 2015; Akhtaruzzaman et al. 2021; Salisu et al. 2021; Yousaf et al. 2021; among others), Bitcoin (Yang et al. 2022; Guesmi et al. 2019; Ji et al. 2020; Mroua et al. 2020; Mariana et al. 2021), commodities (Domanski and Heath 2007; Erb and Harvey 2006; Silvennoinen and Throp 2013; Zghal et al. 2022); Islamic indexes (Salisu and Sikiru 2020; Kenourgios et al. 2016; Yarovaya et al. 2021); Credit Default Swaps (Zghal et al. 2018; Hachicha et al. 2022) and the volatility index (Hood and Malik 2013; Zghal and Ghorbel 2020; Tarchella and Dhaoui 2021; Shahzad et al. 2021; Ali et al. 2022; Nekhili and Sultan 2022).

CDSs can be an effective hedging instrument for both conventional and Islamic stock indices due to several key mechanisms, despite some specific considerations for Islamic indices.

Five reasons can explain the use of CDSs to hedge stock indices: (1) Stock indices, especially those heavy in financials, energy, or high-yield sectors, are highly sensitive to the credit risk of their constituent companies. A credit event such as default or restructuring can imply a severe drop in that company’s stock price, impacting the index. Buying CDS protection on a specific company (or index) provides a payout if that entity experiences a credit event. This payout directly offsets losses incurred from holding the stock or index due to the credit shock. It is a more precise hedge against credit deterioration than broad market hedges. (2) CDSs offers significant cost efficiency and leverage. CDS premiums are often cheaper, especially for investment-grade entities. In contrast, hedging by shorting individual stocks or the entire index requires significant capital and involves borrowing costs. This capital efficiency is enhanced by leverage, as a modest premium payment protects a much larger notional exposure. (3) The liquidity and flexibility of CDS markets enhance their utility. Major indices (e.g., CDX, iTraxx) and single-name CDSs trade in deep, liquid markets, enabling swift entry and exit at transparent prices. Investors gain granular hedging options; they can protect against specific high-risk holdings using single-name CDSs, hedge sector-level credit risk via sectoral CDS indices, or mitigate portfolio-wide exposure through broad index CDSs. (4) CDSs also hedge systemic risk and contagion. During crises, credit events in one entity or sector can spark market-wide sell-offs. Broad CDS index protection generates payouts amid such systemic stress, offsetting correlated equity index losses. (5) Unlike short-selling, CDS hedging is purely contractual, avoiding direct impacts on underlying share prices or borrowing requirements. Hull (2022) clearly outlines the hedging function of a CDS while Chacko (2006) provides detailed examples of how different entities (banks, insurance companies, pension funds) can use CDSs to precisely manage their credit exposure without having to buy or sell the underlying bonds or loans, which can be operationally difficult and expensive.

Islamic indices adhere to Shariah principles, prohibiting interest (Riba), excessive leverage, and certain industries. Conventional CDSs are inherently controversial under the principles of Shariah for several reasons. (1) Gharar (excessive uncertainty) exists regarding trigger events, timing, and payouts. (2) Critics argue it resembles Maysir (gambling/speculation), as protection buyers pay premiums betting on a negative event without an underlying asset ownership need. (3) Pure risk trading without underlying asset transfer is problematic. (4) Premium pricing linked to interest rates raises Riba concerns. Khan (2013) provides the philosophical and technical foundation for why instruments like conventional CDSs are inherently problematic. His arguments support our points on Riba and the pricing mechanisms. Al-Suwailem (2006) directly addresses the challenge of designing Shariah-compliant hedges, arguing that while risk management is encouraged, contracts must avoid Gharar and Maysir. The study distinguishes between legitimate risk-sharing (where all parties have a potential upside and downside) and gambling (a zero-sum bet where one wins only if the other loses, like a CDS). This supports our point that critics see CDSs as a bet on a negative outcome.

The primary argument for permissibility hinges on genuine risk mitigation using CDSs solely to protect existing investments that align with Islamic principles, allowing such tools to manage existing risk. Some scholars may accept it under Darurah (necessity) if no Shariah-compliant alternatives exist (El-Gamal 2006; Ayub 2009).

Structurally, some institutions structure Shariah-compliant alternatives that mimic CDSs, using concepts like Wa’ad (promise) or Takaful (mutual guarantee), where the structure and underlying contracts are designed to avoid prohibited elements (ISRA 2023). Dusuki (2020) examines the regulatory and practical aspects of Islamic hedging, while Hassan and Aliyu (2021) review Sharia-compliant derivatives, including equity hedging. Bank Negara Malaysia (2021) presents guidelines on Islamic Derivatives and a regulatory framework for Sharia-compliant hedging in Malaysia.

These are complex and not universally accepted. Crucially, while Islamic index constituents comply with Shariah screens, their stock prices remain vulnerable to financial system credit events (e.g., counterparty defaults), which CDSs can technically hedge (Islamic Financial Services Board (IFSB) 2017; Ayub 2009; Sundararajan 2007; Hassan and Kayed 2009).

CDSs are a powerful, liquid, and capital-efficient tool for hedging the credit risk component embedded within both conventional and Islamic stock indices. Their effectiveness stems from directly offsetting losses caused by credit events impacting index constituents or the broader market. However, for Islamic indices, their use is exceptionally complex and contentious due to compliance requirements with Islamic finance principles (such as the prohibition of Gharar (excessive uncertainty) and Riba (interest)). While they can technically hedge the financial risk exposure of Shariah-compliant stocks, CDSs themselves generally violate core Islamic finance principles.

This paper distinguishes itself from prior studies in several key aspects. To start with, there is a lack of studies that analyze the hedging efficacy of various alternative assets simultaneously, involving VSTOXX, gold, and Bitcoin, and especially sectoral CDS indices, to reduce market risk in emerging-country contexts. The widespread use of these indices as hedging tools justifies their selection for the Dow Jones Conventional and Islamic emerging market indices.

Second, in line with Kroner and Sultan (1993), our aim is to determine time-varying optimal hedge ratios applicable to the Conventional and Islamic emerging market indices, using the conditional volatility estimates derived from the MGARCH models’ specifications (DCC, ADCC and GO-GARCH) and applying a rolling estimation approach to estimate time-varying MGARCH parameters.

Third, existing studies on alternative assets have not distinguished the benefits of CDS, VSTOXX, Bitcoin, and gold to investors in the EMERGC and EMERGI markets. Thus, we compute the conditional diversification benefits (CDBs) of these alternative assets following the method of Christoffersen et al. (2017). The measure of CDBs, which is defined based on the expected shortfall at a given confidence level, permits us to measure the time-varying diversifications related to portfolio composition and probability levels during periods of bubble crypto currency and the COVID-19 pandemic. In this context, we identify three specific events that contributed to global uncertainty and in turn had global effects throughout our sample period. The first event is before bubble crypto currency. The second event is during bubble crypto currency and before the COVID-19 period. Finally, the last event is during the COVID-19 period.

Finaly, one of the objectives of this paper is to examine the extent to which hedging Islamic stock indices with CDSs is useful and can be an optimal hedging strategy and whether a sectoral CDS that offers the best hedging performance in the conventional stock index remains the same as in the Islamic one. In addition, we will compare the optimal hedge ratios obtained with conventional and Islamic stock indices for the same model, the same sub-periods, and the same sectoral CDS.

The novelty and the main contribution of this paper lie in its examination of the hedging and safe haven properties of Credit Default Swaps (CDSs) at the sectoral level during turbulent periods, such as the COVID-19 pandemic and the financial bubble crisis. Unlike prior studies, we specifically investigate whether sectoral CDS indices can serve as effective hedging instruments for both conventional and Islamic stock markets during extreme market stress. CDSs are derivatives designed to hedge against credit risk (e.g., the default risk of a company or sovereign entity). While they are not directly tied to equity markets, their effectiveness in hedging stock market risk depends on correlations between credit risk and equity performance. We compare the hedging effectiveness of a sectoral CDS used to cover the conventional stock index and the one used to cover the Islamic stock index for various sub periods to show whether CDSs can be a good alternative to hedge the two indices. To the best of our knowledge, this is the first work that studies eventual change in the hedging effectiveness of a sectoral CDS to cover conventional and Islamic stock indices between various sub-periods, using various multivariate GARCH models.

We follow the methodology adopted by Hachicha et al. (2022) but extend it by dividing the entire analysis period into three distinct sub-periods and by studying the safe haven properties of a sectoral CDS compared to the most effective alternative in the literature. This segmentation allows us to evaluate the resilience of sectoral CDS indices across varying market conditions and to assess whether industrial CDS indices consistently retain their hedging superiority during volatility.

Our main contribution is not in the selection of the econometric model applied to estimate the optimal hedge ratio but in the novel focus on sectoral CDS indices as alternative hedging tools during crises. By comparing their performance in conventional and Islamic equity markets, we provide insights into the diversification benefits of CDSs across different financial systems and regulatory environments.

This study provides valuable insights for market participants’ decision-making, as it helps to identify the most effective alternative assets that can hedge risk in relation to both conventional and Islamic stock markets. Accordingly, portfolio managers and investors can develop more effective investment strategies by comparing these alternative assets for possible inclusion in their equity portfolios.

Furthermore, our analysis demonstrates its value for financial advisors, who frequently look for unconventional assets to shield stock portfolios from downside risk, especially during periods of market stress when such protection becomes especially beneficial.

The remainder of this paper is organized as follows. Section 2 exhibits a literature review. Section 3 discusses the methodology. Section 4 deals with data and descriptive statistics. Section 5 presents the empirical results. Eventually, Section 6 draws conclusions.

2. Literature Review

This present work relates to the literature that discusses the hedging role of various assets classes such as gold, Bitcoin, CDSs, and VIX (VSTOXX) against market downturns.

2.1. Hedging Role of Gold and Bitcoin

Gold is generally seen as a hedge and safe haven asset, with its value tending to rise during market disruptions caused by negative shocks. Previous researchers have examined gold’s role as a hedge and safe haven. Specifically, Hillier et al. (2006) found that precious metals, such as gold, exhibited the capability to hedge against stock-related risks.

Moreover, Baur and Lucey (2010) explored whether gold could serve as a hedge, diversifier, or safe haven for stocks and bonds. Their findings provided the first empirical evidence that gold could act as a hedge against stocks during calm periods and as a safe haven during extreme market conditions. Baur and McDermott (2010) extended this research by incorporating a multi-country analysis. They considered testing the safe haven effect across world stock markets and found that gold could serve as a hedge and a strong safe haven in developed markets but not in emerging markets like the BRICS countries.

Hood and Malik (2013) found that while gold serves a hedge for the U.S. stock market, its safe haven characteristics are relatively weak when compared to the volatility index. Lucey and Li (2014) investigated the role of precious metals as safe havens and found that gold’s effectiveness as a safe haven changes over time.

Moreover, Chkili (2016) analyzed the dynamic correlations between gold and stock market indices in each BRICS member country, concluding that gold acted as a strong safe haven for the financial assets studied. Similarly, Kang et al. (2016) examined the co-movement between the stock market indices of BRICS countries, oil, and gold. They found that gold could function simultaneously as a hedge and as a stabilizing tool for the assets traded in these financial markets.

In addition, Chkili (2017) examined whether gold could be considered a hedge or a safe haven for Islamic stocks. The study found that gold serves as a safe haven against risks in the Islamic stock market during both stable and volatile periods. Additionally, Raza et al. (2019) highlight that gold and commodity futures are the most effective hedging instruments for U.S. real estate investments, providing protection in both the short and long term.

Akhtaruzzaman et al. (2021) also investigated the gold’s role as a safe haven during the COVID-19 outbreak. Their findings reveal that in phase I (before 16 March 2020) gold acted as a strong safe haven, but its safe haven properties weakened in phase II (starting from 17 March 2020).

In addition, gold provided significant hedging effectiveness against risks. Notably, Salisu et al. (2021) showed that gold was highly effective in hedging against oil price risks during the COVID-19 crisis. Similarly, Sikiru and Salisu (2021) concluded that gold offered the most reliable hedge against the risk related to Asia–Pacific equities during the COVID-19 pandemic, although its hedging effectiveness was reduced during this period.

Ali et al. (2021) investigated the diversification potentials of precious metals in Dow Jones Islamic (DJI) equity index portfolios. Their findings showed that while dynamic conditional correlations between sample assets rose significantly, adding gold to a portfolio with any DJI index reduced the downside risk. Nevertheless, other precious metals do not provide the same advantage.

Bitcoin’s role as a digital alternative to gold is widely referenced, with a growing number of studies focusing on whether Bitcoin could act as a hedging instrument. In this regard, Dyhrberg (2016) demonstrated that Bitcoin can serve as a hedge against the FTSE 100 index and against the US dollar.

Bouri et al. (2017a) investigated Bitcoin’s potential as a hedge against global uncertainty. Their findings suggest that Bitcoin’s hedging properties vary depending on the region and the investment horizon. In another study, Bouri et al. (2017b) examined the relationship between Bitcoin and commodities. Their estimated results revealed that Bitcoin demonstrates hedging and safe haven properties for the energy commodity index.

Moreover, Mroua et al. (2020) examined the diversification benefits of introducing Bitcoin into a traditional diversified financial portfolio. Their analysis reveals that an optimal portfolio, which includes Bitcoin, the US stock market, and commodity indices, can serve as an effective hedge, offering risk-averse investors a superior portfolio performance during financial crises.

Corbet et al. (2020), utilizing a sample of gold and cryptocurrencies, provided evidence of a “flight to safety” during the COVID-19 pandemic period. In addition, Conlon et al. (2020) investigated safe haven and flight-to-safety behavior in the crypto currency markets during the same period.

Additionally, some researchers have focused on the safe haven properties of Bitcoin during the COVID-19 pandemic, investigating its potential to exceed gold in portfolio diversification. Consequently, investors have increasingly turned to alternative assets like Bitcoin to reduce the risk in their portfolios.

Several previous studies have compared the role of gold and Bitcoin as hedging instruments and safe havens for various commodities and financial assets. In this context, Popper (2015) argues that Bitcoin shares several characteristics with gold, particularly in its ability to hedge risks and in its potential as a diversifier.

Furthermore, Klein et al. (2018) analyzed the volatility, correlation, and portfolio performance of Bitcoin and gold. Their findings suggest that the correlations of Bitcoin with other markets often differ from those of gold. While Bitcoin’s volatility dynamics share some similarities with gold, the results found show that Bitcoin does not serve as an effective safe haven during market downturns, a key characteristic of gold. Ultimately, they argued that Bitcoin should not be viewed as a substitute for gold.

Bouri et al. (2020) examined the safe haven roles of Bitcoin, gold, and the commodity index relative to global, developed, emerging, US, and Chinese stock market indices. Their study proved that the diversification benefits vary across various time frequencies, with Bitcoin outperforming both gold and commodities.

Despite exhibiting higher volatility than gold and the S&P 500, Bitcoin displayed short-term safe haven properties both prior to and during the pandemic (Mariana et al. 2021). Separately, Pho et al. (2021) emphasize that investor risk aversion plays a pivotal role in diversifier selection; their analysis reveals that in China, risk-averse investors favor gold over Bitcoin for portfolio diversification, while risk-seeking investors exhibit the inverse preference.

Tarchella and Dhaoui (2021) investigated the hedging performance of alternative assets, including financial assets and commodity futures, for the Chinese stock market in a multi-scale framework, both before and during the pandemic crisis. Their results indicate that Bitcoin offered the most effective hedge for the Shanghai stock market. While WTI provided the most hedging effectiveness, gold came in second, with only a small difference in effectiveness.

Chkili et al. (2021) examined the role of Bitcoin as a hedge and safe haven for Islamic stock markets during the COVID-19 crisis, in comparison with gold. Their findings substantiate that Bitcoin served as a safe haven during downturns in these markets. Moreover, they found that adopting a Bitcoin-based hedging strategy results in higher costs during the crisis period.

Chemkha et al. (2021) analyzed the hedging and safe haven properties of gold and Bitcoin. Their findings indicate that both assets effectively mitigate risk in international portfolios, functioning as reliable hedging instruments. However, during the COVID-19 pandemic, gold exhibited limited safe haven capabilities for the studied assets, whereas Bitcoin’s heightened volatility rendered it ineffective as a protective shelter.

Moreover, Yang et al. (2022) examined the hedging and safe haven properties of Bitcoin, gold, crude oil, and commodities against six currencies across multiple investment horizons, with a particular emphasis on their performance during the COVID-19 outbreak. Their results prove that Bitcoin offers superior hedging performance in the long term. In addition, commodities can be considered the most favorable asset for optimal currency portfolios over all time horizons. Additionally, their analysis shows that these assets were more effective at mitigating risk during the early stages of pandemic, with gold being an effective safe haven for currencies.

Yousaf et al. (2021) analyzed the return and volatility transmission mechanisms between oil–Bitcoin and oil–gold pairs before and during the COVID-19 outbreak. Their results indicate that hedge ratios were elevated during the COVID-19 period, implying increased hedging costs compared to the pre-pandemic period. Furthermore, the study reveals that gold functioned as a hedge and, at the same time, a strong safe haven instrument for the oil market, while Bitcoin served as a diversifier asset for the oil market during the pandemic.

The Hedging Role of CDSs and Volatility Indices

The remarkable growth of the CDS market underscored their outstanding efficiency as a tool for both hedging and speculating on credit risk.

In this regard, Calice et al. (2013) investigated the role of Credit Default Swaps (CDSs) as potential hedging instruments for stocks, using single-name corporate CDS data within the U.S context. Their findings indicate that holding a diversified basket of CDSs can greatly mitigate default and capital-associated risks. The study further concludes that holding CDSs without exposure to the actual reference entity (naked CDSs) serves as an effective partial hedge against investments in stocks, commodities, and foreign exchange investments. Similarly, Ratner and Chiu (2013) highlight the safe haven properties of CDSs during financial crises, observing that CDS levels tend to rise rapidly while stock values decline.

Moreover, Zghal et al. (2018) show that CDS indices can serve as effective hedging and safe haven instruments against fluctuations in stock sectors. Likewise, Hachicha et al. (2022) highlight that CDS indices exhibit superior hedging capabilities for both Islamic and conventional portfolios, offering the highest hedging effectiveness.

In addition, several recent studies have examined the impact of the COVID-19 pandemic on credit risk. Agca et al. (2022) revealed that the Credit Default Swap (CDS) spreads of U.S. firms with supply chain connections to China increased significantly due to disruptions caused by lockdown restrictions.

Kwan and Mertens (2020) estimated the impact of COVID-19 on firms’ CDS spreads. They found a significant widening across all sectors. Among investment-grade firms, those within the energy sector experienced the most pronounced increase.

Daehler et al. (2020) utilized a two-stage econometric approach to investigate the dynamics of emerging market (EM) sovereign CDS spreads during the first half of 2020. Their findings suggest that EM CDS spreads were influenced more by traditional factors, such as fiscal space, oil price fluctuations, and monetary policies, rather than by risks specifically related to COVID-19. The study also focused on the pandemic’s impact on credit risk by examining the changes in sovereign CDS spreads during this period.

Moreover, equity volatility derivatives are widely regarded as effective diversifiers due to their remarkable negative correlations with stock market variables during times of crisis. For instance, Hood and Malik (2013) compared the VIX with oil, gold, other precious metals, and various commodities, providing evidence that the VIX outperforms these assets, serving as a superior hedge and safe haven asset for U.S. equity markets. Similarly, Chen et al. (2011) explored the diversification advantages of volatility-related assets, concluding that incorporating these assets into investment portfolios enhances investors’ opportunities.

Furthermore, several studies emphasize the diversification benefits of investing in the VIX or VSTOXX. In this respect, McFarren (2013) and Moran (2014) note that while the VIX offers diversification benefits of equity portfolios, these advantages tend to be short-lived.

Fernandes et al. (2014) discovered that the VIX offers superior hedging opportunities for portfolios compared to other alternatives, such as CDSs and commodity futures. Similarly, Ahmad et al. (2018) used the time-varying correlations among crude oil, US bonds, gold, the VIX, OVX, and European carbon prices to estimate time-varying, optimal hedge ratios and deduce the most effective hedging instrument in clean energy markets. Their results show that the VIX is the most effective asset for hedging and ensuring portfolio stability.

More recently, Tarchella and Dhaoui (2021) identified the VIX as having optimal diversification for the Shanghai stock market during the pandemic period.

Shahzad et al. (2021) compared the hedging effectiveness of three alternative assets (VIX, Bitcoin, and gold) in mitigating downside movements in BRICS stock market indices. Their study reveals that VIX futures provided greater diversification benefits in Brazil, Russia, India, and South Africa, particularly during the onset of the COVID-19 outbreak.

Ali et al. (2022) constructed optimal portfolios composed of G-12 countries’ stock market returns, national benchmark bonds, crude oil, gold, and volatility index (VIX) returns. They highlight that the VIX provides the most effective hedge against stock returns in these markets. Additionally, the risk and downside risk measures suggest that individual stocks show the highest risk and expected maximum loss compared to mixed portfolios involving bonds and stocks, VIX and stocks, or gold and stocks.

Several previous studies attempted to compare the VIX, VSTOXX, and CDSs in terms of hedging capability. Indeed, Caporin (2012) compared the VIX and CDS indices and found that models based on CDS indices are more efficient than those relying solely on the VIX. Moreover, Hkiri et al. (2018) investigated the dependence between US financial sector CDS spreads and global risk factors, such as the interest rate, oil price, and VIX. Their findings suggest that the VIX, a leading risk factor, drives financial sector CDS spread dynamics, although its impact fluctuates with data frequency.

Unlike this study, Zghal and Ghorbel (2020) highlight that the VIX and sovereign CDSs are identified as potentially effective hedging instruments for most of the stock markets examined. Specifically, the VIX is considered to be a strong safe haven for the Chinese stock market, while sovereign CDSs are considered to be a strong safe haven for the Japanese and Philippian stock markets. Noteworthy, however, is that the safe haven roles and diversification properties of the VIX and CDS indices are sensitive to data frequency and the models used.

3. Methodology

Researchers have predominantly used the BEKK model (Baba et al. 1990)), the Dynamic Conditional Correlation (DCC) model (Engle 2002), or the tVARMA-GARCH model (Ling and McAleer 2003). However, these methods present certain limitations. For instance, both the BEKK model and VARMA-GARCH modeling-based estimations are challenging to implement, especially in a three-dimensional and higher dimensional context. This is largely due to the presence of numerous free parameters, which might contribute to significant optimization difficulties when the likelihood function is flat. In the same way, the DCC model fails to adequately capture asymmetric relationships between underlying assets, as its estimation is often restricted by the model’s specific limitations.

Additionally, numerous studies employ DCC-GARCH models to determine optimal hedge ratios. Therefore, we will assess the optimal hedge ratios using the ADCC-GARCH model proposed by Cappiello et al. (2006) and the GO-GARCH model designed by Van der Weide (2002). Following this, we will select the appropriate model to handle the estimation challenges resulting from the presence of numerous variables in vast datasets. This approach will provide a comprehensive insight into how optimal hedge ratios differ across diverse multivariate GARCH frameworks.

Moreover, the GARCH model approach is applied in this case to develop a one-period-ahead hedge ratio. This approach procedure is different compared to those in other studies, particularly those developed through the use of the current hedge ratio as a proxy. Consequently, the hedge ratio for the next period should be estimated. Specifically, the one-step-ahead optimal hedge ratios are calculated through a rolling window analysis that takes into account the fluctuating nature of data variability.

Let $r_t$ be a n × 1 vector of asset returns. An AR (1) process for $r_t$ conditional on the information set $I_{t-1}$, can be expressed as

$$r_t=\mu +a{r}_{t-1}+{\epsilon }_t$$

(1)

The residuals are modeled as

$${\epsilon }_t=H_t^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{z}_t,$$

(2)

where $H_t$ denote n × n, and the conditional covariance matrix of $r_t$ and $z_t$ designates n × 1 i.i.d random vector of errors.

3.1. DCC-GARCH Model

The Dynamic Conditional Correlation (DCC) model proposed by Engle (2002) is implemented using a two-step estimation process. In the first step, the GARCH parameters are estimated, and in the second step, the conditional correlations are calculated as follows:

$$H_t=D_t{R}_t{D}_t,$$

(3)

where $R_t$ denotes the conditional correlation matrix, while $D_t$ represents a diagonal matrix containing the time-varying standard deviations along its diagonal. Therefore,

$$D_t=diag\left(h_{1,t}^{1/2},\dots h_{n,t}^{1/2}\right)$$

(4)

$$R_t=diag\left(q_{1,t}^{-1/2},\dots q_{n,t}^{-1/2}\right)Q_{t}diag\left(q_{1,t}^{-1/2},\dots q_{n,t}^{-1/2}\right)$$

(5)

The expressions of $h$ correspond to univariate GARCH models. In the GARCH(1,1) model, the components of $H_t$ can be reformulated as follows:

$$h_{i,t}={\omega }_i+{\alpha }_i{\epsilon }_{i,t-1}^2+{\beta }_i{h}_{i,t-1},$$

(6)

and $Q_t$, the symmetric positive definite matrix of elements $q_{ij;t}$, could be explained as

$$Q_t=\left(1-{\theta }_1-{\theta }_2\right)\overline{Q}+{\theta }_t{z}_{t-1}{z^{\prime }}_{t-1}+{\theta }_2{Q}_{t-1}$$

(7)

$\overline{Q}$ denotes the $n\times n$ unconditional correlation matrix of the standardized residuals, $z_{i;t}\left(z_{i,t}={\epsilon }_{i,t}/{\sqrt{h}}_{i,t}\right)$. The parameters ${\theta }_1$ and ${\theta }_2$ are non-negative and are associated with the exponential smoothing process. These parameters are fundamental in deriving the dynamic conditional correlations. The DCC model retains mean-reverting properties, provided that ${\theta }_1+{\theta }_2<1$. The correlation estimate is expressed as follows:

$${\rho }_{i,j,t}={\displaystyle \frac{q_{i,j,t}}{\sqrt{q_{i,i,t}{q}_{j,j,t}}}}$$

(8)

The DCC model adapts to changing market conditions by allowing both market volatilities and correlations between assets to evolve over time. This flexibility improves hedge ratios by reflecting current market dynamics rather than relying on historical averages, enhancing risk reduction during periods of volatility and correlation regime changes (e.g., transitions between low/high-volatility regimes or shifts between high/low-correlation regimes). The DCC model is well-suited for portfolios where correlations exhibit gradual changes without strong asymmetry.

3.2. ADCC-GARCH Model

In addition to the DCC model, we also examine the asymmetric DCC (ADCC) specification proposed by Cappiello et al. (2006). This approach extends the DCC model and incorporates the asymmetric GARCH framework introduced by Glosten et al. (1993) by adding an asymmetric term, thereby formulating the asymmetric DCC (ADCC) model, defined as follows:

$$h_{i,t}={\omega }_i+{\alpha }_i{\epsilon }_{i,t-1}^2+{\beta }_i{h}_{i,t-1}+d_i{\epsilon }_{i,t-1}^{2}I\left({\epsilon }_{i,t-1}\right)$$

(9)

The indicator function $I\left({\epsilon }_{i,t-1}\right)=1$ if ${\epsilon }_{i,t-1}<0$, and 0 otherwise. In this framework, a positive value of d indicates that negative residuals have a greater impact on increasing variance compared to positive residuals. This asymmetric or “leverage” effect aims to reflect a common trait of financial assets, where a sudden decrease in asset prices tends to amplify volatility more than an equivalent rise in prices would. Consequently, it highlights that adverse news typically leads to greater volatility than favorable news. In the context of the ADCC model, the dynamics of Q are defined as follows:

$$Q_t=\left(\overline{Q}-A^{\prime }\overline{Q}A-B^{\prime }\overline{Q}B-G^{\prime }\overline{Q}G\right)+A^{\prime }{z}_{t-1}{z^{\prime }}_{t-1}A+B^{\prime }{Q}_{t-1}B+G^{\prime }{z}_t^{-}{z^{\prime }}_{t-1}^{-}G$$

(10)

In the equation above, A, B, and G represent $n\times n$ parameter matrices. The term $z_t^{-}$ denotes zero-threshold standardized errors, which are defined as $z_t$ when $z_t\langle 0$, and zero otherwise. $Q$ and $Q^{-}$ correspond to the unconditional matrices of $z_t$ and $z_t^{-}$, respectively.

The ADCC model incorporates asymmetric responses to positive versus negative shocks, recognizing that correlations often spike during market downturns. This feature improves hedge effectiveness during crisis periods (e.g., the 2008 financial crisis and the COVID-19 pandemic) by anticipating heightened downside correlations. While ADCC excels in volatile conditions, DCC remains sufficient for stable regimes. Both DCC and ADCC use a two-step estimation procedure, making them computationally tractable for moderate-sized portfolios.

3.3. The GO-GARCH Model

The Generalized Orthogonal (GO)-GARCH model, proposed by Van der Weide (2002), represents returns $r_t$ as a function of the conditional mean ($m_t$) and an error term (${\epsilon }_t$). The conditional mean can also account for an AR(1) component in this specification.

$$r_t=m_t+{\epsilon }_t$$

(11)

The GO-GARCH model maps $r_t-m_t$ on a set of unobservable independent factors $f_t$ are

$${\epsilon }_t=A{f}_t$$

(12)

In addition, the mixing matrix $A$ can be decomposed into an unconditional covariance matrix $\sum$ and an orthogonal (rotational) matrix $U$, as follows:

$$A={\sum }^{1/2}U$$

(13)

In the mixing matrix $A$, the rows represent the assets, and the columns refer to the factors $\left(f\right)$.

$$f_t=H_t^{1/2}{z}_t$$

(14)

The random variable $z_t$ is characterized by ${\rm E}\left(z_{i,t}\right)=0$, and ${\rm E}\left(z_{i,t}^2\right)=1$. The conditional variances of the factors can be represented using a GARCH process. The factors’ unconditional distribution $f$ satisfies ${\rm E}\left(f_t\right)=0$, and ${\rm E}\left(f_i{f^{\prime }}_t\right)=I$. By integrating Equations (11), (12), and (14), the resulting equation is expressed as

$$r_t=m_t+A{H}_t^{1/2}{z}_t$$

(15)

The conditional covariance matrix of the returns $\left(r_t-m_t\right)$ is

$${\sum }_t=A{H}_t{A}^{\prime }$$

(16)

From the GO-GARCH model, two key assumptions can be identified. First, the matrix $A$ is assumed to be time-invariant. Second, $H_t$ is considered to potentially represent a diagonal matrix. Additionally, it is worth noting that the OGARCH modeling approach involves constraining $A$ to be orthogonal. Initially proposed by Van der Weide (2002), the GO-GARCH model was formulated as a one-step maximum likelihood method, which simultaneously estimates the rotation matrix and the associated dynamics. However, this approach has proven to be less practical when applied to multi-asset scenarios.

Alternatively, the matrix U can also be estimated using nonlinear least squares or the method of moments, as proposed by Boswijk and Van der Weide (2011). It has been suggested that U can be estimated using independent component analysis (ICA), as outlined by Broda and Paolella (2009), which is the approach adopted in our study. Using three asset returns can effectively illustrate cases of autocorrelation, particularly volatility clustering and fat tails. This leads to the introduction of an AR(1) mean equation for each GARCH model. We assume that the residual series obtained from the DCC and ADCC models follow the multivariate Student-t distribution. For the GO-GARCH model, Normal Inverse Gaussian (NIG) distribution is used.

GOGARCH decomposes asset returns into orthogonal (uncorrelated) factors, isolating independent sources of risk. This simplifies hedging by targeting specific risk drivers (e.g., macroeconomic factors or sector trends) and reduces dimensionality in large portfolios, ensuring computational efficiency for high-dimensional datasets. If the orthogonal factors align with systemic risks (e.g., interest rates or inflation), GOGARCH can provide robust hedging during structural market shifts. A key advantage of these three models in hedging applications is their simplicity in updating optimal hedge ratios as new data becomes available. GOGARCH is generally preferable for high-dimensional portfolios (>30 assets) due to its factor-based structure. The GO-GARCH model provides superior hedging performance in environments where factor-driven dependencies and dimensionality reduction matter most, while ADCC shines when asymmetric correlations dominate. The choice depends on the portfolio’s characteristics, market regime, and the presence of tail risks. By aligning model choice with portfolio characteristics and market conditions, risk managers can optimize hedging strategies to minimize variance and tail risks effectively.

4. Data Presentation and Descriptive Statistics

We use daily data on the Dow Jones Conventional and Islamic emerging market indices (EMERG, EMERGI), seven sectoral CDSs (Telecom, Industrial, Banks, Goods, Energy, Metals, Other Financial), the VSTOXX, gold prices, and Bitcoin. The analysis period runs from 19 July 2010 to 8 October 2021. The sample consists of 2929 daily observations.

The sample period is partitioned into three: (i) before bubble crypto currency (Period 1), from 19 July 2010 to 25 December 2017; (ii) during bubble crypto currency and before COVID-19 (Period 2), from 26 December 2017 to 31 December 2019; and (iii) during COVID-19 (Period 3), from 1 January 2020 to 8 October 2021. These data were extracted from Datastream.

Table 1. Descriptive statistics and preliminary tests.

	Mean	Min	Max	Sd.	Skewness	Kurtosis	JB Test	ADF Test	Q(12)	Q2(12)
EMERGC	0.0097	−6.9433	5.5818	0.9961	−0.5944	4.7640	2948.80 ***	−13.74	127.07 ***	1927.90 ***
EMERGI	0.0197	−6.7254	7.5080	0.9710	−0.5694	5.9457	4481.80 ***	−13.63	100.88 ***	1022.50 ***
CDS TEL	−0.0344	−50.7063	60.8856	4.9530	0.5699	51.8918	32,963.00 ***	−14.67	352.41 ***	1306.40 ***
CDS IND	−0.0308	−12.5791	28.8322	2.1040	1.8534	21.3409	57,348.00 ***	−13.20	118.99 ***	631.80 ***
CDS BANKS	−0.0478	−71.4489	70.7189	5.7652	−0.1123	32.3276	127,740.00 ***	−15.04	340.84 ***	833.56 ***
CDS GOODS	−0.0236	−25.3067	22.1544	2.0801	0.9551	33.4898	137,528.00 ***	−13.31	67.23 ***	356.57 ***
CDS ENERGY	−0.0236	−59.1570	69.7830	3.5932	2.9412	113.3324	1,573,958.00 ***	−12.82	79.11 ***	310.02 ***
CDS METALS	−0.0183	−107.6675	97.0970	6.2012	−1.2154	102.7174	1,290,178.00 ***	−16.27	115.50 ***	83.71 ***
CDS OTHER FIN	−0.0551	−142.8112	152.1618	9.2989	0.5344	151.0904	2,790,029.00 ***	−15.19	529.34 ***	748.74 ***
VSTOXX	−0.0116	−43.4376	47.0666	6.8544	0.6263	3.6856	1853.70 ***	−15.98	36.40 ***	319.70 ***
Gold	0.0102	−9.8095	5.6000	1.0104	−0.6566	7.1701	6497.10 ***	−13.93	11.09 *	197.45 ***
Bitcoin	0.4558	−50.4021	36.3626	5.2116	−0.2728	13.2355	21,452.00 ***	−11.08	190.53 ***	1018.20 ***

***, ** and * indicates significance levels at 1%, 5% and 10% respectively.

shows the persistence of negative means for both the CDS index returns of all sectors and the VSTOXX return. Bitcoin has the highest average daily return (0.4558), and CDS Other Fin. shows the lowest average return (−0.0551).

All return series were discovered to be leptokurtic, characterized by an asymmetrical distribution, as skewness appears to be almost negative. Additionally, The Jarque–Bera test statistics are significant in all cases, indicating that the null hypothesis of normality is rejected for all return distributions. The augmented Dickey–Fuller (ADF) test shows that all return series are stationary. Such results are confirmed by Figure 1, which presents the daily raw returns for all indices over time.

We observe intense fluctuations in the returns of assets throughout the studied period. Interestingly, variations in returns were even more pronounced during extreme events such as the bubble crypto currency (period 2) and the COVID-19 outbreak (period 3).

5. Empirical Results

The first objective of the model is to estimate various versions of the MGARCH framework, each incorporating a constant in the mean equation along with a GARCH (1,1) variance specification. Modifications include the addition of an AR(1) term in the mean equation and the exploration of different distributional assumptions. The model selection process indicates that the DCC specification with an AR(1) term in the mean equation provides the best fit. All GARCH model variants (DCC, ADCC, GO-GARCH) have been estimated with an AR(1) term included in the mean equation. To address the non-normality typically present in return distributions, both the DCC and ADCC models have been estimated, assuming that residuals follow a multivariate skewed t-student distribution. For the GO-GARCH model, where the multivariate t-distribution is not applicable, estimation was performed assuming a multivariate affine negative inverse Gaussian (MANIG) distribution.

5.1. Dynamic Conditional Correlation

In this step, we use the rolling window analysis to construct one-step-ahead dynamic conditional correlations. The estimation window is set at 2929 observations, and a total number of 1000 one-step-ahead dynamic conditional correlations have been attained. We then refit each MGARCH model for every 20 and 60 daily observations. We aim to determine the conditional correlations and then time-varying optimal hedge ratios for different time horizons using three MGARCH versions (DCC, ADCC, and GO-GARCH). Therefore, the objective consists of distinguishing between the short- and long-run hedging effectiveness of sectoral CDSs, VSTOXX, gold, and Bitcoin to reduce the risk of both conventional and Islamic portfolios.

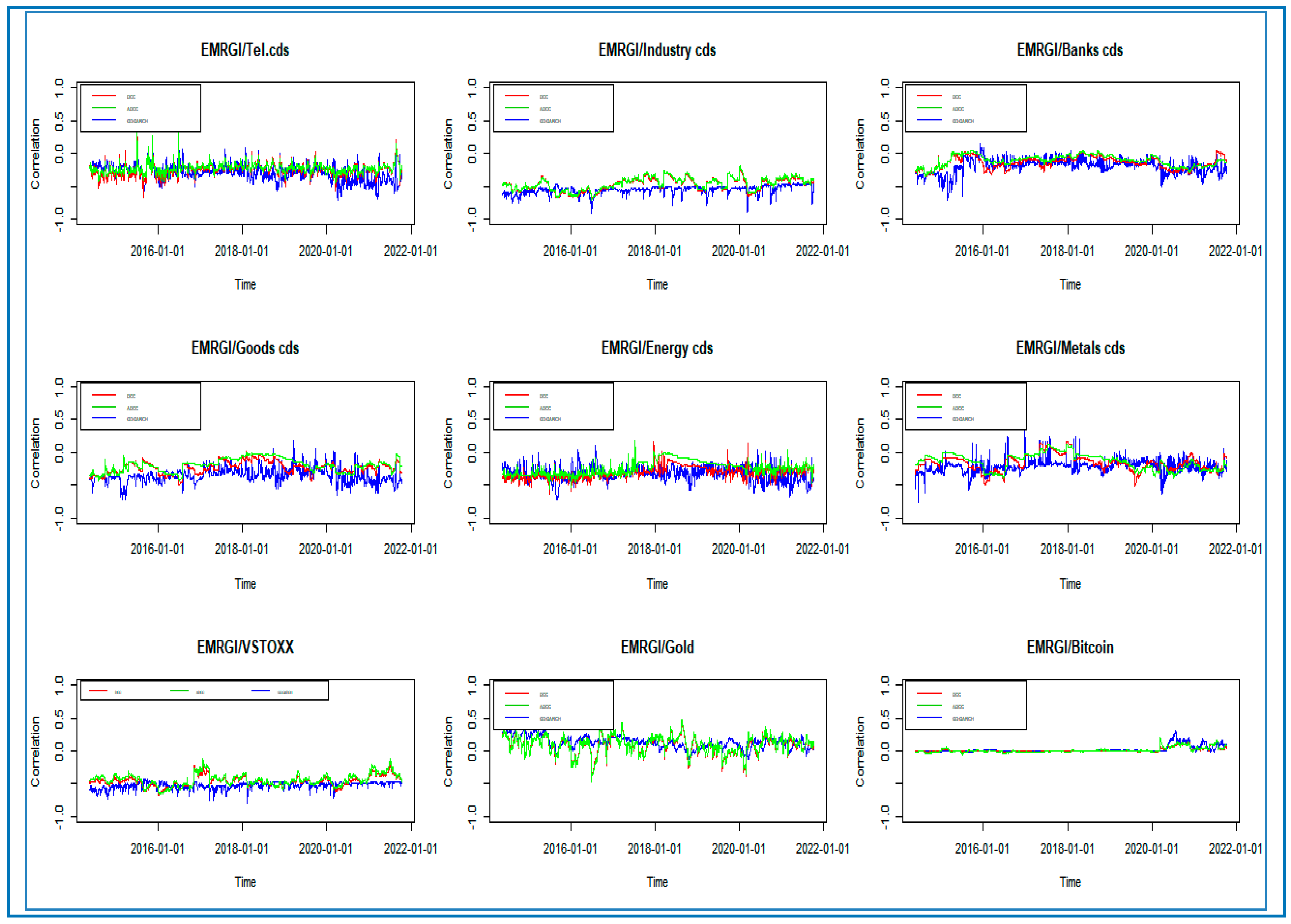
Figure 2 presents the rolling one-step-ahead conditional correlations between emerging stocks indices and each considered alternative assets using the three versions of the MGARCH models.

While the dynamic conditional correlations of the DCC and ADCC models exhibit nearly identical patterns, the GO-GARCH model yields conditional correlations that diverge significantly from both. Notably, despite a synchronized rise in correlation estimates across all three models in early 2020, the DCC model’s correlations gradually weakened thereafter. In contrast, the correlations derived from the GO-GARCH model remained robust and reliable, a finding consistent with prior studies by Ahmad et al. (2018), Basher and Sadorsky (2016), Hachicha et al. (2022), and Zghal et al. (2022). Overall, while the DCC and ADCC models produce similarly volatile correlation dynamics, the GO-GARCH model generates more stable linkages.

Touching upon the dynamic conditional correlations linking the conventional (EMERGC) and Islamic (EMERGI) stock indices and five sectoral CDSs (TEL, Banks, Goods, Energy Metals) and gold, they appear to fluctuate between negative and positive values. During 2020, however, the correlation increased remarkably in both the conventional and Islamic stock indices, and conditional correlations obtained from MGARCH models displayed significantly greater variability.

In addition, the conditional correlations for EMERGC/CDS-IND and EMERGC/VSTOXX, and EMERGI/CDS-IND and EMERGI/VSTOXX, are predominantly negative in terms of each estimation model. This empirical finding suggests that CDS IND and VSTOXX could be considered significant hedging instruments in both conventional and Islamic portfolios. Furthermore, the GO-GARCH model’s estimated correlation recorded the more negative values.

Moreover, the conditional correlation between Bitcoin and the two emerging stock indices is positive for each MGARCH model. However, Bitcoin can play the role of diversifier instrument in both conventional and Islamic indices.

Overall, the correlations estimated by the DCC and ADCC models show a high degree of similarity, whereas those from the GO-GARCH model exhibit a distinct pattern. Notably, all three MGARCH models demonstrated an upward trend in correlation levels throughout 2020, which was further amplified by the onset of the COVID-19 pandemic. However, while the DCC model correlations gradually weakened over time, the GO-GARCH model correlations remained relatively stable.

Table 2. Correlation between conditional correlations obtained by each MGARCH model.

EMERGC	DCC/ADCC	DCC/GO-GARCH	ADCC/GO-GARCH
CDS TEL	0.9708	0.3845	0.3890
CDS IND	0.9937	0.3266	0.3282
CDS BANKS	0.9064	0.5000	0.5516
CDS GOODS	0.8736	0.2032	0.2242
CDS ENERGY	0.9354	0.2211	0.2460
CDS METALS	0.8970	0.2564	0.1421
CDS OTHER FIN	0.9416	0.3783	0.3936
VSTOXX	0.9676	0.3174	0.2108
Gold	0.9946	0.3272	0.3026
Bitcoin	0.9565	0.4570	0.4119
EMERGI	DCC/ADCC	DCC/GO-GARCH	ADCC/GO-GARCH
CDS TEL	0.9663	0.2859	0.2895
CDS IND	0.9897	0.3668	0.3895
CDS BANKS	0.8733	0.3258	0.5020
CDS GOODS	0.8422	0.2038	0.2460
CDS ENERGY	0.8376	0.0868	0.1243
CDS METALS	0.8388	0.2851	0.1770
CDS OTHER FIN	0.9404	0.3429	0.3932
VSTOXX	0.9774	0.0942	0.0626
Gold	0.9913	0.3539	0.2894
Bitcoin	0.9454	0.7371	0.6945

presents the Pearson’s correlation coefficient between each pair of conditional correlation series obtained using the DCC, ADCC, and GOGARCH models.

For the conventional and Islamic equity indices, the dynamic conditional correlations modeled by the DCC show a strong alignment with those produced by the ADCC model. In contrast, the correlation pairs associated with the DCC and GO-GARCH models, as well as those between the ADCC and GO-GARCH models, tend to exhibit significantly weaker relationships for each individual pair.

5.2. Diversifier, Hedge, and Safe Haven Properties of Sectoral CDSs, VSTOXX, Gold, and Bitcoin

To examine CDSs’, VSTOXX’s, gold’s, and Bitcoin’s capabilities as a diversifier, hedge, and safe haven against movements in EMERGC and EMERGI equity markets, we follow the method used by Baur and McDermott (2010). A safe haven instrument is an asset that is expected to retain or increase in value during periods of market turmoil or economic uncertainty. It performs well during crises (e.g., recessions, geopolitical shocks). Following the ADCC-GARCH estimation, the pairwise dynamic conditional correlations between both the Dow Jones conventional and Islamic emerging market indices stock markets, and each of the alternative assets, are extracted from Equation (17) into separate time series. $ADC{C}_t$ are regressed on dummy variables (D) as follows:

$${ADDC}_t={\gamma }_0+{\gamma }_{1}D\left(r_{\mathit{a}\mathit{s}\mathit{s}\mathit{e}\mathit{t}}{q}_{10}\right)+{\gamma }_{2}D\left(r_{\mathit{a}\mathit{s}\mathit{s}\mathit{e}\mathit{t}}{q}_5\right)+{\gamma }_{3}D\left(r_{asset}{q}_1\right)$$

(17)

where D represents the dummy variables used to take into account the extreme movements at the 10%, 5%, and 1% quantiles of the most negative stock returns.

In effect, the CDSs, VSTOXX, gold, and Bitcoin would act as a weak hedge if ${\gamma }_0$ is zero and as a strong hedge in case ${\gamma }_0$ proves to be negative, thus standing as significant for the individual sector. Still, CDSs, VSTOXX, gold, and Bitcoin turn out to be a weak safe haven once the ${\gamma }_1$, ${\gamma }_2$, or ${\gamma }_3$ coefficients appear to be negative and non-significant, and a strong safe haven in case they prove to be negative and significant. Accordingly, CDSs, VSTOXX, gold, and Bitcoin should not represent a safe haven in case the ${\gamma }_1$, ${\gamma }_2$, or ${\gamma }_3$ coefficients turn out to be positive.

Equations (18)–(20) show the theoretical model used to investigate the role of CDSs, VSTOXX, gold, and Bitcoin during the three periods.

$$ADC{C}_{t(beforebubblecryptocurrency)}={\gamma }_0+{\gamma }_{1}D(r_{asset}{q}_{10})+{\gamma }_{2}D(r_{asset}{q}_5)+{\gamma }_{3}D(r_{asset}{q}_1)$$

(18)

$$ADC{C}_{t(beforeCOVID19andduringbubblecryptocurrency)}={\gamma }_0+{\gamma }_{1}D(r_{asset}{q}_{10})+{\gamma }_{2}D(r_{asset}{q}_5)+{\gamma }_{3}D(r_{asset}{q}_1)$$

(19)

$$ADC{C}_{t(duringCOVID19)}={\gamma }_0+{\gamma }_{1}D(r_{asset}{q}_{10})+{\gamma }_{2}D(r_{asset}{q}_5)+{\gamma }_{3}D(r_{asset}{q}_1)$$

(20)

Following the estimation of the ADCC model, dynamic conditional correlations are extracted from Equation (17) into separate time series and then used to assess the hedge and safe haven properties of sectoral CDSs, VSTOXX, gold, and Bitcoin for conventional and Islamic portfolios.

Table 3. The estimation results for the role of CDSs, VSTOXX, gold, and Bitcoin as a hedge and safe haven asset for EMERGC stock return.

	$\mathbf{Hedge}\left({\mathit{\gamma }}_0\right)$	$0.01\left({\mathit{\gamma }}_1\right)$	$0.05\left({\mathit{\gamma }}_2\right)$	$0.1\left({\mathit{\gamma }}_3\right)$
Before bubble crypto currency
CDS TEL	−0.2539 ***	−0.0094	0.0216 *	−0.0246 **
CDS IND	−0.5110 ***	−0.0005	0.0084	0.0102 *
CDS BANKS	−0.1687 ***	0.0056	0.0069	0.0033
CDS GOODS	−0.2668 ***	0.0016	0.0082	0.0014
CDS OIL GAS	−0.2947 ***	−0.0004	0.0115	0.0021
CDS MTLS	−0.2407 ***	−0.0024	0.0184	0.0211
CDS OTHER FIN	−0.2407 ***	−0.0218	0.0140	−0.0007
VSTOXX	−0.4889 ***	−0.0001	0.0082	0.0123 *
Gold	0.1216 ***	0.0324 *	0.0034	0.0038
Bitcoin	0.0123 ***	−0.0043	−0.0005	−0.0026
During bubble crypto currency and before COVID-19
CDS TEL	−0.2406 ***	−0.0050	0.0286	−0.0282 *
CDS IND	−0.4546 ***	0.0096	0.0040	−0.0101
CDS BANKS	−0.0761 ***	0.0082	0.0100	−0.0107
CDS GOODS	−0.2265 ***	−0.0048	0.0030	−0.0234 *
CDS OIL GAS	−0.2842 ***	0.0032	0.0135	−0.0231 *
CDS MTLS	−0.1395 ***	0.0206	0.0151	−0.0438 *
CDS OTHER FIN	−0.1365 ***	−0.0090	0.0137	−0.0307 *
VSTOXX	−0.4858 ***	−0.0059	0.0088	0.0007
Gold	0.0799 ***	0.0334	0.0194	−0.0331
Bitcoin	0.0086 ***	0.0093	−0.0079	0.0001
COVID-19 period
CDS TEL	−0.2923 ***	0.0363 *	−0.0012	0.0020
CDS IND	−0.4823 ***	0.0223 *	0.0131	−0.0064
CDS BANKS	−0.1975 ***	0.0066	0.0064	−0.0094
CDS GOODS	−0.2699 ***	0.0183 *	−0.0080	0.0131
CDS OIL GAS	−0.3039 ***	−0.0124	−0.0136	−0.0003
CDS MTLS	−0.2860 ***	−0.0244 **	0.0062	0.0008
CDS OTHER FIN	−0.2421 ***	0.0130	0.0146	−0.0022
VSTOXX	−0.4607 ***	0.0173 *	0.0212 *	−0.0174 *
Gold	0.1131 ***	−0.0099	−0.0072	0.0183
Bitcoin	0.1106 ***	−0.0030	0.0005	0.0040

***, ** and * indicates significance levels at 1%, 5% and 10% respectively.

and

Table 4. The estimation results for the role of CDSs, VSTOXX, gold, and Bitcoin as a hedge and safe haven asset for EMERGI stock return.

	$\mathbf{Hedge}\left({\mathit{\gamma }}_0\right)$	$0.01\left({\mathit{\gamma }}_1\right)$	$0.05\left({\mathit{\gamma }}_2\right)$	$0.1\left({\mathit{\gamma }}_3\right)$
Before bubble crypto currency
CDS TEL	−0.2376 ***	0.0166	−0.0190 *	0.0058
CDS IND	−0.4892 ***	−0.0072	0.0088	0.0185 **
CDS BANKS	−0.1802 ***	0.0051	0.0066	0.0062
CDS GOODS	−0.2585 ***	−0.0052	0.0075	0.0122
CDS OIL GAS	−0.2756 ***	−0.0084	0.0160 *	0.0019
CDS MTLS	−0.2350 ***	−0.0133	0.0036	0.0550 ***
CDS OTHER FIN	−0.2402 ***	−0.0251	−0.0120	0.0344 *
VSTOXX	−0.4708 ***	−0.0057	0.0104	0.0182 **
Gold	0.1031 ***	0.0305 *	0.0098	−0.0091
Bitcoin	0.0131 ***	−0.0019	−0.0079 *	0.0018
Before COVID-19 and during bubble crypto currency
CDS TEL	−0.2293 ***	0.0158	−0.0057	−0.0064
CDS IND	−0.4172 ***	0.0225	0.0040	−0.0201
CDS BANKS	−0.0633 ***	0.0119	0.0129	−0.0204 *
CDS GOODS	−0.1960 ***	0.0063	0.0021	−0.0262 *
CDS OIL GAS	−0.2652 ***	0.0227	−0.0111	−0.0053
CDS MTLS	−0.1468 ***	0.0174	0.0110	−0.0362 *
CDS OTHER FIN	−0.1243 ***	0.0016	0.0083	−0.0288 *
VSTOXX	−0.4688 ***	0.0027	−0.0097	0.0159 *
Gold	0.0588 ***	0.0248	−0.0151	0.0074
Bitcoin	0.0113 ***	0.0082	0.0069	−0.0140 *
COVID-19 period
CDS TEL	−0.2576 ***	0.0377 **	0.0136	−0.0175
CDS IND	−0.4252 ***	0.0263 *	0.0180	−0.0174
CDS BANKS	−0.1835 ***	0.0009	0.0089	−0.0115
CDS GOODS	−0.2508 ***	0.0191 *	0.0111	−0.0083
CDS OIL GAS	−0.2786 ***	−0.0056	−0.0089	−0.0073
CDS MTLS	−0.2446 ***	−0.0138	−0.0093	0.0106
CDS OTHER FIN	−0.2330 ***	0.0095	0.0215	−0.0149
VSTOXX	−0.4125 ***	0.0165	0.0259	−0.0240
Gold	0.0900 ***	−0.0145	0.0121	−0.0001
Bitcoin	0.0941 ***	−0.0115	−0.0002	0.0025

***, ** and * indicates significance levels at 1%, 5% and 10% respectively.

report the coefficient estimates from the regression models specified in Equations (18)–(20). The estimated results on the role of sectoral CDSs, VSTOXX, gold, and Bitcoin as a hedge and safe haven for EMERGC stock return are reported in Table 3.

Table 3 highlights that the hedge parameter $\left({\mathit{\gamma }}_0\right)$ is negative and statistically significant, which indicates that sectoral CDS spreads and VSTOXX can be considered as a strong hedge for EMERGC index in all periods. In contrast, the positive and significant parameter $\left({\mathit{\gamma }}_0\right)$ indicates that gold and Bitcoin act only as an effective diversifier for the EMERGC index.

Concerning the safe haven capability, the sectoral CDS spread, except for the Banks and Goods sectors, can be regarded as a weak safe haven asset before bubble crypto currency. In contrast, it can be considered as a strong safe haven for the EMERGC before the COVID-19 period. Furthermore, CDS metals and VSTOXX were a strong safe haven for the EMERGC index during the COVID-19 pandemic.

Moreover, gold and Bitcoin serve neither as a strong hedge nor as a strong safe haven, which implies that sectoral CDSs and VSTOXX have more preferable characteristics for EMERGC investors. These results are of interest to investors in terms of portfolio diversification and hedging strategies during a crisis.

These results corroborate those of Shahzad et al. (2019) that compare the safe haven properties of Bitcoin and gold during extreme market conditions. They verify whether such properties are similar or different for the two assets. Furthermore, they conclude that both Bitcoin and gold can be regarded as weak safe haven assets in most cases.

Table 4 depicts the estimated results on the role of CDSs, VSTOXX, gold, and Bitcoin as a hedge and safe haven for EMERGI stock return.

As shown in Table 4, the EMERGI index is found to be negatively and significantly correlated with the sectoral CDS indices and VSTOXX during the three periods under study. This result indicates that both assets are a strong hedge for the emerging Islamic financial index. As such, it could be beneficial for investors in emerging Islamic countries to include sectoral CDSs and VSTOXX in their equity portfolios for hedging purposes. However, gold and Bitcoin cannot be considered hedge alternatives, as all the coefficients (${\mathit{\gamma }}_0$) are positive and significant. This implies that gold and Bitcoin are only effective diversifiers for investors in the EMERGI market.

As for safe haven capability, we find evidence of Bitcoin being a strong safe haven for emerging Islamic financial indices, before bubble crypto currency, in the 5% quantile. These findings suggest that investors react to shocks in the emerging Islamic countries.

In addition, before the COVID-19 period, CDS spreads for banks, goods, metals, and other financial sectors and Bitcoin served as a strong safe haven for the EMERGI index. That is, in times of extreme market turmoil and uncertainty, investors with exposure to the EMERGI sell stocks and buy CDSs for the four sectors and Bitcoin. It is also worth noting that sectoral CDSs, VSTOXX, gold, and Bitcoin acted as a weak safe haven for the EMERGI during the COVID-19 period. Our results corroborate those of Conlon and McGee (2020), which considered Bitcoin to not act as a safe haven during times of crisis.

5.3. Optimal Hedge Ratio and Hedging Effectiveness

The conventional and Islamic stock index return hedged by CDSs, VSTOXX, gold, and Bitcoin can be reformulated as follows:

$$R_{P,t}=R_{S,t}-{\gamma }_t{R}_{A,t},$$

(21)

where $R_{P,t}$ is the return on the hedged portfolio; $R_{S,t}$ denotes the conventional or Islamic emerging stock index return; $R_{A,t}$ represents the alternative asset returns (sectoral CDSs, VSTOXX, gold, and Bitcoin); and ${\gamma }_t$ is the hedge ratio. When an investor holds a long position in the stock index, the hedge ratio indicates the quantity of alternative asset indices to be sold. Consequently, the variance of the hedged portfolio, given the information available at time $t-1$, is expressed as

$$\mathrm{var}\left(R_{P,t}{I}_{t-1}\right)=\mathrm{var}\left(R_{S,t}{I}_{t-1}\right)-2{\gamma }_t\mathrm{cov}\left(R_{A,t},R_{S,t}{I}_{t-1}\right)+{\gamma }_t^2\mathrm{var}\left(R_{A,t}{I}_{t-1}\right).$$

(22)

The optimal hedge ratios (OHRs), represented by ${\gamma }_t$, are utilized to minimize the conditional variance of the hedged portfolio. The OHR, given the information set as $I_{t-1}$, is computed after taking the partial derivative of the variance of ${\gamma }_t$ with respect to the hedge ratio and equating it to zero, as proposed by Baillie and Myers (1991). The resulting expression is as follows:

$${\gamma }_t^{*}{I}_{t-1}={\displaystyle \frac{\mathrm{cov}\left(R_{S,t},R_{A,t}\left|I_{t-1}\right.\right)}{\mathrm{var}\left(R_{A,t}\left|I_{t-1}\right.\right)}}$$

(23)

The conditional volatility estimates from the GARCH models can be utilized to determine hedge ratios, as discussed by Kroner and Sultan (1993). In this approach, a long position in one asset (e.g., asset i) can be hedged by taking a short position in another asset (e.g., asset j). The optimal hedge ratio for mitigating stock market risk using alternative asset indices is calculated as follows:

$${\gamma }_t^{*}\left|I_{t-1}\right.={h_{SA,t}/h}_{A,t},$$

(24)

Here, $h_{A,t}$ refers to the conditional variance of returns for alternative assets, while $h_{SA,t}$ represents the conditional covariance between the conventional and Islamic stock market indices and other indices, including sectoral CDSs, VSTOXX, gold, and Bitcoin. The effectiveness of various optimal hedge ratios (OHRs), derived from different GARCH model specifications, can be assessed using the hedging effectiveness (HE) index, as outlined by Chang et al. (2011) and Ku et al. (2007).

$$HE={\displaystyle \frac{{\mathrm{var}}_{unhedged}-{\mathrm{var}}_{hedged}}{{\mathrm{var}}_{unhedged}}},$$

(25)

In this context, ${\mathrm{var}}_{unhedged}$ refers to the variance of the unhedged portfolio, while ${\mathrm{var}}_{unhedged}$ indicates the variance of the optimally hedged portfolio. Hedging effectiveness is a measure of how well a hedging instrument reduces the risk exposure of a portfolio or position. It quantifies the reduction in volatility, variance, or downside risk achieved through hedging.

A higher HE index demonstrates greater hedging effectiveness. Additionally, out-of-sample hedge ratios are derived using a rolling window approach. At each time period t, one-step-ahead conditional volatilities are predicted, and these predictions are subsequently employed to calculate one-step-ahead hedge ratios. We fix the size of the rolling window at 1929 observations with the objective of obtaining 1000 one-step-ahead hedge ratios.

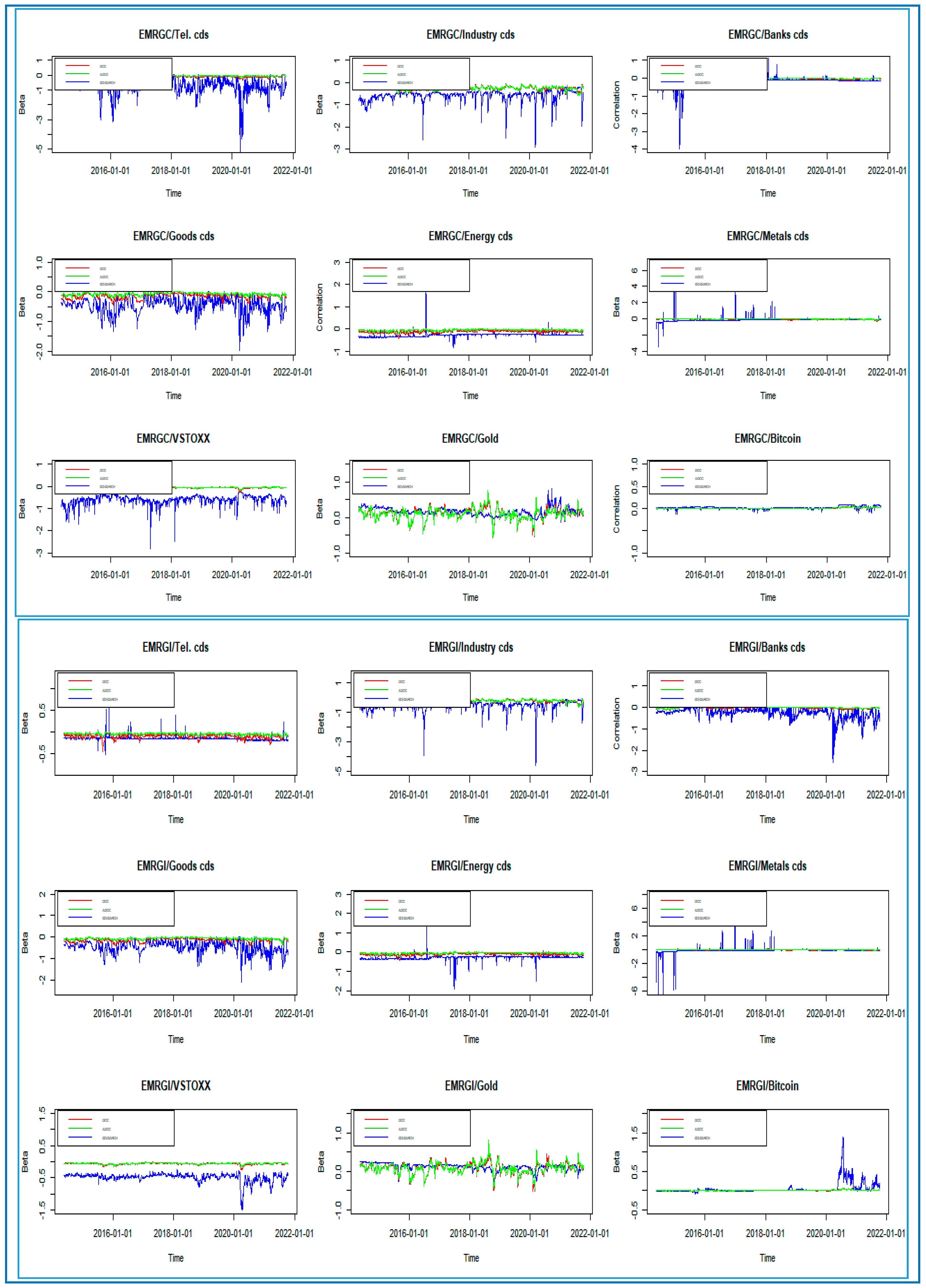
Figure 3 depicts the daily optimal hedge ratios between conventional and Islamic emerging stock indices and the sectoral CDSs, VSTOXX, gold, and Bitcoin based on the three MGARCH models (DCC, ADCC, and GO-GARCH).

Accordingly, we notice that the GO-GARCH hedge ratios mostly exhibit greater variations, but there are some exceptions as in the case of EMERGC/gold, EMERGC/Bitcoin, and EMERGI/gold. It is also worth noting that DCC hedge ratios are similar to the ADCC model’s hedge ratios. Similarly, we find that time-varying hedge ratios can capture significant events related to the global economic system viz., bubble crypto currency and the COVID-19 pandemic.

Table 5. Correlations between hedge ratios.

EMERGC	DCC/ADCC	DCC/GO-GARCH	ADCC/GO-GARCH
CDS TEL	0.8704	0.7813	0.7676
CDS IND	0.9050	−0.6459	−0.5811
CDS BANKS	0.8408	0.0707	0.1849
CDS GOODS	0.7617	0.5466	0.5881
CDS ENERGY	0.8666	0.1705	0.1468
CDS METALS	0.7731	0.0667	0.0638
CDS OTHER FIN	0.8426	−0.0189	0.0256
VSTOXX	0.8821	−0.6072	−0.5708
Gold	0.9773	0.2277	0.1584
Bitcoin	0.9346	0.6994	0.6628
EMERGI	DCC/ADCC	DCC/GO-GARCH	ADCC/GO-GARCH
CDS TEL	0.8543	0.1594	0.2317
CDS IND	0.9085	−0.4891	−0.4452
CDS BANKS	0.8243	0.3954	0.3729
CDS GOODS	0.7354	0.5093	0.5612
CDS ENERGY	0.8334	0.0560	0.0875
CDS METALS	0.7563	0.0051	0.0021
CDS OTHER FIN	0.8498	−0.0512	0.0009
VSTOXX	0.8756	0.7847	0.6155
Gold	0.9663	0.2113	0.1025
Bitcoin	0.9439	0.8232	0.7752

displays the registered correlations between the inter-hedge ratios calculated from three versions of MGARCH models viz., DCC, ADCC, and GO-GARCH.

We find that the hedge ratios obtained from the DCC/ADCC models exhibit a high correlation, indicating that the two models captured the properties of the data similarly.

In addition, the DCC/GO-GARCH hedge ratio correlations, in the EMERGC index, are considerably lower than the ADCC and GO-GARCH for the CDS of IND, banks, goods, other fin., and VSTOXX hedge ratio binding correlations. Further, hedge ratios calculated from DCC/GO-GARCH, in the EMERGI, are significantly lower than ADCC and GO-GARCH for the CDS of TEL, IND, goods, energy, and other fin. sectors’ hedge ratio binding correlations.

Table 6. Summary statistics of hedge ratio and hedging effectiveness (HE) obtained from the DCC model for each period and each refit.

Refit = 20
	Period 1 (19 July 2010 to 25 December 2017)				Period 2 (26 December 2017 to 31 December 2019)				Period 3 (1 January 2020 to 16 October 2021)
EMERGC	Min	Max	Mean	HE	Min	Max	Mean	HE	Min	Max	Mean	HE
CDS TEL	−0.3263	0.0373	−0.0948	0.0784	−0.2100	0.0131	−0.0844	0.0572	−0.3004	0.0275	−0.1192	0.0933
CDS IND	−0.5455	−0.0936	−0.2609	0.2817	−0.3902	−0.0601	−0.2384	0.2126	−0.5370	−0.0914	−0.2796	0.2525
CDS BANKS	−0.1533	0.0033	−0.0304	0.0272	−0.0790	0.0038	−0.0214	0.0119	−0.1693	0.0218	−0.0581	0.0475
CDS GOODS	−0.4609	−0.0086	−0.1600	0.0759	−0.4220	0.0067	−0.1014	0.0463	−0.7460	−0.0063	−0.1753	0.0929
CDS ENERGY	−0.4320	0.0096	−0.1415	0.1319	−0.1692	0.0089	−0.0856	0.0639	−0.2472	0.0061	−0.1096	0.0946
CDS METALS	−0.2059	0.0122	−0.0431	0.0379	−0.2536	0.0469	−0.0638	0.0410	−0.2588	0.0016	−0.0780	0.0517
CDS OTHER FIN	−0.2343	0.0063	−0.0507	0.0329	−0.1169	0.0071	−0.0352	0.0189	−0.2178	−0.0280	−0.0983	0.0662
VSTOXX	−0.1682	−0.0186	−0.0688	0.2490	−0.1325	−0.0310	−0.0613	0.2309	−0.2508	−0.0199	−0.0741	0.1919
GOLD	−0.4164	0.4075	0.0812	0.0309	−0.5620	0.5833	0.1057	0.0299	−0.5427	0.4358	0.1033	0.0276
BITCOIN	−0.0011	0.0084	0.0018	0.0001	−0.0013	0.0034	0.0006	0.0000	−0.0026	0.0644	0.0204	0.0069
EMERGI	Min	Max	Mean	HE	Min	Max	Mean	HE	Min	Max	Mean	HE
CDS TEL	−0.4296	0.0455	−0.0848	0.0748	−0.2434	0.0068	−0.0718	0.0527	−0.2834	0.0172	−0.1124	0.0733
CDS IND	−0.6194	−0.0828	−0.2282	0.2636	−0.4193	−0.0506	−0.2182	0.1848	−0.5902	−0.0845	−0.2682	0.2032
CDS BANKS	−0.1346	0.0034	−0.0284	0.0304	−0.0772	0.0094	−0.0187	0.0098	−0.1714	0.0138	−0.0569	0.0386
CDS GOODS	−0.4289	−0.0104	−0.1484	0.0774	−0.3944	0.0054	−0.0919	0.0400	−0.7195	−0.0284	−0.1657	0.0755
CDS ENERGY	−0.4422	0.0082	−0.1242	0.1207	−0.1764	−0.0045	−0.0743	0.0527	−0.2163	−0.0015	−0.1082	0.0774
CDS METALS	−0.3118	0.0141	−0.0401	0.0407	−0.2536	0.0469	−0.0638	0.0410	−0.2588	0.0016	−0.0780	0.0517
CDS OTHER FIN	−0.2314	0.0076	−0.0467	0.0332	−0.1169	0.0071	−0.0352	0.0189	−0.2178	−0.0280	−0.0983	0.0662
VSTOXX	−0.1654	−0.0146	−0.0599	0.2312	−0.1325	−0.0310	−0.0613	0.2309	−0.2508	−0.0199	−0.0741	0.1919
GOLD	−0.3583	0.3586	0.0623	0.0280	−0.4811	0.5832	0.0774	0.0240	−0.5265	0.4649	0.0938	0.0207
BITCOIN	−0.0098	0.0062	−0.0009	0.0001	−0.0112	0.0084	−0.0001	0.0001	−0.0077	0.0680	0.0217	0.0058
Refit = 60
	Period 1 (19 July 2010 to 25 December 2017)				Period 2 (26 December 2017 to 31 December 2019)				Period 3 (1 January 2020 to 16 October 2021)
EMERGC	Min	Max	Mean	HE	Min	Max	Mean	HE	Min	Max	Mean	HE
CDS TEL	−0.3347	0.0373	−0.0949	0.0782	−0.2067	0.0132	0.0847	0.0571	−0.3049	0.0183	−0.1206	0.0949
CDS IND	−0.5208	−0.0926	−0.2605	0.2827	−0.3902	−0.0601	−0.2382	0.2127	−0.5348	−0.0917	−0.2793	0.2526
CDS BANKS	−0.1542	0.0032	−0.0310	0.0280	−0.0790	0.0038	−0.0213	0.0119	−0.1693	0.0218	−0.0576	0.0467
CDS GOODS	−0.4479	−0.0085	−0.1610	0.0765	−0.4220	0.0067	−0.1043	0.0476	−0.3978	−0.0079	−0.1519	0.0772
CDS ENERGY	−0.4331	0.0095	−0.1425	0.1328	−0.1692	0.0024	−0.0840	0.0603	−0.2601	0.0061	−0.1104	0.0952
CDS METALS	−0.1953	0.0109	−0.0424	0.0361	−0.2196	0.0718	−0.0587	0.0409	−0.1859	−0.0099	−0.0798	0.0668
CDS OTHER FIN	−0.2328	0.0060	−0.0511	0.0333	−0.1077	0.0134	−0.0400	0.0224	−0.2480	−0.0371	−0.0985	0.0729
VSTOXX	−0.1539	−0.0192	−0.0684	0.2477	−0.1219	−0.0299	−0.0642	0.2450	−0.2688	−0.0271	−0.0781	0.2287
GOLD	−0.4164	0.4075	0.0830	0.0307	−0.5620	0.5680	0.1047	0.0295	−0.5427	0.4265	0.1042	0.0275
BITCOIN	−0.0009	0.0081	0.0018	0.0001	−0.0013	0.0029	0.0006	0.0000	−0.0025	0.0644	0.0186	0.0063
EMERGI	Min	Max	Mean	HE	Min	Max	Mean	HE	Min	Max	Mean	HE
CDS TEL	−0.4335	0.0455	−0.0849	0.0747	−0.2434	0.0044	−0.0807	0.0528	−0.2835	0.0163	0.1125	0.0731
CDS IND	−0.6190	−0.0818	−0.2284	0.2655	−0.4193	−0.0506	−0.2179	0.1845	−0.5821	−0.0833	−0.2679	0.2033
CDS BANKS	−0.1339	0.0020	−0.0290	0.0312	−0.0745	0.0086	−0.0185	0.0097	−0.1714	0.0138	−0.0565	0.0380
CDS GOODS	−0.4251	−0.0102	−0.1490	0.0772	−0.3944	0.0054	−0.0967	0.0439	−0.4111	−0.0287	−0.1449	0.0607
CDS ENERGY	−0.4410	0.0078	−0.1246	0.1206	−0.1771	−0.0045	−0.0750	0.0517	−0.2244	−0.0015	−0.1080	0.0771
CDS METALS	−0.1866	0.0141	−0.0377	0.0373	−0.2502	0.0420	−0.0574	0.0411	−0.2088	−0.0038	−0.0663	0.0405
CDS OTHER FIN	−0.2382	0.0108	−0.0471	0.0335	−0.1169	0.0061	−0.0354	0.0192	−0.2279	−0.0292	−0.0989	0.0663
VSTOXX	−0.1558	−0.0149	−0.0597	0.2300	−0.1317	−0.0314	−0.0615	0.2309	−0.2543	−0.0209	−0.0749	0.1931
GOLD	−0.3583	0.3586	0.0645	0.0276	−0.4811	0.5602	0.0766	0.0236	−0.5279	0.4512	0.0944	0.0207
BITCOIN	−0.0083	0.0047	−0.0009	0.0001	−0.0061	0.0084	−0.0001	0.0000	−0.0074	0.0625	0.0188	0.0049

,

Table 7. Summary statistics of hedge ratio and hedging effectiveness (HE) obtained from the ADCC model for each period and each refit.

Refit = 20
	Period 1 (19 July 19 2010 to 25 December 2017)				Period 2 (26 December 2017 to 31 December 2019)				Period 3 (1 January 2020 to 16 October 2021)
EMERGC	Min	Max	Mean	HE	Min	Max	Mean	HE	Min	Max	Mean	HE
CDS TEL	−0.1054	0.0195	−0.0392	0.0608	−0.0922	0.0050	−0.0430	0.0518	−0.1844	0.0210	−0.0560	0.0804
CDS IND	−0.5295	−0.0890	−0.2562	0.2712	−0.4083	−0.0669	−0.2385	0.2077	−0.6022	−0.0829	−0.2716	0.2415
CDS BANKS	−0.1409	0.0030	−0.0188	0.0182	−0.0321	0.0047	−0.0075	0.0057	−0.0997	−0.0007	−0.0278	0.0377
CDS GOODS	−0.2386	−0.0002	−0.0789	0.0582	−0.1399	0.0128	−0.0427	0.0277	−0.2924	−0.0063	−0.0937	0.0697
CDS ENERGY	−0.2376	0.0082	−0.0729	0.1080	−0.0997	0.0232	−0.0332	0.0381	−0.1592	0.0027	−0.0518	0.0798
CDS METALS	−0.1241	0.0265	−0.0224	0.0263	−0.1252	0.0390	−0.0225	0.0269	−0.2251	−0.0047	−0.0552	0.0906
CDS OTHER FIN	−0.1978	0.0068	−0.0303	0.0265	−0.0514	0.0199	−0.0188	0.0162	−0.1378	−0.0116	−0.0532	0.0562
VSTOXX	−0.1371	−0.0147	−0.0625	0.2244	−0.1113	−0.0242	−0.0601	0.2284	−0.1726	−0.0244	−0.0631	0.2041
GOLD	−0.4547	0.3579	0.0777	0.0331	−0.5522	0.7869	0.1217	0.0320	−0.4817	0.5812	0.1089	0.0309
BITCOIN	−0.0067	0.0059	0.0001	0.0001	−0.0022	0.0089	0.0000	0.0000	−0.0022	0.0733	0.0199	0.0120
EMERGI	Min	Max	Mean	HE	Min	Max	Mean	HE	Min	Max	Mean	HE
CDS TEL	−0.1034	0.0272	−0.0343	0.0572	−0.1042	−0.0007	−0.0400	0.0462	−0.1385	0.0148	−0.0531	0.0627
CDS IND	−0.5451	−0.0638	−0.2225	0.2536	−0.3649	−0.0549	−0.2149	0.1769	−0.6564	−0.0629	−0.2557	0.1862
CDS BANKS	−0.1327	0.0048	−0.0165	0.0176	−0.0305	0.0055	−0.0066	0.0048	−0.1085	−0.0017	−0.0286	0.0314
CDS GOODS	−0.2423	−0.0017	−0.0720	0.0600	−0.1353	−0.0006	−0.0348	0.0217	−0.3573	−0.0063	−0.0929	0.0609
CDS ENERGY	−0.2285	0.0045	−0.0644	0.1029	−0.0858	−0.0003	−0.0246	0.0226	−0.1751	0.0052	−0.0517	0.0642
CDS METALS	−0.1169	0.0190	−0.0192	0.0256	−0.1197	0.0278	−0.0243	0.0253	−0.2227	−0.0040	−0.0512	0.0683
CDS OTHER FIN	−0.1843	0.0046	−0.0278	0.0264	−0.0452	0.0051	−0.0161	0.0127	−0.1340	−0.0102	−0.0534	0.0497
VSTOXX	−0.1280	−0.0089	−0.0543	0.2102	−0.1248	−0.0225	−0.0580	0.2187	−0.1505	−0.0151	−0.0593	0.1681
GOLD	−0.3844	0.3239	0.0614	0.0295	−0.4277	0.8465	0.1023	0.0260	−0.4459	0.5711	0.1039	0.0243
BITCOIN	−0.0141	0.0077	−0.0017	0.0003	−0.0066	0.0191	−0.0002	0.0001	−0.0037	0.0667	0.0172	0.0065
Refit = 60
	Period 1 (19 July 19 2010 to 25 December 2017)				Period 2 (26 December 2017 to 31 December 2019)				Period 3 (1 January 2020 to 16 October 2021)
EMERGC	Min	Max	Mean	HE	Min	Max	Mean	HE	Min	Max	Mean	HE
CDS TEL	−0.1081	0.0199	−0.0391	0.0610	−0.0922	0.0051	−0.0429	0.0518	−0.1832	0.0129	−0.0562	0.0807
CDS IND	−0.5126	−0.0876	−0.2559	0.2727	−0.4004	−0.0669	−0.2382	0.2079	−0.5954	−0.0826	−0.2707	0.2416
CDS BANKS	−0.1464	0.0036	−0.0194	0.0189	−0.0317	0.0047	−0.0076	0.0057	−0.0960	−0.0007	−0.0275	0.0364
CDS GOODS	−0.2387	−0.0005	−0.0811	0.0608	−0.1399	0.0128	−0.0420	0.0271	−0.2910	−0.0063	−0.0933	0.0694
CDS ENERGY	−0.2509	0.0083	−0.0727	0.1072	−0.1155	0.0232	−0.0349	0.0377	−0.1586	0.0027	−0.0519	0.0797
CDS METALS	−0.1241	0.0261	−0.0216	0.0250	−0.1136	0.0380	−0.0221	0.0258	−0.2279	−0.0047	−0.0551	0.0900
CDS OTHER FIN	−0.1884	0.0072	−0.0303	0.0267	−0.0514	0.0232	−0.0183	0.0160	−0.1410	−0.0118	−0.0528	0.0569
VSTOXX	−0.1343	−0.0178	−0.0625	0.2240	−0.1103	−0.0244	−0.0602	0.2288	−0.1700	−0.0244	−0.0630	0.2040
GOLD	−0.4547	0.3579	0.0790	0.0331	−0.5522	0.7656	0.1199	0.0315	−0.4817	0.5594	0.1091	0.0308
BITCOIN	−0.0045	0.0071	0.0002	7.696 ×${10}^{-5}$	−0.0022	0.0089	0.0000	0.0000	−0.0022	0.0733	0.0193	0.0117
EMERGI	Min	Max	Mean	HE	Min	Max	Mean	HE	Min	Max	Mean	HE
CDS TEL	−0.1051	0.0272	−0.0343	0.0574	−0.1042	−0.0007	−0.0401	0.0463	−0.1365	0.0106	−0.0536	0.0631
CDS IND	−0.5216	−0.0649	−0.2226	0.2559	−0.3620	−0.0532	−0.2144	0.1764	−0.6472	−0.0616	−0.2548	0.1851
CDS BANKS	−0.1392	0.0057	−0.0169	0.0182	−0.0302	0.0059	−0.0066	0.0048	−0.1049	−0.0017	−0.0286	0.0312
CDS GOODS	−0.2371	−0.0032	−0.0725	0.0607	−0.1353	−0.0006	−0.0336	0.0204	−0.3573	−0.0029	−0.0895	0.0591
CDS ENERGY	−0.2405	0.0047	−0.0637	0.1005	−0.0799	−0.0006	−0.0237	0.0204	−0.1739	0.0056	−0.0517	0.0638
CDS METALS	−0.1169	0.0186	−0.0184	0.0236	−0.1104	0.0267	−0.0240	0.0246	−0.2245	−0.0040	−0.0512	0.0679
CDS OTHER FIN	−0.1832	0.0050	−0.0279	0.0267	−0.0426	0.0052	−0.0158	0.0125	−0.1281	−0.0100	−0.0528	0.0501
VSTOXX	−0.1206	−0.0108	−0.0543	0.2097	−0.1238	−0.0228	−0.0581	0.2192	−0.1494	−0.0154	−0.0591	0.1677
GOLD	−0.3844	0.3239	0.0630	0.0292	−0.4277	0.8103	0.1006	0.0253	−0.4459	0.5526	0.1041	0.0242
BITCOIN	−0.0154	0.0083	−0.0015	0.0003	−0.0028	0.0191	−0.0002	0.0001	−0.0037	0.0640	0.0159	0.0060

and

Table 8. Summary statistics of hedge ratio obtained from the GO-GARCH model and hedging effectiveness (HE) for each period and each refit.

Refit = 20
	Period 1 (19 July 19 2010 to 25 December 2017)				Period 2 (26 December 2017 to 31 December 2019)				Period 3 (1 January 2020 to 16 October 2021)
EMERGC	Min	Max	Mean	HE	Min	Max	Mean	HE	Min	Max	Mean	HE
CDS TEL	−3.1838	0.0491	−0.6183	0.0915	−2.1626	0.0421	−0.6743	0.1041	−5.6765	0.0374	−0.9845	0.1821
CDS IND	−1.4297	−0.2409	−0.6470	0.3683	−1.3110	−0.2527	−0.6337	0.3326	−1.3738	−0.1912	−0.7056	0.3236
CDS BANKS	−2.8739	0.7082	−0.2326	0.0450	−0.1287	1.1239	−0.0949	0.0275	−0.1631	0.1546	−0.1455	0.0766
CDS GOODS	−1.4395	−0.0245	−0.4503	0.1536	−1.2857	0.0101	−0.3718	0.0986	−2.3923	−0.0085	−0.5814	0.1659
CDS ENERGY	−1.6153	0.0167	−0.4228	0.1365	−1.6480	−0.0178	0.4414	0.1034	−3.7874	0.0243	−0.6266	0.1677
CDS METALS	−6.3525	7.0617	−0.1521	0.0794	−0.1349	2.1704	−0.1060	0.0429	−0.1333	0.3282	−0.1224	0.0630
CDS OTHER FIN	−3.1269	0.0341	−0.6396	0.1015	−2.8766	−0.0159	−0.9148	0.0741	−7.6550	−0.0816	−1.3232	0.1196
VSTOXX	−1.1068	−0.2052	−0.4700	0.2868	−0.8791	−0.1824	−0.4578	0.2569	−2.6532	−0.2460	−0.6130	0.2791
GOLD	0.0858	0.5599	0.1946	0.0386	−0.1746	0.1694	0.0918	0.0108	−0.3560	0.3291	0.1326	0.0395
BITCOIN	−0.0261	0.6153	0.0936	0.0027	−0.0154	0.5473	0.0504	0.0010	−0.0330	2.0941	0.2916	0.0236
EMERGI	Min	Max	Mean	HE	Min	Max	Mean	HE	Min	Max	Mean	HE
CDS TEL	−0.4613	0.5871	−0.1326	0.0697	−0.1470	0.3774	−0.1358	0.0952	−0.1906	0.2347	−0.1711	0.1814
CDS IND	−3.9191	−0.2211	−0.6086	0.3363	−2.2017	−0.2135	−0.5304	0.2931	−4.5494	−0.1494	−0.4925	0.2786
CDS BANKS	−0.7723	0.0236	−0.1787	0.0493	−0.8193	0.0059	−0.2292	0.0244	−3.2809	−0.0010	−0.5429	0.0754
CDS GOODS	−1.4586	−0.0238	−0.4078	0.1434	−1.3533	0.0198	−0.3812	0.0977	−2.0313	0.0026	−0.6500	0.1778
CDS ENERGY	−1.8671	0.0062	−0.3716	0.1147	−1.8437	−0.0329	−0.4444	0.0982	−3.0577	0.0087	−0.6869	0.1737
CDS METALS	−2.1864	0.0243	−0.3388	0.0632	−1.1714	0.0217	−0.3533	0.0430	−4.6849	0.0119	−0.5722	0.0671
CDS OTHER FIN	−3.4590	0.0194	−0.5599	0.0858	−3.2345	−0.0256	−0.9208	0.0678	−7.2257	−0.0755	−1.4547	0.1223
VSTOXX	−1.9855	−0.2411	−0.6952	0.3012	−2.7094	−0.2741	−0.5973	0.2626	−1.7593	−0.2154	−0.4658	0.2512
GOLD	−0.0311	0.5866	0.2038	0.0388	−0.0562	0.2582	0.0666	0.0087	−0.0603	0.4011	0.1063	0.0149
BITCOIN	−0.1071	0.0607	−0.0005	4.8966 × 10−5	−0.0016	0.1914	0.0146	8.4171 × 10−5	−0.0091	1.4095	0.2385	0.0143
Refit = 60
	Period 1 (19 July 19 2010 to 25 December 2017)				Period 2 (26 December 2017 to 31 December 2019)				Period 3 (1 January 2020 to 16 October 2021)
EMERGC	Min	Max	Mean	HE	Min	Max	Mean	HE	Min	Max	Mean	HE
CDS TEL	−1.0188	1.3005	−0.1452	0.0947	−0.1599	0.9576	−0.1403	0.1044	−0.2059	0.8383	−0.1774	0.1773
CDS IND	−1.4586	−0.2409	−0.6461	0.3688	−1.3113	−0.2525	−0.6376	0.3352	−1.3838	−0.1913	−0.7240	0.3245
CDS BANKS	−1.1211	0.0286	−0.2021	0.0471	−0.7690	0.0204	−0.2313	0.0275	−3.0410	0.0160	−0.4898	0.0702
CDS GOODS	−1.3244	−0.0239	−0.4506	0.1539	−1.2857	0.0100	−0.3730	0.0993	−1.9934	−0.0085	−0.5706	0.1609
CDS ENERGY	−1.6318	0.0148	−0.4185	0.1364	−1.6675	−0.0177	−0.4446	0.1043	−2.6604	0.0242	−0.5992	0.1595
CDS METALS	−1.7755	0.0195	−0.4266	0.0806	−0.9923	0.0173	−0.3484	0.0434	−4.8285	0.0113	−0.5279	0.0651
CDS OTHER FIN	−14.1272	4.8447	−0.2021	0.1034	−0.1875	−0.0747	−0.0833	0.0753	−0.1059	−0.0626	−0.0926	0.1173
VSTOXX	−2.7792	−0.3119	−0.6614	0.2875	−2.4663	−0.3576	−0.5913	0.2568	−1.4921	−0.2291	−0.5318	0.2794
GOLD	0.1134	0.5669	0.2019	0.0406	−0.1528	0.1682	0.0996	0.0113	−0.3301	0.3283	0.1201	0.0394
BITCOIN	−0.0269	0.6320	0.0970	0.0028	−0.0163	0.5066	0.0495	0.0010	−0.0324	1.3047	0.2213	0.0167
EMERGI	Min	Max	Mean	HE	Min	Max	Mean	HE	Min	Max	Mean	HE
CDS TEL	−0.5099	0.5774	−0.1323	0.0695	−0.1470	0.3776	−0.1358	0.0955	−0.1906	0.2282	−0.1694	0.1771
CDS IND	−3.9181	−0.2202	−0.6097	0.3369	−2.2016	−0.2123	−0.5301	0.2941	−4.5740	−0.1509	−0.4794	0.2737
CDS BANKS	−11.2704	0.8836	−0.3504	0.0540	−0.1185	0.3075	−0.1004	0.0244	−0.1473	−0.0062	−0.1347	0.0705
CDS GOODS	−1.2846	−0.0233	−0.4087	0.1445	−1.3535	0.0197	−0.3827	0.0985	−2.1163	0.0027	−0.6418	0.1743
CDS ENERGY	−1.9107	0.0061	−0.3685	0.1148	−1.8609	−0.0331	−0.4482	0.0992	−2.0767	0.0084	−0.6645	0.1674
CDS METALS	−2.2134	0.0243	−0.3419	0.0662	−1.1609	0.0217	−0.3562	0.0436	−4.1185	0.0117	−0.5786	0.0691
CDS OTHER FIN	−3.5932	0.0197	−0.5634	0.0881	−3.2346	−0.0256	−0.9335	0.0690	−6.6988	−0.0755	−1.4448	0.1200
VSTOXX	−1.8964	−0.2401	−0.6955	0.3017	−2.7094	−0.2718	−0.5975	0.2629	−1.7613	−0.1917	−0.4642	0.2467
GOLD	−0.0318	0.5827	0.2046	0.0390	−0.0511	0.2588	0.0677	0.0087	−0.0618	0.4142	0.1024	0.0149
BITCOIN	−0.0150	0.0060	−0.0018	5.1124 × 10−5	−0.0127	0.0068	0.0034	7.1380 × 10−5	−0.0194	0.0667	0.0406	0.0118

report the summary statistics of the hedge ratios and hedging effectiveness between the two Dow Jones emerging market indices and hedging instruments obtained from the three variants of the MGARCH models. We discuss the sensitivity of the results to refit used (every 20 and 60 days) to compare the hedging effectiveness in the long and short term and the sensitivity to periods to analyze the effect of crises on hedging strategies.

Table 6 displays the hedge ratios and hedging effectiveness obtained by using the DCC model. A rolling estimation approach is employed to estimate these parameters, with two refit intervals (20 and 60 days) selected to evaluate the effectiveness of sectoral CDSs, VSTOXX, gold, and Bitcoin to hedge Islamic and conventional stock markets in short and long-run horizons during the three periods.

Our analysis reveals that hedge ratios and hedge effectiveness values remain consistent across both refits. Notably, negative mean hedge ratios characterize all alternative assets except gold and Bitcoin. This suggests that hedging benefits for EMERGC and EMERGI can be realized through either short or long positions in sectoral CDSs and VSTOXX—results consistent with those of Basher and Sadorsky (2016) and Raza et al. (2019).

However, positive mean hedge ratios emerge for EMERGC/gold, EMERGI/gold, EMERGC/Bitcoin, and EMERGI/Bitcoin across all three periods. This implies an optimal strategy of long positions on Islamic/conventional stocks paired with short positions on gold and Bitcoin. Specifically, gold’s hedge ratios average between 0.0812 and 0.1057 for EMERGC and between 0.0623 and 0.0944 for EMERGI. Practically, hedging a USD 1 long position in EMERGC and EMERGI indices during Period 3 requires an average short position of USD 0.1033 and USD 0.0944 in gold, respectively. Critically, hedging USD 1 in the conventional index proves more costly within the Islamic index framework, underscoring divergent risk mitigation dynamics between the two.

Therefore, according to the maximum HE criterion, the CDS IND sector yields the highest hedging effectiveness level (0.2827) for the EMERGC, followed by EMERGI (0.2625) during the first period under study and for the longest forecasts. The VSTOXX index ranks as the second instrument, providing the highest hedging effectiveness (0.2490) for EMERGC and (0.2312) for the EMERGI stock market.

In addition, for each period analyzed, we observe that the values of the hedge ratio and hedging effectiveness are quite consistent across the various model refits.

Such findings have important implications for investors seeking to reduce risk in their Islamic and conventional portfolios. In this context, our results corroborate those of Hachicha et al. (2022), considering that opting for the industrial sector CDS index implies a rather beneficial portfolio design objective.

Table 7 highlights the results of the hedge ratio and hedging effectiveness values estimated with the ADCC model. Compared to Table 6, we find that the different hedging values achieved with the ADCC model are statistically similar to those calculated by the DCC model during the three periods. In fact, among the ten pairs, EMERGC/gold, EMERGI/gold, EMERGC/Bitcoin, and EMERGI/Bitcoin exhibit positive average hedge ratio values. For instance, the mean value of the hedge ratio of EMERGC/gold is 0.0777 (Table 7, period 1, refit = 20). We interpret this value as a USD 1 long position in EMERGC, which can be hedged on average for 7.77 cents with a short position in gold.

Moreover, the different hedging effectiveness values for both Islamic and conventional stock market indices are very similar.

One could also conclude that both CDS-IND and VSTOXX keep the highest values during the first period. Hence, hedging using industrial CDSs and VSTOXX for both Islamic and conventional emerging indices can be highly effective and profitable for investors in the short and long term and during calm and volatile periods.

Furthermore, the different hedge ratios and HE values are very similar, regardless of which period is studied (Period 1, Period 2, and Period 3).

Table 8 depicts the results highlighting the optimal hedge ratios and the hedging effectiveness calculated from the estimates of GO-GARCH.

Generally, the GO-GARCH model records the highest values of the hedge ratios and hedging effectiveness regarding the different periods and refits used in this study. Indeed, all of the alternative assets have the same sign of the average mean hedge ratio values (positive values for gold and Bitcoin and negative values for all other indices).

However, both Islamic and conventional stock market indices differ with respect to the GO-GARCH model, in comparison to the DCC and ADCC models. For instance, the hedging values of the pair EMERGC/Bitcoin are 0.0204, 0.0199, and 0.2916, respectively, for the DCC, ADCC, and GO-GARCH models.

Additionally, based on the maximum HE criterion, the industrial CDS sector achieves the highest hedging effectiveness level (36.88%) for the shortest forecast horizon during the first period. As a result, the GO-GARCH model demonstrates relatively high hedging efficiency, particularly in the EMERGC/CDS-IND case.

In this context, our results corroborate those of Zghal et al. (2022), considering that selecting for the GO-GARCH model maximizes the efficiency of the various hedging measures.

The superiority of GOGARCH model can be explained by various factors.

If asset returns are driven by a small set of latent factors (e.g., macroeconomic or sector-specific drivers), GO-GARCH’s orthogonal decomposition better isolates these factors, leading to more accurate covariance estimates and more accurate factor identification that improves hedge ratio calculations (e.g., minimizing portfolio variance).

-

With many assets, GO-GARCH’s parsimonious structure (via orthogonalization) avoids the “curse of dimensionality” that plagues ADCC, which requires estimating pairwise correlations.

-

Orthogonal factors reduce multicollinearity, making the model less sensitive to noisy or redundant data.

-

Correlation estimates in ADCC can become unstable if asset pairs exhibit erratic dependencies.

-

GO-GARCH out-performs ADCC models when markets have clear factor structures (e.g., sector ETFs, commodities) or if they are stable correlation regimes (no abrupt asymmetry).

In addition, through the comparison of both of the econometric models, statistical evidence reveals that there is no significant differences between DCC and ADCC models in term of hedging effectiveness. Investors in the EMERGC and EMERGI stock market have the same opportunity to hedge their portfolios because of these models, by using sectoral CDS indices and VSTOXX. In contrast, GO-GARCH model provide optimal hedge ratio and effectiveness hedging significantly not the same than DCC and ADCC models which confirms empirical results founded in previous works.

Industrials (e.g., manufacturing, machinery, aerospace, and transportation firms) are highly cyclical, meaning their performance is closely tied to macroeconomic trends (GDP growth, industrial production, and commodity prices).

Stock markets often decline during economic downturns, which simultaneously increases the default risk for cyclical sectors like industrials. This dual sensitivity amplifies the correlation between industrial CDS spreads (cost of insuring against default) and equity market downturns.

In a recession, industrials face reduced demand, tighter margins, and higher default risk, causing their CDS spreads to widen sharply. This mirrors equity market declines, making industrial CDS a natural hedge.

During crises, industrial CDS spreads widen more dramatically than non-cyclical sectors, providing stronger offsetting gains when equities fall.

Industrial firms’ equity prices and CDS spreads are often strongly negatively correlated. When stock prices fall, CDS spreads rise (due to perceived higher default risk), creating a natural hedge. Empirical studies show that correlation is stronger for cyclicals like industrials than for sectors with stable cash flows (e.g., consumer staples). Industrials are exposed to risks that drive broad market selloffs, such as rising interest rates (increasing borrowing costs), supply chain disruptions (e.g., COVID-19, trade wars), and commodity price volatility. These factors simultaneously pressure industrial equities and widen CDS spreads, enhancing hedging effectiveness.

Finally, industrial CDSs are particularly effective for hedging stock market risk due to their cyclicality, liquidity, and strong correlation with systemic economic stressors. They act as a “macro hedge” during broad downturns, outperforming CDSs tied to less cyclical or defensive sectors. However, their effectiveness depends on the nature of the equity risk (systemic vs. sector-specific) and the economic context driving market movements. Thus, it is necessary to always validate these via historical stress-testing and correlation analysis.

5.4. Diversification Benefits

Diversification benefits refer to the reduction in overall portfolio risk achieved by investing in assets with low or negative correlations. Diversification minimizes unsystematic risk (asset-specific risk) without sacrificing expected returns.

We assess the diversification benefits arising from combining both Dow Jones conventional and Islamic emerging stock indices and CDSs, VSTOXX, gold, and Bitcoin via the CDB measure of Christoffersen et al. (2017), which is captured in terms of the expected shortfall for probability q as follows:

$$CD{B}_t\left({\omega }_{t,}q\right)={\displaystyle \frac{{\omega }_{t,}E{S}_{i,t}\left(q\right)+(1-{\omega }_t)E{S}_{g,t}\left(q\right)-E{S}_{p,t}\left({\omega }_{t,}q\right)}{{\omega }_{t,}E{S}_{i,t}\left(q\right)+(1-{\omega }_t)E{S}_{g,t}\left(q\right)-VA{R}_t\left(q\right)}}$$

(26)

where ${\omega }_t$ represents the weight of the asset $i$ (CDS, VSTOXX, gold, and Bitcoin) in the portfolio $p$ at time $t$. The expected shortfall (ES) is given by

$$E{S}_{z,t}\left(q\right)=-E\left[r_{z,t}\left|r_{z,t}\le F_{z,t}^{-1}\left(q\right)\right.\right]$$

(27)

where $z=i,g;F_{z,t}^{-1}\left(q\right)$ represents the inverse of the distribution function of asset $z$ at time $t$, which is the upper bound of the expected shortfall.

$H$ and $h$ show a cumulative distribution function with υ degrees of freedom and standard Student’s t density function, respectively.

Table 9. Diversification benefits of CDSs, VSTOXX, gold, and Bitcoin for various portfolio compositions.

	Period 1	Period 2	Period 3
EMERGC	Mean (std. dev)	Mean (std. dev)	Mean (std. dev)
CDS TEL	0.0262 (0.6783)	0.0174 (0.3921)	−0.0422 (0.8804)
CDS IND	0.6291 (0.1012)	0.6172 (0.0897)	0.6221 (0.0945)
CDS BANKS	0.0775 (0.2128)	0.0728 (0.1664)	0.0438 (0.2902)
CDS GOODS	0.5933 (0.2364)	0.6124 ((0.1787)	0.5797 (0.2317)
CDS ENERGY	0.5196 (0.2063)	0.5286 (0.1702)	0.5097 (0.3027)
CDS METALS	−0.1958 (1.5568)	−0.6686 (5.3607)	−0.0229 (1.9954)
CDS OTHER FIN	0.0874 (0.4843)	−0.0336 (0.4870)	−0.1111 (4.7650)
VSTOXX	0.3653 (0.0880)	0.3455 (0.0735)	0.3514 (0.0900)
GOLD	0.5921 (0.0839)	0.5713 (0.1171)	0.5828 (0.0883)
BITCOIN	0.4752 (0.1310)	0.4589 (0.1500)	0.4008 (0.1939)
EMERGI	Mean (std. dev)	Mean (std. dev)	Mean (std. dev)
CDS TEL	0.0246 (0.6413)	0.0021 (0.4019)	−0.0066 (3.1428)
CDS IND	0.6153 (0.1045)	0.6086 (0.0942)	0.5989 (0.1025)
CDS BANKS	0.0781 (0.1993)	0.0575 (0.1742)	−0.0175 (0.3693)
CDS GOODS	0.5840 (0.2281)	0.5896 (0.1848)	0.5196 (0.2974)
CDS ENERGY	0.5027 (0.1962)	0.4960 (0.1840)	0.4532 (0.4023)
CDS METALS	−0.0752 (1.3401)	−0.0674 (2.5085)	−0.4349 (1.5195)
CDS OTHER FIN	0.1432 (0.4397)	−0.3582 (0.5114)	−0.0529 (2.2454)
VSTOXX	0.3583 (0.0883)	0.3462 (0.0776)	0.3619 (0.0951)
GOLD	0.6008 (0.0864)	0.5842 (0.1083)	0.5723 (0.0979)
BITCOIN	0.4779 (0.1029)	0.4542 (0.1510)	0.3888 (0.2252)

presents the mean values and standard deviations of the CDB for varying portfolio weights.

The results show that the CDB is higher for the EMERGC/IND-CDS portfolio (62.91%) during the first period, followed by CDS Goods (59.33%).

For EMERGI, like the case of EMERGC, the CDB is higher for CDS-IND during the first period (61.53%). However, the CDB decreases during the second and third periods, and the CDS-IND sector always records the highest values compared to the other alternatives assets, while the CDB results confirm that CDS-IND offers particular value to investors in conventional and Islamic stock markets.

In addition, the diversification benefits of Bitcoin are stable during the three periods. This result is in line with those of Chkili et al. (2021) highlighting that the diversification benefits of Bitcoin are, at most times, stable during turbulent periods. Therefore, adding Bitcoin to a portfolio of conventional or Islamic stocks reduce the risk of the portfolio.

6. Conclusions

This paper conducted a comparative analysis of the potential roles of CDSs, VSTOXX, gold, and Bitcoin in both conventional and Islamic stock markets. As a starting point, we adopted the approach proposed by Baur and McDermott (2010) to examine their roles as safe haven assets and hedges during stock market downturns. Then, we evaluated the out-of-sample hedging effectiveness of these assets for conventional and Islamic portfolios, using the DCC, ADCC, and GO-GARCH models. Additionally, we explored the conditional diversification benefits across various portfolio compositions, following the methodology of Christoffersen et al. (2017).

Our key findings indicate that CDSs, VSTOXX, gold, and Bitcoin reveal significant differences in the safe haven, hedging, and diversification abilities for conventional and Islamic stock markets, with gold and Bitcoin being strong safe havens for emerging Islamic financial indices, before bubble crypto currency. Also, CDS metals and VSTOXX served as strong safe havens for the EMERGC index during the COVID-19 pandemic. Most CDS sectors served as strong safe havens for the EMERGI and EMERGC indices. Moreover, the CDS-IND sector provided the highest hedging effectiveness in both conventional and Islamic portfolios. Furthermore, the CDS-IND sector offered stronger and more stable diversification benefits, followed by CDS-Goods during the three periods under study. Additionally, the GO-GARCH model recorded the highest values of the hedge ratios and hedging effectiveness regarding the different periods and refits used in this study. As regards the conditional diversification benefits, the CDS-IND sector offered higher benefits to investors in conventional and Islamic stock markets.

Our empirical analysis is particularly important for investors and portfolio managers, as it enables them to design more effective investment strategies by comparing CDSs, VSTOXX, gold, and Bitcoin for potential inclusion in their conventional and Islamic equity portfolios. Our findings are also useful to financial advisors who now have empirical evidence that the industrial CDS sector’s hedging effectiveness and diversification benefits are much higher than those of other alternative assets. The results found are sensitive to several factors, namely the period of the study, the dates chosen for the separation between the sub-periods, the refits, the windows, the market conditions, and the proposed model. In our study, we investigated how the results change depending on the model, sub-periods, and refit. Future researches can study the effect of the proposed approach to identify whether each asset is a safe haven or not and the effect of window size and/or data frequency on the results. In addition, the hedging effectiveness of the MGARCH model can be compared with wavelet theory methods and other new proposed approaches.